A hybrid fuzzy MCDM method for measuring the performance of publicly held pharmaceutical companies

Abstract

Maximizing shareholders’ value has always been an indispensable goal for publicly traded companies. Shareholders value is highly dependent on the operating expenses, profit margin, return on investment and the overall performance in public companies. We propose a hybrid fuzzy multi-criteria decision making method for measuring the performance of publicly held companies in the Pharmaceutical industry. The proposed method helps investors choose a proper portfolio of stocks in the presence of environmental turbulence and uncertainties. The proposed method is composed of three distinct but inter-related phases. In the pre-screening phase, a set of financial and non-financial evaluation criteria are selected based on the balanced scorecard (BSC) approach. In the efficiency measurement phase, the DEMATEL method is used first to determine the inter-relationships among the BSC perspectives. A fuzzy ANP method is used next to determine the relative importance of the criteria based on the resulting DEMATEL interactive network. In the third step, two different fuzzy data envelopment analysis (DEA) methods are used to evaluate the relative efficiency of the decision making units (DMUs). The fuzzy DEA models are modified by using the relative importance of the criteria and the precedence relations among the input and output weights as additional constraints. Finally, the modified fuzzy DEA models are used to calculate the relative efficiency scores of the DMUs. In the ranking phase, an integration method grounded in the Shannon’s entropy concept is used to combine different efficiency scores and calculate the final ranking of the DMUs. The method proposed in this study is used to evaluate the performance of publicly held pharmaceutical companies actively trading on the Swiss Stock Exchange (SSE).

1 Introduction

It has been well established that performance measurement should be an essential component of a rational and efficient investment management system. Yet there is little agreement on what guidelines are appropriate for choosing the most suitable performance measurement methods or how to implement them in practice. Because traditional performance measurement systems have often been criticized, many studies have investigated ways that qualitative and non-financial information can help address issues such as internal process, learning and growth, and customer needs and satisfaction (Creamer and Freund 2010).

We propose a hybrid fuzzy multi-criteria decision making (MCDM) approach for measuring the performance of publicly held pharmaceutical companies. The three-phase approach proposed in this study is based on the decision-making trial and evaluation laboratory (DEMATEL) method, the fuzzy analytic network process (ANP), and fuzzy data envelopment analysis (DEA). First, a set of financial and non-financial evaluation criteria are identified using the balanced scorecard (BSC) framework. In the first phase, a literature review and expert opinions are used to identify a set of performance measurement criteria and cluster them according to the BSC perspectives. In the second phase, the DEMATEL method is used to construct an interactive network of BSC perspectives by identifying the inter-relationships among the BSC perspectives. A fuzzy ANP method is used next to determine the relative importance of the criteria based on the interactive network of DEMATEL. Two different fuzzy DEA (FDEA) approaches are used to evaluate the relative efficiency of the pharmaceutical companies represented by decision making units (DMUs) in the DEA models. The relative importance of the criteria, based on fuzzy ANP, is established next and the precedence relations between the weights of the inputs and outputs in the fuzzy DEA models are represented in the form of additional constraints. Then the relative efficiency scores of the DMUs are calculated using the modified fuzzy DEA models. Finally, a method grounded in the Shannon’s entropy concept is used to combine different efficiency scores and to calculate the final ranking of the DMUs. The proposed method is applied to measure the performance of 21 pharmaceutical companies publicly traded on the Swiss Stock Exchange (SSE).

The overall contribution of this study is fivefold: (1) using the BSC framework to identify the most important indices for measuring the performance of publicly held pharmaceutical companies; (2) using the DEMATEL method to capture the network of interdependencies among these indices; (3) using the fuzzy ANP method to measure the relative importance of these indices; (4) using the fuzzy DEA method to calculate the relative efficiency scores and develop an overall ranking of the publicly held pharmaceutical companies; and (5) using statistical analysis to determine the most efficient method.

The remainder of this paper is organized as follows. In Sect. 2 we present a brief review of the literature on performance evaluation, BSC, DEMATEL, ANP, and DEA. In Sect. 3 we present the mathematical details of the hybrid approach proposed in this study. In Sect. 4 we use the method proposed here to evaluate the performance of publicly held pharmaceutical companies. In Sect. 5 we present our conclusions and future research directions.

2 Literature review

In this section, we present a brief review of the literature on performance evaluation, BSC, DEMATEL, ANP, and DEA.

2.1 Performance evaluation

There are two basic views with regards to corporate performance evaluation: traditional and modern. The traditional view is heavily influenced by financial criteria such as earnings per share, return on assets, debt ratio, and so on. On the other hand, the modern view is more concerned with the growth and development and improvement of the unit under evaluation.

Wang (2008) proposed a method for evaluating the financial performance of domestic airline in Taiwan. Ertuğrul and Karaşoğlu (2009) proposed a method to evaluate the performance of Turkish cement firms. Yalcin et al. (2012) proposed a methodology for evaluating the financial performance of Turkish manufacturing industries. Bulgurcu (2012) proposed a method for evaluating the financial performance of the high-technology firms on the Istanbul Stock Exchange Market. Halkos and Tzeremes (2012) proposed a procedure to evaluate the performance of manufacturing industries.

It is undisputed that sole consideration of financial criteria cannot lead to an equitable and comprehensive performance assessment system. Non-financial and qualitative criteria affecting the prospects of companies, such as customer satisfaction, innovation and learning, technology, quality products and services should also be considered in a balanced and fair performance assessment methodology.

2.2 BSC applications in performance evaluation

BSC is a performance management system developed by Kaplan and Norton (1992) for plotting the future vision of an organization and codifying strategic objectives. BSC is used to specify critical success factors and the causal relationship between these factors based on the future perspectives and the organization’s strategic objectives. BSC evaluates organizational performance from the four perspectives of financial, customer, internal process and learning and growth. BSC is a well-established tool for strategic management used by many researchers and practicing managers. Eilat et al. (2008) embedded the BSC in the DEA model through a hierarchical structure of constraints that reflected the BSC balance considerations. They illustrated the proposed approach with a case study in research and development project selection. Wu et al. (2009) proposed a fuzzy MCDM model based on the BSC for banking performance evaluation. Wang et al. (2010) integrated the hierarchical BSC with a non-additive fuzzy integral for evaluating high technology firm performance. Tzeng et al. (2011) presented a BSC approach to establish a performance evaluation and relationship model for hot spring hotels. Wu et al. (2011) used BSC to evaluate the performance of extension education centers in universities. Wu (2012) used BSC to construct a strategy map for banking institutions. Amado et al. (2012) combined the BSC method with DEA to enhance performance assessment and provided a set of recommendations relating to the successful application of DEA and its integration with the BSC. Lin et al. (2013) proposed a hybrid model of hierarchical BSC with fuzzy linguistic variables to evaluate the performance of operating rooms in hospitals.

2.3 Fuzzy analytic network process

The analytic hierarchy process (AHP) has been widely used in MCDM to measure quantitative and qualitative criteria (Saaty 1977, 1980). AHP decomposes a MCDM problem into a hierarchical structure by assuming that the relationships of criteria in different levels are independent. Conventional AHP uses precise and crisp pair-wise judgments to derive weights without considering any uncertainties in human understanding and intuition. In response, Saaty and Vargas (1987) proposed an interval AHP to handle interval judgments. However, this approach for interval judgment was found to be very difficult to implement in real-life problems. In addition, the assumption of independent relationship in different levels of the hierarchical structure in AHP was not always true in most MCDM problems. Saaty (1996) proposed ANP, a generalization of AHP, to cope with problems involving interdependent relationships among criteria. ANP extends the AHP to problems with dependence and feedback among criteria by using a network structure instead of a hierarchical structure.

Despite the popularity and wide spread use of the ANP, this method is not useful for problems involving uncertainty. The judgments of individuals concerning their preferences are often imprecise or ambiguous, and very hard to estimate with crisp numbers. In recent years, many researchers have used fuzzy ANP to capture the impreciseness and ambiguity in human decision making. Dağdeviren and Yüksel (2010a) used fuzzy ANP to assess the sectorial competition level in manufacturing firms based on vision and strategy. Liu and Wang (2010) used fuzzy ANP in an advanced quality function deployment model. Vinodh et al. (2011) used fuzzy ANP to select suppliers in a manufacturing organization. Sevkli et al. (2012) developed a fuzzy ANP model to evaluate the strength–weakness–opportunity–threat method in the Turkish airline industry. Tavana et al. (2013a, b) introduced a hybrid group decision support system based on fuzzy ANP for evaluation of the advanced technologies at NASA.

2.4 Fuzzy DEA

DEA is a non-parametric method to evaluate the relative efficiency of homogenous decision making units (DMUs) with multiple inputs and multiple outputs. The field of DEA has grown enormously since the pioneering work of Farrell (1957). The first DEA model was formally introduced by Charnes et al. (1978). The model is also known as CCR by which the efficiency of DMUs with constant returns to scale is calculated. Banker et al. (1984) developed the CCR model for variable returns to scale and introduced the BCC model. In order to measure the efficiency of DMUs using conventional DEA models, inputs and outputs should be positive, quantitative, and precise. However, in many real-life problems, data is expressed as qualitative, imprecise and with ambiguity. Fuzzy logic has been used in DEA to overcome these limitations. Sengupta (1992) presented a fuzzy programming approach for fuzzy DEA modeling. Guo and Tanaka (2001) proposed a perceptual evaluation method for fuzzy DEA. Lertworasirikul et al. (2003) developed fuzzy DEA models in the form of fuzzy linear programming. Jahanshahloo et al. (2004) developed a slack based DEA model for evaluating the efficiency and the ranking of DMUs with fuzzy inputs and outputs. Wen and Li (2009) developed a fuzzy DEA model using fuzzy simulation and the genetic algorithm. Zerafatangiz et al. (2010) introduced a non-radial fuzzy DEA method for evaluating the performance of DMUs. Wang and Chin (2011) proposed a fuzzy DEA method based on expected value. Zhou et al. (2012) proposed a fuzzy DEA model with an assurance region.

Abtahi and Khalili-Damghani (2011) proposed a mathematical formulation for measuring the performance of agility in supply chains using single-stage fuzzy DEA. Khalili-Damghani et al. (2011) applied the proposed formulation of Abtahi and Khalili-Damghani (2011) to measure the efficiency of agility in supply chains and used simulation to rank the interval efficiency scores. Khalili-Damghani and Abtahi (2011) measured the efficiency of just in time productions systems using fuzzy DEA approach. Khalili-Damghani and Taghavifard (2012) proposed a fuzzy two-stage DEA approach for performance measurement in supply chains.

Khalili-Damghani et al. (2012) used the ordinal data in a new two-stage DEA approach for agility performance and illustrated the efficacy of their approach in a supply chain. Khalili-Damghani and Taghavifard (2013) performed sensitivity and stability analysis in two-stage DEA models with fuzzy data. They proposed several models for calculating the stability radius in DEA problems with considerable input and output variations and uncertainties. Khalili-Damghani and Tavana (2013) proposed a new network DEA model for measuring the performance of agility in supply chains. The uncertainty of the input and output data were modeled with linguistic terms and the proposed model was used to measure the performance of agility in a real-life case study in the dairy industry. Tavana et al. (2013a, b) proposed a fuzzy group DEA model for high-technology project selection at NASA.

Liu (2014) proposed a fuzzy two-stage DEA model where the weights were restricted in ranges and the input and output data were treated as fuzzy numbers. The assurance region approach was utilized to restrict weight flexibility and a pair of two-level mathematical programs was formulated to calculate upper and lower bounds for the fuzzy efficiency scores based on Zadeh’s extension principle (Dubois and Prade 1980). This pair of two-level programs was then transformed into a pair of conventional one-level programs to calculate the bounds for the fuzzy efficiency scores.

Tavana and Khalili-Damghani (2014) proposed a new fuzzy two stage DEA model based on the Stackelberg (leader–follower) game theory approach to prioritize and sequentially decompose the efficiency score of the DMU into a set of efficiency scores for its sub-DMUs. The proposed models were linear (allowing for a quick identification of the global optimum solution) and independent of the $\alpha$-cut variables (allowing for a significant reduction in the computational efforts). They also used Monte Carlo simulation to discriminately rank the efficiencies in their model.

Kao et al. (2014) proposed a multi-objective programming method for solving network DEA problems. They formulated the divisional efficiencies and the overall efficiency of the organization as separate objective functions and measured the organization’s overall efficiency without neglecting the efficiencies of its subunits. Khalili-Damghani et al. (2014) proposed fuzzy DEA models for assessing the efficiency of agility in supply chains under uncertainty and applied their models to study two agility patterns. They also introduced a real-world case study to demonstrate the applicability of the proposed models.

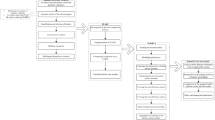
3 Proposed hybrid approach

We use a three-phase hybrid fuzzy MCDM approach to evaluate the performance of a set of companies in the pharmaceutical industry. Figure 1 presents a schematic view of the proposed approach:

Fig. 1

Schematic view of the proposed hybrid fuzzy MCDM approach

3.1 Pre-screening phase (Module 1)

In the pre-screening phase we first identify the relevant performance evaluation criteria using a literature review and then use expert opinions to cluster the selected performance criteria according to the BSC perspectives (i.e., financial, customer, internal process, and learning and growth).

3.2 Efficiency measurement phase (Module 2)

In the efficiency measurement phase we first use the DEMATEL method (Module 1) to determine the interdependencies among the BSC perspectives by following the four procedures proposed by Gabus and Fontela (1972, 1973):

Procedure 1. Construct the direct-relation matrix In this step we ask our experts to specify the impact of perspective $i$ on perspective $j$ using a five point scale from 0 to 4. Zero indicates that perspective $i$ has no impact on perspective $j$. Four means that perspective $i$ has a high impact on perspective $j$. The mean direct relation matrix D is obtained by collecting ideas and calculating the means for the degree of influence the perspectives have on each other as follows:

$$\begin{aligned} D=\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {d_{11} }&{} \cdots &{} {d_{1j} }&{} \cdots &{} {d_{1n} } \\ \vdots &{} &{} \vdots &{} &{} \vdots \\ {d_{i1} }&{} \cdots &{} {d_{ij} }&{} \cdots &{} {d_{in} } \\ \vdots &{} &{} \vdots &{} &{} \vdots \\ {d_{n1} }&{} \cdots &{} {d_{nj} }&{} \cdots &{} {d_{nn} } \\ \end{array} }} \right] \end{aligned}$$

(1)

$d_{ij}$ indicates the direct impact of factor $i$ on factor $j$; the main diagonal elements $d_{ij}= 0$ corresponding to $i=j$.

Procedure 2. Normalize the initial direct-relation matrix The normalized direct-relation matrix can be obtained by using (2).

$$\begin{aligned} X&= s \cdot D \nonumber \\ s&= \min \left[ {\frac{1}{\max _i \sum _{j=1}^n {\left| {d_{ij} } \right| } },\frac{1}{\max _j \sum _{i=1}^n {\left| {d_{ij} } \right| } }} \right] \end{aligned}$$

(2)

Procedure 3. Construct the total-relation matrix The total-relation matrix $T$ is calculated by using (3).

$$\begin{aligned} T=[t_{ij} ]_{n\times n} =X+X^{2}+\cdots +X^{k}=X(I-X)^{-1},\quad i,j=1,2,\ldots ,n \end{aligned}$$

(3)

where $I$ is the identity matrix, $t_{ij}$ (an element of $T$) indicates the indirect effects of factor $i$ on factor $j$, and Matrix $T$ reflects the total relationship between the factors.

Procedure 4. Determining the interconnection matrix We then determine the network relations by using (4) to calculate the totals of the rows and totals of the columns of Matrix $T$ as $r$ and $c$ vectors:

$$\begin{aligned} \vec {\hbox {r}}=\left[ {r_i } \right] _{n\times 1} =\left[ {\sum \limits _{j=1}^n {t_{ij} } } \right] _{n\times 1}\nonumber \\ \vec {\hbox {c}}=\left[ {c_j } \right] _{1\times n} =\left[ {\sum \limits _{i=1}^n {t_{ij} } } \right] _{1\times n} \end{aligned}$$

(4)

where $r_{i}$ (the sum of the $i$-th row of Matrix $T$) shows the total direct and indirect effects of Factor $i$ on the other factors. In addition, $c_{j}$ (the sum of the $j$-th column of Matrix $T$) shows the total direct and indirect effects of the other factors on Factor $j$.

Furthermore, when $i=j, r_{i} + c_{i}$ shows all the effects given and received by Factor $i$. That is, $r_{i} +c_{i}$ indicates both Factor $i$’s impact on the whole system and the other system factors’ impact on Factor $i$. Therefore, the indicator $r_{i} +c_{i}$ represents the degree of importance factor $i$ on the system. On the contrary, the difference between the two $(r_{i} -c_{i})$ shows the net effect of Factor $i$ on the system. More specifically, if the value of $r_{i} -c_{i}$ is positive, Factor $i$ is a net cause, i.e. having a net causal effect on the system. When $r_{i} -c_{i}$ is negative, Factor $i$ is a net result clustered into an effect group.

In the efficiency measurement phase we then use the fuzzy ANP method (Module 2) to determine the relative importance of the criteria. We should note the interdependencies of the evaluation criteria due to the interdependency relations between the BSC perspectives in module (1). Fuzzy ANP as suggested by Dağdeviren and Yüksel (2010b) can be used to determine the relative importance of the criteria using the following five procedures:

Procedure 1. Determinate the network structure In this step we determine the network structure based on the goals, perspectives, and evaluation criteria.

Procedure 2. Determine the pairwise comparisons matrices Our experts are then asked to provide their pair-wise comparisons by assuming no interdependency among the factors (similar to a simple hierarchy) using linguistic variables parameterized through triangular fuzzy numbers (TFNs) as presented in Table 1. Figure 2 presents a schematic view of the TFNs. Among the various types of fuzzy numbers, triangular and trapezoidal fuzzy numbers are most often used in real-world applications. We use TFNs because they are intuitive, easy to use, computationally simple, and useful in promoting representation and information processing in a fuzzy environment.

Table 1 Linguistic variables and the TFNs used for the relative importance of the criteria

Fig. 2

Linguistic terms used for representing the relative importance

Procedure 3. Calculate the local weights of the BSC perspectives and performance criteria We then use the method proposed by Chang (1996) to determine the local weights of the perspectives and criteria. We do not describe the method and its steps here for the sake of brevity. Details can be found in Chang (1996) and Dağdeviren and Yüksel (2010a). Finally, we use (5) to calculate the weight vector of criteria, called W, based on the method proposed by Dağdeviren and Yüksel (2010b).

$$\begin{aligned} W=\left[ {W(A_1 ),W(A_2 ),\ldots ,W(A_n )} \right] ^{T} \end{aligned}$$

(5)

Procedure 4. Determine the interdependent weights

Procedure 5. Determine the global weights of the criteria

3.3 Calculate the efficiency scores of the DMUs (Module 3) using fuzzy DEA approaches

In last part of the efficiency measurement phase we calculate the efficiency scores of the DMUs. Fuzzy DEA is proposed to calculate the efficiency scores because the inputs and outputs are qualitative and mixed with uncertainty.

Assume that we have $n$ DMUs that consume $m$ fuzzy inputs as $\tilde{x}_{ij} ,i=1,2,\ldots ,m$ to produce $s$ fuzzy outputs as $\tilde{y}_{rj} , r=1,2,\ldots ,s$. Based on the CCR model proposed by Charnes et al. (1978), the fuzzy CCR-Input oriented is represented by (6).

$$\begin{aligned} \begin{array}{lll} Max &{} Z_0 =\displaystyle \sum \limits _{r=1}^s {\tilde{u}_r \tilde{y}_{r\circ }} &{}\\ s.t. &{} \displaystyle \sum \limits _{i=1}^m {\tilde{v}_i \tilde{x}_{i\circ } } =1 &{}\\ &{} \displaystyle \sum \limits _{r=1}^s {\tilde{u}_r \tilde{y}_{rj} } -\displaystyle \sum \limits _{i=1}^n {\tilde{v}_i \tilde{x}_{ij} } \le 0 &{}\quad j=1,2,\ldots ,n \\ &{} \tilde{v}_i ,\tilde{u}_r \ge 0;\quad r=1,2,\ldots ,s ; &{}\quad i=1,2,\ldots ,m \\ \end{array} \end{aligned}$$

(6)

Several approaches have been proposed in the literature to handle fuzziness in DEA models. Hatami-Marbini et al. (2011) has classified the fuzzy DEA methods into four primary categories: the tolerance approach, the alpha-level based approach, the fuzzy ranking approach, and the possibility methods. We used two well-known approaches: the expected value method proposed by Wang and Chin (2011) and the alpha-cut based approach proposed by Khalili-Damghani et al. (2011). We further modified both methods to handle the additional constraints prescribed in the process. Real-world fuzzy DEA models are usually customized using triangular or trapezoidal fuzzy numbers. Similar to both Wang and Chin (2011) and Khalili-Damghani et al. (2011), the methods developed in this research are based upon triangular fuzzy numbers which allows us to make a fair comparison of the performances of the different methods. In addition triangular fuzzy numbers are simple to use and easy to understand.

3.3.1 Wang and Chin’s (2011) expected value method

Wang and Chin (2011) consider the inputs and outputs in the form of trapezoidal fuzzy numbers (TrFNs) and calculate the efficiency scores based on the optimistic and pessimistic scenarios. The optimistic model is presented as Model (7).

$$\begin{aligned} \begin{array}{ll} Maximize&{}\quad \theta _\circ ^{best} =\displaystyle \sum \limits _{r=1}^s {\left( u_r^l y_{r\circ }^l +u_r^m y_{r\circ }^m +u_r^n y_{r\circ }^n +u_r^u y_{r\circ }^u \right) } \\ s.t.&{} \quad \displaystyle \sum \limits _{i=1}^m {\left( v_i^l x_{i\circ }^l +v_i^m x_{i\circ }^m +v_i^n x_{i\circ }^n +v_i^u x_{i\circ }^u \right) } =1 \\ &{}\quad \displaystyle \sum \limits _{r=1}^s {\left( u_r^l y_{rj}^l +u_r^m y_{rj}^m +u_r^n y_{rj}^n +u_r^u y_{rj}^u \right) } \\ &{}\qquad -\displaystyle \sum \limits _{i=1}^n {\left( v_i^l x_{ij}^l +v_i^m x_{ij}^m +v_i^n x_{ij}^n +v_i^u x_{ij}^u \right) } \le 0,\quad j=1,2,\ldots ,n \\ &{}\quad u_r^u \ge u_r^n \ge u_r^m \ge u_r^l \ge 0,\quad r=1,2,\ldots ,s \\ &{}\quad v_i^u \ge v_i^n \ge v_i^m \ge v_i^l \ge 0,\quad i=1,2,\ldots ,m \\ \end{array} \end{aligned}$$

(7)

Theorem I

Model (7) is always feasible and bounded.

Proof

The dual form of Model (7) can be written as follows:

$$\begin{aligned} \begin{array}{ll} Minimize&{}\quad \omega _o \\ s.t. &{}\quad \sum \limits _{j=1}^n {\lambda _j x_{ij}^l } \le \omega x_{io}^l,\quad i=1,\ldots ,m \\ &{}\quad \displaystyle \sum \limits _{j=1}^n {\lambda _j x_{ij}^m } \le \omega x_{io}^m,\quad i=1,\ldots ,m \\ &{}\quad \displaystyle \sum \limits _{j=1}^n {\lambda _j x_{ij}^n } \le \omega x_{io}^n,\quad i=1,\ldots ,m \\ &{}\quad \displaystyle \sum \limits _{j=1}^n {\lambda _j x_{ij}^u } \le \omega x_{io}^u,\quad i=1,\ldots ,m \\ &{}\quad \displaystyle \sum \limits _{j=1}^n {\lambda _j y_{rj}^l } \ge y_{ro}^l,\quad r=1,\ldots ,s \\ &{}\quad \displaystyle \sum \limits _{j=1}^n {\lambda _j y_{rj}^m } \ge y_{ro}^m,\quad r=1,\ldots ,s \\ &{}\quad \displaystyle \sum \limits _{j=1}^n {\lambda _j y_{rj}^n } \ge y_{ro}^n,\quad r=1,\ldots ,s \\ &{}\quad \displaystyle \sum \limits _{j=1}^n {\lambda _j y_{rj}^u } \ge y_{ro}^u,\quad r=1,\ldots ,s \\ &{}\quad \lambda _j \ge 0,\quad j=1,2,\ldots ,n \\ \end{array} \end{aligned}$$

Consider an arbitrary solution for the dual model as follows:

$$\begin{aligned} \begin{array}{l} \lambda _j =0,\quad j=1,2,\ldots ,n,\quad j\ne o \\ \lambda _o =1 \\ \omega =1 \\ \end{array} \end{aligned}$$

It is clear that the above solution satisfies all the constraints in the dual model and hence it is a feasible solution for the dual model. Therefore, it can be concluded that independent of the values of inputs and outputs of DMUs, there is at least one feasible solution for the dual model, and sequentially there is a feasible solution for the primal model (7). Thus, model (7) is always feasible.

According to the direction of the objective function for the dual model (i.e., minimization), the optimum value of the objective function (i.e., $\omega ^{*}$) is always less than or equal to any arbitrary objective function value associated with a feasible solution (i.e. $\omega ^{*}\le \omega$ is always satisfied). Since $\omega =1$ in the proposed arbitrary solution, it can be concluded that $\omega ^{*}\le 1$. According to the basic theorem of linear programming, the optimum value of the primal and dual models are equal. Therefore, $\theta _\circ ^{best*} =\omega ^{*}\le 1$. This completes the proof. $\square$

The pessimistic model is presented as Model (8).

$$\begin{aligned} Minimize&\quad \theta _\circ ^{worst} =\sum \limits _{r=1}^s {\left( u_r^l y_{r\circ }^l +u_r^m y_{r\circ }^m +u_r^n y_{r\circ }^n +u_r^u y_{r\circ }^u\right) } \nonumber \\ s.t.&\quad \sum \limits _{i=1}^m {\left( v_i^l x_{i\circ }^l +v_i^m x_{i\circ }^m +v_i^n x_{i\circ }^n +v_i^u x_{i\circ }^u \right) } =1 \nonumber \\&\quad \sum \limits _{r=1}^s {\left( u_r^l y_{rj}^l +u_r^m y_{rj}^m +u_r^n y_{rj}^n +u_r^u y_{rj}^u \right) }\nonumber \\&\qquad -\sum \limits _{i=1}^n {\left( v_i^l x_{ij}^l +v_i^m x_{ij}^m +v_i^n x_{ij}^n +v_i^u x_{ij}^u \right) } \ge 0, \quad j=1,2,\ldots ,n \nonumber \\&\quad u_r^u \ge u_r^n \ge u_r^m \ge u_r^l \ge 0, \quad r=1,2,\ldots ,s \nonumber \\&\quad v_i^u \ge v_i^n \ge v_i^m \ge v_i^l \ge 0, \quad i=1,2,\ldots ,m \end{aligned}$$

(8)

Solving Models (7) and (8) results in two different sets of efficiency scores for the DMUs. In Model (7), if the optimum value of $\theta _\circ ^{best}$ is equal to unity, the associated DMU is called efficient and if the optimum value of $\theta _\circ ^{best}$ is less than unity, the associated DMU is called inefficient. In Model (8), if the optimum value of $\theta _\circ ^{worst}$ is equal to unity, the associated DMU is called efficient and if the optimum value of $\theta _\circ ^{worst}$ is greater than unity, the associated DMU is called inefficient. Details can be found in Wang and Chin (2011).

Theorem II

Model (8) is always feasible.

Consider an arbitrary solution for Model (8) as follows:

$$\begin{aligned} v_i^l&= \frac{1}{4\times m\times x_{ij}^l },\quad v_i^m =\frac{1}{4\times m\times x_{ij}^m },\quad v_i^n =\frac{1}{4\times m\times x_{ij}^n },\quad v_i^u =\frac{1}{4\times m\times x_{ij}^u }\\ u_r^l&= \frac{1}{4\times s\times y_{rj}^l },\quad u_r^m =\frac{1}{4\times s\times y_{rj}^m },\quad u_r^n =\frac{1}{4\times s\times y_{rj}^n },\quad u_r^u =\frac{1}{4\times s\times y_{rj}^u }\\&\theta _\circ ^{worst} =1 \end{aligned}$$

It is clear that the above solution satisfies all the constraints in Model (8) and hence it is a feasible solution for Model (8). Therefore, it can be concluded that, there is at least one feasible solution for Model (8). Thus, Model (8) is always feasible. This completes the proof. $\square$

Lemma I

The optimality conditions of Model (8) are as follows: (a) $\theta _\circ ^{worst} =1$ for efficient DMUs; and (b) $\theta _\circ ^{worst} >1$ for inefficient DMUs.

According to the following constraints in Model (8):

$$\begin{aligned}&\sum \limits _{r=1}^s {(u_r^l y_{rj}^l +u_r^m y_{rj}^m +u_r^n y_{rj}^n +u_r^u y_{rj}^u )} -\sum \limits _{i=1}^n {(v_i^l x_{ij}^l +v_i^m x_{ij}^m +v_i^n x_{ij}^n +v_i^u x_{ij}^u )} \ge 0,\\&\quad j=1,2,\ldots ,n \end{aligned}$$

For each $\hbox {DMU}_\mathrm{o}$ under consideration we have:

$$\begin{aligned} \sum \limits _{r=1}^s {(u_r^l y_{ro}^l +u_r^m y_{ro}^m +u_r^n y_{ro}^n +u_r^u y_{ro}^u )} \ge 1 \end{aligned}$$

If the above inequality is prescribed as an equality, $\sum _{r=1}^s (u_r^l y_{ro}^l +u_r^m y_{ro}^m +u_r^n y_{ro}^n +u_r^u y_{ro}^u ) =1$ and hence $\theta _\circ ^{worst} =1$; otherwise, $\sum _{r=1}^s {(u_r^l y_{ro}^l +u_r^m y_{ro}^m +u_r^n y_{ro}^n +u_r^u y_{ro}^u )>} 1$ and hence $\theta _\circ ^{worst} >1$. Therefore, the optimum value for the objective function of Model (8) is equal to 1 for the efficient DMUs and it is greater than 1 for the inefficient DMUs.

Khalili-Damghani et al.’s (2011) alpha-cut based method

Khalili-Damghani et al. (2011) proposed an $\alpha$-cut based fuzzy DEA model. They used TrFNs and demonstrated the uncertainty of the inputs and the outputs. Khalili-Damghani et al. (2011) calculated the upper- and lower-limit of the fuzzy inputs and outputs as follows:

$$\begin{aligned}&(x_{ij}^L )_{\alpha _i } =x_{ij}^l +\alpha _i (x_{ij}^m -x_{ij}^l );\quad \alpha _i \in [0,1],\quad i=1,\ldots ,m;\quad j=1,\ldots ,n\end{aligned}$$

(9)

$$\begin{aligned}&(x_{ij}^U )_{\alpha _i } =x_{ij}^u -\alpha _i (x_{ij}^u -x_{ij}^n );\quad \alpha _i \in [0,1],\quad i=1,\ldots ,m;\quad j=1,\ldots ,n\end{aligned}$$

(10)

$$\begin{aligned}&(y_{rj}^L )_{\alpha _r } =y_{rj}^l +\alpha _r (y_{rj}^m -y_{rj}^l );\quad \alpha _r \in [0,1],\quad r=1,\ldots ,s;\quad j=1,\ldots ,n\end{aligned}$$

(11)

$$\begin{aligned}&(y_{rj}^U )_{\alpha _r } \!=\!y_{rj}^u \!-\!\alpha _r (y_{rj}^u \!-\!y_{rj}^n );\quad \alpha _r \in [0,1],\quad r=1,\ldots ,s;\quad j=1,\ldots ,n \end{aligned}$$

(12)

Using this method, the upper- and lower-limit for the efficiency scores can be obtained for each DMU by Replacing (9)–(12) in Model (6). The upper-limit for the efficiency scores can be calculated by using Model (13).

$$\begin{aligned}&\displaystyle Max\quad E^{U}=\sum \limits _{r=1}^s {u_r } y_{ro}^u -\eta _r (y_{ro}^u -y_{ro}^n ) \nonumber \\&\displaystyle s.t. \quad \sum \limits _{r=1}^s {u_r } y_{rj}^l \!+\!\eta _r (y_{rj}^m -y_{rj}^l )\!-\!\sum \limits _{i=1}^m {v_i } x_{ij}^u \!-\!\lambda _i (x_{ij}^u \!-\!x_{ij}^n )\!\le \! 0;\quad j=1,\ldots ,n,\quad j\ne o, \nonumber \\&\displaystyle \quad \sum \limits _{r=1}^s {u_r } y_{ro}^u -\eta _r (y_{ro}^u -y_{ro}^n )-\sum \limits _{i=1}^m {v_i } x_{io}^l +\lambda _i (x_{io}^m -x_{io}^l )\le 0, \nonumber \\&\displaystyle \sum \limits _{i=1}^m {v_i } x_{io}^l +\lambda _i (x_{io}^m -x_{io}^l )=1, \nonumber \\&\displaystyle v_i \ge 0, \quad i=1,2,\ldots ,m,\nonumber \\&\displaystyle u_r \ge 0, \quad r=1,2,\ldots ,s, \nonumber \\&\displaystyle 0\le \lambda _i \le v_i; \quad i=1,2,\ldots ,m, \nonumber \\&\displaystyle 0\le \eta _r \le u_r; \quad r=1,2,\ldots ,s. \end{aligned}$$

(13)

Theorem III

Model (13) is always feasible and bounded.

Proof

Defining proper dual variables, the dual form of Model (13) can be written as follows:

$$\begin{aligned} Min&\quad z=\theta \\ s.t.&\quad \sum \limits _{\begin{array}{l} j=1 \\ j\ne o \\ \end{array}}^n {y_{rj}^l } \alpha _j +y_{ro}^u \alpha _o -\mu _r \ge y_{ro}^u ,\quad r=1,2,\ldots ,s, \\&\quad \sum \limits _{\begin{array}{l} j=1 \\ j\ne o \\ \end{array}}^n {(y_{rj}^m -y_{rj}^l )} \alpha _j -(y_{ro}^u -y_{ro}^n )\alpha _o -\gamma _r +\mu _r \ge -(y_{ro}^u -y_{ro}^n ),\quad r=1,2,\ldots ,s, \\&\quad -\sum \limits _{\begin{array}{l} j=1 \\ j\ne o \\ \end{array}}^n {x_{ij}^u } \alpha _j -x_{io}^l \alpha _o +x_{io}^l \theta -\phi _i \ge 0,\quad i=1,2,\ldots ,m, \\&\quad \sum \limits _{\begin{array}{l} j=1 \\ j\ne o \\ \end{array}}^n {(x_{ij}^u -x_{ij}^n )\alpha _j -} (x_{io}^m -x_{io}^l )\alpha _o +(x_{io}^m -x_{io}^l )\theta -\beta _i +\phi _i \ge 0,\quad i=1,2,\ldots ,m, \\&\quad \alpha _j \ge 0,\quad \quad \,\, j=1,2,\ldots ,n, \\&\quad \phi _i ,\beta _i \ge 0,\quad i=1,2,\ldots ,m,\\&\quad \mu _r ,\gamma _r \ge 0,\quad r=1,2,\ldots ,s, \\&\quad \theta \quad free \end{aligned}$$

Consider a solution for the dual model as follows:

$$\begin{aligned}&\alpha _j =0,\quad j=1,2,\ldots ,n,\quad j\ne o \\&\alpha _0 =1 \\&\phi _i =\beta _i =0,\quad i=1,2,\ldots ,m,\\&\mu _r =\gamma _r =0,\quad r=1,2,\ldots ,s, \\&\theta =1 \end{aligned}$$

It is obvious that the above solution is a feasible solution for the dual model. Therefore, independent of the input and output variables, there is always at least one feasible solution for the dual and the primal models. Consequently, the optimum value for the objective function of the dual model is definitely less than or equal to 1 (i.e., $Z^{{*}}\le 1$). By the virtue of the duality theorem in linear programming, the objective function of the dual and the primal models are equal for the optimal solution (i.e., $Z^{{*}}=E_o^{{*}U}$). Therefore, it can be concluded that $E_o^{{*}U} \le 1$ is always true. Hence, the Model (13) is always bounded. This completes the proof. $\square$

The lower-limit for the efficiency score can be calculated by using Model (14).

$$\begin{aligned} Max&\quad E^{L}=\sum \limits _{r=1}^s {u_r } y_{ro}^l +\eta _r (y_{ro}^m -y_{ro}^l ) \nonumber \\ s.t.&\quad \sum \limits _{r=1}^s {u_r } y_{rj}^u -\eta _r (y_{rj}^u -y_{rj}^n )-\sum \limits _{i=1}^m {v_i } x_{ij}^l +\lambda _i (x_{ij}^m -x_{ij}^l )\le 0;\quad j=1,\ldots ,n,\quad j\ne o \nonumber \\&\quad \sum \limits _{r=1}^s {u_r } y_{ro}^l +\eta _r (y_{ro}^m -y_{ro}^l )-\sum \limits _{i=1}^m {v_i } x_{io}^u -\lambda _i (x_{io}^u -x_{io}^n )\le 0 \nonumber \\&\quad \sum \limits _{i=1}^m {v_i } x_{io}^u -\lambda _i (x_{io}^u -x_{io}^n )=1 \nonumber \\&\quad v_i ,u_r \ge 0; \quad r=1,2,\ldots ,s;\quad i=1,2,\ldots ,m \nonumber \\&\quad 0\le \lambda _i \le v_i;\quad i=1,2,\ldots ,m \nonumber \\&\quad 0\le \eta _r \le u_r;\quad r=1,2,\ldots ,s \end{aligned}$$

(14)

Theorem IV

Model (14) is always feasible and bounded.

Proof

Defining proper dual variables, the dual form of Model (14) can be written as follows:

$$\begin{aligned} Min&\quad z=\theta \\ s.t.&\quad \sum \limits _{\begin{array}{l} j=1 \\ j\ne o \\ \end{array}}^n {y_{rj}^u } \alpha _j +y_{ro}^l \alpha _o -\mu _r \ge y_{ro}^l ,\quad r=1,2,\ldots ,s,\\&\sum \limits _{\begin{array}{l} j=1 \\ j\ne o \\ \end{array}}^n {(y_{rj}^u -y_{rj}^n )} \alpha _j -(y_{ro}^m -y_{ro}^l )\alpha _o -\gamma _r +\mu _r \ge -(y_{ro}^m -y_{ro}^l ),\quad r=1,2,\ldots ,s,\\&-\sum \limits _{\begin{array}{l} j=1 \\ j\ne o \\ \end{array}}^n {x_{ij}^l } \alpha _j -x_{io}^u \alpha _o +x_{io}^u \theta -\phi _i \ge 0,\quad i=1,2,\ldots ,m,\\&\sum \limits _{\begin{array}{l} j=1 \\ j\ne o \\ \end{array}}^n {(x_{ij}^m -x_{ij}^l )\alpha _j -} (x_{io}^u -x_{io}^n )\alpha _o +(x_{io}^u -x_{io}^n )\theta -\beta _i +\phi _i \ge 0,\quad i=1,2,\ldots ,m,\\&\alpha _j \ge 0,\quad \quad \,\, j=1,2,\ldots ,n,\\&\phi _i ,\beta _i \ge 0,\quad i=1,2,\ldots ,m,\\&\mu _r ,\gamma _r \ge 0,\quad r=1,2,\ldots ,s,\\&\theta \quad free \end{aligned}$$

Consider a solution for the dual model as follows:

$$\begin{aligned}&\alpha _j =0,\quad j=1,2,\ldots ,n,\quad j\ne o \\&\alpha _0 =1 \\&\phi _i =\beta _i =0,\quad i=1,2,\ldots ,m,\\&\mu _r =\gamma _r =0,\quad r=1,2,\ldots ,s, \\&\theta =1 \end{aligned}$$

It is obvious that the above solution is a feasible solution for the dual model. Therefore, independent of the input and output variables, there is always at least one feasible solution for the dual and the primal models. Therefore, the optimum value of the objective function for the dual model is definitely less than or equal to 1 (i.e., $Z^{{*}}\le 1$). By the virtue of the duality theorem in linear programming, the objective function of the dual and the primal models are equal for the optimal solution (i.e., $Z^{{*}}=E_o^{{*}L}$). Therefore, it can be concluded that $E_o^{{*}L} \le 1$ is always true. Hence, Model (14) is always bounded. This completes the proof. $\square$

3.3.2 Proposed fuzzy DEA method

We modify the Wang and Chin’s (2011) and Khalili-Damghani et al.’s (2011) method to consider the preferences of the DMs on the priority of the inputs and the outputs criteria. To accomplish this modification, the weights of the criteria achieved by fuzzy ANP are considered in the form of additional constraints. The efficiency scores are recalculated and compared with the efficiency scores in the original models using TFNs.

Models (7)–(8) and Models (13)–(14), which are the original models proposed by Wang and Chin’s (2011) and Khalili-Damghani et al. (2011), respectively, were developed based on trapezoidal fuzzy numbers. The modified models, which used the relative importance of the inputs and the outputs attained from the ANP, also were developed using triangular fuzzy numbers which are easy to interpret and sensible to use in terms of consistency and comparability.

We first use the criteria weights and rank them. We then introduce a set of linear constraints using Wang and Chin’s (2011) and Khalili-Damghani et al.’s (2011) models based on these priorities. As a result of this modification, the weight of each input and output criteria (i.e., $u_{r}$ or $v_{i}$) can be controlled based on the DM preferences.

Modified Wang and Chin’s (2011) method Assume that inputs and outputs are ranked based on their priorities. The most important input is ranked 1 and the least important input is ranked $m$ (there are $m$ inputs, $i=1,2,\ldots ,m$). Also, the most important output is ranked 1 and the least important output is ranked $s$ (there are s outputs, $r=1,2,\ldots ,s$). The ranks of inputs and outputs are assigned based on the fuzzy ANP weights. Consequently, the following sets of constraints are added to Wang and Chin’s (2011) model.

$$\begin{aligned}&\forall i:v_i \ge v_p ;\quad i=1,\ldots ,m-1,\quad p=i+1,\ldots ,m \nonumber \\&\forall r:u_r \ge u_k ;\quad r=1,\ldots ,s-1,\quad k=r+1,\ldots ,s \end{aligned}$$

(15)

Next, the following sets of constraints are considered in order to derive the relative dominance of the inputs and outputs since fuzzy weights were used in the original Wang and Chin’s (2011) method.

$$\begin{aligned}&\forall i:\tilde{v}_i \ge \tilde{v}_p ;\quad i=1,\ldots ,m-1,\quad p=i+1,\ldots ,m \nonumber \\&\forall r:\tilde{u}_r \ge \tilde{u}_k ;\quad r=1,\ldots ,s-1,\quad k=r+1,\ldots ,s \end{aligned}$$

(16)

where, $\tilde{v}_i =(v_i^l ,v_i^m ,v_i^u)$ and $\tilde{u}_r =(u_r^l ,u_r^m ,u_r^u)$. Therefore, constraints (16) will be represented as constraints (17).

$$\begin{aligned}&(v_i^l ,v_i^m ,v_i^u )\ge (v_p^l ,v_p^m ,v_p^u);\quad i = 1,\ldots ,m-1,\quad p = i+1,\ldots ,m \nonumber \\&(u_r^l ,u_r^m ,u_r^u )\ge (u_k^l ,u_k^m ,u_k^u) ;\quad r = 1,\ldots ,s-1, \quad k = r+1,\ldots ,s \end{aligned}$$

(17)

The practical set of constraints added to the original method of Wang and Chin (2011) are presented as follows in constraints (18):

$$\begin{aligned} \begin{array}{l} \left\{ {{\begin{array}{l} {v_i^l \ge v_p^l } \\ {v_i^m \ge v_p^m } \\ {v_i^u \ge v_p^u } \\ \end{array} }} \right. ;\quad {\begin{array}{l} {i=1,\ldots ,m-1} \\ {p=i+1,\ldots ,m} \\ \end{array} }\\ \left\{ {{\begin{array}{l} {u_r^l \ge u_k^l } \\ {u_r^m \ge u_k^m } \\ {u_r^u \ge u_k^u } \\ \end{array} }} \right. ;\quad {\begin{array}{l} {r=1,\ldots ,s-1} \\ {k=r+1,\ldots ,s} \\ \end{array} } \\ \end{array} \end{aligned}$$

(18)

Model (7) is modified using (18) and a modified version of the optimistic model by Wang and Chin (2011) is developed as Model (19).

$$\begin{aligned} Maximize&\quad \theta _\circ ^{best} =\sum \limits _{r=1}^s {(u_r^l y_{r\circ }^l +2u_r^m y_{r\circ }^m +u_r^u y_{r\circ }^u )} \nonumber \\ s.t.&\quad \sum \limits _{i=1}^m {(v_i^l x_{i\circ }^l +2v_i^m x_{i\circ }^m +v_i^u x_{i\circ }^u )} =1 \nonumber \\&\quad \sum \limits _{r=1}^s {(u_r^l y_{rj}^l +2u_r^m y_{rj}^m +u_r^u y_{rj}^u )} -\sum \limits _{i=1}^n {(v_i^l x_{ij}^l +2v_i^m x_{ij}^m +v_i^u x_{ij}^u )} \le 0,\nonumber \\&\qquad j=1,2,\ldots ,n,\nonumber \\&\quad {\begin{array}{l} {v_i^l \ge v_p^l ;\quad i=1,\ldots ,m-1,\quad p=i+1,\ldots ,m} \\ {v_i^m \ge v_p^m ;\quad i=1,\ldots ,m-1,\quad p=i+1,\ldots ,m} \\ {v_i^u \ge v_p^u ;\quad i=1,\ldots ,m-1,\quad p=i+1,\ldots ,m} \\ \end{array} }\nonumber \\&\quad {\begin{array}{l} {u_r^l \ge u_k^l ;\quad r=1,\ldots ,s-1,\quad k=r+1,\ldots ,s} \\ {u_r^m \ge u_k^m ;\quad r=1,\ldots ,s-1,\quad k=r+1,\ldots ,s} \\ {u_r^u \ge u_k^u ;\quad r=1,\ldots ,s-1,\quad k=r+1,\ldots ,s} \\ \end{array} } \nonumber \\&\quad u_r^u \ge u_r^m \ge u_r^l \ge 0; \quad r=1,2,\ldots ,s \nonumber \\&\quad v_i^u \ge v_i^m \ge v_i^l \ge 0;\quad i=1,2,\ldots ,m \end{aligned}$$

(19)

Model (8) is also modified using (18) and a modified version of the pessimistic model by Wang and Chin (2011) is developed as Model (20).

$$\begin{aligned} Minimize&\quad \theta _\circ ^{worst} =\sum \limits _{r=1}^s {\left( u_r^l y_{r\circ }^l +2u_r^m y_{r\circ }^m +u_r^u y_{r\circ }^u \right) } \nonumber \\ s.t.&\quad \sum \limits _{i=1}^m {\left( v_i^l x_{i\circ }^l +2v_i^m x_{i\circ }^m +v_i^u x_{i\circ }^u\right) } =1 \nonumber \\&\quad \sum \limits _{r=1}^s {\left( u_r^l y_{rj}^l +2u_r^m y_{rj}^m +u_r^u y_{rj}^u \right) } -\sum \limits _{i=1}^n {\left( v_i^l x_{ij}^l +2v_i^m x_{ij}^m +v_i^u x_{ij}^u \right) } \ge 0,\nonumber \\&\qquad j=1,2,\ldots ,n,\nonumber \\&\quad {\begin{array}{l} {v_i^l \ge v_p^l ;\quad i=1,\ldots ,m-1, \quad p=i+1,\ldots ,m} \\ {v_i^m \ge v_p^m ;\quad i=1,\ldots ,m-1, \quad p=i+1,\ldots ,m} \\ {v_i^u \ge v_p^u ;\quad i=1,\ldots ,m-1, \quad p=i+1,\ldots ,m} \\ \end{array} }\nonumber \\&\quad {\begin{array}{l} {u_r^l \ge u_k^l ;\quad r=1,\ldots ,s-1, \quad k=r+1,\ldots ,s} \\ {u_r^m \ge u_k^m ;\quad r=1,\ldots ,s-1, \quad k=r+1,\ldots ,s} \\ {u_r^u \ge u_k^u ;\quad r=1,\ldots ,s-1, \quad k=r+1,\ldots ,s} \\ \end{array} } \nonumber \\&\quad u_r^u \ge u_r^m \ge u_r^l \ge 0; \quad r=1,2,\ldots ,s \nonumber \\&\quad v_i^u \ge v_i^m \ge v_i^l \ge 0; \quad i=1,2,\ldots ,m \nonumber \\&\quad u_r^u \ge u_r^m \ge u_r^l \ge 0; \quad r=1,2,\ldots ,s \nonumber \\&\quad v_i^u \ge v_i^m \ge v_i^l \ge 0; \quad i=1,2,\ldots ,m \end{aligned}$$

(20)

Models (19) and (20) consider the decision makers’ preferences on the priority of the inputs and outputs. This leads to more reasonable coefficients for the inputs and outputs and more accurate efficiency scores for the DMUs.

Modified Khalili-Damghani et al.’s (2011) method We then develop Models (21) and (22) by adding a set of constraints (15) to Models (13) and (14). Model (21) is used to calculate the upper-bound for the efficiency scores of the DMUs.

$$\begin{aligned} Maximize&\quad E^{U}=\sum \limits _{r=1}^s {u_r } y_{ro}^u -\eta _r (y_{ro}^u -y_{ro}^n ) \nonumber \\ s.t.&\quad \sum \limits _{r=1}^s {u_r } y_{rj}^l +\eta _r (y_{rj}^m -y_{rj}^l )-\sum \limits _{i=1}^m {v_i } x_{ij}^u -\lambda _i (x_{ij}^u -x_{ij}^n )\le 0;\nonumber \\&\qquad j=1,\ldots ,n,\quad j=1,2,\ldots ,n,\quad j\ne o \nonumber \\&\quad \sum \limits _{r=1}^s {u_r } y_{ro}^u -\eta _r (y_{ro}^u -y_{ro}^n )-\sum \limits _{i=1}^m {v_i } x_{io}^l +\lambda _i (x_{io}^m -x_{io}^l )\le 0 \nonumber \\&\quad \sum \limits _{i=1}^m {v_i } x_{i\circ }^l +\lambda _i (x_{i\circ }^m -x_{i\circ }^l )=1 \nonumber \\&\quad \sum \limits _{i=1}^m {v_i } x_{i\circ }^l +\lambda _i (x_{i\circ }^m -x_{i\circ }^l )=1 \nonumber \\&\quad v_i \ge v_p ;\quad i=1,\ldots ,m-1,\quad p=i+1,\ldots ,m \nonumber \\&\quad u_r \ge u_k ;\quad r=1,\ldots ,s-1,\quad k=r+1,\ldots ,s \nonumber \\&\quad v_i ,u_r \ge 0;\quad r=1,2,\ldots ,s ;\quad i=1,2,\ldots ,m\nonumber \\&\quad 0\le \lambda _i \le v_i ;\quad i=1,2,\ldots ,m \nonumber \\&\quad 0\le \eta _r \le u_r ;\quad r=1,2,\ldots ,s \end{aligned}$$

(21)

Model (22) is used to calculate the lower-bound for the efficiency scores of the DMUs.

$$\begin{aligned} Maximize&\quad E^{L}=\sum \limits _{r=1}^s {u_r } y_{ro}^l +\eta _r \left( y_{ro}^m -y_{ro}^l \right) \nonumber \\ s.t.&\quad \sum \limits _{r=1}^s {u_r } y_{rj}^u \!-\!\eta _r (y_{rj}^u \!-\!y_{rj}^n )\!-\!\sum \limits _{i=1}^m {v_i } x_{ij}^l \!+\!\lambda _i \left( x_{ij}^m \!-\!x_{ij}^l \right) \!\le \! 0;\quad j\!=\!1,\ldots ,n,\quad j\!\ne \! o\nonumber \\&\quad \sum \limits _{r=1}^s {u_r } y_{ro}^l +\eta _r \left( y_{ro}^m -y_{ro}^l \right) -\sum \limits _{i=1}^m {v_i } x_{io}^u -\lambda _i \left( x_{io}^u -x_{io}^n \right) \le 0 \nonumber \\&\quad \sum \limits _{i=1}^m {v_i } x_{io}^u -\lambda _i \left( x_{io}^u -x_{io}^n \right) =1 \nonumber \\&\quad v_i \ge v_p ;\quad i=1,\ldots ,m-1,\quad p=i+1,\ldots ,m \nonumber \\&\quad \forall r:u_r \ge u_k ;\quad r=1,\ldots ,s-1,\quad k=r+1,\ldots ,s \nonumber \\&\quad v_i ,u_r \ge 0 ;\quad r=1,2,\ldots ,s ;\quad i=1,2,\ldots ,m \nonumber \\&\quad 0\le \lambda _i \le v_i ;\quad i=1,2,\ldots ,m \nonumber \\&\quad 0\le \eta _r \le u_r ;\quad r=1,2,\ldots ,s \end{aligned}$$

(22)

The main advantages of the two modified methods over the original models are: (1) the modified approaches take into consideration the preferences of the DMs on the priority of the inputs and outputs criteria and result in a fair and exact efficiency score for each DMU; and (2) the DMUs cannot select coefficients of inputs and outputs in an unconstrained situation. However, restricting the coefficients of the inputs and outputs according to the DMs’ preferences in a constrained situation enhances the discrimination power of the DEA models.

3.3.3 Ranking the DMUs

The proposed fuzzy DEA methods do not provide similar results and it is necessary to use a procedure to combine the results of the proposed fuzzy DEA approaches systematically. The following procedure is proposed to accomplish this goal.

Step 1. The rank assigned to each DMU in each method is determined for both the optimistic and pessimistic scenarios. Then, using the Spearman correlation test, the correlations between the achieved ranks from different methods are determined. The following method is used to calculate the rank correlation coefficient for the paired data:

$$\begin{aligned} r_s =1-\frac{6\left( {\sum _i {d_i^2 } } \right) }{n(n^{2}-1)} \end{aligned}$$

(23)

where $d_{i}$ represents the difference between the rank order of each pair. Consider the case where the rankings for each pair are equal. In that case, all the values of $d_{i}$ are zero which shows there is a strong correlation between the two methods. In contrast, if the ranks are not equal and the difference between $d_{i}$ is large, the Spearman correlation will produce a small value. The Spearman test has a t-student distribution with degrees of freedom $n-2$ as follow:

$$\begin{aligned} t=r_s \sqrt{\frac{n-2}{1-r_s^2 }} \end{aligned}$$

(24)

The null hypothesis is rejected if the test statistic is greater than the theoretical value $t_{\alpha ,n-2}$ from the t-student table. Otherwise, the null hypothesis is accepted.

Step 2 After the Spearman correlation test, the low-correlated methods are selected in order to determine the final ranking of the DMUs. We then use the method introduced by Soleimani-damaneh and Zarpisheh (2009) to combine the efficiency scores obtained from different DEA models and determine the final rankings for the DMUs. The method is revisited here briefly.

Suppose the efficiency scores of $n$ DMU’s are calculated according to the $k$ DEA methods and the Matrix $E$ is obtained as follows:

$$\begin{aligned} E=\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {E_{11} }&{} {E_{12} }&{} \cdots &{} {E_{1k} } \\ {E_{21} }&{} {E_{22} }&{} \cdots &{} {E_{2k} } \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {E_{n1} }&{} {E_{n2} }&{} \cdots &{} {E_{nk} } \\ \end{array} }} \right) \end{aligned}$$

(25)

where $E_{jl}$, $j=1,2,\ldots ,n$; $l=1,2,\ldots ,k$ represent the efficiency scores of $\hbox {DMU}_{j}$ achieved from the $l$-th model. The efficiency scores are normalized using (26).

$$\begin{aligned} \bar{{E}}_{jl} =\frac{E_{jl} }{\sum _{j=1}^n {E_{jl} } };\quad j=1,2,\ldots ,n;\quad l=1,2,\ldots ,k \end{aligned}$$

(26)

The entropy values are then calculated using (27).

$$\begin{aligned} e_l =-(\ln n)^{-1}\sum _{j=1}^n {\bar{{E}}_{jl} .\ln } \bar{{E}}_{jl} ;\quad l=1,2,\ldots ,k \end{aligned}$$

(27)

Next, the degree of diversification $(d_{l})$ is calculated using (28).

$$\begin{aligned} d_l =1-e_l ;\quad l=1,2,\ldots ,k \end{aligned}$$

(28)

The importance weight of the $l$-th model is calculated using (29).

$$\begin{aligned} w_l =\frac{d_l }{\sum _{l=1}^k {d_l } };\quad l=1,2,\ldots ,k \end{aligned}$$

(29)

Finally, a final efficiency index is calculated for each $\hbox {DMU}_{j}$ using (30).

$$\begin{aligned} \beta _j =\sum _{l=1}^k {w_l E_{jl};\quad j=1,2,\ldots ,n} \end{aligned}$$

(30)

The entire process represented by Eqs. (25)–(30) is based on both the optimistic and pessimistic models of the low-correlated method and therefore the two final efficiency indices are calculated using these models.

4 Case study: stock exchange for pharmaceutical companies

One of the most important financial markets is the Securities Exchange. Active participation of investors in the Securities Exchange guarantees the viability of the investment market and sustainable development of countries. One of the strategic industries in this market that is extremely sensitive to others, is the pharmaceutical industry. The pharmaceutical industry has direct effect on the living conditions and health of the community. Improving health standards are a predisposing factor for economic development. This industry requires large investments particularly in research and development in order produce the most effective products and ultimately achieve appropriate returns. Thus effective performance evaluation is particularly critical for this industry.¹

4.1 Case study

We used the method proposed in this study to evaluate the performance of 21 pharmaceutical companies actively trading on the SSE for Morgan Bank, a New York investment banking firm specialized in pharmaceutical companies worldwide. We first utilized the expertise of six pharmaceutical investment bankers at Morgan Bank to identify the most important and widely used performance evaluation criteria in the pharmaceutical companies considering the BSC framework with the four perspectives of financial, customer, learning and growth and internal processes. The criteria considered for each perspective are presented in Table 2.

Table 2 Evaluation criteria based on the BSC

4.2 Determine the network of the BSC perspectives

We then determined the interdependence between the BSC perspectives based on the DEMATEL method by preparing a questionnaire and distributing them among our six investment bankers. The total correlation matrix is presented in Table 3. Using the threshold of relations (i.e., the mean of the matrix elements, 1.7938), the network relationship is presented in Fig. 3.

Table 3 Total interactions among the BSC perspectives

Fig. 3

Interdependence among the BSC perspectives

As shown in Table 3, the financial perspective has the highest relation with the customer perspective and the lowest relation with the learning and growth perspective. The customer perspective has the highest relation with the financial perspective and the lowest relation with itself. The learning and growth perspective has the highest relation with the financial perspective and the lowest relation with the internal process perspective. The internal process perspective has the highest relation with the financial perspective and the lowest relation with itself.

The relations between the financial–internal process, customer–customer, customer–internal process, learning and growth-learning and growth, learning and growth–internal process, internal process–internal process, are discarded because they are lower than the threshold value of 1.7938. The remaining relations are the subject for further study.

The column “$r$” and column “$c$” in Table 3 are the sum of the rows and columns of the total correlation matrix, respectively. For instance, 7.426 is the sum of 1.8768 $+$ 2.037 $+$ 1.9244 $+$ 1.5877. The “r” column indicates the sum of the impacts a certain perspective puts on the other perspectives. Therefore, the financial perspective is the strongest criteria among the impact group. For instance, in column “$c$”, 7.9991 is the sum of the first column of total correlation matrix (i.e., 1.876 $+$ 2.1112 $+$ 2.0947 $+$ 1.9164). The “$c$” column indicates the sum of the impacts a certain perspective receives from the other perspectives. Therefore, the financial perspective is the strongest criteria among the effect groups.

The column “$r+c$” in Table 3 presents the sum of effect and cause behavior of a criterion. It indicates the degree of interaction of a criterion with other criterion in the network. The most interactive criterion is financial perspective while the least interactive criterion in the network is internal process.

Fig. 4

Hierarchical evaluation structure

The column “$r-c$” in Table 3 indicates the difference between the cause and effect of a criterion. A positive value for “$r-c$” indicates that the impact of a criterion is stronger than its receiving effects and therefore it is a cause criterion. A negative value for “$r-c$” indicates that the impact of a criterion is weaker than its receiving effects and therefore it is an effect criterion. Hence, financial and customer perspectives are effect criteria while learning and growth and internal process are cause criteria.

4.3 Determine the local and global weights of the perspectives and criteria

We then constructed the hierarchical structure of the criteria and the perspectives presented in Fig. 4. A questionnaire was given to our six investment bankers and they were asked to present their preferences assuming no interdependence between the perspectives using the linguistic variables in Table 1. The pair-wise comparisons are summarized in Tables 4, 5 and 6. The geometric mean was used to aggregate the opinions of the six investment bankers.

Using the proposed fuzzy ANP method, the local weights of the BSC perspectives and the performance criteria were determined. The results are presented in Table 7.

Table 4 Interdependence matrix of the perspectives with respect to the financial perspective

Table 5 Interdependence matrix of the perspectives with respect to the customer perspective

Table 6 Interdependence matrix of the perspectives with respect to the learning and growth perspective

Table 7 Local weights of the BSC perspectives and the evaluation criteria

The interdependence matrix of the perspectives was then calculated as follows:

$$\begin{aligned} W_{BSC} =\left[ {{\begin{array}{l} F \\ C \\ L \\ I \\ \end{array} }} \right] =\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {0.5775}&{} {0.8092}&{} {0.7041}&{} 0 \\ {0.2062}&{} 0&{} {0.2959}&{} 0 \\ {0.0862}&{} {0.1255}&{} 0&{} 0 \\ {0.1301}&{} {0.0654}&{} 0&{} 0 \\ \end{array} }} \right] \otimes \left[ {{\begin{array}{l} {0.5667} \\ {0.2440} \\ {0.1063} \\ {0.0830} \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {0.5996} \\ {0.1483} \\ {0.0794} \\ {0.0897} \\ \end{array} }} \right] \end{aligned}$$

The interdependent weights for the BSC perspectives are obtained by normalizing the above vector as follows:

$$\begin{aligned} W_{BSC} =\left[ {{\begin{array}{l} F \\ C \\ L \\ I \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {0.6538} \\ {0.1617} \\ {0.0866} \\ {0.0978} \\ \end{array} }} \right] \end{aligned}$$

The global weights of the criteria were calculated next and the results are given in Table 8.

Table 8 Global weights of the performance criteria

4.4 Calculate the efficiency scores of the DMUs using the proposed fuzzy DEA model

The criteria are prioritized and clustered next as inputs and outputs in Table 9 according to the global weights obtained in the previous step.

Table 9 Inputs and outputs of the fuzzy DEA models

As shown in Table 9, operating budget and cost of goods sold are classified as inputs and market share, EPS, P/E ratio, sales growth, rank of liquidity, and volume of exports are classified as outputs. These inputs and outputs are used in the proposed fuzzy DEA models. If a new input or output is created based on the ratio of two distinct variables (i.e., inputs or outputs) from the production possibility, then, the final model may cause some infeasibility or may perturb the convexity assumption of the production possibility set (Hollingsworth and Smith 2003; Emrouznejad and Amin 2009). We should note that infeasibility does not occur in the case of the P/E ratio, which has been used in the proposed model as an output, since this is a very well-known financial ratio and is not made based on two distinct variables from the production possibility set. The estimates presented in Table 10 are provided by SSE based on 3 years of historical data.

Table 10 Inputs and outputs of the DMUs

It is notable that a crisp number $m$ is a special case of a TFN number $(m, m, m)$. The efficiency scores of each DMU in both the optimistic and pessimistic scenarios were calculated using the proposed fuzzy methods. As a result, 4 optimistic efficiency scores and 4 pessimistic efficiency scores were calculated for each DMU. All models were coded using LINGO software on a Pentium IV 2.4 GHz, PC with 2G of RAM, and MS-XP. The resulting efficiency scores are represented in Table 11.

Table 11 Efficiency scores of the DMUs

Table 11 shows that the efficiency scores of all the DMUs have been calculated in both the optimistic and pessimistic scenarios. In the classical DEA methods, the efficient DMU has an efficiency score equal to 1 while the inefficient DMUs have efficiency scores less than 1. This situation is correct for the optimistic and pessimistic scenarios in both the modified and the original Khalili-Damghani et al. (2011) methods. Therefore, the DMUs can be categorized into three classes for the optimistic and pessimistic scenarios in the modified and original Khalili-Damghani et al. (2011) methods.

In the first class, a DMU is efficient in both the optimistic and the pessimistic scenarios (the efficiency score is always equal to 1). These DMUs (called $\hbox {E}^{++}$) are not sensitive to the inputs and outputs, and are always efficient. As shown in Table 11, eleven DMUs are classified in the $\hbox {E}^{++}$ group using the original Khalili-Damghani et al. (2011) method, while only two DMUs are classified in the $\hbox {E}^{++}$ group using the modified Khalili-Damghani et al. (2011) method. This means that the extra information used in the modified Khalili-Damghani et al. (2011) method not only considers the decision makers’ preferences on the priority of the inputs and outputs, but also improves the discrimination power in DEA modeling.

In the second class, a DMU is inefficient in both the optimistic and the pessimistic scenarios (efficiency score is always less than 1). These DMUs (called $\hbox {E}^{-}$) are not sensitive to the inputs and outputs, and are always inefficient. As shown in Table 11, six DMUs are classified in the this group using the original Khalili-Damghani et al. (2011) method, while eighteen DMUs are classified in the $\hbox {E}^{-}$ group using the modified Khalili-Damghani et al. (2011) method. This means that the extra information used in the modified Khalili-Damghani et al. (2011) method not only considers the decision makers’ preferences on the priority of the inputs and outputs, but also provides a fair assessment and ensures the proper classification of the DMUs

In the third class, a DMU is efficient in the optimistic scenario and inefficient in the pessimistic scenario. Such DMUs (called $\hbox {E}^{+}$) are sensitive to the input and output values and therefore may be either efficient or inefficient. As shown in Table 11, four DMUs are classified in the $\hbox {E}^{+}$ group using the original Khalili-Damghani et al. (2011) method, while just one DMU is classified in the $\hbox {E}^{+}$ group using the modified Khalili-Damghani et al. (2011) method. Thus, the extra information used in the modified Khalili-Damghani et al. (2011) method not only considers the decision makers’ preference on the priority of the inputs and outputs, but also improves the discrimination power in DEA modeling.

As indicated in Sect. 3.3.1, the definition of an efficient DMU in the pessimistic scenario for both the original and modified Wang and Chin (2011) methods are not typical. However, the definition of the efficient and inefficient DMUs are typical in the optimistic scenario. In the pessimistic scenario, if the optimum value of the objective function is equal to 1, the associated DMU is called efficient and if the optimum value of the objective function is greater than 1, the associated DMU is called inefficient. Therefore, the DMUs in the optimistic and pessimistic scenarios in both the original and modified Wang and Chin (2011) methods are classified into the following three classes.

In the first class (called $\hbox {E}^{++}$), a DMU is always efficient in the optimistic and pessimistic scenarios. In the original Wang and Chin (2011) method, none of the DMUs are classified in this group. However, six DMUs are classified in this group in the modified Wang and Chin (2011) method. In the second class (called $\hbox {E}^{-}$), seventeen DMUs are classified in this group in the original Wang and Chin (2011) method and five DMUs are classified in this group in the modified Wang and Chin (2011) method. Finally, in third class (called $\hbox {E}^{+}$), a DMU is efficient in the optimistic scenario and inefficient in the pessimistic scenario. Two DMUs are classified in this group in the original Wang and Chin (2011) method and five DMUs are classified in this group in the modified Wang and Chin (2011) method.

4.5 Rank the DMUs

The method proposed by Soleimani-damaneh and Zarpisheh (2009) was used to combine different efficiency scores and obtain a final ranking for the DMUs. First, the Spearman test was used to check the different rankings. The results of the Spearman rank correlation test between each pair of methods in both the optimistic and pessimistic scenarios are presented in Tables 12 and 13, respectively. The test was run with a 99 % confidence level.

Table 12 Results of the Spearman test for the optimistic scenario

Table 13 Results of the Spearman test for the pessimistic scenario

The results of the Spearman test for the optimistic scenario in Table 12 shows that the modified methods have produced different rankings when compared with the classical methods. As shown in Table 12, the correlation between the modified expected value approach of Wang and Chin (2011) and the modified approach of Khalili-Damghani et al. (2011) is high (0.993). This means that these methods produce rankings that are statistically similar since there is not enough evidence to accept the null hypothesis. The correlation between the original method of Wang and Chin (2011) and the original method of Khalili-Damghani et al. (2011) is similar with a high correlation of 0.860. In all other pairwise comparisons in Table 12 where one side is an original method and other side is a modified method, the null hypothesis is accepted. This means that the modifications of the original methods, which incorporates the opinion of the decision makers, is effective and produce different rankings. Thus, the efficiency scores from the modified methods were used to determine the final ranking of the DMUs based on the method proposed by Soleimani-damaneh and Zarpisheh (2009). In the optimistic scenario, when using this final ranking of the DMUs, the relative importance scores are 0.5160 and 0.4839 for the modified Wang and Chin (2011) and the modified Khalili-Damghani et al. (2011) methods, respectively.

Table 13 presents the results of the Spearman test for the pessimistic scenario. Again, the modified methods have produced different rankings when compared with the classical methods. As shown in Table 13, the correlation between the modified expected value approach of Wang and Chin (2011) and the modified method of Khalili-Damghani et al. (2011) is high (0.772). This means that these methods produce rankings which are statistically similar and there is not enough evidence to accept the null hypothesis. In all other pairwise comparisons in Table 13, the null hypothesis is accepted. Thus the modification of both methods, which incorporates the opinions of the decision makers is effective and can result in different rankings. In the pessimistic scenario, when using the final ranking of the DMUs based on the method proposed by Soleimani-damaneh and Zarpisheh (2009), the relative importance scores are 0.5683 and 0.4316 for the modified Wang and Chin (2011) and the modified Khalili-Damghani et al. (2011) methods, respectively. The final rankings of the DMUs in both the optimistic and pessimistic scenarios is presented in Table 14.

Table 14 Final rankings of the DMUs

5 Conclusion and future research directions

The effects of financial markets on the economic growth and progress of developing economies is undeniable. The primary function of the financial markets is to effectively move capital markets and allocate financial resources to various sectors of the economy. Various performance evaluation methods can be used to help investors make informed decisions by following the measured growth and the dynamics of companies on the Stock Exchange.

In this study we proposed a new method for measuring the efficiency of pharmaceutical companies. Financial and non-financial metrics were used in the proposed method within a BSC framework. The DEMATEL approach was used to capture the causal relationships and the interaction between the BSC perspectives. Fuzzy ANP was used next to determine the relative importance of the factors within a network structure. High priority factors were then divided into the input and output factors. To measure the performance of the pharmaceutical companies (represented by DMUs), two fuzzy DEA models [i.e., the model proposed by Wang and Chin (2011) and the model proposed by Khalili-Damghani et al. (2011)], were modified based on the weight constraints developed using the fuzzy ANP. Finally, statistical tests were performed to check whether there were differences between the achieved ranks. The high correlated methods were discarded and an aggregation method based on Shannon’s entropy proposed by Soleimani-damaneh and Zarpisheh (2009) was applied to rank the DMUs.

The contribution of the proposed performance measurement system is fivefold: (1) the proposed method helps investors choose a proper portfolio of stocks in the presence of environmental turbulence and uncertainties; (2) it considers fuzzy logic and fuzzy sets to represent ambiguous, uncertain or imprecise information; (3) a comprehensive performance measurement method is proposed to combine ANP and DEMATEL within a DEA system; (4) an integration method grounded in the Shannon’s entropy concept is used to combine different efficiency scores and calculate the final ranking of the DMUs; and (5) the proposed method synthesizes a representative outcome based on qualitative judgments and quantitative data.

The method proposed in this study is flexible and versatile. It can be easily customized to handle a large number of different problems in different application domains. In addition, triangular and trapezoidal fuzzy numbers were used in the model proposed in this study. The models can be easily modified to handle other well-known fuzzy numbers such as Gaussian or left–right fuzzy numbers. Finally, ranking methods other than the Shannon’s entropy method can be utilized in the proposed model to rank the DMUs.