1 Introduction

Generally, the banks manage collections of funds available to their clients as potential buy-and-hold investors. Each client is invited by the bank to invest in either an available fund or in a portfolio of funds. This should be designed as a lifelong investment appealing to the bank client’s preferences for risk and returns. A sector of these potential investors is more concerned about downside risk than about other risk measures which are less intuitive to bank clients. Then, the bank should create and offer funds oriented to downside risk minimization. On the other hand, the bank managers and executives should advise their clients about it. In addition to bank managers who take responsibility for mutual funds and pension funds, there are potential users of our research such as financial consultants who advise their clients about their investments. The results from this paper are understandable to bank managers whatever their ability to handle the mathematical aspects of the method. These managers are able to use practical information from the proposed method in order to build their own funds minimizing downside risk.

Hence, we here deal with an actual case of portfolio choice to demonstrate how downside risk can be converted into the bank manager’s objective for the purpose of designing funds satisfying the above described sector of investors. This problem is solved by the mean-semivariance efficient frontier model (E-SV; Ballestero 2005), whose results will be compared to those from the classical mean-variance efficient frontier model (E-V). Using E-SV instead of E-V is justified when downside risk is a clearer and more interesting notion of risk than the variance of returns. While variance measures up and down movements, semivariance (below the mean value) measures movements of returns below the mean.

This paper aims at the following objectives.

First objective: to apply E-SV to a well-known opportunity set of blue chips, namely, the Dow Jones opportunity set.

Second objective: to make comparisons of results between efficient portfolios obtained from E-V and E-SV in terms of expected return and risk.

Literature on efficient frontiers, portfolio choice and related issues (concerning papers published from year 2000 onwards) includes the following papers. (a) Efficient frontiers from linkages between utility theory and compromise programming to bound the optimum portfolio (Ballestero and Pla-Santamaria 2004, 2005). (b) Efficient frontiers from beta parameters (Bilbao et al. 2006; Ballestero et al. 2009). (c) New approaches based on multi-objective programming (Steuer et al. 2005; Steuer et al. 2007; Ben Abdelaziz et al. 2007). (d) Goal programming to select equity funds portfolios (Pendaraki et al. 2004). (e) Selection from neural networks and hybrid models (Ong et al. 2005; Huang et al. 2006; Lin et al. 2006). (f) Portfolio choice from fuzzy techniques (Arenas et al. 2001; Ben Abdelaziz and Masri 2005; Pérez-Gladish et al. 2007). (g) Portfolio choice from multi-attributes (Aouni 2009). References related to downside risk measures for the portfolio selection problem, before and after year 2000, are Sortino and Van der Meer (1991), Speranza (1993), Konno et al. (2002) and Vercher et al. (2007). Concerning mean-downside risk efficient frontiers, some meta-heuristic techniques have being used in order to find efficient portfolios in the presence of cardinality constraints. See Chang et al. (2009) and Bermúdez et al. (2012).

The paper is organized as follows. In Sect. 2, the E-SV model is motivated and reviewed. In Sect. 3, basic numerical information for the actual case study is provided in detail. In Sect. 4, the E-SV model is developed for the Dow Jones actual case. The paper closes with a concluding remark.

2 Background

2.1 Motivating semivariance: an example of two lotteries

Suppose you are willing to choose one of the following lotteries taking expected profitability and risk into account.

Lottery 1

You can win $ 4 with probability of 90 % or lose $ 36 with probability of 10 %. Therefore, we have:

Lottery 2

You can win $ 12 or lose $ 12, both with equal probability. Therefore, we have:

Notice that lotteries 1 and 2 have equal expected return and equal variance. Therefore, you cannot make your choice by minimizing the variance, namely, by penalizing upside and downside volatility. Your choice will be here made by minimizing downside risk, namely, semivariance. This leads to select Lottery 2. This is consistent with a drawdown policy. In fact, if you choose Lottery 1, then your maximum potential loss is $ 36, while if you choose Lottery 2 your maximum loss is $ 12 only.

2.2 Analytical models

A widely used method to select portfolios of securities is mean-variance (Markowitz 1952), which is formulated as follows:

$$ \min XVX^{T} $$
(1)

subject to

(2)
(3)

together with the non negativity conditions x i ≥0 for all i, where:

  • m is the number of assets in the opportunity set

  • X=(x 1,x 2,…,x i ,…,x m ) is the row vector of portfolio weights, namely, the decision variables of the problem

  • X T is the transposed vector of X

  • V is the covariance matrix of random returns on the assets

  • E is the row vector of expected returns on the assets

  • E 0 is the investor’s target or aspiration level for the portfolio expected return.

Mean-variance (1)–(3) relies on classical Eu(R) utility theory under uncertainty (Arrow 1965) thorough (Pratt 1964) approximation. This model generally requires using historical information on monthly or weekly returns, which involves adopting the Sharpe’s (1994) principle that historic results have predictive ability.

From decades, there is a wide range of literature dealing with downside risk and semivariance. In this literature, a relevant problem is to derive mean-semivariance efficient frontiers from an analytical model like Markowitz E-V model, so that the new objective function is the portfolio semivariance instead of being the Markowitz portfolio variance. A solution to this problem has been recently given (Ballestero 2005) as follows.

$$ \min\sum_{j, h} \bigl[ v_{jh} - \beta_{j}\beta_{h} v ( \tilde{R}_{M} > E_{M} ) \bigr] x_{j} x_{h} $$
(4)

or equivalently if using vectorial notation:

$$ \min XV_{S}X^{T} = X(V - B)X^{T} $$
(5)

subject to

(6)
(7)
(8)

together with the non-negativity conditions. Symbols have the following meaning:

  • X=(x 1,…,x i ,…,x m ) is the row vector of portfolio weights

  • X T is the transposed vector of X

  • x j , x h are generic components in vector X

  • V S is the m∗m semivariance matrix-core of objective function (5)

  • V is the m∗m covariance matrix of random returns on the assets

  • v jh is the (j,h) generic element of covariance matrix V

  • β j , β h are Sharpe’s betas for assets j and h, respectively.

  • \(v( \tilde{R}_{M} > E_{M} )\) is semivariance (above the mean value) for market portfolio M, whose random returns and expected returns are denoted as \(\tilde{R}_{M}\) and E M , respectively.

  • B is the m∗m matrix whose generic element is \(\beta_{j}\beta_{h} v( \tilde{R}_{M} > E_{M} )\)

  • x 0 is an upper limit to be imposed on every portfolio weight for diversification purposes. This parameter should be fixed at a low level, such as 5 % or less. This bound is according to mutual funds regulations in some countries.

Notice that both models (1)–(3) and (4)–(8) have similar structure, with a quadratic objective function and linear constraints. Notice also that the constraints are the same in both models, with the exception of diversification constraint (8), which is needed for the validity of the mean-semivariance approach.

Remarks to facilitate suitable applications of the mean-semivariance model are as follows.

Remark 1

To compute the semivariance for a single stock or for a single market index is a simple problem indeed. An example can be made. Suppose a market index M whose weekly returns over the last 5 weeks are 0.087, 0.076, 0.0335, 0.0385 and 0.077. Obviously, in real world problems the time series of past returns should be much longer than 5 weeks but we here assume a short number of weeks for simplicity. From these observed returns the following results are obtained.

Meaning is as follows. Over the 5-week observation period, the returns have dropped for 3 weeks below the mean value. Investors are concerned with this result. Notice that the “semivariance below the mean” to “semivariance above the mean” ratio is as high as 0.000281/0.000201=1.4, namely, the falls have been around one and a half higher than the rises. This involves a serious risk, especially for conservative investors.

Remark 2

However, the analyst is faced with a more difficult problem: how to determine the algebraic equation of the semivariance for a portfolio of stocks, this semivariance being a quadratic function of the unknown (x 1,…,x i ,…,x m ) portfolio weights, namely, the objective function to minimize. A solution to this problem is Eq. (4). To make clear how this equation can be specified, the following example can be helpful.

  1. (a)

    Opportunity set: A two-stock set (S 1,S 2) whose portfolio weights are denoted by x 1 and x 2, respectively. For simplicity, this simplistic opportunity set is here used although a two-stock portfolio is quite impossible to be diversified (see Remark 3 below).

  2. (b)

    Time series of weekly returns (5 weeks for simplicity):

  3. (c)

    Covariance matrix: From the time series in paragraph (b), this matrix is obtained by a statistical software (e.g., Excel), namely,

    $$\left [\begin{array}{c@{\quad}c} 0.00068 & -0.00012\\ -0.00012 & 0.000944\end{array} \right ] $$
  4. (d)

    Market index: We assume the same market index M as in Remark 1.

  5. (e)

    Beta coefficients: From the time series given in Remark 1 and paragraph (b) the beta coefficients are straightforwardly computed by a statistical software, namely,

  6. (f)

    Semivariance above the mean of market index M: This value is given in Remark 1, namely, \(v( \tilde{R}_{M} > E_{M} ) =0.000201\)

  7. (g)

    Specifying the objective function: This is performed by introducing the just obtained numerical parameters into Eq. (4), namely,

Remark 3

In Remark 2, simplicity is achieved to the expense of mathematical strictness. Objective function (4) is proven to be valid if and only if the portfolios are sufficiently diversified by constraint (8), which requires an opportunity set of around 25 stocks or more.

Remark 4

By introducing the algebraic expressions of the beta coefficients into Eq. (4) and after making some routine calculus, this equation becomes:

$$\min\sum_{j, h} \biggl[ v_{jh} \biggl( 1 - \biggl( \frac{\rho_{jM}\rho_{hM}}{ \rho_{jh}} \biggr)\frac{v ( \tilde{R}_{M} > E_{M} ) }{ v_{M} }\biggr) \biggr] $$

where ρ jM , ρ hM and ρ jh denote correlation coefficients between (j,M), (h,M) and (j,h), respectively. Symbol v M denotes the variance of the market index. Suppose a particular (j ∗,h ∗) pair of stocks which are characterized by strong comovement between: (a) stock j ∗ and the M market index; (b) stock h ∗ and the M market index; (c) both stocks j ∗ and h ∗. Then, (ρ jM ρ hM /ρ jh )≅1 for j=j ∗ and h=h ∗. Therefore, the (j ∗,h ∗) term in the portfolio semivariance objective function just formulated becomes approximately:

$$v_{jh} \biggl( 1 - \frac{v ( \tilde{R}_{M} > E_{M} )}{v_{M}} \biggr) = v_{jh}v ( \tilde{R}_{M} < E_{M} ) / v_{M} \quad \mbox{for }j = j^*\mbox{ and }h = h^* $$

Therefore, the particular (j ∗,h ∗) term is approximately proportional to the semivariance below the mean of the market index. In terms other than (j ∗,h ∗) the influence of the market semivariance is not characterized by proportionality.

3 Numerical actual case (I): basic information

This case deals with portfolio selection of stocks, the opportunity set of assets being the 30 Dow Jones blue chips. Efficient frontiers of portfolios will be determined either by using mean-semivariance model (4)–(8) or by using Markowitz’s mean-variance model, so that results from both methods can be compared.

3.1 Weekly returns and expected returns

In Table 1, the time series of Friday close prices from September, 23, 2005 to September, 18, 2009 are recorded for each Dow Jones stock as well as for the Dow Jones Index (DJI), which is the M market portfolio in our scenario. From Table 1, the respective time series of weekly returns have been computed together with the respective expected returns (mean values) and beta coefficients, the latter being computed by the following equation:

$$\beta_{i}=\frac{\operatorname{cov}(\tilde{R}_{i},\tilde {R}_{M})}{\operatorname{var}(\tilde{R}_{M})}; \quad i = 1, 2, \dots, 30 $$

where “cov” and “var” denote covariance and variance respectively, while \(\tilde{R}_{i}\) and \(\tilde{R}_{M}\) are random returns on the ith stock and on the market portfolio (DJI), respectively.

Table 1 Dow Jones Index (DJI) and its 30 stocks: Friday close price of every week. September 2005–September 2009. Unit: dollars per share
Full size table

In Table 2, this information is displayed. Covariance matrix V is computed from Table 2 and displayed in Table 3. Due to space limitations, these large tables and others below are presented as fragments.

Table 2 Dow Jones Index and its 30 stocks: Weekly returns, expected returns and betas. September 2005–September 2009
Full size table
Table 3 Dow Jones opportunity set: covariance matrix V from random returns on the 30 stocks. September 2005–September 2009
Full size table

3.2 Determining the V S semivariance matrix

From the weekly returns on market portfolio M (namely, the DJI random returns), the process to compute semivariance V S is conducted as follows.

First step. Compute the \(v( \tilde{R}_{M} > E_{M} )\) semivariance (above the mean value) of market portfolio M. This is carried out in Table 4. From the second and third columns of this table, square deviation \(( \tilde{R}_{M} - E_{M} )^{2}\) is computed and written in the fourth column if and only if weekly return \(\tilde{R}_{M}\) is greater than expected return E M . If, on the contrary, a weekly return is less than (or equal to) the expected return, then zero is written in the fourth column instead of the square deviation. Market semivariance above the mean value is then obtained by aggregating the fourth column of the table, the sum being multiplied by the frequency (probability) equal to 1/209, as there are 209 observed returns. Thus, we obtain \(v( \tilde{R}_{M} >\nobreak E_{M} ) = 0.000393\).

Table 4 Dow Jones Index (market portfolio M): Computing \(v( \tilde{R}_{M} > E_{M} )\) semivariance above the mean value. September 2005–September 2009
Full size table

Second step. From the beta values (see Table 2, bottom) and the semivariance obtained in the first step above, compute matrix B, whose generic element is:

$$\beta_{j}\beta_{h}v ( \tilde{R}_{M} > E_{M} ) = 0.000393\beta_{j}\beta_{h} $$

Matrix B is numerically displayed in Table 5 (fragment).

Table 5 Dow Jones opportunity set: matrix B whose generic element (j,h) is \(\beta_{j}\beta_{h}v( \tilde{R}_{M} > E_{M} )\). September 2005–September 2009
Full size table

Third step. Compute matrix V S as the difference between matrix V (Table 3) and matrix B (Table 5). In Table 6 (fragment), matrix V S is recorded.

Table 6 Dow Jones opportunity set: semivariance matrix (V−B). September 2005–September 2009
Full size table

4 Numerical actual case (II): mean-semivariance efficient frontier model and results

4.1 Formulating and solving the model

Semivariance matrix V S (Table 6) is the core of the objective function (5) to be minimized. By using numerical information on expected returns (Table 2, bottom) and taking x 0=0.05 as diversification level, the model constraints are as follows.

(9)

where parameter E 0 moves over a feasible range.

(10)
(11)

together with the non-negativity conditions.

This numerical model is straightforwardly solved by Lingo special GenPRT.lg4 software.

4.2 Results: a comparison of portfolios from the mean-semivariance and mean-variance models

By using the mean-semivariance model with the numerical information above, an efficient frontier of 7 portfolios has been determined. Here, the targets are between E 0=0.00100 and E 0=0.00160. Lowest bound E 0=0.00100 is due to the bullet shaped arc of frontier, while the highest bound E 0=0.00160 is because no feasible solution is found above. In Table 7, the main characteristics of this frontier are recorded.

Table 7 Results: a comparison between mean-semivariance and E-V frontiers
Full size table

For the purpose of comparison, the Markowitz E-V model is applied to the same portfolio problem, namely, by minimizing the portfolio variance (from covariance matrix V in Table 3) subject to the same constraints (9)–(11) already used in the mean-semivariance model. For ease of comparison, every target E 0 is here fixed at the same level of the respective E 0 target in the mean-semivariance frontier. As above, expected returns higher than E 0=0.00160 lead to infeasible solutions. In both models, expected returns lower than E 0=0.00100 lead to a typically irregular (bullet shaped) arc of frontier (Haugen 1997), which has been removed.

In Table 7, let us compare the resulting mean-semivariance frontier to the classical E-V frontier.

  1. (a)

    Volatility as measured by the portfolio variance. For each expected return E 0, the volatility from the mean-semivariance model is slightly higher than the respective volatility from the E-V model. This result is consistent as E-V, but not mean-semivariance, minimizes the portfolio variance. However, the respective discrepancies are very small. In percentage, these discrepancies decrease from 0.35 % (for the lowest E 0 return) to almost zero for the highest E 0 return.

  2. (b)

    Downside risk as measured by the semivariance. For each expected return E 0, the semivariance from the E-V model is slightly higher than the respective semivariance from the mean-semivariance model. Again, the result is consistent as mean-semivariance, but not E-V, minimizes the portfolio semivariance. Like in paragraph (a), we obtain small discrepancies, namely, from 0.42 % (for the lowest E 0 return) to almost zero for the highest expected return.

  3. (c)

    Assets in the portfolio. In both frontiers, each E 0 portfolio includes 21–23 assets with non-zero weight. More precisely, if we compare portfolios of equal E 0 in both frontiers, there are 3 portfolios with 22 assets and 3 portfolios with 21 assets. Frequently, for each E 0 portfolio, the assets, but not their weights, coincide in both frontiers. To be exact, this coincidence occurs in 4 portfolios and does not occur in 2 portfolios.

  4. (d)

    Portfolio weights. For each E 0 portfolio, those assets, which are not weighted at 5 % level, are weighted at levels mostly different from a frontier to another frontier. There are two exceptions for E 0=0.00150 and E 0=0.00160. However, most assets reach the upper limit of 5 % allowed by the diversification constraints.

  5. (e)

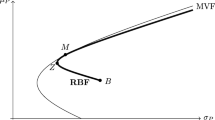
    In Fig. 1, the variable plotted on the horizontal axis is portfolio expected return while the variable on the vertical axis is portfolio semivariance. Polygon ABC (solid line) is the mean-semivariance efficient frontier given by the proposed E-SV model. Dotted polygon A′B′C′ represents the semivariances obtained by the Markowitz E-V model. Notice that polygon ABC lies below the dotted polygon. This is a coherent result as the E-SV model minimizes the portfolio semivariance while Markowitz E-V minimizes the portfolio variance. The gaps between both polygons are as follows: AA′=0.42 %, BB′=0.39 % and CC′=0.05 %. Therefore, the higher the expected return the narrower the gap.

    Fig. 1
    figure 1

    Mean-semivariance efficient frontier from the E-SV model and semivariance polygonal line from the E-V model

    Full size image
  6. (f)

    In Fig. 2, the variable plotted on the horizontal axis is portfolio expected return while the variable on the vertical axis is portfolio variance. Dotted polygon H′I′J′K′ is the mean-variance efficient frontier given by the Markowitz E-V model. Polygon HIJK represents the variances obtained by the proposed E-SV model. Notice that dotted polygon H′I′J′K′ lies below the solid polygon. This is a coherent result as the Markowitz E-V model minimizes the portfolio variance while the proposed model minimizes the portfolio semivariance. The gaps between both polygons are as follows: HH′=0.35 %, II′=0.48 %, JJ′=0.01 % and KK′=0.10 %.

    Fig. 2
    figure 2

    Mean-variance efficient frontier from the Markowitz E-V model and variance polygonal line from the E-SV model

    Full size image

5 Concluding remarks

To highlight the value added by this paper notice that a model of portfolio choice such as E-SV needs to be tested from actual opportunity sets of stocks appropriately. An appropriate test should discern if the new model is relevant in the sense that the results of the model differ from the results given by the classic E-V model and they are consistent with the objective of reflecting downside risk. So far E-SV has been nearly illustrated from fictitious opportunity sets including a short number of assets. Such illustrations are insufficient for testing purposes. As we have developed an accurate test from Down Jones opportunity set of stocks, this paper can be viewed as a contribution to finance, and more precisely, to the field of portfolio efficient frontiers in the framework of downside risk.

Future research could be conducted to construct and test models in which targets of downside risk other than the mean value are used from the investors preferences.