Effect of Interface Properties on Mechanical Behavior of 3D Four-Directional Braided Composites with Large Braid Angle Subjected to Uniaxial Tension

Abstract

A Representative Volume Cell (RVC) chosen to epitomize the entire three dimensional four-directional braided composites is investigated to evaluate the mechanical behavior of the material by computational micromechanics. In addition to including several damage modes of braid yarn and matrix within the braided composites, the numerical model also takes into account interface damage mode by using a Cohesive Zone Model (CZM). A parametrical study is conducted to evaluate the influence of interface properties on the macro stress-strain curve and the interaction of different failure modes of the braided composites under uniaxial tensile loading. The interface damage evolution of the braided composites with large braid angle is also provided further. Preliminary results indicate that the interface damage, which is one of the key factors to cause the nonlinearity of the stress-strain relationship, can decrease the elastic modulus but not obviously control the ultimate strength of the braided composites with large braid angle.

1 Introduction

Textile composites are being widely used in the fields of astronautics, space, marine, automotive and off-shore due to the special properties compared with traditional laminate composites, combing high stiffness and strength at low density, high tolerance, high-specific energy absorption behavior and excellent in plane shear behavior [1]. Three dimensional four-directional braided composites are manufactured by braided preforms impregnating and solidifying with resin material. The braided preforms are formed of braid yarns (an assembly of fibers) in an interlacing pattern by four-step 1 × 1 method. In the braid process, rows and columns carriers with braid yarns are moved in alternating directions four times to complete one machine cycle as shown in Fig. 1 [2]. Therefore, the microscopic geometry of the composites exhibits periodic behavior. A Representative Volume Cell (RVC) can be chosen to analyze the macroscopic mechanical properties by numerical method, which is a general method adopted by many scholars [3–6]. In addition, the braided composites have complex damage and failure modes due to the complexity of mesoscopic geometrical structure. Except of braid yarn damage modes (longitudinal fiber breakage and transverse matrix cracking) and pocket matrix damage, the damage of interface between braid yarn and pocket matrix is a dominated failure mode either [7, 8].

Fig. 1

Four-step braid process for the braided composites

The literatures regarding the delamination of laminate composites, interfacial debonding of particle reinforced composites and related interfacial crack and damage problems are large. With the rapid development of computation hardware and software, numerical computation is becoming an economical and feasible method for evaluating interfacial crack and damage problems. One popular approach is the Virtual Crack Closed Technique (VCCT) which is performed to calculate the strain energy release rates in conjunction with finite element analysis [9–12]. Such the approach requires complex numerical algorithms to detect the crack tip and release constraints on the duplicate nodes with crack propagation. Therefore, the crack propagation path must be known in advance. In addition, the technique is widespread used to perform the 2D crack propagation problems. Another way to study the interface damage and development is the Cohesive Zone Methods (CZM) which is similar as Barenblatt-Dugdale model in fracture mechanics. The CZM was first proposed by Needleman to model the void nucleation by particle and matrix decohesion [13–15]. Tvergaard proposed a CZM similar as Needleman model to predict the interfacial debonding with any mixture forms by normal and tangential separations [16]. Because the CZM introduces the crack separations and cohesive tractions, the mechanical behavior can be characterized by the traction-separation relations. Therefore, The CZM can avoid the stress singularity at the crack tip in the fracture mechanics. At present, there are a lot of constitutive relations for CZM, such as bilinear, polynomial, sinusoidal and exponential forms. For fiber reinforced composites, Allen et al. [17] predicted the interface cracking and delamination of metal matrix continuous fiber composites by CZM with a nonlinear interface constitutive model. Swaminathan et al. [18] implemented a 3D CZM to study the effect of the fiber-fiber interactions and the orientation and spacing of fibers on the nature of initiation and propagation of interfacial debonding in three-dimensional composite microstructures. It was concluded that the certain combinations of spacing and alignment of fibers in composites layers might delay the onset of damage due to interface damage. Jiang et al. [19] further developed a concise CZM, in which a damage variable was introduced to quantify the extent of accumulated interface damage, to model the mixed-mode delamination propagation of laminate composites. Balzani and Wagner [20] adopted a CZM with exponential and linear constitutive law to simulate the delamination of unidirectional fiber composites. The results indicated that the CZM with exponential form constitutive law could improve the numerical convergence of numerical algorithm. Xie and Waas [21] introduced a discrete CZM with a rod type element in which the stiffness matrix was sparse. In this CZM, the direct nodal displacements were used in the traction-separation laws rather than the interpolated values as in the continuum framework. The results indicated that the approach was not sensitive to the mesh size and the load increment. Recently, Harper and Hallett [22] presented a cohesive zone interface element degradation law to analyze delamination crack propagation of laminate composites under cyclic loading. Numerical results were in good agreement with analytical crack propagation rates under mode I and mixed mode loading. As mentioned above, the CZM is an effective model to evaluate the interface damage and cracking propagation in finite element analysis for 2D and 3D problems in comparison with VCCT. However, the CZM is mainly implemented in laminate composites and particle reinforced composites. For 3D braided composites, the complex mesoscopic damage states of constituents and their interactions need to be recognized in detail. And the interface damage states of yarn/yarn and yarn/matrix within the 3D braided composites are required to be evaluated as well.

In the present paper, the mesoscopic damage modes of constituents within 3D four-directional braided composites are included in mesoscopic damage model to study the effect of mesoscopic damage, especially the interface damage, on the mechanical properties of the braided composites under uniaxial tension. An RVC with interface elements, which are characterized by CZM, is established. Then, the macroscopic stress-strain curve of the braided composites is obtained. And the interface damage development for the braided composites is provided as well. Meanwhile, a parametrical study is conducted to assess the influence of interfacial properties on the mechanical properties of the braided composites with large braid angle. Because the mechanical properties of yarn/yarn and yarn/matrix interfaces are difficult to be obtained by experiments, some interfacial properties are required to be assumed in advance in the computation. However, the trends obtained by the analysis technique can improve our understanding of the effect of interfacial properties.

2 Experiment Analysis

The 3D four-directional braided composites are manufactured by Tianjin Polytechnic University of China. The braid yarn and matrix are 12 K T700 carbon fibers and TDE-86 epoxy resin, respectively. A tensile experiment of the braided composites is conducted to obtain the macroscopic longitudinal tensile stress-strain curve and the fracture behavior. The size of specimen is shown in Fig. 2. H is the thickness of the specimen, which has three types of size 3 mm, 5 mm and 8 mm.

Fig. 2

Geometry size of the specimen

Figure 3 shows the macroscopic tensile stress-strain curve. It can be found that the braided composites with large braid angle (45°) exhibit a little nonlinear characteristic, which can be attributed to the mesoscopic damage of the braided composites. And failure strain appears large, which can exceed 2%. From the macroscopic fracture section of the braided composites as shown in Fig. 4 where the subpicture b) is the enlarged microscopic images of the wireframe part in the subpicture a), it can be observed that several yarns are pulled out in the fracture surface. In addition, some epoxy matrix cracks are appeared in the specimen surface. The results show that the mechanical properties of the braided composites with large braid angle are controlled be several mechanisms, such as fiber breakage, the localization of matrix cracking and damage development of interfacial debonding. These mechanisms can be included in the subsequent mesoscopic computational model in which the mechanical properties of the braided composites will be analyzed by using the finite element simulation of an RVC of the braided composites. The longitudinal breakage and transverse cracking of braid yarns and matrix cracking within the braided composites can be taken into account by introducing a mesoscopic damage model. In addition, the interface debonding of yarn/yarn and yarn/matrix interface within the braided composites can also be modeled by means of interface element whose behavior is controlled by a CZM.

Fig. 3

Macroscopic stress-strain curves of the braided composites

Fig. 4

Tensile fracture photographs of specimen of the braided composites. b is the enlarge microscopic image of the wireframe part in the subfigure (a)

3 Computation Model

3.1 RVC Generation and FE Discretization

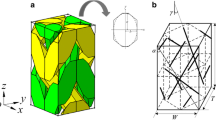
Because the geometrical configuration of the braided composites exhibits periodical characteristic in the micro-scale as shown in Fig. 5a, a smallest RVC can reproduce the geometrical structure of the braided composites when it is piled up periodically. In this paper, an RVC including four braid yarns with different directions, indicated as ABCD in Fig. 5a and shown in Fig. 5b, is chosen from the interior braid structure of the braided composites to analyze their mechanical properties. The cross-section of braid yarn in the RVC is assumed as hexagonal shape to consider the squeezing of braid yarns each other.

Fig. 5

Layout of RVC. a RVC chosen in the periodical geometry structure; b geometry model of RVC; c cross-section of braid yarn

The layout of the RVC is shown in Fig. 5b. The braid angle γ and the height h of the RVC can be measured by microscopic image analysis. The relations of geometrical parameters (shown in Fig. 5c) of the RVC can be expressed as follows:

$$ h = 8b/\tan \gamma $$

(1)

$$ {L_a} = 2b\cos \gamma $$

(2)

$$ {L_b} = 2b - (2a - {L_a})\cos \gamma \quad {L_b} \leqslant 2a \leqslant {L_m} $$

(3)

$$ {L_m} = 4b\cos \gamma $$

(4)

where, the height of cross-section 2a can be determined by K-number (a thousand fiber is counted as 1 K.) of yarn and cross-section area $A = 6{b^2}\cos \gamma - {({L_m} - 2a)^2}/(2\cos \gamma )$. All geometrical parameters of the braided composites are given in Table 1. The properties of constituents within the braided composites are shown in Table 2

Table 1 Geometrical parameters of RVC

Table 2 Material properties of constituents of the braided composites

In order to study the influence of interface properties, many yarn/yarn and yarn/matrix interface elements are established in an RVC as shown in Fig. 6. Figure 6a is the whole FE model of the RVC in which the braid yarns and matrix can be distinguished easily. Figure 6b shows the interface elements between braid yarns and matrix. Due to the complex braid structure of the braided composites, the zero thickness of interface element between braid yarn and matrix is required to avoid the effect on the braid configuration of the RVC. However, these zero thickness interface elements with complex geometry configuration are difficulty to generate by the mature mesh generation tools at present. Therefore, these interface elements are needed to be constructed by some FORTRAN pre-programmed codes combining with mesh generation tools. In the 3D four-directional braided composites, there are two kinds of interface forms: yarn/yarn and yarn/matrix interface elements which can be denoted as Y/Y and Y/M interface elements for convenience. Usually, the interface bonding strengths of the Y/Y and Y/M are different due to the squeezing of braid yarns.

Fig. 6

Finite element model. a a RVC of the braided composites; b interface phase

3.2 Damage Model

When the braided composites are subjected to uniaxial tensile loading, the failure mechanisms of yarns within the braided composites can be categorized into two types: longitudinal (L direction) fiber-matrix shear failure and transverse (in T and Z direction) matrix failure. Therefore, we can introduce two damage indicators, d _L and d _T, to characterize the damage mechanisms of braid yarns. The matrix within the braided composites is recognized as a homogeneous material for simplicity in this paper. Therefore, the damage state of matrix within the braided composites can be characterized by one damage indicator, d _M.

The longitudinal fiber-matrix shear damage initiation criterion in different forms with respect to the positive and negative of stress in the L direction can be expressed as

$$ {f_{\rm{L}}} = \left\{ {\begin{array}{*{20}{c}} {{{\left( {\frac{{{\sigma_{\rm{L}}}}}{{{X_{\rm{L}}}}}} \right)}^2} + \alpha {{\left( {\frac{{{\tau_{\rm{LT}}}}}{{{S_{\rm{L}}}}}} \right)}^2} + \alpha {{\left( {\frac{{{\tau_{\rm{ZL}}}}}{{{S_{\rm{L}}}}}} \right)}^2} \geqslant 1\quad ({\sigma_{\rm{L}}} \geqslant 0)} \hfill \\{\quad \quad \quad \quad \,\,\,{{\left( {\frac{{{\sigma_{\rm{L}}}}}{{{X_{{{\rm{L}} - }}}}}} \right)}^2} \geqslant 1\quad ({\sigma_{\rm{L}}} < 0)} \hfill \\\end{array} } \right. $$

(5)

where, σ _L and τ _LT(ZL) are the longitudinal direct and shear stresses, respectively. X _L, X _L− and S _L the longitudinal tensile strength, compressive strength and shear strength of braid yarns within the braided composites, respectively.

The transverse matrix damage initiation criterion of braid yarns adopts the puck criterion, which can be categorized into two forms with respect to the magnitude of normal stress σ _N. That is

$$ {f_{\rm{L}}} = \left\{ {\begin{array}{*{20}{c}} {{{\left( {\frac{{{\tau_{\rm{T}}}}}{{{S_{\rm{T}}} - {\mu_{\rm{T}}}{\sigma_{\rm{N}}}}}} \right)}^2} + {{\left( {\frac{{{\tau_{\rm{L}}}}}{{{S_{\rm{L}}} - {\mu_{\rm{L}}}{\sigma_{\rm{N}}}}}} \right)}^2} \geqslant 1\,\;({\sigma_{\rm{N}}} < 0)} \hfill \\{{{\left( {\frac{{{\sigma_{\rm{N}}}}}{{{X_{\rm{T}}}}}} \right)}^2} + {{\left( {\frac{{{\tau_{\rm{T}}}}}{{{S_{\rm{T}}} - {\mu_{\rm{T}}}{\sigma_{\rm{N}}}}}} \right)}^2} + {{\left( {\frac{{{\tau_{\rm{L}}}}}{{{S_{\rm{L}}} - {\mu_{\rm{L}}}{\sigma_{\rm{N}}}}}} \right)}^2} \geqslant 1\,\;({\sigma_{\rm{N}}} \geqslant 0)} \hfill \\\end{array} } \right. $$

(6)

where, σ _N, τ _T and τ _L are the normal and shear stresses on the fracture plane of one braid yarn as shown in Fig. 7. X _T, S _T and μ _T(L) are the transverse tensile strength, shear strength and friction coefficient in the failure plane, respectively.

Fig. 7

The transverse compressive failure plane and stress components of braid yarn

It can be found from Fig. 7 that the transverse matrix damage initiation criterion of braid yarn is depended on the fracture plane angle θ. In the present paper, to simplify the complexity of the problem, the transverse shear strength and friction coefficients can be determined as

$$ {S_{\rm{T}}} = {X_{{{\rm{T}} - }}}\cos {\phi_0}\left( {\sin {\theta_0} + \frac{{\cos {\theta_0}}}{{\tan 2{\theta_0}}}} \right) $$

(7)

$$ \tan (2{\theta_0}) = - \frac{1}{{{\mu_{\rm{T}}}}} $$

(8)

$$ \frac{{{\mu_{\rm{L}}}}}{{{S_{\rm{L}}}}} = \frac{{{\mu_{\rm{T}}}}}{{{S_{\rm{T}}}}} $$

(9)

where, X _T− is the transverse compressive strength of braid yarn. θ ₀ is the angle of fracture plane in pure compression of unidirectional fiber composites. The typical values of θ ₀ are in the range of 50°–60°[8]. In the present study, the value of angle θ ₀ equals 53°. Therefore, only the stress components, σ _N, τ _T and τ _L, are changed with the variation of θ in the Eq. 6. And the fracture plane angle θ can be found to make the value of f _T attain the maximum.

The damage initiation criterion of matrix within the braided composites can adopt the maximum principle stress criterion which can be expressed as

$$ {f_{\rm{M}}} = {\left( {\frac{{{\sigma_{{\max }}}}}{{X_{\rm{M}}^{\rm{t}}}}} \right)^2} \geqslant 1 $$

(10)

where, σ _max is the maximum principle stress of matrix of the braided composites.

In order to utilize the Murakami-Ohno damage theory, the damage variables d _L and d _T of braid yarn should be associated with the damage variables Ω_L, Ω_T, Ω_Z in the direction of L, T, Z which can be written as

$$ \begin{array}{*{20}{c}} {{\Omega_{\rm{L}}} = {d_{\rm{L}}}} \\{{\Omega_{\rm{T}}} = {d_{\rm{T}}}\cos \theta } \\{{\Omega_{\rm{Z}}} = {d_{\rm{T}}}\sin \theta } \\\end{array} $$

(11)

The matrix damage variable d _M also can be extended to the damage variables Ω_L, Ω_T, Ω_Z in the direction of L, T, Z, that is

$$ {\Omega_{\rm{L}}} = {\Omega_{\rm{T}}} = {\Omega_{\rm{Z}}} = {d_{\rm{M}}} $$

(12)

To improve the convergence of the numerical algorithm, an artificial Duvaut-Lions viscous model [23, 24] is used. The damage variables Ω_I(I = L, T, Z) can be regularized as

$$ {\dot{D}_{\rm{I}}} = \frac{1}{{{\eta_{\rm{I}}}}}({\Omega_{\rm{I}}} - {D_{\rm{I}}})\quad {\hbox{I}} = ({\hbox{L}},{\hbox{T}},{\hbox{Z}}) $$

(13)

here, η _I and D _I are viscous parameter and regularized damage variable of damage mode I, respectively.

The evolvement of damage variables (d _L, d _T and d _M) and Murakami-Ohno damage model can be documented in Ref. [25]. The damage evolvement model is controlled by element characteristic length, material fracture energy of braided composites constituents, equivalence displacements. The equivalence displacements and equivalence stresses of the damage variables (d _L and d _T) can be constructed in the forms as listed in Table 3

Table 3 The equivalence displacements and stresses corresponding to different failure modes

The progressive interface debonding can be simulated by 3D 6-nodes isoparametric linear interface elements (COH3D6 in ABAQUS/Standard [23]). The interface constitutive behavior can be described by the traction-separation law which is associated with three tractions (σ _n , σ _s1, σ _s2) and corresponding separations (δ _n , δ _s1, δ _s2), one normal and two shear components. The initial traction-separation law of the interface elements without damage keeps the linear characteristic, that is

$$ {\sigma_n} = K{\delta_n},\quad {\sigma_{{s1}}} = K{\delta_{{s1}}},\quad {\sigma_{{s2}}} = K{\delta_{{s2}}} $$

(14)

here, K is the elastic stiffness of the interface which is difficult to be measured in experiment. In order to ensure the displacement continuity at the interface and to reduce the modification of the stress distribution around the braid yarn, a large magnitude of elastic stiffness of the interface should be chosen appropriately. The elastic stiffness equals 10⁷ GPa/m chosen in this paper. With the increase of the external loading, the response of the interface does not keep linearity. The onset of interface damage is judged by the quadratic nominal stress criterion, which can be expressed as

$$ {\left\{ {\frac{{ < {\sigma_n} > }}{N}} \right\}^2} + {\left\{ {\frac{{{\sigma_{{s1}}}}}{S}} \right\}^2} + {\left\{ {\frac{{{\sigma_{{s2}}}}}{S}} \right\}^2} \geqslant 1 $$

(15)

where, N and S are the normal and tangential strength of the interface, respectively. For simplicity, it is assumed that N is equal to S in the present study. <σ _n > is equal to $({\sigma_n} + \left| {{\sigma_n}} \right|)/2$ to neglect the contribution of normal compressive stress to the interfacial initial damage. An interface damage indicator, d_i, is introduced to measure the extent of interface damage. Therefore, the traction-separation law of the interface with damage will become

$$ \begin{array}{*{20}{c}} {{\sigma_n} = K(1 - {d_{\rm{i}}}){\delta_n},\quad ({\sigma_n} \geqslant 0)} \\{{\sigma_n} = {K_n},\quad ({\sigma_n} < 0)} \\{{\sigma_{{s1}}} = K(1 - {d_{\rm{i}}}){\delta_{{s1}}}} \\{{\sigma_{{s2}}} = K(1 - {d_{\rm{i}}}){\delta_{{s2}}}} \\\end{array} $$

(16)

The development of the interface damage variable d _i can be constructed to be associated with the equivalence displacement, which can be written as

$$ {d_{\rm{i}}} = \frac{{{{\bar{\delta }}_f}(\bar{\delta } - {{\bar{\delta }}_0})}}{{\bar{\delta }({{\bar{\delta }}_f} - {{\bar{\delta }}_0})}} $$

(17)

where, $\bar{\delta }$ is the equivalence displacement. ${\bar{\delta }_0}$ and ${\bar{\delta }_f}$ are the equivalence displacements corresponding to initial damage and final failure of interface, respectively. The equivalence displacement $\bar{\delta }$ can be defined as

$$ \bar{\delta } = \sqrt {{ < {\delta_n}{ >^2} + {\delta_{{s1}}}^2 + {\delta_{{s2}}}^2}} $$

(18)

The variation of traction-separation law of interface with equivalence displacement is provided in Fig. 8. In this cohesive model, the interface fracture energy regardless of the loading history keeps a constant when the interface is completely cracking. If not indicated otherwise, the interface fracture energy in the simulations presented below is 75 J/m².

Fig. 8

The traction-separation law of damage of interface element

4 Numerical Results and Discussion

4.1 The Influence of Interface Strength and Energy

In order to study the influence of the interface strength of Y/Y and Y/M on the properties of the braided composites, the following discussion can be divided into three cases. In Case 1, the damage model of braid yarn and matrix is not added in the computation. Yarn and matrix within the RVC all keep linear characteristic. However, the computation model includes the interface damage of Y/Y and Y/M. And the interface strength of Y/Y and Y/M with the same values varies from c/3 to 5c/3 $(c = X_{\rm{M}}^{\rm{t}} = 80{\hbox{MPa}})$. In Case 2, the numerical model not only takes into account the damage of braid yarn and matrix but also includes the interface damage of Y/Y and Y/M with the same interface strength which changes from c/3 to 8c/3. In Case 3, the damage states of braid yarn, matrix, Y/Y interface and Y/M interface are also all considered in the numerical model as well. The variation of interface strength of Y/M is from c/3 to 8c/3 in the numerical model, while the interface strength of Y/Y with a constant value is equal to 3c.

Figure 9 displays the influence of the interface strength on the uniaxial tensile mechanical behavior of the 45° braided composites in Case 1. It can be found that the initial stiffness is not affected by the interface strength, but the stress-strain curve of the composites with low interface strength departs early from initial linearity due to interface debonding. When the interface debonding approaches some extent, the stress-strain curve becomes linear again. It also can be concluded that the interfacial properties do not obviously control the failure of the braided composites with large braid angle which can be attributed to the development of all damage modes with increase of macro strain.

Fig. 9

The influence of interface strength on the stress-strain curve of the braided composites

Figure 10 shows the effect of interface strength on the tensile mechanical properties of the braided composites in the Case 2 and Case 3. It can be found that the trend of predicted stress-strain curves in Fig. 10a and b is significantly different from that shown in Fig. 10c–h. The interface strength in Fig. 10a and b is lower than the matrix strength, namely weaker interface. The weaker interface easily produces damage when the RVC is subjected to the uniaxial tension. With the development of interface damage, the ability of stress transfer of interface will be decreased. Thus, the braid yarns within the RVC will be difficult to emerge damage. With the increase of macro strain, the braid yarns still have the loading capacities to result in the stress-strain curves with the upward trend. Eventually, the numerical computation ends due to the lower convergence rate. With the increase of interface strength, the damage of braid yarns and matrix within the RVC occurs gradually when the interface appears damage. With the increasing load, the macro stress-train curves all appear the downward trend. When the interface strength increases to a certain level, the interface damage may occurs later than the damage of braid yarn and matrix or even does not emerge during the applied loading. It also can be found from Fig. 10 that the stress-strain curve obtained in the Case 2 has some difference in comparison with that obtained in the Case 3 with same interface strength. When the interface strength is equal to the matrix strength, the strength of stress-strain curve obtained in the Case 2 is lower than that obtained in the Case 3. And the stress-strain curve emerges nonlinearity earlier in the Case 2 as shown in Fig. 10c. However, when interface strength is equal to 4c/3, 5c/3, 2c, 7c/3 and 8c/3 as shown in Fig. 10d–h, the strength of stress-strain obtained in Case 2 is higher than that obtained in the Case 3. And with the increase of the interface strength, the stress-strain curve of Case 2 is closer to that obtained in the Case 3 gradually. These phenomena can be attributed to the interface damage which can delay the damage of braid yarns and matrix within the RVC happened. In addition, the overall trend of predicted stress-strain curve is controlled by the interaction of braid yarn damage, matrix damage and interface damage.

Fig. 10

The comparison stress-strain curves of Case 2 and Case 3. a c/3; b 2c/3; c c; d 4c/3; e 5c/3; f 2c; g 7c/3; h 8c/3

Figure 11 is the effect of interface fracture energy on the unidirectional stress-strain curves of the 45° braided composites. Three interface fracture energies: 75 J/m², 7.5 J/m², 0.75 J/m² are adopted in the simulation, while the interface strength of Y/Y and Y/M is equal to c and remains unchanged. The fracture energy can modify the equivalence displacement at failure, ${\bar{\delta }_f}$ as shown in Fig. 8. The equivalence displacement at failure increases with the increase of the fracture energy. Therefore, the interface of Y/Y and Y/M will become brittle when the fracture energy is a smaller value. It can be found as shown in the Fig. 11 that the magnitude of the interface fracture energy is almost not affected the variation of stress-strain curve when the interface fracture energy is varied from small to large. It can be explained that the interface still keeps brittle when it reaches 75 J/m².

Fig. 11

The influence of interface fracture energy on the stress-strain curve of the braided composites

4.2 The Damage Development of the Braided Composites

To study the damage development and interaction of damage modes of the braided composites, all the damage modes mentioned in Section 3.2 are taken into account in the computation. And the interface strength in the simulations presented below is equal to c. Figure 12 shows the predicted stress-strain curve in comparison with the experimental results of the 45° braided composites. It can be found that the initial slope of the predicted stress-strain curve is lower than that obtained by the experimental results. In addition, the predicted results more approach the experiment results which are obtained by the specimen with the thickness 8 mm. That is because the RVC utilized in the simulation is only the inner structure of the braided composites. In fact, the specimens of the braided composites have other mesoscopic structures which locate in the surface and corner of the specimens. When the thickness of specimen increases, the percentage of inner structure will increase as well. Therefore, the simulated results will have in good agreement with the experimental results obtained by the thicker specimen.

Fig. 12

Predicted stress-strain curve comparing with experimental results

Figure 13 gives the variation of damage initiation and failure element percentages of braid yarn, matrix and interface elements of the 45° braided composites with the macro strain. It is noted that the element percentage of braid yarn (matrix or interface) is the ratio of damage initiation (d _L, d _T, d _M and d _i ≥ 0) or failure element numbers (d _L, d _T, d _M and d _i ≥ 0.98) of braid yarn (matrix or interface) to the whole element numbers of braid yarn (matrix or interface) within the RVC. As shown in Fig. 13, the damage initiation points of braid yarn and matrix pockets, respectively, are observed at 1.2% ε and 1.7% ε, while the damage initiation point of interface element appears at 0.2% ε. When the value of macro strain approaches 1.2% ε, the failure element percentages of Y/Y and Y/M have reached 27% and 15%, respectively. It also can be found that the slope of the macroscopic stress-strain curve degrades obviously as shown in Fig. 13 when the strain reaches 1.05% ε. Therefore, the initial nonlinearity of the stress-strain curve can be attributed to the interface damage of Y/Y and Y/M of the braided composites. With the increase of the macro strain, the damage of braid yarn and matrix pockets is emerged and developed. And the nonlinearity of stress-strain curve becomes more and more obvious. When the value of macro strain approaches 2.3% ε, the interface damage and failure element percentages all have been larger 80%. After the macro strain reaches the 3.005% ε, the macro stress starts to decline gradually. And the damage of braid yarn continues increase. The descending reason of the stress-strain curve is due to the interaction of matrix pockets damage, transverse damage of braid yarn and interface damage. It can be concluded that the fiber-matrix damage control the failure of the braided composites with big braid angle. Figure 14 is the interface damage development of the RVC at the points of the macro strain 0.5% ε, 1.05% ε, 1.5% ε, 2.025% ε, 2.512% ε and 3.005% ε. It can be observed that the debonding areas are mainly distributed in the yarn/yarn interfaces and the yarn/matrix interfaces whose normal directions with respect to the tensile direction are all close to 45°. When the strain reaches 2.025% ε, the slope of the macroscopic stress-strain curve degrades again as shown in Fig. 13. In addition, the damage of interfacial has reached the saturated state as shown in Fig. 14d. It can be concluded that the interface debonding is the direct reason to induce the nonlinearity of the braided composites with large braid angle.

Fig. 13

The variation of damage and failure element percentages with the strain history for the 45° braided composites

Fig. 14

Damage development of interface within the RVC

5 Conclusions

A Representative Volume Cell (RVC) with interface elements is established to study the effect of interfacial properties of yarn/yarn and yarn/matrix on the uniaxial tensile stress-strain curves of the 3D four-directional braided composites with large braid angle. The interface mechanical properties are characterized by a Cohesive Zone Model (CZM). The macroscopic stress-strain curve of the 45° braided composites is obtained. The interaction and damage development of braid yarn damage, matrix damage and interface damage is provided as well. The results show that the interface damage is one of factors to cause the nonlinearity of stress-strain relation. The interface strength is one of main parameters to influence the interface damage. It is noted that the interface behavior of yarn/yarn and yarn/matrix within the braided composites should be studied by experimental method further.