1 Introduction

With the increasing requirements of energy efficiency and environment protection, composite materials have become an attractive alternative to traditional materials because of the advantages of low density, high strength, high stiffness to weight ratio, excellent durability, and design flexibility.

The coefficients of thermal expansion (CTE) of fibre reinforced composites are very important parameters in the design and analysis of composite structures. Since the CTE of polymer matrix are typically much higher than those of fibres, and the fibres often exhibit anisotropic thermal and mechanical properties, the stress induced in composites due to temperature change is very complex.

For the purpose of calculating the CTE of unidirectional composites, analytical models have been developed by simple rule of mixtures to thermoelastic energy principles. When different models for the transverse CTE are compared, large discrepancies exist. Which model to use becomes a question. Bowles and Tompkins [1] critically reviewed some of the analytical models. These models were compared with the experimental measurements and finite element analysis. Islam et al. [2] studied the linear thermal expansion of unidirectional composites using the finite element method. Karadeniz and Kumlutas [3] performed finite element analysis using a representative unit cell and compared several analytical models.

This study aims to clarify the discrepancies among different models for the transverse CTE of composites and provide a more convenient model. First, the transverse CTE of unidirectional carbon fibre composites were calculated by finite element analysis using a representative unit cell. Second, the analytical micromechanical models from literature were reviewed by comparing with the FEA data. Finally, by using FEA, Design of Experiments, and Response Surface Method, a simple model for predicting the transverse CTE of unidirectional carbon fibre composites was developed. The model was validated against the data from reference and it shows that the accuracy is satisfactory.

2 Comparison of Micromechanical Models and Finite Element Analysis

2.1 Review of Micromechanical Models

As a starting point, a number of analytical micromechanical models for calculating the transverse CTE of composites from literature were reviewed. These models, as summarised in Table 1, were based on the assumption of perfect bonding existing between fibre and matrix.

Table 1 Analytical micromechanical models for transverse CTE of composites
Full size table

The rule of mixture [4] was developed without considering any phase interaction. Schapery model [5] was based on the simple planar model of alternating fibre and matrix strips. The modified strip model [6] was developed based on Schapery model by introducing the constraint effects from thermal expansion and Poisson’s ratio mismatch of fibre and matrix. Chamis model [7] was developed based on a simple force-balance. Hashin’s concentric cylinder model [8] was developed from a cylinder assemblage model. Scheneider model [6] was also developed from a cylinder assemblage model and is often cited in German literature. Geier model [6] is also often cited in German literature. Chamberlain model [9] was developed using plane stress thick walled cylinder equations for the case of transversely isotropic fibres embedded in an isotropic cylindrical matrix. Among these models, Schapery model and Chamis model are taken to be an upper bound and lower bound, respectively.

2.2 Finite Element Analysis

With the development of computer technologies, the CTE of composites were also studied numerically by finite element analysis. FEA has been proved to offer better accuracy than analytical models. Thus, in this study, the CTE of composites of composites were calculated by FEA using a representative unit cell. The finite element formulation assumes that a condition of generalised plane strain exists in the unidirectional composites.

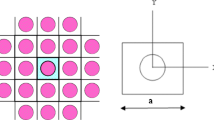
Fibres in a bundle can be in either hexagonal array or square array. The representative unit cells for these two arrays were constructed as shown in Fig. 1. The size of the unit cell was determined as per the fibre volume fraction. With reference to Fig. 1, for hexagonal array, the width of unit cell a is given by

$$a = \sqrt {\frac{\pi }{{2\sqrt 3 V_f }}} d$$
(1)

and the height of unit cell is\(\sqrt {3a} \).

Fig. 1
figure 1

Construction of a representative unit cell. Left: hexagonal array; right: square array

Full size image

For square array, the size of unit cell is given by

$$a = \sqrt {\frac{\pi }{{V_f }}} \frac{d}{2}$$
(2)

where d is the diameter of fibre.

Three dimensional steady state analyses were conducted to calculate the effective coefficients CTE using the unit cells constructed for both hexagonal array and square array of different fibre volume fractions. A commercial FEA package MSC. Marc Mentat was employed in this study. By applying symmetric boundary conditions, only one quarter of the unit cell was modelled in FEA. The initial grid size was 0.5 μm. When the fibre volume fraction is 50%, the meshes for the unit cells are as shown in Fig. 2.

Fig. 2
figure 2

Meshes for the unit cells at 50% fibre volume fraction

Full size image

The boundary conditions used in FEA are as follows: along the planes x, y, and z = 0, the model was restricted to move in the x, y, and z directions, respectively. Along the opposite planes, the periodic boundary conditions were applied, which were achieved by defining links in MSC.Marc Mentat. The model underwent a unit temperature drop. The displacements in the x, y, and z directions were obtained respectively. The transverse CTE of the composite is derived from the original dimension in the x direction l x and the displacement in the x direction Δl x as

$$ \alpha _{{22}} = \frac{{\Delta l_{x} }} {{l_{x} \Delta T}} $$
(3)

As an example, AS4 graphite/epoxy composites were studied. The properties of AS4 graphite fibres were taken from [10]. The properties of epoxy were experimentally measured by Dynamic Mechanical Analysis (DMA) and Thermal Mechanical Analysis (TMA). These data are as shown in Table 2.

Table 2 Material properties of AS4 fibres and epoxy matrix
Full size table

The fibre volume fractions studied were from 1% to the maximum (90.69% for hexagonal array and 78.54% for square array).

First, the grid convergence was studied. For the hexagonal array of the maximum fibre volume fraction, the FEA was conducted using the original mesh and the refined mesh, as shown in Fig. 3. The relative difference is approximately 0.09%. Thus, sufficient accuracy had been met.

Fig. 3
figure 3

Mesh refinement for grid convergence study

Full size image

2.3 Results and Discussion

The transverse CTE of AS4/epoxy composites in hexagonal and square arrays calculated from FEA are shown in Fig. 4.

Fig. 4
figure 4

Transverse CTE of AS4/epoxy composites calculated assuming hexagonal and square arrays

Full size image

The transverse CTE in hexagonal and square arrays are in good agreement, except at the maximum fibre volume fraction of square array. For higher fibre volume fractions, it is more reasonable to assume hexagonal array.

With the assumption of hexagonal array, the transverse CTE of AS4/epoxy composites were calculated using the analytical micromechanical models and FEA, respectively. The results are as shown in Fig. 5. For better presentation, the relative difference of each micromechanical model from the FEA ε M was also calculated.

$$\varepsilon _M = \frac{{\alpha _{22M} - \alpha _{22FEA} }}{{\alpha _{22FEA} }}$$
(4)

where α 22M and α 22FEA are the CTE calculated using any analytical model, e.g. rule of mixture, and FEA, respectively.

Fig. 5
figure 5

Transverse CTE of AS4/epoxy composites calculated using various micromechanical models and FEA

Full size image

The relative differences at three different fibre volume fractions 30%, 50%, and 70% are as shown in Fig. 6. For all fibre volume fractions, Chamis model and Chamberlain model give much lower CTE than the FEA. These large differences were attributed to the Poisson restraining effects which were not included in these two models [1]. The CTE calculated by the rule of mixture and Schneider model are lower than those by FEA. Schapery model gives the highest CTE. Geier model gives the second highest CTE. At lower fibre volume fractions, Hashin’s concentric cylinder model gives the best results and at higher fibre volume fractions, the modified strip model gives the best results. Overall, Hashin’s concentric cylinder model best matches the FEA data.

Fig. 6
figure 6

Relative differences of micromechanical models and FEA at three different fibre volume fractions 30%, 50%, and 70%

Full size image

3 Model Development

Our study has already shown that Hashin model is the best. However, the calculating process of Hashin model is very complicated and inconvenient for practical applications. In this study, a simple micromechanical model for calculating the transverse CTE of composites was developed using FEA, Design of Experiments, and Response Surface Method.

3.1 Screening Design

First, a screening design was conducted to uncover the individual contributions to the transverse CTE. A factorial design was conducted to identify the significant factors. With reference to [1], the factors affecting the transverse CTE to be investigated were chosen to be E fT , α fT , E m , α m , and ν m . Fibre reinforced composites are constituted by two distinct material phases: fibre and matrix. Based on dimensional analysis, dimensionless variables E fT /E m , α fT /α m , and ν m were derived and thus the number of variables being investigated was significantly reduced. Accordingly, the dimensionless transverse CTE was α 22/α m . The elastic modulus of matrix were fixed at 2,581 MPa and 64 × 10−6/°C. The ranges of E fT and α fT were chosen so that most carbon fibres were included. ν m was varied between 0.2 and 0.4. The levels for each variable are as shown in Table 3.

Table 3 Levels of variables to be investigated
Full size table

The micromechanical model was assumed to be in the form as follows.

$$\alpha _{22} = \alpha _m \left( {1 + \nu _m } \right) + \left[ {\alpha _{fT} - \alpha _m \left( {1 + \nu _m } \right)} \right]f\left( {V_f } \right)$$
(5)

where f(V f ) is a function of V f to be determined.

Eq. (5) can be rewritten as

$$f\left( {V_f } \right) = \frac{{\alpha _{22} - \alpha _m \left( {1 + \nu _m } \right)}}{{\alpha _{fT} - \alpha _m \left( {1 + \nu _m } \right)}}$$
(6)

For each variable combination, the transverse CTE were calculated by FEA. The data were converted into f(V f ) using Eq. (6). As shown in Fig. 7, f(V f ) can be represented by a non-linear function of V f , i.e.

$$f\left( {V_f } \right) = a_0 V_f^{a_1 } $$
(7)

Coefficients a 0 and a 1 were chosen as the responses.

Fig. 7
figure 7

f(V f ) vs. V f

Full size image

A full 23 factorial design with three centre points were chosen. The complete data are as shown in Table 4.

Table 4 Result from factorial design
Full size table

The data were analysed using Design-Expert software. The percentage contribution of each term for a 0 and a 1 is as shown in Fig. 8. For both a 0 and a 1, the significant factors are E fT /E m and ν m . a 0 increases with E fT /E m and decreases with ν m ; a 1 increases with ν m and decreases with E fT /E m . The ANOVA also indicates that significant curvature exists, which means that a linear model might not be sufficient.

Fig. 8
figure 8

Percent contribution of terms

Full size image

3.2 Response Surface Method

The result from the screening design shows that α fT /α m is an insignificant variable so that only E fT /E m and ν m were used in the further analysis. When a linear model is not sufficient, a second-order response surface model needs to be developed. One effective way to develop such a model is the Central Composite Design (CCD). First, the previous screening design was reorganised into a 22 design with two replicates and three centre points. The design was then augmented by adding eight axial runs and two additional centre points, as shown in Table 5 .

Table 5 Additional runs for central composite design
Full size table

Based on the data as shown in Tables 4 and 5, regression models were developed for a 0 and a 1. Due to the non-linearity, the models were assumed to in the following form.

$$\matrix {a_0 = b_0 \left( {{{E_{fT} } \mathord{\left/ {\vphantom {{E_{fT} } {E_m }}} \right. \kern-\nulldelimiterspace} {E_m }}} \right)^{b_1 } \nu _m^{b_2 } } \\ {a_1 = c_0 \left( {{{E_{fT} } \mathord{\left/ {\vphantom {{E_{fT} } {E_m }}} \right. \kern-\nulldelimiterspace} {E_m }}} \right)^{c_1 } \nu _m^{c_2 } } \ $$

By using LSE, the final regression model was fitted as

$$\alpha _{22} = \alpha _m \left( {1 + \nu _m } \right) + \left[ {\alpha _{fT} - \alpha _m \left( {1 + \nu _m } \right)} \right]0.96\left( {{{E_{fT} } \mathord{\left/ {\vphantom {{E_{fT} } {E_m }}} \right. \kern-\nulldelimiterspace} {E_m }}} \right)^{0.013} \nu _m^{ - 0.036} V_f^{1.24\left( {{{E_{fT} } \mathord{\left/ {\vphantom {{E_{fT} } {E_m }}} \right. \kern-\nulldelimiterspace} {E_m }}} \right)^{ - 0.053} \nu _m^{0.20} } $$
(8)

3.3 Model Validation

The developed model was validated against FEA and experimental data presented by Bowles and Tompkins [1]. Six different composite material systems were used, as shown in Table 6 . The properties of constituents can be found in [1]. The CTE predicted using the current model presented in this paper were compared against the FEA and experimental data, as shown in Fig. 9.

Fig. 9
figure 9

Comparison of current model, FEA and experimental data

Full size image
Table 6 Material systems used for model validation
Full size table

It shows from Fig. 9 that the CTE calculated using the current model is in excellent agreement with the FEA results (within 1%). They are in reasonably good agreement with the experimental data.

3.4 Model Extrapolation

Although the presented model was developed for carbon fibre composites, it was extrapolated to S-glass/epoxy composites. In this case, E fT /E m  = 56.18. The predicted CTE is compared with the FEA data as shown in Fig. 10.

Fig. 10
figure 10

Comparison of current model and FEA data for S-glass/epoxy composites

Full size image

It shows this developed model still provides reasonable accuracy (within 15%), which proves its physical validity. To improve the accuracy, the model development process can be repeated and a new model can be developed for glass fibre composites.

4 Conclusions

A model for predicting the transverse coefficients of thermal expansion for carbon fibre composites is presented in this paper. The transverse CTE were calculated by finite element analysis using a representative unit cell. The analytical micromechanical models from literature were reviewed by comparing with the FEA data. It shows that overall Hashin model provides the best accuracy. However, the calculating process of Hashin model is very complicated and inconvenient for practical applications. By using FEA, Design of Experiments, and Response Surface Method, the transverse CTE of unidirectional carbon fibre composites were studied and a regression-based model was developed. The model was validated against the FEA and experimental data. It shows that the developed model offers excellent accuracy while reduces complicated computation process. The advantage of this model is that it provides a simple and accurate method for predicting the transverse CTE of composites, which helps effective and efficient design of composite structures.