Introduction

The structural organization of the artery wall and its mechanical behavior has been the object of research for a long time. Arteries are key parts of the circulatory system in terms of feeling the blood flow features and supplying the extra pressure needed to transport nutrients to the organs and tissue. Therefore, cardiovascular diseases can affect or even destroy the normal workings of the organism. For this reason the study of the arteries, whether from a biological or a mechanical point of view, has gained so much attention. What may be described as the normal behavior of materials, as a purely mechanical response to a stimulus, is only a small part of the biological tissue behavior. They undergo damage11 and viscoelastic effects,32 like many conventional materials (rubbers, steel, aluminum etc.). But they also constitute a very active component where chemical reactions, cell synthesis and apoptosis, growth,23,27,28 remodeling,7,22,29 creation of atheroma plaque25 etc., are involved in their response.

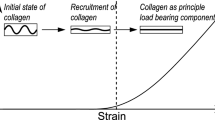
Arteries are made up of four main components and have a clear composite-like structure.14 They are made of collagen, elastin, smooth muscle cells (SMC), and water. SMC are responsible for the so called myogenic tone and react mechanically to external stimuli by contracting or dilating the vessel. Collagen exhibits high non-linear behavior bearing the major part of the load transmitted through the tissue. A great deal of research has been devoted to understanding its hierarchical microstructure at and across different scales (see Ref. 13 for a review). Its highly non-linear behavior causes the arterial wall to “block” under large deformation, preventing damage to the tissue. Elastin has important flexibility and extensibility features for blood vessels and endows the ECM with resilience during the loading of the cardiac cycle. The elastic fibers are randomly packed, forming sheets.

The arterial wall has three differentiated layers called intima, media and adventitia.5 In most arteries, SMC are placed in the media layer and bundles of collagen fibers are placed along the SMC. The adventitia is made up of collagen in a more randomly packed fashion. Fibroblasts are also an important component of the adventitia and are mainly the responsible for the synthesis of collagen. O’Connell et al.31 shows a nice reconstruction of a rat aorta artery (see Fig. 1).

Figure 1
figure 1

Microstructural representation of aortic medial lamellar unit in rats31 (with permission)

Full size image

Based on these observations, research has investigated different phenomenological models to capture the behavior of arterial tissue (see e.g. Refs. 9, 15, 19, among others). Usually, elastin is modeled as a Neo-Hookean model while collagen is commonly modeled by exponential-type expressions, given the mechanical response of collagen fibers.

Although these phenomenological models reproduce very nicely some types of tissues or arteries, others do not fit so well. In some situations, although they reproduce the mechanical behavior, the fitted parameters do not have physical meaning or they do not match with some experimental observations. The micro-structural characterization of its components, both in terms of organization and mechanical behavior, can help to achieve a more realistic constitutive modeling of soft tissue.

The carotid artery has been widely studied because it is prone to develop atherosclerosis, stenosis, remodeling, etc. An extensive range of experimental results relating to the carotid artery can be found in the literature. However, these studies tend to be focused on a specific aspect of the tissue, using different species (human, pig, dog), etc. Some studies rely on the mechanical properties of the wall using uniaxial or inflation tests. Others also present values of the residual stresses of the carotid. However there are few cases where a complete characterization of the tissue is performed for a specific study. Therefore, researchers have to rely on different studies using different samples, species, etc. Here, two studies17,35 are reviewed that, in our view, present the most complete set of experimental tests.

In this work, the mechanical behavior and structural organization of carotid arteries are studied in order to overcome some limitations of previous models and to describe more accurately the features of the arterial wall. We start by describing the basic kinematics and elasticity of arterial tissue. Two previous experimental data and hyperelastic models are reviewed before suggesting an approach that improves previous limitations and drawbacks. Finally, a real human carotid geometry is reconstructed as well as its internal organization. We introduce our new model with which the geometry can be simulated within a finite element framework.

Baseline Elasticity

We start by recalling some basic notions of the kinematic assumption. The deformation gradient is the tangent of the motion and represents a two-point linear map over the reference configuration. Based on the motion \(\phi \) the deformation gradient is defined as \({\mathbf {F}} = \nabla _{\mathbf {X}} \varvec{\phi }\) and the right Cauchy Green tensor as \({\mathbf {C}} = {\mathbf {F}}^{\mathrm{t}} \cdot {\mathbf {F}} \). The Jacobians of the deformation gradient will be denoted as \(J = \text{ det } ({\mathbf {F}})\).

The quasi-incompressibility of the tissue is modeled based on the so called volumetric-isochoric decomposition of the deformation gradient, which was first proposed by Flory.12 The deformation gradient F is decoupled into dilatational and volume-preserving part as \(\mathbf {F}=\text {J}^{1/3}\bar{\mathbf {F}}\). We use the prefix isochoric to describe any term affected by the volume-preserving part \(\bar{\mathbf {F}}\). In connection with this description and with the treatment of highly non-linear materials, the use of finite hyperelasticity is a convenient framework. Constitutive theories in the context of hyperelasticity rely on the definition of a Helmmholtz strain energy function (SEF) in its material description \(\Psi (\mathbf {C})\). For the particular definition of a SEF for soft biological tissue, we write \(\Psi =\Psi_{\text{vol}}(J)+\Psi _{\text{ich}}(\bar{\mathbf{C}})\). \(\Psi_{\text{vol}}\) is related with the water content in the cardiovascular tissue. The second term is associated with the isochoric contribution of the deformation gradients.

Following the Clausius–Plank inequality, the momentum fluxes can be obtained by derivation of the SEF with respect to its associated strain measure (see, e.g., Refs. 18, 26 for more details). We can obtain

$$\begin{aligned} {\mathbf {S}=}2\partial_{\mathbf {C}} \Psi ={\mathbf{S}}_{\text{vol}}{\mathbf(J)}+{\mathbf{S}}_{\text{ich}}(\bar{\mathbf{C}}). \end{aligned}$$
(1)

The tangent modulus, a quantity that relates incremental stresses and strains, is essential for a consistent finite element implementation. We evaluate the total derivative of \(\mathbf {S}\) with respect to \(\mathbf {C}\) and we split it again into volumetric-isochoric terms

$$ \begin{aligned} {\boldsymbol{\mathsf{C}}} = 2d_{\mathbf{C}}{\mathbf{S}}={\boldsymbol{\mathsf{C}}}_{\text{vol}}({\mathbf{J}})+{\boldsymbol{\mathsf{C}}}_{\text{ich}}(\bar{\mathbf{C}}). \end{aligned}$$
(2)

Constitutive Modeling of Arterial Tissue

It is common to split the isochoric part of the SEF into an isotropic part, associated to the elastin, and an anisotropic part, associated to the collagen fibers as \( \Psi_{\text{ich}}(\bar{I}_1,\bar{I}_4) = \Psi_{\text{iso}}(\bar{I}_1)+ \Psi_{\text{ani}}(\bar{I}_4)\). The elastin, which is usually described with an isotropic behavior, was described with a Neo-Hookean model as \(\Psi _\text {iso}(\overline{I}_1)=C_{10}[\overline{I}_1-3]\), where \(C_{10}\) is a stress-like parameter, \(\overline{I}_1=tr \overline{\mathbf {C}}\) and \(\overline{I}_4=\overline{\mathbf {C}}:\mathbf {N}\) is the first and fourth invariant of the isochoric part of the deformation, respectively. The anisotropic part of the SEF is described below.

Previous Pig Carotid Artery Experiments and Fitting

Before proposing the model, the experimental results of Garcia et al.17 are reviewed. They used pig carotid arteries in their studies to perform uniaxial tests in both longitudinal and circumferential directions of the vessel to find the material parameters. They focused on the proximal and distal sides of the common carotid artery (CCA). For the description of the collagen fibers, they adopted the exponential-type model.19 This model represents a symmetric helicoidal distribution of the fiber within the vessel thickness.

The fitting of material parameters using exclusively macroscopic information could result in values that could not have a real interpretation. For example, the fitted fiber orientation could not match with the real distribution of the fibers. This is a common problem of ill-posed problems. A non-constraint minimization problem is prone to such non-uniqueness of the results. To this end, some limitation to the optimization problem should be provided. To obtain extra information, Garcia16 also performed polarized light microscopy studies in order to find the preferential direction of the collagen fibers as well as a statistical dispersion of those fibers. For the visualization of the collagen fibers, Picrosirius red staining with the polarization method enhances the light intensity due to the birefringence of the collagen.4,20 Garcia16 found that collagen fibers are located in a circumferential direction for both the distal and proximal location. Using the information of the fiber direction an acceptable fitting result was not achieved as shown in Fig. 2.

Figure 2
figure 2

Experimental data and fitting results performed by Garcia16 considering orientation distribution recovered by polarized light microscopy. Error values were \(\epsilon =0.1419\) and \(\epsilon =0.0621\) for the proximal and distal specimens respectively

Full size image

It was only possible to fit the experimental curves when considering the angle of the fibers to be variable although this did not match the microstructural organization that was found in the polarized light experimental data. Therefore, there must have been something missing in the approach that the authors used. This could be because the chosen constitutive model was not appropriate for fitting this material.

A Cross-Link Model Approach

In this section different aspects of the arterial tissue are included in order to fit the above-mentioned data to better describe the mechanical behavior of the carotid considering the microstructure findings described by, e.g., Garcia16 and O’Connell et al.31

There is some evidence of non-isotropic behavior of the elastin in arterial walls; however, we will ignore the anisotropic contribution in this work. As pointed out by Zou and Zhang,37 the behavior of the first part of the stress–strain curve of the arterial wall is due to the compliance of the elastin. The elastin behavior of the material, as stated above, is usually modeled by means of a Neo-hookean law.

O’Connell et al.,31 in rat aorta, and Garcia et al.,17 in pig carotid, have shown that the collagen fibers distribution follows a helicoidal distribution from the outer to the inner layer. As they stated, collagen fibers are bundled around the SMC with some collagen fibrils linking the main fiber in a predominant perpendicular direction. In the media layer there are several sublayers, every one with a preferential direction of the SMC and therefore of collagen fibers, and elastin sheets separating these sublayers. In the case of the media layer of carotid arteries, previous studies report that SMC keep a very circumferential direction.16 Following these observations, we can consider that the preferential direction of the fibers is in the circumferential direction.16

It is well known that collagen fibers are attached each other and themselves by collagen cross-links31 attaching the main fibers in a mesh-like structure with no preferential orientation. The amount of these cross-links is modeled by a factor \(\alpha \). Given that the cross-links are isotropically connected to the main fibers, an isotropic contribution of the cross-links is proposed. The most important physical meaning of this parameters \(\alpha \) is the incorporation of the attachments between the main fibers which provide to the collagen tissue compliance in the transverse direction of the main fibers. A linear interpolation of well known isotropic and anisotropic SEF is used to obtain this behavior as

$$\begin{aligned} \Psi _\text {ani}(\overline{I}_1,\overline{I}_4)&=\sum _{i=1}^N [1-\alpha ]\Psi _{fib}^i +\alpha \left[ \frac{k_{1}}{2k_{2}}[\text {exp}(k_{2}[\overline{I}_1-3]^{2})-1] -\Psi _{fib}^i\right]&\nonumber \\&=\sum _{i=1}^N [1-2\alpha ]\Psi _{fib}^i +\alpha \frac{k_{1}}{2k_{2}}[\text {exp}(k_{2}[\overline{I}_1-3]^{2})-1],&\end{aligned}$$
(3)

where \(k_1\in \mathbb R ^+\) represents a stress-like parameter, \(k_2\in \mathbb R ^+\) measures the exponential behavior of the response, \(\overline{I}_4=\overline{\mathbf {C}}:\mathbf {N}\) with \(\mathbf {N}=\mathbf {n} \otimes \mathbf {n}\), being \(\mathbf {n}\) the direction of the fibers. \(\alpha \) represents the amount of cross-links being \(\alpha \in [0 , 0.5]\). \(\alpha =0\) represents no cross-links and \(\alpha =0.5\) that the degree of links is high enough to consider a fully isotropic distribution of the fibers and

$$\begin{aligned} \Psi _\text {fib}^i(\overline{I}_4)= \frac{k_{1}}{2k_{2}}[\text {exp}(k_{2}[\overline{I}_4-1]^{2})-1]. \end{aligned}$$
(4)

Fitting of Experimental Data of Pig Carotid

The model presented above is used to fit the experimental results presented in Garcia et al.17 The fitting process is split into two parts. First, we focus on the elastin which works mainly in the first part of the uniaxial test. This procedure fits the material parameters corresponding with the first part of the test up to 3–4% of strain. Later, and using the value of the elastin as seed, we fit the rest of the parameters related with the collagen fibers.

The optimization problem (Eq. 5) is used to minimize the goal function \({\mathcal{F}}\).

$$\begin{aligned} \text {(OP1) For }p\text { given minimize } {\mathcal{F}}(C_{10}) =\sum _{j=1}^{n} \left[ \left[ \sigma _\mathrm{c}^j - {\hat{\sigma }_\mathrm{c}^j} \right] ^2 + \left[ \sigma _\mathrm{l}^j - \hat{\sigma }_\mathrm{l}^j \right] ^2 \right] , \end{aligned}$$
(5)

where j represents every experimental data point, \(\sigma _\mathrm{c}^j\) and \(\sigma _\mathrm{l}^j\) are the Cauchy stresses in circumferential and longitudinal direction, respectively, achieved by the constitutive model and \(\hat{\sigma }_\mathrm{c}^j\) and \(\hat{\sigma }_\mathrm{l}^j\) the circumferential and longitudinal stresses obtained from the experimental test. The goodness of the fitting was measured by computing the coefficient of determination \(R^2\), defined as \( R^2 = 1- \left[ \Sigma _{j=1}^{n} \left[ \sigma ^j_\mathrm{c}-\hat{\sigma }^j_\mathrm{c} \right] ^2 \right] \Big / \left[ \Sigma _{j=1}^{n}\left[ \sigma ^j_\mathrm{c}-\mu _\mathrm{c} \right] ^2 \right] - \left[ \Sigma _{j=1}^{n} \left[ \sigma ^j_\mathrm{l}-\hat{\sigma }^j_\mathrm{l} \right] ^2 \right] \Big / \left[ \Sigma _{j=1}^{n}\left[ \sigma ^j_\mathrm{l}-\mu _\mathrm{l} \right] ^2 \right] \) where \(\mu \) is the mean value of the measured longitudinal and circumferential stresses \(\mu _\mathrm{l}=\Sigma _{j=1}^n \sigma _\mathrm{l}^j /n\) and \(\mu _\mathrm{c}=\Sigma _{j=1}^n \sigma _\mathrm{c}^j /n\). Also the normalized mean square root error \(\varepsilon \) was computed for each fitting \(\varepsilon = \sqrt{\chi ^2 / [n-q]} / \mu \). In this equation \(q\) is the number of parameters of the SEF, so \(n-q\) is the number of degrees of freedom. The results from the fitting process are presented in Table 1.

Regarding the collagen fibers, a single family of fibers in the circumferential direction is considered (see Eq. 3). Now we apply a new optimization procedure, OP2, which take the same form as in Eq. 5, but is applied to the whole range of data and includes the collagen contribution, to extract the rest of the material parameters, which gives a goal function as \({\mathcal{F}}(C_{10},k_{1},k_{2},\alpha ).\) The parameter C 10 is allowed to change to take into account the small amount of collagen that actually works during the low strain regime and is used as seed value for this latter fitting procedure. The experimental and fitted curves are presented in Figs. 3 and 4 for the proximal and distal position, respectively. The material parameters are summarized in Tables 2 and 3. A comparison of the material parameters obtained with the model fitted in Garcia et al.17 and the fitting proposed here is shown in Table 4.

Patient Specific Human Carotid Artery Modeling

Finally, the proposed constitutive model has been applied to model the elastic response of a real patient carotid geometry. The geometry obtained in Alastrue et al.2 using computed tomography (CT), which is being used here, provided a substantial amount of customized information about the geometrical description of the human carotid artery.

Table 1 Results of the OP1 for pig carotid specimens17
Full size table
Figure 3
figure 3

Experimental curves for the circumferential (+) and longitudinal (\(\circ \)) directions of the uniaxial tests in the proximal pig CA.17 (-) and (–) represents the fitted curves of the circumferential and longitudinal experimental data respectively

Full size image
Figure 4
figure 4

Experimental curves for the circumferential (+) and longitudinal (\(\circ \)) directions of the uniaxial tests in the distal pig CA.17 (-) and (–) represents the fitted curves of the circumferential and longitudinal experimental data respectively

Full size image
Table 2 Results of the OP2 for proximal pig carotid specimens
Full size table
Table 3 Results of the OP2 for distal pig carotid specimens
Full size table
Table 4 Comparison of the material parameters fitted with the model proposed in this work (top) and the previous model by Garcia et al.17 (bottom)
Full size table

Experimental Fitting

Data from Sommer et al.35 are used to fit the proposed model (see Eq. 4). Although the authors performed an extensive study, to be able to fit their data we have had to restrict ourselves to \(p{-}\lambda _{\theta }\) curves since no information of the axial direction can be found. The material parameters are obtained by means of the minimization of the optimization function34

$$\begin{aligned} &{\text{For}} \, p \, {\text{given minimize}} \nonumber \\ & {\mathcal{F}}(C_{10},k_1,k_2,\alpha )=\sum \limits _{j=1}^{N}\left[ p_j - p_j^\psi \right] ^2. \end{aligned}$$
(6)

\(p_j\) and \(p_j^\psi \) are the pressures given by the experimental and numerical result at every point from 0 to 13 [kPa]. The analytical expression for \(p_j\) is given in Eq. 7, see Ref. 34 for more details on the kinematic and mechanical description of incompressible thick-walled cylindrical tube subjected to inflation.

$$\begin{aligned} p_i=\mathop \int \limits ^{r_0}_{r_i} (\sigma _{\theta \theta } - \sigma _{rr})dr / r. \end{aligned}$$
(7)

Table 5 shows the numerical values of the fitted parameters. Values of the Neo-Hookean part are higher for the media layer since it is known that elastin is mainly in the media layer. Values related with the anisotropic part (\(k_1\) and \(k_2\)) are much higher in the adventitia layer since collagen is the main component in the adventitia. The higher value of the \(\alpha \) parameter in the adventitia layer reflects a more random organization of the fibers. From these results it can be also observed that the behavior of the tissue in a low strain regime is stiffer in the internal carotid artery (ICA) than in the CCA.

Table 5 Results of the OP2 for the material parameters of human carotid specimens in Sommer et al.35
Full size table

Unusually in the computational modeling of blood vessels we adopt a variable distribution of the mechanical parameters. In a similar fashion, interpolating linearly the values of the mechanical properties obtained at both parts of the artery to describe the mechanical properties along the artery length. The material parameter values for the external carotid artery (ECA) are taken equal to the values in the ICA. The results of the three mechanical constants are pictured in Fig. 5.

Figure 5
figure 5

Spatial distribution of the material parameter values in the carotid artery. The figure shows the C10, \(k_1\) and \(k_2\) value along the artery in the cut plane shown on the left

Full size image

Finite Element Model

In this context we first discretize the model in a finite element mesh (Fig. 6a and 6b) and simulate it with Abaqus FEA.1 The meshing procedure was performed in Ansys Icem CFD (Ansys, Inc., Software, Canonsburg, PA, USA) and the resulting mesh was later imported into Abaqus. The resulting mesh contains 128,008 standard bricks with linear interpolation, resulting in a total of 434,484 degrees of freedom. The meshing process results in very homogeneous, undistorted elements. As the CT data does not provide information about the internal composition and structure of the arterial wall, we make use of the experimental data in Sommer et al.35 to describe the thickness for the different layers of the arterial wall. This data provides thickness values of the media and adventitia layer in the CCA and ICA. A linear transition of the thickness over the arterial wall from the CCA and the ICA is applied. Therefore, the finite element mesh consists of five elements in the radial direction representing the media layer and three representing the adventitia layer of the carotid artery.

To complete the mechanical and structural description of the model at hand, it remains to describe the structural organization of the constituents. An isotropic distribution of the elastin component is assumed as well as the collagen and SMC are preferentially oriented in the circumferential direction. Figures 6c and 6d shows details of the fiber distribution in some representative places. The orientation of the fibers is gathered by means of the directions of the principal stresses of the carotid modeled with an isotropic model, under internal pressure and with the displacement of the external face constrained (see Ref. 2). This method provides a radial, longitudinal and circumferential direction in every integration direction, that can be used for creating the fiber orientation.

An important issue in this kind of finite element model is the imposition of boundary conditions reproducing the actual in situ conditions of the vessel. A set of spring elements are included on the surface of the carotid model to simulate the surrounding tissue and also to avoid rigid body motions due to the internal pressure in the non-homogeneous geometry. These springs block rigid solid motion but allow deformation of the arterial wall. The mechanical properties of these springs have been chosen so that this condition is fulfilled. The area associated to every node is taken into account in the spring stiffness to avoid zones of high concentrated nodes. We include the area in the nodes to impose the same equivalent stiffness to the spring.

Figure 6
figure 6

Finite element mesh on top and detail of the fiber distribution in the carotid artery model. Mesh shows a good quality even in the bifurcation. The fiber orientation shows a circunferential distribution

Full size image

FEM Results in Carotid Artery

Figure 7 shows the maximum principal stresses for the whole artery, in different longitudinal cuts and the three slices of the CCA, ICA and ECA for normotensive pressure at 13.3 [kPa] load state. As we can see, due to the mechanical properties of the carotid, stresses in the ICA and ECA are higher than those in the CCA. We can also appreciate the transition of the media and adventitia layer in the stress field. The stresses in media layer are lower than in the adventitia layer because of the higher material parameters \(k_1\) and \(k_2\) in the adventitia layer. The maximum principal stress is in the direction of the collagen fibers, mainly circumferential, since is the most bearing structure. The minimum principal stress is mainly in the radial direction while the middle is in the longitudinal.

Figure 7
figure 7

The maximum principal stress at the whole CA is shown on top of the figure. In the middle the maximum principal stress are shown at the different longitudinal cut planes outlined on the left side. On the bottom the maximum principal stress are shown at three different slices of the CCA, ECA and ICA (outlined in dark gray). The stress values correspond with homeostatic conditions (13.3 kPa)

Full size image

Besides the stress differences in the CCA, the ICA and the ECA a similar stress concentration is appreciable in a ring just before the bifurcation and a ring at the bifurcation part of the ICA.

Discussion

In this work we have examined several structural data of the arterial wall and the mechanical behavior of the elastin21,24 and the collagen fibers,36 which are known to be the most important constituents in terms of mechanical behavior. A well-known and widely-used SEF has been modified to describe some features that this previous model did not include. Garcia16 and O’Connell et al.31 showed that carotid and aorta arteries have a preferentially circumferential direction. Using this previous model, the experimental data could not be fitted since no collagen fibers or fibrils cross-links are included in their constitutive model. The modification of previous SEF has been introduced by including the collagen cross-links attached to the main fibers. These cross-links confer a non-negligible stiffness in the transversal direction of the fibers. Our approach overcome the limitations observed in previous models.

The fitting of the experimental data by means of the presented approach shows similar errors and lower standard deviations than previous models. However, the most important fact is that we were able to include the structural information obtained from experimental observations into the SEF presented here and obtain a good material fitting. The approach adopted in Garcia16 did not fit the mechanical test when they include the information of the fiber orientation in the model. The elastin-related parameters are comparable although our results show lower deviation between distal and proximal locations. The Young modulus of elastin fibrils is 560–740 kPa21 although the value of the elastic modulus for the elastic fibrils depends on the fibrillin and the degree of cross-linking. In a low strain regime \(C_{10}\) is usually approached as \(C_{10} = E/6\), so \(C_{10}\approx 100 \, {\text{kPa}}\) is obtained. Interestingly, applying the content values of elastin in carotid arteries as a rough averaged of 20–30% we obtain the \(C_{10}\) values for our fitting of \(\approx 20{-}30 \, {\text{kPa}}.\) Note that this is an upper bound, since there will be some collagen working in the strain regime. Note also that the values presented by Koenders et al.21 are for individual elastin fibers. The elastin lamelae have other cross-linking that probably stiffens the material up to a certain level.24 In terms of the collagen-related parameter, \(k_1\) presents a very similar tendency. In terms of the \(k_2\) the parameter that establishes the exponential-type behavior of the collagen, our results produce very similar values between the distal and proximal location while the values from Garcia et al.17 differ in one order of magnitude. Our results indicate, by means of the parameter \(\alpha \), that collagen fibers are very aligned with the circumferential direction (with a low degree of cross-links) for the distal samples while this degree of links increases to 25\(\%\) for the proximal samples. Garcia et al.17 showed angles of the fiber orientation of 75\(^\circ \) and \(80^\circ \) which represent a relatively low variability between distal and proximal samples.

The final goal in this work was to apply this mechanical model to a real patient-specific carotid artery in order to be able to simulate it computationally in a finite element framework. We used a geometrical model using CT images of a human carotid artery and a circumferential distribution of the fibers over the arterial thickness. This distribution correlated well with experimental data.16,31 A carotid geometry with variable thickness along the carotid artery is reconstructed. A model with variable mechanical properties in the media and adventitia layer and along the CCA, the ICA and the ECA, which have been shown to have different mechanical behaviors, was also created. In terms of other FE simulations, our results showed similar2 or slightly lower stress values than other carotid models.6,8 Usually the external face of the artery is a free face which does not reflect the physiological conditions of the artery, surrounded by connective tissue. In our opinion, the direct inclusion of this tissue or spring elements in the external face, as in our case, describes the physiology of the arterial tissue in a more realistic way.

There are also important limitations in the current model. Firstly, residual stresses of the arterial wall were not considered, known to be an important issue for the accurate modeling of blood vessels. This is not a trivial topic when dealing with general geometries. Pre-stress has been extensively studied in analytical models19,33 and simple FE models.3 However, approaches to general geometries represent a more unusual task.2 It would also be interesting to consider the myogenic tone of SMC30,38 since this active force can considerably modify the stress field over the arterial wall.

In summary, we have extended a previous SEF by means of a cross-link-related parameter that includes structural features that previous models were unable to address. The behavior of collagen cross-links that can be observed, e.g. in O’Connell et al.31 were included. With this approach we have been able to fit the results of a set of mechanical tests on carotid arteries that previous models could not reproduce.