Impact of Fluid–Structure Interaction on Direct Tumor-Targeting in a Representative Hepatic Artery System

Abstract

Direct targeting of solid tumors with chemotherapeutic drugs and/or radioactive microspheres can be a treatment option which minimizes side-effects and reduces cost. Briefly, computational analysis generates particle release maps (PRMs) which visually link upstream particle injection regions in the main artery with associated exit branches, some connected to tumors. The overall goal is to compute patient-specific PRMs realistically, accurately, and cost-effectively, which determines the suitable radial placement of a micro-catheter for optimal particle injection. Focusing in this paper on new steps towards realism and accuracy, the impact of fluid–structure interaction on direct drug-targeting is evaluated, using a representative hepatic artery system with liver tumor as a test bed. Specifically, the effect of arterial wall motion was demonstrated by modeling a two-way fluid–structure interaction analysis with Lagrangian particle tracking in the bifurcating arterial system. Clearly, rapid computational evaluation of optimal catheter location for tumor-targeting in a clinical application is very important. Hence, rigid-wall cases were also compared to the flexible scenario to establish whether PRMs generated when based on simplifying assumptions could provide adequate guidance towards ideal catheter placement. It was found that the best rigid (i.e., time-averaged) geometry is the physiological one that occurs during the diastolic targeting interval.

Introduction

Local intra-arterial administration of therapeutic agents (such as chemotherapeutic drugs, multifunctional nanoparticles, or radioactive microspheres) is a promising technique for the treatment of unresectable solid tumors, particularly for those found in the liver. Ideally, direct injection into tumor-supplying arteries is desired in this approach to allow for maximum drug dosage with minimal side-effects. However, given the difficulties in advancing the drug-infusion catheter directly to the target site (for example, due to a vessel’s small diameter or high degree of tortuosity), direct injection is often not feasible. Thus, the potential for aberrant drug deposition, which can result in severe side-effects and diminished treatment effectiveness, remains.

To address this problem, a patented, direct tumor-targeting methodology has been developed in which precise catheter location (i.e., radial positioning in the arterial particle-injection plane) as well as particle velocity and infusion interval allows for the drugs to be carried by the blood flow directly to the target site.10 These conditions can be determined via computational simulations which predict the fluid–particle dynamics in a given arterial system. Specifically, tens-of-thousands of particles are randomly infused over the entire arterial inlet plane and tracked through the modeled system. Via a method of backtracking along the particle trajectories, a patient-specific particle release map (PRM) is generated, which visually links particle injection regions with associated exit branches, some potentially connected to tumors. Such PRMs then determine radial catheter positions to achieve optimal targeting. A Computational Medical Management Program (CMMP) has been proposed to implement this targeting methodology into clinical practice. This three-stage program can be executed as follows: (1) patient evaluation; (2) computer modeling; and (3) clinical implementation. The first stage includes classification of the tumor, determination of the best treatment route, and collection of the patient’s geometry and flow conditions. In the second stage, computational analyses, which use the truncated geometry and boundary conditions from the first stage, are performed to determine the PRMs and optimal targeting conditions. In the final stage, optimal catheter positioning and injection is achieved using a proposed Smart Micro-Catheter (SMC) and Medicine Supply Apparatus (MSA).

Several computational simulations and experimental bench-top tests have demonstrated this approach in a representative hepatic artery system.2,3,5,9,11,16 While providing an initial proof-of-concept, all of these studies assumed rigid arterial walls. Given their increasing stiffness in the physiological pressure range and with a patient’s age, this may be an adequate simplification; however, this assumption has yet to be validated. Thus, this study models fluid–structure interaction (FSI) and blood-particle transport in a representative hepatic artery system (see Fig. 1) to explore the impact of arterial wall motion on the feasibility of direct microparticle targeting to a predetermined daughter branch connected to a solid tumor.

Figure 1

(a) Representative hepatic artery system and (b) associated physiological inlet flow and outlet pressure waveforms. The colors at each outlet in (a) correspond to their injection region in the PRM

Methods

To demonstrate the impact of arterial wall motion on the feasibility of direct microsphere targeting, two-way FSI with Lagrangian particle tracking was modeled in a representative hepatic artery system, and PRMs were generated and analyzed throughout the cardiac pulse. Two rigid-wall cases at the approximate diastolic and time-averaged geometries were also compared to this flexible-wall scenario to determine whether PRMs generated using the rigid-wall assumption could provide adequate guidance towards best catheter placement.

The two-way FSI analysis was accomplished using the ANSYS^® MFX Multi-field solver which coupled the fluid code, ANSYS^® CFX^®, with the structural code, ANSYS^® Mechanical™, via a routine in which the individual solvers successively computed and passed information (i.e., displacements and forces) across the fluid–solid interface until convergence was achieved within each time step. For the rigid-wall cases, only the fluid solver, ANSYS^® CFX^®, was required. The following sections summarize the methods used to perform these analyses.

Representative Hepatic Artery System

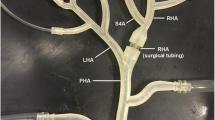
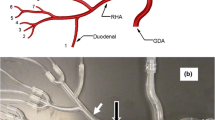
The representative hepatic artery system, whose dimensions were prescribed using population-averaged values, consists of the common hepatic artery (CHA), gastroduodenal artery (GDA), proper hepatic artery (PHA), left and right hepatic arteries (LHA and RHA, respectively), and four daughter branches bifurcating from the LHA and RHA (D1–D4), as illustrated in Fig. 1a. The GDA, which leads to the gastrointestinal (GI) tract, was included in this system to model a worst case scenario in which the catheter cannot be advanced past the GDA bifurcation. For the FSI and fluid–particle analyses, symmetry was assumed along the z–x plane in order to reduce the computational expense. Also, because patient-specific geometries obtained from in vivo imaging are already in a pressurized state, this system was assumed to be around the diastolic minimum pressure.

To generate the structural domain, a uniform wall thickness of 0.378 mm was extruded outward from the lumen wall. This thickness assumed negligible adventitia thickness and was obtained by using the measurements of Hirokawa et al. 7 who found the average thicknesses of the intima and media of 57 hepatic arteries from 36 human cadavers to be 120 and 258 μm, respectively.

Governing Equations

Fluid Transport

For transient, incompressible fluid flow under isothermal conditions, the mass and momentum conservation equations are:

$$ \frac{{\partial u_{i} }}{{\partial x_{i} }} = 0, $$

(1)

$$ \rho \left( {\frac{{\partial u_{i} }}{\partial t} + \frac{{\partial u_{j} u_{i} }}{{\partial x_{j} }}} \right) = - \frac{\partial p}{{\partial x_{i} }} + \rho g_{i} + \frac{\partial }{{\partial x_{j} }}\left[ {\eta \left( {\dot{\gamma }} \right)\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)} \right], $$

(2)

where $u_{i}$ is the velocity vector, $x_{i}$ is the spatial vector, $p$ is the pressure, $\rho$ is the fluid density, $g_{i}$ is the gravitational acceleration vector, and $\eta \left( {\dot{\gamma }} \right)$ is the fluid dynamic viscosity as a function of the shear rate. To account for the fluid–structure interface motion, the transient terms in the conservation equations require differentiation of integrals whose integrand and limits are functions of time. Using the Leibniz theorem where $W_{j}$ is the velocity of the control volume boundary, the mass and momentum conservation equations (in integral form) respectively become1:

$$ \int\limits_{CS} {\left( {u_{j} - W_{j} } \right)n_{j} dA = 0} , $$

(3)

$$ \rho \frac{d}{dt}\int\limits_{CV(t)} {u_{i} dV} + \rho \int\limits_{CS} {\left( {u_{j} - W_{j} } \right)} u_{i} n_{j} dA = - \int\limits_{CS} {pn_{j} dA} + \int\limits_{CS} {\eta \left( {\dot{\gamma }} \right)} \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)n_{j} dA. $$

(4)

Blood can be sufficiently modeled with a constant density (1060 kg m⁻³) and a non-Newtonian shear-thinning viscosity. Here, a simplified Quemada viscosity model was used in the form:

$$ \eta \left( {\dot{\gamma }} \right) = \hbox{max} \left[ {\mu_{0} , \left( {\sqrt {\eta_{\infty } } + \frac{{\sqrt {\tau_{0} } }}{{\sqrt \lambda + \sqrt {\dot{\gamma }} }}} \right)^{2} } \right], $$

where $\mu_{0}$ (minimum viscosity) is 0.03090 g cm⁻¹ s⁻¹, $\eta_{\infty }$ (asymptotic viscosity) is 0.02654 g cm⁻¹ s⁻¹, $\tau_{0}$ (apparent yield stress) is 0.04360 g cm⁻¹ s⁻¹, $\lambda$ (shear stress modifier) is 0.02181 s⁻¹, and $\dot{\gamma }$ is the shear rate.4

Particle Transport

Particle transport was modeled with the Lagrangian particle tracking approach which employs the conservation of momentum (i.e., the particle’s time rate of change of linear momentum is balanced by the forces acting on the particle):

$$ m_{\text{p}} \frac{{du_{i}^{\text{p}} }}{dt} = \sum {F_{i}^{\text{p}} } , $$

(5)

where $m_{\text{p}}$ is the particle’s mass, $u_{i}^{\text{p}}$ is the velocity vector of the particle, and $F_{i}^{\text{p}}$ is a force vector acting on the particle. Here, the only forces acting on the particle were assumed to be the drag force and the pressure gradient force. Based on the assumption of dilute particle suspensions, only one-way fluid–particle coupling was modeled. At the walls, the interaction was assumed to be purely elastic. Thus, the parallel and perpendicular restitution coefficients were both set to one in all simulations. To mimic the radioembolization procedure, the injected microspheres were modeled after one of two commercially available radioactive microspheres on the market. Specifically, they have a density of 1600 kg m⁻³ and a maximum, average, and minimum diameter of 60, 32, and 20 μm, respectively, with a standard deviation of 10 μm.

Structural Dynamics

The vessel wall motion was modeled using the conservation of momentum:

$$ \rho_{wall} \frac{{\partial^{2} \hat{u}_{i} }}{{\partial t^{2}}} = \frac{{\partial \sigma_{ji} }}{{\partial x_{j} }} + f_{i} ,$$

(6)

where $\rho_{wall}$ is the vessel wall density, $\hat{u}_{i}$ is the displacement vector for the vessel wall, $\sigma_{ji}$ is the mechanical stress tensor, and $f_{i}$ are body force vectors. Due to the physiological pressures and the distensibility of the vessel walls, the structure can undergo large strains. Hence, large deformation analysis was employed.

For the simulation of vessel-wall response, the results of recent inflation tests on swine and human cadaver hepatic arteries were utilized.6,13 As revealed by these tests, the hepatic arteries can exhibit about a 20% diameter increase in the physiological pressure range (around 75–170 mmHg)6 as well as stiffening with increasing loads.6,13 This is mostly due to their elastin and collagen content and structure. In studying iliac arteries, Roach and Burton17 concluded that this behavior was attributed to the continuous stretch and recruitment of initially wavy collagen fibers.

To model this hyperelastic response, the 2nd order Yeoh model (i.e., 2nd-order reduced polynomial model) was employed:

$$ \psi = \alpha \left( {I_{1} - 3} \right) + \beta \left( {I_{1} - 3} \right)^{2} , $$

(7)

where $I_{1}$ is the first invariant of the left Cauchy–Green deformation tensor, and $\alpha$ and $\beta$ are the material constants. This model is commonly used for abdominal aortic aneurysm modeling15 and is a convenient choice for the current study. Here, the material constants were determined using the swine hepatic artery pressure–diameter data of He et al.,6 due to the limited data available on human hepatic arteries. Given their comparable response, as demonstrated in Li et al.,13 this approximation was deemed acceptable (see Fig. 2a). Furthermore, while arteries often exhibit an anisotropic response, isotropy was assumed due to the lack of available bi- or multi-axial tensile test data.

Figure 2

(a) Comparison of swine and human incremental elastic modulus vs. pressure6,13; (b) second-order Yeoh model fit to swine hepatic artery diameter-pressure data6 in the physiological pressure range

For arteries in which only pressure–diameter data are available, the analytical pressure–radius relationship of a flexible, thick-walled cylinder can be used to estimate the elastic properties. Derived from the equilibrium equation and neglecting body forces,8 this relation can be written as:

$$ p_{{\text{i}}} = \int\limits_{{r_{i} }}^{{r_{0} }} {\left( {\sigma _{{\theta \theta }} - \sigma _{{rr}} } \right)\frac{{{\text{d}}r}}{r}} , $$

(8)

where $\sigma_{\theta \theta }$ is the circumferential stress, $\sigma_{\text{rr}}$ is the radial stress, r _i is the deformed internal radius, r _o is the deformed outer radius, $r = \sqrt {R^{2} - R_{\text{i}}^{2} + r_{\text{i}}^{2} }$ (if $\lambda_{z} = 1$ and there are no residual stresses), R is the un-deformed radius, and R _i is the un-deformed internal radius. Neglecting residual stresses, the difference in the circumferential and radial stresses for a 2nd order Yeoh material is given as:

$$ \sigma_{\theta \theta } - \sigma_{\text{rr}} = \left( {2\alpha + 4\beta \left[ {\left( \frac{R}{r} \right)^{2} + \left( \frac{r}{R} \right)^{2} - 2} \right]} \right)\left[ {\left( \frac{r}{R} \right)^{2} - \left( \frac{R}{r} \right)^{2} } \right]. $$

(9)

After substituting Eq. (9) into Eq. (8) and converting the integral such that it depends on the reference radii rather than the deformed radii, the pressure–radius relation becomes:

$$ p_{\text{i}} =\int\limits_{{R_{\text{i}} }}^{{R_{\text{o}} }} \left( {2\alpha + 4\beta \left[ {\left( \frac{R}{r} \right)^{2} + \left( \frac{r}{R} \right)^{2} - 2} \right]} \right)\left[ {\left( \frac{r}{R} \right)^{2} - \left( \frac{R}{r} \right)^{2} } \right]\frac{R}{{r^{2} }}dR. $$

(10)

Using a MATLAB routine, this relation was numerically integrated, and the pressure was solved at various deformed radii. The material constants, $\alpha$ and $\beta$, were estimated by comparing the model pressure–diameter relation to the experimental pressure–diameter data. Assuming the given hepatic artery system to be at its diastolic state, the approximate diastolic pressure was subtracted from the actual pressure before being applied to the wall. Thus, the model was fit to the data ranging from 9 to 27 kPa (67.5–202.5 mmHg) by shifting the pressure–diameter data by 9 kPa along the pressure axis before curve fitting. The resulting $\alpha$ and $\beta$ values were 0.043 and 0.1 MPa, respectively. Figure 2b illustrates the fit for pressures above 72.18 mmHg (i.e., the estimated diastolic pressure in the representative hepatic arteries). The density and Poisson ratio were set to typical values of 1120 kg m⁻³ and 0.45, respectively.

Boundary Conditions

For the present representative hepatic artery system, population-averaged flow rates and distributions as well as a patient’s pressure waveform were used to approximate the physiological flow conditions (see Basciano2 for details). At the inlet a parabolic velocity profile was assumed, while at the outlets the two or three-element Windkessel (WK2 and WK3) models were employed to prevent un-physiological wave reflections for the flexible case. The WK3 model relates the pressure and flow rate via the differential equation:

$$ \frac{dP}{dt} + \frac{P}{{CR_{\text{d}} }} = R_{\text{p}} \frac{dQ}{dt} + \frac{1}{C}\left( {1 + \frac{{R_{\text{p}} }}{{R_{\text{d}} }}} \right)Q, $$

(11)

where P is the pressure, Q is the flow rate, t is the time, $R_{\text{p}}$ is the proximal resistance, $R_{\text{d}}$ is the distal resistance, and C is the capacitance. The time derivative of the flow rate can be approximated by the first order, backward difference approximation, and Eq. (11) was discretized by the forward Euler method:

$$ P_{i} \approx P_{i - 1} + \Updelta t\left[ {R_{\text{p}} \left( {\frac{{Q_{i - 1} - Q_{i - 2} }}{\Updelta t}} \right) + \frac{1}{C}\left( {1 + \frac{{R_{\text{p}} }}{{R_{\text{d}} }}} \right)Q_{i - 1} - \frac{{P_{i - 1} }}{{CR_{\text{d}} }}} \right]. $$

(12)

To obtain the WK2 model, $R_{\text{p}}$ is set to zero.

The Windkessel parameters (resistances and capacitance) were adjusted such that the inlet flow rate and outlet pressures matched the realistic waveforms given in Fig. 1b and were consistent between the flexible and rigid cases. The best parameters (provided in Table 1) resulted in WK2 models at the outlets. For the remaining fluid boundaries, the wall was set as the fluid–solid interface while the z–x plane was prescribed as the symmetry plane. For the structural domain (vessel wall), the daughter vessel outlet planes were fixed in all degrees of freedom while the inlet and symmetry planes were fixed in the normal direction. For the GDA outlet plane, rotations were fixed as well as motion in the normal direction. The vessel inner wall was set as the fluid–solid interface while the outer wall remained free. Finally, the inner curve of the CHA–PHA vessels was fixed to prevent un-physiological translation of the artery. For the rigid cases, the flow and pressure waveforms of Fig. 1b were directly prescribed at the inlet and outlet boundaries, and the no velocity slip condition was assumed on the walls.

Table 1 WK2 parameters for the representative hepatic artery system

In all, three cases were run: (1) flexible, (2) rigid-diastolic (rigid walls at the approximate diastolic geometry), and (3) rigid-time-averaged (rigid walls at the approximate time-averaged pressure geometry). Two pulses were modeled to achieve pulsatile independence, and particles were uniformly released across the inlet plane at a rate of 50,000 particles per second in the third pulse. One additional pulse was simulated to allow a majority of the particles to exit the domain.

Model Validation

To validate the FSI model setup and computations, a two-way FSI analysis mimicking the experimental study of Kung et al. 12 was performed (Figs. 3 and 4). In this study, fluid flow in a deformable, straight tube having a diameter of 2 cm, a wall thickness of 0.08 cm, and a length of 25 cm was modeled (see Fig. 3a). The deformable wall was made of silicone, and the fluid was a 40% glycerol solution with 0.5% gadolinium and a viscosity of 0.0461 poise. A pulsatile flow rate, given in Fig. 3a, was applied at the inlet using a pulsatile pump while a four-element Windkessel module, which was constructed using capillary tubes and trapped air in a Plexiglas box, was imposed at the outlet to achieve physiological flow rates and pressures.

Figure 3

(a) Kung et al. 12 experimental setup; (b) experimental and numerical outer diameter vs. pressure of silicone tube

Figure 4

(a) Experimental vs. numerical flow rate (left) and pressure (right) at the mid-plane over one pulse; (b) differences in flow rate (left) and pressure (right) along the length of vessel; and (c) maximum total mesh displacement of the inner vessel wall vs. time compared to the mid-plane pressure waveform

In the numerical simulation, axisymmetry was assumed and, thus, only half of the geometry was analyzed. The density and Poisson ratio of the silicone wall were set to typical values for blood vessels, i.e., 1120 kg m⁻³ and 0.45, respectively, while the density of the glycerol solution was set to a typical value for blood, i.e., 1050 kg m⁻³. The elastic modulus of the silicone tube was determined by numerically modeling the static inflation tests and adjusting the modulus to achieve an adequate fit with the experimental pressure–diameter data. This resulted in a modulus of 1.6 MPa, as demonstrated in Fig. 3b. At the fluid inlet, a uniform velocity was imposed using the measured inlet flow rate waveform from the experiment while a 3-element Windkessel (WK3) model was imposed at the outlet. The resistances and capacitance for this model were obtained by fitting Eq. (11) to the measured outlet flow rate and pressure in Kung et al. 12 The best fit produced: R _p = 2.843 × 10⁷ Pa s m⁻³, R _d = 3.844 × 10⁸ Pa s m⁻³, and C = 1.384 × 10⁻⁹ m³ Pa⁻¹. Finally, the wall was set as the fluid–solid interface, and the remaining faces were prescribed as symmetry planes. For the vessel wall (structure), both ends (inlet and outlet) were fixed in all degrees of freedom while symmetry conditions were prescribed on the symmetry planes. The outer boundary of the vessel wall was set to be free while the inner wall was set as the fluid–solid interface. Finally, while the vessel’s bottom edge was further constrained in the experiment to mimic the spine, this was found to have little effect on the results. Thus, for computational reasons, this constraint was excluded in the final results.

Figure 4a demonstrates the good agreement between the flow rate and pressure at the center cross-section, L2, of the 25 cm long tube (see Fig. 3 for L2 position) of the experimental and numerical results. Further, Fig. 4b demonstrates that the numerical simulation was able to model the increasing flow rates and decreasing pressures along the length of the vessel. Lastly, Fig. 4c compares the maximum total mesh displacement of the inner wall over time to the L2 pressure waveform. This demonstrates that the wall displacement follows the pressure waveform and shows that the diameter changes by as much as 3.1 mm at maximum systole from the undeformed state. Given these results, this analysis demonstrates that the applied methods are able to adequately model two-way, FSI in a deformable vessel.

Mesh Generation

Mesh independence tests were separately run in the fluid and solid domains of the representative hepatic artery system. For the fluid domain, tetrahedral elements were utilized with inflation layers near the wall to capture the steep velocity gradients in this region. Steady velocity contours and PRMs were compared for three mesh refinements (coarse: 610,346 elements; intermediate: 1,335,280; fine: 2,223,159). The intermediate mesh demonstrated little difference with the next refined mesh (i.e., the fine mesh); thus, this mesh was chosen for the fluid analyses due to its adequate compromise between accuracy and efficiency. For the structural domain, a hex-dominant mesh was employed. Here, static pressure tests were run in two mesh refinements (0.5 vs. 0.25 mm maximum element size). The difference between the maximum displacements for these two mesh sizes was less than 1%. Thus, the larger element sizing was used. The final structural mesh consisted of 6,556 elements and 27,216 nodes.

Convergence and Computer Resources

For the fluid flow, the solution was considered to be converged when the RMS mass and momentum residuals were less than 1e−5. Additionally, a conservation target of 0.01 (1%) was set to ensure domain mass balance. Convergence of the forces and displacements at the interface was set to 0.01. The time step was set to 0.005 s. With these settings, the FSI case took the CPU, having 40 GB of RAM and using 10 processors of the 3.33 GHz, dual six-core Intel Xeon X5680 processor, approximately 3.5 days to complete, while the rigid cases took approximately 11–14 h to complete.

Results and Discussion

Arterial Wall Displacement

As demonstrated previously, the hepatic arteries can exhibit large deformations under the physiological pressures they bear. Using the material model estimated from the measured response of swine hepatic arteries, a two-way FSI analysis was run in a representative hepatic artery system. Figure 5a illustrates the inner-wall displacement of the flexible case at its diastolic and systolic states as well as the differences in the approximate diameters for both states. This diameter increase ranged from about 15% in D2 to about 27% in the CHA. Figure 5b demonstrates how the size of the PRM (inlet region) changes over the cardiac pulse. Included in this figure are the approximate rigid-diastolic and rigid-time averaged inlet diameters which remain constant. For the flexible case, the diameter changed more drastically in intervals 1 and 2 (the first 20% of the cardiac cycle), while in the last 60% of the cardiac cycle less rapid changes occurred. Thus, targeting may be more readily achieved during the diastolic phase. This is further demonstrated in Figs. 5c and 5d, which are a plot of the approximate CHA, PHA, LHA, RHA, and D1–D4 diameters over time and a comparison of the LHA diameter and pressure over time, respectively. As expected, the change in the LHA diameter closely followed the pressure waveform.

Figure 5

(a) Wall displacement for the FSI scenario; (b) inlet diameter changes over time (demonstrating the PRM size changes over the cardiac cycle); (c) diameter vs. time for various locations along the vessel length (boxed measurements from (a) correspond to the locations for this plot); and (d) diameter and pressure comparison for the LHA location

Blood Flow

In order to more readily compare the flexible and rigid scenarios, the inlet flow and outlet pressure waveforms were kept the same, or very similar, among the cases as demonstrated in Fig. 6a. Thus, the flow rates or pressures at the intermediate locations were subject to the effects of the wall motion. Comparing the flow waveforms at the CHA, PHA, LHA, and RHA locations, Fig. 6b demonstrates that the flexible scenario exhibits lower flow rates in systole and higher or equal flow rates in diastole compared to the rigid cases. This is due to the Windkessel effect which acts to store fluid during systole and ejects it during diastole.

Figure 6

(a) Inlet flow and outlet pressure waveforms; (b) flow rates at the CHA, PHA, LHA, and RHA locations for the flexible and rigid scenarios; (c) CHA to PHA pressure differences for the flexible and rigid scenarios; and (d) time-averaged outflow distributions for the flexible and rigid scenarios

Comparing the rigid cases, the flow rates in the CHA were essentially equivalent. However, the rigid-time averaged case exhibited higher flow rates in the PHA compared to the rigid-diastolic case at the same location. As a result, both the LHA and RHA flow rates were also increased. Because the only significant difference between the rigid cases was the geometry, it was concluded that the expansion of the PHA and distal arteries in the time-averaged geometry causes a decrease in the resistance to these arteries compared to the diastolic case. This is because the resistance is proportional to the inverse of the radius to the fourth power according to Poiseuille’s law. This phenomenon is also demonstrated by the pressure differences between the CHA and PHA for each case, as seen in Fig. 6c. For the rigid-diastolic case, there is a larger pressure difference between the CHA and PHA at systole. This is because the PHA and downstream arteries are smaller and, hence, exhibit a higher resistance to flow than the other cases. At diastole, the rigid-diastolic and flexible scenarios exhibit similar pressure differences because the geometries are relatively the same during this phase of the pulse. The result of these different resistances is demonstrated in Fig. 6d which illustrates the time-averaged outflow distributions for each case. For the rigid-time averaged scenario, the GDA outflow is decreased so that the daughter vessel outflows increase. Despite the significant differences between the flow-rate magnitudes among the flexible and rigid-diastolic cases, their time-averaged outflow distributions are quite similar due to the specification of the WK2 parameters for the flexible case which preserved the flow distributions of the rigid case.

Upon close inspection of Fig. 7, the velocity vectors near the wall of the flexible case point in the direction of the wall motion. Thus, when the vessel expands up to systolic pressure, the vectors point outwards. When the vessel contracts to diastolic pressure, the vectors point inwards. This effect is minimized away from the wall (i.e., towards the center of the vessel). Because this secondary flow is quite small compared to the axial flow, it will likely not have as much of an effect on the particle trajectories as a change in geometric shape. This is demonstrated by the similarities in the flow features between the flexible and rigid scenarios. Here, the rigid-time-averaged case better represents the flexible case at systole while the rigid-diastolic case better mimics the flexible case at diastole. So, it is expected that use of the systolic geometry will provide an even better match at systole. However, because this geometry is only attained in a small interval of the pulse, it would likely not provide the best approximation of the blood and particle transport throughout the pulse. Thus, the time-averaged geometry may be the best compromise between the systolic and diastolic geometries. In the end, this demonstrates the critical role that geometry plays in the blood flow field which will ultimately affect particle transport and tumor-targeting.

Figure 7

Velocity contours and vectors at the symmetry and CHA planes of the flexible and rigid scenarios for systolic and diastolic flows. The secondary velocity vectors in the CHA planes are scaled up for visualization

Particle Trajectories

For all three cases, PRMs were generated for ten equal intervals (i.e., 0.107 s-intervals) of the cardiac cycle (see Fig. 1b for a demonstration of this division). Figure 8a illustrates the PRMs for the flexible case which shows both distinct and overlapping injection regions. Of importance in the direct tumor-targeting methodology is the ability to target only a pre-selected vessel. Thus, the overlapping regions should often be eliminated from consideration. To do this, the inlet plane was divided into subsections to create an inlet grid. Then, subsections were identified in which only one vessel was targeted (see also Fig. 8a). The dark blue subsections represent regions where zero or multiple vessels were targeted. This methodology was also used to eliminate overlapping regions between multiple intervals, or when comparing with the rigid PRMs.

Figure 8

Flexible scenario (a) PRMs (left; the corresponding outlet colors are given in Fig. 1a) and subsections for single vessel targeting (right; D1 = red, D2 = pale blue, D3 = aqua, D4 = orange, GDA = yellow, none/multiple branches = dark blue); and (b) matching subsections over multiple intervals

As demonstrated by the size of the PRM (see also Fig. 5b), the maximum inlet diameter was reached by interval 3 and then decreased until the cycle was repeated at interval 1. The greatest change in flow rate and/or diameter occurred either in or immediately succeeding intervals 1, 2, and 10. Thus, there were fewer and/or smaller injection regions, especially for daughter vessel D2, in these intervals. However, given the distinct injection regions for the remaining intervals, this case shows that direct tumor-targeting would be possible in the presence of flexible walls. This was further demonstrated by the matching subsections over multiple intervals, as shown in Fig. 8b. However, it should be noted that the right side of the PRMs (which was fixed at the center-right point) had fewer differences throughout the pulse than the left, which was free to move. Thus, it is clear that the restriction of arterial motion due to the presence of external organs/tissue can play a significant role in the particle trajectories and PRM generation, as well as optimal catheter placement and hence direct tumor-targeting.

The next step was to determine whether the PRMs from the rigid scenarios could adequately approximate the catheter position for the flexible scenario. Figure 9 illustrates the comparisons between these cases. The “Actual Matching” column illustrates the matching subsections when the rigid and flexible PRMs were directly compared (aligned at the stationary right-center point). The “Scaled Matching” column provides the matching subsections after the size of the PRMs were made equivalent. This last comparison demonstrates how the shapes of the injection regions matched.

Figure 9

Flexible and rigid PRM comparisons—matching subsections for single vessel targeting

Overall, the rigid cases provided better fits to the flexible case during the diastolic phase of the pulse when less rapid changes in geometry occurred. The time-averaged case generates a better overall match when directly comparing its PRMs with the flexible scenario. For the scaled match, the time-averaged case provides a better match for intervals 1 through 7 while the diastolic case results in a superior match for intervals 8 through 10. This is due to their better geometric match to the flexible case during these intervals. Referring back to the blood flow results, the decreased resistance of the PHA and distal arteries in the time-averaged case caused the relative GDA injection region to decrease and the remaining injection regions to increase compared to the diastolic case. Nevertheless, the time-averaged case provides a better overall match to the flexible scenario.

Limitations

Several assumptions were made in this analysis that should be addressed in future studies. First, the entire representative hepatic arterial system was assumed to have the same wall thickness and exhibit the same arterial response (i.e., using the model of Eq. (7) and Fig. 2b for the entire system). While the uniform thickness allowed for increasing stiffness in the distal arteries (due to their larger thickness to diameter ratio), future work should address the effects of increasing elastic moduli from the larger to smaller arteries and variable wall thickness. This work should also include more accurate wall models for each of the hepatic artery generations once they become available. In summary, while presently a uniform material model for the entire system was deemed acceptable to determine the effects of wall motion on blood flow and particle transport, future data sets may be directly integrated into the modeling framework.

The present work also assumed that the inner CHA–PHA curve and daughter vessel outlets were fixed to prevent un-physiological translation of the system, and no external tissue support was applied on the outer wall. Thus, future studies should consider more advanced constraints, such as the Robin boundary condition suggested in Moireau et al. 14 Also, one-way coupling was assumed between the fluid and particles. This assumption is adequate for modeling dilute particle suspensions; however, two-way coupling should be modeled for dense particle suspensions.

It is also important to mention that the peak pressure decreased down the length of the arterial system. This is in contrast with the aorta where a “peaking phenomenon” occurs due to wave reflections from bifurcations and changing stiffness. While it does not occur in every arterial system (for example, the coronary arteries) due to increasing admittance in the distal arteries, it should be confirmed for the present arterial system. The absence of this phenomenon may be physiological, but it may also be a result of the assumed boundary conditions. However, this should not affect the conclusions of this work.

Conclusions

The feasibility of direct tumor-targeting in the presence of arterial wall motion was demonstrated by modeling a two-way FSI analysis with Lagrangian particle tracking in a representative hepatic artery system. Rigid cases were also compared to the flexible scenario to establish whether PRMs that are generated using the assumption of rigid walls could provide adequate guidance for catheter placement. It was found that the best rigid geometry is one that best represents the physiological geometry in the targeting interval (most likely the time-averaged geometry over this interval). Due to its less significant geometric changes, the diastolic phase of the pulse may be this ideal targeting interval. Finally, for the present test case, the computer-time ratio of flexible over rigid was about 7:1.