Introduction

Pressure-induced wall stress has long been submitted as a risk factor for intracranial aneurysms (IAs) and one that is physically relevant to rupture.8,27 Existing studies on IA stress ranged from simple estimations using Laplace law,5,26 to finite element models of idealized aneurysm18,37 and stability analyses,6,18,37 to fully nonlinear finite element analysis of patient-specific aneurysms24 and fluid–structure interaction.4,17 Collectively, these contributions provided significant insight in understanding the stress state in IAs. Finite element method enables the modeling of the aneurysm structure at various levels of fidelity, and may do so on a patient-specific basis. Yet, a fundamental challenge remains that not all information necessary for building patient-specific finite element models is available. An analyst typically has to make necessary assumptions about the missing information whose implications need to be understood better. Perhaps equally important is to reformulate the problem in such ways that some aspects of the solution are insensitive or weakly sensitive to certain assumptions.

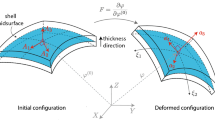
In quasi-static stress analysis, there are two distinct approaches of solving an elastic equilibrium problem—the forward approach and the inverse approach. The forward approach refers to the standard way of determining a deformed shape of a material body from an undeformed configuration and applied force and boundary conditions. The inverse analysis, on the other hand, takes the deformed configuration and the load at this deformed configuration as input, and solves the equilibrium problem by finding a (stress-free) initial configuration that the material body assumes upon removal of the applied load10,11 thereby also determining the stress in the deformed state. This reverted paradigm is possible for nonlinear elastic solids and structures. Membrane- and shell-based inverse analyses were introduced to IAs by the authors,22,48 initially for addressing the problem of unknown stress-free configuration for image-based simulation. In these studies, it was demonstrated that the stress resultant in the deformed state estimated using the inverse scheme was influenced very weakly by the material description (the estimated zero-stress configuration does depend on material description, but we do not necessarily seek that). Thus, the inverse approach of estimating stress in the in vivo aneurysm wall renders moot two critical pieces of missing information in image-based patient-specific modeling: the stress-free configuration and the patient-specific properties of the wall tissue.

There is a growing literature on the identification of quantified geometric indices of IAs23,28,30,42 and their assessment as prognostic indicators of rupture status or risk, but identification of a single indicator or some combinations of them has remained elusive. Because distribution of stress or stress resultant depends on the IA surface size and shape, indices based on them (e.g., spatial peak or spatial average wall stress resultant) may serve as biomechanically grounded indices of surface morphology. In this article, we present further results of inverse analysis for estimation of stress in IAs. We applied the method developed in Zhou and Raghavan48 to a group of 26 image-based, geometrically realistic cerebral aneurysms. The goal was to use a population of human aneurysms to: (1) investigate the material influence on stress estimation and (2) gain further insight into the stress-geometry relation.

Method

Image Segmentation and Geometry Reconstruction

Computed tomography angiographic (CTA) images of 26 saccular, patient-specific IAs were obtained during routine clinical care at University Central Hospital, Helsinki, Finland. The study was approved by the local ethics committee and the patients or their relative gave informed consent. The aneurysms came from middle cerebral artery (12), internal carotid artery (4), anterior communicating artery (3), basilar artery (2), posterior communicating artery (2), and pericallosal artery (3). Maximum diameter of the aneurysms ranged from 3.96 to 12.05 mm with an average of 6.63 mm. Out of the 26 aneurysms, 20 were bifurcation aneurysms while six were side-walled. 3D models of these aneurysms and their contiguous vasculature were created from the source data using levelset segmentation techniques as implemented in the Vascular Modeling ToolKit (VMTK—open source software). The levelset initialization methods, referred to as colliding fronts and fast marching were used to segment the parent vasculature and the aneurysm respectively. The deformable models were evolved by applying segmentation parameters within a set range—number of iterations (200–300), propagation scaling (0–1), curvature scaling (0–1), and advection scaling (1). Detailed reviews of these methods have been published by their authors earlier.1,2,29 Further details on the study population and the implementation of 3D reconstruction may be seen in earlier publications.19,31 Aneurysm domes were isolated from their contiguous vasculature using a cutting plane. The reconstructed surfaces were initially represented by triangular meshes. A convergence study was carried out on the triangular meshes whereby a fine mesh at the maximum element size of 0.2 mm2 was introduced for each aneurysm; the 95th percentile values of the principal stress from the coarse and the fine meshes were linearly fitted. The slope of the linear fit was found to be 1.00,31 indicating that the stress converged in each aneurysm at the utilized coarse level. To further improve the mesh quality, the (coarse mesh) triangular surfaces were re-meshed into quads keeping the maximum element size the same. Representative examples of aneurysm meshes are shown in Fig. 1.

Figure 1
figure 1

Examples of aneurysm mesh

Full size image

Stress Analysis

From the standpoint of mechanics, unruptured cerebral aneurysms can be treated as membrane or shell structures.5,16 IAs start as a small outpouching in the cerebral artery wall, but may enlarge to >10 mm in diameter. Literature values of wall thickness are typically in the range of 16–200 μm25,34 although a slightly larger range of 30–500 μm was also reported.15,35 Taking the average thickness to be ~150 μm, IAs of diameter >3 mm fit well the description of membrane structure. Nevertheless, in analysis it is prudent to model them as shells, because most IAs have undulated surfaces for which the presence of bending stress and transverse shear force may be necessary for achieving equilibrium.

The method of inverse shell analysis22,48 was employed in this study. The method was originally motivated by the need for finding the zero-load configuration21; in the present study, we used it to solve for the stress in the in vivo (deformed) configuration—inaccuracies in the estimation of zero-load geometry notwithstanding. The inverse shell element in Zhou and Lu47 was developed based on the geometrically exact stress-resultant shell formulation by Simo’s group.38–40 By design, the inverse shell can exactly invert deformations predicted by forward analyses. Details of the inverse shell formulation are contained in Zhou and Lu47 and thus omitted here. The inverse element were implemented in FEAP, a finite element program developed by Prof. Taylor at the University of California, Berkeley.41

Surface Curvature

Surface curvature was used later in the study of stress-geometry relation. In the theory of the stress resultant shell, the configuration of a shell structure is described by the position of the middle surface \( {\user2{\varvec{\varphi }}}(\xi^{1} ,\xi^{2} ) \) and a director \( {\mathbf{d}}(\xi^{1} ,\xi^{2} ) \) representing the surface normal. Here \( (\xi^{1} ,\xi^{2} ) \) are a set of convected surface coordinates, which, in finite element kinematics are taken to be the element natural coordinates. In finite element approximation, the fields \( \user2{\varvec{\varphi }}(\xi^{1} ,\xi^{2} ) \) and \( {\mathbf{d}}(\xi^{1} ,\xi^{2} ) \) are constructed by interpolating nodal quantities. In our implementation, the nodal director was defined initially by a weighted average of the normal of elements that share a common node.23 Subsequent orientation of the director was determined by analysis. Components of the curvature tensor \( \user2{\varvec{\kappa}} \) and the metric tensor \( {\mathbf{a}} \) were computed according to

$$ {{\kappa}}_{\alpha \beta } = \frac{1}{2}\left({\frac{{\partial \user2{\varvec{\varphi }}}}{{\partial \xi^{\alpha} }} \cdot \frac{{\partial {\mathbf{d}}}}{{\partial \xi^{\beta }}} + \frac{{\partial \user2{\varvec{\varphi }}}}{{\partial\xi^{\beta } }} \cdot \frac{{\partial {\mathbf{d}}}}{{\partial\xi^{\alpha } }}} \right),\;\;\;\;{{a}}_{\alpha \beta } =\frac{{\partial \user2{\varvec{\varphi }}}}{{\partial \xi^{\alpha} }} \cdot \frac{{\partial \user2{\varvec{\varphi }}}}{{\partial\xi^{\beta } }}. $$
(1)

The principal curvatures \( (\kappa_{1} , \kappa_{2} ) \), used later, were the roots of the characteristic equation \( \det \left[ {{{\kappa}}_{\alpha \beta } - \kappa{{a}}_{\alpha \beta } } \right] = 0 \) and were computed at every Gauss point.

Material Model

We employed the Fung model to describe the wall tissue. The energy function takes the form

$$ W = c\left( {e^{Q} - 1} \right),\;\;\;\; Q = d_{1} E_{11}^{2} + d_{1} E_{22}^{2} + 2 d_{3} E_{11} E_{22} + d_{4} E_{12}^{2} . $$
(2)

This is surface density describing the stored energy per unit surface area. The stiffness parameter c has the dimension of force per unit length. Parameters \( d_{1} , d_{2} , d_{3} , d_{4} \) describe a planar orthotropic material symmetry, and \( (E_{11} , E_{22} ,E_{12} ) \) are the components of the Green–Lagrange strain tensor E with respect to the local material axes. In the aneurysms models, the major symmetry axis was assumed to be parallel to the basal plane (and tangent to the surface). The minor axis was perpendicular to the major and also tangent to the surface. Material parameters were set to be \( c = 0.056\;{\text{N/mm}},\;d_{1} = 17.58,\; d_{2} = 12.18,\;d_{3} = 7.57,\; d_{4} = 4.96, \) as in a previous study.24 This set of material constants was adopted from the experimentally obtained parameters reported in Seshaiyer and Hsu.35 Since the energy function depends only on surface strain, the incompressibility condition was not enforced constitutively, but kinematically by adjusting the current wall thickness.

The wall tension t (i.e., the stress resultant) followed from the formula \( {\mathbf{t}} = \frac{1}{J}{\mathbf{F}}\frac{\partial W}{\partial E}{\mathbf{F}}^{{\text{T}}} \) where F was the surface deformation gradient and \( J = {\text{Det}}\;{\mathbf{F}} \). Since bending moment and transverse shear stress were involved, their constitutive relations needed to be provided. In Zhou and Lu,47 we proposed a strategy for deriving approximate bending and transverse shear functions from the in-plane constitutive equation, and the method was adapted here. The stress couple m was assumed to relate to the curvature change ρ by \( {\mathbf{m}} = \mathbf{D}\varvec{\rho} \), where

$$ {\mathbf{D}} = \frac{{h^{2} c}}{6}\left[ {\begin{array}{*{20}c} {d_{1} } & {d_{3} } & {} \\ {d_{3} } & {d_{2} } & {} \\ {} & {} & {d_{4} } \\ \end{array} } \right] $$

The transverse shear forces \( s_{\alpha } \) was assumed to depend linearly on the transvers shear strain \( \gamma_{\alpha } = {\mathbf{d}} \cdot \frac{{\partial\user2{\varvec{\varphi }}}}{{\partial \xi^{\alpha } }} \) via \( s_{\alpha } = G_{\alpha 3} \gamma_{\alpha } \) (no summation on α). As in the early study24 the shear moduli in the two material directions were set to be \( G_{13} = G_{23} = 8\; {\text{N/mm}} \).

The material model with the parameters described above was regarded as the reference and named Material A. Two comparative models, Materials B and C, were introduced. In Material B, the stiffness parameter c was set to be 5.6 N/mm, which was 100× the reference value. In Material C, the values of \( d_{1} \) and \( d_{2} \) were interchanged to model a swap of symmetry axes.

Finite Element Model

A lumen pressure of 100 mmHg was applied uniformly on the wall surface. Translational degrees-of-freedoms on the cut boundary were fixed. The wall thickness for all models was set uniformly at 0.2 mm. In forward analyses, the image-derived geometry was treated as the undeformed geometry that deformed further under the lumen pressure. In the inverse analyses, the imaged geometry was taken as the deformed geometry, and the undeformed one was computed.

Results

Stresses were obtained by dividing the computed tensions by the assumed uniform thickness. Contours of the first principal stress based on the reference material were compared in six representative subjects (Fig. 2). The magnitude and distribution of the stresses were quite similar between inverse and forward analyses.

Figure 2
figure 2

Contours of the 1st principal stress in six aneurysms, computed using the reference material (unit: N/mm2). Stress values are obtained by dividing the computed wall tensions by the assumed thickness

Full size image

The influence of material parameters was assessed by comparing the stress solutions computed from Materials B and C to that from the reference material. Figure 3 depicts the pointwise percentage difference \( \left( {\frac{{\sigma_{1}^{\text{B}} - \sigma_{1}^{\text{A}} }}{{\sigma_{1}^{\text{A}} }} \times 100} \right) \) in first principal stress between models A and B, in the six samples. In the inverse chart, the blue (dark) color indicates a stress difference below 1%. Higher percentage errors were registered near the boundary or saddle regions. Overall, the stress difference in the forward analysis was much higher than that of the inverse analysis.

Figure 3
figure 3

Percentage difference in the 1st principal stresses between Materials B and A

Full size image

Table 1 presents the population mean of the maximum and mean values of the percentage difference. The maximum and mean percentage differences were first registered in each aneurysm, and then averaged over the population. Evidently, the inverse method exhibited a much smaller difference. In the inverse analysis, Material C appeared to have a stronger influence than Material B. The forward analysis showed an opposite trend.

Table 1 Statistics of percentage difference
Full size table

To further elucidate the stress differences between Materials A and B, the maximum and the mean values of the first principal stresses in all 26 aneurysms were plotted in Figs. 4a and 4b. The abscissae are the stress values from Material A and the ordinates are stresses from Material B. Each figure contains two groups of data, one for inverse analysis and the other for forward analysis. The inverse results fell on or near the 45° line in both figures, indicating that the stress values from the two materials were nearly the same. The forward maximum stresses (Fig. 4a) spread, suggesting a stronger influence of the material description. The forward mean stresses (Fig. 4b) spread less, but again the influence of the material model was evident.

Figure 4
figure 4

Comparison of stress difference between Materials B and A, in inverse and forward analyses. (a) Maximum values of the first principal stress; (b) mean values of the first principal stress. Each data point corresponds to an aneurysm. The abscissa is the stress value from Material A, and the ordinate is the value from Material B

Full size image

The same comparison was repeated for Materials C and A. The results were plotted in Figs. 5a and 5b. The inverse solutions remained close, while the forward predictions of maximum stress showed marginal to moderate differences.

Figure 5
figure 5

Comparison of stresses difference between Materials C and A. (a) Maximum values of the first principal stress; (b) mean values of the first principal stress. Each data point corresponds to an aneurysm. The abscissa is the stress value from Material A, and the ordinate is the value from Material C

Full size image

Since the inverse solutions differed only marginally between materials, we may take the stress values from Material A as the reference and compare them to forward solutions from different material models. Figure 6 presents the forward solutions of the maximum stress in all 26 aneurysm, along with their reference values. As seen from the figure, the forward analysis may over- or under-estimate the stress, depending on the constitutive parameters.

Figure 6
figure 6

Maximum principal stress obtained in inverse and forward analyses. A, B, and C stand for the three material models used in the analyses

Full size image

The mean values of the principal stresses were computed in each aneurysm, along with the mean values \( \bar{\kappa }_{{\mathbf{1}}} \) and \( \bar{\kappa }_{2} \) of the principal curvatures. A “theoretical prediction” of average principal stresses in each aneurysm was computed using the Laplace formula with the mean curvature values:

$$ \bar{\sigma }_{1} = \frac{P}{{\bar{\kappa }_{1} h}}\left( {1 - \frac{{\bar{\kappa }_{2} }}{{2\bar{\kappa }_{1} }}} \right),\;\;\;\;\bar{\sigma }_{2} = \frac{P}{{2 \bar{\kappa }_{1} h}}. $$
(3)

The curvatures were ordered such that \( \bar{\kappa }_{1} \ge \bar{\kappa }_{2} \), so that \( \bar{\sigma }_{1} \ge \bar{\sigma }_{2} \). The “theoretical mean stresses.” \( \bar{\sigma }_{1} \) and \( \bar{\sigma }_{2} \) were plotted against the computed mean values in Fig. 7. Clearly, the Laplace formula fits well with the computed stresses.

Figure 7
figure 7

Mean values of the principal stresses vs. the “Laplace predictions”

Full size image

Discussion and Conclusion

The sensitivity results clearly show that the influence of material description is weak in the inverse analysis. As observed in previous studies,22,48 this weak influence suggests that the IAs are approximately statically determined. In an idealized membrane structure, the wall tension can be viewed as locally in a plane stress state having three components. Since the membrane is curved in space, the equilibrium equation breaks into three component equations. Thus, the equilibrium problem is closed (three equations for three components).22 In a pure traction boundary problem, the wall tension should be completely determined without reference to the mechanical properties of the wall tissue. If the wall thickness is also known, the wall stress can be inferred from the tension. The importance of statically determinate stress solution has been recognized by many scholars. Humphrey called such a solution a universal result. 14 The Laplace solution, Eq. (3), is an example of a universal result. The Laplace solution has been utilized in the analyses of idealized IAs16,36 and abdominal aortic aneurysms.7 It is also the cornerstone of the (axisymmetric) membrane inflation test,12,32 the variants of which have been widely used in biomechanics.

In stress computation the inverse method better captures the static determinacy because it formulates and solves the equilibrium problem on the deformed configuration. If the wall deformation is yet to be determined, as in the forward approach, the influence of material parameters is implicit. Of course, the static determinacy breaks down if there are significant bending moment and transverse shear force in the wall. This study suggests that, for IAs of typical geometry (diameter >3 mm and wall thickness 0.1–0.2 mm), the membrane stress appears to dominate and thus the structure remains approximately statically determinate. Note that we employed a wall thickness of 0.2 mm, which is towards the thicker end of reported thickness range, to avoid underestimating the bending effect. For thinner aneurysms, the static determinacy is expected to be more prominent and the influence of material should be even weaker.

The percentage differences in Table 1 shows that the forward analysis can yield a pointwise stress difference up to ~100% in some aneurysms when the material stiffness was increased 100 times, while the differences in inverse solutions were around ~6%. This 100× stiffness difference, of course, exceeds the typical range of parameter variation employed in analysis, but it helps to make the case for the insensitivity of the inverse solution. Between Material C and A, the inverse solution pointwise differences (14.80 ± 3.02%) appeared to be higher than between B and A (6.79 ± 6.34%), but again the forward solution yielded a higher difference (21.90 ± 16.32%). The moderately higher difference between C and A suggests that change in material symmetry could have a stronger influence than a homogeneous increase or decrease in material stiffness. Thus, material symmetry should be treated with care, even in the inverse analysis. It should be noted that the percentage difference might not be a suitable metric for sensitivity because a high percentage value may be registered by a low baseline stress. Regardless, Table 1 indicates that, in all cases, the inverse method yielded a much smaller stress difference than the corresponding forward analysis.

Could inverse stress solutions be similarly insensitive to the functional form of the stress–strain relationship? To answer this question, we considered an isotropic neo-Hookean material described by the function \( W = \frac{{\mu_{1} }}{2}\left( {I_{1} + I_{2}^{ - 1} - 3} \right) + \frac{{\mu_{2} }}{4}\left( {I_{1} - 2} \right)^{2} \), where \( I_{1} = {\text{tr}}{\mathbf{C}} \) and \( I_{2} = \det {\mathbf{C}} \) are the principal invariants of the in-plane deformation tensor \( {\mathbf{C}} = {\mathbf{F}}^{T} {\mathbf{F}} \). Material parameters were set to be \( \mu_{1} = 0.34\;{\text{N/mm}},\;\mu_{2} = 5.6\;{\text{N/mm}} \). The inverse stress solution was compared to that of the baseline material for all 26 aneurysms. Overall, the stress distributions were fairly close. Figure 8 shows a comparison in one aneurysm; the stress contours are remarkably similar. The population mean of the maximum percentage difference was 15.10 ± 7.52%, similar to the case of Material C (change of symmetric axes). The population average of pointwise difference was −0.677 ± 0.38%.

Figure 8
figure 8

Inverse stress solutions from difference stress–strain functions. Left: Fung function. Right: neo-Hookean function. The average percentage difference is −0.5%

Full size image

Since the geometry is the primary determinant of the wall tension, it is natural to ask the question as to whether certain geometric features are suggestive of high tension and thus imply high stress. That size matters is abundantly clear based on both logic and as detailed in an earlier report31 and again supported by Fig. 8. But do some shape features predispose the IAs to high tension (or stress)? Answers to such questions are of practical interest. In this regard, there is a new finding that could be noteworthy: the peak tension is likely to occur in a saddle surface region. All aneurysms containing saddle regions displayed this pattern. This result is intuitive, because in a saddle region the tension component in the negative curvature direction competes with the one with the positive curvature. Recall that the membrane equilibrium follows the Laplace law \( t_{11 } \kappa_{1} + t_{22} \kappa_{2} = p \). Both \( t_{11 } \) and \( t_{22} \)should be positive as membranes are unlikely to sustain compression. If k 2 is negative, \( t_{22} \) contributes adversely to balancing the pressure. Also, a smaller \( \kappa_{1} \) implies a higher \( t_{11 } \). Thus, high tension is likely to occur in regions where \( \kappa_{2} \) is negative and \( \kappa_{1} \) is small—a flat saddle region, for example the base of a large daughter aneurysm. Figure 9 demonstrates such a case. It should be noted that daughter aneurysms typically have a thinner wall and thus, high stress can actually occur in the dome due to wall thinning.26 In any case, an implication of this finding is that, assuming other conditions the same, aneurysms with large saddle regions are more likely to bear high wall stress. This saddle region high stress postulate based on visual observation needs independent verification in a controlled population of brain aneurysms.

Figure 9
figure 9

Pattern of high stress location (1st principal stress, N/mm2)

Full size image

If we take the inverse solution, which changed minimally across materials, as the “physical stress,” we see from Fig. 6 that the forward analysis tended to overestimate the maximum stress in Material B while under-estimating the stress in Material A. For Material C, the effect was mixed. This complicated influence is understandable. If the maximum stress is induced by a negative curvature as occurring in a saddle region, the forward analysis will tend to reduce the negative curvature and thus under-predict the maximum stress. On the other hand, if an aneurysm is purely convex, the forward computation will tend to over-predict the maximum stress because the current radius of curvature will be enlarged everywhere. In contrast, the inverse approach is unresponsive to the curvature change because it utilizes the geometry fixed at the given deformed state. The complicated influence of geometry in forward analysis underlines the advantage of the inverse approach.

Several limitations of the study need to be discussed. First, all aneurysms considered were saccular and relatively deep (having relatively larger height to diameter ratio). It is known that structures as such are more inclined to be statically determinate than those that are relatively flat. Also, when the sac is deep, the boundary effect induced by displacement constraint is confined locally.9,33,43 Conclusions drawn in this study, therefore, need to be carefully re-evaluated for shallow aneurysms. With regard to the bending and transverse shear stress, we utilized approximate response functions and they could be improved. Nevertheless, since the bending stress is much smaller than the membrane stress (~2% in most surface regions of all aneurysms),13 we do not expect that improvements in bending and/or transverse shear description will change the sensitive results in any significant manner. Another limitation to consider is the ignorance on the perivascular environment—particularly the kind that may mechanically impact the aneurysm, such as differences in intracranial pressure and possibly contact constraints that may exist in some of these aneurysms. Lastly, the assumption of uniform wall thickness is certainly a convenience. While the tension is dictated primarily by surface geometry, the actual stress depends inversely on the thickness.

While significant for stress estimation, the inverse method may have another implication, that is, to facilitate the identification of wall tissue properties. If the wall tension can indeed be determined to a satisfactory accuracy without reference to the tissue properties in question, one could leverage the inversely computed wall tension together with surface strain acquired otherwise to define the wall elasticity, and do so point by point. This approach avoids solving large-scale optimization problems since material properties are characterized point-wisely. It also circumvents the coupled iterations usually seen in optimization based identification methods. The concept of pointwise identification has been proposed by the authors’ team20,44; and numerically tested using aneurysm models.45,46 The method is still in its infancy. To be clinically applicable, patient-specific dynamic scans with sufficient spatial and temporal resolution will be needed. In a remarkable exploratory effort with patient-specific image data, Balocco et al.3 report that current spatial resolution in diagnostic images is insufficient for extracting mechanical properties using a traditional reverse-FE optimization scheme. Whether the pointwise identification scheme may be more effective remains to be seen, but it holds potential.

In conclusion, we have demonstrated that, as along as quasi-static stress analysis is concerned, IAs may be regarded as statically determinate and the inverse method can predict the wall tension reasonably well without accurate constitutive description. The inverse method, therefore, is more reliable in the sense that it is weakly sensitive or even practically insensitive to the uncertainties in material description. This is important for patient-specific analysis, as patient-specific tissue properties are difficult to obtain. The inverse method may also lend itself to new tools for characterizing the wall elastic properties in vivo. This is a promising area, and much remains to be done there.