Surface Curvature as a Classifier of Abdominal Aortic Aneurysms: A Comparative Analysis

Abstract

An abdominal aortic aneurysm (AAA) carries one of the highest mortality rates among vascular diseases when it ruptures. To predict the role of surface curvature in rupture risk assessment, a discriminatory analysis of aneurysm geometry characterization was conducted. Data was obtained from 205 patient-specific computed tomography image sets corresponding to three AAA population subgroups: patients under surveillance, those that underwent elective repair of the aneurysm, and those with an emergent repair. Each AAA was reconstructed and their surface curvatures estimated using the biquintic Hermite finite element method. Local surface curvatures were processed into ten global curvature indices. Statistical analysis of the data revealed that the L2-norm of the Gaussian and Mean surface curvatures can be utilized as classifiers of the three AAA population subgroups. The application of statistical machine learning on the curvature features yielded 85.5% accuracy in classifying electively and emergent repaired AAAs, compared to a 68.9% accuracy obtained by using maximum aneurysm diameter alone. Such combination of non-invasive geometric quantification and statistical machine learning methods can be used in a clinical setting to assess the risk of rupture of aneurysms during regular patient follow-ups.

Introduction

An abdominal aortic aneurysm (AAA) is the abnormal, localized dilation of the aorta over 3 cm of its outer wall diameter below the renal arteries. The incidence of AAA in the adult population is 2–4% in the USA20 and 4.9–9.9% in the UK,6,22 and it is growing with the increase in average life expectancy. The rupture of AAAs is the cause of death in more than 15,000 people in the USA20 and more than 8000 in the UK.6,22

The mortality rate of emergent AAA repair is about 40–50% when an aneurysm ruptures, but about 50% patients die before reaching the hospital.6 To prevent AAA rupture, the most common standard for elective intervention is a maximum transverse diameter of 5.5 cm and an expansion rate over 1 cm/year.2,10 With these criteria, traditional repair is open surgery, which has a mortality rate of 2–4%.8,26 The alternative, minimally invasive endovascular aneurysm repair (EVAR), has a mortality rate of 1.7%.5 However, small aneurysms with maximum diameters less than 5.5 cm do rupture and large aneurysms over 5.5 cm can be stable in the patients’ life time. To this end, biomechanical approaches to assess the AAA rupture risk have shown that peak wall stress (PWS) is more reliable in assessing the rupture risk for small aneurysms, which the traditional approaches cannot assess efficiently.3,27 The location of maximum wall stress is highly correlated with the rupture site and PWS in ruptured AAAs is 60% higher than in unruptured AAAs.27

Clinicians have carefully observed individual contrast-enhanced (CT) images over time for evaluating the maximum AAA transverse diameter and assessing the appropriate medical treatment for pre-surgical planning. Segmented and reconstructed AAAs can provide a qualitative assessment by visual inspection, but radiologists cannot easily evaluate the irregular shape of the AAA quantitatively for predicting its rupture risk. A quantitative approach based on geometric characterization may be a better clinical aid than visual inspection alone.

In recent studies related to geometric assessment, Pappu et al.15 reported that three ruptured aneurysms showed more out of plane growth than axial growth. Similarly, Sacks et al.19 suggested that the complex AAA geometry shows an equivalently complex wall stress distribution, and the location of high curvature also exhibits the location of highest stress. They also developed a reliable method for reconstructing and analyzing anatomical cardiovascular structures with curvatures.23 Correspondingly, Giannoglou et al.4 proposed that the curvatures of mean and maximum centerlines are highly correlated with PWS. In the only study of its kind, Leung and others found that the region of maximum stress appears to coincide with peaks in of Gaussian curvature.9 Overcoming the limitations of the aforementioned studies, Shum et al.24 demonstrated the assessment of AAA rupture risk with the use of shape based features, such as those used in the present work, and non-invasive assessment of regional wall thickness. The basis for this assessment was the work of Batchelor et al.1 who determined that normal and abnormal brain surface shapes can be measures of the relation between the shape of the human brain surface and the function of the underlying tissue. A similar approach was followed by Raghavan and co-workers11,17 who introduced the use of global indices of shape and size of cerebral aneurysms as indicators of rupture potential.

The present work represents a contribution to the long-term goal of individual rupture potential based on the quantitative characterization of AAA shape through non-invasive assessment of the aortic wall surface curvature processed via the standard of care for AAA patients: computed tomography angiography. The objectives of this work are, therefore: (i) to evaluate the suitability of the biquintic Hermite finite element method (BQFE) to discretize the AAA outer wall surface compared to the traditional method of biquadratic surface patching (BSP); and (ii) once validated, to apply BQFE to compute ten global curvature indices and assess their potential utility as discriminators of AAA rupture status. One hundred and ninety-three patient specific AAAs were divided into two subgroups (unruptured vs. ruptured) while twelve patient specific AAAs constituted a third subgroup of surveillance aneurysms (those that were not scheduled for surgical repair at the time of data acquisition). The three subgroups were analyzed with classical statistical analysis to evaluate the differences in the global curvature features. In addition, the first two subgroups were subject to further examination by applying four machine learning algorithms for which their accuracy was calculated to demonstrate the potential use of machine learning classification as a tool that can be used by vascular surgeons to assess AAA rupture risk in the clinic.

Methods

Evaluation of BSP and BQFE for Surface Curvature Quantification

The BSP method is widely used for estimating local curvatures of anatomic structures such as the right ventricular free wall, cerebral, and AAAs.11,17–19 The BQFE method is used for not only estimating local curvatures, but also for constructing surfaces using a single interpolation scheme.25

BQFE has six terms defined at each of four nodes: the radial coordinate and its first, second, and cross derivatives with respect to the element’s local coordinates $\xi$, $\eta$. The internal point P in each element is computed by summation of the product of 24 terms25:

$$ R_{\text{P}} = N_{i}^{jk} \left( {\xi_{\text{P}} ,\eta_{\text{P}} } \right)R_{i}^{jk} \;\;\;\;i = 1,4;\;\;j,k = 0,2;\;\;j + k \le 2, $$

(1)

where $R_{i}^{jk}$ is the vector of nodal variables, subscript $i$ denotes the node number, and superscripts $j,k$ denote the order of the derivatives with respect to the local coordinates $\xi$, and $\eta$, respectively. The magnitudes of the local principal curvatures are calculated by the metric and curvature tensors.

BSP has the following form18:

$$ S\left( {u,v} \right) = au^{2} + 2buv + cv^{2} , $$

(2)

where a, b, and c are best fit constants determined for each surface node using the u-v-n tangent plane coordinate system. The magnitudes $k_{1}$ and $k_{2}$ of the local principal curvatures are computed using Eq. (3)21:

$$ k_{1} = a + c + \sqrt {\left( {a - c} \right)^{2} + 4b^{2} } ,\;\;\;\;k_{2} = a + c - \sqrt {\left( {a - c} \right)^{2} + 4b^{2} } . $$

(3)

From these, ten global curvature indices were defined and calculated for each AAA model13: summation of Gaussian and Mean curvatures (KG, KM), the area-averaged Gaussian, Mean, first principal and second principal curvatures (GAA, MAA, K1AA, K2AA), and the L2-norm of the aforementioned curvatures (GLN, MLN, K1LN, K2LN). The mathematical formulation of these features is described in Appendix I and was postulated by Martufi et al.13 for AAA geometric analysis.

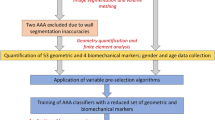
The extent of the AAA is defined by the segmentation of the first contrast-enhanced CT image available immediately below the left renal artery and the last CT image available immediately above the aorto-iliac bifurcation. Hence, we use the binary masks resulting from the segmentation with our in-house code (VESSEG 1.0.2, Carnegie Mellon University, Pittsburgh, PA),23 which define the extent of the outer boundary of the abdominal aorta. AAA surface curvature is then defined by the quantification of the principal curvatures (k ₁ and k ₂) at each of the surface mesh nodes (in the case of BSP) or the fitted surfaces (in the case of BQFE) that make the outer wall surface topology. The ten metrics of curvature are quantified from the local curvatures k ₁ and k ₂ as representative global curvatures of each AAA model. The reconstructed AAA surfaces are converted into linear triangular elements since the BSP method and its derived global curvature indices require surface elements for their assessment. The reader is referred to Appendix II for a detailed mathematical description of the curvature calculation using the BQFE method. Figure 1 illustrates the sequence of the steps followed in the present work starting from the upload of DICOM formatted CT images to the AAA curvature classification using machine learning techniques. A mesh sensitivity analysis was conducted to determine the optimal surface mesh density required for the BSP method to yield the geometric indices within a reasonably small relative error.

Figure 1

Schematic of computational modeling protocol: from CT images to calculation of global curvature features

To compare the performance of the BQFE and BSP methods qualitatively and quantitatively, idealized geometries such as a cylinder and a symmetric AAA were utilized to evaluate the local principal curvatures. The following function was used for generating the geometry of the symmetric AAA model19:

$$ R\left( z \right) = 1 + a_{0} e^{{ - a_{1} \left( {\frac{{z - a_{2} }}{{a_{3} }}} \right)^{2} }} $$

(4)

where $a_{i}$ are constants that define the length and local diameter of the AAA. Figure 2 shows the cylinder and symmetric AAA models. The curvatures of both methods were compared to their analytical counterparts using Eq. (5)16:

Figure 2

Virtual models used for a comparative analysis of the BQFE and BSP methods: (a) cylinder, D = 16 mm and (b) symmetric AAA, D _max = 30 mm

$$ e_{{{\text{L}}2}} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {k_{{{\text{n}}i}} - k_{{{\text{a}}i}} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {k_{{{\text{a}}i}} } \right)^{2} }}} $$

(5)

where $k_{\text{n}}$ and $k_{\text{a}}$ represent the numerical and analytical (first or second) principal curvatures.

In view of the computational cost, the execution time was accounted for in minutes by running the computations of an HP laptop with an Intel Core i5 2.53 GHz processor and 8 GB DDR3 RAM.

Optimization of BQFE Method for AAA Surface Curvature Estimation

To estimate the appropriate number of elements needed to model an AAA in the circumferential and axial directions, we considered the total number of degrees of freedom (DOF) for the meshes against the root mean square error (RMS) between seed and fitted points.14 Figure 3 illustrates least-square fitting of one AAA surface and its seed points.

Figure 3

Least-square fitting used in the BQFE method: seed points (blue) and fitted surfaces (other colors)

Higher order polynomial fits tend to become unstable when the data is sparse. A penalty function such as the Sobolev norm can be added to the error function25:

$$ E\left( R \right) = \sum\limits_{d = 1,D} {\left| {R\left( {\xi_{d} ,\eta_{d} } \right) - R_{d} } \right|^{2} } + \iint {S\left[ {R(\xi ,\eta )} \right]d\xi d\eta } $$

(6)

where

$$ S = A\left( {\frac{\partial R}{\partial \xi }} \right)^{2} + A\left( {\frac{\partial R}{\partial \eta }} \right)^{2} + B\left( {\frac{{\partial^{2} R}}{{\partial \xi^{2} }}} \right)^{2} + B\left( {\frac{{\partial^{2} R}}{\partial \xi \partial \eta }} \right)^{2} + B\left( {\frac{{\partial^{2} R}}{{\partial \eta^{2} }}} \right)^{2} . $$

(7)

Our data in each cross-section consist of 30–50 points and the number of cross-sections is 30–40 in a representative AAA. This amount of data is sufficient so that we do not need to implement the Sobolev norm; the norm is still applied for adjusting errors in the principal, Gaussian, and Mean curvatures.

Application of BQFE Method to the Diverse AAA Subject Population

Three population subgroups were considered for the application of the optimized BQFE method. The ruptured population subgroup (rAAA) consisted of 93 AAAs that had an emergent intervention and ruptured within a month after the last contrast-enhanced CT exam was performed and prior to the repair. The data from these subjects were collected retrospectively following multi-institutional IRB approval, at Allegheny General Hospital (AGH) in Pittsburgh, PA, Northwestern Memorial Hospital (NMH) in Chicago, IL, and Rochester Medical Center (RMC) in Rochester, NY. The unruptured population group (uAAA) consisted of 100 AAAs that underwent elective repair for which the last CT scan available prior to the repair was used as the image source for subsequent segmentation. The third population subgroup consisted of 12 small surveillance AAAs (sAAA), for which the image data was obtained from the first CT exam available in the follow-up history of subjects who were considered at low risk of rupture at the time of diagnosis and placed in a “watchful waiting program” by the treating physician at AGH. The following imagining parameters characterized the majority of the Standard DICOM images: (i) 512 × 512 scan matrix size; (ii) average pixel size = 0.7693 mm (0.6172–0.9688 mm); (iii) pixel intensity = 0–2000; and (iv) average slice thickness = 3.0 mm. This study was subject to Internal Review Board (IRB) approvals at CMU, AGH, NMH, and RMC, and no patient consent was necessary as the data was acquired by a retrospective review of records.

The average maximum diameter of the sAAA subgroup was 44.72 ± 5.41 mm; the average maximum diameter of the uAAA subgroup is 53.74 ± 11.41 mm, and the rAAA subgroup is 69.83 ± 19.93 mm. All CT scan images were segmented with VESSEG.23 Figure 4 illustrates VESSEG’s GUI and its various functions available for CT or MR image segmentation. Each image dataset was then meshed using BQFE method based on the point clouds and centerlines obtained as a product of the VESSEG segmentation protocol.

Figure 4

Graphical User Interface for VESSEG v.1.02, Carnegie Mellon University, used for segmentation of all CT images processed in this work

Statistical Analysis

Aneurysms with a maximum diameter in the range of 50–55 mm are recommended for elective repair as the present clinical standard. To assess the efficacy of this practice, we compared the classification accuracy of maximum diameter to that of ten global curvature indices by means of four statistical analyses using a size-matched approach. The four comparative statistical analyses are as follows: (i) two subgroups: 100 uAAA and 93 rAAA; (ii) two subgroups: size-matched with maximum diameters in the range 50–60 mm resulting in 42 uAAA and 15 rAAA; (iii) three subgroups: size-matched with maximum diameters in the range 50–55 mm resulting in 12 sAAA and 28 uAAA, and size-matched with maximum diameters in the range >60 mm resulting in 65 rAAA; (iv) three subgroups: size-matched with maximum diameters in the range 35–51 mm resulting in 12 sAAA, 34 uAAA, and 10 rAAA. The two-subgroup analyses were conducted by a t test or a Wilcoxon test, and the three-subgroup analyses were conducted by an F-test (ANOVA) or a Kruskal–Wallis test.

For the purpose of classification and prediction of AAA rupture status, the following data mining techniques were utilized with the ten global curvature indices computed for the first comparative analysis (two subgroups: 100 uAAA and 93 rAAA): Decision Tree, Naïve Bayes, k-Nearest Neighbor (kNN), and Support Vector Machine (SVM). In addition, a second classification study was conducted with the same data mining algorithms but using maximum diameter (D _max) as the only classification variable for the first comparative analysis (two subgroups: 100 uAAA and 93 rAAA). The machine learning algorithms were implemented using WEKA (WEKA v.3.6, University of Waikato, Hamilton, New Zealand).12

Results

From the mesh sensitivity analysis performed for the BSP method at mesh sizes ranging from 14,400 to 799,236 elements, all global curvature indices were considered to converge at a mesh size of 500,000 triangular surface elements, for which the percentage difference in the indices was less than 0.2% when compared to the indices calculated with the 799,236-element mesh. A comparison between BQFE and BSP methods was performed with the cylinder phantom shown in Fig. 2, where the errors for both methods with respect to the analytical solution were negligible $\left( {e_{{{\text{L}}2}} \ll 10^{ - 6} } \right)$. Figure 5 illustrates the qualitative results of local Gaussian and Mean curvature distributions for the symmetric AAA phantom, obtained with parameters $a_{0} = 5$, $a_{1} = 0.7$, $a_{2} = 8$, and $a_{3} = 4$ in Eq. (4). The distribution appears to be identical among the two numerical methods and the analytical curvature solution. However, the discrepancies between the two methods can be observed in Fig. 6, which shows the Gaussian and Mean curvatures in the axial direction of the phantom for the analytical, BSP, and BQFE solutions. The following relative errors were quantified for the L2-norm of the Gaussian and Mean curvatures with respect to the analytical solution: $e_{{{\text{L2}},{\text{Gaussian}}}} = 0.0314$ and $e_{{{\text{L}}2,{\text{mean}}}} = 0.0206$ with BQFE, and $e_{{{\text{L}}2,{\text{Gaussian}}}} = 0.0867$ and $e_{{{\text{L2}},{\text{mean}}}} = 0.0366$ with BSP. The lower errors obtained with BQFE, nevertheless, are not significantly different. In view of the computational cost comparison, BQFE curvature calculations takes less than 1 min of CPU time on the aforementioned computational platform, while BSP calculations require 5–10 min of CPU time. From these analyses, the BQFE method provides slightly more accurate and faster surface curvature estimations.

Figure 5

Gaussian and Mean curvature distributions for the symmetric AAA resulting from the analytical solution, and the BQFE and BSP numerical models

Figure 6

Comparison of the analytical curvature with the resulting BSP and BQFE numerical solutions for the (a) Gaussian and (b) Mean curvatures along the longitudinal axis of the AAA axisymmetric phantom illustrated in Fig. 5

The BQFE mesh size analysis with the symmetric AAA phantom was conducted in the axial direction as the geometry has the same curvature in the circumferential direction. RMS errors in Gaussian curvatures calculated for 2, 3, 4, and 6 axial elements were as follows: 0.1387, 0.1177, 0.1237, and 0.2943, respectively. Similarly, RMS errors in Mean curvatures were 0.0299, 0.0619, 0.0664, and 0.1682, respectively. From this analysis, three elements in the axial direction were selected as optimal for all subsequent BQFE computations. Since BQFE is a fitting method with high order (e.g., 10th order) Hermite equations, it becomes unstable when the input data has low spatial resolution; however, errors can be reduced by increasing the number of elements up to an upper bound. This is because the RMS error is defined as the distance between seed points and projected points onto the surfaces. Each AAA model is generated from approximately 40 cross-sections (at the location of the original CT images) and 40 points in each cross-section, on average. In the circumferential direction, each section would have about 40/6 = 6.67 points when using six elements, or 40/4 = 10 points when using four elements. Based on our analysis of various combinations of circumferential elements, we conclude that a section should have more than seven points to avoid unstable fitting of the surfaces. Such analysis indicated that four circumferential elements were sufficient to model AAA topologies using the BQFE method. An increased level of accuracy is achieved when using the Sobolev norm, where one can adjust the L2-norm error by varying the coefficients A and B in Eq. (7). This resulted in the following errors: $e_{{{\text{L2}},{\text{Gaussian}}}} = 0.0309$ and $e_{{{\text{L2}},{\text{mean}}}} = 0.0203$ with $A = B = 0.001$; $e_{{{\text{L2}},{\text{Gaussian}}}} = 0.0258$ and $e_{{{\text{L2}},{\text{mean}}}} = 0.0165$ with $A = 0.01\;\& \;B = 0.001;$ and $e_{{{\text{L2}},{\text{Gaussian}}}} = 0.0330$ and $e_{{{\text{L2}},{\text{mean}}}} = 0.0220$ with $A = 0.001\;\& \;B = 0.01$ for the symmetric AAA phantom.

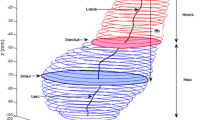
Table 1 describes the mean and standard deviation of 10 global curvature indices and the maximum transverse diameter for the three AAA population subgroups. Figure 7 illustrates the Gaussian and Mean curvature distributions in representative small, unruptured, and ruptured AAAs, showing the heterogeneity of the AAA topology when quantified using complex curvature measures. The outcome of the classical statistical analysis is shown in Tables 2–5 for which the null hypothesis tested was based on the absence of statistical differences in any of the 11 geometric features among a pair or all the population subgroups. Tables 6 and 7 present the outcome of the machine learning studies with the four algorithms using the entire sample size of the ruptured and unruptured AAA population subgroups (i.e., the aforementioned first comparative analysis). kNN resulted in the highest average percentage accuracy with 85.5% when using all 10 surface curvature indices as classifiers, while SVM had 83.4% accuracy, Decision Tree 83.3%, and Naïve-Bayes 80.1% (Table 6). Similarly, the Decision Tree algorithm resulted in the highest average percentage accuracy with 68.9% when using only D _max as a classifier, while SVM had 67.8% accuracy, kNN 66.8%, and Naïve-Bayes 68.8% (Table 7). Due to the underlying correlations between geometric features, we did not consider using feature selection in the machine learning analysis; the correlation of all 11 features is illustrated in Fig. 8.

Table 1 Mean and standard deviation of the 10 global curvature indices and maximum transverse diameter for all small (sAAA), unruptured (uAAA), and ruptured aneurysms (rAAA)

Table 2 Unruptured (U) vs. ruptured (R) comparative analysis

Table 3 Size-matched Unruptured (U) vs. ruptured (R) comparative analysis for 50 mm ≤ D _max ≤ 60 mm

Table 4 Small (S) vs. unruptured (U) vs. ruptured (R) comparative analysis for 35 mm ≤ D _max ≤ 51 mm (S), 50 mm ≤ D _max ≤ 55 mm (U), and D _max > 60 mm (R)

Table 5 Size-matched small (S) vs. unruptured (U) vs. ruptured (R) comparative analysis for 35 mm ≤ D _max ≤ 51 mm

Table 6 Percentage accuracy (%) of the machine learning algorithms with 10-fold validation applied for classification assessment with 10 surface curvature indices

Table 7 Percentage accuracy (%) of the machine learning algorithms with 10-fold validation applied for classification assessment with maximum diameter (D _max) alone

Figure 7

Gaussian (left) and Mean (right) curvature distributions for a representative (a) small AAA, case 7, (b) unruptured AAA, case 11, and (c) ruptured AAA, case 86

Discussion

Sacks et al.18 reported that the right ventricular free wall can be modeled as a thin-walled shell structure by using a BSP for curvature estimations. Their work was extended to the geometric characterization of AAAs as they identified that changes in surface topology in the aneurysmal aorta result not only from localized dilation of the aortic wall, but also due to bending of the abdominal aorta associated with local curvature analysis.19 Smith et al. 25 applied the BQFE method for the first time to compute all geometric variables associated with surface curvature, surface deformation, and strain by using a single interpolation scheme. This approach was implemented in the present work to compare it with the traditional BSP method, optimize it for AAA topologies, and provide reliable curvature estimations in a population-based comparative analysis.

In the present work, we have optimized the BQFE method for AAA topologies resulting in four circumferential and three axial elements that discretize the aneurysmal outer wall surface. Modeling with a single circumferential element causes an opened end at the outer wall boundary at θ = 0 and $2\pi$. Since there are at least 1600 points representing any given AAA topology, the fitted surfaces are stable up to six elements in either (axial or circumferential) direction, which yields more than 44 points per element. When the number of elements in one direction is greater than six, additional points are required or the Sobolev norm should be applied. However, increasing the number of elements does not guarantee greater accuracy in curvature estimation and, thus, more than six elements in either direction are not needed for patient specific AAA topologies. The RMS error quantification reveals that RMS errors decrease with increasing DOFs. Doubling the number of DOFs reduces the error by approximately 27–30%. The point clouds generated by our in-house image segmentation code yields 40–60 axial cross-sections per AAA, each represented by 40–50 points for the surface fitting, which makes it unnecessary to implement the Sobolev norm for gaining additional mesh stability. Alternatively, the Sobolev norm can be applied to adjust the L2-norm errors by optimizing the coefficients A and B in Eq. (7). Errors in the major principal, Gaussian, and Mean curvatures decreased with a higher A coefficient; errors in the minor principal curvatures decreased with a higher B coefficient.

To classify different AAAs between ruptured and unruptured groups, Kultangwattana et al.7 used a Naïve Bayes algorithm with three parameters: area, perimeter, and compactness from normal and abnormal aortas. They obtained accuracy levels of 95%; however, this can be explained in part due to the groups having large differences in the size-related features. Shum et al.24 trained a Decision Tree algorithm with twenty-eight geometric features: seven 1-D size, six 2-D size, four 3-D size, two 3-D shape, four curvature, and three wall thickness indices. The overall accuracy of the algorithm was 86.6% when applied to a sample size of 76 AAAs. It was shown that a centerline length of the AAA sac less than 160.57 mm and an outer wall surface area less than 81.76 cm² correctly classified 45 of 66 unruptured AAAs analyzed in the study. Similarly, 6 of 10 ruptured AAAs were classified correctly for an AAA sac centerline length greater than 160.57 mm. The remaining 25 AAAs were classified correctly using aneurysm tortuosity and the ratio of intraluminal thrombus volume to AAA sac volume. While the limited sample size and skewed sizes of the groups are important limitations of the Shum study,24 it demonstrated the importance of shape-related features in accurately classifying AAA groups based on the nature of the eventual repair (elective or emergent). The quantification of surface curvatures has also been reported for patient specific cerebral aneurysms. Ma et al.11 described the evaluation of four curvature indices, including GAA, MAA, GLN, and MLN, reporting that curvature assessment did not yield a statistical difference between normal and aneurysmal cerebral arteries. However, the sample size used in their study was not sufficiently large to determine if curvatures can be used as classifiers for cerebral aneurysm rupture risk.

Our classical statistical analysis consisted of two parts: (i) two-population subgroup analyses based on ruptured and unruptured AAAs; and (ii) three-population subgroup analyses based on small (surveillance), ruptured, and unruptured AAAs. The first analysis (reported in Table 2) indicates that almost all geometric features except for GAA (p > 0.05) can be adequate discriminators of rupture status. Aneurysms with a maximum diameter near 55 mm, the present clinical standard for recommending elective repair, present a challenge for assessing their rupture potential. An analysis with size-matched AAAs for 50 mm ≤ D _max ≤ 60 mm (Table 3) shows that D _max is no longer a discriminator and that the following six global curvature indices, ranked in order of significance (p < 0.05), are different between ruptured and unruptured AAAs: K2LN, K1LN, GLN, K2AA, MLN, and MAA. When analyzing the three population subgroups allocated according to their size (Table 4), D _max is understandably the only feature that discriminates them. When analyzing pairs of these subgroups, no other geometric feature was found to be different between small and unruptured AAAs. However, five global curvature indices, namely MAA, GLN, MLN, K1LN, and K2LN, were found to be different between small and ruptured AAAs. When repeating the analysis using a size-matched approach with 35 mm ≤ D _max ≤ 51 mm (Table 5), the same outcome was found when comparing the small and unruptured AAAs. In addition, only GLN and MLN were found to be different between small and ruptured AAAs. The statistically different features that are common among the four comparative analyses are the global curvatures GLN and MLN, i.e., the L2-norm of the Gaussian and Mean curvatures, respectively. Therefore, we conjecture that the non-invasive quantification of Gaussian and Mean curvatures may be an important translational tool for evaluating AAA rupture potential in the vascular clinic compared to the use of maximum transverse diameter alone.

Due to the limited data available for small AAAs, the machine learning classification algorithms were applied only for the 100 unruptured and the 93 ruptured AAAs (Tables 6 and 7). For the curvature-based classification analysis, all algorithms yielded overall accuracies greater than 80% with the most accurate algorithm being kNN with three neighbors (85.5%). For the maximum diameter-based classification analysis, all algorithms yielded overall accuracies greater than 66% with the most accurate algorithm being Decision Tree (68.9%). This remarkable outcome indicates that statistical differences in surface curvatures have a higher degree of accuracy in correctly classifying patient specific AAAs as either ruptured or unruptured (once their risk of rupture is perceived to be high according to the vascular surgeon’s size-based assessment or the onset of symptoms) than maximum diameter alone. Feature selection was not possible as a strategy for improving the classification accuracy since almost all features except D _max were highly correlated with each other (see Fig. 8). This is explained by the fact that all global curvature indices are obtained from the spatial distribution of the major and minor principal curvatures (k ₁ and k ₂) (Appendix I).

Figure 8

Correlation among geometric features for the uAAA (n = 100) and rAAA (n = 93) population subgroups. The highest degree of correlation is 1, while the lowest is −0.9132

The present work was subject to some important limitations. For all the statistical analyses there was a mismatch in the sample size of the groups compared. This limitation was mitigated by the sample sizes being greater or equal than the number of features (n = 11) compared. Another factor limiting the clinical impact of this work was the neglect of time dependent surface curvatures for the small AAA subgroup, as the image data were obtained from the first CT scan available for patients placed in a surveillance program. Moreover, this work was limited to evaluating 10 curvature-based indices characterizing the AAA topology; no other shape or size related features were taken into account. Future work will be focused on evaluating the time rate of change of geometric features characterizing small AAAs followed through CT imaging every 6 months.

Conclusion

In this work we assess the potential for AAA outer wall surface curvatures, quantified using the BQFE method, to be used as classifiers of aneurysm population subgroups. A retrospective review of 205 CT AAA image datasets was performed and the images were segmented and reconstructed with the resulting 3D geometries used for curvature estimation with a closed 4 × 3 BQFE interpolation scheme. The geometric indices were analyzed by classical statistical analysis using the entire sample size of the subgroups and with size-matched approaches. An additional classification study was performed using the ruptured and unruptured population subgroups by means of testing the accuracy of four machine learning algorithms.

The implementation of the BQFE is optimized for AAA topologies by using three axial and four circumferential elements, which results in lower errors (albeit not statistically significant) of the surface discretizations compared to the conventional BSP method. However, the computational cost of BQFE is a significant improvement with respect to BSP; BQFE is 7.5 times faster, on average. The classification analysis of surface curvatures using the unruptured and ruptured AAA datasets reveals that the geometric indices GLN and MLN (the L2 norm of the Gaussian and Mean curvatures) yield the highest classification accuracy (85.5%) when using kNN with three neighbors as the classification algorithm. In contrast, using the aneurysm maximum diameter (D _max) as the sole metric of classification resulted in 68.9% classification accuracy.

As patient specific AAAs have asymmetric, tortuous, and complex surfaces, the geometric characterization of their outer wall topology by means of a non-invasive curvature quantification algorithm, combined with a classification strategy, should be considered to assess AAA rupture risk in the vascular clinic. Our work provides an indication that AAA surface curvatures can be more accurate predictors of rupture potential than maximum diameter alone. The translational potential of a tool that can perform a combination of curvature quantification and classification in an automated manner is evident: it would provide the physician with valuable information on the complex AAA shape that is currently unattainable in the vascular suite by simple observation of 3D reconstructed medical images.

Appendices

Appendix I: Definition of Global Curvature Features (i.e., Geometric Indices)

Area of a Triangular Element

$$ S_{i} = \frac{1}{2}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}_{i} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{b}_{j} $$

where the final points of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}_{i}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{b}_{j}$ share one edge of the triangle.

Gaussian and Mean Curvatures

The roots of Eqs. (3) and (8) are defined as the local (nodal) curvatures, $k_{1i}$ and $k_{2i}.$ The local Gaussian (K) and Mean (M) curvatures are given by

$$ K_{i} = k_{1i} \cdot k_{2i} $$

$$ M_{i} = \frac{1}{2}\left( {k_{1i} + k_{2i} } \right) $$

Global Curvature Indices (Calculation Described in Detail by Martufi et al. 13)

KG :

Square root sum of the Gaussian curvature

KM :

Square root sum of the Mean curvature

GAA :

Area averaged Gaussian curvature

MAA :

Area averaged Mean curvature

K1AA :

Area averaged major principal curvature

K2AA :

Area averaged minor principal curvature

GLN :

L2 norm of the Gaussian curvature

MLN :

L2 norm of the Mean curvature

K1LN :

L2 norm of the major principal curvature

K2LN :

L2 norm of the minor principal curvature

   

Appendix II: Brief Description of Curvature Estimation by BQFE Interpolation

A BQFE interpolation has C ² continuity on the surface on which curvatures are probed by having the first and second derivatives defined at the surface nodes such that BQFE derived curvatures are more accurate than those computed with lower order continuity methods. To calculate curvatures directly from BQFE, we use Eq. (8) and the subsequent tensor products:

$$ \left( {g_{\theta \theta } g_{\theta z} - g_{\theta z}^{2} } \right)k_{n}^{2} - \left( {b_{\theta \theta } g_{zz} + g_{\theta \theta } b_{zz} - 2b_{\theta z} g_{\theta z} } \right)k_{n} + \left( {b_{\theta \theta } b_{zz} - b_{\theta z}^{2} } \right) = 0 $$

(8)

where $b_{\alpha \beta } = \sqrt {g_{\theta \theta } g_{\theta z} - g_{\theta z}^{2} } \left| {\begin{array}{*{20}c} {X_{\alpha \beta } } & {Y_{\alpha \beta } } & {Z_{\alpha \beta } } \\ {X_{\theta } } & {Y_{\theta } } & {Z_{\theta } } \\ {X_{z} } & {Y_{z} } & {Z_{z} } \\ \end{array} } \right|$ and $g_{\alpha \beta } = X_{\alpha } X_{\beta } + Y_{\alpha } Y_{\beta } + Z_{\alpha } Z_{\beta } .$

The subscripts of X, Y, and Z represent differentiation with respect to that variable. Equations (9)–(11) demonstrate how the mathematical descriptors of the BQF elements and the corresponding Cartesian coordinates of the surfaces are related to each other:

$$ \begin{aligned} X &= R\cos \theta + \mathop \sum \limits_{k} a_{k} \cos (k\omega z) \hfill \\ Y &= R\sin \theta + \mathop \sum \limits_{j} b_{j} \sin (k\omega z) \hfill \\ Z &= z \hfill \\ \end{aligned} $$

(9)

where $2\omega \pi /\left( {Z_{\hbox{max} } + Z_{\hbox{min} } } \right)$, $a_{k}$ and $b_{j}$ are constants, and k and j are the number of terms in the Fourier series used to represent the longitudinal AAA axis. For example, the derivatives with respect to ${{\uptheta}}$ and z in the X direction are given by

$$ \begin{gathered} X_{\theta } = \frac{\partial R}{\partial \theta }\cos \theta - R\sin \theta \hfill \\ X_{\theta \theta } = \frac{{\partial^{2} R}}{{\partial \theta^{2} }}\cos \theta - 2\frac{\partial R}{\partial \theta }\sin \theta - R\cos \theta \hfill \\ X_{\theta z} = \frac{{\partial^{2} R}}{\partial \theta \partial z}\cos \theta - \frac{\partial R}{\partial z}\sin \theta \hfill \\ X_{z} = \frac{\partial R}{\partial z}\cos \theta - \mathop \sum \limits_{k} \omega ka_{k} \sin (k\omega z) \hfill \\ X_{zz} = \frac{{\partial^{2} R}}{{\partial z^{2} }}\cos \theta - \mathop \sum \limits_{k} \omega^{2} k^{2} a_{k} \cos (k\omega z). \hfill \\ \end{gathered} $$

(10)

The radial coordinate R is the fitted variable and its derivatives are expressed in terms of the element shape functions N which are biquintic hermite shape functions:

$$ \begin{gathered} \frac{\partial R}{\partial \theta } = \frac{\partial \xi }{\partial \theta }\;\frac{{\partial N_{i}^{jk} }}{\partial \xi }R_{i}^{jk} \hfill \\ \frac{{\partial^{2} R}}{{\partial \theta^{2} }} = \left( {\frac{\partial \xi }{\partial \theta }} \right)^{2} \frac{{\partial^{2} N_{i}^{jk} }}{{\partial \xi^{2} }}R_{i}^{jk} \hfill \\ \frac{{\partial^{2} R}}{\partial \theta \partial z} = \frac{\partial \xi }{\partial \theta }\;\frac{\partial \eta }{\partial z}\;\frac{{\partial^{2} N_{i}^{jk} }}{\partial \xi \partial \eta }R_{i}^{jk} \hfill \\ \frac{\partial R}{\partial z} = \frac{\partial \eta }{\partial z}\;\frac{{\partial N_{i}^{jk} }}{\partial \eta }R_{i}^{jk} \hfill \\ \frac{{\partial^{2} R}}{{\partial z^{2} }} = \left( {\frac{\partial \eta }{\partial z}} \right)^{2} \frac{{\partial^{2} N_{i}^{jk} }}{{\partial \eta^{2} }}R_{i}^{jk} . \hfill \\ \end{gathered} $$

(11)

A more detailed calculation is presented by Smith et al.25