Introduction

Interest in the rheology of the erythrocyte in the mid-20th Century grew out of an appreciation of the role of the red cell in diseases like sickle cell anemia and also the susceptibility of red blood cells (RBCs) to hemolysis in medical devices emerging at the time. Cell damage observed even today with prosthetic heart valves,15,39 cardiopulmonary bypass,25 and artificial kidneys contributes to anemia, along with the toxic effects associated with free hemoglobin in the circulatory system.38 The cause of mechanical trauma to blood cells has been attributed to large frictional forces or shear stresses,30 which are associated with the flow of blood through such devices.

Factors and conditions resulting in hemolysis were established by using well-defined flow systems in the laboratory. Such work led to an understanding that hemolysis depends on both exposure time and on the magnitude of the shear stress, when data generated by various techniques at different labs were considered in aggregate.30,35,42 Inversely related, short exposures to high stresses or long exposures at lower stresses cause cell destruction.16

Many investigators sought to develop mathematical expressions to predict the fraction of cells lysed based on this theoretical underpinning.4,8,9,16,40 A power-law equation typically related free hemoglobin to the product of stress and exposure time, each raised to a power determined from a fit to experimental data. While these equations have been helpful in understanding mechanical trauma, empirical models of hemolysis as a function of shear stress and exposure time have fallen short over the years in fully characterizing lethal damage to RBCs. Results from application of correlations to predict hemolysis quantitatively have been disappointing, and for various reasons some researchers have proposed amendments of the power-law model or the use of entirely different models.4,5,10,18,21,22,26,28,37

One of the problems with these empirical models relates to the cell’s exposure. Differences in the nature of shear stress exposure in controlled laboratory conditions compared to the reality of clinical settings contribute to inaccuracies of the power-law model of hemolysis estimation. The clinical situation in blood contacting devices has been described as localized regions of high stress, “hot spots”, with very short exposure times.48 Grigioni et al. 20 cited the fact that prior estimations were derived using experimental set-ups that yielded a constant, uniform shear—which did not take into account repetitive transient loading on the cells, a common scenario in many blood contacting devices. Some investigators have recognized the potential importance of the history of mechanical loading in blood trauma and its combination with resistance of cells to accumulated damage.8,46 As such, the inability of current power-law models to account for the past shear history of a cell adds to the inaccuracy of their predictions,20,22 where, for example, sub-hemolytic trauma to cells can leave them more susceptible to rupture when subjected to shear yet again. Antaki1 also discussed the utility of power-law models and concluded that they are unable to capture the effects of subtle features of the blood contacting geometry, which have been shown to largely affect hemolysis. Previous researchers have attempted to use current blood damage power-law models to estimate hemolysis from CFD results, often using a Lagrangian approach,22,33,45 where damage was calculated along multiple streamlines in the domain of interest. These conventional models provide poor estimates of hemolysis when compared to experimental hemolysis data in the same flow system, thus these investigators have illustrated the inaccuracy of current models for hemolysis prediction. These shortcomings are important because they compromise the validity of catastrophic damage estimates made by engineers working on the design, development and improvement of life-saving medical devices.17,47

Interest in mechanical trauma remains high as evidenced by a recent FDA Critical Path Initiative. In 2009, a total of 28 groups across the country performed numerical simulations to predict stress levels and hemolysis in a model flow with features known to cause hemolysis, particularly turbulent blood flow through a sudden contraction or sudden expansion. Currently, an estimation of hemolysis from computations can vary widely depending on the choices and assumptions made by the user performing the simulation. Specifically, the numerical method, the type of computational mesh, the order of convergence and the turbulence model chosen are among the factors that are important to the simulation outcome. Using experimental measurements by three different laboratories as the basis for validating the computational results, the FDA sought to identify the most accurate model. Preliminary results of this analysis have been presented and the wide variation in results indicates the need for both new physical insights and numerical approaches.23,41

The ongoing problems with predicting hemolysis during flow suggest a continuing need to re-examine the theoretical basis for mechanical trauma. Our group has used computational fluid dynamics (CFD) to analyze a set of classical hemolysis experiments in capillary tubes by Keshaviah.27 Keshaviah studied hemolysis in small diameter capillary tubes with an emphasis on the effect of entrance geometry. His experimental procedure was to force diluted washed RBCs into a capillary, varying the ratio of the larger antechamber diameter to the capillary diameter, as well as the fundamental geometry of the entrance (i.e., sharp edged vs. tapered).

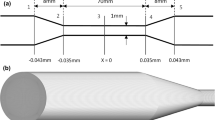
Keshaviah concluded that hemolysis in his experiments was related to the structure of the entrance to the capillary. For example, a tapered entrance caused only 0.1% hemolysis while a blunt entrance region at the same flow conditions resulted in a much higher level of cell damage at 5.9%. These findings suggested that examination of the entrance region with CFD might lead to new insights into mechanism(s) of catastrophic damage to erythrocytes during flow. With CFD, we were able to examine more closely the nature of the flow in the entrance region of Keshaviah’s experimental setup. See Fig. 1 for geometry.

It is clear that the forces associated with blood flow cause hemolysis. We know from basic fluid mechanics that these forces will be high near the wall and will decrease toward the centerline. As such, our approach was an “all or nothing” assumption in which there exists a hemolysis zone near the wall of the capillary, where the higher stresses existed, and a core region where cells passed without overt cell damage (Fig. 2a). In this conceptualization, all cells and only cells in the hemolysis zone experience failure of the cell membrane. The boundary between these two regions was determined so that the fraction of the volumetric flowrate passing through the hemolysis zone corresponded to the observed percent hemolysis reported by Keshaviah. Thus, the spatial location of the threshold streamline or pathline varied with experimental conditions (e.g., an experiment that resulted in more hemolysis would have a larger hemolysis zone) while stresses at the boundary between the hemolysis and hemolysis free regions would presumably be similar in all cases. Figure 2b is an illustration of the stress profile that a cell traveling along the threshold streamline would experience—a constant low shear stress while traveling through the large chamber, followed by a sharp increase in stress as the flow is constricted to enter the capillary, and finally a constant stress while the cell travels through the capillary. Simulations of the various experiments by Keshaviah were run (see supplementary summary table), and characteristics of the flow, such as maximum shear stress along the threshold fluid particle pathline, were calculated and compared.

Our initial aim with this analysis was to ascertain the critical level of shear stress required for cell lysis. In the absence of a consistent finding, we went on to explore extensional flow at the capillary entrance. Results from our analysis provide evidence that hemolysis in this laminar shearing flow can be more closely related to extensional stresses, and indicate that new models should consider extensional stress as well as exposure history for accurate hemolysis predictions.

The nature of steady elongational flow is such that it is difficult to study experimentally with adjacent fluid elements separating at an exponential rate.6 McGraw, in a thesis supervised by Frattini, was the first to examine the deformation of the erythrocyte in a miniaturized extensional flow rheometer under a microscope.32 They obtained larger cell deformations for extensional flows, aspect ratios of 2.0–5.9, than those observed for a shearing flow at comparable stress levels.11 Just recently, Lee et al. examined red cell deformability in a microfluidic device where both extensional and shear flow effects were compared. Deformability as gauged by the deformability index, DI = (L − B)/(L+B) where L and B are semiaxial lengths of the deformed cell, was found to be 0.51 and 0.29 at 3.0 Pa for extensional and shearing flows, respectively.29 Taking the greater deformation into account and the fact that extensional flows of liquids more readily result in drop breakup, Lee noted the insufficiency of existing hemolysis models that focus only on shear stress.

Lee’s observation of relative deformability for extensional and shear stresses is particularly notable in light of an elegant analysis incorporating the stress tensor to characterize mechanical trauma of the red cell.3 In this work, Arora et al. obtained the following equation for hemolysis:

$$ {\frac{{\Updelta {\text{Hb}}}}{\text{Hb}}} = 3.62 \times 10^{ - 7} \left( {\mu_{\text{blood}} \sqrt {{\frac{{f_{1}^{2} {\text{DI}}^{2} }}{{(1 - {\text{DI}}^{2} )f_{2}^{2} }}}} } \right)^{2.416} t^{0.785} $$
(1)

where f 1 and f 2 are constants, Hb is hemoglobin concentration, t is exposure time, μblood is the viscosity of blood, and DI is a distortion index synonymous with the deformability index defined by Lee et al. Ultimately, the tensor analysis by this group is based only on shear stress, but, interestingly, the final expression (Eq. 1) includes as a key dynamic factor the “distortion index” of the cell. According to Lee, DI approaches constant values of 0.6 and 0.55 as stress increases for extensional and shear flows, respectively. If the Arora equation also reflects the dependence on DI for extensional flows, then the small difference in DI above suggests 40% greater likelihood of hemolysis in extensional flow compared to a shearing flow.

Others have reported cell damage in the presence of extensional flow.19,31,33 Lokhandwalla and Sturtevant,31 for example, noted the presence of extensional flow with hemolysis from shock wave lithotripsy. When working with hamster ovary cells, Mollet et al. 34 found that high levels of cell damage were seen in areas of high extensional stress. Although ovarian cells are much different from red blood cells, it would not be unreasonable to assume the same mechanisms might affect RBCs and ovarian cells alike. To date, no one has provided evidence that extensional stresses in a typical flow cause hemolysis. Some studies have speculated that extensional stress may be related to membrane breakup, however, to our knowledge this is the first report providing a link between a threshold value of extensional stress and red cell hemolysis.

Methods

Analysis

In order to analyze the flow results for the effects of the flow-induced stresses, the shear stress and the extensional components of the stress tensor were calculated for blood treated as a Newtonian fluid. The shear stress is given by:7

$$ \tau_{\text{rz}} = - \mu \left( {{\frac{{\partial v_{\text{r}} }}{\partial z}} + {\frac{{\partial v_{\text{z}} }}{\partial r}}} \right) $$
(2)

where μ is the dynamic viscosity of blood, v r is the radial velocity, and v z is the axial velocity. The radial and axial directions are shown in Fig. 1a. The equations for the extensional components of the stress tensor are:7

Figure 1
figure 1

Schematic of simulation domain for a 3:1 contraction. (a) Axial view of constriction geometry. (b) Cross-sectional view of constriction. The average number of nodes for all simulated capillaries was approximately 710,000 with an average computational cell size at the entrance of the capillary on the order of magnitude of 5 × 5 μm

Full size image
$$ \tau_{\text{rr}} = - \mu \left( {2{\frac{{\partial v_{\text{r}} }}{\partial r}}} \right) $$
(3)
$$ \tau_{\text{zz}} = - \mu \left( {2{\frac{{\partial v_{\text{z}} }}{\partial z}}} \right) $$
(4)

These variables were calculated in the entire flow domain as well as along a threshold streamline that originated at the inlet of the flow field.

Flow Simulations

To set up the computational model, a two-dimensional representation of the capillary tube and entrance geometry (Fig. 1) was created and fitted with a quadrilateral grid using the mesh-generation software Gambit 2. The mesh was then imported to the CFD package Fluent 6, as a two-dimensional, axisymmetric model. The dimensions of the capillary tube were 0.035 cm inner diameter and 2.8 cm length for all simulations. The authors are aware that the corner present in the simulation geometry produces a singularity, which can affect the solution.36 The calculation of values used in the analysis of the stresses present in the flow is not performed close to the wall at the corner, so it is expected that the singularity has no effect on the results presented here. Additionally, the simulated grid was refined in the region of the singularity until no change in the solution was found. For each model, an initial simulation was run using the mesh created in Gambit. After this initial simulation, the mesh was refined in regions of high velocity gradient and then refined globally until the velocity magnitude at multiple points in the domain did not change significantly (percent difference <3%) with additional decreases in grid cell size. The average number of nodes for grid-independent results for the simulated capillaries was approximately 710,000, with smaller mesh cells concentrated near the entrance of the capillary and in other regions where high gradients of velocity would be expected. This method of grid refinement led to an average computational cell size at the entrance of the capillary on the order of magnitude of 5 × 5 μm, with smaller cells concentrated closer to the capillary wall. The flow equations were solved using the implicit formulation and the laminar solver available in Fluent, because all capillary Reynolds (Re) numbers were within the laminar regime. The Reynolds number distinguishes laminar (Re < 2000), transition (Re 2000–2500), and turbulent flows (Re > 2500), and is given for the capillary by:

$$ \text{Re} = {\frac{\rho Dv }{\mu }} $$
(5)

where v is the bulk velocity in the capillary, D is the capillary diameter, ρ is the fluid density, and μ is the fluid viscosity. For momentum, the first order upwind interpolation scheme was used; for pressure, the standard Fluent interpolation; and for pressure–velocity coupling, the SIMPLE scheme was used.

The boundary conditions were specified as a mass flow rate inlet condition, which yields a flat flow profile at the upstream boundary, and as an outflow outlet condition at the capillary exit. An outflow boundary condition is appropriate when the flow velocity and pressure details are unknown before simulation; this condition in Fluent extrapolates flow conditions from the interior of the domain to the conditions of the outflow plane. The center line of the capillary was specified as the axis, about which the model was symmetrical.

Twenty-one experiments were reproduced computationally, representing different entrance geometries, flow rates, and fluid viscosity. Four different two-dimensional models were created, representing the variations in contraction ratio (for a sharp contraction) as well as the tapered contraction that was investigated experimentally by Keshaviah. The contraction ratio is the ratio of the larger chamber diameter to the capillary tube diameter (see Fig. 1 for a contraction ratio of 3:1). Specifically, these included a contraction ratio of 27:1 with flows ranging from Re number 700–1050, a contraction ratio of 3:1 with flows ranging from Re number 875–1255, a contraction ratio of 2:1 with flows ranging from Re number 925–1230, as well as simulations with more than double the viscosity of those previously discussed and a contraction ratio of 27:1, with flows ranging from Re number 200–400. These results are presented in Table 1, in the supplementary material. During each simulation, convergence was considered to be achieved when the residuals of the velocity components and the equation of continuity were below 1 × 10−5. The specified fluid for all simulations was considered Newtonian, with a viscosity of 0.005 Pa s for most simulations and a viscosity of 0.013 Pa s for simulations of Keshaviah’s higher viscosity experiments with dextran.

Results

Shear Stress

Because most investigators consider the shear stress to be one of two major factors in hemolysis, the first parameter investigated was τrz. When the shear stress is calculated for the entire domain, it is clear that, as the fluid enters the capillary tube from a larger chamber, an area of high velocity gradients and shear stresses develops at the corner of the contraction (Figs. 2, 3). This area of higher shear is also observed when the shear stress is plotted along the specified threshold streamline—as evidenced by a sharp spike in shear stress magnitude at the capillary entrance (Figs. 2b, 3). When the maximum shear stress along the threshold streamline for all cases is plotted (varying Reynolds number, contraction ratio, and viscosity), no uniform threshold value of stress is observed (Fig. 4). In Fig. 4, a linear regression of the shear stress data vs. percent hemolysis is shown. In the presence of a threshold shear stress value, the slope of shear stress vs. hemolysis should be zero, however, the large slope of this regression line makes clear that the peak value of shear stress does not yield a threshold stress value that applies for all experimental scenarios.

Figure 2
figure 2

(a) Contours of velocity magnitude at the corner of a 27–1 contraction (Re = 1055; μ = 0.005 Pa s). Flow is from left to right. The threshold streamline is shown, and the hemolysis and hemolysis free zones are illustrated. The volumetric flow rate passing through the area between the threshold streamline and the vessel wall as a percentage of the total volumetric flow is equal to the percent hemolysis for this experiment. The boundaries are not shown, but are similar to those given in Fig. 1. (b) The expected shear stress profile along the threshold streamline, with the large increase in shear stress magnitude at the entrance highlighted. CFD simulations indicate that there is a large peak in shear stress at the entrance followed by a constant shear stress value in the capillary. The peak in shear stress occurs at a streamline length, s = 0.45 cm, which corresponds to z = 0.1038 cm

Full size image
Figure 3
figure 3

Contours of shear stress magnitude at the entrance of a sharp contraction (CR = 27:1; Re = 1055; μ = 0.005 Pa s). High shear stresses are seen at the corner of the contraction, and a plume of elevated shear stress magnitude is seen to extend into the capillary. CR contraction ratio

Full size image
Figure 4
figure 4

Peak shear stress on threshold streamline vs. percent hemolysis. The slope of the trendline shows the lack of a consistent threshold peak shear stress across investigated parameters. Hemolysis threshold streamline is chosen such that the “hemolysis zone” shown in Fig. 2 encompasses a fraction of the flow equal to the percent hemolysis from Keshaviah’s data. CR contraction ratio

Full size image

Gradient of Shear with Respect to Displacement Along a Streamline

The second parameter investigated as a possible cause of cell lysis was the gradient of the shear stress with respect to displacement along a given streamline. A large gradient in shear stress might give rise to a tension sufficient to rupture the cell membrane. This analysis also does not yield a threshold value that was common for all experimental scenarios. Instead, a nonlinear relationship with hemolysis was observed and, although hemolysis levels are much higher in the higher viscosity simulations, the gradient of the shear stress along the threshold streamline is much smaller in magnitude than that for the lower viscosity experiments.

Extensional Components of Stress Tensor

The final factors investigated in this work were the extensional components of the stress tensor. Like shear stress, these components exhibited spikes in magnitude in the entrance to the capillary tube. The extensional stresses also vary depending on location within the domain—the magnitude is nearly zero in most of the entrance chamber and the capillary while, close to the wall at the entrance, it is as much as an order of magnitude larger than the maximum value on the threshold streamline. Unlike shear stress and the shear stress gradient, the extensional stresses yield a consistent threshold for hemolysis. When either the maximum radial or axial extensional stress is found along the specified threshold streamline, and these data are compared across all simulated experiments, little variation in the maximum value of extensional stress with hemolysis is seen (Fig. 5).

Figure 5
figure 5

(a) Peak radial stress tensor component on threshold streamline vs. percent hemolysis for various contraction ratios and viscosities. (b) Peak axial stress tensor component on threshold streamline vs. percent hemolysis for various contraction ratios and viscosities. For both plots, a regression of the data is shown—for both extensional components, the slope of the regression is smaller than that for the shear stress

Full size image

The extensional components of the stress tensor are significant in the entrance region of the capillary and similar in magnitude to τrz (Fig. 6). From the figure, it is clear that the radial extensional component is near zero everywhere except the entrance, where a large spike in stress magnitude occurs. In comparison, the shear stress magnitude, which is small in the entrance chamber, peaks during the contraction, but then levels off in the capillary tube at a value of the same order of magnitude as the peak. This indicates that, if lysis were correlated to shear stress only, the damage would not be associated with the entrance region, contrary to Keshaviah’s conclusions.

Figure 6
figure 6

Comparison of τrz and τrr along the threshold streamline for a single experimental scenario (Re = 1055; μ = 0.005 Pa s). This plot shows that τrr has a sharp peak at the entrance of the capillary and then drops to zero once in the capillary, while the shear stress peaks at the entrance, but then maintains a value of the same order of magnitude as the peak through the capillary. This indicates that the effect of τrr is concentrated at the entrance of the capillary, while that of τrz likely would be an important effect throughout the capillary, contrary to the entrance-effect conclusions of Keshaviah

Full size image

Discussion

Shear stress and exposure time have been reported for years as the major factors contributing to hemolysis, but alone in power-law models have not served as an adequate framework for broadly understanding cell damage in the laboratory or clinic. Alternatively or in combination, extensional stress may be a significant factor contributing to failure of the RBC membrane. Zhao et al. 48 examined the deformability of the RBC in a constricted microchannel where cells were subjected to a shear stress up to 5000 Pa. They found that a maximum RBC elongation index (i.e., the same quantity termed as deformability index in Lee et al.) of approximately 0.5 was reached at a shear stress of 123 Pa in the entrance to the constriction. Zhao et al. did not observe cell rupture in their experiments, however, it appears that a chamber with a well-rounded capillary entrance was used, which would lower stress levels at the entrance of the constriction. Using conditions from the worst-case hemolysis experiment by Keshaviah (27:1 contraction ratio, highest flow rate), an additional simulation with a well-rounded entrance (as defined in44) was performed. It was found that the extensional stresses along the threshold streamline decreased significantly, below a level that hemolysis would be expected based on the results presented here (axial stresses were reduced by 1/2, radial stresses were reduced by an order of magnitude). The importance of constriction inlet geometry on hemolysis level has been observed elsewhere,43 and is a valid reason for the lack of cell rupture seen by Zhao et al. The fact that Zhao et al. did not observe cell rupture, even at shear stresses of 5000 Pa, tends to support our conclusion that shear stress was not the determining factor for hemolysis in Keshaviah’s experiments, where shear stresses of the same order of magnitude were present.

The significance of the entrance region to hemolysis is reiterated in the comparison shown in Fig. 7. With a flow rate nearly twice as large, shear stresses for fully developed flow in the capillary region of Fig. 7a with a tapered entrance must be greater than those of the capillary of Fig. 7b with the sharp contraction. Cell damage, however (as measured by hemoglobin loss), was more than three times as great (6 vs. 1.8%) for the abrupt 27:1 contraction when compared to the gradual entrance. Thus, something unique to the capillary orifice seems to be causing hemolysis in this flow system. Also underlining the effect of the entrance region, we found that the maximum shear stress along the threshold streamline is not significantly larger than the shear stress experienced by the fluid while in the capillary—a fact that does not fit well with the conclusion that entrance effects are the predominant cause of blood cell trauma in this system, especially when one considers the exposure time to be orders of magnitude larger within the capillary. In contrast, extensional stresses exist only in the neighborhood of the capillary orifice. That is, they are unique to the entrance and they are similar in magnitude to shear stress.

Figure 7
figure 7

Contours of shear stress magnitude for (a) a tapered geometry with a high volumetric flow rate and (b) a 27:1 sharp contraction with a low flow rate. For (a) Re = 1173; μ = 0.005 Pa s; For (b) CR = 27:1; Re = 706; μ = 0.005 Pa s

Full size image

The more cogent evidence from this study in support of extensional stress comes from the “all-or-nothing” threshold analysis, in which a series of threshold streamlines were calculated for a series of experimental scenarios. Maximum shear stress fails to exhibit a threshold value consistent with the level of hemolysis (Fig. 4). Moreover, the magnitude of the maximum shear stress on the threshold decreases markedly as hemolysis increases! On the other hand, the peak values of the extensional stresses τrr and τzz along the threshold streamline remain relatively constant when plotted against level of hemolysis (Fig. 5). When comparing the four parameters studied, we can look at the spread of the data for each in an attempt to determine which has the characteristics of an appropriate threshold value. The spread is a measure of how close all collected data points are to the average value of those data points and is defined as the range of values divided by the mean of all values. The spread for the peak gradient of the shear and the peak shear stress, 2.00 and 0.85, respectively, was larger than that for the peak radial and axial extensional stresses, with values of 0.43 and 0.55, respectively.

The analysis of each variable discussed thus far is based on the assumption that there is a threshold magnitude of any given variable and that this threshold magnitude is experienced by a cell traveling along a streamline chosen to correspond to the assumed boundary between the hemolysis zone and the hemolysis free zone. Assuming that there is a constant threshold value of any given variable, it would be expected for plots of the maximum magnitude of this variable found on the threshold streamline vs. the percent hemolysis to yield a horizontal line—i.e., the maximum value of the variable on the threshold streamline and percent hemolysis should have no correlation because the percent hemolysis is taken into account when choosing the threshold streamline. One measure of the correlation between two variables is the coefficient of determination, or r 2. The coefficient of determination, r 2, is a measure of how well the data can be predicted by the regression and is equal to the sum of the squared differences between the actual data values and the average of all data values (the total sum of squares) minus the sum of the squared differences between the actual data values and the estimated values from the regression, normalized by the total sum of squares (Excel 2007 User’s Guide). In the absence of randomly distributed points, correlation coefficients r 2 near zero suggest a constant function relationship. Linear regression yielded r 2 values for τrr and τzz of 0.20 and 0.16, which compared to 0.75 for τrz. We believe these results make a strong case for hemolysis by extensional flow. The maximum value of the angular component of the stress tensor on the threshold streamline was also analyzed but yielded a significantly lower magnitude, approximately a quarter of the value of the other components, and an r 2 value of 0.92, thus this component was not considered further. It is difficult to tell whether τrr or τzz might be more important for this flow; in some cases, τzz is slightly larger, but cells experience large values of τrr first and the exposure time is longer while in other cases the reverse is true. In any case, onset of damage in Keshaviah’s experiments occurs at stress levels of approximately 3000 Pa with exposure times on the order of microseconds. The level is comparable to the magnitude of stress reported for jets with a similar exposure time, where shear stresses were assumed to be responsible.30 It is also well above stresses on the order of 10 Pa applied by Lee in his microfluidics system, for which he specifically noted the absence of cell rupture with extensional flow.29

Since extensional flow more effectively increases DI, and DI has been related to cell damage, the findings in the present study are consistent with extensional flows contributing to hemolysis. It is not clear whether shear stress is a necessary element or not. Results from the literature on red cell rheology do help to suggest a mechanism by which shear stress and extensional stress might work in concert. The motion of a RBC in a shearing flow field is unusual. Rather than rotating, the cell membrane revolves around the cytoplasm in a manner characterized as “tank treading.”14 Fischer deduced the motion of the red cell membrane from videomicroscopy images of cells during flow in a device called the rheoscope, essentially a specially constructed cone and plate viscometer.13 Increases in the shear rate result in a higher frequency of revolution with the same basic velocity profile for the membrane. Described in Cartesian components after Fischer, the velocity components in the membrane (Fig. 8) are v x  = fC(y) and v y  = 0 where f is the tank-tread frequency and C(y) represents the circumference parallel to the x-axis. This velocity profile describes a shearing flow within the two-dimensional structure of the red cell membrane.

Figure 8
figure 8

Velocity components in the red blood cell membrane (seen from above) according to Fischer: v x  = fC(y) and v y  = 0 where f is the tank-tread frequency

Full size image

Observations in micropipette deformation experiments led to the characterization of the red cell membrane as essentially a two-dimensional fluid,12 and, since dilation of only a few percent results in rupture, it can be characterized as a two-dimensional incompressible fluid. As such, flow in the membrane must satisfy the two-dimensional continuity equation:

$$ {\frac{{\partial \nu_{x} }}{\partial x}} + {\frac{{\partial \nu_{y} }}{\partial y}} = 0 $$
(6)

We note that Fischer’s velocity profile for the erythrocyte membrane given above satisfies the mathematical constraint of continuity. Moreover, with v y identically equal to zero in a shearing flow, it follows that v x must be a constant at any given value of y to satisfy the continuity equation. A cell entering a region with an extensional flow component in the direction of translation, will encounter a gradient of v x and, constrained by continuity, it dilates with the prospect of failure. This is precisely the situation with the complex flow in the entrance region of the capillary. An implicit assumption to this analysis is that the two-dimensional incompressible fluid character observed at the very low deformation rate of the micropipette experiments and at the intermediate deformation rates of the rheoscope apply at the high deformation rates of the capillary tube.

We emphasize that our findings do not eliminate shear stress as playing an important role in hemolysis, only that extensional components must be considered for accurate predictions. Extensional flow is a feature common to contractions and expansions, geometries notably relevant to many clinical situations and to the FDA Critical Path Initiative. While the present investigation dealt with laminar flows, it perhaps raises the issue as to whether extensional components in turbulence might also be contributing to clinical instances of hemolysis, an area that is also undergoing reexamination.2,24

Conclusions

Simulations of laminar capillary entrance blood flow yield evidence that the hemolysis seen in this type of flow is related to the extensional components of the stress tensor. This, in combination with an available mechanism for rupture due to extensional stresses, leads the authors to propose that extensional stresses can be a significant cause of RBC trauma. This work proposes a threshold value of the extensional stresses for hemolysis of 3000 Pa for exposure times on the order of microseconds. While this explanation does not eliminate the possibility that some hemolysis is caused by shear stress, there is sufficient indication that extensional stresses should be taken into account in blood trauma models. Much more investigation on this topic is required to characterize completely RBC lysis due to mechanical trauma.