Introduction

In recent years, the scientific simulation of cardiovascular blood flow has been of growing importance by recognizing cardiac dysfunction to be the most common cause of death in the western world. Nowadays, the diagnostic discovery of cardiovascular disease is a standard procedure. However, there is still uncertainty about how to evaluate the interdependence of fluid flow and soft tissue deformation. The vast majority of classical engineering applications focus on linear elasticity concepts and Newtonian fluid flows. This is doubly not true for cardiovascular simulation where the solid and fluid materials have complex non-linear properties. Even small structural deviations may cause large changes in fluid behavior. The particular combination of cardiovascular flow and large deformation can be described by “finite haemo-elasticity” and its dimensionless characteristic numbers.

Ventricular Flow Models

Focusing on computational fluid dynamics (CFD), so-called prescribed geometry movement provides a wealth of information that is not available in clinical practice.13 With the introduction of Arbitrary Lagrange–Euler (ALE) methods, Saber et al.17 presented patient-specific flow models based on realistic chamber geometries. Subsequently, Domenichini and Pedrizetti2 evaluated some of the first analysis of realistic 3D vortical flow through the left ventricle. Schenkel et al.,19 among others, investigated the influence of healthy, diseased, and operated ventricle shapes on the asymmetric vortex formation and the overall cavity flow pattern. Recently, Oertel et al. (www.isl.mach.uni-karlsruhe.de) presented perhaps the most comprehensive fluid mechanical heart model to date. The Karlsruher Heart Model (KaHMo) incorporates left ventricle and large vessels for simulating left ventricular flow dynamics based on patient-specific MRI data. Unfortunately, these strategies are not able to capture the effects of out of plane movement or torsion which constrains the vital transfer of momentum between fluid and solid domain. An overall evaluation, however, requires structural influences on the cavity flow to be taken into account; fluid–structure interaction (FSI) becomes of utmost importance.

Fluid–Structure Interaction

As shown by McQueen and Peskin,11 one way of modeling the structural influence of moving boundaries and heart valves is represented by the so-called Immersed-Boundary-Method15 and embedded fiber-like constraints. The solid domain is not explicitly represented within the fluid domain, but rather exists by the additional force field that the solid exerts on the fluid where the two domains overlap. Lemmon and Yoganathan9 further investigated cardiac disease and dysfunctions based on this approach. Apart from the fact that this approach often focuses on shell-like structures, adaptive versions as published by Griffith et al.3 show higher computational requirements compared to classical mesh-movement procedures.

Watanabe et al.23 published coupled MRI heart models in which both the fluid and solid domain deforms. The governing equations are solved monolithically. Former studies by Cheng et al.1 have shown the overall potential of this FSI concept but also a lack in numerical robustness. Penrose and Staples16 presented a different, partitioned method of fluid–solid coupling based on one specific commercial software combination using under-relaxation techniques. However, apart from a potential restriction in modeling flexibility, this method does not allow the arbitrary extension of cardiovascular flow models.

Structural Extension of Flow Models

The novelty of the coupling concept presented within this work is on the the multi-physical extension of existing CFD models rather than on the creation of another stand-alone fluid–solid coupling concept. Partitioned finite hydro-elasticity simulations require a so-called implicit coupling, i.e., an iterative data-exchange during each time-step. For the first time, arbitrary solid and fluid codes can be coupled implicitly. We present a code coupling framework using Abaqus 6.7-1 (www.simulia.com) as FEM and Fluent 6.3.26 (www.fluent.com) as FVM solver. The interface communication is performed by the mesh parallel code coupling interface MpCCI 3.0.5 (www.mpcci.de) developed by the Fraunhofer Institute (SCAI) (www.scai.fraunhofer.de).

The modeling concept is presented using the existing KaHMo stand-alone blood flow model. Unlike the previous approaches, the separated partition concept uses most suitable discretization and modeling techniques but requires special emphasis on momentum and energy equilibrium. The fluid domain representation is similar to the approach published by Oertel et al.14; the representation of myocardial response is mainly based on the ideas of Nash and Hunter12 but simplified towards a macroscopic composite approach. The new KaHMo FSI model is not restricted to the patient-specific status quo but enables further flow prediction due to altering constitutive properties. A functional method to simulate and classify the overall flow structure can help the clinical cardiologist to decide if surgery is necessary and which surgical method is the most effective.

Methods

Continuum Mechanics

The partitioned coupling concept presented within this work uses specialized software capabilities for solving the underlying differential equations of fluid and solid mechanics. As a consequence the two physical domains are usually described by either fixed or moving reference frames. In order to formulate governing equations, numerical coupling and evaluation procedures, the kinematic and kinetic interface conditions must be taken into account.

Arbitrary Lagrangian–Eulerian Description

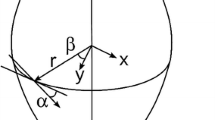
Whereas the structural FEM solution is obtained on a moving Lagrangian reference system, standard FVM flow solutions are usually based on a spatially fixed Eulerian description. However, as the structural deformation also influences the fluid domain boundary, an Arbitrary-Lagrangian–Eulerian (ALE) reference system interconnects both frames at the common interface. In this context, the reference frame motion in Eulerian description in time defines the relative velocity \({{\mathbf{v}}}_{\rm g}.\)

Governing Equations

Referring to Fig. 1 the relative velocity \({{\mathbf{v}}}_{\rm g}\) at the common fluid–solid interface is consistent with the physical velocity \({{\mathbf{v}}}\) and a Lagrangian reference system needs to be used. On the other hand, fixed mesh regions with \({{\mathbf{v}}}_{\rm g}=0\) still refer to a standard Eulerian description for the fluid domain. This relative way of velocity representation in ALE formulation needs to be taken into account in the following. The continuum mechanics equilibrium of mass and momentum is given by Eqs. (1) and (2), respectively. As discussed in Fig. 1 before, this formulation is valid for both fluid \((0 \leq {{\mathbf{v}}} \leq {{\mathbf{v}}}_{\rm g})\) and solid mechanics \(({\dot{{\mathbf{u}}}}={{\mathbf{v}}}={{\mathbf{v}}}_{\rm g}).\)

$$ \nabla\cdot{{\mathbf{v}}}=0 $$
(1)
$$ \rho\left[{\frac{\partial{{\mathbf{v}}}}{\partial t}} + ({{\mathbf{v}}}-{{\mathbf{v}}}_{\rm g})\cdot\nabla {{\mathbf{v}}}\right]=\nabla\cdot {{\varvec{\sigma}}}_{\rm fluid/solid} $$
(2)

The characteristic constitutive properties of each partition are taken into account when defining the Cauchy stress tensor \({{\varvec{\sigma}}}_{\rm fluid/solid}\) for the fluid and solid, respectively (see Eqs. 13 and 15). Whereas Stokes theory of liquid friction yields the fluid mechanical Navier–Stokes equations, a general stress–strain relationship defines the structural equations of motion or balancing equations in general.

Figure 1
figure 1

Moving domains for a simplified heart model

Full size image

Coupling Conditions

Since there is no mass flow passing the fluid–solid interface, the conservation of mass is achieved within each partition independently. Unlike in monolithic approaches, however, the partitioned methodology requires functions on either part to be continuous and steady over the common interface in order to ensure momentum equilibrium. Therefore, the overall momentum balance requires kinematic (3) and kinetic coupling conditions (4) to be satisfied:

$$ {{\mathbf{x}}}_{\rm fluid}={{\mathbf{x}}}_{\rm solid}; \quad{\dot{{\mathbf{x}}}}_{\rm fluid}={\dot{{\mathbf{x}}}}_{\rm solid}; \quad{\ddot{{\mathbf{x}}}}_{\rm fluid}={\ddot{{\mathbf{x}}}}_{\rm solid} $$
(3)
$$ {{\mathbf{t}}}_{\rm fluid}={{\varvec{\sigma}}}_{\rm fluid}\cdot{{\mathbf{n}}}= -{{\varvec{\sigma}}}_{\rm solid}\cdot{{\mathbf{n}}}=-{{\mathbf{t}}}_{\rm solid} $$
(4)

with \({{\mathbf{x}}}_{\rm fluid/solid}\) denoting the interface position and \({{\mathbf{t}}}_{\rm fluid/solid}\) the stress vector for both fluid and structural domain. The vector \({{\mathbf{n}}}\) represents the interface normal vector which points inside the fluid domain. Finally, a residual formulation must reassess energetic equilibrium explicitly.

Partitioned Code-Coupling

The haemo-elastic simulation of cardiovascular blood flow is challenging because of substantial blood inertia and low tissue stiffness. In order to decide which kind of software and coupling strategy is suitable for a given bio-mechanical application, the present fluid forces and the expected solid response have to be taken into account carefully. The high level of complexity underlines the advantage of partitioned approaches where different software packages can be chosen for fluid and solid using specialized numerical simulation features.

Software Packages

For the simulation of the flow the software package Fluent (www.fluent.com) is used, whereas the structural mechanical behavior is described using the FEM-Code Abaqus (www.simulia.com). The coupling of these two codes is performed by MpCCI (www.mpcci.de) which represents an explicit coupling scheme by default. The current software versions correspond to latest releases but can be updated or even replaced if necessary. The implicit modifications are currently placed into Fluent as new coupling “master” (Fig. 2). The approximation schemes used in this work are an Euler implicit time stepping scheme and a second order spatial discretization for the fluid solver which allows both mesh movement and cell-quality based remeshing. For the structural domain an implicit quasi-steady solver scheme has been applied with quadratic basis functions.

Figure 2
figure 2

Implicit FSI Coupling (for KaHMo FSI)8: Iterative solution of fluid and solid mechanics (implemented with fluent user libraries)

Full size image

Iterative Code-Coupling

Figure 2 shows the graphical user interface of the newly implemented coupling procedure where all relevant coupling and simulation parameters can be set (e.g., number and size of time-steps or number of iterations/time-step loops). Whereas the standard coupling of Fluent, MpCCI, and Abaqus is limited to a data exchange of load and node position once per time step, the new coupling concept continues a so-called time-step looping (within one time-step) until the coupling conditions (3)/(4) are satisfied. The data exchange itself is performed by MpCCI but then modified within a specialized relaxation procedure. The decision whether the kinematic or kinetic information are used can also be made within the coupling panel. For each time-step j, the time-step looping k can use under-relaxation of either node-position \({{\mathbf{x}}}_{\rm fluid/solid}\)

$$ {{\mathbf{x}}}^j_{k, {\rm fluid}}=\omega_k\cdot {{\mathbf{x}}}^j_{k, {\rm solid}}+(1-\omega_k)\cdot {{\mathbf{x}}}^j_{k-1, {\rm fluid}} $$
(5)

or load values \({{\mathbf{t}}}_{\rm fluid/solid}\)

$$ {{\mathbf{t}}}^j_{k,{\rm solid}}=\omega_k\cdot {{\mathbf{t}}}^j_{k,{\rm fluid}}+(1-\omega_k)\cdot {{\mathbf{t}}}^j_{k-1,{\rm solid}} $$
(6)

A precise description of the coupling flow chart and engine ( Coupling settings (A) , Time-step settings (B) , and Time-step-looping (C) ) can be found in Appendices A and B.

Interface Equilibrium and Relaxation

A major feature within the coupling concept is built by the convergence control ( Energy analysis (D) ) and the adaptive determination of relaxation factors ( Relaxation engine (E) ) which are discussed subsequently. Regarding the overall multi-physics system the quantities exchanged at the interface must not contribute to the conservation equations (ΣE j k  = 0).

$$ \begin{aligned} \Upsigma E_k^j &=E^j_{k,{\rm fluid}}+E^j_{k,{\rm solid}}\nonumber \\ &=\int\limits_{\Upomega}\left({\mathbf{t}}^j_{k,{\rm fluid}}\cdot {\dot{\mathbf{x}}}^j_{k,{\rm fluid}}+{\mathbf{t}}^j_{k,{\rm solid}}\cdot {\dot{\mathbf{x}}}^j_{k,{\rm solid}}\right)d\Upomega \end{aligned} $$
(7)

The discrete looping procedure needs to ensure the artificial energy difference ΣE j k must fall under a certain threshold in order to satisfy the coupling conditions defined in Eqs. (3) and (4) and to finalize the current time-step. As required by the energy analysis, a coupling residual ([•] j k ) can now be formulated as

$$ \left[{\bullet}\right]_{k}^{j} := {\bullet}_{k-1,{\rm fluid}}^{j}-{\bullet}_{k,{\rm solid}}^{j} $$
(8)

for load \((\bullet={{{\mathbf{t}}}})\) and position relaxation \((\bullet={{{\mathbf{x}}}})\), respectively. Using Eq. (8) an Aitken convergence acceleration 22 determines the relaxation factor ω k for Eqs. (5) and (6) for k > 1 and ω1 = ωstart:

$$ \omega_k= \omega_{k-1}\cdot\left(1+\left[{\frac{\left([{\bullet}]^j_{k-1}- [{\bullet}]^j_{k}\right)^T\cdot [{\bullet}]^j_{k}}{\left([{\bullet}]^j_{k-1}-[{\bullet}]^j_{k}\right)^2}} \right] \right) $$
(9)

Hydro-Elastic Evaluation Methods

The evaluation procedures used within this work are based on classical streamline visualization techniques. However, in order to visualize the complex inner-ventricular flow field additional methods need to be introduced. Furthermore, newly defined dimensionless FSI numbers help to understand cardiovascular fluid–structure interaction effects.

Vortex Visualization (λ2-Method)

Three-dimensional iso-surface representation can be obtained by the so-called λ2 method. The underlying concept relates areas of minimum pressure with vortex structures due to flow field rotation. Using the symmetric (S) and anti-symmetric part (A) of the velocity gradient tensor \(\nabla{{\mathbf{v}}}\) one can show with Eq. (2) that ρ(SS + AA) =  − ∇∇ p. A sufficient criterion for minimum pressure requires the left-hand side to be negative which is true if the second invariant λ2 < 0 with λ1 < λ2 < λ3.13

General Flow Field Quantification

Using the absolute flow simulation results, dimensionless characteristic flow numbers help to judge, and to compare fluid mechanical behavior independent of geometrical circumstances. The following well-known Reynolds number \(Re_{X}^{*}\) and Womersley number \(Wo_{X}^{*}\) shall be studied in more detail:

$$ Re_{X}^{*}={\frac{\rho_*\cdot\bar{v}_{*}\cdot X}{\bar{\mu}_{*}}},\quad Wo_{X}^{*}=\sqrt{{\frac{\rho_*\cdot\omega_0\cdot X^2}{\bar{\mu}_{*}}}} $$
(10)

\(\rho_*, \bar{v}_{*}\), and \(\bar{\mu}_{*}\) are the blood density, mean velocity, and mean viscosity, respectively. X is a characteristic length of the fluid domain and ω0 represents the angular frequency.

Classification of Cardiac Function

Referring to the physical mixing process within the heart chamber the ejection fraction EF and the mixing parameter M n shall be defined in percent units as:

$$ EF={\frac{V_{\rm dia}-V_{\rm sys}}{V_{\rm dia}}},\quad M_n = (1-EF)^n $$
(11)

V sys and V dia represent the systolic and diastolic cavity volume. Measuring the time t b,1-X until X% of initial blood has left the heart, O pV allows the dimensionless representation of the pressure–volume work A pV as defined by Oertel et al.14:

$$ O_{\rm pV}={\frac{A_{\rm pV}\cdot t_{b,20}}{\bar{\mu}_{*}\cdot (V_{\rm dia}-V_{\rm sys})}}. $$
(12)

Classification of Cardiac FSI

In order to classify the coupled system involving fluid and solid quantities, a dimensional analysis checks physical plausibility and provides further multi-physics understanding. The so-called Buckingham theorem describes how every physically meaningful equation involving n variables can be equivalently rewritten as an equation of n − m dimensionless parameters, where m is the number of fundamental dimensions used. Consequently, the physical dimensions of the fluid–solid coupled system described by Eqs. (1) and (2) can be reduced or eliminated through re-dimensioning. Subsequent scaling by characteristic units gives insight into the fundamental properties of cardiovascular fluid–solid interaction.

The space of meaningful physical quantities is represented by the aortic and mitral diameters D A/M, the structural density ρS, the density ρB, and viscosity \(\bar{\mu}_{\rm B}\) of blood, the systolic and diastolic velocities \(\bar{u}_{\rm sys/dia},\) the pressure values p sys/dia, the energy densities W sys/dia, the specific volumes \(V^*_{\rm sys/dia}=V_{\rm ref}-V_{\rm sys/dia},\) as well as the characteristic times T 0 = t sys + t dia. Focusing on these 16 quantities in a three-dimensional space we need to define 13 characteristic numbers capturing the fluid–structure phenomena. From experience, this number can be easily reduced to four by taking ratios of equal physical properties into account. Not surprisingly, the dimensional analysis confirms the importance of the Reynolds and Womersley numbers already given in Eq. (10), and further results in the remaining characteristic numbers ΠP and ΠE:

$$ \begin{aligned} Re_{\rm D}&={\frac{\bar{u}_{\rm sys/dia}\cdot D_{\rm A/M}\cdot\rho_{\rm B}}{\bar{\mu}_{\rm B}}} \widehat{=}{\frac{\hbox{Fluid convection}}{\hbox{Fluid diffusion}}}\\ Wo_{\rm D}^{2}&={\frac{2\pi\cdot\rho_{\rm B}\cdot D_{\rm A/M}^2} {T_0\cdot\bar{\mu}_{\rm B}}} \widehat{=} \frac{\hbox{Fluid acceleration}}{\hbox{Fluid diffusion}}\\ \Pi_{\rm P}&={\frac{p_{\rm sys/dia}}{\rho_{\rm B}\cdot \bar{u}^2_{\rm sys/dia}}} \widehat{=} {\frac{\hbox{Static pressure}}{\hbox{Fluid dynamic pressure}}}\\ \Pi_{\rm E}&=\frac{W_{\rm sys/dia}}{(p\cdot V^*)_{\rm sys/dia}} \widehat{=} \frac{\hbox{Solid energy}}{\hbox{Pump energy}} \end{aligned} $$

The dimensionless numbers given above focus on either fluid or solid part, but can be combined in pairs to produce genuine characteristic FSI numbers:

$$ \begin{aligned} \Pi_{\rm FSI}^{\rm E}&=\frac{\rho_B\cdot \bar{u}_{\rm sys/dia}^2}{(W/V^*)_{\rm sys/dia}} \widehat{=} \frac{\hbox{Fluid pump energy}}{\hbox{Solid energy}}\\ \Pi_{\rm FSI}^{\rm D}&=\frac{(\bar{\mu}_B\cdot \bar{u}_{\rm sys/dia})\cdot V^*_{\rm sys/dia}}{W_{\rm sys/dia} \cdot D_{\rm A/M}} \widehat{=} \frac{\hbox{Fluid diffusion}}{\hbox{Solid energy}}\\ \Pi_{\rm FSI}^A&=\frac{\rho_B\cdot \bar{u}_{\rm sys/dia}\cdot \dot{V}^*_{\rm sys/dia}}{W_{\rm sys/dia}/D_{\rm A/M}} \widehat{=} \frac{\hbox{Fluid acceleration}}{\hbox{Solid energy}} \end{aligned} $$

Modeling Approach

The mechanical interaction of blood flow and cardiovascular tissue can be divided into two main categories: those with passive structural response only, and those with additional active movement. Within this work we focus on a left-ventricular heart model representing both passive inflation and active contraction. However, the modeling and coupling concept described may be applied to any kind of cardiovascular blood flow. Discretization, constitutive models and boundary conditions will be specified depending on patient-specific geometry out of MRI imaging.

Constitutive Fluid and Solid Properties

In classical fluid mechanics the Cauchy stress tensor σfluid in Eq. (2) can be divided into a hydrostatic pressure \(p{{\mathbf{I}}}\) and a deviatoric shear tensor \({{\varvec{\tau}}}_{\rm fluid}.\)

$$ {{\varvec{\sigma}}}_{\rm fluid}= {\frac{1}{3}} tr({{\varvec{\sigma}}}_{\rm fluid}) {{\mathbf{I}}}+{{\varvec{\tau}}}_{\rm fluid}= -p{{\mathbf{I}}}+\mu^{\prime}(\dot\gamma){{\mathcal{D}}} $$
(13)

The shear stress tensor \({{\varvec{\tau}}}_{\rm fluid}\) is defined by the strain rate tensor \({{\mathcal{D}}}\) and the viscosity μ′ which is a function of the shear rate \(\dot\gamma\). Due to the non-Newtonian behavior of blood the Carreau-Model shall be used to fit different conditions of blood viscosity as shown in Fig. 3.

$$ \mu^{\prime}=\mu_{\infty}+(\mu_0-\mu_{\infty}) \cdot\left[1+\left(\lambda\cdot\dot\gamma\cdot k_T\right)^2\right]^{\frac{n-1}{2}} $$
(14)

The parameters n = 0.4 and λ = 0.4 as well μ0 and μ∞ are based on isothermal condition k T  = 1 and can be adapted to the application under consideration.

Figure 3
figure 3

Carreau model for experimental viscosity data

Full size image

Similarly to Eq. (13) the Cauchy stress tensor within a general solid mechanics context is given by

$$ {{\varvec{\sigma}}}_{\rm solid}= \frac{1}{3}tr({{\varvec{\sigma}}}_{\rm solid}){{\mathbf{I}}}+{{\varvec{\tau}}}_{\rm solid} =-p{{\mathbf{I}}}+\frac{1}{J}{{\mathbb{F}}}\frac{\partial W}{\partial{{\mathbb{E}}}} {{\mathbb{F}}}^T $$
(15)

again defined with a pressure \(p{{\mathbf{I}}}\) and a deviatoric shear tensor \({{\varvec{\tau}}}_{\rm solid}.\) Due to the large deformation in bio-mechanical applications, the theory of finite elasticity needs to be used. This requires a constitutive formulation by the strain energy density function W. \({{\mathbb{F}}}\) represents the deformation gradient tensor, \({{\mathbb{E}}}\) the Green strain tensor, and J the determinant of \({{\mathbb{F}}}.\)

Left-Ventricular Heart Model

Figure 4 shows KaHMo FSI’s current ways of defining heart ventricle geometries. Initial heart models were based on a so-called shaper device which ensures a minimum volume and a certain width-to-length ratio during ventricular reconstruction. The successful work-flow for this generic ventricle model has been applied to a patient-specific geometry out of MRI data. Whereas prescribed fluid domain movement requires kinematic information during the whole cardiac cycle, the FSI model requires a realistic start geometry only, corresponding to the initial stress-free configuration at the beginning of atrium contraction. However, the further model behavior now depends strongly on the chosen physiological representation.

Figure 4
figure 4

Geometry creation for KaHMo FSI

Full size image

Model Discretization

Figure 5 shows the discretization of both the fluid and solid domain. The common interface helps to exchange the kinematic and kinetic coupling information. The fluid domain has been discretized with another 100.000 tetrahedral cells. The inlet and outlet valves are modeled as projected surface areas which are initially closed and opened with a restricted area of 100, 75, and 35% until the valve finally opens completely. The cavity volume is 120 mL and the characteristic valve diameters are D M = 24 mm and D A = 21 mm (see Table 1).

Figure 5
figure 5

Discretization of solid and fluid domain

Full size image

The structural model surrounds the fluid domain with a mean wall thickness of 1 cm, discretized by 3.000 quadratic tetrahedral cells. With the focus on cardiovascular fluid mechanics, standard hyper-elastic models were used initially within this study. However, the isotropic constitutive properties do not represent the characteristic fluid domain rotation (see section “Structural Response”). So, additional fiber layers are embedded within the isotropic matrix. Within this modeled composite approach, the endocardial and epicardial fiber layers are most important in order to gain a sufficient deformation behavior. One heart cycle is discretized into 200 time-steps.

Composite Model Approach

In order to compare the flow pattern inside the heart with former models which prescribe the geometry movement, the blood viscosity parameters of Eq. (14) have been set to μ0 = 13.15 mPa s, μ∞ = 3.00 mPa s, n = 0.4, and λ = 0.4 s; the fluid density is assumed to be ρB = 1008 kg/m3. The structural partition is represented by a composite approach whose mathematical foundations can be formulated with an extended strain energy density function:

$$ W=W_{\rm passive}+W_{\rm active} $$
(16)

Within this work a modification of the Holzapfel-Law 20 is used to divide the constitutive behavior into an isotropic and an anisotropic part mathematically. We define I 1 and I 2 as the deviatoric invariants of the Cauchy–Green strain tensor whereas I 4 and I 5 can be described as pseudo invariants which include the initial and current fiber orientation.

The material parameters correspond to Schmid et al.20 and define the passive material properties as follows:

$$ \begin{aligned} W_{\rm passive}=& \underbrace{\sum\limits_{i=1}^2 b_i\cdot(e^{c_i\cdot(I_i-3)^2}-1)}_{W_{\rm iso}}\nonumber \\ &+ \underbrace{\sum\limits_{i=4}^5 b_i\cdot(e^{c_i\cdot(I_i-1)^2}-1)}_{W_{\rm aniso}} \end{aligned} $$
(17)

As described in section “Model Discretization” the structural model is represented by an isotropic matrix and embedded fiber layers. The constitutive behavior of this composite model is represented by Eq. (17). Whereas W iso describes the matrix behavior, W aniso takes the final anisotropic components into account.

Applying the respective terms of Eq. (17) yields a locally transversely isotropic composite with inner and outer fiber orientations α I  = 35° and α A  =  − 45° (see Figs. 5 and 6). The active muscle contraction follows a temporal strain relation in K(t):

$$ W_{\rm active}=-\lambda\cdot\left(\frac{E_J}{(1+K(t))^3}-1\right)^2 $$
(18)

where λ represents a Lagrangian multiplier and K(t) controls the fiber shortening. The initial state is described by E J  = 1 and the Lagrangian constraint becomes obsolete for K(t) = 0. Values K(t) < 0 cause fiber shortening in E J from a quasi-static point of view (E J ∼ (1 + K(t))3). K(t) has been determined in order to gain the correct amount of volume change during contraction.

Figure 6
figure 6

Fiber orientation and composite model7

Full size image

Boundary Conditions

The heart model presented above depends strongly on cavity pressure and structural deformation. Even if the structural model is simplified in terms of the real muscle complexity it is helpful for studying the interaction process. Figure 7 shows the temporal interaction of fluid and solid boundary conditions, i.e., the pressure distribution at the cavity inlet and outlet and the active part of the myocardial structure enabling a characteristic fluid domain deformation. In order to represent the characteristic interaction of pressure load and heart contraction, values are scaled by the respective maximum.

Figure 7
figure 7

Pressure and contraction boundary conditions

Full size image

According to the pressure level in Table 1, the maximum pressure is approximately 160 mbar. The contraction line is mainly driven by the fiber shortening value K(t) in Eq. (18) with a maximum value of approximately 20%. Both boundary conditions have zero magnitudes at different times during the cardiac cycle.

Table 1 Summary of geometry information and reference conditions
Full size table

Results

First physical interpretations towards the inner-ventricular flow pattern can be made based on the coupled fluid domain deformation (KaHMo FSI). The comparison with the prescribed geometry model (KaHMo MRT), based on the same MRI information, and also with characteristic FSI numbers helps to further evaluate the quality of the results.

Fluid Domain Deformation

The focus of this work has been put on the inner-ventricular flow field and the resulting fluid domain deformation. Both the fluid domain behavior and the interaction with the inner ventricular pressure distribution has been compared to measured data and shows a good overall agreement. Figure 8 shows the comparison of the volume change over time which gives an integrated view of the actual flow field deformation.

Figure 8
figure 8

Comparison of volume over time

Full size image

However, in order to evaluate the spatial boundary conditions in more detail, simulated and measured geometries need to be compared directly. This is done in Fig. 9 for characteristic time-frames from the end of systole to the end of diastole phase.

Figure 9
figure 9

Geometrical comparison of flow field deformation for KaHMo FSI and KaHMo MRT

Full size image

Structural Response

Figure 10 confirms a constitutive agreement of KaHMo FSI and KaHMo MRT by comparing the respective pressure–volume relationship. Starting with the stress-free reference configuration, the end-diastolic configuration represents the maximum passive inflation whereas the end-systolic configuration is caused by prescribing the shortening of the embedded fibers. It can be noted that the model represents the characteristic heart shortening in all directions as well as the wall thickening due to the incompressible structural behavior (see Figs. 10 and 11).

Figure 10
figure 10

Comparison of pressure over volume

Full size image
Figure 11
figure 11

Structural deformation from initial state to end systolic configuration (translation and rotation)

Full size image

As a further boundary condition for the fluid mechanics simulation, the heart rotation can be observed as well, indicated by the arrow. Furthermore, it can be discovered that initial and end-systolic configuration are very alike as the corresponding deformation is caused by the relatively small increase in pressure when the atrium contracts (approx. 10%). Whereas the radius-independent structural strain was fairly constant from the endocardial to the epicardial surface (±20% throughout the cardiac cycle) the stress mainly occurred within the discrete stiffer fiber layers.

Cavity Flow Pattern

From the fluid mechanics point of view the resulting fluid domain deformation is of utmost importance for the inner-ventricular flow pattern. Understanding cardiac fluid-mechanics requires both quantitative and qualitative observations due to local fluid domain variations.

For the first time within the KaHMo project a flow pattern inside a heart cavity can be discovered without the prescription of the fluid domain movement—Fig. 12 compares the results of KaHMo MRT with and KaHMo FSI. Following the different time-frames (see time-scale) from left to right one can recognize a good flow-pattern agreement with only small discontinuity due to local fluid domain sensitivity. Whereas KaHMo MRT is based on high-resolution MRI data for the whole cardiac cycle, KaHMo FSI uses the initial MRI configuration only and calculates the following deformation state. Three different visualization techniques are used in order to visualize the corresponding flow field structure.

Figure 12
figure 12

Inner-ventricular flow field in KaHMo FSI/MRT for different time-frames (top left: early filling; top right: late filling; bottom left: atrium contraction; bottom right: mid ejection)

Full size image

Each figure shows 3D streamlines which are also projected onto two-dimensional mid-planes (initially defined by the heart-tip and the valves mid-points) in order to better understand the temporal vortex development. Finally, three-dimensional iso-surface representation can be obtained by the so-called λ2 method.

Hydro-Elastic Quantification

After having evaluated the characteristic 3D deformation of the heart, a quantitative flow evaluation needs to be performed. Using the characteristic fluid mechanical number defined in section “Classification of Cardiac Function” we can confirm a very good agreement in both Reynolds

$$ Re_{\rm FSI}^{\rm sys/dia}=3431/2288,\quad Re_{\rm MRT}^{\rm sys/dia}=3566/2294 $$

and Womersley numbers

$$ Wo_{\rm FSI}^{\rm sys/dia}=25/31,\quad Wo_{\rm MRT}^{\rm sys/dia}=25/31. $$

However, cardiovascular fluid–structure interaction also requires to take characteristic structural properties into account, like the constitutive or contractile behavior of myocardial tissue. Evaluating the newly developed characteristic FSI numbers from section “Classification of Cardiac FSI”, we gain the following result:

$$ \Uppi_{\rm FSI*}^{\rm E\,dia}=1.0 \quad\hbox{and}\quad \Uppi_{\rm FSI*}^{\rm E\,sys}=5.0\cdot 10^{-2} $$
$$ \Uppi_{\rm FSI*}^{\rm A\,dia}=0.1 \quad\hbox{and}\quad \Uppi_{\rm FSI*}^{\rm A\,sys}=3.3\cdot 10^{-3} $$
$$ \Uppi_{\rm FSI*}^{\rm D\,dia}=4.4\cdot 10^{-4} \quad\hbox{and}\quad \Uppi_{\rm FSI*}^{\rm D\,sys}=1.4\cdot 10^{-5} $$

(scaled (*) with \(\Uppi_{\rm FSI}^{\rm E\,dia}=8.36\cdot 10^{-2}\)).

Table 2 summarises the most important fluid mechanical input quantities for ΠFSIs. Although these values need to be evaluated with further heart modeling developments (including potential heart failures) one can already indicate physical phenomena. During filling phase the ratio of fluid to solid quantities is much higher than during systole. Consequently, the fluid dominates the solid during diastole and vice versa during systole. Furthermore, both phases show the dominance of pump energy (\(\Uppi_{\rm FSI*}^{\rm E\,dia/sys}\)) over acceleration (\(\Uppi_{\rm FSI*}^{\rm A\,dia/sys}\)), and diffusion (\(\Uppi_{\rm FSI*}^{\rm D\,dia/sys}\)). Finally, the dimensional cardiac pump work shows very similar characteristics with

$$ O_{\rm FSI}=3.8\times 10^{6}\quad \hbox{and}\quad O_{\rm MRT}=3.5 \times 10^{6} $$

from a fluid mechanics point of view.

Table 2 Quantitative flow field evaluation
Full size table

Discussion

The cardiac flow model KaHMo has been extended by a novel partitioned fluid–solid coupling model specialized for cardiovascular simulations. The model is based on MRI imaging methods and therefore enables results which are not available in current clinical use. The prescribed geometry version KaHMo MRT has been previously validated quantitatively19 by an overall comparison between simulated data and velocity data obtained by additional flux measurements.

Cardiovascular Fluid–Structure Interaction

The focus of this work is on replacing the fluid domain movement by a structural calculation by KaHMo FSI and on comparing the inner-ventricular flow field with the validated model. The evaluation of fluid domain deformation both qualitatively and quantitatively confirmed the functionality of KaHMo FSI; it demonstrates the capabilities of state of the art CFD combined with structural analysis features for fluid domain movement. Although the structural and constitutive behavior of the solid model does not represent local concave/convex deformation changes, the overall visualization of the flow simulation results in Fig. 12 helps to understand the complex inner-ventricular flow-pattern from a stand-alone and coupled perspective. Figure 13 combines the observations of both simulation approaches and shows common behavior. The early ring vortex in Phase 1 develops when the inflow jet enters the cavity with its resting amount of blood inside. With an increase in volume this vortex grows asymmetrically in Phase 2 but both foci stay on a relatively horizontal level. Entering Phase 3, however, the dominating left focus forces the right focus to move alongside the wall towards the heart tip and consequently the whole vortex ring rotates in a clockwise direction. The dominant vortex provides an energetically optimized flow pattern for the upcoming ventricle contraction; the vortex in the heart tip ensures that only a small amount of old blood remains inside the cavity. This also minimizes the risk of developing a thrombus. Both simulation results show the same flow-structure behavior as shown by Krittian et al.8

Figure 13
figure 13

Temporal visualization of inner-ventricular flow field

Full size image

New characteristic FSI numbers have been derived in order to capture the fluid–structure interaction effects quantitatively. First evaluation processes showed the interplay of flow energy, diffusion and acceleration with the structural deformation. One can see that each characteristic number exists for both ventricle filling and ejection comparable to systolic and diastolic pressure measurements. Consequently, systolic or diastolic heart failure phenomena affecting cardiovascular fluid–solid interaction can be captured in future. However, extended simulation variations need to be performed in order to evaluate and calibrate the numbers proposed.

From our experience, the numerical stability depends strongly on phase and characteristics of flow dominance over solid. Consequently, the FSI numbers derived above can be used to gain insight into both physical and numerical fluid–structure interaction.

Model Limitations

At this stage, KaHMo FSI represents rather a feasibility study than a patient-specific analysis. The presented methodology shows considerable potential, however at this stage, it cannot be used for clinical purpose per se as a full in vitro validation of the numerical model is necessary.

Due to corresponding model limitations there remains a certain discrepancy between simulation and measurement due to simplified fiber shortening and inlet/outlet flow conditions. The influence on fluid domain movement depends on geometrical as well as passive/active constitutive properties. However, it should be noted that acquisition of patient-specific structural properties still remains a challenge although promising progress can be seen in terms of tissue-phase mapping, tagging or diffusion MRI techniques.6 The contraction parameter K(t) has to be determined on FSI runtime in order to tune the deformation agreement for KaHMo MRT and KaHMo FSI.

As far as the flow field control is concerned, the inner-ventricular flow field is mainly determined by the formation of the early-filling inlet-jet as shown by Oertel et al.14 The results gained within this study display that more realistic mitral valve dynamics may relocate the early-filling ring vortex further down towards the heart tip. The aortic valve, does not influence the inner-ventricular flow field by active motion and is therefore of less interest in future coupling. However, the probability of valve dysfunction for patient-specific modeling can be captured by valve models developed by Oertel et al.14

Conclusion and Outlook

The numerical results have demonstrated that the strength of the KaHMo project lies in the prediction of the inner-ventricular flow field. The overall agreement of visualized data and quantitative results encourages to further develop the myocardial representation of KaHMo FSI as well as the boundary conditions for either partition (see e.g., Sachse18).

The authors believe that enhanced evaluation of strain and stress throughout the wall is a important further step to evaluate the structural solid component of the model (see e.g., Hunter et al.4 or Taylor et al.21). In order to increase the patient-specific structural influence, future models should be based on advanced MRI measurement techniques such as diffusion tensor and tissue phase mapping MRI. Furthermore, late enhanced MRI techniques provide information of local structural variation which become especially important when investigating cases of myocardial infarction. As far as the spatial model fixation is concerned, the embedding into a fat tissue structure shown by Janoske et al.5 will be reviewed. This can also include an integration of the structural right ventricle as further support for the left-ventricular structure.

In terms of the actual flow pattern, future work will include the representation of the atrial and large vessel geometries for further improving the velocity inlet and outlet boundary conditions for the ventricle. Furthermore, the implementation of a simplified mitral valve geometry will represent a more realistic guidance for the flow into the cavity at the early filling phase, important for the overall vortex development. This will increase the fidelity of the numerical models and make it possible to predict, for the first time, the influence of valve-inflow interaction on the overall vortex formation.