Introduction

Biomechanical understanding of force generation and transmission in skeletal muscle requires the development and implementation of biomechanical models that connect muscle structure to function. Since skeletal muscles involve highly complex 3D fiber architecture, it is clear that high-resolution in vivo probing of skeletal muscle is essential for establishing the connection between structure and function. As alternatives to the highly destructive process of muscle biopsy, novel experimental methods for the non-invasive probing of skeletal muscle have provided the necessary impetus for developing sophisticated biomechanical models that take into consideration the in vivo muscle microstructure and mechanics. Proton magnetic resonance imaging (MRI) methodologies have been applied successfully to extract the gross anatomy of individual muscles,7 , 15 but they can also be used to quantify the directional diffusion of water in tissues.12 Specifically, diffusion tensor imaging (DTI)5 methods have been used to probe the orientation of muscle fibers in mammalian tongue33 , 53 and the human myocardium,49 as well to reconstruct the fiber tracts in the calf muscle.14 , 29 In order to reconstruct the fiber tracts, DTI methods require the use of subvoxel models in order to assign the physical origin of the MRI signal. The present study focuses on the connection between fiber morphology and the reported anisotropy of the diffusion tensor in human skeletal muscle. Before we embark in the problem definition, we need to describe briefly the relevant aspects of skeletal muscle histology.

Human skeletal muscle has a highly hierarchical organization, consisting of bundles of fascicles (1–2 mm wide), each composed of bundles of myofibers (10–100 μm wide), which are the elementary muscle cell (myocyte) and are henceforth referred to as the muscle “fibers”. The contractile element of each fiber is an array of hundreds of parallel myofibrils, each array containing a network of tubules (sarcoplasmic reticulum) and mitochondria. The tubular network consists of two systems; one that runs longitudinally through the cell, and another (transverse) system which is an invagination of the sarcolemma and communicates with the extracellular space. The extracellular structures are arranged within a hierarchical matrix of intramuscular connective (collagenous) tissue organized as follows: the whole muscle is surrounded by the epimysium, the fascicles are delineated by the perimysium, and the myocytes are separated by the endomysium.27 Scanning electron microscopy has revealed a three-level structural organization of the perimysial collagen network, which effectively constitutes an axial and lateral tether between adjacent fibers.35 A key hypothesis has emerged that this hierarchical structure, including the multiple levels of tethering, is intimately related to the generation of shear strain during muscle deformation.36

The results of all the previous DTI studies in the skeletal muscle14 , 17 , 42 have consistently shown a significant difference between the secondary and tertiary eigenvalues, which characterize diffusion in the plane perpendicular to the myofiber orientation. Galban et al. 17 suggested that the secondary eigenvalue is related to the diffusion process within the endomysium, and the tertiary eigenvalue corresponds to the diffusion process within the individual fibers. Experimental studies have also probed the origin of the difference in the two lower eigenvalues of the diffusion tensor by monitoring the variation of eigenvalues while performing extension and contraction experiments.16 , 20 , 21 Specifically, Heemskerk et al. 21 have suggested that the secondary and tertiary eigenvalues have different structural origins, and that the former stays constant while the latter decreases during muscle extension. However, the changes of muscle diffusivity under extension and contraction remain a topic of scientific debate.16 , 20 , 21 We have already proposed,24 and explore here further, an alternative explanation of these findings by invoking individual fiber geometry and muscle mechanics. Inspired by prior reports that the cross-sectional geometry of muscle fibers is asymmetric,4 , 10 , 45 and by evidence of increased cross-sectional ellipticity of older, atrophied or injured skeletal muscle fibers,2 we are advancing the hypothesis that the elliptical shape of skeletal muscle fibers can explain the asymmetry of the diffusion tensor on the transverse plane.

The goal of the present work is to quantify the effect of fiber ellipticity on the diffusion tensor metrics and to characterize the geometrical pattern of diffusion asymmetry on the plane perpendicular to the mean myofiber direction. First, a two-compartmental model of the diffusion MRI signal is built in order to connect the effect of muscle fiber ellipticity with the diffusion tensor metrics. Second, we explore the geometrical pattern of the observed asymmetry in order to examine the coupling between the cross-sectional fiber geometry and whole muscle kinematics, in a way that has been already established for the myocardium. The myocardium wall thickening has been connected to transverse shear in the plane perpendicular to the fiber direction.30 It is also established that the cardio-myocytes adapt by assuming an elliptic cross section,19 which is consistent with the local shear field during cardiac remodeling.54 Although the effect of shear on single fiber geometry has not yet been made explicitly, there is a growing appreciation of the role of shear stress in skeletal muscle models. Driven by systematic experimental studies which reveal non-uniform strain in muscles34 , 50 and ample evidence suggesting that there is lateral transmission of stress between fibers,36 several models based on the assumption that muscle fibers act independently have fallen from favor and were replaced with models that accommodate shear strain both along and across the fibers.8

Materials and Methods

Two-Compartmental Diffusion MR Signal Model

We extend the model formulation developed by Galban et al. 18 by taking into account the muscle fiber size39 and shape in order to model the asymmetry of the diffusion coefficient in the plane perpendicular to the muscle fiber direction. We assume that there are two main compartments contributing to the diffusion properties of the composite medium: the intracellular space (within the muscle fiber) and the extracellular space (collagenous intramuscular connective tissues consisting of endomysium and perimysium). The effect of the intramyocellular organelles and membranes (myofibrils, sarcoplasmic reticulum, and mitochondria) on the restriction of intracellular water diffusion is taken into consideration implicitly by assuming a free intracellular diffusion coefficient lower than the one of free water. Similarly, we account implicitly for the effect of the extracellular collagen fibrils on the restriction of extracellular water diffusion by assuming a free extracellular diffusion coefficient lower than the one of free water.

Due to the random arrangement of collagen fibrils in the endomysium of the relaxed muscle,48 we assume that the endomysium microstructure does not induce any anisotropy in the molecular diffusion tensor of extracellular water. However, molecular water diffusion in the extracellular and intracellular space is restricted by the presence of the myocyte membranes (sarcolemma), and consequently the volume-averaged diffusion coefficient is affected by the shape and packing arrangement of the fibers. Therefore, the idea of an apparent extracellular and intracellular diffusion coefficient which depends on the diffusion encoding direction is introduced in the spirit of Stanisz et al. 44 The modulation of the intracellular and extracellular diffusion coefficients by the diffusion direction relative to the orientation of the elliptical cross-section expresses the dependence of the model on the cross-sectional fiber shape.

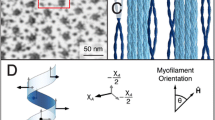
We model the muscle fibers as infinite cylinders with an elliptical cross section of geometric ratio α (= short axis length/long axis length), which is a simplification consistent with muscle histology6 , 43 , 51 and physiology.4 , 47 , 48 Aquin et al. 4 discussed the shape changes of muscle fiber cross-sections in pigs raised at different temperatures. They reported values for α in the range 0.40–0.80 for the two groups of animals studied, and showed that the fibers of cold acclimated animals were more elliptical at the same cross-sectional area than the fibers of the control animals. In a series of morphometric studies, Trotter et al. 47 , 48 proposed that the muscle fiber can be abstracted as a cylinder deforming under two constraints: constant lateral area and constant volume. The first constraint is not universally accepted in the literature but is consistent with the observation that the thickness of the endomysium does not change when the fiber length changes. The endomysium consists of a random network of collagen fibrils which undergo small reorientation as the fiber length changes. The second constraint is less controversial and corresponds to imposing incompressibility of the myocyte. Taken together, the two constraints imply that α decreases (i.e., the cross section deviates more from a circle) as the fiber contracts.

We are now ready to connect the MRI signal to the parameters of the composite model represented in Fig. 1. This connection is made by deriving an analytical expression describing the evolution of the echo attenuation signal by taking into account diffusion, exchange and T 2 effects for the two compartments. The short semi-axis of the ellipse is r s and the long semi-axis is r l. The two compartments have volume fractions υ in and υ ex, so that υ in + υ ex = 1. The evolution of the signal from the intra- (S in) and extracellular (S ex) compartments, in a diffusion-weighted experiment with diffusion gradients of amplitude g and duration δ which are separated by a diffusion time Δ, is governed by the following system of differential equations:

Figure 1
figure 1

Schematic description of bi-compartmental model for water diffusion, on the basis of a composite consisting of fibers (intra-myocellular space) embedded in an extracellular matrix (endomysium)

Full size image
$$ {\frac{{dS_{\text{in}} }}{dt}} = - 4\pi^{2} q^{2} D_{\text{in}}^{\text{app}} S_{\text{in}} - {\frac{1}{{\tau_{\text{in}} }}}S_{\text{in}} + {\frac{1}{{\tau_{\text{ex}} }}}S_{\text{ex}} - {\frac{1}{{T_{{2 , {\text{in}}}} }}}S_{\text{in}} $$
(1)
$$ {\frac{{dS_{\text{ex}} }}{dt}} = - 4\pi^{2} q^{2} D_{\text{ex}}^{\text{app}} S_{\text{ex}} - {\frac{1}{{{{\uptau}}_{\text{ex}} }}}S_{\text{ex}} + {\frac{1}{{{{\uptau}}_{\text{in}} }}}S_{\text{in}} - {\frac{1}{{T_{{ 2 , {\text{ex}}}} }}}S_{\text{ex}} $$
(2)

where q = (γ/2π)δg, γ is the gyromagnetic ratio, D appin and D appex are the apparent diffusion coefficients of the intra- and extracellular compartments, respectively, and τ in, τ ex denote the mean residence times of spins in the two compartments. The above equations are based on Kärger’s model26 enhanced with T 2 effects (corresponding to the last term in each equation). By assuming equal water proton densities for the two compartments and since spin relaxation and diffusion are initiated at t = 0, the following initial conditions have to be satisfied:

$$ \begin{aligned} S_{\text{in}} (t = 0) = \upsilon_{\text{in}} \hfill \\ S_{\text{ex}} (t = 0) = \upsilon_{\text{ex}} \hfill \\ {\frac{1}{{\tau_{\text{in}} }}}S_{\text{in}} (t = 0) = {\frac{1}{{\tau_{\text{ex}} }}}S_{\text{ex}} (t = 0) \hfill \\ \end{aligned} $$
(3)

The total echo attenuation can then be expressed mathematically as a linear superposition of the solutions for the two compartments:

$$ S(q,t) = S_{\text{in}} (q,t) + S_{\text{ex}} (q,t) $$
(4)

The above system of ODEs has a closed-form solution:

$$ S(q,t) = \upsilon^{\prime}_{\text{in}} \,\exp ( - 4\pi^{2} q^{2} tD^{\prime}_{\text{in}} ) + \upsilon^{\prime}_{\text{ex}} \,\exp ( - 4\pi^{2} q^{2} tD^{\prime}_{\text{ex}} ) $$
(5)

where υ′ and D′ represent the modified volume fractions and diffusion coefficients, respectively, defined according to the equations:

$$ \begin{aligned} D^{\prime}_{\text{in,ex}} = {\frac{1}{2}}\left( {D_{\text{in}}^{\text{app}} + D_{\text{ex}}^{\text{app}} + {\frac{1}{{4\pi^{2} q^{2} }}}\left( {{\frac{1}{{{{\uptau}}_{\text{in}} }}} + {\frac{1}{{{{\uptau}}_{\text{ex}} }}} + {\frac{1}{{T_{{ 2 , {\text{in}}}} }}} + {\frac{1}{{T_{{ 2 , {\text{ex}}}} }}}} \right)} \right) \hfill \\ \mp {\frac{1}{2}}\sqrt {\left( {D_{\text{ex}}^{\text{app}} - D_{\text{in}}^{\text{app}} + {\frac{1}{{4\pi^{2} q^{2} }}}\left( {{\frac{1}{{{{\uptau}}_{\text{ex}} }}} - {\frac{1}{{{{\uptau}}_{\text{in}} }}} + {\frac{1}{{T_{{ 2 , {\text{ex}}}} }}} - {\frac{1}{{T_{{ 2 , {\text{in}}}} }}}} \right)} \right)^{2} + {\frac{1}{{4\pi^{4} q^{4} {{\uptau}}_{\text{in}} {{\uptau}}_{\text{ex}} }}}} \hfill \\ \end{aligned} $$
(6)
$$ \upsilon^{\prime}_{\text{ex}} = {\frac{1}{{D^{\prime}_{\text{ex}} - D^{\prime}_{\text{in}} }}}\left( {\upsilon_{\text{in}} \left( {D_{\text{in}}^{\text{app}} + {\frac{1}{{4\pi^{2} q^{2} T_{{ 2 , {\text{in}}}} }}}} \right) + \upsilon_{\text{ex}} \left( {D_{\text{ex}}^{\text{app}} + {\frac{1}{{4\pi^{2} q^{2} T_{{ 2 , {\text{ex}}}} }}}} \right) - D^{\prime}_{\text{in}} } \right) $$
(7)
$$ \upsilon^{\prime}_{\text{in}} = 1 - \upsilon^{\prime}_{\text{ex}} $$
(8)

Diffusion in Intracellular Compartment

Various intracellular membrane and protein structures induce diffusion barriers along directions both parallel and perpendicular to the myofiber. Therefore, the cytoplasmic diffusion coefficient is lower than that of bulk water at body temperature. Although, the hierarchical organization of most of the subcellular barriers inside the tubular myocyte may imply a reduction of the cytoplasmic diffusion coefficient perpendicular to the fiber direction relatively to the diffusion coefficient parallel to it, we assume for simplicity that the free intracellular diffusion coefficient is isotropic and equal to D in. However, owing to the barrier function of the sarcolemma, the transverse intracellular diffusion is restricted. Using the short pulsed gradient approximation, the apparent diffusion coefficient in the intracellular space is computed based on the solution of the diffusion problem between two flat, impermeable barriers spaced a distance r apart:

$$ D_{\text{in}}^{\text{app}} (D_{\text{in}} ,q, \Updelta ,r) = - {\frac{1}{b}}{ \ln }\left[ {2{\frac{{1 - { \cos }\left( {2\pi qr} \right)}}{{\left( {2\pi qr} \right)^{2} }}} + 4\left( {2\pi qr} \right)^{2} \sum\limits_{n = 1}^{\infty } {\exp } \left( { - n^{2} \pi^{2} D_{\text{in}} {\frac{\Updelta}{{r^{2} }}}} \right){\frac{{1 - ( - 1)^{n} { \cos }\left( {2\pi qr} \right)}}{{\left( {\left( {2\pi qr} \right)^{2} - \left( {n\pi } \right)^{2} } \right)^{2} }}}} \right] $$
(9)

where the b-value is given by the equation b = 4π2 q 2(Δ − δ/3).

The length of the individual myocyte is much longer than the diffusion length, therefore r is taken to infinity parallel to the direction of the myofiber. For the two other main diffusion directions, r is approximated by the axes of the elliptical cross section, in order to account for the restriction effects imposed by the shape of the sarcolemma.

$$ \begin{aligned} D_{\text{in}}^{\text{app}} (\parallel ) = D_{\text{in}} \hfill \\ D_{\text{in}}^{\text{app}} ( \bot_{\text{l}} ) = D_{\text{in}}^{\text{app}} (D_{\text{in}} ,q,\Updelta ,r_{\text{l}} ) \hfill \\ D_{\text{in}}^{\text{app}} ( \bot_{\text{s}} ) = D_{\text{in}}^{\text{app}} (D_{\text{in}} ,q,\Updelta ,r_{\text{s}} ) \hfill \\ \end{aligned} $$
(10)

Diffusion in Extracellular Compartment

The endomysium is represented by a random distribution of collagen fibrils, which do not contribute to the MRI signal, surrounded by bulk water. If υ col is the volume fraction of the collagen in the endomysium and D w the water diffusion coefficient at body temperature, the diffusion coefficient for water surrounding a system of cylindrical collagen fibrils of zero diffusivity oriented randomly in space is:

$$ D_{\text{ex}} = D_{\text{w}} (1 - \upsilon_{\text{col}} )^{2/3} $$
(11)

The extracellular diffusion coefficient of water around the myocytes depends on the tortuosity factor. By modeling the myocytes as infinite cylinders with an elliptical cross-section with semi-axes r l and r s, the tortuosity depends on the orientation of the diffusion direction with respect to the cylinder axis. Sen et al. 40 has shown that for a system consisting of ellipsoids, the apparent diffusion coefficient in extracellular space at the long diffusion time limit is anisotropic and can be expressed as:

$$ D_{\text{ex}}^{\text{app}} = D_{\text{ex}} (1 - \upsilon_{\text{in}} )^{L/(1 - L)} $$
(12)

where L expresses the dependence on the orientation of the diffusion gradient with the cylinder axis. For the case of infinite cylinders with an elliptical cross section, it can be shown that:

$$ \begin{aligned} L(\parallel ) = 0 \hfill \\ L( \bot_{\text{l}} ) = {\frac{{{\upalpha}}}{{{{\upalpha}} + 1}}} \hfill \\ L( \bot_{\text{s}} ) = {\frac{1}{{{{\upalpha}} + 1}}} \hfill \\ \end{aligned} $$
(13)

MRI Measurements

Gradient hardware limitations in a clinical platform impose long diffusion gradients in order to achieve large b-values, with the additional problem of causing T 2 decay induced by the need to increase the minimum echo time required to position the two diffusion gradients on the two sides of the 180° RF pulse. In this work, we employ pulsed gradient stimulated-echo (PGSTE) protocols31 which can deliver large b-values while limiting T 2 decay. This occurs because the diffusion sensitivity is proportional to the mixing time between the second and the third RF pulse, during which the magnetization is longitudinal and not subject to T 2 decay. The penalty paid by the stimulated-echo is a signal decrease by a factor of 2 relative to the spin-echo. Nevertheless, in tissues with short T 2, such as skeletal muscle, the echo signal for a stimulated echo preparation exceeds the signal for a spin echo preparation for the typical range of b-values employed in DW-MRI acquisition with eddy current compensation.46

All MR measurements were performed on a 3 T full-body GE scanner (General Electric Healthcare, Waukesha, WI). A single-channel lower extremity coil was used to scan the calf region of the right leg of three healthy male subjects lying supine with feet first into the scanner. Diffusion-weighted images were acquired using a single-shot diffusion weighted stimulated-echo EPI sequence with the following parameters: TR/TE = 2000/52 ms, FOV = 20 cm, slice thickness = 10 mm, acquisition matrix = 64 × 40 (5/8 partial phase encoding), and N ex = 6. Diffusion-weighted gradients were applied along 30 non-collinear directions with a nominal b-value of 541 s/mm2. The diffusion-encoding parameters were: δ = 15 ms, Δ = 40 ms, g max = 30 mT/m. Six axial slices were acquired with the imaging volume centered on the widest cross section of the calf muscle. The total scan time was 6 min and 12 s.

Diffusion Tensor Analysis

The diffusion tensor eigenvalues and eigenvectors are first derived by the experimental diffusion data. The mean diffusion coefficient and fractional anisotropy of the tensor are then defined as follows:

$$ \lambda_{\text{m}} = {\frac{{\lambda_{ 1} + \lambda_{ 2} + \lambda_{ 3} }}{3}} $$
(14)
$$ {\text{FA}} = \sqrt {{\frac{3}{2}}{\frac{{(\lambda_{1} - \lambda_{\text{m}} )^{2} + (\lambda_{2} - \lambda_{\text{m}} )^{2} + (\lambda_{3} - \lambda_{\text{m}} )^{2} }}{{\lambda_{1}^{2} + \lambda_{2}^{2} + \lambda_{3}^{2} }}}} $$
(15)

The asymmetry of the diffusion tensor on the transverse plane can be parameterized via the planar index

$$ {\text{CP}} = {\frac{{2\left( {\lambda_{ 2} - \lambda_{ 3} } \right)}}{{\lambda_{ 1} + \lambda_{ 2} + \lambda_{ 3} }}} $$
(16)

Given known parameters of muscle microstructure, the eigenvalues of the diffusion tensor can be also extracted by applying the proposed microstructural model along the three principal axes

$$ \lambda_{\text{k,sim}} = - {\frac{1}{b}}\ln \left( {{\frac{{S_{\text{k}} (q,\Updelta )}}{{S_{\text{k}} (q,0)}}}} \right) $$
(17)

where k = {∥, ⊥l, ⊥s} = {1, 2, 3}.

The normalized root mean square error for the fitting of the simulated tensor eigenvalues (λk,sim) to the experimental (λk,exp) ones can be computed by

$$ {\text{NRMSE}} = \sqrt {{\frac{{(\lambda_{1,\exp } - \lambda_{{ 1 , {\text{sim}}}} )^{2} + (\lambda_{2,\exp } - \lambda_{{ 1 , {\text{sim}}}} )^{2} + (\lambda_{3,\exp } - \lambda_{{ 3 , {\text{sim}}}} )^{2} }}{{\lambda_{1,\exp }^{2} + \lambda_{2,\exp }^{2} + \lambda_{3,\exp }^{2} }}}} $$
(18)

In the DTI processing, the maps of the planar index and the secondary and tertiary eigenvectors are median filtered using a 3 × 3 window to reduce noise, but no denoising takes place for the rest of the diffusion tensor parameters.

Results

Model Parameters Sensitivity Analysis

The T 2 relaxation times values are taken from the literature T 2,in = 32 ms and T 2,ex = 125 ms.37 , 38 Our model has a total of six parameters: the mean muscle fiber diameter (d m = r l + r s) and ellipticity ratio (α), the intracellular mean residence time (τ in), the intracellular and extracellular diffusion coefficients (D in, D ex) and the intracellular space volume fraction (υ in). To analyze the sensitivity of the model parameters to the derived diffusion tensor eigenvalues, we perform a brute force search for solutions. The total range and resolution of the model parameters used are summarized in Table 1. The best fit (in terms of NRMSE) to the averaged experimental data over 4 muscle regions (λ1/λ2/λ3 = 1.91/1.43/1.29 × 10−9 m2/s) for all parameters are shown in Fig. 2. The range of best solutions is defined based on the constraint NRMSE < 0.04. Table 1 summarizes the ranges of best solutions for all the model parameters. No specific minimum is found for d m, τin and D ex. The best solution for the fiber ellipticity ratio lies between 0.6 and 0.8, and for intracellular diffusion coefficients lies in the range 1.83–1.89 × 10−9 m2/s.

Table 1 Model parameters total range and resolution and model parameters range of best solutions
Full size table
Figure 2
figure 2

Normalized root mean square error between the tensor eigenvalues from the analytical model and the tensor eigenvalues from the experimental data for all parameters for the examined values range and resolution

Full size image

Effect of Fiber Ellipticity on Diffusion Tensor Parameters

In order to assess the effect of the muscle fiber shape on the diffusion tensor parameters, numerical simulations of the diffusion MRI signal were performed with the following parameters derived from the literature and lying within the range examined by the above sensitivity analysis: mean myofiber diameter d m = r l + r s = 80 μm,6 intracellular volume fraction υ in = 0.93,52 intracellular diffusion coefficient D in = 1.9 × 10−9 m2/s, and exchange time τ in = 1.1 s.28 For υ col = 0.50 and D w = 3.2 × 10−9 m2/s, the corresponding extracellular diffusion coefficient is D ex = 2.0 × 10−9 m2/s. The derived DTI parameters are plotted as a function of the fiber ellipticity in Fig. 3. Although the employed diffusion time is such that the root mean square spins displacement on the plane perpendicular to the mean myofiber direction is of the order of 20 μm and therefore four times smaller than the mean cell diameter, the induced difference between the secondary and tertiary eigenvalues is of the order of 0.1–0.3 × 10−9 m2/s for α = 0.6–0.8 and therefore comparable to the experimentally measured value. The difference between the secondary and tertiary eigenvalues of the diffusion tensor decreases as the fiber ellipticity increases and the myofibers become more circular in shape (Fig. 3a). Figures 3b–3d are plots of the mean diffusion coefficient, FA and CP values with the degree of ellipticity for different myofiber diameters. An important conclusion of the present parametric analysis is that both the mean diffusion coefficient and fractional anisotropy (FA) reach a plateau as functions of the fiber ellipticity factor for α > 0.4, which is the range of ellipticity expected for myocytes.51 However, the planar index (CP) shows a significant dependence on the degree of fiber ellipticity for the whole range of α. In fact, the dependence of CP on the fiber ellipticity is approximately linear for α > 0.4. Among the current proposed model parameters, the mean myofiber diameter is one variable reported in the literature to vary significantly for different muscle regions. The plots in Fig. 3 predict that the mean myofiber diameter is one of the parameters with a significant effect on the derived DTI metrics, given the assumptions of the present model.

Figure 3
figure 3

(a) Diffusion tensor eigenvalues dependence on fiber ellipticity for d m = 80 μm, (b) mean diffusion coefficient, (c) FA, and (d) CP dependence respectively on fiber ellipticity for different myocyte diameters d m = 60, 80 or 100 μm

Full size image

In Vivo MRI Results

The fiber direction map and color encoded DTI parameters maps for one central slice of subject 1 are presented in Fig. 4. In the fiber orientation map (Fig. 4a), a vector with the direction of the primary eigenvector is assigned at each voxel. The orientation of the fiber is defined by the zenith angle θ 1 and the azimutal angle ϕ 1 of the primary eigenvector. The zenith angle is a crude estimate of the pennation angle for certain muscles. In general, the pennation angle denotes the angle between the line of action of the muscle (approximately aligned with the leg axis in the case of MG and SOL muscles) and the fiber orientation. Our measurements reveal that the SOL muscle has high pennation angle relative to the GM, GL and TA muscles, and the values are consistent with those reported in the literature.41 , 46 (Notation: Gastrocnemius Medialis, GL; Gastrocnemius Lateralis, GL; Tibialis Anterior, TA; Soleus, SOL.)

Figure 4
figure 4

DTI parameters maps for the central slice of subject 1: (a) primary eigenvector map, (b) map of the zenith angle of the primary eigenvector (values in degrees), (c) FA, and (d) CP maps (non-dimensional parameters). Red lines delineate the aponeurosis between GM and SOL and the anterior aponeurosis of the SOL. Dash line marks the approximate position of part of the anterior aponeurosis. Regions marked (I–IV) pertain to the discussion section

Full size image

The main diffusion parameters for ROIs (of size 1–2 cm2 in plane) placed in specific muscle regions are summarized in Table 2. The diffusion tensor analysis is implemented on a voxel-by-voxel basis and the statistics of the extracted diffusion parameters are computed over the corresponding ROIs for every subject and then averaged for the three subjects. We assume that the diffusion properties do not significantly vary within the ROI of a muscle region. The main output from the diffusion analysis required in the implementation of the proposed composite medium model is the set of three eigenvalues. We assume that T 2,in = 32 ms and T 2,ex = 125 ms and the ranges of the 6 model parameters are derived by satisfying NRMSE < 0.04. The new morphometric parameter extracted from our composite medium model is the fiber cross-sectional aspect ratio α. The previously reported values for the aspect ratio α lie in the range 0.40–0.80.6 , 51 Our predicted values for the mean ellipticity of the muscle fiber shape fall in a similar range (0.6–0.9). As we also expect, the predicted ellipticity follows satisfactorily the measured asymmetry of the diffusion coefficient in the transverse plane. Specifically, the muscle fiber cross section is more elliptical in the GL muscle where the planar index is maximized.

Table 2 In vivo DTI results for four calf muscles
Full size table

In order to explore the geometrical pattern of the asymmetry of the diffusion on the plane perpendicular to the mean myofiber direction, the maps of the secondary and tertiary eigenvectors are plotted. Figure 5 presents the maps of the projection of the secondary eigenvector on the imaging plane superimposed on proton-density weighted images for the two central slices of the three scanned subjects. The orientation of the secondary eigenvector should coincide with the orientation of preferential diffusion on the plane perpendicular to the mean myofiber direction, which in turn coincides with the orientation of the long axis of the elliptical muscle fiber cross section.

Figure 5
figure 5

Maps of the major axis of the ellipse superimposed on a proton-density weighted image for the two central slices of the three subjects (a and b correspond to subject 1, c and d correspond to subject 2, e and f correspond to subject 3)

Full size image

Discussion

Composite Fiber Model Limitations

The present study provides an alternative explanation for the difference in the secondary and tertiary eigenvalues in skeletal muscle diffusion tensor imaging. Although a statistically significant difference between λ2 and λ3 has been observed in the present and previous studies of implementing diffusion tensor imaging in skeletal muscle, we should emphasize that a part of the observed differences may be also related to the presence of noise.3 Muscle DTI has inherently low SNR due to the short T 2 of the muscle, and the dependence of the tensor eigenvalues on SNR should be taken into account in the interpretation of the results.13 Although we do not present any quantitative treatment of noise, we should mention that employing 30 diffusion-encoding directions with 6 averages and stimulated-echo preparation is expected to contribute towards reducing the bias in eigenvalues estimation due to noise. In another recent study using a high number of diffusion encoding directions (equal to 120), we confirmed that the difference between the secondary and tertiary eigenvalues of the diffusion remains and we confirmed the asymmetry of the diffusion process on the plane perpendicular to the myofiber direction using a high order diffusion model.25

The proposed analytical model has a high number of biophysical parameters that can vary significantly. Instead of assigning distinct values for the various biophysical parameters, we opted to perform a sensitivity analysis of the model by allowing the parameters to vary over ranges that agree with the results of existing studies. We have used ranges of values borrowed from the literature for the water residence time,28 the intracellular volume fraction,52 the collagen fraction in extracellular matrix, the muscle fiber diameter6 and ellipticity.4 , 6 The intracellular diffusion coefficient values were selected within a reasonable range, which is of the same order as the extracellular diffusion coefficient and in agreement of the results of Saotome et al.39 Experience with other tissues, suggests that MRI measurements with a higher number of b-values would be useful toward narrowing the ranges for the biophysical parameters.

The predictive ability of the introduced fiber ellipticity model depends on the adequacy of the model to represent the underlying diffusion process and on a priori knowledge of certain biophysical parameters. First, in order to perform a computationally feasible sensitivity analysis of the model to the geometric parameters, we employed the analytical expression for restricted intracellular diffusion between two plates, instead of the exact expression that corresponds to an elliptical cell membrane. Second, the present model formulation is based on Kärger’s approach, which constitutes a simplified phenomenological approach of taking into account diffusion, exchange and T 2 relaxation effects on the diffusion signal. A formal treatment of the above effects requires the numerical solution of the Bloch-Torrey equations following the evolution of the MR signal over the entire period of the PGSTE sequence, and of diffusion inside a realistic tissue geometry (as it has been done in white matter11). The solution of such a problem is computationally demanding, and we are planning to report our progress in this direction in the near future. Third, through plane effects have not been considered in the present analysis. The relatively high slice thickness could induce anisotropy on the transverse plane if the fibers are curved or the fibers are fanning. However, by neglecting extracellular diffusion effects, a first-order geometric analysis shows that the degree of curvature and fanning that would be required to induce such an asymmetry on the transverse plane corresponds to an angle of curvature and dispersion comparable to the pennation angle.

Connection of Eigenvectors with Muscle Kinematics

Having established the asymmetry of the diffusion process on the transverse plane by the eigenvalues analysis and proposed a model-based approach of connecting the asymmetry to muscle fiber shape, we continue with the investigation of the spatial pattern of the observed asymmetry. Although, it is known from histology that the muscle fiber cross-section has an elongated polygonal shape (which can be approximated by an ellipse), there is no direct histological evidence that the alignment of the long axis of the fiber cross sections is meaningful at large spatial scales. (To gather this evidence via optical microscopy investigation, a field of view much larger than the fiber diameter (that is the order of 0.1 mm), is required; we are not aware of any such study.) In the absence of direct validation by performing muscle biopsy on the human volunteers, we hypothesize that there is a functional reason for the fiber cross sectional ellipticity. In order to support this hypothesis, we study the consistency of the cross sectional ellipticity with myocyte shape adaptation during strain predicted from gross muscle kinematics.

Our goal is to correlate the orientation of the elliptical cross-section with potential strain fields in three key calf muscles, one used for dorsiflexion of the ankle (Tibialis Anterior, TA), and two used for plantarflexion (Gastrocnemius Medialis, GM, and Soleus, SOL). With the help of Fig. 6, we provide first some background information on the anatomy and kinematics of these antigravity muscles. TA is a fusiform muscle which originates from the lateral surface of the proximal half of the tibia. GM, the larger of the two gastrocnemius muscles, originates from the medial femoral condyle and inserts (after uniting with the lateral head) into a broad aponeurosis which unites with the deep tendon of SOL to form Achilles tendon. SOL is more complex: it originates at an anterior aponeurosis of complex shape proximally surrounding the fibula, and it inserts at the posterior aponeurosis (having a semi-tubular shape) and at a median septum. The septum is distally attached to the posterior aponeurosis. These aponeuroses divide the soleus into three parts: posterior, anterior, and marginal.1 The posterior soleus is unipennate with fibers oriented along the anterosuperior to posteroinferior direction.

Figure 6
figure 6

Anatomy and function of human calf muscles. (a) Simplified schematic showing the arrangement of gastrocnemius and soleus muscle aponeuroses and the median septum. (b) Wire diagram showing individual fiber orientation (represented by short line segments; blue for gastrocnemius, red for soleus), and the direction (denoted by arrows) of forces exerted by the corresponding tendons upon muscle contraction. (c) Location of calf section studied here

Full size image

The regions pertaining to our discussion are also delineated in the cross sectional view of the calf given in Fig. 4a. Region (I) corresponds to the deep region of TA adjacent to the fibula, region (II) marks the SOL–GM interface, region (III) is on the bifurcated part of the anterior aponeurosis where the median septum penetrates and forms the tendon of insertion for the anterior SOL, and region (IV) belongs to the anterior SOL. Figure 6a is a schematic of a simplified model of the posterior calf muscles, with the SOL muscle drawn on the basis of the 3D reconstruction using MRI by Hodgson et al. 23 As the calf muscles contract isometrically, the two gastrocnemius aponeuroses of origin and the soleus anterior aponeurosis are stretched proximally, while the gastrocnemius broad aponeurosis of insertion and the soleus posterior aponeurosis with the median septum stretch distally via the Achilles tendon. The fiber orientation in the various areas drawn in Fig. 6b is more or less consistent with muscle physiology. Upon isometric contraction, the gastrocnemius muscle moves tangentially (in the plane tangent to the mean myofiber and in the direction indicated by the arrow in region (II))50 and compresses the soleus muscle, Although knowledge of the kinematics of the soleus muscle is less developed, it is expected that the deformation of its various subdomains is consistent with the muscle avoiding acting antagonistically with itself, while at the same time reinforcing the contribution of adjacent calf muscles. This expectation is based on mechanics at the fascicle level. Based on the observations for the variation of the perimysial collagen content between muscles, Purslow36 hypothesized that the sliding of fascicles relative to each other allows the muscle to accommodate shear strain transmission during contraction, which serves to enhance the transmission of force along the fibers.

TA, SOL, and GM are antigravity muscles whose function is to keep the body erect and to contribute to all forms of locomotion.1 Even though the GM and SOL aponeuroses join to Achilles tendon, there is significant shear between them during contraction.9 Therefore, their fibers are continuously subjected to shear during the awake state (a significant portion of 2/3 of a human lifetime), and they are expected to adapt to the mechanical stimulus by adopting a more elliptical cross-section. (This is also consistent with what has been established about the adaptation of the myocardium to mechanical stress). Furthermore, after adopting the geometrical model for myocyte deformation proposed by Trotter and coworker,47 , 48 contraction of the myocyte along the fiber direction causes an increase of the major axis of the ellipse and a decrease of the minor axis. This means that the contracting fiber is stretched in the transverse plane in the direction of the major axis of the ellipse.

The maps of the secondary and tertiary eigenvectors can be used to characterize the orientation of the elliptical fiber cross section. (Colormaps of the secondary and tertiary eigenvalues have been reported in previous studies22 , 41 but have not been put in this context.) The orientation of the major axis of the ellipses in cross sections shown in Fig. 5 is consistent with the direction of transverse shear in regions (I–IV) marked in Fig. 4a. Since the TA fibers in region (I) originate on the tibia with a very small pennation angle, they will tend to stretch toward it upon contraction. The arrows in the muscle regions (II), (III) and (IV) are consistent with the findings of Hodgson et al. 23 (their Fig. 9), as well as Nagarsekar et al. 32 regarding the deformation in GM and SOL during contraction. The results for regions (II) and (IV) imply that GM strains more in the direction which is perpendicular to the longitudinal fiber direction and parallel to the skin surface, and less in the direction perpendicular to both. In addition to the MRI measurements by Hodgson et al.,23 this is indeed consistent with the optical measurements of van Donkelaar et al. 50 for isometric contraction.

Analysis of shear from single slices is not easy in the deep SOL, as its structure varies drastically in the proximal–distal direction (Fig. 6c) and across subjects (Fig. 5). Nevertheless, the alignment of the major axis of the ellipse in region (III) is mostly consistent across the results for three subjects (and in two contiguous slices for each) reported in Fig. 5. This transverse stretching of the region (III) fibers also makes sense from the mechanics point of view: The anterior part of this region corresponds to the domain where the anterior SOL fibers insert into the median septum (shown in Fig. 6a). Upon contraction, the fibers of the anterior SOL stretch toward the putative position of the septum (according to the model of Fig. 6b). The posterior part of region (III) is stretched in the opposite direction by the GM fibers. In agreement with the results of Purslow,36 we hypothesize that the transverse shearing motion of anterior and posterior SOL across the anterior aponeurosis serves to enhance the action of these two muscle compartments.

Broader Implications

Our results place the problem that drives this study on a biomechanical basis, but do not offer a proof that the fiber cross sectional ellipticity is the sole contributor to the DTI transverse eigenvalue asymmetry. It is conceivable that the shape of myofibrils and of the sarcoplasmic reticulum introduce diffusional anisotropy in the direction perpendicular to the muscle fiber, but we have found no evidence from histology to allow us to build a more sophisticated (three-compartment) model. Also, if the sarcoplasmic reticulum network has a topology on the transverse plane that results in the apparent diffusion coefficient asymmetry (λ2 > λ3), then this does not preclude that this asymmetry is also correlated with gross muscle organization and transmission of lateral stress. The latter is related to the shape of the myocyte via the surrounding connective tissue (endomysium), so it has to also be reflected in the shape of the sarcolemma. The point we are making is simple but crucial: a hypothetical sarcoplasmic reticulum asymmetry is connected with a cross-sectional asymmetry of the whole myocyte (since myocytes adapt to stress), and it can therefore be easily incorporated in our diffusion model for the composite medium by modifying, for example, the transverse diffusion coefficients.

There are also important consequences stemming from the model we propose here. As the muscle fibers shorten or elongate, their elliptic cross-section changes shape and, as a result, the ratio λ2/λ3 changes. Although we do not have independent measurements of the various parameters of the model and we cannot provide a quantification of this change at this point, we should point out that such a change was recently reported by other studies.16 , 20 , 21

The present study demonstrates that MRI measurements using DTI coupled with a physically consistent sub-voxel model can provide additional parameters which characterize the structure and function of individual fibers. In addition to providing insight into muscle mechanics, the value of the fiber ellipticity ratio and of the DTI planar index (CP) can be extremely useful in the characterization of morphological changes in skeletal muscle fibers with age, hypertrophy, or following physical inactivity. Numerical simulations show that CP is very sensitive to fiber ellipticity ratio, in contrast to other indices, and therefore CP can be used in lieu of fiber ellipticity ratio. This model-based MRI methodology has potential high translational research value in all clinical areas where alternatives to assess muscle quality are sought. Specifically, although muscle quality has been conventionally defined in the aging or obesity literature via whole limb measures (i.e., knee extension strength or muscle mass), it has been suggested that it can also be assessed in terms of the tertiary eigenvalue of water diffusion tensor in the human calf that has a strong linear correlation to the effective muscle physiological cross-sectional area17—which in turn is proportional to the maximum muscle force. Therefore, connecting water diffusional anisotropy to muscle fiber architecture can help elucidate the connection between structure and muscle quality.

Conclusion

We employed proton MRI and a diffusion-weighted sequence with judiciously chosen directional encoding (under a diffusion tensor imaging (DTI) protocol) to quantify in vivo the microarchitectural properties in multiple contiguous slices of the calf muscles of three healthy volunteers at rest. The map of muscle fiber orientation (given by the primary eigenvector of the diffusion tensor) agrees with local anatomy, and the secondary eigenvalue is significantly higher than the tertiary eigenvalue which is consistent with measurements available in the DTI literature. The main emphasis of this study is on this DTI signal asymmetry on planes perpendicular to the local fiber direction. A composite medium model is developed to simulate water diffusion in the space within the muscle fiber and the extracellular space (endomysium). The muscle fibers are abstracted as infinite cylinders with an elliptical cross section of geometric ratio α (= short axis length/long axis length), a morphometric parameter called fiber ellipticity. The predicted values of fiber ellipticity are within the range 0.4–0.8 which is consistent with the measurements reported in the literature. In order to provide further justification for the proposed model based on mechanics, we show that the orientation of the major axis of the ellipse in selected regions of the Tibialis, Gastrocnemius and Soleus muscles is consistent with the putative direction of transverse shear in these regions, as deduced by independent MRI studies of deformation in active muscle. Given that muscle fibers adapt to mechanical stress and these anti-gravity muscles stay active during the awake state, this observation reinforces our hypothesis that this fiber asymmetry can be an important contributor to the directional DTI signal asymmetry.