Introduction

Bone cells are bathed in the interstitial fluid of the lacunocanalicular porosity. The intimate relation between the fluid and cells provides a method for transduction of stimuli—mechanical, biochemical, or electrical—into cellular responses. The movement of pericellular fluid through the lacunocanalicular network is potentially a primary means of cellular stimulation.42 As the fluid–solid interactions in bone resemble that of a stiff, saturated sponge the flow of fluid through the microchannels may be manipulated via exogenous mechanical loading (cf.,23). Consequently, bone tissue has the ability to model and remodel itself (i.e., functionally adapt) when exposed to a particular mode of excitation or a lack thereof. The exact cellular mechanisms underlying bone’s adaptive ability remain in need of further investigation. An enhanced understanding may lead to the determination of optimal loading regimes that promote a potent osteogenic response.

A key contributor to the knowledge gap surrounding cellular stimulation via fluid flow is the inability to isolate the lacunocanalicular network for experimental study. Theoretical modeling has offered an alternative to describe and quantify intrinsic fluid flow phenomena, including pore fluid pressure, chemotransport, and electrical signals.

Piekarski and Munro in 197733 were among the first to develop a theoretical representation of the lacunocanalicular porosity for the study of stress-induced fluid flow and convective transport. Over the past 30 years theoretical modeling of bone fluid flow has advanced considerably (cf.,17,41,42).

Canaliculi and lacunae have remarkably unique structures, yet they are typically homogenized into a single-continuum “material”. Although a reasonable simplification when dealing with bone fluid flow at the whole-bone (e.g.,16) or osteonal scale (e.g.,15), that was a primary limitation to the investigation of cellular-level phenomena that may generate distinct fluid-mechanical environments for the osteocyte body within the lacuna, and the osteocyte process within the canaliculus, which likely have important implications for pore pressure, fluid shear stress, and the transport of nutrients.

Additionally, the methodologies employed to study lacunocanalicular flow have contributed to uncertainty relating to fundamental parameter values (e.g., permeability values span several orders of magnitude from 10−17 m2  40 down to 10−22 m2  38).

The purpose of this study was thus twofold: firstly, to develop a novel three-dimensional representation of the lacunocanalicular system to quantify parameter values for the lacunar and canalicular structures; and secondly, to apply the model with calculated parameter values to the investigation of small-scale fluid behavior, including pore pressure, fluid shear stress, and species transport, and provide evidence for the validity of computed results.

Methods

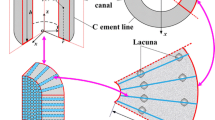
To simulate fluid flow and species transport in mechanically loaded bone, an idealized bone specimen was constructed that represented a radial section of an osteon (Fig. 1). The section consisted of a central osteonal canal (radius r i = 25 μm) and concentric lacunae from which canaliculi emanated radially toward the canal and the cement line (radius r o = 125 μm).

Figure 1
figure 1

Schematic of idealized osteonal section

Full size image

Model Geometry

The idealized osteonal section was simplified for the computational model as a three-dimensional bone specimen of dimensions L × d × d (100 × 21 × 21 μm) (Fig. 2). Three concentric lacunae were distributed in the bone specimen between the osteonal canal surface and the cement line with a lacuna-to-lacuna distance of l = 30 μm.7

Figure 2
figure 2

Schematic of lacunocanalicular model geometry. r i and r o represented boundaries defined by the osteonal canal and the cement line, respectively

Full size image

The complex microstructure of the lacunocanalicular system was replaced by two distinct continuum “materials”: the canaliculi and bone matrix were homogenized as one poroelastic material, referred to as the canalicular material; and the lacuna–osteocyte complex was homogenized as a second poroelastic material, referred to as the lacunar material.

To determine effective poroelastic parameters for the homogenized canalicular and lacunar materials, the following micro-structural descriptions were theorized.

Canaliculi were idealized as straight cylindrical channels of radius b = 0.23 μm, which spanned the canalicular material from the osteonal canal to the cement line (Fig. 3a). An osteocyte process of radius a = 0.1 μm was inserted in the center of each canaliculus. Flow in the collagen-hydroxyapatite porosity was neglected based on the observation of strong chemical bonds between most of the bone fluid and the ionic crystal30; consequently, fluid flowed exclusively in the canalicular material through the annular space defined by the canalicular wall and the surface of the osteocyte process. As proposed in previous studies, we assumed that the annular fluid space was filled with transverse tethering elements that center the process in the canaliculi and a pericellular gel-like proteoglycan fiber matrix that acts as a molecular sieve (cf.,42).

Figure 3
figure 3

(a) Cross-sectional schematic of canalicular material geometry. Twenty-four canaliculi (radius b) (only nine shown here for clarity) were modeled in parallel with a central osteocytic process (radius a) and a fiber-filled annular fluid space. The canalicular channels were encased in solid, impermeable bone matrix. (b) Schematic of lacunar material geometry. Spherical osteocyte (radius R i) was modeled in the center of a spherical lacunar shell (radius R o). The lacuna and cell were housed in a volume of canalicular material

Full size image

The canalicular density on the wall of human secondary osteons of 50 μm diameter has been measured to be 5.5 per 100 μm2.27 Consequently, in the canalicular material of 21 × 21 μm cross section, 24 canaliculi were modeled in parallel.

Each of the three modeled osteocytes were described as a sphere with a radius of R i = 4 μm, and were placed in a spherical lacunar cavity with a radius of R o = 5 μm (Fig. 3b). Although osteocytes and their lacunae tend to be ellipsoidal,28 these simplified geometries and dimensions were reasonable approximations of measured data.40

Similar to the annular fluid space of the canaliculi, the spherical shell defined by the wall of the lacuna and osteocyte surface was assumed to be filled with a fiber matrix and tethering elements.

Each lacuna was placed within a volume of canalicular material measuring 15 × 15 × 10 μm (see Fig. 3b). Altogether, this volume was referred to as lacunar material.

Parameter Values

Based on the structural descriptions of the canalicular and lacunar materials (see Fig. 3), a set of four material constants (E d, ν d, α, and B), porosity, and hydraulic properties (i.e., permeability and dynamic fluid viscosity) were determined in order to characterize fully each material as a linear isotropic poroelastic solid.

The porosity of the canalicular and lacunar material (i.e., the ratio of pore fluid volume to the total bulk volume), including the osteocyte and its processes, was given by

$$ \phi_{\text{c}} = n_{\text{c}} \pi \left( {b^{2} - a^{2} } \right), $$
(1)

and

$$ \phi_{\text{l}} = \phi_{\text{c}} + \frac{{\left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-\nulldelimiterspace} 3}} \right)\pi \left( {R_{\text{o}}^{3} - R_{\text{i}}^{3} } \right)}}{{V_{\text{T}} }}\left( {1 - \phi_{\text{c}} } \right), $$
(2)

respectively, where V T was the total volume of each lacunar material section (i.e., 15 × 15 × 10 μm). We applied the theory of composite materials8, 38 to determine effective elastic constants for the canalicular and lacunar materials based on the porosity and the elastic properties of the solid matrix material. The following relations between drained moduli (K d and G d) and solid phase moduli (K s and G s) were used to determine ν d and E d:

$$ K_{\text{d}} = K_{\text{s}} \left( {1 - \frac{\phi }{{1 - {{K_{\text{s}} } \mathord{\left/ {\vphantom {{K_{\text{s}} } {\left( {K_{\text{s}} + \left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-\nulldelimiterspace} 3}} \right)\,G_{\text{s}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {K_{\text{s}} + \left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-\nulldelimiterspace} 3}} \right)\,G_{\text{s}} } \right)}}}}} \right), $$
(3)
$$ G_{\text{d}} = G_{\text{s}} \left( {1 - \frac{{15\left( {1 - \nu_{\text{s}} } \right)\,\phi }}{{7 - 5\nu_{\text{s}} }}} \right), $$
(4)

and from Detournay and Cheng,12

$$ \nu_{\text{d}} = \frac{{3K_{\text{d}} - 2G_{\text{d}} }}{{2\left( {3K_{\text{d}} + G_{\text{d}} } \right)}}, $$
(5)

and

$$ E_{\text{d}} = 2G_{\text{d}} \left( {1 + \nu_{\text{d}} } \right), $$
(6)

where K s = 17.66 GPa, G s = 6.56 GPa, and ν s = 0.335.38 The porosity ϕ used in the calculation of the effective material constants differs from those computed in Eqs. (1) and (2), in that the osteocyte and its processes are excluded from the calculations (i.e., a → 0 and R i → 0 in Eqs. (1) and (2), respectively; the porosity becomes a ratio of the volume of “not bone” to the total bulk volume). Neglecting the cellular structures, the total lacunocanalicular porosity of the modeled bone specimen was calculated to be 4.4%, which was a robust approximation of reported values (2.3–5.0%11).

With the drained bulk modulus K d from Eq. (3) and the bulk modulus of the contents of the pore space K f (the fluid and cell are assumed to have a modulus equivalent to salt water42), we calculated Biot’s effective stress coefficient α and Skempton’s coefficient B using equations from Detournay and Cheng12:

$$ \alpha = 1 - \frac{{K_{\text{d}} }}{{K_{\text{s}} }}, $$
(7)

and

$$ B = \frac{{\alpha K_{\text{f}} }}{{\left[ {\alpha - \phi \left( {1 - \alpha } \right)} \right]K_{\text{f}} + \phi K_{\text{d}} }}. $$
(8)

The fluid viscosity μ of bone fluid has not been measured and is, therefore, typically assumed to be equivalent to that of salt water (10−3 Pa s). The permeability of cortical bone has been measured experimentally26; but because of the difficulty in isolating the small lacunocanalicular porosity, there are no experimental data for the permeability of the lacunar or canalicular microstructures. Consequently, we calculated effective permeability values for the lacunar and canalicular materials.

The canalicular permeability was determined by first calculating the permeability of a single canaliculus. The permeability for the canalicular fluid annulus was calculated with an equation from Bird et al. 4:

$$ k_{\text{a}} = k_{\text{h}} \left[ {\frac{{1 - q^{4} }}{{1 - q^{2} }} - \frac{{1 - q^{2} }}{{\ln \left( {{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-\nulldelimiterspace} q}} \right)}}} \right], $$
(9)

where k h is the permeability of a hollow canaliculus given by

$$ k_{\text{h}} = {{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } 8}} \right. \kern-\nulldelimiterspace} 8}, $$
(10)

and the bracketed term is an annular correction factor that accounts for the central osteocyte process. A capillaric model37 was applied to calculate the permeability of the canaliculi in parallel:

$$ k_{\text{cap}} = n_{\text{c}} \pi \left( {b^{2} - a^{2} } \right)\,k_{\text{a}} . $$
(11)

Lastly, Weinbaum et al.42 calculated the permeability of the canaliculi with a fiber matrix and transverse fiber spacing of 7 nm to be two orders of magnitude smaller than the permeability of the annular fluid space k cap. Therefore, to account for the presence of the fiber matrix, the final canalicular permeability was achieved by dividing k cap by 100. Thus the canalicular material permeability was

$$ k_{\text{c}} = \frac{{n_{\text{c}} \pi b^{2} \left( {b^{2} - a^{2} } \right)}}{800}\left[ {\frac{{1 - q^{4} }}{{1 - q^{2} }} - \frac{{1 - q^{2} }}{{\ln \left( {{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-\nulldelimiterspace} q}} \right)}}} \right]. $$
(12)

Equation (12) resulted in a canalicular permeability of 1.054 × 10−19 m2. This calculated permeability value was an order of magnitude smaller than that determined by Zhang et al.45 (1.47 × 10−20 m2) using Weinbaum et al.42 model. A greater canalicular density n c used in this study, which appeared to be an accurate representation of the canalicular network,27 resulted in a more permeable bone specimen. To examine the possibility of a more dense fiber matrix or more tortuous canalicular channels, as well as a less dense fiber matrix, canalicular permeability values one order of magnitude above and below that calculated with Eq. (12) were also investigated (see Table 1).The permeability of the lacunar material was determined with a Carman–Kozeny geometric permeability model for flow through concentric spheres13:

$$ k_{\text{l}} = \frac{{\phi^{3} }}{{100K_{0} T_{\text{l}} \left( {1 - \phi^{2} } \right)\,S_{0}^{2} }}, $$
(13)

where ϕ given by

$$ \phi = \frac{{\left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-\nulldelimiterspace} 3}} \right)\pi \left( {R_{\text{o}}^{3} - R_{\text{i}}^{3} } \right)}}{{V_{\text{T}} }} $$
(14)

is the fluid volume enclosed by the lacunar wall and the osteocyte body, normalized by the total lacunar material volume V T; S 0 is the surface area of the spherical shell, normalized by V T, defined as

$$ S_{0} = \frac{{4\pi \left( {R_{\text{o}}^{2} - R_{\text{i}}^{2} } \right)}}{{V_{\text{T}} }}; $$
(15)

K 0 is a shape factor with a value of 2 − 313 (assumed here to be 2.5); and T l is the tortuosity of the pore space, given by

$$ T_{\text{l}} = \left( {\frac{{\delta_{\text{t}} }}{{\delta_{\text{a}} }}} \right)^{2} , $$
(16)

where δ a is the apparent length of the path traveled by a fluid particle (i.e., 2R o), and δ t is the true length of the path taken by a fluid particle through the pore space (assumed to be one half of the lacunar circumference; πR o). The contribution of the surrounding canalicular material permeability was neglected in the calculation of the lacunar material permeability as it was several orders of magnitude smaller, and thus did not have a significant influence.

Table 1 Calculated canalicular and lacunar parameter values
Full size table

To account for the fiber matrix within the spherical shell, a factor of 100 was included in the denominator of Eq. (13), effectively reducing the spherical shell permeability by two orders of magnitude. Although a lacunar fiber matrix permeability factor has not been previously determined, the calculated lacunar material permeability value (7.172 × 10−17 m2) was similar to a value determined by Zhang44 (6.76 × 10−17 m2).

Calculated parameter values used in the poroelastic model were summarized in Table 1.

Computational Model

Derivation of the governing poroelastic field equations has been previously covered in detail (see Cowin11 for a comprehensive review). Briefly, following from the constitutive equations and appropriate conservation laws, the coupled field equations that govern the behavior of the fluid and solid phases are

$$ \nabla \cdot \left( {c\nabla p} \right) = \frac{\partial p}{\partial t} + \Upomega , $$
(17)

and

$$ G_{\text{d}} \nabla^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} + \frac{{G_{\text{d}} }}{{1 - 2\nu_{\text{d}} }}\nabla \left( {\nabla \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} } \right) = \alpha \nabla p - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F} , $$
(18)

respectively, where Ω is a term that accounts for the injection/production of fluid, and F is the body force per unit volume.

The poroelastic model was implemented in STARS, a coupled fluid flow and mechanics simulator (Computer Modelling Group Ltd., Calgary, AB, Canada). The finite difference fluid flow model31 was iteratively coupled39 to the finite element mechanics module such that information was exchanged both ways between the reservoir simulator (computed pressure p) and the mechanics module (computed solid displacement u) until convergence was achieved (i.e., when the norm of pressure change between two consecutive coupling iterations was below a tolerance of 1 × 10−4 Pa).

The three-dimensional lacunocanalicular model was discretized into a Cartesian grid with 1,960 (40 × 7 × 7) elements, which demonstrated convergence. Eight-node hexahedral elements measuring 2.5 × 3.0 × 3.0 μm were used for the canalicular and lacunar materials.

Fluid Flow

Bulk fluid flow was calculated in the trans-osteonal direction (osteonal canal to cement line) with Darcy’s law, which states that fluid velocity is a function of the pressure drop across a given distance and a proportionality constant (permeability divided by fluid viscosity), given by

$$ q = - \frac{k}{\mu }\nabla p, $$
(19)

The shear stress experienced by the osteocyte and its processes was estimated according to the equation

$$ \tau = \frac{8\mu \,v}{\beta }, $$
(20)

where β is the mean pore diameter, given by

$$ \beta = 4\sqrt {2T} \sqrt {\frac{k}{\phi }} , $$
(21)

where v is the interstitial fluid velocity, given by the Dupuit relation

$$ v = \frac{{T{\kern 1pt} q}}{\phi }, $$
(22)

T is the tortuosity of the flow path (T = 1 for straight channels).9

Species Transport

To simulate nutrient transport through the lacunocanalicular network and nutrient consumption by the osteocytes, convective-diffusive-reactive flow was incorporated and governed by

$$ \frac{d}{dt}\left( {\phi \rho C} \right) = \nabla \cdot \left( {J_{\text{con}} + J_{\text{diff}} } \right) + \Uppsi + R, $$
(23)

where C is the concentration of the species, Ψ is the injection/production of the species, R is the reaction of the species, and J con and J diff are the convective flux and diffusive flux, respectively, given by

$$ J_{\text{con}} = - \frac{\rho Ck}{\mu }\nabla p, $$
(24)

and

$$ J_{\text{diff}} = - \phi {\kern 1pt} D\nabla \left( {\rho C} \right), $$
(25)

where D is the species’ diffusion coefficient.

A simulated nutrient was assigned properties representative of glucose, with a mass density of 1540 kg m−3, and a molecular diffusion coefficient D = 1.0 × 10−10 m2 s−1.29 In addition, to examine the ability of osteocytes to receive adequate nutrition via convective transport, a reaction was incorporated in the form of osteocyte consumption of the simulated glucose. A consumption rate of 1.0 × 10−18 kg s−1 was specified for each of the three modeled cells.32 The potential for the cells to receive nourishment was quantified by the amount of glucose consumed by the cells (i.e., the concentration of the reaction product in the lacunae).

Boundary Conditions

The boundaries of the three-dimensional poroelastic model, excluding the boundary defined as the osteonal canal, were specified as impermeable to flow; therefore, trans-osteonal flow through the lacunocanalicular network—the dominant flow direction—was simulated.

The osteonal canals provide the primary space for bone fluid pressure to relax when bone is mechanically loaded.41 Furthermore, it was suggested that in vivo fluid pressure in the canals cannot exceed the vascular pressure (~10 kPa).43 Accordingly, the modeled osteonal canal boundary was maintained at baseline pressure (0 kPa) by injection or production of fluid into or out of the lacunocanalicular porosity, depending on the pore pressure.

Intracortical vessels are important sources for cellular nutrients.10 The osteonal canal was thus the source of the simulated glucose. Fluid entering the lacunocanalicular model from the canal had a glucose concentration of 1%. Also, fluid that drained into the canal was capable of carrying the nutrient, thereby decreasing the concentration in the lacunocanalicular network during outflow.

To simulate the local mechanical environment of the modeled lacunocanalicular bone specimen, a zero-displacement boundary condition was imposed on all nodes of the bottom face, two vertical side faces, and cement line boundary. Exogenous mechanical loading was simulated with a compressive sinusoidal distributed load σ = |σ 0 sin ωt|, applied to the top surface of the model with a maximal loading magnitude σ 0 of 20 MPa, which we have shown to be in the physiological range.16 A range of loading frequencies was investigated to examine the influence of frequency on pore fluid pressure, fluid flow, and species transport. In all cases, 10 complete loading cycles were applied.

Results

In the axially loaded lacunocanalicular bone specimen, the induced normal compressive strain at maximal load was approximately 1070 με in the canalicular material and increased to a maximum of 1460 in the more compliant lacunar material (Fig. 4a).

Figure 4
figure 4

(a) Normal compressive strain plotted from the osteonal canal (0 μm) to the cement line (100 μm) at maximal load during the second loading cycle. (b) Transient pore fluid pressure at cement line plotted for 10 loading cycles (f = 1 Hz) for k c = 10−18, 10−19, and 10−20 m2 (pressure for k c = 10−18 m2 appeared as a nearly flat line at 0 kPa). (c) Pore fluid pressure plotted from the osteonal canal (0 μm) to the cement line (100 μm) at peak pressure during second loading cycle for k c = 10−18, 10−19, and 10−20 m2. Note logarithmic pressure scale for clarity. (d) Maximal pore fluid pressure at cement line plotted for range of loading frequencies

Full size image

Pore fluid pressure was analyzed for canalicular permeability k c values of 10.5, 1.05, 0.105 × 10−19 m2 (referred to hereafter as 10−18, 10−19, and 10−20 m2, respectively). In all reported results the pressure represents a gauge pressure (i.e., an increase or decrease from atmospheric pressure: ~101 kPa), unless explicitly referred to as an absolute pressure.

A decrease in permeability by an order of magnitude produced an order-of-magnitude increase in pressure for f = 1 Hz (Fig. 4b). Maximal pressure magnitudes of 0.86, 8.58, and 85.35 kPa were calculated for k c = 10−18, 10−19, and 10−20 m2, respectively. Maximal pressure was produced at the cement line, whereas fluid drainage at the osteonal canal boundary allowed pressure magnitudes to be maintained at baseline value (Fig. 4c). Consequently, a trans-osteonal pressure gradient was established. The pressure profile across the length of the bone specimen—osteonal canal to cement line—was consistent for all permeability values, with the greatest pressure gradient occurring between the canal and the first lacuna (see Fig. 4c). The lacunae were represented in the pressure profile as regions of constant pressure.

Because we assumed a lacunar fiber matrix permeability factor of 100 (Eq. 13), a sensitivity analysis was performed for this value. Simulations were run with factors of 1, 10, 1000, and 10,000 (i.e., permeability values of 717.2, 71.72, 0.7172, and 0.07172 × 10−17 m2). Analysis revealed no change in pressure response for fiber matrix factors of 1, 10, and 1000, while a factor of 10,000 resulted in a minimal increase in maximal pressure magnitude (~0.8%), relative to a factor of 100. As the lacunar pore space is an order of magnitude larger than that of the canaliculus, it is unlikely that the lacunar permeability approaches the small permeability of the canaliculi. Thus, the assumed fiber matrix factor of 100 appeared to be a reasonable approximation and was utilized for all remaining calculations.

The influence of loading frequency on pore fluid pressure was investigated for 1, 5, 10, 20, and 40 Hz (Fig. 4d). Maximal pressure in the frequency range of 1–40 Hz exhibited an approximately linear relation with loading frequency for k c = 10−18 and 10−19 m2. For k c = 10−20 m2 pressure magnitude had a predominantly nonlinear relation with loading frequency with a small, approximately linear portion up to ~8.0 Hz. Maximal pore pressure magnitude at a given frequency was consistent in all cycles k c = 10−18 and 10−19 m2, whereas a greater pressure magnitude was produced during the first cycle for k c = 10−20 m2; most notably at elevated frequencies. For example, at a loading frequency of 40 Hz, cycle number one exhibited a 33% greater load-induced pressure magnitude, relative to the remaining nine cycles.

Due to the influence of permeability k c on fluid pressure p (i.e., for f = 1 Hz, an order-of-magnitude decrease in permeability resulted in an order-of-magnitude increase in pressure, and vice versa; see Fig. 4c), and the linear proportionality of both terms with fluid velocity in Darcy’s law, fluid velocity magnitudes and profiles across the osteon for f = 1 Hz were nearly identical for the range of canalicular permeabilities investigated.

Corresponding to the pressure profile, a load-induced trans-osteonal fluid velocity gradient was produced (Fig. 5a). Local peaks in fluid velocity magnitude were calculated in the lacunar material, with a maximal value of 0.024 μm s−1 occurring in the first lacuna. Fluid velocity equal in magnitude but opposite in direction was produced during load application (first half of cycle) and load removal (second half of cycle). During loading, positive fluid pressure resulted in flow towards and into the osteonal canal, whereas unloading resulted in flow out of the canal, towards the cement line.

Figure 5
figure 5

(a) Darcy (bulk) fluid velocity plotted from the osteonal canal (0 μm) to the cement line (100 μm) for four time points (see loading/pressure time series; inset) for k c = 10−19 m2 and f = 1 Hz (k c = 10−18 and 10−20 m2 produced identical results). Negative fluid velocity represented fluid flow towards and into the simulated osteonal canal, whereas positive fluid velocity represented flow out of the canal, towards the cement line. (b) Maximal Darcy fluid velocity magnitude at the inlet of first lacuna plotted for range of loading frequencies

Full size image

Fluid velocity magnitude and loading frequency exhibited a similar relationship to that demonstrated for pressure and frequency (i.e., an approximately linear relationship for permeabilities of 10−18 and 10−19 m2, and a nonlinear relationship for 10−20 m2). However, contrary to pressure, at elevated loading frequencies, fluid velocity magnitudes were reduced for k c = 10−20 m2, relative to k c = 10−18 and 10−19 m2 (Fig. 5b).

Although fluid velocity magnitude was similar across the range of permeabilities for f = 1 Hz, fluid shear stress demonstrated a dependence on canalicular permeability (Fig. 6a). Maximal shear stress magnitudes for f = 1 Hz were 0.38, 1.20, and 3.80 Pa for k c = 10−18, 10−19, and 10−20 m2, respectively. The lacunae were sites of minimal shear stress, whereas maximal shear stress occurred in the canaliculi, with local maxima at the inlet and outlet of the lacunae.

Figure 6
figure 6

(a) Fluid shear stress magnitude plotted from the osteonal canal (0 μm) to the cement line (100 μm) at peak pressure during second loading cycle for k c = 10−18, 10−19, and 10−20 m2, and f = 1 Hz. (b) Maximal fluid shear stress magnitude at the inlet of first lacuna plotted for range of loading frequencies

Full size image

Fluid shear stress increased approximately linearly with frequency for permeability values of 10−18 and 10−19 m2, and nonlinearly for 10−20 m2 (Fig. 6b). Although fluid velocity was reduced at elevated frequencies—most notably for k c = 10−20 m2—fluid shear stress was enhanced at all frequencies as canalicular permeability was decreased.

Simulated glucose was transported into the lacunocanalicular system during inflow from the osteonal canal and removed from the system during flow into the canal. At a loading frequency of 1 Hz, the amount of glucose consumed by the osteocytes—quantified by the amount of reaction product in each lacunar material section at the end of the 10-cycle loading regime—was the same across the range of canalicular permeabilities (Fig. 7a). A trans-osteonal gradient in reaction product was evident after 10 loading cycles: lacunae 2 and 3 consumed 18% and 27% less glucose, respectively, relative to lacuna 1.

Figure 7
figure 7

(a) Concentration of reaction product (normalized; C/C max) after 10 loading cycles for f = 1 Hz plotted from the osteonal canal (0 μm) to the cement line (100 μm) for a k c = 10−19 m2 (k c = 10−18 and 10−20 m2 displayed identical results). (b) Concentration of reaction product (normalized; C/C max) in first lacuna after 10 loading cycles plotted for range of loading frequencies

Full size image

The simulated glucose consumed by the modeled cells was frequency dependent (Fig. 7b). For the range of canalicular permeabilities investigated, there was a sharp, linear decline of ~82% in the amount of reaction product as loading frequency was increased from 1 to ~10 Hz. As frequency was increased from ~15 to 40 Hz, there was a dramatically less pronounced, approximately linear reduction of ~8% in reaction product.

Discussion

Pore fluid pressure is an important load-induced phenomenon of the lacunocanalicular system as it in large part dictates the shear stress and degree of chemotransport experienced by the cells. The model presented in this study demonstrated several interesting aspects of the pressure response to loading.

Consistent with the novel two-dimensional lacunocanalicular model developed by Gururaja et al.,17 the homogenized lacuna–osteocyte structures were highlighted herein as the mechanism for the generation of lacunocanalicular fluid pressure. This pore pressure was subsequently dissipated by the flow of fluid into the osteonal canal via the canaliculi.

A change in the pressure behavior was evident as the canalicular permeability k c was decreased from 10−19 to 10−20 m2. Specifically, approximately linear relations between pressure and frequency were calculated for k c = 10−18 and 10−19 m2, whereas a largely non-linear relation was calculated for k c = 10−20 m2 (Fig. 4d). This was explained by a transition from a drained to an undrained system as the permeability was reduced, and as the loading time was decreased (i.e., loading frequency increased), thereby diminishing the time available for fluid to flow freely and dissipate pore pressure.

Moreover, the maximal pressure magnitudes calculated for the range of canalicular permeabilities investigated appear to be more physiologically realistic than those suggested in previous modeling efforts. At a loading frequency typical of human locomotion (1 Hz), pore pressures ranging from 270 kPa46 up to 11 MPa25 have been calculated for the lacunocanalicular porosity. Even at the lower end, these pressure magnitudes present a considerable problem in the event of unloading or in the tensile region of the cortex during loading, as fluid pressure would drop below an absolute value of 6.3 kPa (i.e., −93.7 kPa gauge pressure) (vapor pressure of water at body temperature) and could result in ebullism.18 This is potentially avoided if the system were substantially pressurized, in which case an absolute pressure of 6.3 kPa would never be attained. However, periosteal and endosteal gauge pressures of ~2 and 8 kPa, respectively, have been measured.5 Therefore, as the pore spaces of bone are fully interconnected, it is not possible that the lacunocanalicular system is continuously pressurized above the endosteal pressure of 8 kPa.

Alternatively, it is conceivable that another mechanism prohibits large tensile (negative) gauge pressures, despite high-magnitude compressive pressures; however, such a system has never been proposed, and large negative pressures have not been previously discussed as being physically impossible.

At a loading frequency of 1 Hz, we calculated maximal pore fluid pressures of 0.86, 8.58, and 85.35 kPa for k c = 10−18, 10−19, and 10−20 m2, respectively. The pressure generated with a canalicular permeability of 10−18 m2 is likely unrealistic, as the magnitude would be insufficient to drive fluid against the trans-cortical pressure difference (~6 kPa). Maximal pressure gradients with permeabilities of 10−19 and 10−20 m2 allow fluid to flow against the trans-cortical gradient, yet the magnitudes were consistent with findings that suggested that fluid pressures generated in bone under loading are insufficient to stimulate osteocytes directly.6 Importantly, even at the smallest permeability investigated (i.e., k c = 10−20 m2), the vapor pressure of water at body temperature was never approached during unloading, which suggested a resolution to the issue of large negative fluid pressures calculated in previous theoretical studies.

The dual-continuum model developed in this study approximated the lacunocanalicular pressure response calculated by Anderson et al.1 using computational fluid dynamics. Specifically, pressure gradients were evident in the canaliculi, whereas the greater permeability and porosity of the lacunae allowed for pressure to be relaxed during loading, resulting in a homogeneous pressure response. However, Anderson and colleagues imposed an artificial pressure gradient on the system, whereas the present result was produced in response to a distributed load applied to a compressible solid skeleton (bone matrix), which more closely represents the in situ local mechanical environment.

The pressure profile was also consistent with experimental microelectrode studies. Iannacone et al.19 observed no macroscopic (i.e., transcortical stress generated potentials (SGP); proportional to fluid pressure36) from bone samples subjected to uniform compression, whereas microscopic SGPs were measured local to the osteonal canals. These microscopic SGPs were explained in the present model as large trans-osteonal pressure gradients were developed in response to uniform loading.

Lacunae were shown to be sites of maximal fluid velocity (Fig. 5a), whereas the shear stress in the lacunar material was estimated to be insignificant due to the large porosity and permeability associated with the structure (Fig. 6a). On the other hand, the small permeability of the canaliculi (most notably for k c = 10−19 and 10−20 m2) resulted in significant shear stress in the simulated canalicular channels. Maximal shear stress was predicted to occur on the osteocyte processes at the inlet of the lacunae. The processes have been previously implicated as the primary sensor of shear stress.42 Furthermore, the calculated shear stress magnitudes in the canaliculi approximated the range of values that have induced cellular responses in vitro (cf.,2, 3, 20).

We demonstrated that shear stress increased in response to loading frequency (Fig. 6b). However, all calculations were performed with a maximal loading magnitude of 20 MPa, which induced over 1000 με of normal strain. In reality, at the higher end of the range of physiologically relevant frequencies (~40 Hz), strain magnitudes decrease considerably.14 To examine the case of reduced strain magnitude at high frequency, we decreased the load by a factor of 100 and applied it at a frequency of 40 Hz for k c = 10−19 and 10−20 m2. This loading regime induced ~10 με in the canalicular material. Maximal shear stress magnitudes were 0.14 and 0.57 Pa for k c = 10−19 and 10−20 m2, respectively. With a canalicular permeability of 10−20 m2 the shear stress induced in the canaliculi approximated values in which an intracellular Ca2+ response has been observed. Consequently, our model provides evidence in support of the osteogenic influence of high-frequency low-magnitude loading regimes (cf.,35). Furthermore, it is important to note, in relation to the earlier discussion of pressure magnitude, that with this high-frequency low-magnitude loading regime, the maximal pressure drop upon unloading was 11.0 kPa, which remained within the range of physically plausible values.

In addition, the enhanced magnitude of the first peak in the loading cycle resulted in a shear stress of 0.73 Pa with a canalicular permeability of 10−20 m2. This result indicated the importance of the first cycle in a loading regime and may be a factor in the diminished response of tissue to mechanical loading following a small number of cycles.34

The pressure gradient decreased dramatically past the first lacuna (see Fig. 4c) and was zero at the cement line. As a result, osteocytes located further from the osteonal canal experienced a dramatically reduced level of shear stress, relative to the cells close to the canal. Potentially, cells at a significant distance from the osteonal canal experience insufficient shear stress and instead rely on intercellular signaling molecules via gap junctions from cells that are in a position to experience high levels of shear stress. Alternatively, it is possible that the tortuosity of the channels and the branching of canaliculi serve to decrease the permeability of the flow paths as distance from the osteonal canal is increased, resulting in more homogeneous shear stress throughout the osteon. A wedge-shaped model of a section of an osteon with decreasing canalicular density approaching the cement line may provide additional insights into the fluid-mechanical environment further from the osteonal canal.

Uptake of the simulated glucose exhibited a dramatic decrease as loading frequency was increased from 1 to 10 Hz (Fig. 7b), which corroborated previous theoretical40 and in vivo experimental24 results. Although fluid velocity magnitudes increased with loading frequency, reduced fluid transport distance during each half-loading was a primary factor in the decreased efficiency of transport at higher frequencies.

In contrast to the results of Wang et al.,40 we did not calculate a dramatic difference in transport potential for canalicular permeabilities greater than 10−20 m2. Interestingly, the ability of the simulated osteocytes to obtain the glucose was nearly identical for k c = 10−18 and 10−19 m2. The similarity in transport for larger permeabilities was explained by the fluid velocity results. As permeability was decreased from 10−18 to 10−19 m2, a corresponding order-of-magnitude increase in pressure and trans-osteonal pressure gradient maintained fluid velocity magnitudes, and thus convective transport. Furthermore, this relation was evident at all loading frequencies investigated. A further decrease in canalicular permeability from 10−19 to 10−20 m2 inhibited fluid flow—most notably at higher loading frequencies (see Fig. 5b)—and was, therefore, detrimental to species transport.

A mixing mechanism in the lacunae ostensibly could aid in transport and uptake of nutrients.22,40 By explicitly representing the lacuna in our model, we provided a physical explanation for the proposed mixing. The enhanced fluid velocities calculated in the lacunae would assist in such a mechanism and may provide an important means for cells to maintain an adequate supply of nutrients. Of greater importance to cellular nourishment, however, is the ability of nutrients to be transported to the lacunae in the first place. We calculated that for three lacunae in series, all osteocytes were sufficiently nourished (i.e., all modeled cells were capable of reacting with the simulated glucose at the specified rate) with a high-magnitude low-frequency loading regime. Petrov and Pollack32 suggested that stress-induced fluid flow was not capable of sustaining viability for five osteocytes in series. A more accurate representation of the connections between neighboring osteons would offer better insight into transport processes, as osteocytes at a distance from the osteonal canals likely receive nourishment from a multitude of sources.

Modeling the lacunocanalicular network as a uni-directional, fully-reversible and closed (aside form the osteonal canal) system lacked exact fidelity.21 The lacunocanalicular system is composed of highly tortuous and branching canaliculi with connections across the cement line. Using a straight channel assumption, we calculated a canalicular permeability value of 1.05 × 10−19 m2. However, we showed that calculated fluid pressure and shear stress results suggested a permeability approaching 10−20 m2, which was a robust approximation of the canalicular permeability calculated by Gururaja et al.17 A decrease in permeability from our calculated value of 10−19 m2 towards 10−20 m2 suggested that a tortuosity factor approaching 10 needed to be included in our Eq. (12) for canalicular permeability. The tortuosity factor effectively increases the channel length and decreases the bulk permeability of the canalicular material. Consequently, by simulating the case of k c = 10−20 m2 we simulated the case of tortuous canals in the present model.

Furthermore, theoretical16,41 and experimental19 studies have suggested that each osteon acts as its own drainage system whereby fluid pressure is dissipated via the osteonal canal, regardless of the degree of coupling between neighboring osteons (i.e., permeability of cement lines). Despite a trans-cortical stress gradient, lacunocanalicular fluid flow is dominated by pressure gradients local to the osteonal canals. Thus, the fluid pressure, velocity, and shear stress magnitudes calculated with an impermeable cement line are expected to be accurate approximations of physiological values.

Furthermore, we were restricted to isotropic poroelasticity, whereas the lacunocanalicular system is more aptly described with anisotropic parameters. As canaliculi are oriented principally in the radial direction, trans-osteonal flow is likely the dominant flow direction. However, incorporation of anisotropic parameters would prove useful for a more accurate representation of the different responses of pore pressure and shear stress when loaded with varying regimes (e.g.,17).

Future refinements of the model will address the inherent limitations of a one-dimensional, isotropic description of the lacunocanalicular system. Nevertheless, this study represented a significant step in developing a deformable poroelastic model of the lacunocanalicular system that incorporated explicit representation of canalicular and lacunar porosities.

The model allowed for calculation of lacunar permeability and suggested a narrow range of potential canalicular permeability values. With these permeability values, we calculated physically and physiologically plausible pressure and shear stress magnitudes, species transport, and demonstrated the consistency of calculated results with previous theoretical and experimental studies. This novel study will be of further use in the development of advanced multi-scale bone fluid flow models that seek to elucidate the underlying mechanisms of mechanotransduction.