Micro-scale Dynamic Simulation of Erythrocyte–Platelet Interaction in Blood Flow

Abstract

Platelet activation, adhesion, and aggregation on the blood vessel and implants result in the formation of mural thrombi. Platelet dynamics in blood flow is influenced by the far more numerous erythrocytes (RBCs). This is particularly the case in the smaller blood vessels (arterioles) and in constricted regions of blood flow (such as in valve leakage and hinge regions) where the dimensions of formed elements of blood become comparable with that of the flow geometry. In such regions, models to predict platelet motion, activation, aggregation and adhesion must account for platelet–RBC interactions. This paper studies platelet–RBC interactions in shear flows by performing simulations of micro-scale dynamics using a computational fluid dynamics (CFD) model. A level-set sharp-interface immersed boundary method is employed in the computations in which RBC and platelet boundaries are tracked on a two-dimensional Cartesian grid. The RBCs are assumed to have an elliptical shape and to deform elastically under fluid forces while the platelets are assumed to behave as rigid particles of circular shape. Forces and torques between colliding blood cells are modeled using an extension of the soft-sphere model for elliptical particles. RBCs and platelets are transported under the forces and torques induced by fluid flow and cell–cell and cell–platelet collisions. The simulations show that platelet migration toward the wall is enhanced with increasing hematocrit, in agreement with past experimental observations. This margination is seen to occur due to hydrodynamic forces rather than collisional forces or volumetric exclusion effects. The effect of fluid shear forces on the platelets increases exponentially as a function of hematocrit for the range of parameters covered in this study. The micro-scale analysis can be potentially employed to obtain a deterministic relationship between fluid forces and platelet activation and aggregation in blood flow past cardiovascular implants.

Background

Function and Behavior of Platelets

Platelets play a primary role in the early stages of thrombosis.17,18,43 When subject to unfavorable flow conditions or foreign surfaces, platelets may be activated, and subsequently form aggregates, leading to the initiation of a thrombus. The rheological effects on platelets are well documented and at least the basic mechanisms in the cascade of processes6,8 that lead to the formation of a thrombus are well characterized. Of primary concern from the physical point of view is the shear stress imposed on the platelets. While physiological magnitudes of shear stresses have no effect on platelets, unusually high shear stresses that may develop under conditions of disease (such as in flows through stenosed arteries19,23,26,32,44) or in the presence of prostheses in the circulation, may initiate the cascade of events that lead to thrombosis.

In vivo platelet activation and aggregation takes place in the presence of the far more numerous erythrocytes (RBCs). The normal range of hematocrit in the arteries (the volume fraction of the RBCs) is 0.47 in adult males and 0.42 in adult females. RBCs can be considered as deformable biconcave disc-shaped cells of 8 μm diameter and 2 μm in thickness. Platelets or thrombocytes are discoid in shape with dimensions of 2.0 μm in diameter by 1.0 μm in thickness.12 Based on the relative concentrations of RBCs, platelets, and white blood cells in whole blood, for every 600 RBCs there are 40 platelets and one white blood cell. Therefore, it is important to understand and quantify the effects of RBCs on the platelet response under various flow conditions. The presence of erythrocytes can alter platelet activation behavior biochemically (by release of ADP) as well as mechanically.3,30 These studies have shown that the presence of RBCs enhances platelet activation due to dynamic interactions among the RBCs as well as interactions between RBCs and platelets. These mechanical effects are due to the significant impact of RBCs on platelet distribution in blood, on the collisional frequency of platelets, and due to the modulation of “local”, i.e., microscopic, shear stresses given an overall “macroscopic” shear stress level in the bulk blood.

It is well recognized that in the flow of blood the mutual interactions of the RBCs with each other and with platelets leads to the organization of these individual blood components such that red blood cells tend to accumulate at the centerline of the blood vessels (the Fahraeus–Lindquist effect) while platelets are observed to be displaced laterally towards the walls of the vessels in a non-diffusive manner.15,40 Turitto and Weiss39 suggested that the intercellular collisions of platelets and RBCs greatly increase the diffusion (the lateral transportation) of platelets toward blood vessel walls. This lateral transport is necessary for the interaction between blood platelets and vessel walls. Direct measurements indicate that platelet transport to vessel walls increases several hundred times when red blood cells are added.7,21,27,39 Aarts et al. 1,2 studied the motion of the platelets with and without the presence of the RBCs. In the absence of RBCs, platelets simulated by a distribution of rigid model spherical particles, migrated to an average radial position of 0.6 times the radius from the tube centerline. This behavior of platelets is completely changed by the presence of the RBCs, which caused the platelets to move towards the vessel wall. According to Keller and Skalak22 and Barthes-Biesel and Sgaier,4 RBC motion expel platelets from the core region and cause them to move toward the vessel wall, while the RBCs themselves tend to move towards the vessel centerline, resulting in a platelet-rich, RBC-free zone near the vessel wall. Yeh et al.45 characterize this behavior using a convective-diffusive transport equation for platelets, which incorporates an empirical drift function for directed motion of the platelets in the lateral direction (i.e., towards the wall). In particular the phenomenon of drift of platelets towards the walls is enhanced as the hematocrit increases and was observed only when the hematocrit was significant (>10%).38,42 In addition, the margination of platelets was found to occur only above a threshold value of fluid shear rates which is in the range found in the normal circulation.12,46

Yeh and Eckstein46 point out the platelet motion that leads to margination at moderate hematocrits has a distinctive dispersive character. In addition, since the Peclet number is typically large, convective effects must predominate over diffusion. However, convection alone cannot lead to the margination of platelets, while diffusion (characterized by an enhanced bulk diffusion coefficient for platelets as in Turrito et al.40) cannot account for the directed transport of the rather sparsely distributed platelets. For higher shear rates, the amount of lateral transport was induced by the tumbling, and translational motions of the cells passing the platelets. The red cell dynamics under various flow rates therefore directly impacts on platelet margination. However, margination appears to first increase with flow rates and then to decrease, leading to some optimal range of flow rates (shears) for margination. Yeh and Eckstein discuss the possible mechanical effects that may contribute to the forces that act to induce the drift of platelets towards the fringes of the red blood cell-occupied central region of the blood vessel. They suggest a random walk algorithm for platelet transport that accounts for the motions of the RBCs. Unlike the traditional random walks that yield diffusive transport, a random walk that incorporates non-uniformities in the flow field can lead to a lateral drift, as observed in experiments. This is similar in spirit to the population balance models (which also rely on probabilistic methods to evolve the concentrations of tracer species) used by Hellums and coworkers20 to model platelet dynamics. A key insight highlighted by Yeh and Eckstein is that the large-scale margination of platelets cannot be due only to the displacement of RBCs towards the tube center and the resultant motion of the plasma towards the tube walls. Such a volume exclusion-driven motion5 was found insufficient to explain the extent of displacement of the platelets. The key point from the work of Eckstein and coworkers is therefore that it is the dynamics of RBCs and their interactions with platelets under the influence of shear that results in forces that promote platelet margination rather than the mere static volumetric predominance of RBCs. It is shown later that the present simulations arrive at the same conclusions.

Modeling and Quantifying Platelet Activation

Computational studies have also been reported in the literature in order to understand the behavior of platelets in various flow regimes. In several of these studies, platelets were considered as point rigid particles that are suspended in Newtonian fluid. Fogelson14 developed a macroscopic mathematical model that represents a suspension of discrete mass less platelets in a viscous incompressible fluid. Wang and Fogelson41 developed a continuum model in which the interactions among a viscous, incompressible fluid and a population of non-activated (non-sticky) and activated (sticky) platelets suspended in this fluid were considered. The aggregated particles are modeled by a fluid that is characterized by the presence of link-generated contribution to the fluid force density. Other investigators34,35,43 used a two-dimensional computational model that considered blood as a Newtonian fluid and platelets as a dilute chemical species that is transported by convection and shear-enhanced diffusion.

All the previous computational studies were based on macro-scale models of blood vessels and particles, in which platelets are presented as point particles that move in blood plasma. Such models do not consider the formed elements in their physiological dimensions and shape. While these studies have correlated magnitudes of bulk fluid shear stresses with platelet activation; however, the physical mechanism of the action of the fluid shear stresses on the platelet surface is not clear. Furthermore, most of these studies did not include the effect of RBCs on platelet activation. While point particle treatment of formed blood elements may yield reasonable estimates of particle paths in large blood vessels, effects such as blood flow through constricted geometries, platelet margination due to interactions with blood cells and vessel walls and implants are not captured. In order to understand the mechanics of interaction of RBCs and platelets, a micro-scale model incorporating cell–cell interactions is necessary. The current work aims at developing a micro-scale model that can cover small dimensions in the flow field in order to understand the effect of interaction of RBCs and platelets on platelet behavior. The two-dimensional Navier–Stokes equations for Newtonian, incompressible fluid are solved in micro-scale geometry with dimensions typically representing an arteriolar segment. Red blood cells are assumed to have elliptical shapes that behave as pseudo-rigid particles9 that deform homogeneously under the effect of shear forces. Platelets are assumed to have a circular shape and behave as relatively rigid particles. The translational and rotational motion of the RBCs and platelets are calculated based on the shear and pressure forces that act on each particle separately and the collision forces between particles. The results are presented on the effect of RBCs on the platelet dynamics as a function of the hematocrit and the flow Reynolds number. The effect of the fluid shear stresses on the platelet surface is also analyzed as a function of these parameters.

Computational approach

Governing Equations

The non-dimensionalized governing equations include the incompressibility constraint and conservation of momentum, given by:

$$ \nabla \cdot {\mathbf{u}} = 0, $$

(1)

$$ \frac{{\partial {\mathbf{u}}}} {{\partial t}} + {\mathbf{u}} \cdot \nabla {\mathbf{u}} = - \nabla p + \frac{1} {Re}\nabla^{2} {\mathbf{u}}, $$

(2)

where $Re = {\rho _{0} U_{0} D} \mathord{\left/ {\vphantom {{\rho _{0} U_{0} D} \mu }} \right. \kern-\nulldelimiterspace} \mu$ is the Reynolds number. The variables are non-dimensionalized as

$$ {\mathbf{u}} = \frac{{{\mathbf{u}}^{*} }} {{U_{0} }},\quad L = \frac{{L^{*} }} {{D_{0} }},\quad t = \frac{{t^{*} }} {{D_{0} /U_{0} }},\quad p = \frac{{p^{*} }} {{\rho _{0} U^{2}_{0} }} $$

(3)

where $\mathbf{u}^{\ast}$ is the dimensional velocity field, ρ ₀ and μ are the density and viscosity, and ${p}^{\ast}$ and ${t}^{\ast}$ are the dimensional pressure and time. The average axial velocity at the inlet is denoted by U ₀, the inlet gap width is D ₀, and the characteristic pressure is $\rho _{0} U^{2}_{0} .$

Flow Solver

A cell-centered collocated-variable semi-implicit approach is used to discretize the governing equations. The solution is advanced in time using the two-step fractional step method.47 The presence of the embedded interfaces (RBCs and platelets) is communicated to the flow solver by using a sharp-interface methodology that has been well tested for a variety of moving boundary problems. The method is presented in great detail, including validation for a host of problems in past publications.24,25 Briefly a level-set representation31 of embedded interfaces is used and the discrete form of the governing equations is modified so that the no-slip and no-penetration conditions on the solid surface are supplied to the fluid solver. Moving boundaries are naturally handled in this system and methods to do so are detailed in the above references. Once the flow field is computed the fluid forces experienced by the particles can be determined from the calculated pressure and shear stresses evaluated on the sharp embedded interfaces.

Implicit Interface Representation Using Level-set

Immersed objects or particles are represented implicitly on the mesh using a level-set approach.31,36 In this method, the level-set is represented by a scalar field ϕ _l , where l denotes the lth embedded interface or object. The value of ϕ _l at any point is the signed normal distance from the lth embedded interface, with ϕ _l  < 0 represent the inside of the boundary, ϕ _l  > 0 representing the outside of the boundary, and ϕ _l  = 0 denoting the boundary of the object, also known as the zero level-set.

For moving immersed objects, such as red blood cells and platelets, the motion of the boundaries is tracked by advecting the level-set, such that

$$ (\phi _{l} )_{t} + {\mathbf{V}}_{l} \cdot \nabla \phi _{l} = 0, $$

(4)

where V _l is the velocity of the lth level-set field. As is standard practice in level-set computations a fourth-order ENO scheme31 in space and fourth-order Runge–Kutta integration in time is used to evolve the level-set field. The velocity V _l at the grid points that lie in the narrow band around the level-set is calculated by extension of the interfacial velocity outward from the interface in a direction normal to the interface, as described by Sethian.31 A re-initialization procedure is then carried out to return the ϕ-field to signed distance function.37

Particle Motion

To track the motion of blood constituents (or particles), two coordinate systems are employed. A global coordinate system (x–y coordinate system) is used to predict the motion of the particles with respect to a fixed point (the origin). A local coordinate system is defined for each particle (ξ–η coordinate system), where the origin of this coordinate system is prescribed to be the centroid of each particle. The solution of the individual particle transport, rotation, and deformation is based on the local coordinate system. The translational and angular momentum equations are used to calculate the translational (in both x and y directions) and angular velocities, such that,

$$ m\frac{{d{\mathbf{v}}}} {{dt}} = {\mathbf{F}}, $$

(5)

and

$$ I\frac{{d\omega }} {{dt}} = T. $$

(6)

In these equations, m is the mass of each particle, v is the translational velocity vector, t is the time, F is the force acting on each particle (that includes the fluid forces and collision forces with other particles), I is the moment of inertia of each particle, ω is the particle angular velocity, and T is the sum of torques act on the particle.

Deformation of RBCs

RBCs are assumed to be incompressible elliptical particles9 that deform uniformly (i.e., the RBC retains its elliptical shape) under the effect of the imposed shear stresses. Assuming that the RBCs stretch so as to maintain at a state of local equilibrium with the imposed fluid extensional stress, we obtain an equation for the RBC semi-major axis by taking the moment of the stress equilibrium equation in the ξ-direction to write

$$ 2GA\,{\left( {\frac{{a(t) - a_{0} }} {{a_{0} }}} \right)} = {\int\limits_c {\xi \sigma \,} }dl. $$

(7)

In this equation, G is the shear modulus computed from the specified Young’s modulus E and the Poisson’s ratio for the RBC. A is the cross sectional area of the RBC, a(t) is the semi-major axis of the RBC at any time, a ₀ is the initial RBC semi-major axis, ξ is the local coordinate along the semi-major axis, σ is the component of the stress vector in the ξ-direction, and dl is the length increment along the circumference of the ellipse.

Since the deformation of the RBCs is assumed to be area-preserving

$$ a(t)b(t) = {\text{constant}}{\text{.}} $$

(8)

Equation (8) is used to calculate the minor axis b(t) from a given value of a(t).

Treatment of Collision Between Particles

Collision forces and torques are expected to have a significant influence on the RBC dynamics in the arterial system. While with unlimited resolution these collision forces would be captured through the fluid pressure and stress fields across a lubrication layer between the surfaces of the cells in impending collision, due to the finite resolution provided by the computational grid, it is necessary to impose these collision forces directly in order to avoid overlap of the level sets surrounding each cell. In this study the forces and torques between colliding particles are modeled using an extension of the soft-sphere model described by Crowe et al. 10 In practical terms, to track the distance between particles that are identified as undergoing collision, a buffer-zone is introduced around each particle. This buffer-zone takes the same shape as the particle but with slightly larger area or radius. In the present study buffer-zones are constructed with a radius of 5% increase in the RBC major axis. Information regarding the interfacial points of this buffer zone is stored in the local and global coordinate systems of the corresponding particle. Overlap of the buffer-zones is tracked as described in the next section and the overlap information is employed to compute the distance between the particles during collision.

The collision forces are modeled as spring forces between the surfaces of the colliding particles. The normal collision force is then given by

$$ F_{n} = - k_{n} \delta _{n} , $$

(9)

where δ _n is the measure of the buffer-zones overlap (as shown in the Fig. 1a), and k _n is a spring constant calculated using

$$ k_{n} = \frac{{{\sqrt {2R} }}} {{3(1 - \nu ^{2} )}}E\delta ^{{1/2}}_{n} , $$

(10)

Here, E is the Young’s modulus and ν is the Poisson’s ratio of the particles (for red blood cells these values are 26 kPa and 0.5, respectively11), and R is the effective radius for the two colliding spheres with radii r ₁ and r ₂, defined by

$$ R = \frac{{r_{1} r_{2} }} {{r_{1} + r_{2} }}. $$

(11)

For elliptical particles, the collision forces are modeled by evaluating R using the local radius of curvature at the collision point (Fig. 1b). To apply this equation, it is necessary to calculate the overlap distance δ and the effective radius of the two particles.

Figure 1

Schematic of situation during particle collision, showing: (a) overlapping of circular particles; (b) colliding of a circular particle with an elliptical particle. For the latter case a tangent circle (dashed) is used to evaluate the effective radius of the particles at the collision point

Buffer-zones Overlapping and the Effective Radius

The procedure for detecting overlapping buffer-zones involves two steps. The first step is a rapid inspection of whether buffer-zones are close enough to each other that overlap is possible. The second step involves a more detailed inspection to determine whether or not overlap occurs, and to calculate the overlapped distance and the radius of curvature of the particles at the collision point.

Figure 2a shows a cloud of buffer-zones that will be used as an example to show the two steps (here buffer-zones A, B, and C are specified to simplify the procedure). The first step is achieved by establishing a circle with a radius equal to three times the major dimension of the red blood cell with the same center as the particle. For example if we want to check whether buffer-zone A overlaps with any of the surrounding buffer-zones, the distance between the center of A and the center of any other buffer-zones is calculated. If this distance is greater than the circle radius, then no collision can exist between A and the other particle (e.g., between A and C in Fig. 2a). If this distance is smaller than the radius of the imaginary circle (e.g., between A and B in Fig. 2a) then the second step of inspection is performed. This two-step process enables faster detection of collisions between particles by selecting only pairs that are likely to have collided for closer inspection.

Figure 2

(a) A cloud of RBCs and platelets used to detect overlapping of buffer zones; (b) schematic depicting the treatment of overlapped buffer zones for the computations of the equivalent radius used to calculate the collision forces

In the second step, the coordinates of the points of the buffer-zones that are located inside the imaginary circle are converted to the local coordinate system of A. Then the ellipse equation is applied to see if any of the points of other buffer-zones overlap with A or not. Then the radius of curvature is calculated for those points that overlap with A. For example, consider the case where buffer-zones A1 and B1 overlap as shown in Fig. 2b, where buffer-zone A1 has points P _a1 (with radius of curvature R _A1), P _a2 (with radius of curvature R _A2), and P _a3 (with radius of curvature R _A3) that overlap with B1, and buffer-zone B1 has points P _b1 (with radius of curvature R _B1), P _b2 (with radius of curvature R _B2), P _b3 (with radius of curvature R _B3), and P _b4 (with radius of curvature R _B4) that overlap with A1. Then the average value of the radius of curvature of overlapped points is used as the radius of the local overlapped circles, or

$$ r_{1} = \frac{{R_{{A1}} + R_{{A2}} + R_{{A3}} }} {3}, $$

(12)

$$ r_{2} = \frac{{R_{{B1}} + R_{{B2}} + R_{{B3}} + R_{{B4}} }} {4}. $$

(13)

As a result, r ₁ and r ₂ are now known and these values are used in Eq. (11) to calculate the effective radius for the collision.

The last step in calculating the normal force is to estimate the overlap distance δ. To do so, the values of r ₁ and r ₂ are compared to the values of the radius of curvature of each point in the overlapped region for each particle (i.e., r ₁ is compared to R _A1, R _A2, R _A3, while r ₂ compared to R _B1, R _B2, R _B3, R _B4). The point on the ellipse having a radius of curvature closest to the values r ₁ and r ₂ computed using Eqs. (12) and (13) is considered to be the “contact point” and is used to compute the overlap distance δ. For example if points P _a2 (with global coordinates (x ₁, y ₁)) and P _b4 (with global coordinates (x ₂, y ₂)) are found to have a radius of curvature that is closest to r ₁ and r ₂ on the two elliptical particle surfaces, respectively, then δ is given by

$$ \delta = {\sqrt {(x_{1} - x_{2} )^{2} + (y_{1} - y_{2} )^{2} } }. $$

(14)

Thus, by knowing the values of R and δ, the normal collision force in Eq. (9) can be calculated.

Computational results

Problem Set Up: Geometry

The above algorithms have been applied to compute the dynamics of platelets and RBCs with plasma as a carrier fluid. A two-dimensional straight channel with a height of 42 μm (equivalent to five RBC major axis dimensions) and length of 360 μm is used for the computational simulation (Fig. 3). These dimensions are similar to that of a typical arteriole. RBCs are assumed to be elliptical particles with a major axis dimension of a = 8 μm and minor axis dimension of b = 2 μm. Platelets are assumed to be discoid with a diameter of 2 μm. Values of the Young’s modulus for RBCs11 and platelets16 were specified as 26 kPa and 170 kPa, respectively, while the Poisson’s ratio was assumed to be 0.5 for both RBCs and platelets. The mechanical properties of the RBCs and platelets are based on experimental results using either atomic force microscope11 or a micropipette16 to strain the particles and measure the material response. Plasma is assumed to be a Newtonian fluid and a steady inlet flow is assumed in this micro-scale simulation.

Figure 3

Flow domain for the micro-scale simulation and the various regions in the computations. The inlet and outlet zones are used to allow flow and particle motion to settle into a fully developed state. All data are collected in the computational zone (regions 1–5) which consists of the wall regions (1 and 5) and the core regions (2–4). The domain is divided into equally spaced sections in the y-direction

The computations are set up in a way that will allow the calculation of the dynamics of platelets and RBCs for long enough time that statistically steady behavior of the blood elements can be captured. To do this, the particles (RBCs and platelets) that exit the flow domain need to be reintroduced into the domain at the inflow. To avoid collecting data on the dynamics of the particles in the inlet (x = 0–4) and outlet (x = 7–10) regions where they may be subject to disturbances due to the treatment of flow and particle motion at these boundaries, a centrally placed “computation zone” (extending from x = 4 to 7) is identified. The inlet and the outlet zones are used to allow recycling of the RBCs and platelets. In other words, when any of the particles move out of the computation zone and enter the outlet zone, this particle is re-introduced (with the same velocities and directions) and given a new position in the inlet zone. The computation zone is the region where the collision and motion of RBCs and platelets are computed, and thus all results are presented in this zone. The hematocrit (Ht) is calculated as

$$ Ht = \frac{{{\sum {A{}_{{{\text{RBCs}}}}} }}} {{A_{{{\text{comp}}{\text{.}}}} }}. $$

(15)

Here A _RBCs is the sum of the cross-sectional areas of the RBCs, and A _comp. is the computational zone area. The above definition of Ht is used in this simulation in order to analyze the effect of RBC concentration on the platelet behavior. It should be noted that this area-ratio based hematocrit for the present two-dimensional simulation is different from the conventional three-dimensional volumetric percentage of red blood cells in whole blood. The dimensions of the flow regime as well as the Ht (number of RBCs and the corresponding number of platelets used in our computational model) are representative of flow in the arterioles in the human circulation.

Boundary and Initial Conditions

At the inlet, the following parabolic velocity profile is used,

$$ {\mathbf{u}}(y) = 4{\mathbf{u}}_{{\max }} (d_{{\text{i}}} y - y^{2} )/d_{{\text{i}}} ^{2} . $$

(16)

where u(y) is the velocity at y-location, u _max is the maximum inlet velocity, and d _i is the inlet diameter of the geometry. At the outlet, the standard outflow condition is applied, i.e., the velocities are linearly extrapolated and corrected to be consistent with global mass conservation and a Neumann condition is applied on the pressure.24 Finally, on the top and the bottom boundaries, a wall (no-slip) boundary condition is applied.

Grid Independency

The algorithm and flow code has been validated for a host of moving boundary problems in previous work.24 Nevertheless, grid independence of the computational results in the present setting is established by two different comparisons. First, the motion of a platelet (or circular particle) immersed in a two-dimensional channel flow is computed at Reynolds number of 0.1 (as in the arterioles) and for grid sizes of 0.2, 0.1, and 0.075 times the particle diameter. Plots of the axial velocity of the platelet, given in Fig. 4a, indicates close agreement between the computations with the two finer meshes (0.075 and 0.1), while the results for the coarse mesh (with mesh size 0.2) exhibit small differences with the other two mesh sizes. In a second test, the x-coordinate position of a single platelet is compared for the coarse mesh with the intermediate platelet mesh size (0.1) at Re = 1 and 10% hematocrit (Ht) in Fig. 4b. The two different mesh sizes yield results for the platelet position that are very close to each other. Given that the difference in results between the coarse and intermediate mesh sizes in the two computations did not exhibit significant differences, and in order to include higher Ht values in the computation, the coarse mesh is employed in the analysis of results presented below.

Figure 4

Demonstration of grid independency of the results for particle motion. (a) Axial velocity as a function of time for a single platelet in the flow regime (0% Ht, Re = 1): Solid line—for a fine mesh (0.075 of the platelet diameter); dashed line—for an intermediate mesh size of 0.1 of platelet diameter; dotted line—for a coarse mesh of size 0.2 of platelet diameter; (b) Axial position of a single platelet versus time for the coarse mesh size (dotted line); and with the intermediate mesh size (solid line)

Physiological Assumptions

In this micro-scale simulation, the following assumptions are invoked. The plasma is assumed to be a homogeneous Newtonian fluid with a viscosity coefficient of 1.2 cP in which the RBCs and platelets are suspended. It is also assumed that only viscous and inertial forces affect the motion of the formed elements and the effect of gravity is neglected.

Two different initial configurations of RBCs are considered to examine the effect of these configurations on the results. In the first case, RBCs are initially arranged in a vertical position in which the major axis of each RBC is parallel to the y-axis (90 degrees). In the second case, RBCs are randomly placed and three different initial orientations (45, −45, and 90 degrees) of the RBCs are prescribed. It is shown that the conclusions reached on the eventual steady-state behavior of the cells and platelets are independent of the initial orientation of the elliptical RBCs.

Motion and Distribution of RBCs and Platelets

Lateral Distribution of RBCs

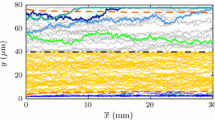
Figures 5, 6, and 7 show the velocity contours of flow at different time steps for Re = 1 and Ht values of 5, 10, and 15%, respectively, for the case where the RBCs are initially oriented in the vertical direction. The position and the distribution of the RBCs and platelets in the flow regime are also included in these figures for the same time instants. The positions of the platelets alone are identified by encircling the same on each of the figures. Note that only those platelets that lie in the region between x = 2 and x = 8 are shown in each case. In all these cases, RBCs are observed to undergo rotation (tumbling) and translation (in x and y directions) in the flow. According to Keller and Skalak22 and Barthes-Biesel and Sgaier4 RBCs move towards the centerline of the vessel and their interactions with platelets cause the latter to move toward the vessel wall, resulting in a platelet-rich, but RBC-depleted zone near the vessel wall. To analyze the effect of Ht on the platelet behavior, the computational domain is divided into five parallel regions in the lateral direction, each of width equal to 0.2 of the inlet diameter (Fig. 3), where regions 1 and 5 are wall regions and regions 2–4 are core regions. Table 1 shows the percentage of RBCs and platelets that are present in each of these regions at t = 0 and at t = 8. For a Ht value of 5%, all platelets remain in the core region at t = 8, whereas 50% and 83% of the platelets have moved to the wall region at Ht values of 10% and 15%, respectively. Figure 8 shows the lateral position of two randomly selected platelets as a function of time for Re = 1, Ht = 15%, with RBCs oriented vertically. In this figure it can be observed that both platelets have moved from region 3 to region 1 or region 5. For times beyond t = 7, both platelets appear to have reached a steady state and remain near the wall for subsequent times.

Figure 5

Velocity contours and RBCs/platelets distribution at different time instants, Re = 1, Ht = 5%. The platelet locations at the various time intervals are shown circled in black. Note that only those platelets that are in the region between x = 2 and x = 8 are shown. When the platelets and RBCs exit the domain (at x = 10) they are recycled back to the inlet zone

Figure 6

Velocity contours and RBCs/platelets distribution at different time instants, Re = 1, Ht = 10%. The platelet locations at the various time intervals are shown circled in black. Greater margination of the platelets than in the 5% Ht case is observed. Note that only those platelets that are in the region between x = 2 and x = 8 are shown. When the platelets and RBCs exit the domain (at x = 10) they are recycled back to the inlet zone

Figure 7

Velocity contours and RBCs/platelets distribution at different time instants, Re = 1, Ht = 15%. The platelet locations at the various time intervals are shown circled in black. Greater margination of the platelets than in the 5% and 10% Ht cases is observed. Note that only those platelets that are in the region between x = 2 and x = 8 are shown. When the platelets and RBCs exit the domain (at x = 10) they are recycled back to the inlet zone

Table 1 RBCs and platelet distribution in the core (2–4) and wall (1 and 5) regions at the beginning (t = 1) and end of the simulation (t = 8)

Figure 8

Lateral position of two selected platelets as a function of time for Re = 1, Ht = 15% as a function of time with RBCs initially in the vertical configuration and the platelets initially placed near the channel centerline

With respect to the RBCs, for the 5% Ht case, at the initial time, 42% of RBCs are present in the wall regions and 58% in the core regions. For this low-hematocrit case, these percentages are approximately maintained throughout the computation. By contrast for the 10% Ht case, it can be clearly observed that RBCs have migrated from the wall regions to the core region. This migration process can be even more clearly observed in the 15% Ht case, where 46% of RBCs were initially present in the wall region, but only 28% remain in this region by t = 8. Therefore, with increasing hematocrit RBCs tend to migrate increasingly towards the core region leading to a depletion of RBCs near the walls. In contrast, platelets move preferentially towards the wall region and away from the core as the hematocrit increases. These observations are consistent with those from experiments.2,12,40,46

Effect of Initial Angular Orientation of the RBCs

The effect of the initial angular orientation of the RBCs (45, −45, and 90 degrees) on the final distribution of the formed elements for Re = 1 and Ht = 15% is shown in Fig. 9. The behavior of RBCs and platelets with the different orientations was found to be similar to those in which the RBCs were initially in the vertical orientation. The steady-state distribution and the fluid forces experienced by the platelets were independent of the initial RBC orientations.

Figure 9

Velocity contours and RBCs/platelets distribution at different time instants with three different initial angular orientations (45, −45, and 90 degrees) of the RBCs. The Re = 1 and Ht = 15%. The platelet locations at the various time intervals are shown circled in black. The margination of platelets is not affected by the initial orientation of the RBCs. Note that only those platelets that are in the region between x = 2 and x = 8 are shown. When the platelets and RBCs exit the domain (at x = 10) they are recycled back to the inlet zone

Effect of RBC Shape

From the above cases it is clear that in the presence of RBCs platelets marginate to the vessel walls. The interactions that lead to this behavior of the platelets have been suggested to be collisions between RBCs and platelets and hydrodynamic effects due to the relative differences in size between the RBCs and platelets. To examine the effect of the RBC shape and size on the platelet motion and concentration distribution, cases are examined with circular particles with radii that are equivalent to: (i) the major radius of the RBC, and (ii) half of the major radius of the RBC, and the results presented in Figs. 10a and 10b, respectively while maintaining the hematocrit constant. With RBCs represented as circular particles of diameter 8 μm, the platelets migrated toward the wall, exhibiting similar behavior to that observed with RBCs represented as elliptical particles. When the RBC diameter was reduced to half of this value, the platelets remained located within the central region of the channel throughout the computation. These results indicate that the migration of the platelets to the wall region is effected primarily due to the difference in size between the platelets and the RBCs, rather than the elliptical RBC shape. The fluid forces in the lateral direction on individual platelets for three different cases were also examined and these are plotted in Fig. 11. As can be observed, the magnitude of the lateral fluid forces on the platelets was comparable for the cases where RBCs were represented as elliptical particles with those in which they were represented as circular particles of 8 μm diameter (Figs. 11a and 11b). The fluid forces in the lateral direction on the platelets were significantly reduced when the RBCs were represented as circular particles of 4 μm diameter (Fig. 11c), which would be expected from the smaller inertia of the RBCs for this case.

Figure 10

Particle distribution at different time steps with: (a) RBCs depicted as circular particles with a diameter equivalent to the major dimension; (b) RBCs depicted as circular particles with a diameter equivalent to one half of the major dimension. Platelet locations are circled in black

Figure 11

Lateral fluid force acting on a single platelet with RBCs depicted as: (a) elliptical particles; (b) circular particles with diameter equivalent to the RBC major axis length; and (c) circular particles with diameter equivalent to half of the major axis length

Deformation of RBCs

In this study RBCs are treated as ellipses that deformed under the effect of fluid forces. The shear modulus of RBCs is calculated using a Young’s modulus of 26 kPa, and Poisson’s ratio of 0.5. To measure the deformation, the average relative change in the length of the major axis to its original length (or the stretch ratio) is calculated as

$$ {\text{stretch ratio}} = \frac{1} {n}{\sum\limits_{i = 1}^n {\frac{{a(t)}} {{a_{0} }}} }, $$

(17)

where, a(t) is the RBC major axis length at any time, a ₀ is the original length of the RBC, and n is the total number of the RBCs in the domain. For comparison, the stretch ratio is calculated for the two hematocrits (10 and 15%) and at t = 8. For both hematocrits the RBCs stretched by a fraction of a percent indicating that for the shear rates considered deformation of the RBCs is negligible. The RBCs can therefore be considered to be mainly transported in translational and rotational modes when they interact with the flow.

Apparent Viscosity

The current study assumed that plasma is a Newtonian fluid with a viscosity of 1.2 cP, and RBCs and platelets are suspended in this fluid. To examine the effect of the RBCs and platelets on the properties of whole blood,33 the apparent viscosity is calculated for all hematocrit values studied according to the laminar flow equation

$$ \mu = \frac{{\Updelta PD^{2} }} {{32Ul}}, $$

(18)

where μ is the apparent viscosity, ΔP is the pressure difference between any two points in the flow regime, D is the diameter, U is the average velocity magnitude, and l is the length of the computational domain. The computed apparent viscosity is found to be 1.8, 2.2, and 2.6 cP for the Ht values of 5, 10, and 15%, respectively. The results for apparent viscosity are compared with the results of Einstein13 and Rand et al.29 Einstein13 analytically developed a formula for the viscosity as a function of volume fraction for spherical particles. Rand et al.29 experimentally studied the relation between the viscosity and hematocrit. They obtained blood from 60 healthy subjects and adjusted the hematocrit to values from 0% to 80%. Then they used a cone-plate micro-viscometer to apply different levels of shear rate up to 250 s⁻¹ (this value is similar to the average shear rate used in the current study). Figure 12 shows the results of the current study and the results found in Einstein13 and Rand et al.29 for hematocrit (particle volume fraction) range of 5–15%. The apparent viscosity appears to have a linear relationship with the hematocrit and the variation of the apparent viscosity with the hematocrit obtained from the present study appears to be similar to that from the experimental results of Rand et al.29 and to the theoretical one of Einstein.13 Also it is important to mention that the current numerical study is limited to the two-dimensional channel flow and as described in Eq. (18), the average inlet velocity and the average pressure gradient are used to calculate the apparent viscosity.

Figure 12

Variation of the apparent viscosity as a function of hematocrit. The variation predicted for the current system is compared with previous experimental34 and theoretical18 results

Flow Effects on the Platelets

Previous experimental studies6,19,26,28 have shown that when the bulk fluid shear stresses exceed a specific magnitude, platelets tend to be activated based on measurements on enzymes such as serotonin. However, the specific effect of bulk shear stresses in inducing activation of individual platelets is not clear. Furthermore, in several of these studies, the effect of the presence of RBCs on the platelets is not taken into account. Interaction of RBCs with platelets introduces short-time fluctuations in shear stress acting on the platelets. In the current study, the platelets are not point particles, but instead exhibit a variation of fluid shear stress around each particle. To determine the effect of shear stress on the straining of each platelet, we integrated the fluid shear stress component acting along the perimeter of the platelet to obtain the surface overall shear force:

$$ D_{\text{s}} = { \sqrt{ \int\limits_c (\xi \tau _{\xi } dl)^{2} + \left( \int\limits_c \eta \tau _{\eta } dl \right)^{2} }}.$$

(19)

Here, ξ and η are the local coordinate systems, τ _ξ and τ _η are the fluid shear stresses acting on each particle in the ξ- and η-directions, respectively, and dl is the circumferential increment. The overall shear force D _s is computed along the platelet paths within the computational region (between x = 4 and x = 7). The computed D _s for a single platelet is plotted as a function of axial distance for Ht = 15% and Re = 1 in Fig. 13 . The computed magnitude contains high frequency fluctuations as the platelets interact with RBCs. The figure shows plots obtained by performing a Fourier analysis with cut-off frequencies of 1.0, 3.0, and 5.0 Hz, The results with a cut-off frequency of 1 Hz exhibit the main trend in the variation of D _s at various positions and hence were employed in further analysis.

Figure 13

Computed overall shear force (D _s) of a single platelet plotted as a function of axial position in the flow regime for the case of Re = 1 and Ht = 15%. Results are plotted with cut-off frequencies of 1, 3, and 5 Hz to filter out the high frequency fluctuations

Figure 14 shows D _s for Re = 1 and different Ht values. For 0% Ht (or single platelet without any RBCs) the magnitude of D _s is very small and does not change significantly as the platelet moves in the axial direction. In the presence of RBCs at a 5% Ht, the surface shear force shows small peaks at various platelet positions and these peaks correspond to times immediately before or after interaction with other particles. As observed in the figure, these peaks increase in magnitude with increasing Ht. The effect of Re on the surface shear force D _s is plotted for Ht of 10% in Fig. 15. It can be observed that as Re increases, the peak values of the D _s on the platelet also increase. Moreover, the average magnitude of the D _s also increases with Re as a result of increased rate of shear in the fluid.

Figure 14

Overall shear force on the particle (D _s) as a function of axial distance for Re = 1: (i) solid line 15% Ht, (ii) dashed line: 10%, (iii) dotted line: 5% Ht, (iv) dashed-dotted: single platelet with no RBCs (0% Ht)

Figure 15

Platelet overall shear force as a function of axial distance for Ht = 10%: (i) solid line Re = 1, (ii) dashed line: Re = 0.1

Finally, to find the relationship between both Ht and the D _s, the average D _s value for all platelets is plotted as a function of Ht for the Re = 1 case in Fig. 16. An exponential curve fit of the data for Re = 1 yields the following relationship,

$$ D_{{\text{s}}} = 9.1 \times 10^{{ - 7}} \;e^{{15Ht}} $$

(20)

where Ht is expressed as a fraction. The coefficient of the data fit in Eq. (20) depends also on the Reynolds number, but insufficient data was obtained in this study to perform a fit with Reynolds number.

Figure 16

Platelet overall shear force for Re = 1 plotted as a function of hematocrit with the computed results as data points and the solid line is the best curve fit of the results

Discussion and conclusions

The current work utilized a fixed-grid sharp-interface method24 to simulate flow dynamics of RBCs and platelets at a micro-scale level. A two-dimensional flow simulation is used to analyze the effect of RBCs on platelet dynamics. Platelets are modeled as relatively rigid circular particles, while RBCs are modeled as elliptical particles that deform under the effect of fluid forces. However, in the range of Re and Ht employed in the present work (Re = 0.1, 1; Ht = 5, 10, and 15%), RBCs exhibit negligible deformation by the flow. With sufficiently high hematocrit, RBCs are observed to migrate to the core region of the vessel while the platelets move toward the walls. These results agree with previous experimental observations. However, with low hematocrit values (e.g., Ht = 5%), such a migratory effect was not present. Our analysis showed that the platelet migration observed is predominantly caused by the difference in size between the RBC and the platelets; computations with RBCs replaced by particles that are closer in size to platelets do not exhibit platelet margination. The tendency of the platelets to marginate was independent of the shape of the RBCs. The predominant effect of RBC size is clearly demonstrated by examination of the lateral fluid forces on the platelets, which are observed to be of similar magnitude for elliptical and circular RBC particles of a similar size. These results indicate that for the hematocrits studied in the paper, the RBCs have a significant effect on the transport of platelets within the vessel. By comparing the velocity fields and RBC distribution in Figs. 5, 6, and 7 it is observed that the tendency of RBCs to migrate towards the centerline is enhanced as the Hematocrit increases. As the hematocrit increases and the red blood cells move towards the centerline the regions adjacent to the wall exhibit larger regions of low velocity, indicating that these regions are one of slower moving fluid. The platelets appear to be marginated to these slower-moving fluid regions while the RBCs locate themselves in the (on the average) faster moving fluid regions away from the wall. The effect of the RBCs on the platelets is not expected to be well replicated by adding an enhanced diffusive force40 to the governing equation for the platelets, since the latter would be equally likely to disperse the platelets from the wall region back into the center as it would be to force the platelets toward the wall region.

The current work uses a measure based on the overall surface shear force acting on the platelets due to the fluid shear stress (D _s) to measure the impact of fluctuating forces imposed by the RBCs on the platelets. To examine the source of the spikes on the computed D _s the corresponding platelets were tracked in both space and time. It is found that these spikes in D _s correspond to the locations where platelets are very close to the RBCs, especially when the platelet is passing through a narrow path between the RBCs or between the RBCs and a wall, and the magnitude of the spike was inversely proportional to the distance between the platelet and the RBC. It can be surmised that the RBCs cause flow fluctuations that significantly increase the local fluid shear stresses acting on the platelets, resulting in higher magnitudes of D _s. Indeed, the fluctuating straining of the platelets due to RBCs was far higher than that due to the averaged fluid flow, as evidenced by computations with a single platelet and no RBCs, for which D _s was very small and devoid of any spikes (Fig. 14). The average magnitudes of D _s increased substantially with increasing Ht and Re, resulting in large-magnitude spikes.

Limitations of the present model

This work represents an initial attempt at a micro-scale dynamic simulation on the effect of RBCs and platelets in blood on the behavior of platelets. There are several limitations to the study that need to be pointed out. In the current study, we restricted the analysis to two-dimensional simulation and restricted the computations to Ht values of up to 15% and the Re magnitudes to 1.0. These assumptions allowed us to simplify the problem. Increasing the hematocrit and Reynolds numbers will lead to larger computational times due to the larger number of immersed boundaries (RBCs, platelets) to be tracked and also due to the finer mesh required at higher Reynolds numbers. While the values of Reynolds numbers employed pertain to the physiological conditions present in arterioles, the values of hematocrit need to be enhanced significantly in order to apply to physiological settings in the larger blood vessels. Methods to efficiently handle larger numbers of particles in the simulation, including multi-scale techniques are being currently investigated. Increasingly the dimensionality of the problem, while simultaneously increasing the hematocrit will present stiff challenges in the foreseeable future. Massively parallel computation will be necessary in 3-dimensions and even then the number of particles that can be handled may not exceed a few hundred. However, 3-dimensional simulations at lower hematocrits can be attempted.

In this study, an integrated value of the surface shear forces (D _s) was used to measure the effect of local fluid shear stress on the surface of the platelets. Since the platelets were assumed to be relatively rigid particles, deformation of platelets due to the fluid shear forces was not computed and it was not possible to determine a specific relationship between the surface shear forces and activation of platelets. Previous experimental studies examined platelets suspended in fluid being subjected to known bulk shear stresses and specific magnitudes of shear stress, suggesting various criteria for shear-induced platelet activation. However, in previous computational studies, platelets were assumed to be point particles moving with the “bulk” fluid flow, and the activation of platelets was based on the bulk fluid shear stress at the platelet location. It is clear from the results of this study that such models omit important aspects of the RBC–platelet interaction, including both the role of RBCs in pushing platelets to the vessel wall and the large fluctuating shear stresses exerted on the platelets due to interaction with nearby RBCs. Further research is necessary to relate the effect of surface shear forces and its fluctuations due to interactions with RBCs on platelet activation.