Introduction

Many different models have been developed that describe the glycemic and hormonal responses to an intravenous glucose load, as well as determining the impact of insulin and glucose sensitivity on these responses. The most widely used is the ‘minimal model’ or variants of this approach.6,9,5,11 However, the intravenous glucose tolerance test (IVGTT) used to obtain parameters in this model is invasive and requires considerable cooperation on the part of the patient. In contrast, the oral glucose tolerance test (OGTT) is a much simpler procedure to perform, with both decreased invasiveness and reduced burden on the patient. OGTT’s are thus routinely performed in clinical laboratories to diagnose impaired glucose tolerance, gestational diabetes and type 2 diabetes.40 Only a few mathematical models of the OGTT have been developed to date, and these models do not explicitly take into account the relatively recent findings of the significant contributions of intestinal hormones to oral glucose-stimulated insulin secretion.1,2,13,18,29,37,49,51,52,53 It has long been known that insulin responses to an oral glucose load are greater than those found after an isoglycemic intravenous glucose infusion.12,17,42 The term ‘incretin’ was therefore coined to describe the unknown gastrointestinal factor(s) released in response to nutrient ingestion that stimulated oral glucose-dependent insulin secretion.17 Thus, it is essential that the role of the incretins be explicitly incorporated into any mathematical model of the OGTT.

Two major incretins have been identified, these being glucose-dependent insulinotropic peptide (GIP) and glucagon-like peptide-1 (GLP-1).17 Both of these hormones are released in response to glucose delivery from the stomach into the duodenum, and levels remain elevated until the ingested glucose is absorbed from the gastrointestinal (GI) tract.50 Studies have demonstrated that GIP and GLP-1 contribute approximately equally to the incretin effect,54 stimulating both first and second phase insulin secretion.24 Since these hormones are believed to be the major contributors to the incretin effect,17 the aggregate effect of these incretins is represented by means of a single variable within which each is assumed to be similarly weighted.

While the model developed here is a model of the OGTT, it is not ad hoc, but rather endeavors to capture the core of the process of normal glucoregulation, and is possibly the simplest that could be constructed that still embraces the known relationships between glucose and its primary regulatory hormones. As such, although we have previously constructed multi-compartment models of glucose kinetics,47 it was decided to invoke a less complex model in the present work. The current model is thus a single compartment representation that is intended primarily to illustrate the importance of the incretins. Moreover, this model aims to reproduce results that lie within the normal ranges observed clinically in humans, which is quite different from matching the model output to a single measured physiological curve by minimizing the sum of squares of residuals. Hence, the simulations should be compared, not to individually measured experimental data but, rather, to the set of curves that constitute the normal range of responses. To represent such data (e.g., changes in circulating levels of glucose and hormones), the model utilizes a number of ‘lumped’ parameters, in which single parameters are used to represent complex molecular reactions that occur at or within the cell membrane. The model thus developed describes the physiological responses, within the limits of a one-compartment model, not only to oral glucose, but also to intravenous glucose injection, as well as changes in both plasma insulin levels and sensitivity to insulin.

The model

The model is built upon the standard OGTT with 50 and 100 g glucose loads taken in liquid form, and is standardized to a 70 kg individual. It consists of a set of ordinary differential equations representing changes in plasma glucose, insulin and the incretins, as well as equations simulating glucose entry into the system and changes in hepatic glucose balance. The model utilizes a single-compartment with a volume of distribution equal to 20% of body weight [e.g., extracellular fluid volume (V) = 14 L]. Typically, the equations were solved for a span of 300 min, beginning with a basal or steady state interval of 5 minutes. The model is, in a sense, the simplest that could be assembled to account quantitatively for nearly all known fundamental functions governing glucoregulation; it was used to test oral loads of differing magnitudes, as well as different rates of metabolic clearances, and conditions of obesity, exercise training, and hypo- and hyperglycemia. In order to achieve a model with this broad embrace and biological validity, it was necessary to introduce non-linear functions into several of the differential equations, as discussed in more detail below. Nomenclature is defined in Tables 1 and 2, which also include basal values, values of rate constants, and the units of measure for each term. To create the model, it was also required to develop a hepatic glucose balance function, which governs the release and uptake of glucose by the liver. This function was formulated with reference both to known tracer studies and the ability to accurately simulate biological responses.

Table 1. Description, basal values and units for variables used in model.
Full size table
Table 2. Description, values, units and sources for constants used in model.
Full size table

Oral Glucose Entry into the System

Glucose entry into the body during an OGTT involves two main compartments: the GI tract and the mesenteric circulation. Within the GI tract, liquid glucose is very rapidly emptied from the stomach into the duodenum. As the shape of this curve has been well described,50 and it was not the explicit intent of this program to model the GI tract, the measured values of Schirra et al.,50 converted to mmol min−1, were approximated using simple linear functions to represent the 50 and 100 g glucose loads. The rate of delivery of glucose to the duodenum (Duod G ) with a 50 g load OGTT is described by Eq. (1a), and the rate for a 100 g load by Eq. (1b):

$$ {Duod}_{G} {\hbox{ }}(50\,{\hbox{g load) }} = \left\{ \begin{aligned}{} & 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t < 5 \\ & 3.854 - 0.0261t,\;\;\;5 \le t \le t_{\max \,50\,{\hbox{g}}} \\ & 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t > t_{\max \,50\,{\hbox{g}}} \\ \end{aligned} \right. $$
(1a)

where t max 50 g   = 147.7 min and,

$$ {Duod}_{G} {\hbox{ }}(100\,{\hbox{g load}}){\hbox{ }} = \left\{ \begin{aligned}{} & 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t >5 \\ & 6.349 - 0.0353t,\;\;\;5 \le t \le t_{\max \,100\,{\hbox{g}}} \\ & 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t > t_{\max \,100\,{\hbox{g}}} \\ \end{aligned} \right. $$
(1b)

where t max 100 g  = 179.9 min; t is time since the start of the simulation, and t max is the t-intercept of the straight lines. Please note that all OGTT simulations began after 5 min of basal metabolism; that t max is used only to refer to the intercepts of these curves and nowhere else in the model; and that these straight lines are simple mathematical descriptions of experimentally measured glucose delivery rates (mmol min−1). Duodenal delivery rates cannot be negative. Furthermore, when the units are converted from mmol back to grams:

$$ \int_5^{t_{\max 50\,{\hbox{g}}} } {{Duod}_{G} (50\,{\hbox{g}}\,{\hbox{load}}){d}t\, = } \,{\hbox{265}}{\hbox{.60}}\,{\hbox{mmol}}\,{\hbox{ = }}\,{\hbox{47}}{\hbox{.81}}\,{\hbox{g}}, $$

and

$$ \int_5^{t_{\max 100\,{\hbox{g}}} } {{Duod}_{G} (100\,{\hbox{g}}\,{\hbox{load}}){d}t\, = \,} {\hbox{539}}{\hbox{.66}}\,{\hbox{mmol}}\,{\hbox{ = }}\,{\hbox{97}}{\hbox{.14}}\,{\hbox{g}} $$

thus retrieving the ingested doses of glucose. Duod G is used subsequently to determine the rate of release of incretins [Eq. (4) below].

Following entry of glucose into the duodenum, the rate of absorption of glucose into the mesenteric circulation (Ra GutG ; mmol min−1) is dependent upon both sodium glucose-luminal transporter- and glucose transporter-mediated uptake.55 Ferrannini et al.,25,26 have measured the rate of appearance of glucose from the GI tract in humans following oral administration of a glucose load enriched with radioactive glucose. These data governing glucose absorption for both a 50 g and a 100 g glucose load have been fitted to a time-weighted exponential function. As the mesenteric circulation drains directly into the portal circulation, Ra GutG is, thus, used to determine changes in blood glucose kinetics [see Eqs. (6) and (8)]. Empirically, from Ferrannini et al.,25,26 converting units to mmol min−1, rates of appearance of glucose from the bowel after the 5 min basal period are given by:

$$ {Ra}_{{GutG}} (50\;{\hbox{g load}})\, = \,\left\{ \begin{aligned}{} & 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t\, < \,5\,\min \\ & 0.255(t - 5)^{1.06\,} e^{ - 0.035(t - 5)} \;\;\;\;\;t\, \ge \,5\min \\ \end{aligned} \right. $$
(2a)
$$ {Ra}_{{GutG}} \;(100\,{\hbox{g}}\,{\hbox{load}})\;{\hbox{ = }}\;\left\{ \begin{aligned}{} & {\hbox{0,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t\,{\hbox{ $ < $ }}\,{\hbox{5}}\,{\hbox{min}} \\ & {\hbox{0}}{\hbox{.36(}}t - {\hbox{5)}}^{{\hbox{1}}{\hbox{.05}}} \,{\hbox{e}}^{ - {\hbox{0}}{\hbox{.029(}}t - {\hbox{5)}}} {\hbox{,}}\;\;\;\;\;t\, \ge \,{\hbox{5}}\,{\hbox{min}}{\hbox{.}} \\ \end{aligned} \right. $$
(2b)

Again, when the units are converted appropriately:

$$ \int_5^{300} {{Ra}_{{GutG}} {d}t\,(50\,{\hbox{g}}\,{\hbox{load}})\, = \,47.03\,{\hbox{g}}\,{\hbox{and}}\,\int_5^{300} {{Ra}_{{GutG}} {d}t\,(100\,{\hbox{g}}\,{\hbox{load}})\, = } \,93.82\,{\hbox{g}}} $$

using Eqs. (2a) and (2b), respectively.

Hepatic Glucose Balance

Hepatic glucose balance (Hepbal G ; mmol min−1) represents the net flux of glucose G (mmol L−1) across the hepatic bed, thereby reflecting the sum of glucose production and glucose uptake from the mesenteric circulation (e.g., following an oral glucose load). A positive balance thus indicates an excess of production over uptake, whilst a negative balance represents a net uptake of glucose. Hepbal GB (mmol min−1) represents basal hepatic glucose balance in the fasting state, and was set to 0.8549 mmol min−1 for a 70 kg person, corresponding to a basal rate of appearance of 2.2 mg kg−1 min−1.25,26 Therefore, the hepatic balance equation for basal equilibrium is:

$$ {Hepbal}_{G} \, = \,{Hepbal}_{{GB}} {\hbox{ }} $$
(3a)

Under non-equilibrium conditions, Hepbal G is regulated primarily by changes in both glucose and insulin. Although the simplest function determining this regulation would be linear, inclusion of interactions between glucose and insulin was found to generate more rapid and appropriate changes in Hepbal G in response to an OGTT.16 Hence, for glucose values near G B , as glucose (G) is displaced from its basal value (G B = 4 mmol L−1) during an OGTT, and as insulin (I) rises, Hepbal G is governed by the regulatory term, M(G B – G)I:

$$ {Hepbal}_{G} \, = \,{Hepbal}_{{GB}} \; + \;M({G}_{B} \, - \,{G}){I} $$
(3b)

M is a modulating factor, which assumes the value 0.02 under non-hypoglycemic conditions. However, when G falls below 3 mmol L−1, a stronger hepatic response was obtained with M = 0.03, encompassing the effects of elevated levels of counter-regulatory hormones (glucagon, epinephrine, cortisol and growth hormone8,14). Thus, as glucose and insulin levels rise during an OGTT, the primary regulatory term becomes large and negative in value, thereby reducing Hepbal G . Such decreases in Hepbal G during an OGTT have been well-described,14,25,26 and are important to prevent hyperglycemia following ingestion of an extremely large glucose load (e.g., 50 g = 278 mmol) relative to total circulating glucose levels. On the other hand, if glucose levels fall below basal (e.g., G < G B), the primary regulatory term becomes greater than zero, thereby increasing Hepbal G above basal and preventing hypoglycemia, consistent with reports in the literature.16

Finally, although Eq. (3b) is effective in controlling Hepbal G in response to physiological changes in insulin, its ability to deal with profound hypoinsulinemia is limited because, as insulin levels fall (i.e., I → 0), the primary regulator is correspondingly driven toward zero. A second regulatory term in the form 1/GI, representing the known inhibitory effects of both glucose and insulin on Hepbal G , was therefore added to the hepatic glucose balance equation:

$$ {Hepbal}_{G} ={Hepbal}_{{GB}} \; + \;M({G}_{B} - {G}){I}\; + \;{\hbox{ }}\alpha [1/({GI})\, - \,1/({G}_{B} {I}_{B} )] $$
(3c)

Thus, as I becomes small, Hepbal G is increased by the secondary regulatory term. This term is balanced to be equal to zero under basal conditions, and therefore has little effect during normal physiological function, but becomes important for simulations of known responses to severe insulin deficiency, such as in Type 1 diabetes.14,41 The value for α was determined by co-analysis of experimentally measured 3-D surface graphs for Hepbal G vs. G and I as determined by Arleth et al. and Moore et al. 3,41 Thus, the Hepbal G function was constructed with attention to measured data reported in the literature.3,41 It is also important to note that the primary and secondary regulatory functions of the liver operate at different times: when the primary term is active, G and I are large enough to suppress most effect from the secondary term, and vice versa. Hence, although there is little published data on hepatic glucose balance in humans, the model presumes that different physiological mechanisms are invoked by these regulators.

Hormonal Responses

As GIP and GLP-1 are thought to contribute equally to the incretin effect,54 circulating concentrations of the incretins (Inc; ng L−1) were combined in this model, rather than being presented individually. Furthermore, in humans, basal levels of GLP-1 are significantly lower than those of GIP [∼10 ng L−1 vs. 200 ng L−1, respectively54,50]. As such, the combined incretin response was modeled on the basis of the reported GIP concentrations during an OGTT.50 Little is known about the factors that control the basal rate of appearance of the incretins (Ra Inc ; ng min−1). However, the major stimulus to the release of these hormones has been clearly demonstrated to be nutrient ingestion, and in particular, the presence of glucose in the upper GI tract [k 5 Duod G 22,50]. Finally, the removal of bioactive GIP and GLP-1 from the circulation is determined by the activity of the enzyme dipeptidylpeptidase IV, which rapidly inactivates both peptides by removal of the two N-terminal amino acids, as well as by renal clearance.21 As enzymatically catalyzed removal and renal clearance are presumed to be linear over the normal range, the removal of bioactive incretins was approximated using the rate constant k 6 . The value of k 6 was set to 0.1 min−1, which agrees with the reported metabolic clearance rates of GIP and GLP-1 [3.2 and 2.4 L min−1, respectively39] given a volume of distribution (e.g., extracellular fluid volume) of 14 L. Consequently, the differential equation governing the kinetics of the incretins becomes:

$$ \frac{{d{Inc}}} {{dt}}\, = \,\frac{{{Ra}_{{Inc}} }} {V}\, + \,k_5 {Duod}_{G} \, - \,k_6 {Inc} $$
(4)

The value of the basal, endogenous secretion of incretins (Ra Inc ) was determined by setting the derivative equal to zero, which occurs when Duod G equals zero. Basal plasma levels of incretins (Inc B ) were taken from Schirra et al.,50 to be 200 ng L−1, and hence, from Eq. (4):

$$ {Ra}_{{Inc}} \; = \;k_6 V{Inc}_{B} \; = \;(0.1)(14)(200)\; = \;280\,{\hbox{ng}\,\min}^{ - 1} $$

Similarly, insulin levels reflect the effects of both glucose (k 7) and the incretins (k 8) on the beta cell.12,17,42,54 The clearance of insulin from the circulation was set in accordance with the reported metabolic clearance rate in humans [i.e., 20 mL kg−1 min−1, which gives rise to the rate constant, k 9 = 0.1 min−1 for a 70 kg human with a volume of distribution of 14 L.36] This clearance value governs the entire disposition of insulin from plasma, about one-half of which occurs on its passage through the liver.23 The differential equation governing insulin kinetics is thus:

$$ \frac{{d{I}}} {{dt}} = {k_{7}} {G}^{1.3} + k_8 {Inc} - k_9 {I} + \beta $$
(5)

It is noted that, although the model works acceptably in the normal OGTT using the linear term k 7 G, findings in the literature show a more rapid rate of rise of insulin, particularly under conditions of hyperglycemia.50 This effect was more faithfully replicated with the nonlinear expression, k 7 G 1.3, which appropriately accelerates the influence of plasma glucose on insulin release. The constant term, β, represents the sum of additional known regulators of the beta cell, including both stimulatory input (e.g., basal rate of secretion, cholinergic, etc.) and inhibitory factors (e.g., somatostatin). The constant value of β was obtained by setting the derivative term, dI/dt equal to zero in Eq. (5), setting G, I and Inc equal to their basal values, and solving for β. When Eq. (5) is combined with Eq. (6) below, it can be seen that the release of insulin responds to both absolute glucose concentration and its rate of change.

Plasma Glucose Kinetics

Changes in blood glucose concentrations during an OGTT are dependent on glucose absorption from the GI tract into the mesenteric circulation [Ra GutG ; Eqs. (2a) and (2b)] and the net absorption/production of glucose by the liver [Hepbal G ; Eq. (3c)], as well as on both glucose- and insulin-dependent glucose uptake by peripheral tissues. It is well established that glucose can promote its own disposal in tissues that include the brain, kidney, splanchnic bed and red blood cells.4,27 In the model, such non-insulin-mediated glucose uptake (NIMGU) is governed by k 1. In contrast, insulin-mediated glucose uptake (IMGU) occurs mainly at the level of the skeletal muscle and heart,4,27 and is governed by k 2 . Assembling the above information into the differential equation governing glucose kinetics therefore results in:

$$ \frac{{d{G}}} {{dt}} = \frac{{{Ra}_{{GutG}} }} {V} + \frac{{{Hepbal}_{G} }} {V} - k_1 {G}^{1.3} - k_2 {I} + \gamma \frac{{d{I}}} {{dt}} $$
(6)

As was the case with insulin kinetics, brisker glucose responses were obtained for NIMGU using k 1 G 1.3 rather than k 1 G. The more rapid rise introduced by this non-linearity corresponds to that observed in the literature.50 Fractional values of exponents such as G 1.3 are known to occur in chemical kinetics, but may also arise as approximations to more complex chemical reactions, which is certainly the case here. For example, if a reaction proceeded in accordance with Michaelis–Menten enzyme kinetics, with velocity of this reaction properly set equal to −V m S/(K m  + S) , one could approximate this velocity over some range of the substrate (S) as −λS n, where n is fractional, 0 < n < 1. A classical example where the exponent, 1 < n < 2, is the dissociation of acetaldehyde, where n = 1.5.48 Therefore, when using a ‘lumped-parameter’ model, the complexities of the intermediary chemical reactions are condensed into a single term (i.e., k 1 G 1.3).

The insulin derivative term, γ dI/dt, is a small corrective term providing some degree of direct insulin derivative control over glucose production and utilization. This term has the effect of sharpening the peak in glucose level following entry of glucose into the circulation. It is introduced empirically as a partial bridge between the current one-compartment model, wherein newly introduced glucose is instantaneously disseminated throughout the entire extracellular fluid, and more detailed multi-compartment models in which the instantaneous distribution occurs over a limited space. Thus, when glucose is entering the system (i.e., Ra GutG  > 0), the value of γ is set to 0.06, and is otherwise = 0.

It has been reported that NIMGU accounts for approximately two-thirds of glucose uptake under basal, post-absorptive conditions.4,27 Given these findings, the values of k 1 and k 2 were established by setting the derivatives in Eq. (6) equal to zero, setting the ratio of NIMGU to IMGU at 2, and utilizing the value of Hepgbal G needed for normal glucose turnover, as shown in Appendix A.

Finally, although Eq. (6) functions well under normoglycemic conditions, the maximal rate of renal re-absorption of glucose in the proximal tubule is exceeded when G > 10 mmol L−1.31 Thus, an additional mechanism was required to account for urinary glucose loss during hyperglycemia. The relationship between the rate of glucose loss to urine and plasma glucose concentration has been reported by Hayford et al. 31 From their data, it was determined:

$${\hbox{Rate of urinary loss of glucose (}}G\, > 10{\hbox{)}}\; = \;0.0718 {G}\, - \,0.717\,({\hbox{mmol}}\;\min ^{ - 1} ) $$
(7)

The two constants in this empirical equation provide values for k 3 and k 4 in the differential equation for glucose when G > 10. Thus:

$${\hbox{If } G > 10 \hbox{ then }}\frac{{d{G}}} {{dt}}\,=\,\frac{{{Ra}_{{GutG}} }} {V} + \frac{{{Hepbal}_{G} }} {V} - k_1 {G}^{1.3} - k_2 {I} + \gamma \frac{{d{I}}} {{dt}} - \frac{{k_3 {G} - k_4 }} {V}$$
(8)

Summary of the Model

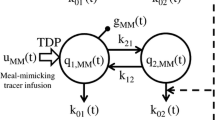
Together, the differential equations (4), (5) and (6), which describe the changes in incretins, insulin and glucose, respectively, are the primary equations used to model the response of the normal human glucoregulatory system to an oral glucose load. A flow diagram of the model is shown in Fig. 1. Basal values and constants are given in Tables 1 and 2, respectively and, of the 15 constants utilized, 10 were derived from specific parametric data in the literature or from steady-state values, while existing human data was used to constrain the model’s output and determine the 5 remaining parameters. Simulations were run, characteristically, to model a 300 min time course, with the first 5 min run in basal steady state. These equations were also used to define the responses to oral glucose under a variety of challenging conditions, including diabetes, obesity and exercise training, as well as during an intravenous glucose infusion (e.g., an IVGTT). It is emphasized again that the parameters of this model were estimated by appeal to the accepted range of clinical data, rather than the responses to a single subject or patient. For all figures presented in this paper, the differential equations were solved numerically by the Euler technique. However, to confirm the accuracy of the solutions, the equations were also solved using a fourth order Runge–Kutta method. In this case, the increase in accuracy provided by the use of the Runge–Kutta method was minimal.

Figure 1.
figure 1

Flow Diagram of OGTT Model. The basic elements of the OGTT model are shown, beginning with Duod G , as initiated by the oral glucose bolus. Duod G , rate of appearance of ingested glucose in the duodenum; G, plasma glucose concentration; Hepbal G , hepatic glucose balance; I, plasma insulin concentration; Inc, plasma incretin concentration; Ra GutG , rate of appearance of Duod G in the blood. Constants used in the model are indicated above the arrows.

Full size image

All code and simulations were written de novo, using a variety of platforms, including BASIC, C, Maple (Maplesoft, Waterloo, ON, Canada) and Labview (National Instruments, Austin, TX).

Results

Introduction of a 50 g oral glucose load into the system at t = 5 min produced a spectrum of changes in all variables that were consistent with normal responses. Hence, the changes in Duod G , as well as in the plasma concentrations of incretins, glucose and insulin all fell within the ranges for normal humans, as shown by the dotted line in Fig. 2a for the mean response reported by Schirra et al.,50 and by the shaded areas in b, e and f, respectively, for the range of responses reported in the same paper. The changes in Ra GutG are also similar to those observed by Ferrannini et al.,26 following administration of a radiolabelled glucose load to humans (Fig. 2c). Finally, although there are no data available for changes in Hepbal G following an OGTT in humans, this parameter has been determined in dogs for a 114 g OGTT,16 and is shown in Fig. 2d for comparative purposes.

Figure 2.
figure 2

Normal Responses to OGTT. Profiles for (a) Duod G , (b) plasma incretins, (c) Ra GutG , (d) Hepbal G , (e) plasma glucose, and (f) plasma insulin during a 50 g (solid line) and 100 g (dashed line) OGTT, administered at t = 5 min. The dotted lines show mean data that is available from the literature, as follows: (a) 50 g OGTT in humans,50 (c) 70 g OGTT in humans, with 83% recovery of ingested glucose,26 and (d) 114 g OGTT in dogs (note that no human data is available for the Hepbal G variable).16 The shaded area in (b, e and f) represents the standard deviation of the mean data for humans.50 The human data shown in (f) is represented as ‘fold-basal (i.e., insulin/basal insulin)’ to account for differences in starting insulin concentrations.

Full size image

Similar findings were made when a 100 g oral glucose load was introduced into the model; however, as compared to the 50 g load, greater increases were seen in the incretins and insulin, while Hepbal G was suppressed to a greater extent (Fig. 2, dashed lines). Nonetheless, glucose levels rose to a higher peak (7.3 as compared to 6.5 mmol L−1) than during the 50 g load and took longer to return to basal (by t = 148 as compared to 121 min). For both of the glucose loads, the return to basal glucose concentrations was associated with a small undershoot (of approximately 0.3 mmol L−1) and a brief oscillatory period, characteristic of a lightly damped system.

One of the major differences between the current model and previously published models of the OGTT is the explicit introduction of a term defining the incretins [Eq. (4)], which thereby permits direct testing of the importance of the incretins in a model of normal insulin and glucose responses to glucose administration. Thus, Duod G was set to zero in order to maintain incretin levels at basal values, while Ra GutG was permitted to rise as during a normal 50 g glucose load. The elimination of the incretin response during a 50 g OGTT resulted in a 28% increase in the maximum plasma glucose levels, reaching a peak of 8.3 mmol L−1 at t = 51 min (Fig. 3), as compared to the normal incretin-mediated response of 6.5 mmol L−1 at t = 33 min. The incretin-deprived response was also more prolonged, not returning to basal until t = 242 min as compared to 121 min under normal conditions. The increase in glycemia due to loss of the glucose-stimulated rise in incretins was mediated through loss of the effect of these hormones on insulin release. Specifically, despite the same total glucose input as during the 50 g OGTT, peak insulin levels (21 mU L−1) were markedly reduced compared with those reached during the oral load (52 mU L−1), and the overall insulin response (as determined by area-under-the-curve) was reduced by 72%. Similar results have been reported by a number of investigators,12,17,42 who have demonstrated that the incretins account for 50–90% of the insulin response following oral administration of glucose to normal humans. Together, these dramatic changes in responses to an OGTT illustrate the importance of the incretin contribution to glucoregulation and the need for their explicit inclusion in models of oral nutrient intake.

Figure 3.
figure 3

Responses to OGTT in the Absence of an Increase in Incretins. Solid lines are profiles for (a) plasma glucose, and (b) plasma insulin when incretins were fixed at the basal value during a 50 g glucose load, administered at t = 5 min. The dotted lines show data from the model during a normal 50 g OGTT, taken from Figure 2e and f.

Full size image

To explore the relationship between Hepbal G and plasma concentrations of glucose and insulin, a 3-D graph was generated, showing changes in Hepbal G (z-axis) in response to glucose and insulin concentrations ranging from 0.4 to 20 mmol L−1 and 0 to 80 mU L−1, respectively (Fig. 4). Hepbal G was highest at low concentrations of insulin and glucose, indicating net hepatic glucose production, but fell into the negative range when levels of glucose and insulin were increased, in accord with net hepatic glucose uptake. The 3-D graph shown in Fig. 4 is consistent with reported measurements,3,41 although it is noted that data obtained by empirical sampling of hepatic glucose balance as a function of both insulin and glucose levels is extremely sparse.

Figure 4.
figure 4

Combined Glucose and Insulin Effects on Hepbal G . The 3-D relationship between Hepbal G (mmol min−1), plasma glucose (mmol L−1) and insulin (mU L−1) concentrations. Hepbal G is plotted on the z-axis.

Full size image

To test the model under conditions for which it had not been explicitly constructed, an insulin infusion-modified IVGTT was simulated, using an intravenous infusion of glucose (1.67 mmol kg−1) from t = 5–7 min, followed by an infusion of insulin (4 mU kg−1 min−1) from t = 25–30 min, in accordance with the protocol described by Quon et al. 46 The resultant changes in glycemia demonstrate a good match with the reported data (Fig. 5).

Figure 5.
figure 5

Glycemic Responses to an Insulin Infusion-modified IVGTT. Changes in plasma levels of glucose in response to an infusion of glucose from t = 5–7 min, followed by infusion of insulin from t = 25–30 min, as per the protocol reported by Quon et al. 46 The solid line is the output generated by the model, while the shaded area represents the standard deviation of the mean data for humans taken from Quon et al. 46

Full size image

The data presented in Fig. 2 represents the model under conditions simulating the responses in a normal individual. However, to simulate hypoglycemia in an individual with an insulin-secreting tumor, circulating insulin concentrations were set to very high levels (i.e., 100 mU L−1) and the system was then allowed to re-equilibrate (Fig. 6). Insulin levels this high are unusual, but will serve as an extreme example. In the first running of this simulation, the value of M, which represents counter-regulatory input, was maintained at the basal value of 0.02. Thus, the high insulin concentrations resulted in a prompt fall in plasma glucose concentrations, to 2.8 mmol L−1, despite a marked increase in Hepbal G , from 0.85 to 3.22 mmol min−1. Since the high levels of circulating insulin prevented larger rises in Hepbal G , plasma glucose levels remained low for the duration of the simulation. However, when M was permitted to increase to 0.03 as glucose fell below 3 mmol L−1, the stimulatory effects of the counter-regulatory hormones on Hepbal G were enhanced by a further 0.07 mmol min−1, and plasma glucose concentrations were thereby increased, to 3.3 mmol L−1. These findings correspond with the known effects of the counter-regulatory hormones to enhance Hepbal G in hypoglycemia.8,14 A second test of the model was the state of severe hypoinsulinemia, as occurs in Type 1 diabetes. In this instance, insulin levels were set to 0.02 mU L−1. When renal glucose clearance was included in the model [i.e., Eq. (8), which allows renal glucose loss when G > 10], plasma glucose concentrations rose in response to the insulin deficiency, to 16.1 mmol L−1. However, when renal glucose loss was prevented [i.e., Eq. (6) was utilized instead of Eq. (8)], glucose levels rose even further, to 17.1 mmol L−1. The moderate renal effects on glucose levels are consistent with the known but relatively small contribution of the kidney to total glucose clearance under conditions of hyperglycemia.31 Interestingly, Hepbal G was not suppressed by the hyperglycemia during simulation of Type 1 diabetes, and indeed, was elevated relative to normal levels (from 0.85 to 3.94 mmol min−1). Based on the primary regulatory term in Eq. (3c) (+M(G B  − G)I), the inhibitory effects of hyperglycemia on Hepbal G are muted by the hypoinsulinemia. Concomitantly, the secondary regulatory term (1/GI) is increased markedly by the extremely low levels of insulin. Thus, Hepbal G increased overall, consistent with findings by others under conditions of severe, acute insulin deficiency.26 Finally, the conditions of obesity and exercise training represented additional challenges to the model due to changes in insulin sensitivity [e.g., k 2 (IMGU)]. For example, insulin sensitivity is well-established to be decreased in obesity.6 Thus, k 2 was decreased by 50% in the model, which led to a very small (12%) increase in basal plasma glucose concentrations, in association with a compensatory (10%) increase in basal insulin levels and a slight decrease (13%) in basal hepatic glucose production, to 0.74 mmol min−1. Similar increases in glycemia have been reported in the literature for obese humans.30 Conversely, a doubling of k 2, consistent with the findings of increased insulin sensitivity in highly trained-individuals,38 induced a slight fall in basal levels of both plasma glucose and insulin, and an associated small increase in Hepbal G .The small decreases in both glucose and insulin are consistent with reports in the literature.45

Figure 6.
figure 6

Responses to changes in Insulin and Insulin Sensitivity. (a) Plasma glucose and (b) hepatic glucose balance. Left: Changes in response to an increase in plasma insulin concentrations to 100 mU L−1 (e.g., hyperinsulinemia) were analyzed both without (M = 0.02) and with (M = 0.03) extra contributions from the counter-regulatory hormones, as introduced through the factor ‘M’. Middle: Changes in response to a decrease in plasma insulin concentrations to 0.02 mU L−1 (e.g., hypoinsulinemia) were analyzed both with and without renal glucose clearance (+ and − RenG, respectively). Right: changes in response to altered insulin sensitivity, such as in obesity (i.e., 0.5 * k 2) or exercise training (i.e., 2 * k 2) as compared to normal sensitivity (i.e., k 2).

Full size image

All of the changes from basal conditions described above (i.e., hyper- and hypoinsulinemia, obesity and exercise training) were accomplished by the re-setting of a single parameter within the model, and all resulted in predictable changes to the simulated responses. In contrast, Type 2 diabetes represents a marked departure, in that both NIMGU (k 1) and IMGU (k 2) have been reported to be significantly decreased (by 50 and 90%, respectively) in this condition.6 However, when k 1 and k 2 were changed in the model accordingly, only small increases in plasma glucose concentrations were observed (data not shown). This unexpected low response indicated that these changes alone were inadequate to simulate Type 2 diabetes. As a number of studies have demonstrated that hepatic glucose production is also inappropriate in patients with Type 2 diabetes, increasing by 15–67%,20,35 Hepbal GB was therefore also increased, by 30%. This change made it necessary to solve two simultaneous equations for basal glucose and insulin utilizing the new values for Hepbal GB , k 1 and k 2, to obtain new values for G B (14.3 mmol L−1) and I B (42 mU L−1). Administration of an OGTT under these conditions resulted in a highly abnormal glucose curve, such that glucose rose from 14.3 to 22.2 mmol L−1 at t = 56 min, and levels remained above basal even after 300 min (Fig. 7). This occurred despite an enhanced, but clearly inadequate insulin response as compared to normal, with insulin rising from 42 to 108 mU L−1 at t = 58 min, consistent with an insulin secretory defect in this condition, as reported by others.4 Furthermore, although Hepbal G was suppressed with the oral glucose load, to −0.60 mmol min−1, this hepatic response was small as compared to the normal response. These dramatic changes in the resultant model output are consistent with those reported for patients with Type 2 diabetes.20

Figure 7.
figure 7

Simulated Type 2 Diabetes. Solid lines are profiles for (a) plasma glucose, (b) plasma insulin, and (c) Hepbal G in response to an OGTT at t = 5 min in simulated Type 2 diabetes. The dotted lines show data from the model during a normal 50 g OGTT, taken from Fig. 2d–f. In order to model Type 2 diabetes, k 1 was decreased by 33% and k 2 by 90%, while Hepbal G was increased by 30%;6,20,35 note the resultant increase in basal levels of glucose and insulin, as well as the axis break and change in scale for glucose.

Full size image

Discussion

This paper describes the development of a one-compartment model to simulate the glycemic and insulin responses to an OGTT, with explicit incorporation of the actions of the incretins based upon known physiological principles. The efficacy of this model was evaluated with regard to the range of values that have been classed as normal responses to glucose challenges. Thus, the changes in plasma levels of both glucose and insulin in response to oral glucose loads of 50 or 100 g were in accord with values reported in the literature for normal individuals,25,26,42,44,50 with concentrations remaining within normal ranges throughout the duration of the experiment. Furthermore, the restoration to basal values of glucose and insulin was also consistent with the reported time frame in normal humans. The model was also tested using settings designed to mimic a variety of conditions, including hyper- and hypoinsulinemia, as well as increases in both insulin resistance (e.g., obesity) and sensitivity (e.g., exercise training). Again, the glucose and insulin responses to all of these challenges fell well within the ranges reported in human studies. Specifically, plasma glucose concentrations decreased markedly during insulin infusion, consistent with findings in patients with insulin-secreting tumors,19 and rose to hyperglycemic levels in response to severe insulin deficiency, as found in Type 1 diabetes.14 Finally, modulation of the ability of insulin to stimulate glucose uptake, through changes in k 2, demonstrated a reciprocal relationship between insulin sensitivity and insulin secretion, a phenomenon that has been widely reported for humans with differing degrees of insulin resistance.6,33 Thus, the model responds appropriately to a variety of different challenges simulating both physiological and pathophysiological states. Type 2 diabetes represents the only example in the present study that required multiple alterations to several parametric values (k 1, k 2, Hepbal G , G B and I B ). Nevertheless, these changes were consistent with the reported literature for patients with Type 2 diabetes.6,20,35

The strength of this model lies in its simplicity and in the fact that 10 of the 15 constants whose numerical values were mandated by the model are known a priori from clinical measurements, leaving only 5 adjustable parameters to incorporate much of known glucoregulation. Moreover, as we are continually discovering, the model’s scope extends considerably beyond the data set on which the parameters were evaluated. More importantly, the major difference between the current model and those proposed by others2,13,18,29,37,49,51,52,53 is the explicit incorporation of an incretin term that allows for the stimulatory effects of the gastrointestinal hormones, GLP-1 and GIP, on glucose-stimulated insulin secretion. Simulation of an IVGTT by preventing the oral glucose-induced rise in incretins (Fig. 3), demonstrated that, for an identical glucose load, the insulin response during the IVGTT was reduced by 72% as compared to that seen during the OGTT. A number of in vivo studies examining the importance of the incretins in humans have similarly demonstrated that the incretins collectively account for approximately 50–90% of the insulin response to oral glucose.12,17,42 Thus, the biological actions of the incretins to stimulate insulin secretion must be an essential component of any model that simulates the glucoregulatory responses to oral nutrients and are, for the first time, explicitly included here in a simple mathematical model.

Two discrete mechanisms were included in the model in order to account for situations in which extreme levels of plasma glucose were reached. In the first instance, M was toggled to a higher value when hypoglycemic conditions were simulated (e.g., G < 3 mmol L−1), to reflect the fact that the counter-regulatory hormones increase to enhance hepatic glucose production under such conditions,8,14 as compared to their normally low levels during an OGTT.34 It is acknowledged that, in actuality, this term would probably be more accurately modeled by a continuous function, rather than the simple threshold function that is currently in place. Nonetheless, during simulated hyperinsulinemia, hypoglycemia was prevented due to appropriately increased stimulation of Hepbal G . Similarly, introduction of a second discrete term governing renal glucose clearance resulted in a small but effective reduction in plasma glucose levels in simulated Type 1 diabetes, consistent with the known glycosuria that occurs in such patients when glycemia exceeds the renal threshold of 10 mmol L−1.31 Together, these discrete terms were a straightforward and physiologically based approach to extend the application of the model to various pathophysiological conditions, rather than being restricted to only the normal state.

Interestingly, the current glucoregulatory model permits the simulation of tracer experiments, performed both in and out of the steady state. The simulations are, of course, limited by the use of a single compartment for glucose, insulin and incretins. As an example, consider the simulation of the kinetics of tritiated glucose after intravenous injection of a bolus of this tracer, with the tracer held in steady state. From the theory of tracer kinetics,32 it is expected that the rate of disappearance of tracer from the well-mixed single compartment will equal the rate of disappearance of tracee, or unlabelled glucose, multiplied by specific activity. Thus, using Eq. (6), it may be shown that the fractional turnover rate of glucose (K) in steady state is approximately 1.5% per minute (see Appendix B). Furthermore, if K (min−1) is defined as the ratio of Hepbal G (mmol min−1) to total extracellular glucose mass (mmol) in the model, then K is, again, equal to 0.015 min−1. This value is in accord with the values of K measured radioisotopically in humans,28 as well as with more recent data obtained using stable isotopes.15

Although the model functions well under a variety of conditions, there are several limitations that must be discussed. The first concerns the response to prolonged periods of intravenous glucose infusion. The glucose response to such infusions is handled very well by the model, with glycemic levels returning to basal within the appropriate time frame (data not shown). However, the model’s insulin response over an extended time course falls short of that which is observed experimentally,10 apparently due to a “physiological” resistance to the action of insulin that develops when glucose is maintained above basal for a prolonged period. In order to accommodate such resistance, one or more of the rate constants would be required to change with time when glucose concentrations are held at an elevated level. However, sufficiently detailed observations are not yet available in the literature, and a better physiological understanding of this phenomenon is therefore required in order to make such an adjustment.

A second issue concerns the terms k 7 G 1.3  + k 8 Inc that appear in Eq. (5) governing the rate of change of insulin. Current knowledge in cell biology suggests that these two terms are interactive and should be combined in some form, such as the product G.Inc. However, such changes greatly magnify the stimulation of the beta cell and rate of insulin release, such that proper glucose control is maintained only when the liver Hepbal G function oscillates with great precision. The Hepbal G function in the model is, indeed, up to the task, and glucose control is properly maintained. However, these changes were not implemented in the current model as experimental data on hepatic glucose balance in humans is lacking for verification purposes. Under these circumstances, the more slowly responding terms of the form k 7 G 1.3  + k 8 Inc were retained. Nonetheless, because the model is implemented using numerical solutions to the differential equations, subsequent versions can easily accommodate such complex modifications of rate constants within subprograms as data becomes available.

Finally, several other limitations of the model must be acknowledged. For example, although the use of a single compartment in the model captures the most critical components of the system, it does not admit subtleties such as remote action by insulin on glucose56 or the mechanisms governing biphasic insulin release.24 Also, no consideration has been given to possible changes in hepatic extraction of insulin, which has been reported to occur under conditions of hyperlipidemia.7 Furthermore, as gastric emptying and nutrient absorption are quite different between liquid and solid meals, as well as between different types of nutrients,50 the current model of liquid glucose ingestion would require alterations to simulate meal-related tolerance tests. Additionally, in constructing the model, linear functions were used initially, and were replaced with non-linear terms only when such changes provided additional accuracy (e.g., through the use of G 1.3 and GI in the hepatic balance function).

It is also acknowledged that, although 10 of the 15 constants utilized in the model were derived from known values, the remaining one-third of the parameters were adjusted to produce the best overall accommodation of normal clinical guidelines or benchmarks. However, despite such evaluations, the model retained the ability to simulate new clinical and physiological tests, not in any way associated with the building of the model. Most notably, the model was found to reproduce with reasonable verisimilitude the findings obtained in an insulin infusion-modified IVGTT without changes in any of the parameters.

The potential utility of this model lies in several areas. As one example, expression of the model in LabView has permitted its use for several years as a teaching tool in undergraduate physiology laboratories. Parameters can be altered, body weight adjusted, etc., and the response of the system can be clearly observed without the need for experimental human subjects. One additional intriguing application of the model is to provide, by non-invasive methods, approximations of differential glucose flux across the hepatic bed. Currently Hepbal G (t) can only be determined by transhepatic vascular catheterization. The use of this model may therefore allow prediction of parameters that have yet to be studied or may otherwise be unavailable clinically.

In summary, the model presented in the current paper represents a unique approach by which the glucose and insulin responses to oral glucose can be simulated using only 6 equations [representing Duod G , Ra GutG , Hepbal G , Inc, I and G; Eqs. (1)–(6), respectively]. The incorporation of incretins into this model allows for a more accurate representation of the known physiology of the glucoreregulatory system. When taken in combination with a specific term to simulate changes in hepatic glucose handling, this model permits simulation of glucose dynamics under a wide variety of physiological and pathophysiological conditions.