Optimal feedback gains of a delayed proportional-derivative (PD) control for balancing an inverted pendulum

Abstract

In the dynamics analysis and synthesis of a controlled system, it is important to know for what feedback gains can the controlled system decay to the demanded steady state as fast as possible. This article presents a systematic method for finding the optimal feedback gains by taking the stability of an inverted pendulum system with a delayed proportional-derivative controller as an example. First, the condition for the existence and uniqueness of the stable region in the gain plane is obtained by using the D-subdivision method and the method of stability switch. Then the same procedure is used repeatedly to shrink the stable region by decreasing the real part of the rightmost characteristic root. Finally, the optimal feedback gains within the stable region that minimizes the real part of the rightmost root are expressed by an explicit formula. With the optimal feedback gains, the controlled inverted pendulum decays to its trivial equilibrium at the fastest speed when the initial values around the origin are fixed. The main results are checked by numerical simulation.

1 Introduction

An inverted pendulum serves as an important model in many applications, such as in the study of the human body in a quiet standing position [1,2,3] or a biped robot locomotion [4, 5]. It is also an important part of some personal transportation devices, such as two-wheeled motorized vehicles that offer drivers enhanced mobility [6] or power-assist wheelchair robots that help patients climb steps or curbs [7]. In addition, a missile in attitude control during launch and a rocket booster “balanced” on their own thrust vector can be regarded as an inverted pendulum model [8, 9]. An inverted pendulum is a nonlinear and open-loop unstable system that can be stabilized using different control strategies. In Ref. [10], numerical simulations demonstrated that the stability border could be well predicted using the linearized approximation of an inverted pendulum. Actually, most studies involving stability analysis have been based on linear control theories, where the controllers are in the form of state feedback, such as proportional-derivative (PD) controllers [2, 11], proportional-integral-derivative (PID) controllers [3], or linear quadratic regulator (LQR) controllers [12], for example. In addition, nonlinear feedback controllers [13, 14], fuzzy controllers [15,16,17], and adaptive controllers [18] have also been used in controlling inverted pendulums.

A delay effect on controlled inverted pendulums has been discussed in many papers. In Ref. [2], it was confirmed that when a time delay exceeds some critical delay, an inverted pendulum system cannot be stabilized by a PD controller. In addition, it was shown that under an increasing time delay, a digitally controlled inverted pendulum system will be out of control [11]. A time delay is usually unavoidable in digital controllers, filters, hydraulic-servo actuators, and human–machine interactions. Time-delayed systems are described by delay differential equations and are infinite-dimensional systems, no matter how small the delays are. The feature of infinite dimensionality makes the analysis and synthesis of time-delayed systems complicated compared with delay-free ones. Although an inverted pendulum with a delayed feedback controller is essentially nonlinear, the control design in most applications is based on linear control theories. In addition, although lots of different control strategies have been developed, PID controllers constitute the main control strategy used in controlling inverted pendulums. Actually, as pointed out in Ref. [19], PID controllers are the most important class of controllers since 98% of the controllers in use in applications worldwide fall in this category. When the delay is short, a delayed proportional (P) controller can be regarded as an alternative to a PD controller because it responds quickly to input changes but is insensitive to high-frequency noise [20, 21]. Delayed PD control is useful for controlling inverted pendulums, as shown in a study of three paradigms of human balance control: mechanical inverted time-delayed pendulum, stick balancing at the fingertip, and human postural sway during quiet standing [22]. In a study of a mechanical model of postural balancing, delayed proportional-derivative-acceleration (PDA) feedback control was used, and acceleration feedback benefited the stabilization of an inverted pendulum [23]. In Ref. [24], it was shown that even in the presence of time delay, a wheeled inverted pendulum can be well stabilized with only one accelerometer as the sensor when the mechanical structure is slightly modified. In a study of human balancing, delayed PDA control proved helpful in enlarging the stable region [25, 26]. Delayed acceleration feedback was shown effective in vibration absorption [27].

Optimal feedback control has been used for controlling inverted pendulums with different control objectives. One objective is to identify feedback gains that lead to optimal responses, as shown in Ref. [28], where a fuzzy control is combined in the control strategies. Another objective is to minimize the quadratic performance index [29]. To determine the optimal weight matrices in the quadratic performance index of a LQR, a genetic algorithm (GA) can be effective [12]. A third objective is to return the pendulum from the downward to the upward position with a minimum number of swings, for which a nonlinear controller was used to swing up a pendulum attached to a cart in a minimum amount of time [30]. These optimal feedback gains (OFGs) that minimize the performance criteria are sensitive to changes in the parameter values and initial values, and they can be obtained numerically only. Thus, a question arises as to whether it is possible to define the optimal control with less sensitivity in a different sense and whether or not the optimal gains can be determined easily.

Similar to delay-free systems described by ordinary differential equations, the general solution of linear time-delay systems can be expressed in terms of characteristic functions. Thus, the decaying ratio of a solution can be determined simply by the real part of the rightmost characteristic roots (characteristic roots with the largest real parts). The smaller (the larger in absolute value) the real part of the rightmost characteristic root(s) is, the faster the solution decays to zero. In this sense, the real part of the rightmost characteristic roots can be used as an index of stability, and it can be obtained using the iteration method [31, 32] or a combination of integration and iteration [33]. However, no results have been reported in the literature on finding the OFGs that minimize the real part of the rightmost characteristic roots within a given stable region. The aim of this article is to present an approach for finding the OFGs of time-delayed systems, demonstrated on a controlled inverted pendulum under a delayed PD feedback controller.

The rest of this article is organized as follows. In Sect. 2, the problem and main results are stated. Sections 3 and 4 are devoted to the proof of the main results. In Sect. 3, first the properties of critical stable curves are discussed, and then the unique connected stable region in the gain plane is determined. In Sect. 4, based on the repeated analysis of the so-called $\sigma$-stability, the explicit formula for OFGs within the stable region and the minimal real part of the rightmost characteristic roots are derived. In Sect. 5, numerical simulation results are given for demonstration purposes. Finally, some concluding remarks are made in Sect. 6.

2 Problem statement and main results

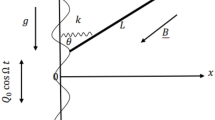
An inverted pendulum is one of the most important mechanical models. In active vibration control, many systems and structures can be modeled directly using an inverted pendulum, or they can be simplified to an inverted pendulum. In dimensionless form, an inverted pendulum model can be described by

$$\begin{aligned} \ddot{x}(t)+2\xi \varOmega \dot{x}(t)-\varOmega ^{2}\sin (x(t))=u(t), \end{aligned}$$

(1)

where x(t) is the angle of deviation of the inverted pendulum, $\varOmega >0$, $\xi \in {\mathbb {R}}$. The free vibration is unstable, and u(t) is a linear feedback control to make the closed loop stable. The linearized system around $x(t)=0$ reads

$$\begin{aligned} \ddot{x}(t)+2\xi \varOmega \dot{x}(t)-\varOmega ^{2}x(t)=u(t). \end{aligned}$$

(2)

Under a time-delayed PD control of the form $u(t)=-k_{\mathrm{p}}x(t-\tau )-k_{\mathrm{d}}\dot{x}(t-\tau )$, the system equation becomes a retard delay differential equation

$$\begin{aligned} \ddot{x}(t)+2\xi \varOmega \dot{x}(t)-\varOmega ^{2}x(t) =-k_{\mathrm{p}}x(t-\tau )-k_{\mathrm{d}}\dot{x}(t-\tau ).\qquad \end{aligned}$$

(3)

The corresponding characteristic function is

$$\begin{aligned} p(\lambda )=\lambda ^{2}+2\xi \varOmega \lambda -\varOmega ^{2}+k_{\mathrm{p}}\mathrm{e}^{-\lambda \tau }+k_{\mathrm{d}}\lambda {\mathrm{e}^{-\lambda \tau }}. \end{aligned}$$

(4)

The characteristic equation $p(\lambda )=0$ has infinitely many roots, denoted by $\sigma _{1}+\mathrm{i}\omega _{1}, \sigma _{2}+\mathrm{i}\omega _{2}, \cdots$, and satisfying $\sigma _{1}>\sigma _{2}> \cdots$ without loss of generality. Then the general solution of Eq. (3) can be expressed as

$$\begin{aligned} {x}(t)=\sum _{n=1}^{\infty }\mathrm{e}^{\sigma _{n}t}\left( p_n(t)\cos (\omega _{n}t)+q_n(t)\sin (\omega _{n}t)\right) , \end{aligned}$$

(5)

where $p_n(t)$ and $q_n(t)$ are polynomials depending on the initial conditions and the multiplicity of the characteristic root $\lambda _n=\sigma _n+\mathrm{i}\omega _n$. For sufficiently large t, the solution is dominated by the terms in x(t) related to $\lambda _1=\sigma _1+\mathrm{i}\omega _1$. In the case of $\sigma _1<0$, the unique equilibrium $x=0$ of Eq. (3) is asymptotically stable, and the smaller the real part of the rightmost characteristic roots $\sigma _1$ is, the faster the general solution x(t) decays to zero. Thus, regarding $\sigma _1$ as a function with respect to $(k_\mathrm{p},k_\mathrm{d})$, it is important to know under what conditions $\sigma _1$ is negative and for what gain values within a given domain $\sigma _1$ takes the minimum. The main objective of this article is to find a pair of $(k_\mathrm{p},k_\mathrm{d})=(k_\mathrm{p}^*,k_\mathrm{d}^*)$ in the asymptotically stable region $S_0$ such that

$$\begin{aligned} \min \limits _{(k_\mathrm{p},k_\mathrm{d})\in {S_0}}\sigma _1=\sigma _1^*. \end{aligned}$$

(6)

Within the stable region $S_0$, the minimum $\sigma _1^*$ can be obtained by using a combination of the D-subdivision method [34] and stability switch theory [35] repeatedly, on the basis of the critical-stable curves determined by $p(\sigma +\mathrm{i}\omega )=0$. The main results can be stated as follows

Theorem 1

• (1) For a given delay $\tau$ ($\tau \geqslant 0$), the stable region $S_0$ in the $(k_\mathrm{p},k_\mathrm{d})$-plane of Eq. (3) is a connected domain that exists and is unique if and only if $\varDelta _0=4\xi \varOmega \tau +2-\varOmega ^2\tau ^2>0$.

• (2) In the stable region $S_0$, the minimum $\sigma _1^*$ can be expressed explicitly

  $$\begin{aligned} \sigma _1^*=\frac{-\xi \varOmega \tau -2 +\sqrt{\xi ^{2}\varOmega ^{2}\tau ^{2}+\varOmega ^{2}\tau ^{2}+2}}{\tau }, \end{aligned}$$

  (7)

and the corresponding gains $k_\mathrm{p}^*$ and $k_\mathrm{d}^*$ are given by

$$\begin{aligned} \begin{aligned} k_{\mathrm{p}}^*&=\mathrm{e}^{\sigma _1^*\tau }\left[ \tau {\sigma _1^*}^{3}+ (2\xi \varOmega \tau +1){\sigma _1^*}^{2} -\varOmega ^2\tau \sigma _1^*+\varOmega ^{2}\right] ,\\ k_{\mathrm{d}}^*&=\mathrm{e}^{\tau \sigma _1^*}\left[ -\tau {\sigma _1^*}^{2} -2(\xi \varOmega \tau +1)\sigma _1^*+\varOmega ^{2}\tau -2\xi \varOmega \right] . \end{aligned} \end{aligned}$$

(8)

This theorem will be proved in the next two sections. Here, it is worth noting that the minimum $\sigma _1^*$ given in Eq. (7) can be rewritten in the following form

$$\begin{aligned} \sigma _1^*=-\frac{\varDelta _0}{\tau \left( \xi \varOmega \tau +2 +\sqrt{\xi ^{2}\varOmega ^{2}\tau ^{2} +\varOmega ^{2}\tau ^{2}+2}\right) }. \end{aligned}$$

As a direct application of Theorem 1, $\varDelta _0=0$ gives the critical delay as follows

$$\begin{aligned} \tau _\mathrm{c}=\frac{2\xi +\sqrt{4\xi ^2+2}}{\varOmega }. \end{aligned}$$

(9)

In particular, $\tau _\mathrm{c}=\sqrt{2}/\varOmega$ if $\xi =0$, which is the same as the one obtained in Ref. [2].

When $\varDelta _0>0$, the stable region $S_0$ exists uniquely, and the corresponding minimum $\sigma _1^*$ is given in Eq. (7), depending on $\xi$ and $\tau$. Direct computation gives

$$\begin{aligned} \frac{\mathrm{d}\sigma _1^*}{\mathrm{d}\xi }=-{\frac{\varOmega \left( -\xi \varOmega \tau +\sqrt{{\xi }^{2}{\varOmega }^{ 2}{\tau }^{2} +{\varOmega }^{2}{\tau }^{2}+2} \right) }{\sqrt{{\xi }^{2}{ \varOmega }^{2}{\tau }^{2} +{\varOmega }^{2}{\tau }^{2}+2}}}. \end{aligned}$$

Hence $\mathrm{sgn}\left( \frac{\mathrm{d}\sigma _1^*}{\mathrm{d}\xi }\right) =-1<0$. This means that $\sigma _1^*$ decreases with respect to $\xi$ and

$$\begin{aligned} \inf _{\xi \in {\mathbb {R}}}\sigma _1^*=\lim _{\xi \rightarrow +\infty }\sigma _1^*=-\frac{2}{\tau }. \end{aligned}$$

(10)

Thus, $\sigma _1^*\geqslant -2/\tau$ holds for any positive number $\xi$, and the effects of damping on the decaying ratio of the solution of Eq. (3) are limited. Similarly,

$$\begin{aligned} \frac{\mathrm{d}\sigma _1^*}{\mathrm{d}\tau }=2\,{\frac{-1 +\sqrt{{\xi }^{2}{\varOmega }^{2}{\tau }^{2} +{\varOmega }^{2}{\tau }^{2}+2}}{\tau ^2\sqrt{{\xi }^{2}{\varOmega }^{2}{\tau }^{2} +{\varOmega }^{2}{\tau }^2 +2}}}>0. \end{aligned}$$

It follows that $\sigma _1^*$ increases with respect to $\tau$. Moreover, $\lim _{\tau \rightarrow +\infty }\sigma _1^*=(-\xi +\sqrt{1+\xi ^2})\varOmega >0$ and $\lim _{\tau \rightarrow +0}\sigma _1^*=-\infty$, so there is a $\tau ^*>0$ such that $\sigma _1^*>0$ for all $\tau >\tau ^*$. Thus, when the OFGs $(k_\mathrm{p}^*, k_\mathrm{d}^*)$ are fixed, increasing the delay value leads to a deterioration of the stability, and the controlled inverted pendulum must be unstable for sufficiently large delay $\tau$ for any given gain values. A similar result is obtained when the frequency $\varOmega$ varies.

3 Existence and uniqueness of stable region in the gain plane

3.1 Key properties of critical-stable curves

When system (3) is in a critical-stable state, namely $p(\mathrm{i}\omega )=0$, two cases are considered. Case (1): $\omega =0$. In this case, $p(0)=0$ yields $k_\mathrm{p}=\varOmega ^2$, which defines a straight line $\tilde{L}_0$. Case (2): $\omega \ne 0$. In this case, separating the real and imaginary parts of $p(\mathrm{i}\omega )=0$ gives

$$\begin{aligned} \begin{aligned}&\mathfrak {R}(p(\mathrm{i}\omega ))=-\omega ^{2}-\varOmega ^{2} +k_{\mathrm{p}}\cos (\omega \tau )+k_{\mathrm{d}}\omega \sin (\omega \tau )=0,\\&\mathfrak {I}(p(\mathrm{i}\omega ))=2\xi \varOmega \omega -k_{\mathrm{p}}\sin (\omega \tau ) +k_{\mathrm{d}}\omega \cos (\omega \tau )=0, \end{aligned} \end{aligned}$$

(11)

where $\mathfrak {R}(z)$ and $\mathfrak {I}(z)$ denote the real and imaginary parts of the complex number z, respectively. It follows that

$$\begin{aligned} \begin{aligned}&\cos (\omega \tau )=\frac{\left( \omega ^{2}+\varOmega ^{2}\right) k_{\mathrm{p}}-2k_{\mathrm{d}}\xi \varOmega \omega ^{2}}{k_{\mathrm{p}}^{2}+k_{\mathrm{d}}^{2}\omega ^{2}},\\&\sin (\omega \tau )=\frac{\left( k_{\mathrm{d}}\left( \omega ^{2}+\varOmega ^{2}\right) +2k_{\mathrm{p}}\xi \varOmega \right) \omega }{k_{\mathrm{p}}^{2}+k_{\mathrm{d}}^{2}\omega ^{2}}, \end{aligned} \end{aligned}$$

(12)

and

$$\begin{aligned} \begin{aligned} k_{\mathrm{p}}&=2\xi \varOmega \omega \sin (\omega \tau )+\left( \varOmega ^{2}+\omega ^{2}\right) \cos (\omega \tau ),\\ k_{\mathrm{d}}&=\frac{-2\xi \varOmega \omega \cos (\omega \tau )+\left( \varOmega ^{2}+\omega ^{2}\right) \sin (\omega \tau )}{\omega }. \end{aligned} \end{aligned}$$

(13)

As $\omega$ varies from 0 to $+\infty$, Eq. (13) defines a critical-stable curve $L_{0}$ in the $(k_\mathrm{p}, k_\mathrm{d})$-plane, and the critical-stable curve of the closed-loop (3) is composed of $L_{0}$ and $\tilde{L}_{0}$. Denote the intersection points of the curve $L_{0}$ and $k_{\mathrm{p}}$ axis by $P_{1},P_{2},\cdots ,P_{k},\cdots$. The corresponding values of $\omega$ at these intersection points satisfy $0<\omega _{1}<\omega _{2}<\cdots<\omega _{k}<\cdots$.

Lemma 1

$L_0$ does not intersect with itself on the right side of $\tilde{L}_0$.

Proof

Equation (11) can be rewritten as

$$\begin{aligned} \left[ \begin{array}{cc} \cos (\omega \tau ) &{}\quad \sin (\omega \tau )\\ -\sin (\omega \tau ) &{}\quad \cos (\omega \tau ) \end{array} \right] \left[ \begin{array}{c} k_{\mathrm{p}}\\ k_{\mathrm{d}}\omega \end{array} \right] = \left[ \begin{array}{c} \varOmega ^{2}+\omega ^{2}\\ -2\xi \varOmega \omega \end{array} \right] . \end{aligned}$$

(14)

Let $\alpha =4\xi ^{2}\varOmega ^{2}+2\varOmega ^{2}-k_{\mathrm{d}}^{2}$ and $\beta =\varOmega ^{4}-k_{\mathrm{p}}^{2}$; then calculating the modulus of both sides of Eq. (14) gives $F_0(\omega )=0$, where

$$\begin{aligned} F_0(\omega )=\left( \varOmega ^{2}+\omega ^2\right) ^2 +(-2\xi \varOmega \omega )^2-k_{\mathrm{p}}^{2}-k_{\mathrm{d}}^{2}\omega ^{2}, \end{aligned}$$

or is simply denoted by $F_0(\omega )=\omega ^{4}+\alpha \omega ^{2}+\beta$. The curve $L_0$ intersects at $(k_\mathrm{p}, k_\mathrm{d})$ with itself only if $F_0(\omega )$ has two different positive roots. This is true if and only if

$$\begin{aligned} \alpha <0,\quad \beta>0,\quad \alpha ^{2}-4\beta >0. \end{aligned}$$

On the right side of $\tilde{L}_0$, one has $k_\mathrm{p}>\varOmega ^2$, which leads to $\beta <0$. Thus, $L_0$ cannot intersect with itself on the right side of $\tilde{L}_0$.

Moreover, when $\alpha>0, \beta >0$, i.e., $k_{\mathrm{p}}^2<\varOmega ^{4}, k_{\mathrm{d}}^{2}<4\xi ^{2}\varOmega ^{2}+2\varOmega ^{2}$, which define a rectangle $M_{0}$ in the $(k_\mathrm{p}, k_\mathrm{d})$-plane, then $F_0(\omega )=0$ has no positive roots. In this case, $L_{0}$ cannot pass through $M_{0}$.

Actually, Eq. (14) can be rewritten as

$$\begin{aligned} \left[ \begin{array}{c} k_{\mathrm{p}}\\ k_{\mathrm{d}} \end{array} \right] = \left[ \begin{array}{cc} 1 &{}\quad 0\\ 0 &{}\quad \frac{1}{\omega } \end{array} \right] \left[ \begin{array}{cc} \cos (\omega \tau ) &{}\quad -\sin (\omega \tau )\\ \sin (\omega \tau ) &{}\quad \cos (\omega \tau ) \end{array} \right] \left[ \begin{array}{c} \varOmega ^{2}+\omega ^{2}\\ -2\xi \varOmega \omega \end{array} \right] , \end{aligned}$$

(15)

where the two matrices stand for a scaling transformation and a rotation transformation, respectively. Thus, $L_0$ is the mapping of a parabola after a rotation transformation and a scaling transformation. In particular, when $\tau =0$, the parabola after a scaling transformation becomes a straight line. When $\omega \gg 1$, Eq. (15) gives

$$\begin{aligned} \begin{aligned} k_\mathrm{p}&=O(\omega ^2)\cos (\omega \tau ),\\ k_\mathrm{d}&=O(\omega )\sin (\omega \tau ). \end{aligned} \end{aligned}$$

(16)

Thus, for a fixed $\tau >0$ and sufficiently large $\omega$, the critical stable curve $L_0$ looks like a spiral that goes to infinity.

Lemma 2

At the intersection points $P_n$ on the left half of the $k_\mathrm{p}$-axis, where the corresponding gain value $k_\mathrm{p}^{(n)}<0$, one has

$$\begin{aligned} \mathrm{sgn}\left( \mathfrak {R}\left( \frac{\mathrm{d}\lambda }{\mathrm{d}k_{\mathrm{d}}}\right) \right) _{P_{n}}>0,\quad \mathrm{sgn}\left( \frac{\mathrm{d}k_{\mathrm{p}}}{\mathrm{d}\omega }\right) _{P_{n}}<0. \end{aligned}$$

(17)

And at the intersection points $P_n$ on the right half of the $k_\mathrm{p}$-axis, where $k_\mathrm{p}^{(n)}>0$, one has

$$\begin{aligned} \mathrm{sgn}\left( \mathfrak {R}\left( \frac{\mathrm{d}\lambda }{\mathrm{d}k_{\mathrm{d}}}\right) \right) _{P_{n}}<0,\quad \mathrm{sgn}\left( \frac{\mathrm{d}k_{\mathrm{p}}}{\mathrm{d}\omega }\right) _{P_{n}}>0. \end{aligned}$$

(18)

Proof

A straightforward application of the implicit function theorem gives

$$\begin{aligned} \frac{\mathrm{d}\lambda }{\mathrm{d}k_{\mathrm{d}}}=-\dfrac{\frac{{\partial }p(\lambda )}{{\partial }k_{\mathrm{d}}}}{\frac{{\partial }p(\lambda )}{{\partial }\lambda }}. \end{aligned}$$

(19)

At $P_{n} (n=1,2,\cdots )$, one has $|\frac{{\partial }p(\lambda )}{{\partial }k_{\mathrm{d}}}|=|\omega _n\sin (\omega _n\tau )+\mathrm{i}\omega _n\cos (\omega _n\tau )|=|\omega _n|\ne 0$. Thus,

$$\begin{aligned} \begin{aligned}&\mathrm{sgn}\left( \mathfrak {R}{\left( \frac{\mathrm{d}\lambda }{\mathrm{d}k_{\mathrm{d}}}\right) }\right) _{P_{n}}=\mathrm{sgn}\left( \mathfrak {R}{\left( \frac{\mathrm{d}\lambda }{\mathrm{d}k_{\mathrm{d}}}\right) ^{-1}}\right) _{P_{n}}\\&\quad =-\mathrm{sgn}\left( \frac{2\xi \varOmega \sin (\omega _n\tau )-k_{\mathrm{d}}^{(n)}\omega _n\tau +2\omega _n\cos (\omega _n\tau )}{\omega _n}\right) . \end{aligned} \end{aligned}$$

(20)

Because $L_0$ does not pass through $M_0$, which includes the origin, $k_\mathrm{p}^{(n)}\ne 0$. Substituting Eq. (12) into the preceding equation yields

$$\begin{aligned} \mathrm{sgn}\left( \mathfrak {R}\left( \frac{\mathrm{d}\lambda }{\mathrm{d}k_{\mathrm{d}}}\right) \right) _{P_{n}}&=\mathrm{sgn}\left( -\frac{2\left( 2\xi ^{2}\varOmega ^{2}+\omega ^{2}+\varOmega ^{2}\right) }{k_{\mathrm{p}}^{(n)}}\right) _{P_{n}}\\&=-\mathrm{sgn}\left( k_{\mathrm{p}}^{(n)}\right) . \end{aligned}$$

In addition, because $\tan (\omega \tau )=\frac{2\xi \varOmega \omega }{\omega ^2+\varOmega ^{2}}$, one has

$$\begin{aligned} \left. \frac{\mathrm{d}k_{\mathrm{p}}}{\mathrm{d}\omega }\right| _{P_{n}}&=2\xi \varOmega \omega _n\tau \cos (\omega _n\tau )+2\xi \varOmega \sin (\omega _n\tau )\\&\quad +2\omega _n\cos (\omega _n\tau )-\left( \omega _n^{2}+\varOmega ^{2}\right) \tau \sin (\omega _n\tau )\\&=\frac{2\omega _n\cos (\omega _n\tau )\left( 2\xi ^{2}\varOmega ^{2}+\omega _n^{2}+\varOmega ^{2}\right) }{\omega _n^{2}+\varOmega ^{2}}. \end{aligned}$$

It follows that

$$\begin{aligned} \mathrm{sgn}\left( \frac{\mathrm{d}k_{\mathrm{p}}}{\mathrm{d}\omega }\right) _{P_{n}}=\mathrm{sgn}(\cos (\omega _n\tau )). \end{aligned}$$

Moreover, at $P_n^{(n)}$, one has $k_\mathrm{d}=0$. Owing to Eq. (12), it holds that

$$\begin{aligned} \cos (\omega _n\tau )=\frac{\omega _n^{2}+\varOmega ^{2}}{k_{\mathrm{p}}^{(n)}}, \end{aligned}$$

where $k_{\mathrm{p}}^{(n)}$ is the corresponding value of $k_\mathrm{p}$ at $P_n, k_\mathrm{p}^{(n)}\ne 0$. It follows that

$$\begin{aligned} \mathrm{sgn}\left( \frac{\mathrm{d}k_{\mathrm{p}}}{\mathrm{d}\omega }\right) _{P_{n}}=\mathrm{sgn}\left( k_{\mathrm{p}}^{(n)}\right) . \end{aligned}$$

(21)

As a result, both Eqs. (17) and (18) are true.

Lemma 2 implies that as $k_\mathrm{p}$ or $k_\mathrm{d}$ varies and passes through the critical-stable curve $L_0$ from one region to another, the number of characteristic roots with positive real parts changes by 2. That is to say, with a fixed $k_\mathrm{d}$, the closed loop increases (or decreases) one pair of conjugate complex characteristic roots with a positive real part when $k_\mathrm{p}$ passes through $L_0$ from left to right on the right half-plane $k_\mathrm{p}>\varOmega ^2$ (or the left half-plane $k_\mathrm{p}<\varOmega ^2$). This fact is demonstrated in Fig. 1a, where $P_1, P_2, P_3, P_4, \cdots$ are the intersection points of $L_0$ with the $k_\mathrm{p}$-axis, the arrows are tangent to the solid curve $L_0$ at the intersection points, and the integers are the numbers of unstable characteristic roots. The plot around the origin is magnified as shown in Fig. 1b, where the dashed line is the straight line $\tilde{L}_0$, and the connected region $S_0$ is a possible stable region of the controlled inverted pendulum. The gray rectangle represents $M_0$, for which the controlled inverted pendulum has exactly one unstable root.

Fig. 1

a Plot of critical-stable curve for (3) with $\xi =0.1, \varOmega =1, \tau =0.1$. b Zoom around origin of plot given in a

3.2 Existence of stable region

The region $S_0$ given in Fig. 1b is an asymptotically stable region; here $\varDelta _0=2.03>0$ holds. Moreover, a general statement is true, namely, the first statement of Theorem 1 holds. In fact, let $\varDelta _0=4\xi \varOmega \tau +2-\varOmega ^{2}\tau ^{2}$. On the straight line $\tilde{L}_{0}$ defined by $p(0)=0$, one has

$$\begin{aligned} s_0=\mathrm{sgn}\left( \frac{\mathrm{d} \lambda }{\mathrm{d}k_{\mathrm{p}}}\right) =\mathrm{sgn}\left( \varOmega ^{2}\tau -2\xi \varOmega -k_{\mathrm{d}}\right) . \end{aligned}$$

(22)

The start point $(\varOmega ^{2},\varOmega ^{2}\tau -2\xi \varOmega )$ of $L_0$ divides $\tilde{L}_{0}$ into two parts: points on the upper part that lead to $s_0<0$ and points on the lower part that result in $s_0>0$. With a fixed $k_\mathrm{d}$ satisfying $s_0>0$ (or $s_0<0$), the closed loop increases (or decreases) one unstable root when $k_\mathrm{p}$ passes through $\tilde{L}_0$ from left to right. Note that the upper right region of the start point must be an asymptotically stable region if the start point is located on the right boundary of $M_0$ because the number of its unstable roots must be less than $M_0$.

The lower and upper right endpoints on the boundary of $M_{0}$ are $(\varOmega ^2, -\varOmega \sqrt{4\xi ^2+2})$ and ($\varOmega ^2, \varOmega \sqrt{4\xi ^{2}+2}$). The start point must be located above the lower one owing to $\varOmega ^2\tau -2\xi \varOmega >-\varOmega \sqrt{4\xi ^2+2}$.

On the one hand, if $\varDelta _0>0$, then $\varOmega ^2(4\xi ^{2}+2)-(\varOmega ^{2}\tau -2\xi \varOmega )^{2}=\varOmega ^{2}\varDelta _0>0$, which means the start point stands between the two endpoints, so that the asymptotically stable region $S_0$ exists and is located on the upper right side of the start point.

On the other hand, the stable region $S_0$ on the upper right side of the start point exists only if the tendency of $L_0$ at the beginning is toward the right side of $\tilde{L}_0$, namely, $\frac{\mathrm{d}k_\mathrm{p}}{\mathrm{d}\omega }|_{\omega =0}>0$. A Taylor series expansion gives

$$\begin{aligned} \frac{\mathrm{d}k_\mathrm{p}}{\mathrm{d}\omega }=\varDelta _0 \omega -\tau ^2\left( 2\varDelta _0+\varOmega ^2\tau ^2+8\right) \omega ^3+O\left( \omega ^5\right) , \end{aligned}$$

(23)

for $\omega \in B(0,\delta )$, where $B(0, \delta )$ is a $\delta$-neighbor of 0 in ${\mathbb {R}}^1$. When $\varDelta _0\leqslant 0$, the slope is negative. Thus, $\frac{\mathrm{d}k_\mathrm{p}}{\mathrm{d}\omega }|_{\omega =0}>0$ if and only if $\Delta _0>0$. As a result, $\varDelta _0>0$ is the sufficient and necessary condition that governs the existence of the stable region $S_0$.

3.3 Uniqueness of stable region

Now the uniqueness of the stable region is guaranteed if $\varDelta _0>0$. Actually, the critical stable curves $L_0$ and $\tilde{L}_0$ divide the $(k_\mathrm{p}, k_\mathrm{d})$-plane into many regions. As shown earlier, for any two adjacent regions with $L_{0}$ as the common boundary, the number of unstable roots must differ by two. While for any two adjacent regions with $\tilde{L}_{0}$ as the common boundary, the number of unstable roots must differ by one. That is to say, the number of unstable roots in a selected region is odd (even) when the region is in the left (right) plane of $\tilde{L}_{0}$. So the stable region only exists on the right side of $\tilde{L}_0$. Thus, $S_0$ is the unique stable region in the $(k_\mathrm{p}, k_\mathrm{d})$-plane.

Here are three examples that distinguish the case of $\varDelta _0>0, \varDelta _0=0$, and $\varDelta _0<0$. In Fig. 1, the start point is on the right boundary of $M_0$. In Fig. 2b, the start point almost coincides with the upper right endpoint, the stable region $S_0$ is nearly empty, and $\varDelta _0=0.000816\approx 0$. In Fig. 3, the start point is in the upper part of $M_0$, $\varDelta _0=-2.01<0$, and the stable region $S_0$ does not exist.

Fig. 2

a Plot of critical–stable curve for (3), with $\xi =0.1, \varOmega =1, \tau =1.628$. b Zoom around origin of plot given in a

Fig. 3

a Plot of critical–stable curve for (3), with $\xi =-10, \varOmega =1, \tau =0.1$. b Zoom around origin of plot given in a

4 Determination of optimal gains within unique stable region $S_0$

The key idea in finding the OFGs is to shrink the stable region by repeated use of critical $\sigma$-stable curves, defined by the plot of $p(\sigma +\mathrm{i}\omega )=0$ with a fixed $\sigma <0$.

When $\omega =0$, $p(\sigma )=0$ defines a line $\tilde{L}_{\sigma }$ passing through the start point $(p_{\mathrm{s}}, d_{\mathrm{s}})$, with the slope $-\frac{1}{\sigma }$. When $\omega \ne 0$, solving $k_{\mathrm{p}}$ and $k_{\mathrm{d}}$ from the critical conditions $\mathfrak {R}(p(\sigma +\mathrm{i}\omega ))=0, \mathfrak {I}(p(\sigma +\mathrm{i}\omega ))=0$ gives

$$\begin{aligned} \begin{aligned} k_{\mathrm{p}}&=\frac{\mathrm{e}^{\sigma \tau }}{\omega }\left[ \sin (\omega \tau )\sigma ^{3} +\left( 2\xi \varOmega \sin (\omega \tau )+\omega \cos (\omega \tau )\right) \sigma ^{2}\right. \\&\quad \,+\left( \omega ^{2}-\varOmega ^{2}\right) \sin (\omega \tau )\sigma +2\xi \varOmega \omega ^{2}\sin (\omega \tau )\\&\left. \quad +\,(\omega ^{2}+\varOmega ^2)\omega \cos (\omega \tau )\right] , \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} k_{\mathrm{d}}=&\frac{\mathrm{e}^{\sigma \tau }}{\omega }\left[ -\sin (\omega \tau )\sigma ^{2} -2\left( \xi \varOmega \sin (\omega \tau )+\omega \cos (\omega \tau )\right) \sigma \right. \\&\left. \quad +\,\left( \omega ^{2}+\varOmega ^2\right) \sin (\omega \tau )-2\xi \varOmega \omega \cos (\omega \tau )\right] , \end{aligned} \end{aligned}$$

(24)

which defines a curve, denoted by $L_{\sigma }$, as $\omega$ increases from 0 to +$\infty$. Let

$$\begin{aligned} \begin{aligned} p_{\mathrm{s}}&=\lim _{\omega \rightarrow 0}k_{\mathrm{p}}=\mathrm{e}^{\sigma \tau }\left( \tau \sigma ^{3}+\left( 2\xi \varOmega \tau +1\right) \sigma ^{2} -\varOmega ^2\tau \sigma +\varOmega ^{2}\right) ,\\ d_{\mathrm{s}}&=\lim _{\omega \rightarrow 0}k_{\mathrm{d}}=\mathrm{e}^{\tau \sigma }\left( -\tau \sigma ^{2}-2(\xi \varOmega \tau +1)\sigma +\varOmega ^{2}\tau -2\xi \varOmega \right) . \end{aligned} \end{aligned}$$

(25)

4.1 Sufficient condition for existence of $\sigma$-stable region

The critical conditions $\mathfrak {R}(p(\sigma +\mathrm{i}\omega ))=0$ and $\mathfrak {I}(p(\sigma +\mathrm{i}\omega ))=0$ can be written as

$$\begin{aligned}&\left[ \begin{array}{cc} \cos (\omega \tau ) &{}\quad \sin (\omega \tau )\\ -\sin (\omega \tau ) &{}\quad \cos (\omega \tau ) \end{array} \right] \left[ \begin{array}{c} k_{\mathrm{p}}+{k_\mathrm{d}}\sigma \\ k_{\mathrm{d}}\omega \end{array} \right] \nonumber \\&\quad =\mathrm{e}^{\sigma \tau } \left[ \begin{array}{l} \varOmega ^{2}+\omega ^{2}-\sigma ^2-2\xi \varOmega \sigma \\ -2\omega (\sigma +\xi \varOmega ) \end{array} \right] , \end{aligned}$$

(26)

which holds only if $F_{\sigma }(\omega )=0$, where $F_{\sigma }(\omega )=\omega ^{4}+\alpha _{\sigma }\omega ^{2}+\beta _{\sigma }$, with $\alpha _{\sigma }=-\mathrm{e}^{-2\sigma \tau }k_\mathrm{d}^2+\sigma ^2+2\varOmega ^2+(2\varOmega \xi +\sigma )^2, \beta _{\sigma }=-\mathrm{e}^{-2\sigma \tau }(k_\mathrm{d}\sigma +k_\mathrm{p})^2+(-2\xi \varOmega \sigma +\varOmega ^2-\sigma ^2)^2$. $F_{\sigma }(\omega )=0$ has two positive real roots, namely, the critical $\sigma$-stable curve $L_{\sigma }$ intersects with itself if and only if

$$\begin{aligned} \alpha _{\sigma }<0,\quad \beta _{\sigma }>0,\quad \alpha _{\sigma }^{2}-4\beta _{\sigma }>0. \end{aligned}$$

(27)

Obviously, when $\beta _{\sigma }<0$, or $\alpha _{\sigma }>0$, $F_{\sigma }(\omega )=0$ does not have two different positive real roots, namely, the critical $\sigma$-stable curve $L_{\sigma }$ does not intersect with itself. The latter case, with $\alpha _{\sigma }>0$, defines a parallelogram $M_{\sigma }$ in the $(k_\mathrm{p}, k_\mathrm{d})$-plane. $L_{\sigma }$ cannot pass through $M_{\sigma }$.

Let $S_{\sigma }$ be the $\sigma$-stable region, where the real part of each root of $p(\lambda )=0$ is less than $\sigma$; then $S_{a}$ must be contained in $S_{b}$ if both $S_a$ and $S_b$ exist, and $a<b$.

On the line $\tilde{L}_{\sigma }$, one has

$$\begin{aligned} \begin{aligned} s_\sigma&=\mathrm{sgn}\left( \frac{\mathrm{d}\lambda }{\mathrm{d}k_\mathrm{p}}\right) =\mathrm{sgn}\left( \left( \frac{\mathrm{d}k_\mathrm{p}}{\mathrm{d}\lambda }\right) ^{-1}\right) \\&=\mathrm{sgn}\left( -2\xi \varOmega \tau \sigma +\varOmega ^2\tau -\sigma ^2\tau -2\xi \varOmega -2\sigma -k_\mathrm{d}\right) \\&=\mathrm{sgn}(d_\mathrm{s}-k_\mathrm{d}). \end{aligned} \end{aligned}$$

(28)

Thus, if the start point $(p_\mathrm{s}, d_\mathrm{s})$ is on the right boundary of $\tilde{M_\sigma }$, then $S_\sigma$ is not empty.

The vertical ordinates of the upper right endpoint and start point are $q_1=\mathrm{e}^{\sigma \tau }\sqrt{(2\xi \varOmega +\sigma )^2+2\varOmega ^2+\sigma ^2}$ and $q_2=\mathrm{e}^{\sigma \tau }(-2\xi \varOmega \tau \sigma +\varOmega ^2\tau -\tau -\xi \varOmega -2\sigma )$, respectively. Let $G=\mathrm{sgn}(q_1^2-q_2^2)$, and let

$$\begin{aligned} \varDelta _{\sigma }=\tau ^2\sigma ^2+\left( 2\varOmega \tau ^2\xi +4\tau \right) \sigma -\tau ^2\varOmega ^2+4\xi \tau \varOmega +2, \end{aligned}$$

which has two roots with respect to $\sigma$ as follows:

$$\begin{aligned} \tilde{\sigma }_1&=\frac{-\xi \varOmega \tau -2 +\sqrt{\xi ^{2}\varOmega ^{2}\tau ^{2}+\varOmega ^{2}\tau ^{2}+2}}{\tau },\\ \tilde{\sigma }_2&=\frac{-\xi \varOmega \tau -2-\sqrt{\xi ^{2}\varOmega ^{2}\tau ^{2} +\varOmega ^{2}\tau ^{2}+2}}{\tau }. \end{aligned}$$

Then $G=\mathrm{sgn}((-2\varOmega \sigma \xi +\varOmega ^2-\sigma ^2)\varDelta _{\sigma })$. The start point is on the boundary of $M_\sigma$ if and only if $G=1$.

The region $M_{\sigma }$ is defined by

$$\begin{aligned} \begin{aligned}&(k_\mathrm{d})^2<2\mathrm{e}^{2\sigma \tau }\left( \varOmega ^2+(\varOmega \xi +\sigma )^2\right) ,\\&(k_\mathrm{d}\sigma +k_\mathrm{p})^2<\mathrm{e}^{2\sigma \tau }\left( -2\xi \varOmega \sigma +\varOmega ^2-\sigma ^2\right) ^2. \end{aligned} \end{aligned}$$

(29)

When $-2\xi \varOmega \sigma +\varOmega ^2-\sigma ^2=0$, the second inequality gives $k_\mathrm{d}\sigma +k_\mathrm{p}=0$; thus, $M_{\sigma }$ is reduced to a straight line passing through the origin. But when $-2\xi \varOmega \sigma +\varOmega ^2-\sigma ^2>0$, $M_{\sigma }$ always has exactly one $\sigma$-unstable root. Using the method of stability switch, the $\sigma$-stable region $S_\sigma$ exists if $-2\xi \varOmega \sigma +\varOmega ^2-\sigma ^2>0, G=1$ and $\sigma <0$, namely,

$$\begin{aligned}&\mathrm{max}\left\{ \tilde{\sigma }_1,\quad \mathrm{min}\left\{ -\xi -\varOmega \sqrt{\xi ^2+1},-\xi +\varOmega \sqrt{\xi ^2+1}\right\} \right\} \nonumber \\&\quad<\sigma <0. \end{aligned}$$

(30)

4.2 Optimal feedback gains

Condition (30) is not a necessary condition. To find a necessary condition, let us first calculate the slope of $L_{\sigma }$ when $\omega$ approaches zero as follows

$$\begin{aligned} \lim _{\omega \rightarrow 0}\frac{\mathrm{d}k_\mathrm{d}}{\mathrm{d}\omega } =\frac{A_\sigma }{B_\sigma }, \end{aligned}$$

where $A_\sigma =\tau [-\tau ^2\sigma ^2+(-2\varOmega \tau ^2\xi -6\tau )\sigma +\tau ^2\varOmega ^2-6\xi \tau \varOmega -6]$, $B_\sigma =-\tau ^3\sigma ^3+(-2\xi \varOmega \tau ^3-3\tau ^2)\sigma ^2+(\varOmega ^2\tau ^3+6\tau )\sigma -3\varOmega ^2\tau ^2+12\xi \varOmega \tau +6$. Hence, $S_c$ ($c<0$) exists in $S_0$ only if at the start point, with $\sigma \in (c, 0)$, the slope of $\tilde{L}_\sigma$ is greater than $L_\sigma$, namely,

$$\begin{aligned} \mathrm{sgn}\left( -\frac{1}{\sigma }-\frac{A_\sigma }{B_\sigma }\right) =\mathrm{sgn}\left( -\frac{\sigma A_\sigma +B_\sigma }{\sigma B_\sigma }\right) =\mathrm{sgn}\left( \frac{\varDelta _\sigma }{B_\sigma }\right) =1, \end{aligned}$$

(31)

for all $\sigma \in (c, 0)$. When $\varDelta _0>0$, assume that $b_1$ and $b_2$ ($b_2<b_1$) are the two negative real roots of $B_\sigma$; then $b_2<\tilde{\sigma }_2^*<b_1<\tilde{\sigma }_1^*<0$.

In fact, substituting $\xi \varOmega \tau =\frac{\varDelta _0+\varOmega ^2\tau ^2-2}{4}$ into $B_\sigma$, $\tilde{\sigma }_1^*$, and $\tilde{\sigma }_2^*$ leads to

$$\begin{aligned} B_\sigma= & {} -\tau ^3\sigma ^3-\left( 2+\frac{1}{2}\varOmega ^2\tau ^2 +\frac{1}{2}\varDelta _0\right) \sigma ^2\tau ^2 \\&+\,\left( \varOmega ^2\tau ^2+6\right) \sigma \tau +3\varDelta _0,\\ \tilde{\sigma }_1^*= & {} \frac{-\frac{1}{4}\varOmega ^2\tau ^2 -\frac{1}{4}\varDelta _0-\frac{2}{3}+\frac{1}{4}\sqrt{a}}{\tau },\\ \tilde{\sigma }_2^*= & {} \frac{-\frac{1}{4}\varOmega ^2\tau ^2 -\frac{1}{4}\varDelta _0-\frac{2}{3}-\frac{1}{4}\sqrt{a}}{\tau }, \end{aligned}$$

where $a=\varOmega ^4\tau ^4+2\varDelta _0\varOmega ^2\tau ^2+(\varDelta _0-2)^2+32>0$. Let $c_1=\frac{1}{8}\varDelta _0+\frac{1}{8}\varOmega ^2\tau ^2+\frac{3}{4}, c_2=-\frac{1}{8}{\varDelta _0}^2+(\frac{1}{2}-\frac{1}{4}\varOmega ^2\tau ^2)\varDelta _0-\frac{1}{8}\varOmega ^4\tau ^4-\frac{3}{2}\tau ^2\varOmega ^2-\frac{9}{2}$. Because $B_{\tilde{\sigma }_1^*}=c_1\sqrt{a}+c_2, B_{\tilde{\sigma }_2^*}=-c_1\sqrt{a}+c_2$ and $c_1^2a-c_2^2=(4\varOmega ^2\tau ^2\xi ^2+4\varOmega ^2\tau ^2+8)\varDelta _0>0$, one has $B_{\tilde{\sigma }_1^*}>0$ and $B_{\tilde{\sigma }_2^*}<0$. Moreover, $\lim _{\sigma \rightarrow -\infty }B_{\sigma }>0, B_0=3\varDelta _0>0$ and $\lim _{\sigma \rightarrow +\infty }B_{\sigma }<0$, according to the Zero Theorem, the roots of the cubic polynomial $B_{\sigma }$ must be located in the three intervals $(-\infty ,\tilde{\sigma }_2^*)$, $(\tilde{\sigma }_2^*, \tilde{\sigma }_1^*)$, and $(0, +\infty )$. Thus, $b_2<\tilde{\sigma }_2^*<b_1<\tilde{\sigma }_1^*<0$. It follows that Eq. (31) is true only if $\sigma \in (\tilde{\sigma }_1^*,0)$. When $\sigma =\tilde{\sigma }_1^*$, tangency occurs, and $S_\sigma$ disappears entirely. As a result, the minimum of $\sigma _1$ is $\tilde{\sigma }_1^*$, which represents the minimum of the real part of the rightmost characteristic roots in Eq. (4). Substituting the value of $\sigma ^*$ above into Eq. (25), the corresponding value of $(p_{\mathrm{s}}, d_{\mathrm{s}})$ is optimal in the sense that the solution of Eq. (25) decays at the fastest speed.

Remark

The maximal real part of the optimal selection $\sigma ^*$ is a repeated root. Set $k_\mathrm{p}=k_\mathrm{p}^*, k_\mathrm{d}=k_\mathrm{d}^*$; then the derivatives of Eq. (4) at $\lambda =\sigma ^*$ are found to be

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}p(\lambda )}{\mathrm{d}\lambda }=0,\quad \frac{\mathrm{d^2}p(\lambda )}{\mathrm{d}\lambda ^2}=0, \quad \frac{\mathrm{d^3}p(\lambda )}{\mathrm{d}\lambda ^3}=0, \quad \frac{\mathrm{d^4}p(\lambda )}{\mathrm{d}\lambda ^4}>0. \end{aligned} \end{aligned}$$

(32)

Hence, $\lambda =\sigma ^*$ is a triple root of $p(\lambda )=0$.

5 Illustrative examples

Example 1

We consider the equation used for modeling human balance in Ref. [36]:

$$\begin{aligned} I\ddot{x}-mgh\sin (x)=u, \end{aligned}$$

where I is the moment of inertia of the human body around the ankle, x is the tilt angle, m is the body mass, g is the gravity acceleration, h is the distance from the ankle joint to the body center of mass, u is the ankle torque, and $I=60, m=60, g=9.81, h=1$. With $u(t)=-Kx(t-\tau )-D\dot{x}(t-\tau )$, the closed loop reads

$$\begin{aligned} \ddot{x}(t)-\varOmega ^2\sin (x(t))=-k_{\mathrm{p}}x(t-\tau )-k_{\mathrm{d}}\dot{x}(t-\tau ), \end{aligned}$$

(33)

where $\varOmega ^2=\frac{mg}{I}=9.81, \tau =0.1, k_\mathrm{p}=\frac{K}{I}$, and $k_\mathrm{d}=\frac{D}{I}$. Linearizing the nonlinear controlled system gives a retarded delay differential equation

$$\begin{aligned} \ddot{x}(t)-\varOmega ^2x(t)=-k_{\mathrm{p}}x(t-\tau )-k_{\mathrm{d}}\dot{x}(t-\tau ). \end{aligned}$$

(34)

Figure 4a shows the plots of $S_\sigma$ with different values of $\sigma$, where the largest region is the stable region $S_0$. As $\sigma$ decreases, $S_\sigma$ shrinks and finally disappears entirely at $\sigma _1\approx -0.5515$. Figure 4b shows how $S_\sigma$ disappears, where the integers denote the number of $\sigma _1^*$-unstable roots in each closed region and the gray parallelogram represents $M_{\sigma _1^*}$. Therefore, the critical value $\sigma _1^*$ is the minimal real part of the rightmost characteristic roots. Accordingly, the OFGs are $k_\mathrm{p}^*\approx 16.626$, $k_\mathrm{d}^*\approx 5.167$.

To check the results, the time histories are given in Figs. 5 and 6 for linear system (34) and nonlinear system (33), respectively, where the solutions are calculated using MATLAB code dde23, under two initial conditions: $x(t)=-1, \dot{x}(t)=1$ or $x(t)=1, \dot{x}(t)=1$ for $t\in [-\tau , 0]$. The controller with OFGs stabilizes the two systems at the fastest speed.

Fig. 4

a Plots of $\sigma$-critical stable curves with $\xi =0, \varOmega ^2=9.81, \tau =0.1$. b Zoom around start point for case $\sigma =\sigma _1^*\approx -5.515$, where tangency occurs and $S_{\sigma _1^*}$ disappears entirely

Fig. 5

Time histories of linear system (34) and nonlinear system (33) with $\varOmega ^2=9.81, \tau =0.1$ and under the first initial condition, for different feedback gains $k_\mathrm{p}$ and $k_\mathrm{d}$. OFG represents $k_\mathrm{p}^*\approx 16.626$, $k_\mathrm{d}^*\approx 5.167$. a Displacement of linear system. b Displacement of nonlinear system

Fig. 6

Time histories of linear system (34) and nonlinear system (33) with $\varOmega ^2=9.81, \tau =0.1$ and under the second initial condition, for different feedback gains $k_\mathrm{p}$ and $k_\mathrm{d}$. OFG represents $k_\mathrm{p}^*\approx 16.626,\, k_\mathrm{d}^*\approx 5.167$. a Displacement of linear system. b Displacement of nonlinear system

Example 2

We include a small damping in the controlled inverted pendulum

$$\begin{aligned} \ddot{x}(t)+2\xi \varOmega \dot{x}(t)-\varOmega ^2\sin (x(t)) =-k_\mathrm{p}x(t-\tau )-k_\mathrm{d}\dot{x}(t-\tau ), \end{aligned}$$

(35)

where $\xi =0.1, \varOmega =6, \tau =0.1$. Equation (3) is the linearized form of this system.

The plots of $S_\sigma$ are presented in Fig. 7a, which is similar to Fig. 4a. However, the position of $M_{\sigma }$ is different in Fig. 7b. Actually, as stated in Sect. 4, the number of $\sigma$-unstable roots of $M_{\sigma }$ can be one or two. In Example 1, one has $\sigma _1^*\approx -5.515$ and

$$\begin{aligned} \min \left\{ -\xi +\varOmega \sqrt{\xi ^2+1},\quad -\xi -\varOmega \sqrt{\xi ^2+1}\right\} \approx -3.13>\sigma _1^*. \end{aligned}$$

Thus, $M_{\sigma }$ is to the right of $\tilde{L}_{\sigma }$ and has two $\sigma$-unstable roots. In this example, it goes to $\sigma _1^*\approx -5.226$ and

$$\begin{aligned} \min \left\{ -\xi +\varOmega \sqrt{\xi ^2+1},\quad -\xi -\varOmega \sqrt{\xi ^2+1}\right\} \approx -6.13<\sigma _1^*. \end{aligned}$$

Thus, $M_{\sigma }$ is to the left of $\tilde{L}_{\sigma }$, which has only one $\sigma$-unstable root. The time histories of linear and nonlinear systems with feedback gains are shown in Figs. 8 and 9, where, again, the OFG decays to 0 at the fastest speed compared with others. Moreover, by observing the eight charts of the time history, we notice that the OFG in a nonlinear system takes less time to decay than in a linear system.

Fig. 7

a Plots of $\sigma$-critical stable curves for $\xi =0.1, \varOmega =6, \tau =0.1$. b Zoom around start point for the case $\sigma =\sigma _1^*\approx -5.226$, where tangency occurs and $S_{\sigma _1^*}$ disappears entirely

Fig. 8

Time histories of linear system (3) and nonlinear system (35), with $\xi =0.1, \varOmega =6, \tau =0.1$, under the first initial condition, for different feedback gains $k_\mathrm{p}$ and $k_\mathrm{d}$. OFG represents $k_\mathrm{p}^*\approx 42.178, k_\mathrm{d}^*\approx 6.373$. a Displacement of linear system. b Displacement of nonlinear system

Fig. 9

Time histories of linear system (3) and nonlinear system (35), with $\xi =0.1, \varOmega =6, \tau =0.1$, under second initial condition, for different feedback gains $k_\mathrm{p}$ and $k_\mathrm{d}$. OFG represents $k_\mathrm{p}^*\approx 42.178, k_\mathrm{d}^*\approx 6.373$. a Displacement of linear system. b Displacement of nonlinear system

6 Conclusion

Stability analysis of an inverted pendulum with a delayed PD controller is not a new problem; it has been studied by many researchers. Unlike previous studies, which address mainly stable regions or stable delay intervals, this paper presents a systematic approach to finding OFGs that minimize the real part of rightmost characteristic roots within a unique stable region, and the optimal gains make the open-loop system stable at the fastest speed. One key step is to determine when the boundary of the $\sigma$-stable region will disappear as $\sigma$ varies. One major feature of this paper is that OFGs are expressed in an explicit and simple formula in closed form and can be used directly in applications, as demonstrated in human balancing problems under delayed PD control. Theoretically, the proposed procedure for finding the OFGs works also for other systems with delayed feedback.