1 Introduction

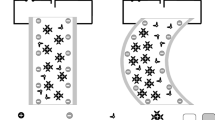
Ionic polymer–metal composite (IPMC) is an electrically actuated functional material. An IPMC actuator is generally composed of a layer of ionic exchange membrane (e.g., Nafion, Flemion, and Aciplex) plated with noble metal electrodes [1,2,3,4,5]. In the free state, the hydrated cations inside an IPMC are distributed uniformly within the membrane. When applied with an electric field, the hydrated cations are forced to move toward the cathode, thereby causing the IPMC to bend in the anode direction [6,7,8,9,10]. This actuation process is schematically shown in Fig. 1. IPMC actuators have many inherent advantages, such as low excitation voltage, low mass, large strain, flexibility, fast response, and simple design compared to traditional actuators [11,12,13]. Because of these attractive characteristics, a wide range of industrial and medical applications has been achieved [13, 14], for example, flapping wings [15], grippers [16, 17], fishlike robots [18,19,20], artificial muscles [21], and biomedical devices [22].

The behavior of IPMC actuators exhibits coupling among three physical properties: electrical, chemical, and mechanical. In recent decades, considerable efforts have been devoted to developing models for predicting the deformation behavior of IPMC actuators under excitation voltages. These models can be classified into three categories, black [23,24,25], gray [12, 26,27,28,29], and white [6, 7, 30, 31] box models.

Fig. 1
figure 1

a Schematic diagram of actuation principle of IPMC. b Deformation image of IPMC cantilever actuator under voltage

Full size image

For simplification, many models did not take into account the large bending deformation of IPMC actuators. However, IPMC actuators in functional devices often experience large nonlinear deformation. Kothera and Leo [32] experimentally studied the harmonic distortion arising in actuation responses of IPMC actuators using solvents with different properties; they chose Volterra series as an identification technique to extract information about the nonlinearities. Bonomo et al. [26] proposed a lumped nonlinear circuit model to describe the dependence of absorbed currents on the voltage applied across the thickness of IPMCs and a linear transduction of the current into mechanical reactions to predict the dynamic behavior of IPMC actuators. Anto et al. [33] presented a mechanical model of IPMC cantilever actuators with electrically induced bending moments to explain large bending deflections. Alici [34] introduced an equivalent modeling method to illustrate the large nonlinear bending deformation of cantilever polymer actuators based on the Euler–Bernoulli beam theory. Using the model introduced by Bonomo, Vahabi et al. [27] proposed a parametric identification approach using linear and nonlinear least square methods for the nonlinear relationship between the absorbed current and the applied voltage and the linear relationship between the absorbed current and the blocking force of IPMC actuator. Based on a nonlinear autoregressive exogenous (NARX) model and a particle swarm optimization (PSO) method, Nam and Ahn [35] developed a nonlinear black-box model for IPMC actuators to identify nonlinearities. Annabestani and Naghavi [24] presented a dynamic nonlinear black-box model to describe the displacement features of IPMC actuators using a combination of an adaptive neuro fuzzy inference system (ANFIS) and a NARX structure. Truong and Ahn [25] developed an innovative and accurate nonlinear black-box model via a general multilayer perceptron neural network (GMLPNN) integrated with a smart learning mechanism (SLM) based on a self-decoupling extended Kalman filter to predict the bending behavior of IPMC actuators. Caponetto et al. [29] characterized IPMC nonlinearities and proposed an improved electromechanical gray-box model via single-objective and multiobjective optimization algorithms. Most of these models considered a uniform curvature of an IPMC.

However, the imperfect electrical conductivity of metallic electrodes leads to a decrease in the electric field applied to an IPMC actuator along the longitudinal direction and causes a nonuniform bending curvature of the IPMC actuator. Annabestani and Naghavi [36] first identified the nonuniform curvature of IPMC actuators using ANFIS-NARX model. Punning et al. [37] developed a technique to describe the bending strain of IPMC actuators using a digital image correlation (DIC) method [38] and revealed the nonuniform bending curvature of IPMC actuators.

A distributed equivalent electrical circuit is very useful for describing the electric properties of IPMC actuators. An IPMC strip was divided into ten segments consisting of resistor-capacitor (RC) circuits by Kanno et al. [39], and a distributed RC model was first proposed. Punning et al. [40] developed the model using RC transmission line theory by dividing the IPMC piece into an infinite number of infinitesimally short similar segments. Moeinkhah et al. [12] used RC transmission line theory to derive an analytical impedance and actuation model based on a similar distributed RC electric circuit.

In this study, the standard Onsager formulation based on linear irreversible thermodynamics [6] was used to describe actuation phenomena and predict the deformation of a unit part of IPMC actuators, and the difference in the resistances of the two electrodes caused by the bending curvature of the actuator was investigated experimentally and theoretically. The distributed electrical model considering the influence of the bending deformation was presented to analyze the effect of voltage on the actuator. Finally, an analytical solution was obtained to illustrate the large nonlinear deformation behavior of the actuators.

2 Materials and experimental procedures

2.1 Sample preparation

Materials. Nafion 117 (DuPont, Wilmington, DE, USA); dimethyl sulfoxide (DMSO, Shanghai Shiyi Chemical Reagent Co., Shanghai, China); tetrammineplatinum (II) chloride \((\hbox {Pt}[\hbox {NH}_{3}]_{4}\hbox {Cl}_{2}\), Shanghai Jiuyue Chemical Co., Shanghai, China); sodium borohydride, glucose, hydrazine hydrate \((\hbox {NaBH}_{4}, \hbox {N}_{2}\hbox {H}_{4}.\hbox {H}_{2}\hbox {O}\), and \(\hbox {C}_{6}\hbox {H}_{12}\hbox {O}_{6}\) (Sinopharm Chemical Reagent Co., Shanghai, China); ammonium hydroxide, sulfuric acid, hydrochloric acid, sodium hydroxide, and silver nitrate \((\hbox {NH}_{3}.\hbox {H}_{2}\hbox {O}, \hbox {HCl}, \hbox {H}_{2}\hbox {SO}_{4}, \hbox {NaOH}\), and \(\hbox {AgNO}_{3}\), Nanjing Chemical Reagent Co., Nanjing City, China).

Fig. 2
figure 2

SEM micrographs of IPMC sample. a Surface. b Cross-sectional images of Pt-IPMC sample. c Surface. d Cross-sectional images of Ag-IPMC sample

Full size image

Pretreatment of Nafion 117 membrane. Strips of Nafion 117 were roughened with a metallographic sandpaper (W10). They were then cleaned by ultrasonic irradiation for 10 min, boiling 2  mol/L\(^{-1}\) HCL for 1 h, and deionized water consecutively [3, 5, 13].

Preparation of Pt electrodes. One of the pretreated strips was soaked in 0.1  mol/ L\(^{-1}\) \(\hbox {H}_{2}\hbox {SO}_{4}\) solution for 30  min and then in 0.01 mol/L\(^{-1}\) \(\hbox {Pt}(\hbox {NH}_{3})_{4}\hbox {Cl}_{2 }\) solution for 14 h to perform the ion-exchanging process at room temperature. Finally, Pt-IPMC was produced through two-step reduction. The first reduction step was conducted using \(\hbox {NaBH}_{4}\) as the reducing agent, and the second reduction step (or electrode development) was performed with \(\hbox {N}_{2}\hbox {H}_{4 }\) as the reducing agent [3, 5].

Preparation of Ag electrodes. One of the pretreated strips was soaked in 0.25 mol/L\(^{-1}\) NaOH solution for 30  min and then in 0.03 mol/L\(^{-1}\) \(\hbox {Ag}(\hbox {NH}_{3})_{2}\hbox {OH}\) solution for 14 h at room temperature. Ag electrodes were manufactured using silver mirror reaction [41].

Ion exchange. All IPMC samples were placed in 1 mol/ L\(^{-1}\) NaCl solution for 24 h to perform the ion-exchanging process and form samples containing \(\hbox {Na}^{+}\) cations at room temperature.

Figure 2 shows surface and cross-sectional scanning electron microscope (SEM) micrographs of the fabricated IPMC samples. Note that Pt and Ag particles are both uniformly distributed. The Ag electrode is thicker than the Pt electrode. However, more apparent cracks were generated in the Ag electrode.

2.2 Experimental setup

2.2.1 Testing of surface electrode resistances

Surface electrode resistances depend on the contact areas of the metal particles [42]. In IPMC cantilever actuators bent under excitation voltages, the cathode side is stretched, and the anode side is compressed, according to Euler–Bernoulli beam theory. This leads to different changes in the resistance of the two surface electrodes of the IPMC actuators. We investigated the influences of the curvature on the resistances of both surface electrodes of IPMC actuators.

As shown in Fig. 3, a series of poly(methyl methacrylate) (PMMA) tubes with different radii (0–80 mm) were used to produce corresponding curvatures of the IPMC actuators, and the resistances of the two surface electrodes were measured using an ST-2258C multifunction digital four-probe tester. The Young’s modulus and the thickness of the PMMA tubes were approximately 3000 MPa and 2 mm, respectively, while those of the IPMC sample were approximately 100 MPa and 0.8 mm, respectively. Therefore, the flexural rigidity of the PMMA segment was much larger than that of the IPMC sample, and the influence of the IPMC sample on PMMA segments was neglected.

2.2.2 Measurement of deflection curves

To analyze the characteristics of the bending deformation of the IPMC actuators and verify the validation of the model presented in the following sections, the deflection curves of the IPMC actuators under excitation voltages were tested using a two-dimensional (2D) laser displacement sensor (Gocator 2330, LMI Technologies, Vancouver, BC, Canada).

The experimental setup is schematically shown in Fig. 4. An Agilent Technologies (Santa Clara, CA) E3631A direct-current (DC) power supply was used to provide excitation to the IPMC actuator samples. A 2D laser displacement sensor, the LMI Gocator 2330, was used to measure the deflection curves of the actuators over the entire cantilever beam length, not only the tip displacements of the actuators. The LMI Gocator 2330 has 1280 pixels and a maximum measurement range of 80 mm. The field of view (FOV) of this sensor can be adjusted to between 47 and 85 mm. Depending on the selected FOV, the resolution of the sensor in the x-direction varies between 0.044 and 0.075 mm, while that in the z-direction ranges from 0.006 to 0.014 mm.

Fig. 3
figure 3

Experimental configuration to measure resistances of surface electrodes of IPMC actuators with different curvatures

Full size image
Fig. 4
figure 4

Schematic representation of experimental configuration to measure bending deflection curves of IPMC actuators

Full size image

All the samples were cut into \(34 \ \times 4~\hbox {mm}\) strips. The effective length of the cantilever beam actuators when clamped (between two Ag electrodes) was approximately 24 mm. The specifications of the IPMC samples are listed in Table 1. All samples were hydrated, and all measurements of the deflection curves were carried out in air at room temperature.

2.3 Results analysis

2.3.1 Influence of curvature of IPMC actuators on surface electrode resistance

Figure 5 shows the dependence of the surface electrode resistances on the curvatures of the IPMC actuators with Pt electrodes. The testing results reveal that the surface resistance of the anode electrode of the IPMC actuators decreases, while that of the cathode electrode and the difference between the resistances of the two electrodes increase with increasing curvature. A similar result was also obtained by Punning et al. [42]. The surface resistance of the cathode electrode (9.30 \(\Omega \cdot \hbox {cm}^{-1}\)) is approximately 1.3 times that of the anode electrode (7.20 \(\Omega \cdot \hbox {cm}^{-1}\)) when the curvature is 12.5 \(\hbox {m}^{-1}\). When the curvature reaches approximately 35 \(\hbox {m}^{-1}\), the value of the former (11.93 \(\Omega \cdot \hbox {cm}^{-1}\)) is approximately 2.38 times that of the latter (5.02 \(\Omega \cdot \hbox {cm}^{-1}\)). Obviously, the difference between the resistances of the two electrodes cannot be neglected when the strip is bent.

Table 1 Specifications of IPMC samples
Full size table
Fig. 5
figure 5

Dependence of surface resistances of two electrodes on curvature of IPMC actuators

Full size image

The surface electrode resistances can be expressed as functions of the curvatures of the IPMC sample by linearly fitting the experimental data,

$$\begin{aligned} \begin{array}{l} R_{sa} =8.19-0.084(1/\rho ), \\ R_{sb} =8.50+0.095(1/\rho ), \\ \end{array} \end{aligned}$$
(1)

where \(R_{sa}\) and \(R_{sb}\) are the surface electrode resistances of the anode and cathode of the IPMC sample, respectively, and \(1/\rho \) is the curvature.

2.3.2 Bending deformation of IPMC actuators

The typical bending deformation behavior of an IPMC cantilever actuator is shown in Fig. 1b. When excitation voltage is applied across the electrodes, but no other external load is involved, the IPMC cantilever actuator demonstrates significant nonlinear bending deformation toward the anode. In this case, no torsional deformation exists. Regardless of the shear and axial deformations, the deflection of the IPMC cantilever actuator can be treated as a large geometric nonlinear deformation. The geometric structure and deformation of the IPMC actuator are assumed to be longitudinally symmetric, and its thickness is sufficiently small compared to its length. In this event, the longitudinal axis or any line parallel to it can be used to represent the structure of the IPMC actuator for analyzing its deformation.

Figure 6a shows a three-dimensional (3D) graph of deflections versus position and time of the Pt-IPMC cantilever actuator (measured by the equipment shown in Fig. 4) under 2 V DC voltage. It shows that the deflection of the actuator is not stable under DC voltage. A back relaxation of the IPMC actuator occurs after the maximum deflection is reached. Figure 6b shows the time-dependent tip displacements of the actuator. It is apparent from Fig. 6b that the deformation of the actuator can be divided into three stages: I (fast deformable stage, 0–2.54 s), II (stable stage, 2.54–6.10 s), and III (back relaxation stage, 6.10 s). The deformation reaches its maximum at 4.12 s, and the deflections of the demarcation points of the three stages represent 95% of the maximum deflection. The back relaxation of the actuator has been studied by several researchers and can be avoided when a current driving signal is applied [31, 43]. However, the main purpose of this article is to try to describe the whole nonlinear deflection curve of IPMC cantilever actuators analytically considering the electrical and mechanical properties of IPMC, not the deformation process of the actuator. In this case, the maximum deflection curves of the actuator under DC excitation voltages were examined in this study.

The maximum deflection curve of the actuator is shown in Fig. 6c. All the deflection curves studied in this paper are the maximum deflection curves of the IPMC cantilever actuators under different DC excitation voltages.

Fig. 6
figure 6

Measured deformation of Pt-IPMC Actuator under 2 V excitation voltage. a 3D graph of deflections versus position and time. b Tip deflection versus time. c Maximum deflection curve (4.12 s)

Full size image

3 Electromechanical model

3.1 Geometric model

A schematic diagram and the coordination system of the actuator are presented in Fig. 7, where l is the length, \(1/\rho \) and \(\theta \) represent respectively the curvature and deflection angle at coordinate s, and W and \(\theta _{0}\) are the deflection and rotational angles at the free end, respectively. The geometric deformation relationship of the IPMC can be described as follows

$$\begin{aligned}&\sin \theta =\frac{\mathrm{d}w}{\mathrm{d}s}, \end{aligned}$$
(2)
$$\begin{aligned}&\cos \theta =\frac{\mathrm{d}x}{\mathrm{d}s}, \end{aligned}$$
(3)
$$\begin{aligned}&\frac{1}{\rho }=\frac{\mathrm{d}\theta }{\mathrm{d}s}. \end{aligned}$$
(4)

3.2 Actuation model

The relationship between the bending curvature of the IPMC actuator and external excitation voltage is necessary for analyzing the deformation of the IPMC actuator. De-Gennes et al. [6] proposed an irreversible thermodynamic model to describe the shift of hydrated cations inside IPMC actuators. In this model, a linear coupling equation between the electric field intensity E and osmotic pressure gradient \(\nabla p\) is presented (for details see Ref. [6]). With a constant excitation voltage U, the surface resistance of IPMC electrodes decreases the field intensity E starting from the clamped side and ending at the free end. Consequently, the bending deformation curvature also decreases from the clamped end to the free end.

Owing to the decrease in the voltage along the arc length (s) arising from the imperfect electric conductibility of the metallic electrodes of the IPMC sample, the irreversible thermodynamic model may not be accurate enough for the structural integral deformation of IPMC actuators. However, the model is very suitable for a small element cut out of IPMC. The curvature of a unit part of IPMC actuators could be considered uniform (Fig. 1a).

Fig. 7
figure 7

Geometric definitions of parameters of IPMC deformation and coordinate systems

Full size image
Fig. 8
figure 8

a Distributed RC model of IPMC actuator. b Equivalent single-unit circuit

Full size image

The deformation of a unit part of an IPMC actuator caused by excitation voltage or an osmotic pressure gradient \(\nabla p\) is elastic [6]. The bending curvature of the unit part is proportional to the electric field intensity E(s) or excitation voltage u(s) when the thickness of the IPMC is constant [31, 44]:

$$\begin{aligned} \frac{1}{\rho (s)}=\frac{L}{KY}E(s)=\frac{L}{KYh}u(s), \end{aligned}$$
(5)

where constant coefficient L is the Onsager coefficient, and K is the Darcy permeability of the Nafion 117 membrane, and Y and h are the Young’s modulus and thickness of the IPMC strip, respectively.

At the same time, the curvature affects the surface resistance of the IPMC electrodes, changing the electric field intensity E. Therefore, it is important to study the distribution of the electric field intensity E along the length (s) of IPMC actuators.

3.3 Distributed electrical model

To obtain the deflection curve equation of an IPMC actuator when it reaches its maximum deflection under a steady voltage, it is necessary to investigate the distribution of voltage along the length of the IPMC sample. However, the bending deformation curvature decreases from the clamped end to the free end. This inevitably causes variations in the surface electrode resistances along the arc coordinate (s). To improve the accuracy of the electromechanical model of the IPMC actuators, the effect of the variations of electrode resistances on the distributed electric circuit is examined.

Considering the effect of a bending deformation, the resulting distributed RC model can be described by a series of similar circuits distributed along the arc length (s) of the IPMC actuators (Fig. 8a). \(R_{sa}(s)\) and \(R_{sb}(s)\), the surface resistances per unit length of the anode and cathode electrodes respectively, can be expressed as functions of the arbitrary position s along the actuator’s axis by substituting Eq. (5) into Eq. (1). \(R_{2}\) is a shunt resistor between the surface electrodes in a single unit.

To simplify the analysis, the single-unit circuit shown in Fig. 8a was transferred to the equivalent single-unit circuit shown in Fig. 8b by replacing \(R_{s}(s)=R_{sa}(s)+R_{sb}(s)\). According to Eq. (1), \(R_{s}(s)=16.69+0.011(1/\rho )\). It is assumed that the sum of the two surface electrode resistances does not change with curvature. In other words, the value of \(R_{s}(s)\) can be assumed to be a fixed value along the s-direction \((R_{s}=16.69~\Omega \cdot \hbox {cm}^{-1})\).

All parameters in the equivalent circuit are defined per unit length along the s-coordinate and assumed to be time-invariant and uniform. Under a constant input voltage U, the deflection of the IPMC cantilever actuator reaches its maximum deformation owing to the maximum electric charge caused by ion movement in the polymer matrix. The capacitance C was charged completely in the equivalent circuit. It can be inferred from Fig. 8 that the distributed resistive network formed by \(R_{s}\) and \( R_{2}\) still works, but the \( R_{1}-C\) branch of the unit circuit no longer comes into play. The following relations can be obtained according to Kirchhoff’s and Ohm’s laws:

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}s}i(s)= & {} - i_2 (s), \end{aligned}$$
(6)
$$\begin{aligned} i_2 (s)= & {} R_2 u(s). \end{aligned}$$
(7)

The voltage drop on the unit segment is given by

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}s}u(s)=-R_s i(s). \end{aligned}$$
(8)

By first substituting Eqs. (6) and (7) into Eq. (8) and then applying a derivative operation to both sides of the equation, a differential equation that describes the distribution of voltages can be obtained:

$$\begin{aligned} \frac{\mathrm{d}^{2}}{\mathrm{d}s^{2}}u(s)=R_s R_2 (s). \end{aligned}$$
(9)

The general solution of Eq. (9) is \(u(s)=A\exp \left( {\sqrt{R_s R_2 }x} \right) +B\exp \left( {-\sqrt{R_s R_2 }x} \right) \). Based on the boundary conditions of the IPMC actuators \(u \vert _{s=0}=U\) and \(i \vert _{s=0}=0\), the following equation is derived:

$$\begin{aligned} u(s)=U\frac{\cosh \left( {\sqrt{R_s R_2 }(s-l)} \right) }{\cosh \left( {\sqrt{R_s R_2 }l} \right) }. \end{aligned}$$
(10)

A similar equation was given by Punning et al. [40].

By substituting Eqs. (3) and (10) into Eq. (5), the following curvature equation is obtained:

$$\begin{aligned} \frac{1}{\rho (s)}=\frac{\mathrm{d}\theta }{\mathrm{d}s}=aU\cosh \left( {b(s-l)} \right) , \end{aligned}$$
(11)

where \(a=\frac{L}{KYh\cosh (\sqrt{R_s R_2 }l)}\) and \(b=\sqrt{R_s R_2 }\). By integrating Eq. (11) and using the clamped boundary condition of \(\theta \vert _{s=0=0}\), a slope equation is derived:

Table 2 Parameters of Pt-IPMC sample
Full size table
$$\begin{aligned}&\theta =\frac{aU}{b}\left[ {\sinh \left( {bl} \right) +\sinh \left( {b(s-l)} \right) } \right] ,\quad s\in \left[ {0,l} \right] , \end{aligned}$$
(12)
$$\begin{aligned}&\theta _0 =\frac{aU}{b}\sinh (bl), \end{aligned}$$
(13)
$$\begin{aligned}&\begin{array}{l} \displaystyle x=\int _0^s {\cos \left\{ {\frac{aU}{b}\left[ {\sinh \left( {bl} \right) +\sinh \left( {b(s-l)} \right) } \right] } \right\} \hbox {d}s} , \\ \displaystyle w=\int _0^s {\sin \left\{ {\frac{aU}{b}\left[ {\sinh \left( {bl} \right) +\sinh \left( {b(s-l)} \right) } \right] } \right\} \hbox {d}s} , \\ \end{array} s\in \left[ {0,l} \right] .\nonumber \\ \end{aligned}$$
(14)

The analytical solutions to Eq. (14) are not easily obtained. Because its value is very small, the first item of its Taylor expansion, sinh(\(b(s-l))\), is replaced by \( b(s-l)\). Using the clamped boundary condition of \(x\vert _{s=0}=w \vert _{s=0}=0\), we obtain the expressions

$$\begin{aligned} x= & {} \frac{1}{aU}\left\{ {\sin \left[ {aU\left( {s-l+\frac{1}{b}\sinh (bl)} \right) } \right] }\right. \nonumber \\&\left. -\sin \left[ {aU\left( {-l+\frac{1}{b}\sinh (bl)} \right) } \right] \right\} ,\quad s\in \left[ {0,l} \right] , \nonumber \\ w= & {} \frac{1}{aU}\left\{ {\cos \left[ {aU\left( {s-l+\frac{1}{b}\sinh (bl)} \right) } \right] }\right. \nonumber \\&\left. -\cos \left[ {aU\left( {-l+\frac{1}{b}\sinh (bl)} \right) } \right] \right\} ,\quad s\in \left[ {0,l} \right] , \end{aligned}$$
(15)

as well as the free-end (tip of actuators) coordinates:

$$\begin{aligned} \begin{array}{l} X=\frac{1}{aU}\left\{ {\sin \left[ {\frac{aU}{b}\sinh \left( {bl} \right) } \right] -\sin \left[ {aU\left( {-l+\frac{1}{b}\sinh (bl)} \right) } \right] } \right\} , \\ W=\frac{1}{aU}\left\{ {\cos \left[ {\frac{aU}{b}\sinh \left( {bl} \right) } \right] -\cos \left[ {aU\left( {-l+\frac{1}{b}\sinh (bl)} \right) } \right] } \right\} . \\ \end{array}\nonumber \\ \end{aligned}$$
(16)

4 Model verification

In this study, verification experiments were conducted on two IPMC actuator samples. The results from the Pt-IPMC sample were used to describe the application and validity of the electromechanical model, while those from the Ag-IPMC actuator sample were employed to evaluate the accuracy of the derived IPMC electromechanical model.

4.1 Verification of Pt-IPMC actuator

4.1.1 Parameter estimation

The parameters used in the derived model were assumed to be time-invariant and uniform (Table 2). The sum of the resistances of the two surface electrodes \((R_{s})\) was calculated from the surface square resistance, according to the size of the IPMC sample. The Young’s modulus of the IPMC sample was tested using a universal testing machine, QUASAR 2.5, as per ASTM D882 standards. The values of the parameter \(R_{2}\) were obtained using the technique introduced by Punning et al. [40]. K and L, measured by Shahinpoor and Kim [2, 44], are also shown in Table 2.

An excitation voltage was applied to the Pt-IPMC actuator sample, which was exposed to a large deflection, to calculate the value of \(a=\frac{L}{KYh\cosh (\sqrt{R_s R_2 }l)}\) using Eq. (13). The value of \(b=\sqrt{R_s R_2 }\) was calculated using the parameters listed in Table 2.

Table 3 Parameters of Pt-IPMC sample
Full size table
Fig. 9
figure 9

Measured and calculated deformation curves of Pt-IPMC actuator under 2 V excitation voltage

Full size image
Fig. 10
figure 10

Comparison of calculated and measured maximum deflection curves for Pt-IPMC actuator under different excitation voltages. a 1.5 V. b 2.5 V. c 3.0 V. d 3.5 V

Full size image
Table 4 Comparisons of calculated and measured deflection parameters at free end
Full size table

4.1.2 Model verification

The deformation of the Pt-IPMC actuator sample at the free end under a 2 V excitation is listed in Table 3, along with the values of a and b obtained for the electromechanical model.

As long as the values of a, b and U are determined, the solution to Eq. (15) is analytical. According to the effective length of the IPMC sample (\(l=24\) mm, as listed in Table 1) and the value of b listed in Table 2, the range of \(b(s-l)\vert _{s\in [0,l]}\) was obtained, [−0.062, 0]. Since the range of \(b(s-l)\) is pretty small, the usage of \(b(s-l)\) can replace sinh\((b(s-l))\) efficiently and the analytical solution of Eq. (14) is accurate enough. The calculated deflection curve of the Pt-IPMC actuator can be obtained using Eq. (15). The calculated coordinates of the tip of the actuator was (21.87, 8.49) mm.

The calculated and experimentally measured deflection curves were compared to evaluate the accuracy of the electromechanical model. Figure 9 shows a comparison of the calculated and measured deflections of the Pt-IPMC sample under 2 V DC. It can be found that the deformations, measured three times, are very similar to each other. In particular, the deflection curves were compared at excitation voltages varying between 1.5 and 3.5 V (Fig. 10). Accordingly, the findings revealed that the deflection curves exhibited consistent trends. For quantitative evaluation, the tip displacements of the Pt-IPMC actuator were compared as specified in Table 4.

Table 5 Parameters of Ag-IPMC sample
Full size table
Fig. 11
figure 11

Measured and calculated deflection curves of Ag-IPMC actuator at different excitation voltages. a 0.60 V. b 0.55 V. c 0.65 V. d 0.75 V

Full size image

The maximum error for displacement prediction was \(+\)6.6%, which was related to the excitation voltage of 2.5 V. These results confirmed that the electromechanical model represented the large deformation behavior of the Pt-IPMC actuators with a reasonable accuracy over the entire actuator length.

4.2 Model verification using Ag-IPMC actuators

Apart from the validation of the Pt-IPMC actuator at various voltages, an Ag-IPMC actuator was also tested to evaluate the validity of the proposed electromechanical model for other IPMC actuators. Table 5 shows the parameters of the Ag-IPMC sample. The deflection curve of the Ag-IPMC actuator at the excitation voltage of 0.6 V is shown in Fig. 11a. Based on the measured slope at the free end of the actuator, the constant a was identified using the same procedure as was used for the Pt-IPMC actuator. The deflection curves of the Ag-IPMC actuator over the entire actuator length at various excitation voltages were obtained based on the determined constants a and b, and they were then compared with the measured deflection curves. The results are presented in Fig. 11b–d.

Table 6 Comparison of displacement and rotational angles for Ag-IPMC actuator
Full size table

Despite the consistent deflection curves shown in Fig. 11, a quantitative evaluation was still performed by comparing the calculated and measured displacements at the free end of the Ag-IPMC actuator at various excitation voltages. The errors are listed in Table 6. The maximum error in terms of displacement was −5.6%, which was related to the excitation of 0.6 V.

The model verification shows that there is no difference in the application of the developed model for the two IPMC samples. The surface electrode resistance of the Ag-IPMC sample (0.194 \(\Omega \cdot \hbox {cm}^{-1}\)) is much smaller than that of the Pt-IPMC sample (16.69 \(\Omega \cdot \hbox {cm}^{-1}\)), showing that the former sample requires a lower excitation voltage but responds faster than the latter, so the Ag-IPMC actuator is more sensitive to voltage.

By comparing the electromechanical model with the experimental results from the two sets of IPMC actuators consisting of different electrodes, it is verified that the electromechanical model reliably describes the large nonlinear deflection behavior of the actuators. Given that the IPMC cantilever actuators were structurally flexible and not perfectly aligned, the initial deflections were deemed the major causes of the errors between the electromechanical model and the measured deflection results of the IPMC actuators.

5 Conclusion

This study has developed an analytical electromechanical model to describe large nonlinear quasi-static deflections of IPMC actuators. The voltage distribution of the actuators was analyzed using a distributed electrical model under DC voltage considering the influence of curvature of the IPMC samples. This model takes into account the electrical and mechanical properties of the IPMC samples and gives the analytical solution for the whole deflection curves. The accuracy of the electromechanical model was experimentally validated using two types of IPMC actuator subjected to various DC driving voltages.

The experimental results lead to the following conclusions:

  1. (1)

    The surface resistances of electrodes are dependent on the curvatures of the IPMC sample, and the difference between the resistances of two electrodes increases with increasing curvature. However, the sum of two corresponding surface resistances in an equivalent single-unit circuit can be assumed to be a fixed value along the axis of IPMC.

  2. (2)

    The model can be taken as an analytical engineering model that could be used to predict the large nonlinear deflections of IPMC actuators with satisfactory accuracy.