Rotating electroosmotic flow of an Eyring fluid

Abstract

A perturbation analysis is presented in this paper for the electroosmotic (EO) flow of an Eyring fluid through a wide rectangular microchannel that rotates about an axis perpendicular to its own. Mildly shear-thinning rheology is assumed such that at the leading order the problem reduces to that of Newtonian EO flow in a rotating channel, while the shear thinning effect shows up in a higher-order problem. Using the relaxation time as the small ordering parameter, analytical solutions are deduced for the leading- as well as first-order problems in terms of the dimensionless Debye and rotation parameters. The velocity profiles of the Ekman–electric double layer (EDL) layer, which is the boundary layer that arises when the Ekman layer and the EDL are comparably thin, are also deduced for an Eyring fluid. It is shown that the present perturbation model can yield results that are close to the exact solutions even when the ordering parameter is as large as order unity. By this order of the relaxation time parameter, the enhancing effect on the rotating EO flow due to shear-thinning Eyring rheology can be significant.

1 Introduction

Owing to their portability and high throughput, microfluidic devices have now been in common use for chemical or biological assays, where the fluid transport is often driven by electrokinetic pumping. For a variety of reasons, such as the ionization of surface groups, many solid surfaces acquire an electric charge when brought into contact with an electrolyte solution, which in return upsets the charge balance of the solution. The charged surface furthermore determines the distribution of free ions in the solution. Ions with a charge opposite to that of the surface (or counterions) will be attracted while those of the same charge (or coions) will be repelled. As a result, a so-called electric double layer (EDL) develops near the solid surface, where a Stern layer is formed by immobile ions sorbed onto the surface and a diffuse layer develops under the influence of electric attraction and random thermal motion. The electric potential at the slipping plane of the EDL is known as the zeta potential. Outside the EDL, the solution is essentially electrically neutral. When an electric field is applied externally, the net charges in the EDL will move, thereby causing the bulk fluid to move as well through the viscous action. Such flow is termed electroosmotic (EO) flow. Electrokinetic pumping is known to be better than hydrodynamic pumping in several respects, for example, easy control and fabrication, less sensitivity of flow rate to channel size, negligible sample dispersion, low noise, and an absence of mechanical moving parts.

Microfluidics are often applied to the assay of biofluids, such as blood and DNA solutions, which exhibit non-Newtonian behaviors when sheared in a microscale environment. Studies on the EO flow of a non-Newtonian fluid in microchannels have been reported extensively in the literature in recent years [1]. For the EO flow of non-Newtonian fluids, the most commonly chosen model us the power-law model, as studied by, among many others, Chakraborty [2], Zhao et al. [3], Zhao and Yang [4, 5], Babaie et al. [6], Deng et al. [7], Dhar et al. [8], and Ng and Qi [9]. The power-law model is a relatively simple two-parameter nonlinear model that can conveniently represent the rheological behaviors of shear thinning, Newtonian, or shear thickening fluid by a behavior index that is smaller than, equal to, or larger than unity, respectively. Besides the power-law fluid, other models have also been used to describe EO flow of non-Newtonian fluids. Examples include viscoelastic fluids [10,11,12] and viscoplastic materials [13, 14].

Compared with other models, EO flow of Eyring fluid has received much less attention than it deserves. The Eyring model is a kind of structural viscosity model that can represent a wide range of non-Newtonian fluids, such as colloidal suspensions. In fact, this non-Newtonian model, although more complicated in form, is superior to other models in some aspects. First, the Eyring model is derived from the kinetic theory of liquid rather than from an empirical reasoning, as in the case of power-law fluid. Second, an Eyring fluid will tend to a Newtonian fluid of finite viscosity at both low and high shear rates, while the apparent viscosity of a power-law fluid is infinite at zero shear rate. There exist in the literature only a couple of studies on the EO flow of Eyring fluid, however. Berli and Olivares [15] developed a two-zone model for EO flows of various types of non-Newtonian fluids (power-law, Bingham, and Eyring), where the outer zone is a Newtonian depletion layer covering the EDL, and the inner zone is non-Newtonian but without electric body force. More recently, Goswami et al. [16] looked into the EO flow of a Powell–Eyring fluid through a slit microchannel and obtained an analytical solution by employing the homotopy perturbation method. The need to further understand the EO flow of Eyring fluid has motivated us to pursue the present study.

Another key aspect of the present study is to consider EO flow in a rotating environment. This is germane to centrifugal microfluidics [17, 18], which is an emerging technology using centrifugation for mass separation and flow control on the microscale. This technology may offer a convenient way to integrate liquid handling for sample preparation and subsequent detection [19]. Rapid mixing can also be achieved in a centrifugal microfluidic platform by the alternate rotation (clockwise and counterclockwise) of microchambers containing the mixture [20,21,22,23]. In a rotating environment, secondary flow is induced in the plane perpendicular to the primary flow by the Coriolis force. As the direction of the secondary flow depends on the sense of rotation, the secondary flow can be used to generate directional switching at high rotation frequencies [24, 25]. To enhance the efficiency of flow control and separation, some researchers have fabricated systems incorporating electrokinetics into centrifugal pumping [26,27,28,29]. In particular, Wang et al. [26] developed a dual-pumping CD-like microfluidic system for biomedical separation. It was a multichannel electrophoretic separation CD system that worked under the interaction between the centrifugal and electric forces. These authors found that, through the adjustment of the applied electric field, a higher separation efficiency could be attained by centrifugation, with the advantages of lower joule-heat generation, low chemical reaction, and steadiness of ion concentration during processes.

Motivated by Duffy et al. [17], Chang and Wang [30] pioneered a theoretical study on rotating EO flow over an infinite plate or in a parallel-plate channel. They developed analytical solutions for the axial and transverse flows as functions of the parameters characterizing the rotation, viscous effect, and electrokinetics. The work by Chang and Wang [30] was subsequently extended by Xie and Jian [31] and Li et al. [32] for the rotating EO flow of power-law and third-grade fluids between two parallel plates. Lateral confinement due to side walls was, however, ignored by these authors. More recently, Ng and Qi [33] presented an analytical model for the EO flow of a Newtonian fluid through a rotating rectangular channel, where the confinement due to side walls was taken into account. They deduced in particular the velocity profiles in an electrokinetically modulated Ekman layer, known as an Ekman–EDL layer, that develops near a wall under conditions of fast rotation and a thin EDL.

The aim of the present study is to develop an analytical solution for the EO flow of an Eyring fluid in a rotating wide rectangular channel. The channel is assumed to be so wide that the primary and secondary flows are functions of the coordinate along the axis of rotation only. It is also assumed that the dimensionless relaxation time, which can be interpreted as the ratio of the EO stress to the stress parameter of the Eyring model, is a small parameter. The Eyring model can thereby be expanded into two terms, where the first term corresponds to the Newtonian model valid at small shear rates and the second term corresponds to a first-order correction accounting for the shear-thinning behavior of the material. On this basis, we may carry out a perturbation analysis using the square of the dimensionless relaxation time as the small ordering parameter. In the leading-order problem, we allow the zeta potentials on the upper and lower walls to be different, which extends the work by Ng and Qi [33] in the limiting case of a very wide channel. For simplicity, only the condition of equal zeta potentials is considered in the first-order problem. We shall further look into the limiting case where the rotation speed is so high that the Ekman layer becomes as thin as the EDL. The resulting Ekman–EDL layer is shown to be characterized by the Ekman layer thickness normalized by the Debye length. This extends the solution deduced by Ng and Qi [33] for a Newtonian Ekman–EDL layer to a higher order for an Eyring fluid. Finally, with some numerical results, we shall examine how rotation may change the velocity profiles depending on the zeta potential distribution on the two walls. We shall also confirm that the effects of rotation on primary and secondary flows are qualitatively the same in the leading and the first orders.

2 Problem formulation

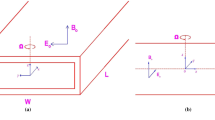
The present problem is to consider the rotating EO flow of an Eyring fluid through a wide rectangular channel. As shown in Fig. 1, a right-handed coordinate system that is attached to the rotating channel is defined such that the x- and y-axes point along the longitudinal and transverse directions, respectively, while the z-axis points vertically upward. The upper and lower walls, located at $z={\pm }h$, are charged with different zeta potentials, $\zeta _1$ and $\zeta _2$, respectively. The channel rotates about the z-axis at a constant rotation speed, $\varOmega$. Primary flow occurs along the x-direction resulting from an electric field $E_x$ applied in this direction, while secondary flow arises in the (y, z) plane as driven by the Coriolis force induced by the system rotation. It is assumed that the channel is long in the x-direction and wide in the y-direction such that the flow, in the fully developed region, is essentially independent of x and y [30,31,32]. As a result, the velocity component in the z-direction is identically zero. Owing to the lateral side walls, the net flux in the y-direction is zero. To satisfy this condition, a pressure gradient in this direction is induced to generate a counterbalancing flow.

Fig. 1

Schematic diagram of problem: EO flow through a wide rectangular channel of height 2h and width 2b ($b\gg h$) rotating about z-axis at speed $\varOmega$, with primary and secondary flow velocities u(z), v(z) in x- and y-directions. The zeta potentials are $\zeta _1$ and $\zeta _2$ on the upper and lower walls, respectively

Further assuming negligible inertia and gravity effects, the governing equations in a rotating frame for steady incompressible flow read as follows

$$\begin{aligned}&\nabla \cdot \varvec{u}=0,\end{aligned}$$

(1)

$$\begin{aligned}&2\rho \varvec{\varOmega }\times \varvec{u}=-\nabla P+\nabla \cdot \varvec{T} +\rho _e\varvec{E}, \end{aligned}$$

(2)

where $\varvec{T}$ is the stress tensor, $\varvec{u}=(u, v, 0)$ is the velocity vector seen in the rotating frame, with u and v denoting respectively the axial and transverse velocities, $\varvec{\varOmega }=(0, 0, \varOmega ), \varvec{E}=(E_x, 0, 0), \rho$ is the fluid density, P is the reduced pressure, and $\rho _e$ is the free charge density in the fluid. It follows from the assumption of a very long and wide channel that the variables are functions of z only: $u=u(z), v=v(z)$, and $\rho _e=\rho _e(z)$. The pressure gradient is nonzero only in the y-direction, as reasoned previously.

The electric potential distribution $\psi (z)$ in the EDL is related to the free charge density $\rho _e$ by the following Poisson equation:

$$\begin{aligned} \frac{\mathrm{d}^2\psi }{\mathrm{d} z^2}=-\frac{\rho _e}{\epsilon }, \end{aligned}$$

(3)

where $\epsilon$ is the dielectric permittivity of the liquid electrolyte. With the further assumptions of a Boltzmann distribution for the ions in the EDL and a 1:1 symmetrical electrolyte of valence Z, the free charge density is given by

$$\begin{aligned} \rho _e=-2Zen_{\infty }\sinh \left( \frac{Ze\psi }{k_\mathrm{B}T}\right) , \end{aligned}$$

(4)

where e is the fundamental charge, $n_{\infty }$ is the bulk concentration, $k_\mathrm{B}$ is the Boltzmann constant, and T is the absolute temperature. On applying the Debye–Hückel approximation, which is valid for very small potential, $|Ze\psi /(k_\mathrm{B}T)|\ll 1$, a linearized Poisson–Boltzmann equation results from Eqs.  (3) and (4):

$$\begin{aligned} \frac{\mathrm{d}^2\psi }{\mathrm{d} z^2}-\kappa ^2 \psi =0, \end{aligned}$$

(5)

where $\kappa =[2Z^2e^2n_{\infty }/(\epsilon k_\mathrm{B}T)]^{1/2}$ is called the Debye parameter, whose inverse is the Debye shielding thickness of the EDL. With the following boundary conditions for the potential $\psi$:

$$\begin{aligned} \psi= & {} \zeta _1\quad \text { at }z=h,\nonumber \\ \psi= & {} \zeta _2\quad \text { at }z=-h, \end{aligned}$$

(6)

the solution to Eq. (5) is given by

$$\begin{aligned} \psi (z)=a\frac{\cosh (\kappa z)}{\cosh (\kappa h)}+ b\frac{\sinh (\kappa z)}{\sinh (\kappa h)}, \end{aligned}$$

(7)

with $a=(\zeta _1+\zeta _2)/2$ and $b=(\zeta _1-\zeta _2)/2$.

By virtue of the simplifying assumptions stated earlier, the Cauchy momentum equations reduce to the following component form:

$$\begin{aligned}&-2\rho \varOmega v=\frac{\mathrm{d} \tau _{xz}}{\mathrm{d} z}-\epsilon \kappa ^2\psi E_x, \end{aligned}$$

(8)

$$\begin{aligned}&2\rho \varOmega u=-\frac{\mathrm{d} P}{\mathrm{d} y}+ \frac{\mathrm{d} \tau _{yz}}{\mathrm{d} z}, \end{aligned}$$

(9)

where $\tau _{xz}$ and $\tau _{yz}$ are the only nonzero stress components, and $\mathrm{d} P/\mathrm{d} y$ is the pressure gradient induced in the y-direction to maintain a zero net flux in this direction.

Under simple shear, the rheology of an Eyring fluid can be expressed as [34]

$$\begin{aligned} \frac{{\dot{\gamma }}}{{\dot{\gamma }}_0}=\sinh \left( \frac{\tau }{\tau _0}\right) , \end{aligned}$$

(10)

where ${\dot{\gamma }}$ is the shear rate, $\tau$ is the shear stress, and ${\dot{\gamma }}_0$ and $\tau _0$ are material constants characterizing the shear rate and shear stress. For three-dimensional shear, a more formal constitutive relationship in terms of the stress tensor $\tau _{ij}$ and the rate-of-deformation tensor ${\dot{\gamma }}_{ij}$ can be obtained as follows

$$\begin{aligned} \tau _{ij}=\mu ({\dot{\gamma }}){\dot{\gamma }}_{ij}, \end{aligned}$$

(11)

where

$$\begin{aligned} \mu ({\dot{\gamma }})=\mu _0\frac{\sinh ^{-1}(\lambda {\dot{\gamma }})}{\lambda {\dot{\gamma }}}, \end{aligned}$$

(12)

in which

$$\begin{aligned} {\dot{\gamma }}=\sqrt{\textstyle {\frac{1}{2}}{\dot{\gamma }}_{ij}:{\dot{\gamma }}_{ij}},\quad {\dot{\gamma }}_{ij}=\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}, \end{aligned}$$

(13)

and $\mu _0$ and $\lambda$ are parameters characterizing the viscosity and relaxation time of the material, respectively. On comparing with the model for simple shear, one can readily identify that

$$\begin{aligned} \mu _0=\tau _0/{\dot{\gamma }}_0,\quad \lambda ={\dot{\gamma }}_0^{-1}. \end{aligned}$$

(14)

Also note the two extremes of $\mu$:

$$\begin{aligned} \mu \rightarrow \left\{ \begin{array}{ll} \mu _0, &{}\quad \text{ as } \lambda {\dot{\gamma }}\ll 1, \\ 0, &{}\quad \text{ as } \lambda {\dot{\gamma }}\gg 1. \end{array}\right. \end{aligned}$$

(15)

Hence, the Eyring fluid described by Eqs. (11) and (12) will behave like a Newtonian fluid with viscosity $\mu _0$ when ${\dot{\gamma }}$ is much smaller than ${\dot{\gamma }}_0$ but like a shear-thinning fluid (i.e., with a diminishing effective viscosity) when ${\dot{\gamma }}$ is of order ${\dot{\gamma }}_0$ or larger.

To allow the present problem to be solved analytically, we assume that the fluid is only subjected to relatively low shear rates such that $\lambda {\dot{\gamma }}\ll 1$, by which we may expand $\sinh ^{-1}(\lambda {\dot{\gamma }})\approx \lambda {\dot{\gamma }}-\lambda ^3{\dot{\gamma }}^3/6$, thereby leading to the approximation

$$\begin{aligned} \mu\approx & {} \mu _0\left( 1 -\frac{\lambda ^2{\dot{\gamma }}^2}{6}\right) \nonumber \\= & {} \mu _0\left\{ 1-\frac{\lambda ^2}{6}\left[ \left( \frac{\mathrm{d} u}{\mathrm{d} z}\right) ^2+\left( \frac{\mathrm{d} v}{\mathrm{d} z}\right) ^2\right] \right\} , \end{aligned}$$

(16)

where the error of the approximation is $O(\lambda ^4{\dot{\gamma }}^4)$. Obviously, in this two-term expansion, the first term corresponds to the Newtonian model, which is recovered when $\lambda =0$, while the second term, which is of order $\lambda ^2{\dot{\gamma }}^2$, represents the shear-thinning property of the material.

Based on the simplified Eyring model, the stress components are now given by

$$\begin{aligned} \tau _{xz}=\mu _0\left\{ \frac{\mathrm{d} u}{\mathrm{d} z}-\frac{\lambda ^2}{6} \left[ \left( \frac{\mathrm{d} u}{\mathrm{d} z}\right) ^3+\left( \frac{\mathrm{d} v}{\mathrm{d} z}\right) ^2\frac{\mathrm{d} u}{\mathrm{d} z}\right] \right\} \end{aligned}$$

(17)

and

$$\begin{aligned} \tau _{yz}=\mu _0 \left\{ \frac{\mathrm{d} v}{\mathrm{d} z}-\frac{\lambda ^2}{6} \left[ \left( \frac{\mathrm{d} u}{\mathrm{d} z}\right) ^2\frac{\mathrm{d} v}{\mathrm{d} z}+\left( \frac{\mathrm{d} v}{\mathrm{d} z}\right) ^3\right] \right\} . \end{aligned}$$

(18)

Substituting Eqs. (17) and (18) into Eqs. (8) and (9) gives

$$\begin{aligned} -2\rho \varOmega v= & {} \mu _0\left\{ \frac{\mathrm{d}^2 u}{\mathrm{d} z^2}-\frac{\lambda ^2}{6} \left[ 3\left( \frac{\mathrm{d} u}{\mathrm{d} z}\right) ^2\frac{\mathrm{d}^2 u}{\mathrm{d} z^2}+\left( \frac{\mathrm{d} v}{\mathrm{d} z}\right) ^2 \frac{\mathrm{d}^2u}{\mathrm{d} z^2}\right. \right. \nonumber \\&\left. \left. +\,2\frac{\mathrm{d} u}{\mathrm{d} z}\frac{\mathrm{d} v}{\mathrm{d} z}\frac{\mathrm{d}^2 v}{\mathrm{d} z^2}\right] \right\} -\epsilon \kappa ^2\psi E_x,\end{aligned}$$

(19)

$$\begin{aligned} 2\rho \varOmega u= & {} -\frac{\mathrm{d} P}{\mathrm{d} y}+\mu _0 \left\{ \frac{\mathrm{d}^2 v}{\mathrm{d} z^2}-\frac{\lambda ^2}{6} \left[ 3\left( \frac{\mathrm{d} v}{\mathrm{d} z}\right) ^2\frac{\mathrm{d}^2 v}{\mathrm{d} z^2}\right. \right. \nonumber \\&\left. \left. +\,\left( \frac{\mathrm{d} u}{\mathrm{d} z}\right) ^2\frac{\mathrm{d}^2 v}{\mathrm{d} z^2} +2\frac{\mathrm{d} u}{\mathrm{d} z}\frac{\mathrm{d} v}{\mathrm{d} z}\frac{\mathrm{d}^2 u}{\mathrm{d} z^2}\right] \right\} . \end{aligned}$$

(20)

Let us introduce the following normalized variables and dimensionless parameters (distinguished by an overhead caret):

$$\begin{aligned} \left. \begin{array}{l} ({\hat{y}},{\hat{z}})=(y,z)/h,\quad ({\hat{u}},{\hat{v}})=(u,v)/U,\quad ({\hat{\psi }}, {\hat{a}}, {\hat{b}})=(\psi , a, b)/\zeta _0,\\ {\hat{\kappa }}=\kappa h,\quad {\hat{P}}=Ph/(\mu _0 U),\quad {\hat{\lambda }}=\lambda \kappa U, \end{array}\right\} \end{aligned}$$

(21)

in which $U=-\epsilon \zeta _0 E_x/\mu _0$ is the Helmholtz–Smoluchowski (or EO slip) velocity, and $\zeta _0$ is a characteristic value for the electric potential. Note that in pure EO flow the velocity gradient is largely zero outside the EDL, and hence the shear rate is scaled by the EO slip velocity divided by the EDL thickness (instead of the channel height): ${\dot{\gamma }}\sim \kappa U$. This explains the normalization for the relaxation time parameter ${\hat{\lambda }}$ introduced earlier. Further note that, from Eq. (14), $\lambda =\mu _0/\tau _0$, by which we may also express the dimensionless time relaxation parameter as a ratio of stresses:

$$\begin{aligned} {\hat{\lambda }}=\tau _E/\tau _0, \end{aligned}$$

(22)

where $\tau _E=-\epsilon \kappa \zeta _0 E_x$ is known as the characteristic shear stress in EO flow. We may therefore interpret that a small shear rate ${\hat{\lambda }}\ll 1$ amounts to a small ratio of the applied EO stress to the stress parameter of the material, which accords with the simple-shear relationship (10).

In terms of the normalized variables, the momentum equations can be expressed in the following nondimensional form:

$$\begin{aligned} -\omega \hat{v}= & {} \frac{\mathrm{d}^2 \hat{u}}{\mathrm{d} \hat{z}^2}-\frac{{\hat{\lambda }}^2}{6{\hat{\kappa }}^2}\left[ 3\left( \frac{\mathrm{d} {\hat{u}}}{\mathrm{d}{\hat{z}}}\right) ^2 \frac{\mathrm{d}^2{\hat{u}}}{\mathrm{d}{\hat{z}}^2}+\left( \frac{\mathrm{d}{\hat{v}}}{\mathrm{d}{\hat{z}}}\right) ^2\frac{\mathrm{d}^2{\hat{u}}}{\mathrm{d}{\hat{z}}^2}\right. \nonumber \\&\left. +\,2\frac{\mathrm{d}{\hat{u}}}{\mathrm{d}{\hat{z}}}\frac{\mathrm{d}{\hat{v}}}{\mathrm{d}{\hat{z}}}\frac{\mathrm{d}^2{\hat{v}}}{\mathrm{d}{\hat{z}}^2}\right] +\hat{\kappa }^2 \hat{\psi }, \end{aligned}$$

(23)

$$\begin{aligned} \omega \hat{u}= & {} \hat{K}_y+\frac{\mathrm{d}^2 \hat{v}}{\mathrm{d} \hat{z}^2}-\frac{{\hat{\lambda }}^2}{6{\hat{\kappa }}^2} \left[ 3 \left( \frac{\mathrm{d}{\hat{v}}}{\mathrm{d}{\hat{z}}}\right) ^2\frac{\mathrm{d}^2{\hat{v}}}{\mathrm{d}{\hat{z}}^2}+\left( \frac{\mathrm{d}{\hat{u}}}{\mathrm{d}{\hat{z}}}\right) ^2 \frac{\mathrm{d}^2{\hat{v}}}{\mathrm{d}{\hat{z}}^2}\right. \nonumber \\&\left. +\,2\frac{\mathrm{d}{\hat{u}}}{\mathrm{d}{\hat{z}}}\frac{\mathrm{d}{\hat{v}}}{\mathrm{d}{\hat{z}}}\frac{\mathrm{d}^2{\hat{u}}}{\mathrm{d}{\hat{z}}^2}\right] , \end{aligned}$$

(24)

where $\omega =2\rho \varOmega h^2/\mu _0$ is the inverse Ekman number, ${\hat{K}}_y=-\mathrm{d} {\hat{P}}/\mathrm{d} {\hat{y}}$ is the normalized pressure gradient induced in the ${\hat{y}}$-direction, and the nondimensional electric potential distribution ${\hat{\psi }}$ is given by

$$\begin{aligned} {\hat{\psi }}({\hat{z}})={\hat{a}} \frac{\cosh ({\hat{\kappa }}{\hat{z}})}{\cosh ({\hat{\kappa }})} +{\hat{b}}\frac{\sinh ({\hat{\kappa }} {\hat{z}})}{\sinh ({\hat{\kappa }})}, \end{aligned}$$

(25)

where ${\hat{a}}=({\hat{\zeta }}_1+{\hat{\zeta }}_2)/2$ and ${\hat{b}}=({\hat{\zeta }}_1-{\hat{\zeta }}_2)/2$. Note that the Ekman number is a dimensionless number representing the ratio of viscous force to Coriolis force in a rotating fluid system. The smaller the Ekman number, the thinner the Ekman layer, which is a boundary layer where the viscous effect is balanced by the Coriolis effect.

As explained earlier, the internally triggered pressure gradient ${\hat{K}}_y$ that appears in Eq. (24) generates a counterbalancing flow in the transverse direction so as to maintain a zero net flux in this direction, as required by the lateral confinement of the channel. To determine ${\hat{K}}_y$, we need to impose the following condition for the flow:

$$\begin{aligned} \int _{-1}^1 {\hat{v}}({\hat{z}}) \mathrm{d} {\hat{z}}=0. \end{aligned}$$

(26)

Our assumption of small shear rates, namely $\lambda {\dot{\gamma }}\ll 1$, which was used to approximate the Eyring model, means that we may use ${\hat{\lambda }}\ll 1$ as a small ordering parameter here. Let us expand the variables into the following perturbation series:

$$\begin{aligned}&{\hat{u}}={\hat{u}}_0+{\hat{\lambda }}^2{\hat{u}}_1+\cdots ,\end{aligned}$$

(27)

$$\begin{aligned}&{\hat{v}}={\hat{v}}_0+{\hat{\lambda }}^2{\hat{v}}_1+\cdots ,\end{aligned}$$

(28)

$$\begin{aligned}&{\hat{K}}_y={\hat{K}}_{y0}+{\hat{\lambda }}^2{\hat{K}}_{y1}+\cdots . \end{aligned}$$

(29)

To be consistent with the approximation in Eq. (16), it suffices for us to consider the first two orders in the perturbation expansions. Again, the O(1) solution $({\hat{u}}_0, {\hat{v}}_0, {\hat{K}}_{y0})$ corresponds to that for Newtonian fluid flow, while the $O({\hat{\lambda }}^2)$ solution $({\hat{u}}_1, {\hat{v}}_1, {\hat{K}}_{y1})$ gives the correction to the leading-order solution to account for the shear-thinning behavior of the material.

Substituting the preceding expansions into Eqs. (23), (24), and (26), and collecting terms of the same order, we get the following perturbation problems, where a single/double prime denotes a first/second derivative with respect to ${\hat{z}}$.

O(1) problem:

$$\begin{aligned}&-\omega {\hat{v}}_0={\hat{u}}_0''+\hat{\kappa }^2 \hat{\psi },\end{aligned}$$

(30)

$$\begin{aligned}&\omega {\hat{u}}_0=\hat{K}_{y0}+{\hat{v}}_0'',\end{aligned}$$

(31)

$$\begin{aligned}&\int _{-1}^1 {\hat{v}}_0 \mathrm{d} {\hat{z}}=0; \end{aligned}$$

(32)

$O({\hat{\lambda }}^2)$ problem:

$$\begin{aligned}&-\omega {\hat{v}}_1={\hat{u}}_1''-f_0, \end{aligned}$$

(33)

$$\begin{aligned}&\omega {\hat{u}}_1={\hat{K}}_{y1}+{\hat{v}}_1''-g_0, \end{aligned}$$

(34)

$$\begin{aligned}&\int _{-1}^1 {\hat{v}}_1 \mathrm{d} {\hat{z}}=0, \end{aligned}$$

(35)

where

$$\begin{aligned} f_0= & {} \left( 3{\hat{u}}_0'^{2}{\hat{u}}_0''+{\hat{v}}_0'^{2}{\hat{u}}_0''+2{\hat{u}}_0'{\hat{v}}_0'{\hat{v}}_0''\right) /6{\hat{\kappa }}^2, \end{aligned}$$

(36)

$$\begin{aligned} g_0= & {} \left( 3{\hat{v}}_0'^{2}{\hat{v}}_0''+{\hat{u}}_0'^{2}{\hat{v}}_0''+2{\hat{u}}_0'{\hat{v}}_0'{\hat{u}}_0''\right) /6{\hat{\kappa }}^2. \end{aligned}$$

(37)

With the no-slip condition at the two walls,

$$\begin{aligned} {\hat{u}}_0={\hat{u}}_1={\hat{v}}_0={\hat{v}}_1=0\qquad \text{ at } {\hat{z}}=\pm 1, \end{aligned}$$

(38)

the two problems can be solved in sequence, as detailed in the following sections.

3 Solution to O(1) problem

As remarked earlier, the solution to the O(1) problem, $({\hat{u}}_0, {\hat{v}}_0, {\hat{K}}_{y0})$, corresponds to the Newtonian limit of the Eyring model. Therefore, presented in this section is essentially the problem of the EO flow of Newtonian fluid in a very wide rotating channel. A similar problem, but for equal zeta potentials on the two walls, has been studied by Ng and Qi [33].

For $\omega \ne 0$, Eqs. (30) and (31) can be rewritten as

$$\begin{aligned}&{\hat{u}}_0^{(4)}+\omega ^2 {\hat{u}}_0=\omega {\hat{K}}_{y0}-{\hat{\kappa }}^4 {\hat{\psi }}, \end{aligned}$$

(39)

$$\begin{aligned}&{\hat{v}}_0=-\omega ^{-1}\left( {\hat{u}}_0^{''}+{\hat{\kappa }}^2 {\hat{\psi }}\right) , \end{aligned}$$

(40)

in which the normalized potential distribution ${\hat{\psi }}$ is given by Eq. (25). Equation (39) is a fourth-order inhomogeneous ordinary differential equation, of which the particular solution ${\hat{u}}_0^{\text {p}}$ and the complementary solution ${\hat{u}}_0^{\text {c}}$ can be readily found as follows

$$\begin{aligned} {\hat{u}}_0^{\text {p}}= & {} \frac{{\hat{K}}_{y0}}{\omega }-\left( \frac{{\hat{\kappa }}^4}{{\hat{\kappa }}^4+4\eta ^4}\right) \left[ {\hat{a}}\, {{\mathrm{sech}}}({\hat{\kappa }}) \cosh ({\hat{\kappa }} {\hat{z}})\right. \nonumber \\&\left. +\,{\hat{b}}\ \text {csch}({\hat{\kappa }}) \sinh ({\hat{\kappa }} {\hat{z}})\right] \end{aligned}$$

(41)

and

$$\begin{aligned} {\hat{u}}_0^{\text {c}}= & {} \frac{1}{2}\mathrm{e}^{\eta {\hat{z}}}\left[ C_1\cos (\eta {\hat{z}})+C_2\sin (\eta {\hat{z}})\right] \nonumber \\&+\,\frac{1}{2}\mathrm{e}^{-\eta {\hat{z}}} \left[ C_1'\cos (\eta {\hat{z}})+C_2'\sin (\eta {\hat{z}})\right] , \end{aligned}$$

(42)

in which $C_{1,2}$ and $C_{1,2}'$ are four yet-to-be-determined coefficients, and $\eta =(\omega /2)^{1/2}$ is a dimensionless rotation parameter. Substituting ${\hat{u}}_0={\hat{u}}_0^{\text {p}}+{\hat{u}}_0^{\text {c}}$ into Eq. (40) then gives

$$\begin{aligned} {\hat{v}}_0= & {} -\left( \frac{2{\hat{\kappa }}^2\eta ^2}{{\hat{\kappa }}^4+4\eta ^4}\right) \left[ {\hat{a}} {{\mathrm{sech}}}({\hat{\kappa }})\cosh ({\hat{\kappa }}{\hat{z}}) +{\hat{b}}\ \text {csch}({\hat{\kappa }})\sinh ({\hat{\kappa }} {\hat{z}})\right] \nonumber \\&+\,\frac{1}{2}\mathrm{e}^{\eta {\hat{z}}} \left[ C_1\sin (\eta {\hat{z}})-C_2\cos (\eta {\hat{z}})\right] \nonumber \\&-\,\frac{1}{2}\mathrm{e}^{-\eta {\hat{z}}} \left[ C_1'\sin (\eta {\hat{z}})-C_2'\cos (\eta {\hat{z}})\right] . \end{aligned}$$

(43)

Using the no-slip boundary conditions in Eq. (38), the four coefficients can be determined as follows

$$\begin{aligned} C_1= & {} -\frac{2\cos (\eta )\cosh (\eta )}{\cos (2\eta )+\cosh (2\eta )}\left( \frac{{\hat{K}}_{y0}}{\omega }\right) \nonumber \\&+\,\frac{2{\hat{a}} {\hat{\kappa }}^2 \left[ {\hat{\kappa }}^2\cos (\eta )\cosh (\eta )+2\eta ^2\sin (\eta )\sinh (\eta )\right] }{\left( {\hat{\kappa }}^4+4\eta ^4\right) \left[ \cos (2\eta )+\cosh (2\eta )\right] }\nonumber \\&-\frac{2{\hat{b}}{\hat{\kappa }}^2 \left[ {\hat{\kappa }}^2\cos (\eta )\sinh (\eta ) +2\eta ^2\sin (\eta )\cosh (\eta )\right] }{({\hat{\kappa }}^4+4\eta ^4) \left[ \cos (2\eta )-\cosh (2\eta )\right] }, \nonumber \\\end{aligned}$$

(44)

$$\begin{aligned} C_2= & {} -\frac{2\sin (\eta )\sinh (\eta )}{\cos (2\eta )+\cosh (2\eta )} \left( \frac{{\hat{K}}_{y0}}{\omega }\right) \nonumber \\&+\,\frac{2{\hat{a}}{\hat{\kappa }}^2 \left[ {\hat{\kappa }}^2\sin (\eta )\sinh (\eta ) -2\eta ^2\cos (\eta )\cosh (\eta )\right] }{\left( {\hat{\kappa }}^4+4\eta ^4\right) \left[ \cos (2\eta )+\cosh (2\eta )\right] }\nonumber \\&-\frac{2{\hat{b}} {\hat{\kappa }}^2 \left[ {\hat{\kappa }}^2\sin (\eta )\cosh (\eta ) -2\eta ^2\cos (\eta )\sinh (\eta )\right] }{({\hat{\kappa }}^4+4\eta ^4) \left[ \cos (2\eta )-\cosh (2\eta )\right] }, \nonumber \\\end{aligned}$$

(45)

$$\begin{aligned} C_1'= & {} -\frac{2\cos (\eta )\cosh (\eta )}{\cos (2\eta )+\cosh (2\eta )} \left( \frac{{\hat{K}}_{y0}}{\omega }\right) \nonumber \\&+\,\frac{2{\hat{a}} {\hat{\kappa }}^2 \left[ {\hat{\kappa }}^2\cos (\eta )\cosh (\eta )+2\eta ^2\sin (\eta )\sinh (\eta )\right] }{\left( {\hat{\kappa }}^4+4\eta ^4\right) \left[ \cos (2\eta )+\cosh (2\eta )\right] }\nonumber \\&+\,\frac{2{\hat{b}}{\hat{\kappa }}^2 \left[ {\hat{\kappa }}^2\cos (\eta )\sinh (\eta ) +2\eta ^2\sin (\eta )\cosh (\eta )\right] }{({\hat{\kappa }}^4+4\eta ^4) \left[ \cos (2\eta )-\cosh (2\eta )\right] },\nonumber \\\end{aligned}$$

(46)

$$\begin{aligned} C_2'= & {} \frac{2\sin (\eta )\sinh (\eta )}{\cos (2\eta )+\cosh (2\eta )} \left( \frac{{\hat{K}}_{y0}}{\omega }\right) \nonumber \\&-\frac{2{\hat{a}}{\hat{\kappa }}^2 \left[ {\hat{\kappa }}^2\sin (\eta )\sinh (\eta ) -2\eta ^2\cos (\eta )\cosh (\eta )\right] }{\left( {\hat{\kappa }}^4+4\eta ^4\right) \left[ \cos (2\eta )+\cosh (2\eta )\right] }\nonumber \\&-\frac{2{\hat{b}} {\hat{\kappa }}^2 \left[ {\hat{\kappa }}^2\sin (\eta )\cosh (\eta ) -2\eta ^2\cos (\eta )\sinh (\eta )\right] }{({\hat{\kappa }}^4+4\eta ^4) \left[ \cos (2\eta )-\cosh (2\eta )\right] }.\nonumber \\ \end{aligned}$$

(47)

Finally, the transverse pressure gradient ${\hat{K}}_{y0}$ can be found by substituting ${\hat{v}}_0$ into Eq. (32). After some algebra, we get

$$\begin{aligned} \frac{{\hat{K}}_{y0}}{\omega }= & {} \frac{{\hat{a}}{\hat{\kappa }}^4}{{\hat{\kappa }}^4+4\eta ^4} +\left( \frac{2{\hat{a}} {\hat{\kappa }}^2\eta ^2}{{\hat{\kappa }}^4+4\eta ^4}\right) \frac{\sin (2\eta )+\sinh (2\eta )}{\sin (2\eta )-\sinh (2\eta )} \nonumber \\&-\left[ \frac{4{\hat{a}}{\hat{\kappa \eta }}^3\tanh ({\hat{\kappa }})}{{\hat{\kappa }}^4+4\eta ^4} \right] \frac{\cos (2\eta )+\cosh (2\eta )}{\sin (2\eta )-\sinh (2\eta )}. \end{aligned}$$

(48)

Integrating the axial velocity across the channel gives the flow rate of the primary flow:

$$\begin{aligned} {\hat{q}}_0= & {} \int _{-1}^1{\hat{u}}_0\mathrm{d} {\hat{z}} =\frac{2{\hat{K}}_{y0}}{\omega } -\frac{2{\hat{a}}{\hat{\kappa }}^3\tanh ({\hat{\kappa }})}{{\hat{\kappa }}^4+4\eta ^4}\nonumber \\&+\,\left( \frac{4{\hat{a}}{\hat{\kappa }}^2\eta }{{\hat{\kappa }}^4+4\eta ^4}\right) \frac{\cos (2\eta )-\cosh (2\eta )}{\sin (2\eta )-\sinh (2\eta )}\nonumber \\&+\,\left[ \frac{4{\hat{a}}{\hat{\kappa \eta }}^2\tanh ({\hat{\kappa }})}{{\hat{\kappa }}^4+4\eta ^4}\right] \frac{\sin (2\eta )+\sinh (2\eta )}{\sin (2\eta )-\sinh (2\eta )}. \end{aligned}$$

(49)

It is worth pointing out that ${\hat{K}}_{y0}$ and ${\hat{q}}_0$ depend only on the average of the two zeta potentials (i.e., ${\hat{a}}$), but not their difference (i.e., ${\hat{b}}$). In fact, both these quantities are linearly proportional to ${\hat{a}}$. Hence, when ${\hat{\zeta }}_1=-{\hat{\zeta }}_2$ or ${\hat{a}}=0$, both the pressure gradient and the flow rate are zero.

In the particular case where the two zeta potentials are the same, ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$, the solution can be obtained by setting ${\hat{a}}=1$ and ${\hat{b}}=0$ as follows

$$\begin{aligned} {\hat{u}}_0^{(\text {s})}= & {} \frac{{\hat{K}}_{y0}}{\omega }-\left[ \frac{{\hat{\kappa }}^4{{\mathrm{sech}}}({\hat{\kappa }})}{{\hat{\kappa }}^4+4\eta ^4}\right] \cosh ({\hat{\kappa }} {\hat{z}})\nonumber \\&+\,C_1\cosh (\eta {\hat{z}})\cos (\eta {\hat{z}})+C_2\sinh (\eta {\hat{z}})\sin (\eta {\hat{z}}),\end{aligned}$$

(50)

$$\begin{aligned} {\hat{v}}_0^{(\text {s})}= & {} -\left( \frac{2{\hat{\kappa }}^2\eta ^2}{{\hat{\kappa }}^4+4\eta ^2}\right) {{\mathrm{sech}}}({\hat{\kappa }})\cosh ({\hat{\kappa }}{\hat{z}})\nonumber \\&+\,C_1\sinh (\eta {\hat{z}})\sin (\eta {\hat{z}})-C_2\cosh (\eta {\hat{z}})\cos (\eta {\hat{z}}), \end{aligned}$$

(51)

where the term ${\hat{K}}_{y0}/\omega$ is given by Eq. (48), with ${\hat{a}}=1$. This solution for the particular case of equal zeta potentials on the two walls agrees with that previously obtained by Ng and Qi [33].

For a nonrotating channel, $\omega =0$, the secondary flow is identically zero (${\hat{v}}_0\equiv 0$), and the axial velocity can be readily found as

$$\begin{aligned} {\hat{u}}_0^{\text {nr}}({\hat{z}})={\hat{a}} \left[ 1-\frac{\cosh ({\hat{\kappa }} {\hat{z}})}{\cosh ({\hat{\kappa }})}\right] +{\hat{b}} \left[ {\hat{z}}-\frac{\sinh ({\hat{\kappa }}{\hat{z}})}{\sinh ({\hat{\kappa }})}\right] , \end{aligned}$$

(52)

and the flow rate of the axial flow is given by

$$\begin{aligned} {\hat{q}}_0^{\text {nr}}=\int _{-1}^1 {\hat{u}}_0^{\text {nr}} \mathrm{d} {\hat{z}}= 2{\hat{a}} \left[ 1-\frac{\tanh ({\hat{\kappa }})}{{\hat{\kappa }}} \right] . \end{aligned}$$

(53)

4 Solution to $O({\hat{\lambda }}^2)$ problem

For simplicity, we consider only the case of equal zeta potentials, ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$, on deducing solutions to the $O({\hat{\lambda }}^2)$ problem. By symmetry, we may reduce the domain of analysis to the upper half of the channel, $0\leqslant {\hat{z}}\leqslant 1$. The algebra for this problem is much more tedious and lengthy than that for the preceding problem, and we have obtained the analytical expressions presented below with the aid of the package Mathematica 9.0.

Let us first rewrite Eqs. (33) and (34) as follows (again, $\omega \ne 0$ is assumed here; the case for $\omega =0$ will be discussed separately in Sect. 6)

$$\begin{aligned}&{\hat{u}}_1^{(4)}+\omega ^2{\hat{u}}_1=\omega {\hat{K}}_{y1}+f_0''-\omega g_0,\end{aligned}$$

(54)

$$\begin{aligned}&{\hat{v}}_1 =\omega ^{-1}\left( f_0-{\hat{u}}_1''\right) , \end{aligned}$$

(55)

where $f_0$ and $g_0$ are given in Eqs. (36) and (37), respectively. The complementary solution (${\hat{u}}_1^{\text {c}}, {\hat{v}}_1^{\text {c}}$) and the particular solution (${\hat{u}}_1^{\text {p}}, {\hat{v}}_1^{\text {p}}$) are expressible by

$$\begin{aligned} {\hat{u}}_1^{\text {c}}= & {} C_3\cos (\eta {\hat{z}})\cosh (\eta {\hat{z}}) +C_4\sin (\eta {\hat{z}})\sinh (\eta {\hat{z}}),\end{aligned}$$

(56)

$$\begin{aligned} {\hat{v}}_1^{\text {c}}= & {} C_3\sin (\eta {\hat{z}})\sinh (\eta {\hat{z}})-C_4\cos (\eta {\hat{z}})\cosh (\eta {\hat{z}}),\end{aligned}$$

(57)

$$\begin{aligned} {\hat{u}}_1^{\text {p}}= & {} \frac{{\hat{\kappa }}^4{{\mathrm{sech}}}^2({\hat{\kappa }})}{12\left( {\hat{\kappa }}^4 +4\eta ^4\right) } \left( \eta {\hat{z}}\right) \left[ (C_1-C_2)\sin (\eta {\hat{z}}) \cosh (\eta {\hat{z}})\right. \nonumber \\&\left. -(C_1+C_2)\cos (\eta {\hat{z}}) \sinh (\eta {\hat{z}})\right] \nonumber \\&+\,\frac{{\hat{K}}_{y1}}{\omega } +U_{\kappa }({\hat{z}}) +\left( \frac{\eta ^2}{{\hat{\kappa }}^2} \right) U_{\eta }({\hat{z}}) , \end{aligned}$$

(58)

$$\begin{aligned} {\hat{v}}_{1}^{\text {p}}= & {} -\frac{{\hat{\kappa }}^4{{\mathrm{sech}}}^2({\hat{\kappa }})}{12\left( {\hat{\kappa }}^4+4\eta ^4\right) } \left( \eta {\hat{z}}\right) \left[ \left( C_1-C_2\right) \cos (\eta {\hat{z}}) \sinh (\eta {\hat{z}})\right. \nonumber \\&\left. +\,\left( C_1+C_2\right) \sin (\eta {\hat{z}})\cosh (\eta {\hat{z}}) \right] \nonumber \\&+\, V_\kappa ({\hat{z}}) +\left( \frac{\eta ^2}{{\hat{\kappa }}^2} \right) V_\eta ({\hat{z}}), \end{aligned}$$

(59)

where $C_{3, 4}$ are yet-to-be-determined coefficients, and $U_{\kappa , \eta }({\hat{z}})$ and $V_{\kappa , \eta }({\hat{z}})$ are four functions given in Appendix. By applying the no-slip boundary conditions, the coefficients $C_{3,4}$ can be found as follows

$$\begin{aligned} C_3= & {} -\frac{2\cos (\eta )\cosh (\eta )}{\cos (2\eta )+\cosh (2\eta )} \left( U_c +\frac{{\hat{K}}_{y1}}{\omega }\right) \nonumber \\&-\frac{2\sin (\eta )\sinh (\eta )V_c}{\cos (2\eta )+\cosh (2\eta )},\end{aligned}$$

(60)

$$\begin{aligned} C_4= & {} \frac{2\cot (\eta )\coth (\eta )}{\cos (2\eta )+\cosh (2\eta )} \left[ \cos (\eta )\cosh (\eta ) \left( U_c+\frac{{\hat{K}}_{y1}}{\omega }\right) \right. \nonumber \\&\left. +\,\sin (\eta )\sinh (\eta )V_c\right] -\csc (\eta )\text {csch}(\eta )\left( U_c+ \frac{{\hat{K}}_{y1}}{\omega } \right) ,\nonumber \\ \end{aligned}$$

(61)

where

$$\begin{aligned} U_c= & {} M_\kappa +\left( \frac{\eta ^2}{{\hat{\kappa }}^2}\right) M_\eta \nonumber \\&+\,\frac{{\hat{\kappa }}^4\eta {{\mathrm{sech}}}^2({\hat{\kappa }})}{12 \left( {\hat{\kappa }}^4+4\eta ^4\right) } \left[ \left( C_1-C_2\right) \sin (\eta ) \cosh (\eta )\right. \nonumber \\&\left. - \left( C_1+C_2\right) \cos (\eta ) \sinh (\eta )\right] \end{aligned}$$

(62)

and

$$\begin{aligned} V_c= & {} N_\kappa +\left( \frac{\eta ^2}{{\hat{\kappa }}^2}\right) N_\eta \nonumber \\&-\frac{{\hat{\kappa }}^4\eta {{\mathrm{sech}}}^2({\hat{\kappa }} ) }{12 \left( {\hat{\kappa }}^4+4\eta ^4\right) } \left[ \left( C_1-C_2\right) \cos (\eta ) \sinh (\eta )\right. \nonumber \\&\left. +\,\left( C_1+C_2\right) \sin (\eta ) \cosh (\eta )\right] , \end{aligned}$$

(63)

in which $M_\kappa =U_\kappa ({\hat{z}}=1), M_\eta =U_\eta ({\hat{z}}=1), N_\kappa =V_\kappa ({\hat{z}}=1)$, and $N_\eta =V_\eta ({\hat{z}}=1)$. Their expressions are given in Appendix.

The transverse pressure gradient ${\hat{K}}_{y1}$ is then found by substituting ${\hat{v}}_1={\hat{v}}_1^{\text {c}}+{\hat{v}}_1^{\text {p}}$ into Eq. (35):

$$\begin{aligned} \frac{{\hat{K}}_{y1}}{\omega }= & {} - U_c- V_c\left[ \frac{\sin (2 \eta )+\sinh (2 \eta )}{\sin (2 \eta )-\sinh (2 \eta )}\right] \nonumber \\&-\left( \frac{K_c}{2}\right) \left[ \frac{\cos (2 \eta )+\cosh (2 \eta )}{\sin (2 \eta )-\sinh (2 \eta )}\right] , \end{aligned}$$

(64)

where

$$\begin{aligned} K_c= & {} K_\kappa +\left( \frac{\eta ^2}{{\hat{\kappa }}^2} \right) K_\eta +\left[ \frac{{\hat{\kappa }}^4\eta {{\mathrm{sech}}}^2({\hat{\kappa }} )}{3 \left( {\hat{\kappa }}^4+4\eta ^4\right) }\right] \left[ C_1\sin (\eta )\sinh (\eta )\right. \nonumber \\&\left. - C_2 \cos (\eta )\cosh (\eta ) \right] , \end{aligned}$$

(65)

in which the two coefficients $K_\kappa$ and $K_\eta$ are also given in Appendix.

After obtaining the particular and complementary solutions, the $O({\hat{\lambda }}^2)$ flow rate of the primary flow can then be found:

$$\begin{aligned} {\hat{q}}_1=2\int _0^1 {\hat{u}}_1 \mathrm{d} {\hat{z}}=2\int _0^1 ({\hat{u}}_1^{\text {p}}+{\hat{u}}_1^{\text {c}}) \mathrm{d} {\hat{z}}, \end{aligned}$$

(66)

which can be numerically computed using Simpson’s rule. Adding this flux to the leading-order flux gives the total flux

$$\begin{aligned} {\hat{q}}={\hat{q}}_0+{\hat{\lambda }}^2{\hat{q}}_1 \quad \text { for } \omega \ne 0, \end{aligned}$$

(67)

where ${\hat{q}}_0$ is the O(1) flow rate given by Eq. (49), with ${\hat{a}}=1$, corresponding to the condition ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$ under which the $O({\hat{\lambda }}^2)$ solution has been deduced.

5 Ekman–EDL layer

Let us consider in this section a limiting flow structure, which happens when the rotation and Debye parameters are both large, corresponding to a high-speed rotation and a thin EDL. The boundary layer structure that arises under such a limiting condition is known as an Ekman–EDL layer [33]. It is a thin near-wall layer incorporating effects due to pressure, Coriolis, viscous, and electric forces. Outside this layer, where the viscous and electric forces vanish, the flow is geostrophic because it results from a balance between the pressure gradient and the Coriolis force.

Recall that the dimensionless rotation parameter is $\eta =(\omega /2)^{1/2}$, where $\omega =2\rho \varOmega h^2/\mu _0$ is the inverse Ekman number. Alternatively, we may write $\eta =h/\delta _E$, where $\delta _E=[\mu _0/(\rho \varOmega )]^{1/2}$ is the Ekman layer thickness. An Ekman layer shows up when the Ekman thickness is much smaller than the channel height, $\delta _E\ll h$, or $\eta \gg 1$. Also recall that the dimensionless Debye parameter ${\hat{\kappa }}=\kappa h$ is the ratio of the channel height to the Debye length. Hence, a thin EDL corresponds to ${\hat{\kappa \gg }} 1$. An Ekman–EDL layer arises when ${\hat{\kappa }}$ and $\eta$ are both large and comparable to each other.

To fix ideas, let us consider an Ekman–EDL that develops near the upper wall. In this regard, we introduce the following stretched local coordinate:

$$\begin{aligned} z^*=\eta (1-{\hat{z}}). \end{aligned}$$

(68)

We further introduce a modified dimensionless Debye parameter, which is the Debye parameter normalized by the Ekman layer thickness instead of the channel height:

$$\begin{aligned} \xi ={\hat{\kappa }}/\eta . \end{aligned}$$

(69)

The electric potential near the upper wall then simplifies to ${\hat{\psi }}=\exp (-\xi z^*)$. In terms of the newly defined variable $z^*$, the velocities in the Ekman–EDL layer can be obtained by taking the limits of $\eta \gg 1$ and ${\hat{\kappa \gg }} 1$ in the solutions given in Sects. 3 and 4. Again, the condition of equal zeta potentials ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$ is assumed here.

Table 1 Exact and approximate values of axial velocity ${\hat{u}}({\hat{z}})$ in nonrotating channel for ${\hat{\lambda }}=O(1)$, where ${\hat{\kappa }}=10$

The axial and transverse velocities, denoted by ${\hat{u}}^*(z^*)$ and ${\hat{v}}^*(z^*)$, can be expressed as follows. First are the perturbation expansions

$$\begin{aligned} {\hat{u}}^*(z^*)= {\hat{u}}_0^*(z^*)+{\hat{\lambda }}^2 {\hat{u}}_1^{*}(z^*)+\cdots \end{aligned}$$

(70)

and

$$\begin{aligned} {\hat{v}}^*(z^*)={\hat{v}}_0^*(z^*)+{\hat{\lambda }}^2 {\hat{v}}_1^{*}(z^*)+\cdots . \end{aligned}$$

(71)

The O(1) velocities are

$$\begin{aligned} {\hat{u}}_0^*= & {} {\hat{K}}_{y0}^* -\frac{\xi ^4}{\xi ^4+4} \mathrm{e}^{-\xi z^*}+\frac{2\xi ^2-4\xi }{\xi ^4+4}\mathrm{e}^{-z^*}\cos (z^*)\nonumber \\&+\,\frac{2\xi ^2}{\xi ^4+4} \mathrm{e}^{-z^*}\sin (z^*),\end{aligned}$$

(72)

$$\begin{aligned} {\hat{v}}_0^*= & {} -\frac{2\xi ^2}{\xi ^4+4}\mathrm{e}^{-\xi z^*} -\frac{2\xi ^2-4\xi }{\xi ^4+4} \mathrm{e}^{-z^*}\sin (z^*)\nonumber \\&+\,\frac{2\xi ^2}{\xi ^4+4}\mathrm{e}^{-z^*}\cos (z^*), \end{aligned}$$

(73)

where

$$\begin{aligned} {\hat{K}}_{y0}^*=\lim _{{\hat{\kappa }},\eta \gg 1} \left( \frac{ {\hat{K}}_{y0}}{\omega } \right) =\frac{\xi ^4-2\xi ^2+4\xi }{\xi ^4+4}. \end{aligned}$$

(74)

These leading-order velocities, which are velocities in a Newtonian Ekman–EDL layer, were obtained previously by Ng and Qi [33]. The $O({\hat{\lambda }}^2)$ velocities are

$$\begin{aligned} {\hat{u}}_1^*= & {} {\hat{K}}_{y1}^* +U_\kappa ^*(z^*)+\frac{U_\eta ^*(z^*)}{\xi ^2} -\left( N_\kappa ^*+\frac{N_\eta ^*}{\xi ^2} \right) \mathrm{e}^{-z^*}\sin (z^*)\nonumber \\&-\left( N_\kappa ^*+\frac{N_\eta ^*}{\xi ^2}+\frac{K_\kappa ^*}{2} +\frac{K_\eta ^*}{2\xi ^2} \right) \mathrm{e}^{-z^*}\cos (z^*),\end{aligned}$$

(75)

$$\begin{aligned} {\hat{v}}_1^*= & {} V_\kappa ^*(z^*)+\frac{V_\eta ^*(z^*)}{\xi ^2}\nonumber \\&+\,\left( N_\kappa ^*+\frac{N_\eta ^*}{\xi ^2}+\frac{K_\kappa ^*}{2} +\frac{K_\eta ^*}{2\xi ^2} \right) \mathrm{e}^{-z^*}\sin (z^*)\nonumber \\&-\left( N_\kappa ^*+\frac{N_\eta ^*}{\xi ^2} \right) \mathrm{e}^{-z^*}\cos (z^*), \end{aligned}$$

(76)

where

$$\begin{aligned} {\hat{K}}_{y1}^*= \lim _{{\hat{\kappa }},\eta \gg 1} \left( \frac{{\hat{K}}_{y1}}{\omega }\right) = -M_\kappa ^*-\frac{M_\eta ^*}{\xi ^2} +N_\kappa ^*+\frac{N_\eta ^*}{\xi ^2} +\frac{K_\kappa ^*}{2}+\frac{K_\eta ^*}{2\xi ^2}, \end{aligned}$$

(77)

in which the six coefficients $M_{\kappa ,\eta }^*, N_{\kappa ,\eta }^*$, and $K_{\kappa ,\eta }^*$ are given in Appendix.

In the inviscid core (i.e., outside the Ekman–EDL layer), the transverse velocity tends to zero, while the axial velocity tends to the following geostrophic limit:

$$\begin{aligned} \lim _{z^*\rightarrow \infty }{\hat{u}}^* ={\hat{K}}_{y0}^*+{\hat{\lambda }}^2{\hat{K}}_{y1}^* . \end{aligned}$$

(78)

6 Nonrotating channel

For completeness of this paper, let us also consider the case of EO flow of an Eyring fluid through a nonrotating parallel-plate channel. Only ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$ is considered here.

6.1 Exact solution

When the channel is not rotating ($\omega =0$), the secondary flow vanishes, and the flow becomes purely electroosmotic. In this case Eq. (8) reduces to

$$\begin{aligned} \frac{\mathrm{d}\tau _{xz}}{\mathrm{d} z}=\epsilon \kappa ^2E_x\psi . \end{aligned}$$

(79)

Upon integrating this equation, and using the symmetry condition, $\tau _{xz}=0$ at $z=0$, the shear stress distribution is obtained as follows

$$\begin{aligned} \tau _{xz}=-\tau _E\frac{\sinh (\kappa z)}{\cosh (\kappa )}, \end{aligned}$$

(80)

where $\tau _E=-\epsilon \kappa E_x\zeta _0$. Under simple shear, the rheological behavior of an Eyring fluid is given by Eq. (10). Combining Eqs. (10) and (80) gives

$$\begin{aligned} \frac{\mathrm{d} u}{\mathrm{d} z}=\frac{\tau _0}{\mu _0} \sinh \left[ -\frac{\tau _E\sinh (\kappa z)}{\tau _0 \cosh (\kappa )}\right] \end{aligned}$$

(81)

or, in dimensionless form,

Fig. 2

Axial and transverse velocity profiles ${\hat{u}}({\hat{z}}), {\hat{v}}({\hat{z}})$ for $\omega =10,\,50$ and ${\hat{\lambda }}=0,1,3,4$, where ${\hat{\kappa }}=10$ and ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$, under the condition of no lateral confinement. The solid lines and the circles denote results of the perturbation model and the numerical model, respectively. a Axial velocity for $\omega = 10$. b Transverse velocity for $\omega = 10$. c Axial velocity for $\omega = 50$. d Transverse velocity for $\omega = 50$

$$\begin{aligned} \frac{\mathrm{d} {\hat{u}}}{\mathrm{d} {\hat{z}}} =\frac{{\hat{\kappa }}}{{\hat{\lambda }}} \sinh \left[ -{\hat{\lambda }} \frac{\sinh ({\hat{\kappa }}{\hat{z}})}{\cosh ({\hat{\kappa }})}\right] . \end{aligned}$$

(82)

Integrating the preceding equation while applying the no-slip boundary condition gives a formal expression for the velocity,

$$\begin{aligned} {\hat{u}}({\hat{z}})=\frac{{\hat{\kappa }}}{{\hat{\lambda }}} \int _{{\hat{z}}}^1 \sinh \left[ {\hat{\lambda }} \frac{\sinh ({\hat{\kappa }}{\hat{z}})}{\cosh ({\hat{\kappa }})}\right] \mathrm{d} {\hat{z}} \quad \text { for } 0\le {\hat{z}}\le 1, \end{aligned}$$

(83)

where the integral can be numerically evaluated using Simpson’s rule. This velocity profile is an exact solution to the problem because it is applicable for any values of ${\hat{\lambda }}$. The flow rate in a nonrotating channel is then given by

$$\begin{aligned} {\hat{q}}=2 \int _0^1 {\hat{u}}({\hat{z}}) \mathrm{d}{\hat{z}}\quad \text { for } \omega =0, \end{aligned}$$

(84)

which is also found numerically.

6.2 Perturbation solution

Using the method of perturbation, an approximate solution can also be found for ${\hat{\lambda }}\ll 1$. For a nonrotating channel, the perturbation problems reduce to

$$\begin{aligned}&{\hat{u}}_0''+{\hat{\kappa }}^2{\hat{\psi }}=0,\end{aligned}$$

(85)

$$\begin{aligned}&{\hat{u}}_1''-{\hat{u}}_0'^{2}{\hat{u}}_0''/(2{\hat{\kappa }}^2)=0. \end{aligned}$$

(86)

The solutions to these problems can be readily found as follows

$$\begin{aligned}&{\hat{u}}_{\text {appr}}={\hat{u}}_0+{\hat{\lambda }}^2 {\hat{u}}_1 =1-\frac{\cosh ({\hat{\kappa }}{\hat{z}})}{\cosh ({\hat{\kappa }})}\nonumber \\&\quad -{\hat{\lambda }}^2 \left[ \frac{\cosh (3{\hat{\kappa }}{\hat{z}}) -9\cosh ({\hat{\kappa }}{\hat{z}})+9\cosh ({\hat{\kappa }})-\cosh (3{\hat{\kappa }}) }{72\cosh ^3({\hat{\kappa }})}\right] , \nonumber \\ \end{aligned}$$

(87)

which accords with the perturbation solutions (for zero interfacial slip) deduced recently by Goswami et al. [16].

In Table 1, we compare, for various values of ${\hat{\lambda }}$, the axial velocity as computed by the exact Eq. (83) with that by the approximate Eq. (87). In theory, the value of ${\hat{\lambda }}$ should be much smaller than unity for the perturbation solution to be close to the exact solution. In practice, the requirement can often be relaxed. Table 1 shows that the approximate values can be very close to the exact ones, even when ${\hat{\lambda }}=1$.

Fig. 3

Axial and transverse flow rates $({\hat{q}}_x,\, {\hat{q}}_y)$ as functions of ordering parameter ${\hat{\lambda }}$, for $\omega =10,\,50$, where ${\hat{\kappa }}=10$ and ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$, under the condition of no lateral confinement. The solid lines and the circles denote results of the perturbation model and the numerical model, respectively. a Axial flow rate for $\omega = 10$. b Transverse flow rate for $\omega = 10$. c Axial flow rate for $\omega = 50$. d Transverse flow rate for $\omega = 50$

7 Discussion

For electrokinetic transport in microchannels, the thickness of EDL typically ranges from 10  nm to 10 $\upmu \hbox {m}$, and the cross-sectional dimension of a rotating microchannel can vary over a wide range of $O(1-10^3)~\upmu \hbox {m}$ [17]. Hence, the normalized Debye parameter ${\hat{\kappa }}=\kappa h$ is usually O(10) or larger. To examine theoretical trends, we may also consider ${\hat{\kappa }}=O(1)$, however. Depending on the design, the rotation speed $\varOmega$ of a centrifuge can be as fast as $O(10^3)$rad/s. For a fluid with a kinematic viscosity of $10^{-6}~\hbox {m}^2\cdot \mathrm{s}^{-1}$, an Ekman layer is thinner than $O(100)~\upmu \hbox {m}$, which allows the rotation parameter $\omega$ to vary over a wide range. We shall consider $\omega \le 200$ in the following discussion.

7.1 Without lateral side walls

Although we have been considering flow in the presence of lateral confinement, our model can be readily adapted to the case of no lateral confinement. Without side walls, the channel will become open in both the axial and transverse directions. This amounts to rotating the EO flow between two parallel plates. To model this case, we may simply set the transverse pressure gradients ${\hat{K}}_{y0}=0$ and ${\hat{K}}_{y1}=0$ in Eqs. (31) and (34), respectively. Zero net flux conditions, as in Eqs. (32) and (35), are not imposed. In other words, by setting ${\hat{K}}_{y0}={\hat{K}}_{y1}=0$, our solutions deduced earlier will reduce to the solutions for the case of flow without lateral confinement. The O(1) problem is then exactly the same problem studied previously by Chang and Wang [30].

Let us first demonstrate the limit of validity of our perturbation model. To this end, we shall compare results with those generated by a numerical model that uses the original exact expression for the Eyring viscosity, as in Eq. (12). The objective is to check the upper bound of the ordering parameter ${\hat{\lambda }}$ within which the perturbation analysis, which is based on the simplified Eyring viscosity as in Eq. (16), may produce results in close agreement with the numerical solutions based on the full Eyring model.

Adopting an iterative finite-difference numerical scheme that we have recently developed for the rotating EO flow of viscoplastic material between two parallel plates [35], we may solve numerically the Cauchy momentum equations, where the full Eyring rheological model is used to describe the effective viscosity: ${\hat{\mu }}=\sinh ^{-1}({\hat{\lambda }}\hat{{\dot{\gamma }}})/({\hat{\lambda }}\hat{{\dot{\gamma }}})$.

In Fig. 2, we show the axial and transverse velocity profiles $({\hat{u}},{\hat{v}})$ for $\omega =10, 50$, where ${\hat{\kappa }}=10, {\hat{\zeta }}_1={\hat{\zeta }}_2=1$. For four values of the dimensionless relaxation time parameter, ${\hat{\lambda }}=0,1,3,4$, we compare the results generated by the perturbation model (solid lines) with those computed using the numerical model (circles). At ${\hat{\lambda }}=0$ (Newtonian limit), the two models are identical, as are their results, as expected. As remarked earlier, the perturbation analysis is in theory valid only when the ordering parameter is small. In practice, this condition can often be relaxed as far as the accuracy of results is concerned. We see here again when ${\hat{\lambda }}$ is as large as 1, the perturbation model can generate results that are still in close agreement with those obtained using the numerical model. The figure suggests that the close agreement may persist as long as ${\hat{\lambda }}<3$. The discrepancy between the two sets of results will become appreciable when ${\hat{\lambda }}>3$.

Fig. 4

(Color online) Leading-order axial and transverse velocity profiles, ${\hat{u}}_0({\hat{z}})$ and ${\hat{v}}_0({\hat{z}})$, for $\omega =0,40,200$ and ${\hat{\kappa }}=10,50$, where ${\hat{\zeta }}_1=2$ and ${\hat{\zeta }}_2=0$ (i.e., asymmetrical zeta potential distribution). a ${\hat{\kappa }}=10$. b ${\hat{\kappa }}=10$. c ${\hat{\kappa }}=50$. d ${\hat{\kappa }}=50$

The corresponding axial and transverse flow rates $({\hat{q}}_x,{\hat{q}}_y)$, as functions of the ordering parameter ${\hat{\lambda }}$, are shown in Fig. 3. This figure confirms our observation made earlier: the results yielded by the perturbation model are in close agreement with the numerical solutions as long as ${\hat{\lambda }}<3$. The difference is limited to 2 % or smaller. The error of the perturbation model will not be very significant until ${\hat{\lambda }}>3$.

A larger value of ${\hat{\lambda }}$ also amounts to a higher degree of shear thinning of the fluid. This will, as a matter of course, result in a larger flow rate under the same forcing. Figure 2 reveals that the shear-thinning-induced enhancement of the flow rate is caused mainly by an increase in the near-wall peak velocity. This can be explained by the fact that the shear stress is at its maximum at the wall, which will, by virtue of the shear-thinning rheology, lower the effective viscosity near the wall, thereby causing the fluid to flow more readily in this region for larger ${\hat{\lambda }}$. A similar shear-thinning effect on rotating EO flow velocity profiles has been reported by Xie and Jian [31].

7.2 With lateral side walls

Let us consider in the following sections the O(1) and $O({\hat{\lambda }}^2)$ perturbation problems for rotating EO flow subject to lateral confinement.

7.2.1 Newtonian fluid

We first look into the O(1) solution, corresponding to the Newtonian limiting case. This will extend the previous work by Ng and Qi [33], who studied the EO flow of a Newtonian fluid in a rotating channel with equal potentials on the upper and lower walls. The problem is reexamined here, allowing possibly unequal zeta potentials on the two walls.

Figure 4 shows velocity distributions in the axial and transverse directions, ${\hat{u}}_0({\hat{z}})$ and ${\hat{v}}_0({\hat{z}})$, for ${\hat{\zeta }}_1=2$ and ${\hat{\zeta }}_2=0$, or ${\hat{a}}={\hat{b}}=1$. Owing to the unequal zeta potentials, the axial velocity profiles are as a result asymmetrical about the centerline. The degree of asymmetry, however, decreases as the rotation rate increases. As $\omega$ gets larger, ${\hat{u}}({\hat{z}})$ becomes increasingly symmetrical about ${\hat{z}}=0$. One can reason that under the effect of rotation, the axial velocity in the interior will tend to a Taylor–Proudman profile [36], where the velocity gradient is essentially zero. This trend is clearly seen in Fig. 4a, c. For a rotation speed as high as $\omega =200$ or $\eta =10, {\hat{u}}_0$ is essentially uniform in the interior region, where the velocity, known as the geostrophic velocity, is given by ${\hat{K}}_{y0}/\omega$. Near the walls are the Ekman–EDL layers, where the velocity is affected by all the parameters: ${\hat{\kappa }}, \omega$, and ${\hat{K}}_{y0}$. As is typical for a Taylor–Proudman profile, the boundary layer exhibits an overshoot before matching the geostrophic core.

The transverse velocity profiles ${\hat{v}}_0({\hat{z}})$ shown in Fig. 4b, d exhibit a very different trend as $\omega$ increases. They are mostly antisymmetrical about the centerline. In other words, the transverse flow near one wall has largely the same distribution as, but is opposite in direction to, that near the other wall. The flow in one half of the channel counterbalances that in the other half of the channel. Also, the magnitude of the peak transverse velocity has a nonmonotonic relation with the rotation speed. In one half of the channel, the transverse flow is at its maximum magnitude for a finite value of $\omega$ and will diminish to zero at the two limits: $\omega \rightarrow 0$ and $\omega \rightarrow \infty$. This nonmonotonic dependence of the transverse flow on the rotation speed was observed previously by Chang and Wang [30].

Fig. 5

(Color online) Leading-order axial and transverse velocity profiles, ${\hat{u}}_0({\hat{z}})$ and ${\hat{v}}_0({\hat{z}})$, for $\omega =0,40,200$ and ${\hat{\kappa }}=10,50$, where ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$ (i.e., symmetrical zeta potential distribution). a ${\hat{\kappa }}=10$. b ${\hat{\kappa }}=10$. c ${\hat{\kappa }}=50$. d ${\hat{\kappa }}=50$

It is of interest to compare Figs. 4 and 5, which show the velocity distributions for the same values of ${\hat{\kappa }}$ and $\omega$ but for ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$, or ${\hat{a}}=1$ and ${\hat{b}}=0$. With the same ${\hat{a}}$, the corresponding cases shown in Figs. 4 and 5 have the same axial flow rate ${\hat{q}}_0$ and the same transverse pressure gradient ${\hat{K}}_{y0}$. The corresponding velocity profiles are, however, dramatically different. With equal zeta potentials, both the axial and transverse velocity profiles are always symmetrical about the centerline. The axial velocity in the interior, which is the Helmholtz–Smoluchowski velocity at $\omega =0$, is reduced when the geostrophic velocity takes over for $\omega \gg 1$. The reduction in the axial velocity is caused by a favorable pressure gradient in the transverse direction, which is induced to generate a zero net flux in this direction.

Fig. 6

(Color online) Leading- and first-order flow rates: a ${\hat{q}}_0$, b ${\hat{q}}_1$, as functions of $\omega$ for ${\hat{\kappa }}=1,10,50$, where ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$

Fig. 7

(Color online) Leading- and first-order flow rates: a ${\hat{q}}_0$, b ${\hat{q}}_1$, as functions of ${\hat{\kappa }}$ for $\omega =0,40,200$, where ${\hat{\zeta }}_1={\hat{\zeta }}_2=1$

Fig. 8

(Color online) Leading- and first-order axial and transverse velocity profiles in an Ekman–EDL layer: a ${\hat{u}}_0^*(z^*)$, b ${\hat{u}}_1^*(z^*)$, c ${\hat{v}}_0^*(z^*)$, d ${\hat{v}}_1^*(z^*)$, for various values of the modified dimensionless Debye parameter $\xi$

Fig. 9

(Color online) For the leading- and first-order axial velocities in an Ekman–EDL layer. a Ratio of peak to geostrophic velocity ${\tilde{u}}_{\mathrm{m}}^*={\hat{u}}_{\mathrm{m}}^*/{\hat{u}}_{\infty }^*$ as function of $\xi$. b Location of peak velocity ${\hat{z}}_{\mathrm{m}}^*$ as function of $\xi$

Among the cases shown in Figs. 4 and 5, the only case where the corresponding axial velocity profiles look alike is the one for ${\hat{\kappa }}=10$ and $\omega =200 (\eta =10)$. This suggests that, for the same ${\hat{a}}$, when ${\hat{\kappa }}$ and $\eta$ are both large and comparable to each other, the same Ekman–EDL axial flow will develop near each of the walls, irrespective of the distribution of zeta potentials on these walls.

In the symmetrical case, the transverse flow reverses direction, thereby satisfying the condition of a net zero flux, within one half of the channel. This is in sharp contrast to the transverse flow in the asymmetrical case. In the symmetrical case (Fig. 5), the transverse flow is positive near both the upper and lower walls. In the asymmetrical case (Fig. 4), the transverse flow is positive near the lower wall but negative near the upper wall. In either case, as $\omega$ increases, the transverse flow tends to zero in the geostrophic core.

On comparing Figs. 2 and 5, one can further see the following effects on flow owing to the lateral confinement. First, the net transverse flow is always negative in the case of no lateral confinement, but it is exactly zero in the case of lateral confinement. Second, for $\omega >0$, the axial flow rate is in general higher under the condition of lateral confinement than without lateral confinement. As explained earlier, at sufficiently high rotation speed, the flow in the interior is geostrophic where the velocity is proportional to the transverse pressure gradient. Therefore, the transverse pressure gradient that is induced in the case of lateral confinement but not in the case of no lateral confinement will bring forth a larger axial flow rate in the former than in the latter.

7.2.2 Shear-thinning effect

Recall that the $O({\hat{\lambda }}^2)$ solution is the correction to the leading-order solution to account for the shear-thinning effect of the fluid rheology.

We show in Figs. 6 and 7 the O(1) and $O({\hat{\lambda }}^2)$ flow rates, ${\hat{q}}_0$ and ${\hat{q}}_1$, as functions of $\omega$ and ${\hat{\kappa }}$. From these figures, the following observations can be made. First, for both orders, the flow rate decreases with increasing $\omega$. The decreasing effect on the flow rate due to rotation is most appreciable when ${\hat{\kappa }}\approx 10$. For ${\hat{\kappa }}> 50$, the effect of rotation on the flow rate is much weakened. Second, the figures reveal that the flow rates ${\hat{q}}_0$ and ${\hat{q}}_1$ vary with the parameters ${\hat{\kappa }}$ and $\omega$ in almost the same manner. Both flow rates are subject to nearly the same rate of change with respect to each of the two parameters. This means that the effect of rotation on the EO flow is qualitatively the same whether the fluid is Newtonian or Eyring, that is, irrespective of ${\hat{\lambda }}$. Third, ${\hat{q}}_1$ is in general approximately 10 times smaller than ${\hat{q}}_0$. This means that for the shear-thinning effect to be appreciable, the parameter ${\hat{\lambda }}$ must be sufficiently large. As was found earlier, our perturbation model may yield reasonably accurate results even when ${\hat{\lambda }}$ is as large as 3. Hence, as long as $\lambda =O(1)$, for which our perturbation solutions remain accurate, the shear-thinning behavior of the fluid may enhance the flow by an amount comparable to the base Newtonian flow.

We finally show in Fig. 8 the O(1) and $O({\hat{\lambda }}^2)$ velocity profiles in the Ekman–EDL layer, $({\hat{u}}_0^*, {\hat{v}}_0^*)$ and $({\hat{u}}_1^*, {\hat{v}}_1^*)$, as computed by Eqs. (72), (73), (75), and (76). The key features of the leading-order velocity profiles $({\hat{u}}_0^*, {\hat{v}}_0^*)$ were discussed previously by Ng and Qi [33]. It is seen here that the velocity profiles of the two orders vary with the parameter $\xi$, mostly in the same manner. The profiles of ${\hat{u}}_1^*$ have a sharper overshoot, which is located closer to the wall, compared with the corresponding profiles of ${\hat{u}}_0^*$. Otherwise, the velocity profiles of the two orders look similar in form. The first-order velocity is in general an order of magnitude smaller than the leading-order velocity. Nevertheless, after multiplying the ordering parameter ${\hat{\lambda }}^2$, where ${\hat{\lambda }}$ can be as large as 3, the first-order correction can be a finite fraction of the leading-order solution, as was noted earlier. We have shown here that the validity of the present perturbation analysis can be extended to a range where the shear-thinning rheology as described by the Eyring model may have a finite effect on the flow.

To further look into the difference between the leading- and first-order axial velocity profiles in the Ekman–EDL layer, we show in Fig. 9 two quantities as a function of $\xi$ in panels a and b. The quantity ${\tilde{u}}_{\mathrm{m}}^*={\hat{u}}_{\mathrm{m}}^*/{\hat{u}}_{\infty }^*$ (Fig. 9a) is a ratio of the maximum to the geostrophic core axial velocities, while ${\hat{z}}_{\mathrm{m}}^*$ (Fig. 9b) is the location where the axial velocity reaches its maximum. The degree of overshoot of the axial velocity profile is measured by the quantity ${\tilde{u}}_{\mathrm{m}}^*$, which is always more pronounced in the first-order than in the leading-order profile, or a sharper overshoot of ${\hat{u}}^*_1$ than that of ${\hat{u}}^*_0$. As $\xi$ increases, the overshoot of ${\hat{u}}^*_1$ will become milder, which also can be seen from Fig. 8b. For the leading-order axial velocity ${\hat{u}}_0^*$, it does not follow a monotonous trend as $\xi$ increases, although the change in the overshoot is very gentle within the range of $\xi$ shown in the figure. There are also distinct trends of dependence of ${\hat{z}}_{\mathrm{m}}^*$ on $\xi$ for the leading- and first-order axial velocities. In the range $0\le \xi \le 1$, the location of the peak ${\hat{u}}^*_1$ varies slightly as $\xi$ increases, while it is always closer to the wall than for ${\hat{u}}^*_0$. As $\xi$ further increases, ${\hat{z}}_{\mathrm{m}}^*$ will decrease monotonically, for both the leading- and first-order axial velocities.

8 Concluding remarks

We have performed a perturbation analysis on the EO flow of a mildly shear-thinning fluid through a very wide rectangular channel that rotates about an axis perpendicular to its own. The fluid rheology is described by the Eyring model, which has the Newtonian model as its limit at small shear rates. We deduced solutions to the leading-order as well as the first-order problems, where in the leading-order problem we allowed the zeta potentials on the upper and lower walls to be different. We have seen how the zeta potential distribution on the two walls may affect the axial and transverse velocity profiles. We have explained the effect of rotation on the velocity profiles in terms of the Taylor–Proudman profile, geostrophic interior, and Ekman–EDL boundary layer. On comparing with numerical solutions that take into account the full Eyring model, our perturbation analysis is shown to be able to generate accurate results as long as the dimensionless relaxation time parameter does not exceed order unity. We have also shown that the first-order flow rate is always positive, confirming that the shear-thinning rheology of an Eyring fluid always enhances the flow rate. Also, the dependence of the first-order flow on the electrokinetic and rotation parameters is qualitatively almost the same as that of the leading-order flow. We may therefore conclude that, within the range of validity of the present perturbation model, the higher-order shear-thinning correction can be a finite fraction of the base Newtonian fluid flow.

In this work, a no-slip boundary condition was assumed, which is applicable when the substrate is a wetting substance. When the substrate is nonwetting, hydrophobic interactions may give rise to an apparent wall slip [37] on the edge of the Stern layer. It will be of interest in the future to look into such apparent slip effects on electrokinetic flow [16, 38] in a rotating channel.

Appendix

This Appendix contains the lengthy expressions for functions or parameters introduced in Sects. 4 and 5. In Eqs. (58) and (59), the four functions are given by

$$\begin{aligned} U_{\kappa }({\hat{z}})= & {} \frac{{\hat{\kappa }}^2\eta ^2C_1C_2}{3({\hat{\kappa }}^4+4\eta ^4)} {{\mathrm{sech}}}({\hat{\kappa }})\cosh ({\hat{\kappa }} {\hat{z}})\nonumber \\&+\,{{\mathrm{sech}}}^3({\hat{\kappa }}) \cosh ({\hat{\kappa }} {\hat{z}}) [U_1 \sinh ^2({\hat{\kappa }} {\hat{z}})+U_2\cosh ^2({\hat{\kappa }} z)]\nonumber \\&+\,{{\mathrm{sech}}}^2({\hat{\kappa }})\cosh (2 {\hat{\kappa }} {\hat{z}}) [U_3\sin (\eta {\hat{z}}) \sinh (\eta {\hat{z}})\nonumber \\&+\,U_6 \cos (\eta {\hat{z}}) \cosh (\eta {\hat{z}})]\nonumber \\&+\,{{\mathrm{sech}}}^2({\hat{\kappa }})\sinh (2 {\hat{\kappa }} {\hat{z}})[U_4\sin (\eta {\hat{z}})\cosh (\eta {\hat{z}})\nonumber \\&+\,U_5\cos (\eta {\hat{z}}) \sinh (\eta {\hat{z}})]\nonumber \\&+\,{{\mathrm{sech}}}({\hat{\kappa }})\cosh ({\hat{\kappa }} {\hat{z}}) [U_7 \sin (2 \eta {\hat{z}})\sinh (2 \eta {\hat{z}})\nonumber \\&+\,U_{10}\cos (2 \eta {\hat{z}})\cosh (2\eta {\hat{z}})]\nonumber \\&+\,{{\mathrm{sech}}}({\hat{\kappa }})\sinh ({\hat{\kappa }} {\hat{z}}) [U_8\sin (2 \eta {\hat{z}})\cosh (2 \eta {\hat{z}})\nonumber \\&+\, U_9\cos (2\eta {\hat{z}}) \sinh (2 \eta {\hat{z}})]\nonumber \\&+\,U_{11}{{\mathrm{sech}}}({\hat{\kappa }}) \sin (2 \eta {\hat{z}}) \sinh ({\hat{\kappa }}{\hat{z}})\nonumber \\&+\,U_{12}{{\mathrm{sech}}}({\hat{\kappa }}) \cos (2\eta {\hat{z}}) \cosh ({\hat{\kappa }} {\hat{z}})\nonumber \\&+\,U_{13}{{\mathrm{sech}}}({\hat{\kappa }}) \sinh (2\eta {\hat{z}})\sinh ({\hat{\kappa }}{\hat{z}})\nonumber \\&+\,U_{14}{{\mathrm{sech}}}({\hat{\kappa }}) \cosh (2\eta {\hat{z}})\cosh ({\hat{\kappa }}{\hat{z}}), \end{aligned}$$

(A1)

$$\begin{aligned} U_{\eta }({\hat{z}})= & {} \sin (\eta {\hat{z}})\sin (2\eta {\hat{z}}) [U_{15}\sinh (2\eta {\hat{z}}) \sinh (\eta {\hat{z}})\nonumber \\&+\,U_{16}\cosh (2\eta {\hat{z}})\cosh (\eta {\hat{z}})] \nonumber \\&+\,\sin (\eta {\hat{z}})\cos (2\eta {\hat{z}}) [U_{17}\cosh (2\eta {\hat{z}})\sinh (\eta {\hat{z}})\nonumber \\&+\,U_{18}\sinh (2\eta {\hat{z}})\cosh (\eta {\hat{z}})]\nonumber \\&+\, \cos (\eta {\hat{z}})\sinh (\eta {\hat{z}}) [U_{19}\sin (2\eta {\hat{z}})\cosh (2\eta {\hat{z}})\nonumber \\&+\,U_{20}\cos (2\eta {\hat{z}}) \sinh (2\eta {\hat{z}})]\nonumber \\&+\,U_{21}\sin (\eta {\hat{z}}) \sin (2\eta {\hat{z}}) \cosh (\eta {\hat{z}})\nonumber \\&+\,U_{22}\sin (\eta {\hat{z}})\cos (2\eta {\hat{z}})\sinh (\eta {\hat{z}})\nonumber \\&+\,U_{23}\sin (\eta {\hat{z}})\sinh (\eta {\hat{z}}) \cosh (2\eta {\hat{z}})\nonumber \\&+\,U_{24}\cos (\eta {\hat{z}}) \sinh (\eta {\hat{z}}) \sinh (2\eta {\hat{z}}),\end{aligned}$$

(A2)

$$\begin{aligned} V_\kappa ({\hat{z}})= & {} \frac{{\hat{\kappa }}^2\eta ^2( C_1^2-C_2^2)}{6({\hat{\kappa }}^4+4\eta ^4)} {{\mathrm{sech}}}({\hat{\kappa }})\cosh ({\hat{\kappa }}{\hat{z}})\nonumber \\&+\,\frac{{\hat{\kappa }}^4{{\mathrm{sech}}}^2({\hat{\kappa }})}{6({\hat{\kappa }}^4+4\eta ^4)} [C_2\cos (\eta {\hat{z}}) \cosh (\eta {\hat{z}})\nonumber \\&-\,C_1 \sin (\eta {\hat{z}}) \sinh (\eta {\hat{z}})] \nonumber \\&+\,V_1 {{\mathrm{sech}}}^3({\hat{\kappa }})\cosh ({\hat{\kappa }} {\hat{z}}) \sinh ^2({\hat{\kappa }} {\hat{z}})\nonumber \\&+\,V_2{{\mathrm{sech}}}^3({\hat{\kappa }})\cosh ^3({\hat{\kappa }} z)\nonumber \\&+\,V_3{{\mathrm{sech}}}^2({\hat{\kappa }}) \sin (\eta {\hat{z}}) \sinh (\eta {\hat{z}})\nonumber \\&+\,V_4 {{\mathrm{sech}}}^2({\hat{\kappa }}) \cos (\eta {\hat{z}}) \cosh (\eta {\hat{z}})\nonumber \\&+\,{{\mathrm{sech}}}^2({\hat{\kappa }})\cosh (2 {\hat{\kappa }}{\hat{z}}) [V_5 \sin (\eta {\hat{z}}) \sinh (\eta {\hat{z}})\nonumber \\&+\,V_8 \cos (\eta {\hat{z}}) \cosh (\eta {\hat{z}}) ] \nonumber \\&+\, {{\mathrm{sech}}}^2({\hat{\kappa }})\sinh (2 {\hat{\kappa }} {\hat{z}}) [V_6\sin (\eta {\hat{z}})\cosh (\eta {\hat{z}})\nonumber \\&+\, V_7\cos (\eta {\hat{z}}) \sinh (\eta {\hat{z}})]\nonumber \\&+\,V_9{{\mathrm{sech}}}({\hat{\kappa }}) \sin (2 \eta {\hat{z}}) \sinh ({\hat{\kappa }}{\hat{z}})\nonumber \\&+\,V_{10} {{\mathrm{sech}}}({\hat{\kappa }})\cos (2 \eta {\hat{z}}) \cosh ({\hat{\kappa }} {\hat{z}})\nonumber \\&+\,V_{11}{{\mathrm{sech}}}({\hat{\kappa }}) \sinh (2 \eta {\hat{z}}) \sinh ({\hat{\kappa }}{\hat{z}})\nonumber \\&+\,V_{12} {{\mathrm{sech}}}({\hat{\kappa }})\cosh (2\eta {\hat{z}})\cosh ({\hat{\kappa }}{\hat{z}})\nonumber \\&+\, {{\mathrm{sech}}}({\hat{\kappa }})\cosh ({\hat{\kappa }}{\hat{z}}) [V_{13}\sin (2\eta {\hat{z}}) \sinh (2\eta {\hat{z}})\nonumber \\&+\,V_{16} \cos (2\eta {\hat{z}})\cosh (2\eta {\hat{z}}) ]\nonumber \\&+\, {{\mathrm{sech}}}({\hat{\kappa }})\sinh ({\hat{\kappa }}{\hat{z}}) [V_{14}\sin (2 \eta {\hat{z}})\cosh (2\eta {\hat{z}})\nonumber \\&+\, V_{15}\cos (2\eta {\hat{z}}) \sinh (2\eta {\hat{z}})],\end{aligned}$$

(A3)

$$\begin{aligned} V_\eta ({\hat{z}})= & {} -\frac{5}{12} (C_1^2+C_2^2) [C_1\cos (\eta {\hat{z}}) \cosh (\eta {\hat{z}})\nonumber \\&-\,C_2\sin (\eta {\hat{z}}) \sinh (\eta {\hat{z}})]\nonumber \\&+\,V_{17} \sin (\eta {\hat{z}}) \sin (2\eta {\hat{z}})\cosh (\eta {\hat{z}})\nonumber \\&+\,V_{18} \sin (\eta {\hat{z}})\cos (2\eta {\hat{z}}) \sinh (\eta {\hat{z}}) \nonumber \\&+\,V_{19}\cos (\eta {\hat{z}}) \sin (2\eta {\hat{z}}) \sinh (\eta {\hat{z}})\nonumber \\&+\,V_{20}\cos (\eta {\hat{z}}) \cos (2\eta {\hat{z}}) \cosh (\eta {\hat{z}})\nonumber \\&+\,V_{21}\sin (\eta {\hat{z}}) \sinh (\eta {\hat{z}})\cosh (2\eta {\hat{z}})\nonumber \\&+\,V_{22}\sin (\eta {\hat{z}})\cosh (\eta {\hat{z}})\sinh (2\eta {\hat{z}})\nonumber \\&+\,V_{23}\cos (\eta {\hat{z}}) \sinh (\eta {\hat{z}}) \sinh (2\eta {\hat{z}})\nonumber \\&+\,V_{24}\cos (\eta {\hat{z}}) \cosh (\eta {\hat{z}}) \cosh (2\eta {\hat{z}})\nonumber \\&+\,\sin (\eta {\hat{z}})\sin (2\eta {\hat{z}}) [V_{25}\sinh (\eta {\hat{z}}) \sinh (2\eta {\hat{z}})\nonumber \\&+\, V_{26}\cosh (\eta {\hat{z}})\cosh (2\eta {\hat{z}})]\nonumber \\&+\, \sin (\eta {\hat{z}})\cos (2\eta {\hat{z}}) [V_{27}\sinh (\eta {\hat{z}})\cosh (2\eta {\hat{z}})\nonumber \\&+\, V_{28}\cosh (\eta {\hat{z}})\sinh (2\eta {\hat{z}})]\nonumber \\&+\,\cos (\eta {\hat{z}})\sin (2\eta {\hat{z}}) [V_{29}\sinh (\eta {\hat{z}})\cosh (2\eta {\hat{z}})\nonumber \\&+\, V_{30}\cosh (\eta {\hat{z}}) \sinh (2\eta {\hat{z}})]\nonumber \\&+\,\cos (\eta {\hat{z}}) \cos (2\eta {\hat{z}}) [V_{31}\sinh (\eta {\hat{z}}) \sinh (2\eta {\hat{z}})\nonumber \\&+\, V_{32}\cosh (\eta {\hat{z}}) \cosh (2\eta {\hat{z}})], \end{aligned}$$

(A4)

where, with the introduction of $\xi ={\hat{\kappa }}/\eta$ (for $\eta \ne 0$), the constants $U_{1{-}24}$ and $V_{1{-}32}$ are given as follows

$$\begin{aligned} U_1= & {} \frac{\xi ^8 \left( -27\xi ^8+56\xi ^4+16\right) }{2 \left( \xi ^4+4\right) ^3 \left( 81 \xi ^4+4\right) },\end{aligned}$$

(A5)

$$\begin{aligned} U_2= & {} \frac{\xi ^{12} \left( 9 \xi ^4-44\right) }{\left( \xi ^4+4\right) ^3 \left( 81 \xi ^4+4\right) },\end{aligned}$$

(A6)

$$\begin{aligned} U_3= & {} \frac{\xi ^6\left[ \left( 3 \xi ^4-10\right) C_1-\xi ^2 C_2\right] }{24 \left( \xi ^4-1\right) \left( \xi ^4+4\right) ^2}, \end{aligned}$$

(A7)

$$\begin{aligned} U_4= & {} \frac{\xi ^3\left[ 2 \xi ^2 \left( \xi ^4+1\right) \left( C_1+C_2\right) -\left( 3 \xi ^8-2 \xi ^4-4\right) \left( C_1-C_2\right) \right] }{24 \left( \xi ^4-1\right) \left( \xi ^4+4\right) ^2},\nonumber \\\end{aligned}$$

(A8)

$$\begin{aligned} U_5= & {} \frac{\xi ^3\left[ 2 \xi ^2 \left( \xi ^4+1\right) \left( C_1-C_2\right) +\left( 3 \xi ^8-2 \xi ^4-4\right) \left( C_1+C_2\right) \right] }{24 \left( \xi ^4-1\right) \left( \xi ^4+4 \right) ^2},\nonumber \\ \end{aligned}$$

(A9)

$$\begin{aligned} U_6= & {} -\frac{\xi ^6\left[ \xi ^2C_1+\left( 3\xi ^4-10\right) C_2\right] }{24 \left( \xi ^4-1\right) \left( \xi ^4+4\right) ^2},\end{aligned}$$

(A10)

$$\begin{aligned} U_7= & {} \frac{\xi ^2\left[ \left( \xi ^4+180\right) \left( C_1^2-C_2^2\right) +16\xi ^2C_1 C_2 \right] }{6 \left( \xi ^4+4\right) \left( \xi ^4+324\right) }, \end{aligned}$$

(A11)

$$\begin{aligned} U_8= & {} -\frac{\xi \left[ \left( \xi ^4\,{-}\,12\xi ^2+108\right) \left( C_1^2\,{-}\,C_2^2\right) +2 \left( \xi ^4+12\xi ^2+108\right) C_1 C_2\right] }{3 \left( \xi ^4+4\right) \left( \xi ^4+324\right) },\nonumber \\\end{aligned}$$

(A12)

$$\begin{aligned} U_9= & {} -\frac{\xi \left[ \left( \xi ^4+12\xi ^2+108\right) \left( C_1^2\,{-}\,C_2^2\right) \,{-}\,2 \left( \xi ^4\,{-}\,12 \xi ^2+108\right) C_1 C_2\right] }{3\left( \xi ^4+4\right) \left( \xi ^4+324\right) },\nonumber \\ \end{aligned}$$

(A13)

$$\begin{aligned} U_{10}= & {} \frac{\xi ^2\left[ 4 \xi ^2 \left( C_1^2-C_2^2\right) -\left( \xi ^4+180\right) C_1 C_2\right] }{3 \left( \xi ^4+4\right) \left( \xi ^4+324\right) },\end{aligned}$$

(A14)

$$\begin{aligned} U_{11}= & {} \left[ \frac{2\xi \left( \xi ^2+2\right) \left( \xi ^2+10\right) }{3 \left( \xi ^4+4\right) \left( \xi ^4+16\xi ^2+100\right) }\right] \left( C_1^2+C_2^2\right) ,\nonumber \\\end{aligned}$$

(A15)

$$\begin{aligned} U_{12}= & {} \left[ \frac{\xi ^2\left( \xi ^4+12\xi ^2+44\right) }{3\left( \xi ^4+4 \right) \left( \xi ^4+16\xi ^2+100\right) }\right] \left( C_1^2+C_2^2\right) ,\nonumber \\\end{aligned}$$

(A16)

$$\begin{aligned} U_{13}= & {} \left[ \frac{2\xi \left( \xi ^2-10\right) \left( \xi ^2-2\right) }{3\left( \xi ^4+4\right) \left( \xi ^4-16\xi ^2+100\right) }\right] \left( C_1^2+C_2^2\right) ,\nonumber \\\end{aligned}$$

(A17)

$$\begin{aligned} U_{14}= & {} -\left[ \frac{\xi ^2\left( \xi ^4-12\xi ^2+44\right) }{3\left( \xi ^4+4 \right) \left( \xi ^4-16\xi ^2+100\right) }\right] \left( C_1^2+C_2^2\right) ,\nonumber \\\end{aligned}$$

(A18)

$$\begin{aligned} U_{15}= & {} -C_2 \left( C_1^2+C_2^2\right) /40,\end{aligned}$$

(A19)

$$\begin{aligned} U_{16}= & {} \left( -4 C_1^3+3 C_1^2 C_2-4 C_1 C_2^2+3 C_2^3\right) /240,\end{aligned}$$

(A20)

$$\begin{aligned} U_{17}= & {} -C_1 \left( C_1^2+C_2^2\right) /40,\end{aligned}$$

(A21)

$$\begin{aligned} U_{18}= & {} \left( 3 C_1^3+4 C_1^2 C_2+3 C_1 C_2^2+4 C_2^3\right) /240,\end{aligned}$$

(A22)

$$\begin{aligned} U_{19}= & {} \left( 3 C_1^3-4 C_1^2 C_2+3 C_1 C_2^2-4 C_2^3\right) /240,\end{aligned}$$

(A23)

$$\begin{aligned} U_{20}= & {} -\left( 4 C_1^3+3 C_1^2 C_2+4 C_1 C_2^2+3 C_2^3\right) /240,\end{aligned}$$

(A24)

$$\begin{aligned} U_{21}= & {} \left( 4 C_1^3-3 C_1^2 C_2+4 C_1 C_2^2-3 C_2^3\right) /48,\end{aligned}$$

(A25)

$$\begin{aligned} U_{22}= & {} -\left( 3 C_1^3+4 C_1^2 C_2+3 C_1 C_2^2+4 C_2^3\right) /48,\end{aligned}$$

(A26)

$$\begin{aligned} U_{23}= & {} -\left( 3 C_1^3-4 C_1^2 C_2+3 C_1 C_2^2-4 C_2^3\right) /48,\end{aligned}$$

(A27)

$$\begin{aligned} U_{24}= & {} \left( 4 C_1^3+3 C_1^2 C_2+4 C_1 C_2^2+3 C_2^3\right) /48,\end{aligned}$$

(A28)

$$\begin{aligned} V_1= & {} -\frac{16 \xi ^{10} \left( 3 \xi ^4+2\right) }{\left( \xi ^4+4\right) ^3 \left( 81\xi ^4+4\right) },\end{aligned}$$

(A29)

$$\begin{aligned} V_2= & {} \frac{2\xi ^{10}\left( 19\xi ^4-4\right) }{\left( \xi ^4+4\right) ^3 \left( 81\xi ^4+4\right) },\end{aligned}$$

(A30)

$$\begin{aligned} V_3= & {} \frac{\xi ^4 \left[ \left( 3\xi ^4+4\right) C_1-4\xi ^2 C_2\right] }{12 \left( \xi ^4+4\right) ^2},\end{aligned}$$

(A31)

$$\begin{aligned} V_4= & {} -\frac{\xi ^4 \left[ 4\xi ^2C_1+\left( 3\xi ^4+4\right) C_2\right] }{12 \left( \xi ^4+4\right) ^2},\end{aligned}$$

(A32)

$$\begin{aligned} V_5= & {} -\frac{\xi ^4\left[ \left( -9 \xi ^4+8\right) C_1+\xi ^2 \left( \xi ^4+6 \right) C_2\right] }{24 \left( \xi ^4-1\right) \left( \xi ^4+4\right) ^2}, \end{aligned}$$

(A33)

$$\begin{aligned} V_6= & {} \frac{\xi ^3\left[ \left( \xi ^8+6\xi ^4-4\right) \left( C_1+C_2\right) -2\xi ^2\left( 3\xi ^4 -1\right) \left( C_1-C_2\right) \right] }{24 \left( \xi ^4-1\right) \left( \xi ^4+4\right) ^2},\nonumber \\\end{aligned}$$

(A34)

$$\begin{aligned} V_7= & {} \frac{\xi ^3\left[ \left( \xi ^8+6\xi ^4-4\right) \left( C_1-C_2\right) +2\xi ^2\left( 3\xi ^4 -1\right) \left( C_1+C_2\right) \right] }{24 \left( \xi ^4-1\right) \left( \xi ^4+4\right) ^2},\nonumber \\ \end{aligned}$$

(A35)

$$\begin{aligned} V_8= & {} -\frac{\xi ^4\left[ \xi ^2\left( \xi ^4+6\right) C_1+\left( 9 \xi ^4-8 \right) C_2\right] }{24 \left( \xi ^4-1\right) \left( \xi ^4+4\right) ^2},\end{aligned}$$

(A36)

$$\begin{aligned} V_9= & {} \frac{16\xi \left( \xi ^2+5\right) \left( C_1^2+C_2^2\right) }{3 \left( \xi ^4+4\right) \left( \xi ^4+16\xi ^2+100\right) },\end{aligned}$$

(A37)

$$\begin{aligned} V_{10}= & {} \frac{4\xi ^2\left( \xi ^2+2\right) \left( C_1^2+C_2^2\right) }{3 \left( \xi ^4+4\right) \left( \xi ^4+16\xi ^2+100\right) },\end{aligned}$$

(A38)

$$\begin{aligned} V_{11}= & {} \frac{16\xi \left( \xi ^2-5\right) \left( C_1^2+C_2^2\right) }{3\left( \xi ^4+4\right) \left( \xi ^4-16 \xi ^2 +100\right) },\end{aligned}$$

(A39)

$$\begin{aligned} V_{12}= & {} -\frac{4\xi ^2\left( \xi ^2-2\right) \left( C_1^2+C_2^2\right) }{3\left( \xi ^4+4\right) \left( \xi ^4-16 \xi ^2 +100\right) },\end{aligned}$$

(A40)

$$\begin{aligned} V_{13}= & {} -\frac{\xi ^2\left[ -4\xi ^2 (C_1^2-C_2^2)+\left( \xi ^4+180\right) C_1 C_2\right] }{3 \left( \xi ^4+4\right) \left( \xi ^4+324\right) }, \end{aligned}$$

(A41)

$$\begin{aligned} V_{14}= & {} -\frac{\xi \left[ \left( \xi ^4+12\xi ^2+108\right) (C_1^2-C_2^2)-2 \left( \xi ^4-12\xi ^2+108\right) C_1 C_2\right] }{3 \left( \xi ^4+4\right) \left( \xi ^4+324\right) },\nonumber \\\end{aligned}$$

(A42)

$$\begin{aligned} V_{15}= & {} \frac{\xi \left[ \left( \xi ^4-12\xi ^2+108\right) (C_1^2-C_2^2)+2 \left( \xi ^4+12\xi ^2+108\right) C_1 C_2\right] }{3 \left( \xi ^4+4\right) \left( \xi ^4+324\right) },\nonumber \\ \end{aligned}$$

(A43)

$$\begin{aligned} V_{16}= & {} -\frac{\xi ^2\left[ \left( \xi ^4+180\right) (C_1^2-C_2^2)+16 \xi ^2 C_1 C_2\right] }{6 \left( \xi ^4+4\right) \left( \xi ^4+324\right) },\end{aligned}$$

(A44)

$$\begin{aligned} V_{17}= & {} \left( 2 C_1^3-5 C_1^2 C_2+2 C_1 C_2^2-5 C_2^3\right) /24,\end{aligned}$$

(A45)

$$\begin{aligned} V_{18}= & {} \left( C_1^3+5 C_1^2 C_2+C_1 C_2^2+5 C_2^3\right) /24, \end{aligned}$$

(A46)

$$\begin{aligned} V_{19}= & {} -\left( 6 C_1^3+7 C_1^2 C_2+6 C_1 C_2^2+7 C_2^3\right) /48, \end{aligned}$$

(A47)

$$\begin{aligned} V_{20}= & {} \left( 7 C_1^3-6 C_1^2 C_2+7 C_1 C_2^2-6 C_2^3\right) /48, \end{aligned}$$

(A48)

$$\begin{aligned} V_{21}= & {} -\left( C_1^3-5 C_1^2 C_2+C_1 C_2^2-5 C_2^3\right) /24, \end{aligned}$$

(A49)

$$\begin{aligned} V_{22}= & {} \left( 6 C_1^3-7 C_1^2 C_2+6 C_1 C_2^2-7 C_2^3\right) /48, \end{aligned}$$

(A50)

$$\begin{aligned} V_{23}= & {} -\left( 2 C_1^3+5 C_1^2 C_2+2 C_1 C_2^2+5 C_2^3\right) /24, \end{aligned}$$

(A51)

$$\begin{aligned} V_{24}= & {} \left( 7 C_1^3+6 C_1^2 C_2+7 C_1 C_2^2+6 C_2^3\right) /48, \end{aligned}$$

(A52)

$$\begin{aligned} V_{25}= & {} C_1 \left( C_1^2+C_2^2\right) /60, \end{aligned}$$

(A53)

$$\begin{aligned} V_{26}= & {} -\left( 7 C_1^3-4 C_1^2 C_2+7 C_1 C_2^2-4 C_2^3\right) /240, \end{aligned}$$

(A54)

$$\begin{aligned} V_{27}= & {} C_2 \left( C_1^2+C_2^2\right) /15, \end{aligned}$$

(A55)

$$\begin{aligned} V_{28}= & {} \left( 4 C_1^3-13 C_1^2 C_2+4 C_1 C_2^2-13 C_2^3\right) /240, \end{aligned}$$

(A56)

$$\begin{aligned} V_{29}= & {} -\left( 4 C_1^3+13 C_1^2 C_2+4 C_1 C_2^2+13 C_2^3\right) /240, \end{aligned}$$

(A57)

$$\begin{aligned} V_{30}= & {} C_2 \left( C_1^2+C_2^2\right) /24, \end{aligned}$$

(A58)

$$\begin{aligned} V_{31}= & {} \left( 7 C_1^3+4 C_1^2 C_2+7 C_1 C_2^2+4 C_2^3\right) /240, \end{aligned}$$

(A59)

$$\begin{aligned} V_{32}= & {} -C_1 \left( C_1^2+C_2^2\right) /24, \end{aligned}$$

(A60)

in which $C_1$ and $C_2$ are given in Eqs. (44) and (45), respectively.

Setting ${\hat{z}}=1$ in the functions $U_\kappa ({\hat{z}}), U_\eta ({\hat{z}}), V_\kappa ({\hat{z}})$, and $V_\eta ({\hat{z}})$, we obtain the parameters $M_{\kappa , \eta }$ and $N_{\kappa , \eta }$ as follows

$$\begin{aligned} M_\kappa= & {} \frac{\xi ^2 C_1C_2}{3\left( \xi ^4+4\right) } +U_1\tanh ^2({\hat{\kappa }} )+U_2\nonumber \\&+\,U_3 \left[ 1+\tanh ^2({\hat{\kappa }})\right] \sin (\eta ) \sinh (\eta ) \nonumber \\&+\, 2\tanh ({\hat{\kappa }}) \left[ U_4\sin (\eta ) \cosh (\eta ) + U_5\cos (\eta ) \sinh (\eta )\right] \nonumber \\&+\,U_6\left[ 1+\tanh ^2({\hat{\kappa }})\right] \cos (\eta ) \cosh (\eta )\nonumber \\&+\, U_7 \sin (2 \eta ) \sinh (2 \eta )\nonumber \\&+\, \tanh ({\hat{\kappa }})[U_8\sin (2 \eta ) \cosh (2 \eta )\nonumber \\&+\, U_9\cos (2 \eta ) \sinh (2 \eta )] \nonumber \\&+\, U_{10}\cos (2 \eta ) \cosh (2 \eta )\nonumber \\&+\,U_{11}\tanh ({\hat{\kappa }} )\sin (2 \eta ) +U_{12} \cos (2 \eta )\nonumber \\&+\, U_{13}\tanh ({\hat{\kappa }})\sinh (2\eta )+U_{14}\cosh (2 \eta ),\end{aligned}$$

(A61)

$$\begin{aligned} M_\eta= & {} \sin (\eta ) \sin (2 \eta )[U_{15} \sinh (\eta ) \sinh (2 \eta )\nonumber \\&+\,U_{16} \cosh (\eta ) \cosh (2 \eta )]\nonumber \\&+\, \sin (\eta ) \cos (2 \eta )[U_{17} \sinh (\eta ) \cosh (2 \eta )\nonumber \\&+\, U_{18} \cosh (\eta ) \sinh (2 \eta )]\nonumber \\&+\, \cos (\eta )[U_{19} \sin (2 \eta ) \sinh (\eta ) \cosh (2 \eta )\nonumber \\&+\, U_{20} \cos (2 \eta ) \sinh (\eta ) \sinh (2 \eta )]\nonumber \\&+\, U_{21} \sin (\eta ) \sin (2 \eta ) \cosh (\eta )\nonumber \\&+\, U_{22} \sin (\eta ) \cos (2 \eta ) \sinh (\eta )\nonumber \\&+\, U_{23} \sin (\eta ) \sinh (\eta ) \cosh (2 \eta )\nonumber \\&+\, U_{24} \cos (\eta ) \sinh (\eta ) \sinh (2 \eta ),\end{aligned}$$

(A62)

$$\begin{aligned} N_\kappa= & {} \frac{\xi ^2\left( C_1^2-C_2^2\right) }{6\left( \xi ^4+4\right) }\nonumber \\&+\,\frac{\xi ^4{{\mathrm{sech}}}^2({\hat{\kappa }})}{6(\xi ^4+4)} [C_2 \cos (\eta ) \cosh (\eta )-C_1 \sin (\eta ) \sinh (\eta )]\nonumber \\&+\,V_1\tanh ^2({\hat{\kappa }})+ V_2+{{\mathrm{sech}}}^2({\hat{\kappa }}) [V_3\sin (\eta )\sinh (\eta ) \nonumber \\&+\, V_4\cos (\eta )\cosh (\eta )]\nonumber \\&+\,V_5[1+\tanh ^2({\hat{\kappa }})]\sin (\eta ) \sinh (\eta )\nonumber \\&+\,2 V_6\tanh ({\hat{\kappa }}) \sin (\eta ) \cosh (\eta ) \nonumber \\&+\,2V_7\tanh ({\hat{\kappa }})\cos (\eta )\sinh (\eta ) \nonumber \\&+\, V_8[1+\tanh ^2({\hat{\kappa }})]\cos (\eta ) \cosh (\eta ) \nonumber \\&+\, V_9\tanh ({\hat{\kappa }})\sin (2\eta )+V_{10}\cos (2\eta )\nonumber \\&+\,V_{11}\tanh ({\hat{\kappa }})\sinh (2\eta ) +V_{12}\cosh (2\eta ) \nonumber \\&+\, V_{13}\sin (2 \eta ) \sinh (2 \eta )+ \tanh ({\hat{\kappa }}) [V_{14}\sin (2 \eta ) \cosh (2 \eta )\nonumber \\&+\, V_{15}\cos (2 \eta ) \sinh (2 \eta )] \nonumber \\&+\, V_{16}\cos (2 \eta ) \cosh (2 \eta ),\end{aligned}$$

(A63)

$$\begin{aligned} N_\eta= & {} \frac{5}{12} (C_1^2+C_2^2)[C_2 \sin (\eta ) \sinh (\eta )\nonumber \\&-\,C_1 \cos (\eta ) \cosh (\eta )]\nonumber \\&+\,\sin (\eta )[V_{17}\cosh (\eta ) \sin (2 \eta )\nonumber \\&+\, V_{18}\sinh (\eta ) \cos (2 \eta )]\nonumber \\&+\, \cos (\eta )[V_{19}\sinh (\eta )\sin (2 \eta )\nonumber \\&+\, V_{20}\cosh (\eta ) \cos (2 \eta )] \nonumber \\&+\,\sin (\eta ) [V_{21} \sinh (\eta ) \cosh (2 \eta )\nonumber \\&+\, V_{22} \sinh (2 \eta ) \cosh (\eta )]\nonumber \\&+\,\cos (\eta ) [V_{23} \sinh (\eta ) \sinh (2 \eta )\nonumber \\&+\, V_{24} \cosh (\eta ) \cosh (2 \eta )]\nonumber \\&+\, \sin (\eta ) \sin (2 \eta ) [V_{25} \sinh (\eta ) \sinh (2 \eta )\nonumber \\&+\, V_{26} \cosh (\eta ) \cosh (2 \eta )]\nonumber \\&+\, \sin (\eta ) \cos (2 \eta ) [V_{27} \sinh (\eta ) \cosh (2 \eta )\nonumber \\&+\, V_{28} \sinh (2 \eta ) \cosh (\eta )]\nonumber \\&+\, \sin (2 \eta ) \cos (\eta ) [V_{29} \sinh (\eta ) \cosh (2 \eta )\nonumber \\&+\, V_{30} \sinh (2 \eta ) \cosh (\eta )]\nonumber \\&+\, \cos (\eta ) \cos (2 \eta ) [V_{31} \sinh (\eta ) \sinh (2 \eta )\nonumber \\&+\, V_{32} \cosh (\eta ) \cosh (2 \eta )]. \end{aligned}$$

(A64)

In Eq. (65), the two coefficients $K_{\kappa , \eta }$ are

$$\begin{aligned} K_\kappa= & {} -\frac{2\xi (C_1^2-C_2^2)}{3 (\xi ^4+4)} \tanh ({\hat{\kappa }} )\nonumber \\&+\,\frac{4 \xi ^9 (4-119 \xi ^4)}{3 (\xi ^4+4)^3 (81 \xi ^4+4)} {{\mathrm{sech}}}^2({\hat{\kappa }} ) \tanh ({\hat{\kappa }} )\nonumber \\&+\,\frac{20 \xi ^9}{3 (\xi ^4+4)^2 (81 \xi ^4+4)} {{\mathrm{sech}}}^2({\hat{\kappa }} )\tanh ({\hat{\kappa }} )\cosh (2 {\hat{\kappa }} )\nonumber \\&+\,\frac{\xi ^4 \text {sech}^2({\hat{\kappa }} )}{6 (\xi ^4+4)} [\sin (\eta ) \cosh (\eta )(C_1-C_2)\nonumber \\&-\cos (\eta ) \sinh (\eta )(C_1+C_2)]\nonumber \\&-2{{\mathrm{sech}}}^2({\hat{\kappa }} )[\sin (\eta ) \cosh (\eta ) (V_3+V_4)\nonumber \\&-\cos (\eta )\sinh (\eta ) (V_3-V_4)]\nonumber \\&+\,\frac{\text {sech}^2({\hat{\kappa }})}{2\xi ^2-2\xi +1} [K_1 \sin (\eta ) \cosh (\eta -2 {\hat{\kappa }} )\nonumber \\&+\,K_2 \cos (\eta ) \sinh (\eta -2 {\hat{\kappa }} )]\nonumber \\&+\,\frac{\text {sech}^2({\hat{\kappa }} )}{2 \xi ^2+2\xi +1} [-K_3 \sin (\eta ) \cosh (\eta +2 {\hat{\kappa }} )\nonumber \\&+\,K_4 \cos (\eta ) \sinh (\eta +2 {\hat{\kappa }} )]\nonumber \\&+\,\frac{4}{4+\xi ^2} [-K_5 \sin (2 \eta ) +K_6 \tanh ({\hat{\kappa }})\cos (2 \eta ) ]\nonumber \\&+\,\frac{4}{4-\xi ^2} [K_7 \sinh (2\eta ) +K_8\tanh ({\hat{\kappa }})\cosh (2 \eta ) ]\nonumber \\&-\frac{4\sin (2 \eta )}{64+\xi ^4} [K_9 \tanh ({\hat{\kappa }} )\sinh (2 \eta )+K_{10} \cosh (2 \eta )]\nonumber \\&+\,\frac{4 \cos (2 \eta )}{64+\xi ^4} [K_{11} \sinh (2 \eta )+K_{12}\tanh ({\hat{\kappa }} ) \cosh (2 \eta ) ],\nonumber \\\end{aligned}$$

(A65)

$$\begin{aligned} K_\eta= & {} \frac{5}{6} (C_1^2+C_2^2) [(C_1-C_2) \sin (\eta ) \cosh (\eta )\nonumber \\&+\,(C_1+C_2) \cos (\eta ) \sinh (\eta )]\nonumber \\&+\,\frac{K_{13}}{5} \sin (\eta ) \cosh (3 \eta )+\frac{K_{14}}{5} \sin (3 \eta ) \cosh (\eta )\nonumber \\&+\,\frac{K_{15}}{5} \cos (\eta ) \sinh (3 \eta )\nonumber \\&+\,\frac{K_{16}}{5} \cos (3 \eta ) \sinh (\eta )+K_{17} \sin (\eta ) \cosh (\eta )\nonumber \\&+\,K_{18} \cos (\eta ) \sinh (\eta )\nonumber \\&+\, \frac{K_{19}}{2} \sin (\eta ) \cosh (\eta )+\frac{K_{20}}{2} \cos (\eta ) \sinh (\eta )\nonumber \\&+\, \frac{K_{21}}{6} \sin (3 \eta ) \cosh (3 \eta )\nonumber \\&+\,\frac{K_{22}}{6} \cos (3 \eta ) \sinh (3 \eta )+ \frac{K_{23}}{10} \sin (\eta ) \cosh (3 \eta )\nonumber \\&+\,\frac{K_{24}}{10} \sin (3 \eta ) \cosh (\eta )\nonumber \\&+\,\frac{K_{25}}{10} \cos (\eta ) \sinh (3 \eta )+\frac{K_{26}}{10} \cos (3 \eta ) \sinh (\eta ),\nonumber \\ \end{aligned}$$

(A66)

in which $K_{1{-}26}$ are given as follows

$$\begin{aligned} K_1= & {} (1-2\xi )(-V_5+V_6)+V_7-V_8,\end{aligned}$$

(A67)

$$\begin{aligned} K_2= & {} V_5-V_6+(1-2\xi )(V_7-V_8),\end{aligned}$$

(A68)

$$\begin{aligned} K_3= & {} (1+2\xi )(V_5+V_6)+V_7+V_8, \end{aligned}$$

(A69)

$$\begin{aligned} K_4= & {} V_5+V_6-(1+2\xi )(V_7+V_8), \end{aligned}$$

(A70)

$$\begin{aligned} K_5= & {} \xi V_9+2V_{10}, \end{aligned}$$

(A71)

$$\begin{aligned} K_6= & {} 2V_9-\xi V_{10}, \end{aligned}$$

(A72)

$$\begin{aligned} K_7= & {} \xi V_{11}-2V_{12}, \end{aligned}$$

(A73)

$$\begin{aligned} K_8= & {} -2V_{11}+\xi V_{12} ,\end{aligned}$$

(A74)

$$\begin{aligned} K_9= & {} \xi ^3V_{13}+(16-2\xi ^2)V_{14}\nonumber \\&+\,(16+2\xi ^2)V_{15}-8\xi V_{16}, \end{aligned}$$

(A75)

$$\begin{aligned} K_{10}= & {} (16-2\xi ^2)V_{13}+\xi ^3V_{14} -8\xi V_{15}\nonumber \\&+\,(16+2\xi ^2)V_{16}, \end{aligned}$$

(A76)

$$\begin{aligned} K_{11}= & {} (16+2\xi ^2)V_{13}-8\xi V_{14} -\xi ^3 V_{15}\nonumber \\&-(16-2\xi ^2)V_{16}, \end{aligned}$$

(A77)

$$\begin{aligned} K_{12}= & {} -8\xi V_{13}+(16+2\xi ^2)V_{14}\nonumber \\&+\,(-16+2\xi ^2)V_{15}-\xi ^3V_{16}, \end{aligned}$$

(A78)

$$\begin{aligned} K_{13}= & {} -3V_{21}-3V_{22}-V_{23}-V_{24}, \end{aligned}$$

(A79)

$$\begin{aligned} K_{14}= & {} 3V_{17}-V_{18}-V_{19}-3V_{20}, \end{aligned}$$

(A80)

$$\begin{aligned} K_{15}= & {} V_{21}+V_{22}-3V_{23}-3V_{24}, \end{aligned}$$

(A81)

$$\begin{aligned} K_{16}= & {} V_{17}+3V_{18}+3V_{19}-V_{20}, \end{aligned}$$

(A82)

$$\begin{aligned} K_{17}= & {} -V_{17}+V_{18}-V_{19}-V_{20}\nonumber \\&+\,V_{21}-V_{22}+V_{23}-V_{24}, \end{aligned}$$

(A83)

$$\begin{aligned} K_{18}= & {} -V_{17}-V_{18}+V_{19}-V_{20}-V_{21}\nonumber \\&+\,V_{22}+V_{23}-V_{24}, \end{aligned}$$

(A84)

$$\begin{aligned} K_{19}= & {} V_{25}-V_{26}-V_{27}+V_{28}+V_{29}\nonumber \\&-V_{30}+V_{31}-V_{32} ,\end{aligned}$$

(A85)

$$\begin{aligned} K_{20}= & {} V_{25}-V_{26}+V_{27}-V_{28}-V_{29}\nonumber \\&+\,V_{30}+V_{31}-V_{32}, \end{aligned}$$

(A86)

$$\begin{aligned} K_{21}= & {} V_{25}+V_{26}-V_{27}-V_{28}-V_{29}\nonumber \\&-V_{30}-V_{31}-V_{32}, \end{aligned}$$

(A87)

$$\begin{aligned} K_{22}= & {} V_{25}+V_{26}+V_{27}+V_{28}+V_{29}\nonumber \\&+\,V_{30}-V_{31}-V_{32}, \end{aligned}$$

(A88)

$$\begin{aligned} K_{23}= & {} -V_{25}-V_{26}+3V_{27}+3V_{28}-3V_{29}\nonumber \\&-3V_{30}-V_{31}-V_{32}, \end{aligned}$$

(A89)

$$\begin{aligned} K_{24}= & {} -3V_{25}+3V_{26}+V_{27}-V_{28}+V_{29}\nonumber \\&-V_{30}+3V_{31}-3V_{32}, \end{aligned}$$

(A90)

$$\begin{aligned} K_{25}= & {} -3V_{25}-3V_{26}-V_{27}-V_{28}+V_{29}\nonumber \\&+\,V_{30}-3V_{31}-3V_{32}, \end{aligned}$$

(A91)

$$\begin{aligned} K_{26}= & {} -V_{25}+V_{26}-3V_{27}+3V_{28}-3V_{29}\nonumber \\&+\,3V_{30}+V_{31}-V_{32}. \end{aligned}$$

(A92)

Under the assumptions of ${\hat{\kappa }}\gg 1$ and $\eta \gg 1$, the four functions $U_{\kappa , \eta }({\hat{z}})$ and $V_{\kappa , \eta }({\hat{z}})$ in Eqs. (A1)–(A4) can be simplified and expressed in terms of the variable $z^*$ as follows

$$\begin{aligned} U_\kappa ^*(z^*)= & {} -\frac{8 \xi ^3 \left( \xi ^5+10 \xi ^4+46 \xi ^3+84 \xi ^2+16 \xi -24\right) \mathrm{e}^{-(\xi +2) z^*}}{3 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^2+6 \xi +10\right) \left( \xi ^2+6 \xi +18\right) }\nonumber \\&+\,\frac{\xi ^4 \left( 6 \xi ^6+9 \xi ^5+9 \xi ^4+6 \xi ^3-4 \xi ^2-4 \xi -4\right) }{6 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^3+\xi ^2+\xi +1\right) }\nonumber \\&\times \,\mathrm{e}^{-(2 \xi +1) z^*} \sin \left( z^*\right) \nonumber \\&-\frac{\xi ^4 \left( 3 \xi ^5+5 \xi ^4+8 \xi ^3+8 \xi ^2+8 \xi +4\right) }{6 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^3+\xi ^2+\xi +1\right) }\nonumber \\&\times \, \mathrm{e}^{-(2 \xi +1) z^*} \cos \left( z^*\right) +\frac{\xi ^8 \left( 4-9 \xi ^4\right) \mathrm{e}^{-3\xi z^*}}{2 \left( \xi ^4+4\right) ^2 \left( 81 \xi ^4+4\right) }, \end{aligned}$$

(A93)

$$\begin{aligned} U_{\eta }^*(z^*)= & {} \frac{8 \xi ^3 \left[ (7 \xi -6) \sin \left( z^*\right) +(\xi -8) \cos \left( z^*\right) \right] }{15 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) } \mathrm{e}^{-3 z^*}, \end{aligned}$$

(A94)

$$\begin{aligned} V_\kappa ^*(z^*)= & {} -\frac{10 \xi ^{10} \mathrm{e}^{-3 \xi z^*}}{\left( \xi ^4+4\right) ^2 \left( 81 \xi ^4+4\right) }\nonumber \\&-\frac{64 \xi ^3 (\xi +2) \mathrm{e}^{-(\xi +2) z^*}}{3 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^2+6 \xi +10\right) }\nonumber \\&+\,\frac{\xi ^4 \left( \xi ^5+15 \xi ^4+20 \xi ^3+20 \xi ^2+16 \xi +4\right) }{6 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^3+\xi ^2+\xi +1\right) }\nonumber \\&\times \, \mathrm{e}^{-(2 \xi +1) z^*} \sin \left( z^*\right) \nonumber \\&+\,\frac{\xi ^4 \left( 2 \xi ^6+3 \xi ^5+3 \xi ^4-2 \xi ^3-4 \xi -4\right) }{6 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^3+\xi ^2+\xi +1\right) }\nonumber \\&\times \, \mathrm{e}^{-(2 \xi +1) z^*} \cos \left( z^*\right) \nonumber \\&+\,\frac{8 \xi ^3 \left[ 6 (\xi +2) \cos \left( 2z^*\right) -\left( \xi ^3+4 \xi ^2+8 \xi -12\right) \sin \left( 2 z^*\right) \right] }{3 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^2+6 \xi +18\right) }\nonumber \\&\times \, \mathrm{e}^{-(\xi +2) z^*}, \end{aligned}$$

(A95)

$$\begin{aligned} V_\eta ^*(z^*)= & {} \frac{8 \xi ^3 \left[ (7 \xi -6) \cos \left( z^*\right) -(\xi -8) \sin \left( z^*\right) \right] }{15 \left( \xi ^2+2 \xi +2\right) \left( \xi ^4+4\right) ^2} \mathrm{e}^{-3 z^*}. \end{aligned}$$

(A96)

Similarly, the six coefficients $M_{\kappa ,\eta }^*, N_{\kappa , \eta }^*$, and $K_{\kappa , \eta }^*$ corresponding to $M_{\kappa , \eta }, N_{\kappa , \eta }$, and $K_{\kappa , \eta }$ reduce to

$$\begin{aligned} M_\kappa ^*= & {} \frac{\xi ^8 \left( 4-9 \xi ^4\right) }{2 \left( \xi ^4+4\right) ^2 \left( 81 \xi ^4+4\right) }\nonumber \\&-\frac{\xi ^4 \left( 3 \xi ^5+5 \xi ^4+8 \xi ^3+8 \xi ^2+8 \xi +4\right) }{6 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^3+\xi ^2+\xi +1\right) }\nonumber \\&-\frac{8 \xi ^3 \left( \xi ^5+10 \xi ^4+46 \xi ^3+84 \xi ^2+16 \xi -24\right) }{3 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^2+6 \xi +10\right) \left( \xi ^2+6 \xi +18\right) }, \nonumber \\\end{aligned}$$

(A97)

$$\begin{aligned} M_\eta ^*= & {} \frac{8\xi ^3(\xi -8)}{15 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) }, \end{aligned}$$

(A98)

$$\begin{aligned} N_\kappa ^*= & {} -\frac{10 \xi ^{10}}{\left( \xi ^4+4\right) ^2 \left( 81 \xi ^4+4\right) }\nonumber \\&+\,\frac{\xi ^4 \left( 2 \xi ^6+3 \xi ^5+3 \xi ^4-2 \xi ^3-4 \xi -4\right) }{6 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^3+\xi ^2+\xi +1\right) } \nonumber \\&-\frac{16 \xi ^3 (\xi +2) \left( \xi ^2+6 \xi +42\right) }{3 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) \left( \xi ^2+6 \xi +10\right) \left( \xi ^2+6 \xi +18\right) }, \nonumber \\&\end{aligned}$$

(A99)

$$\begin{aligned} N_\eta ^*= & {} \frac{8 \xi ^3 (7 \xi -6)}{15 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) }, \end{aligned}$$

(A100)

$$\begin{aligned} K_\kappa ^*= & {} \left[ \frac{32 \left( \xi ^3+7 \xi ^2+16 \xi +42\right) }{\left( \xi ^2+6 \xi +10\right) \left( \xi ^2+6 \xi +18\right) }\right. \nonumber \\&\left. -\frac{\xi ^2 \left( \xi ^4+\xi ^3+\xi ^2+2 \xi +2\right) }{\xi ^3+\xi ^2+\xi +1}\right] \frac{2\xi ^3 }{3 \left( \xi ^2+2 \xi +2\right) \left( \xi ^4+4\right) ^2}\nonumber \\&+\, \frac{40 \xi ^9}{3 \left( \xi ^4+4\right) ^2 \left( 81 \xi ^4+4\right) }, \end{aligned}$$

(A101)

$$\begin{aligned} K_\eta ^*= & {} -\frac{32 \xi ^3 (2 \xi -1)}{15 \left( \xi ^4+4\right) ^2 \left( \xi ^2+2 \xi +2\right) }. \end{aligned}$$

(A102)