1 Introduction

Malaria afflicts 300–500 million people worldwide and consumes 40 % of the health expenditures of over 100 countries. The World Health Organization (WHO) estimates nearly one million deaths annually, 85 % of which are children under five years of age (WHO 2013). It has been known for many decades that the malaria-infected, parasitized RBCs (pRBCs) exhibit paramagnetic properties; therefore, it is possible to separate and remove the pRBCs by applying a force via a high magnetic field gradient (Paul et al. 1981; Zborowski et al. 2003; Moore et al. 2006; Hackett et al. 2009). This has motivated the development of a magnetic apheresis (mPharesis™) system to continuously purify a patient’s blood, much like a dialyzer (Kim et al. 2012; Gandini et al. 2013) (see Fig. 1). The unique challenge of this application is its ability to target ring-stage pRBCs, which have a relatively weak magnetic susceptibility, and the need for high throughput on the order of 100 mL/min—similar to standard hemodialysis.

Fig. 1
figure 1

The envisioned mPharesis™ system (top) in clinical setting, and (bottom) principle of operation of one of several magnetic separation channels. a Blood inlet, b Bleed slit, c Return outlet (Kim et al. 2012)

Full size image

The mPharesis™ filter design includes a stack of laminar flow microchannels through which the infected blood is transported and exposed to a high magnetic field gradient (>1000 T/m) created by an array of ferromagnetic wires embedded on one wall of the channel (see Fig. 1, bottom). This causes the pRBCs to migrate or “marginate” toward the wall toward the source of the magnetic force whereupon they can be skimmed off by a side branch (bleed-slit) downstream. The purified blood is then returned to the patient. The engineering challenge is to optimize the efficiency of this magnetophoretic separator to maintain the overall size of the system within the desired envelope and limit the treatment time under 4 h (Kim et al. 2012).

This present numerical study focused on the influence of the geometry of an individual separation channel of the mPharesis™ device on the efficiency of magnetic separation. Specifically, it explored the hypothesis that the introduction of a constriction at the entrance of the channel would improve the efficiency compared to a standard parallel-plate channel. The assumption was that since the magnetic force diminishes very rapidly with distance from the magnet poles, it would be advantageous to initially divert the magnetic cells in close proximity to the greatest force where they would be retained by the magnetic force. Downstream of the constriction, the nonmagnetic healthy cells would diffuse across the height of the channel, while the magnetic cells would remain close to the wall. An added diffuser is introduced to further streamline the flow and prevent remixing.

2 Methods

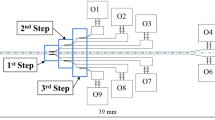
Numerical simulations were performed with two computational domains, depicted in Figs. 2 and 3. Figure 2 depicts a three-way magnetophoretic separator in a previously reported experiment by Han and Frazier (2006) which was used for validation of the computational model described here. For economy of computational cost, a symmetry condition was assumed, reducing the domain to half the width (see Fig. 2b). Figure 3 represents a single separation channel of the mPharesis™ device (not drawn to scale). In both devices, blood flows within the channel along the positive x direction. A magnetic gradient is generated by an external uniform magnetic field, provided by a permanent magnet (not shown) in proximity with a ferromagnetic wire. The solutions to the equations of motion were solved using computational fluid dynamics discrete element method (CFD-DEM). This was chosen as a reasonable alternative to mesoscale simulations, such as the Lattice Boltzmann and/or immersed boundary methods, but with more economical computational cost. The details of the constitutive models and numerical methods are provided below.

Fig. 2
figure 2

Schematic of the magnetophoretic separator with a rectangular ferromagnetic wire. a Top view and b Cross-sectional view of the microchannel (Han and Frazier 2006)

Full size image
Fig. 3
figure 3

Individual separation channel of mPharesis device (not drawn to scale) a without constriction; b with step constriction; and c with constriction and diffuser. For all cases, the length of the channels was 10 mm (along x direction) and the entrance/exit height of the channel was 100 µm (along y direction). The simulations were two dimensional; therefore, there is no dimension along z direction

Full size image

2.1 Governing equations for blood flow

Blood was treated as a multi-component system, comprised of RBCs and plasma. White cells are considered too dilute to affect the flow system. The plasma was treated as a Newtonian fluid, obeying the following conservation of mass,

$$\frac{{\partial \rho_{p} }}{\partial t} + {\text{div}}\left( {\rho_{p} \varvec{v}_{p} } \right) = 0$$
(1)

where \(\frac{\partial }{\partial t}\) is the derivative with respect to time, div is the divergence operator, \(\rho_{p} = \varepsilon \rho_{p0}\), is the density of plasma, ρ p0 is the density of the plasma in the reference configuration, ɛ is the volume fraction of plasma (1-hematocrit), and \(\varvec{v}_{{p}}\) is the velocity field. ɛ in turn is computed using the method introduced by Link et al. (2005). The corresponding balance of linear momentum is:

$$\rho_{p} \frac{{D^{p} \varvec{v}_{p} }}{Dt} = div\left( {\varvec{T}_{p} } \right) + \rho_{p} \varvec{b}_{p} + \varvec{F}_{pr}$$
(2)

where \(\varvec{T}_{p} = \left[ { - \varepsilon p + \varepsilon \lambda_{p} tr\varvec{D}_{p} } \right]\varvec{I} + 2\mu_{p} \varepsilon \varvec{D}_{p}\), p is the pressure of the mixture, λ p and μ p are the (constant) first and second coefficients of viscosity of the pure plasma, where \(\varvec{D}_{p} = \frac{1}{2}\left[ {\left( {grad \varvec{v}_{p} } \right) + \left( {grad \varvec{v}_{p} } \right)^{T} } \right]\). In general, for any scalar β, \(\frac{{D^{\alpha } \beta }}{Dt} = \frac{\partial \beta }{\partial t} + \varvec{v}^{\alpha } \cdot \nabla \beta , \alpha = f,s\), and (for any vector w), \(\frac{{D^{\alpha } \varvec{w}}}{Dt} = \frac{{\partial \varvec{w}}}{\partial t} + \left( {\nabla \varvec{w}} \right)\varvec{v}^{\alpha }\), \(\varvec{T}_{p}\) represents the Cauchy stress tensors, \(\varvec{F}_{\text{pr}}\) represents the interaction forces (exchange of momentum) between the plasma and RBCs (for more details, see Johnson et al. 1990; Wu et al. 2014a, b), and \(\varvec{b}_{p}\) refers to the body force. The balance of the angular momentum implies that, in the absence of couple stresses, the total Cauchy stress tensor is symmetric.

The equation of motion of the RBC component is represented in a similar fashion:

$$m_{r} \frac{{D^{2} \varvec{x}_{r} }}{Dt} = \varvec{F}_{contact} + \varvec{F}_{pr} + \varvec{F}_{ext}$$
(3)

where m r is the mass of a RBC, \(\varvec{x}_{r}\) is the instantial space position of RBCs, \(\varvec{F}_{contact}\) is the force of collision with other RBCs or boundaries, \(\varvec{F}_{pr}\) is the interaction force with continuous phase (plasma), and \(\varvec{F}_{ext}\) is the external force field, in this case the magnetic force. In current study, \(\varvec{F}_{pr}\) includes only the drag force and is represented by the drag model of Rusche and Issa (2000).

2.1.1 RBCs collision: soft-sphere model

The soft-sphere model incorporates multiple particle–particle interactions with the trajectories determined by integrating Newton’s second law. According to Cundall and Strack (Cundall and Strack 1979), the normal component of the contact force, \(\varvec{F}_{\text{contact}}^{m,n}\), acting on particle m by particle n (or wall) is

$$\hat{\varvec{F}}_{\text{contact}}^{m,n} = - \hat{k}\delta \varvec{n}^{m,n} - \hat{n}\varvec{v}_{r}^{m,n}$$
(4)

where \(\hat{k}\) and \(\hat{\eta }\) are the normal “spring” stiffness and damping coefficient, respectively, \(\delta = \left( {R_{m} + R_{n} } \right) - \left| {\varvec{r}_{m} - \varvec{r}_{n} } \right|\) is a (fictitious) overlap between two RBCs, R is the radius of a RBC, \(\varvec{n}^{m,n} = \left( {\varvec{r}_{m} - \varvec{r}_{n} } \right)/\left| {\varvec{r}_{m} - \varvec{r}_{n} } \right|\) is the normal unit vector between two RBCs, \(\varvec{v}_{r}^{m,n} = \left( {\varvec{v}_{m} - \varvec{v}_{n} } \right) + \left( {R_{m}\varvec{\omega}_{m} + R_{n}\varvec{\omega}_{n} } \right) \times \varvec{n}^{m,n}\) is the relative velocity, \(\hat{\varvec{v}}_{r}^{m,n} = \left( {\varvec{v}_{r}^{m,n} .\varvec{n}^{m,n} } \right)\varvec{n}^{m,n}\) is the normal relative velocity, and \(\varvec{\omega}\) is the angular velocity. The tangential component of the contact force between particles is likewise:

$$\tilde{\varvec{F}}_{\text{contact}}^{m,n} = \left\{ {\begin{array}{l} { - \tilde{k}\tilde{\delta } - \tilde{\eta }\tilde{\varvec{v}}_{r}^{m,n} for \left| {\tilde{\varvec{F}}_{\text{contact}}^{m,n} } \right| \le \mu_{f} \left| {\hat{\varvec{F}}_{\text{contact}}^{m,n} } \right|} \\ { - \mu_{f} \left| {\left| {\hat{\varvec{F}}_{\text{contact}}^{m,n} } \right|} \right|\varvec{t}^{m,n} for \left| {\tilde{\varvec{F}}_{\text{contact}}^{m,n} } \right| > \mu_{f} \left| {\hat{\varvec{F}}_{\text{contact}}^{m,n} } \right| } \\ \end{array} } \right.$$
(5)

where \(\tilde{k}\), \(\tilde{\eta }\), and μ f are the tangential spring stiffness, tangential damping coefficient, and friction coefficient, respectively, and \(\tilde{\varvec{v}}_{r}^{m,n} = \varvec{v}_{r}^{m,n} - \tilde{\varvec{v}}_{r}^{m,n}\) is the relative tangential velocity.

The tangential displacement \(\tilde{\delta }\) is given by:

$$\tilde{\delta } = \left\{ {\begin{array}{*{20}l} {\hat{\delta }_{0} H + \mathop \smallint \limits_{to}^{t} \tilde{\varvec{v}}_{r}^{m,n} {\text{dt}}} \hfill & {{\text{for }} \left| {\tilde{\varvec{F}}_{\text{contact}}^{m,n} } \right| \le \mu_{f} \left| {\hat{\varvec{F}}_{\text{contact}}^{m,n} } \right|} \hfill \\ { - \mu_{f} \left| {\hat{\varvec{F}}_{\text{contact}}^{m,n} } \right|\varvec{t}^{m,n} /k_{t} {\text{ for }} \left| {\tilde{\varvec{F}}_{\text{contact}}^{m,n} } \right| > \mu_{f} \left| {\hat{\varvec{F}}_{contact}^{m,n} } \right| } \hfill & {{\text{for }} \left| {\tilde{\varvec{F}}_{\text{contact}}^{m,n} } \right| > \mu_{f} \left| {\hat{\varvec{F}}_{contact}^{m,n} } \right| } \hfill \\ \end{array} } \right.$$
(6)
$$\varvec{H} = \left[ {\begin{array}{*{20}c} {qh_{x}^{2} + c} & {qh_{x} h_{y} - sh_{z} } & {qh_{x} h_{z} + sh_{y} } \\ {qh_{x} h_{y} + sh_{z} } & {qh_{y}^{2} + c} & {qh_{y} h_{z} - sh_{x} } \\ {qh_{x} h_{z} - sh_{y} } & {qh_{y} h_{z} + sh_{x} } & {qh_{z}^{2} + c} \\ \end{array} } \right]$$
(7)

where \(\varvec{t}^{m,n} = \tilde{\varvec{v}}_{r}^{m,n} /\tilde{\varvec{v}}_{r}^{m,n}\) is the tangential unit vector, \(\varvec{h} = \left( {\varvec{n}^{m,n} \times \varvec{n}_{0}^{m.n} } \right)/\left| {\varvec{n}^{m,n} \times \varvec{n}_{0}^{m.n} } \right|\), c = cos φ, s = sin φ, q = 1 − c, \(\varphi = \arcsin \left| {\varvec{n}^{m,n} \times \varvec{n}_{0}^{m.n} } \right|\), \(\hat{\delta }_{0}\) and \(\varvec{n}_{0}^{m.n}\) are the tangential displacement and normal direction in the previous time step, respectively, and μ f is the frictional coefficient. The mechanism of the particle–wall collision is same as the particle–particle collision. (For further details of the derivation, the reader is referred to Su et al. 2011 and van der Hoef et al. 2006.) The determination of the stiffness and damping coefficient can be found in Tsuji et al. (1992) or van der Hoef (2006).

2.2 Magnetic field

According to Han and Frazier (2004, 2006), the expression for the magnetic force produced by a magnetically saturated, ferromagnetic rectangular wire placed under a uniform external magnetic field referenced to a coordinate system centered at the origin as shown in Fig. 2 is

$$\begin{aligned} \varvec{F}_{\text{magnetic}} \left( {z^{'} ,y^{'} } \right) = & \mu_{0} M_{s} \left( {\chi_{\text{rbc}} - \chi_{p} } \right)V_{\text{rbc}} a^{2} H_{0}\,\times\, \frac{{\left( {\frac{{M_{s} }}{{2H_{0} }}a^{2} + 3\left( {a + y^{'} } \right)^{2} - z^{'2} } \right)z^{'} }}{{\left( {z^{'2} + \left( {a + y^{'} } \right)^{2} } \right)^{3} }}\varvec{e}_{{z^{'} }} \\ & + \mu_{0} M_{s} \left( {\chi_{\text{rbc}} - \chi_{p} } \right)V_{\text{rbc}} a^{2} H_{0}\,\times\, \frac{{\left( {\frac{{M_{s} }}{{2H_{0} }}a^{2} - 3z^{'2} + \left( {a + y^{'} } \right)^{2} } \right)\left( {a + y^{'} } \right)}}{{\left( {z^{'2} + \left( {a + y^{'} } \right)^{2} } \right)^{3} }}\varvec{e}_{{y^{'} }} \\ \end{aligned}$$
(8)

where \(\varvec{e}_{{z^{'} }}\) and \(\varvec{e}_{{y^{'} }}\) are the unit vectors in the \(z^{{\prime }}\) and \(y^{{\prime }}\) directions, respectively, and \(y^{'} \ge 0\); \(k = \frac{{\mu_{w} - \mu_{0} }}{{\mu_{w} + \mu_{0} }}\) = 1, where \(\mu_{w}\) and μ 0 are the magnetic permeability of the ferromagnetic wire and free space, respectively; M s is the saturation magnetization field of the rectangular wire; χ p and χ rbc are the magnetic susceptibilities of the plasma and the RBCs; V rbc is the volume of the RBCs; and a is the nominal radius of the wire, which for a rectangular wire is half of the wire height, 25 μm; H 0 is the applied external magnetic field. The above governing equations were implemented in OpenFOAM (OpenCFD 2011) and solved on a PC workstation (Dell T7910). The mesh dependency studies were performed and discussed in detail in the channel optimization part of the results section. All the symbols used in current paper are summarized in the “Appendix.”

3 Results

3.1 Computational model validation: deoxyhemoglobin RBC separation

Simulations of the magnetophoretic microfluidic separator used by Han and Frazier (2004, 2006) were performed for four flow rates, corresponding to average velocity of 0.1, 0.2, 0.4, and 0.6 mm/s. The Re is about 0.0094 for the inlet velocity of 0.1 mm/s, and the apparent kinematic viscosity of plasma was 0.94e−6 m2/s. The hematocrit was assumed to be 4 %, based on the reported dilution of bovine whole blood of 1:10 (Han and Frazier 2006), and assuming a nominal hematocrit of bovine whole blood as 44 % (Oshima and Sankai 2009). Additional physical parameters are provided in Table 1. The initial condition for all the simulations were a cell-free domain. A uniform inlet boundary condition was applied. All simulations were run for a duration of 5× (length of the channel/mean velocity) to assure steady-state conditions. For economy of computational cost, all simulations were performed in 2D on x − y plane at z = 0, with coordinates shown in Fig. 2 and assumed symmetric geometry; however, the geometries replicate the salient features. Accordingly, the inlet velocity boundary condition was assumed to be 1.5 times the average velocity, to correspond with the centerline velocity. The magnetic field was prescribed by Eq. (8) with z = 0 corresponding to the centerline of the channel:

$$\begin{aligned}&\varvec{F}_{\text{magnetic}} \left( {y^{'} } \right) \\&\;\;= \mu_{0} M_{s} \left( {\chi_{\text{rbc}} - \chi_{p} } \right)V_{\text{rbc}} a^{2} H_{0} \frac{{\left( {\frac{{M_{s} }}{{2H_{0} }}a^{2} + \left( {a + y^{'} } \right)^{2} } \right)}}{{\left( {a + y^{'} } \right)^{5} }}\varvec{e}_{{y^{'} }} \end{aligned}$$
(9)

Figure 4 shows the distribution of paramagnetic deoxyhemoglobin RBCs passing through the separator near the outlet region. Both simulations and experiments demonstrate that the applied magnetic force has an obvious effect on the distribution of RBCs. (The simulation appears less dense because it is two dimensional.) Figure 5 compares the simulated versus measured percentage of RBCs exiting the central outlet (outlet2 in Fig. 2) for the four velocities considered as well as the control case in which there is no magnet. There was a small systematic overprediction of RBC percentage by simulation of 0.8–4.7 %, which was observed to be a function of flow rate.

Table 1 Physical properties and flow condition (to economize computational cost, the diameter of the RBCs is specified as 8 µm)
Full size table
Fig. 4
figure 4

Comparison of simulated to experimentally observed deoxyhemoglobin RBCs passing through the microchannel magnetophoretic separator at an average flow velocity of 0.1 mm/s without (left) and with (right) applied magnetic field (0.2T). Experimental figures were reused with permission (Han and Frazier 2006).

Full size image
Fig. 5
figure 5

Comparison of simulated and experimental separation percentage of deoxyhemoglobin RBCs at outlet2 of the separator for various average flow velocities (Han and Frazier 2006)

Full size image

3.2 Channel optimization for separation of malaria-infected RBCs

Based on the excellent agreement between the numerical and experimental results in the above case, the CFD-DEM model was applied to a parametric study of the mPharesis separation channel. Some of the conditions were adjusted to correspond to the realistic application of the device clinically. In particular, the hematocrit was prescribed as 40 %, with a ratio of malaria-infected, parasitized RBCs (pRBCs) to healthy RBCs of 1:9. Also, the magnetic susceptibility difference between the pRBCs (χ pRBC = −6.2e−6) and plasma was prescribed as 1.5e−6 (SI units), corresponding to ring-stage malaria (Hackett et al. 2009; Kim et al. 2012); approximately 2.5 × less than deoxyhemoglobin RBCs (χ deoxyRBC = −3.8e−6) used in the Han et al.’s experiment. All simulations were performed in 2D to economize computational costs, similar to the previous simulation. Furthermore, the domain was limited to the middle region of the channel, which excluded entrance effects and the bleed slit, as shown in Fig. 3. The computed magnitude of the magnetic force was found to decay very quickly with distance from the wire, resulting in significantly less force (<1 %) at the far wall (y = H) than the near wall (see Fig. 3). However, these cells near the far wall have the farthest to travel to completely stratify the blood. For this reason, we introduce an upstream constriction, shown Fig. 3b, to initially bring all cells in close proximity to the greatest magnetic force. Thereafter, when the channel expands to its full height, the uninfected RBCs can transport away from the magnetic wall leaving the pRBCs trapped in a boundary layer. An added diffuser is introduced to streamline the flow downstream of the constriction (see Fig. 3c). Without loss of generality, the length of the channels was specified as 10 mm.

The inlet velocity for all the cases was set as 1.0 mm/s, corresponding to Re = 0.057 based on an apparent kinematic viscosity of whole blood as 3.32e−6 m2/s. All simulations were run for a duration of 5x (length of the channel/mean velocity) to assure steady-state conditions were reached. To account for the discretization of the pRBCs and RBCS phases, all data shown in the following sections are averaged from 100 different time steps. Prior to simulations of the various geometries of the channels, a mesh dependency study was first performed using the 10-mm-length rectangular channel (see Fig. 3a). It was found that meshes of 18,288 and 31,248 nodes both closely approximated the theoretical (Newtonian) prediction; therefore, a mesh with 18,288 nodes was chosen. Mesh dependency studies were confirmed for the other geometries as well.

For quantifying the separation efficiency, the pRBCs density distribution across the channel was evaluated at the outlet. To accommodate the discrete size of the cells, the outlet was discretized into 20 regions, each 5 µm in height. Although the bleed slit was not included in the simulation, the presumption was that the flow exiting the outlet would be split such that the concentrated pRBCs layer of blood would be collected, and the remaining blood returned to the patient. The specific split ratio would be chosen based on clinical considerations, such as availability of blood and risk of anemia.

3.2.1 Effect of constriction height, H c (L c = 2 mm)

The pRBCs distributions are provided in Fig. 6 for rectangular constrictions of 50 and 80 %, 2 mm in length, and are compared with the baseline (no constriction). Table 2 shows the percentage of the pRBCs in the near-wall subzone (20 µm). We defined two metrics to assess the degree of separation. The first was simply the relative quantity of pRBCs captured within the 20-µm subzone at the outlet:

Fig. 6
figure 6

Percentage density distribution at the outlet along the y direction, effect of H c

Full size image
Table 2 Effect of constriction height on pRBCs separation rate
Full size table
$${\text{pRBC Capture }}\% = \frac{{\text{pRBCs near wall}}}{{\text{total pRBCs}}}$$

A value of 20 % (percent of RBCs that are infected pRBCs) would imply no stratification of pRBCs, and 100 % would correspond to complete stratification. A second index, pRBC enrichment, describes the relative increase in concentration of pRBCs in the sublayer compared to the bulk,

$${\text{pRBC enrichment}} = \frac{\text{pRBCs concentration near wall}}{\text{bulk pRBCs concentration}}-1$$
(10)

The above index ranges from 0 % for no stratification to a maximum of 400 % if all cells are stratified to the sublayer (i.e., pRBC concentration from 4 to 16 %).

As contrasted with the channel without constriction, which provided very limited enrichment (28 %), the channels with constrictions were markedly more efficient (91.5 % and 139 % for the 50-µm and 20-µm constriction, respectively).

3.2.2 Effect of constriction length L c (H c = 80 %)

To evaluate the relative benefit of lengthening the constriction L c, six different lengths were evaluated (0.2, 0.5, 1.0, 2.0, 4.0, and 8.0 mm), each having a height of 20 µm. These results are provided in Fig. 7 and Table 3. It can be seen that there is a slight improvement with length from 0.2 mm up to 4 mm, beyond which further extension to 8 mm yields diminishing returns.

Fig. 7
figure 7

Percentage density distribution at the outlet along the y direction, effect of L c

Full size image
Table 3 Effect of constriction length on pRBCs separation rate (H c = 80 µm)
Full size table

3.2.3 Effect of the diffuser after the constriction L d (L c = 2 mm, H c = 80 %)

Following the constriction, it is desired for the RBCs to gradually advect from the wall, leaving the pRBCs trapped in the magnetic boundary layer. However, a sudden expansion was observed to cause a flow disturbance that draws pRBCs away from the wall (see Fig. 8a). Therefore, a tapered diffuser was introduced for the case of 80 µm × 2 mm constriction (see Fig. 8b). The corresponding concentration profiles at the exit of the channel are provided in Fig. 9 and Table 4, which reveals a dramatic improvement (from 139 to 261 %) by introducing a diffuser of just 1 mm. The incremental improvement by extending the diffuser to 2 mm was negligible.

Fig. 8
figure 8

Snapshot of RBC distribution in the channel region near the outlet of the constriction. Black: Infected RBCs; White: Normal RBCs. a Channel with H c = 80 µm, L c = 2 mm constriction and no diffuser; b Channel with H c = 80 µm, L c = 2 mm constriction and L d = 1 mm diffuser

Full size image
Fig. 9
figure 9

Percentage density distribution at the outlet along the y direction, effect of L d

Full size image
Table 4 Effect of diffuser length on pRBCs separation rate (H c = 80 µm)
Full size table

4 Discussion

Many groups over the past decades have proposed unique microfluidic geometries designed to improve the magnetic separation of cells (Melville et al. 1975; Kumar and Lykke 1984; Zborowski et al. 1999), particles (Gerber 1984; Lien et al. 2007; Wu et al. 2011; Zhu et al. 2011; Verbruggen et al. 2015), and other suspensions. A common practice involves attaching magnetic particles to target cells, proteins, fungi, or viruses to improve separation efficiency (Hayes et al. 2001; Furdui and Harrison 2004; Inglis et al. 2004; Kim and Park 2005; Pamme et al. 2006; Xia et al. 2006; Chen et al. 2007; Hahn et al. 2007; Earhart et al. 2009; Yung et al. 2009; Kang et al. 2012). High magnetic gradient microfluidic separators involving RBCs and pRBCs have been published using an external permanent magnet (Chikov et al. 1993; Karl et al. 2008), external magnets in combination with ferromagnetic bead or steel wool packed columns (Owen 1978; Fairlamb et al. 1984; Nalbandian et al. 1995; Ahn et al. 1996; Carter et al. 2003; Trang et al. 2004; Ribaut et al. 2008; Karl et al. 2009; Bhakdi et al. 2010), embedded ferromagnetic elements (Melville et al. 1975; Paul et al. 1981; Takayasu et al. 1982; Han and Frazier 2006; Furlani 2007; Iliescu et al. 2009), and/or saline buffer clearance streams (Nam et al. 2013). Although high separation efficiencies have been reported, none of these separators are practical for a continuous, high-throughput blood purification system to treat a malaria-infected patient. Batch devices can collect only small quantities at a time and must either be repeatedly replaced or purged. Reported continuous systems require highly diluted blood (e.g., <5 % hematocrit), and sometimes the addition of a sheath fluid layer, to efficiently capture the target cells. In both cases, it would be necessary to reconcentrate the blood prior to returning it to the patient. Furthermore, very few studies attempted the separation of ring-stage malaria-infected cells with only one showing significant success, though with a low throughput (73 % separation efficiency at approximately 200–300 pRBCs per minute) (Nam et al. 2013). Most high-gradient magnetic separators target ferromagnetic particles, which are 1000× or more paramagnetic than mature pRBCs, or often deoxygenated RBCs which are 2.5× more paramagnetic. Unlike these other separators, the mPharesis design is also capable of capturing immature ring-stage pRBCs with its novel, parametrically optimized magnetic force field. The parallel-plate type geometry reported here is attractive for treating severe malaria as it offers the possibility of selectively removing weakly magnetic infected cells without wasting healthy cells or diluting the filtered blood. It is also more amenable for upscaling because it can be extended in the width direction and can be stacked in layers.

The rapid decay of the magnetic force with distance restricts the range over which it can attract and maintain malaria-infected cells to within a few tens of microns. The hypothesis of improved pRBC separation efficiency with the introduction of an upstream constriction was confirmed with parametric optimization. The constriction diverted the flow within 20–50 µm of the magnetic wall and, upon exiting the constriction, retained the pRBCs near while the nonmagnetic RBCs would diffuse back into the bulk flow. The addition of a short diffuser allowed the separation to occur more gradually, avoiding remixing and resulting in markedly improved separation efficiency. It was observed that the length of the constriction needs not be very long, which is fortuitous as it limits its effect on pressure drop. For example, the performance of a 1-mm-long constriction was comparable to 2 mm yet exhibited approximately half the pressure drop.

The CFD-DEM method applied in this study was advantageous inasmuch as it allowed discrimination between pRBCs and healthy RBCs. Several approaches were considered for current problem, including multi-component Eulerian model, CFD-DEM model, and mesoscale simulation such as immersed boundary method combined with the Lattice Boltzmann method (LBM-IBM) (Zhang et al. 2008; Fenech et al. 2009; Yin et al. 2013; Wu et al. 2014b; 2015). The limitation with the multi-component Eulerian model, however, is the necessity to identify the interaction forces between pRBCs and RBCs, which is not currently known. Also the computational cost of applying LBM-IBM method would be prohibitively expensive, considering that the number of the particles in the system is about 0 (105).

The size of the problem also poses numerical challenges for the general CFD-DEM method. Usually, when the CFD mesh contains 0 (102) particles, the volume fraction of the fluid can be directly calculated as proposed by Hoomans et al. (1996); however, when the size of the particle is in the same order of the CFD mesh, this method may cause numerical instability. Therefore, in current study, the volume fraction of RBCs, ϕ, was computed using the method introduced by Link et al. (2005). Another limitation relates to necessary assumptions regarding the interaction forces, and specifically the drag forces on the cells. In this study, we did not explicitly model the biconcave geometry of the red blood cell; however, the model does not have any provision for cell shape, but rather accounts for the presence of cells mathematically in terms of their drag force and collision force. Excellent numerical replication of Han’s experimental data confirmed the applicability of our implementation of CFD-DEM approach to the problem of RBCs separation using magnetic force (Han and Frazier 2006).

Although the optimized channel yielded much better separation efficiency compared to baseline, it is still far from perfect: capturing up to 73 % of the pRBCs in the near-wall layer versus 100 % if the separator was able to stratify all the pRBCs. Furthermore, the above capture index is based on the presumption that 20 % of the channel height is skimmed off into a waste slit or branch, which would also imply that a significant proportion of healthy cells would be discarded as well. Therefore, for the current case of 1:9 pRBC/RBC with 40 % hematocrit, the ideal device would concentrate all the infected cells within a 4-µm skimming layer. Although this is not a likely prospect, as this would restrict the pRBCs to a monolayer adjacent to the magnetic wall, it is evident from comparison of Fig. 8a, b, that the degree of remixing can be mitigated by replacing a sudden expansion with a gradual diffuser. Therefore, there is an opportunity to improve the stratification efficiency if the upward forces acting on these cells (i.e., lift, drag, and collisions with RBCs) could be reduced, for example, by additional shape optimization, in both the height and width of the channel (y and z dimensions).

Although this optimization was performed in the context of a specific parallel-plate geometry, the results may be applicable to any magnetophoretic separator geometry with a single ferromagnetic pole or array of poles. For example, continuous microfluidic high-gradient magnetic separators such as Han and Frazier (2006), Nam et al. (2013), and Furlani (2007) could potentially be improved by introducing a constriction and diffuser as reported here (Han and Frazier 2006; Furlani 2007; Nam et al. 2013). Additionally, experimental results could be extrapolated to target cells with different magnetic susceptibilities by appropriately scaling the flow conditions. We illustrated this by performing an additional simulation to consider an earlier stage of malaria infection (ring stage) in which the magnetic susceptibility of pRBCs is reduced by 1/3 from 1.5 to 0.5e−6 (SI) corresponding to approximately 10–15 h after parasite invasion. The best performing channel (H c = 80 µm, L c = 2 mm, and L d = 2 mm) was simulated with a proportionately decreased inlet velocity (from 1.0 to 0.33 mm/s), and the resultant capture rate and pRBC enrichment were 66 and 232 %, respectively, which is comparable to the results shown in the previous section.

5 Conclusions

Magnetic separation of parasitized, malaria-infected red blood cells within a parallel-plate system was simulated using a CFD-DEM (Eulerian–Lagrangian) approach. The plasma was treated as a Newtonian fluid (as the Eulerian phase), and the RBCs were treated as soft spheres (as the Lagrangian phase) influenced by drag, collisions with other RBCs, and a magnetic field. The CFD-DEM approach was shown to accurately predict previously reported experimental observations by Han et al. Using this model, we determined that the introduction of a constriction and diffuser into an otherwise parallel-plate channel was effective for improving the retention of the paramagnetic cells within the magnetic force field and hence the overall separation efficiency. For the cases studied, it was found that a constriction of 50 µm in height, 2 mm in length followed by a 2-mm diffuser performed almost as well as a narrower and longer constriction of 20 µm × 8 mm, suggesting that a subtle modification to the blood flow channel can provide a profound beneficial effect. The constriction introduced a greater pressure drop (from 17 to 495 Pa), which should be considered when scaling up this design for a clinical-sized device. The ability to accommodate physiological hematocrit and high throughput motivates further consideration for translation to a treatment-scale device.