Droplet coalescence and hydrodynamic interactions that occur during the process of film drainage form a basis for many applications, such as mineral processing, food science, printing and sintering processes and the field of microfluidics (Aarts et al. 2005; Tan et al. 2007; Butt and Kappl 2010). This film drainage process has also gained significance in biological studies such as the drainage of tear film (Braun and Fitt 2003) and interaction of biological cells (Shelduko 1967). The recent advancement of experimental observations coupled with modeling techniques has made it possible to advance our knowledge of the film drainage process (Klaseboer et al. 2000; Yang et al. 2002; Carnie et al. 2005; Dagastine et al. 2006).

Film drainage between droplets of identical liquids has been investigated extensively during the last few decades. These studies were based on free spherical droplets colliding with each other (Dai and Leal 2008), pendant droplets in contact with the planar liquid surface (Aarts and Lekkerkerker 2008; Zeng et al. 2009) or the contact of two sessile droplets (Case and Nagel 2008). Generally, these studies found that the time taken for coalescence of identical droplets moving toward one another depends on the interfacial tension of the droplets, which in turn controls the time of film drainage. This concept of film drainage has attracted a lot of interest due to the physics involved during droplet interactions. It is suggested that even a small change in the size of the droplets can affect the scales of thin films (Sanfield and Steinchen 2008; Guriyanova et al. 2010). The drainage process of this thin film between interacting droplets is time-dependent; thus, different length scales need to be measured with precision (Fisher et al. 1992). With the increasing availability of high precision experimental measurements over the past decade, several studies have been performed to predict the static and dynamic interacting forces between the droplets. Deformation, surface forces and hydrodynamic drainage effects are considered to make relative contributions to the film drainage process between two identical droplets (Yeo et al. 2001; Chan et al. 2011). During the head-on collision of two identical droplets, film drainage time decreases with an increase in the capillary number, Ca = μV/γ, where μ is the viscosity of liquid, V is the characteristic velocity and γ is the interfacial tension between two liquids (Yoon et al. 2007).

Recently, droplets and particles with multiple surfaces, known as Janus droplets or particles, have gained wide interest. Janus particles are defined as particles with differently functionalized properties at different regions of the surface. These droplets and particles have been investigated for applications such as self-assembly, organic phase separation and as dimers. For example, these particles can be used as optical probes for chemical and biological measurements (Choi et al. 2003; Huang et al. 2006). Due to their wide range of applications, several studies have been carried out to improve the fabrication technique for producing Janus particles with different morphologies. However, to our knowledge, no study has been performed to understand the drainage process of the surrounding film when immiscible droplets coalesce to form a Janus droplet. The film drainage time between immiscible droplets of the same size can be beneficial in the fabrication and synthesis of Janus particles.

Here, we focus on the film drainage process during a very slow head-on collision between two partially immiscible droplets suspended in a third fluid. In this case, when droplets are very close to each other, the nonlinear Marangoni flow can be induced by the formation of three different interfacial tensions [(a) between the interfaces of droplets, (b) between the droplet interfaces and surrounding fluid]. However, the effect of this Marangoni flow is unknown from a physics standpoint. While the film drainage between two partially engulfing immiscible droplets has not been studied previously, the only studies we have found to closely resemble the above problem are studies of coalescence time between two miscible droplets (Riegler and Lazar 2008; Blanchette 2010). Their studies indicate that a greater difference between the interfacial tensions of two miscible droplets increases the coalescence speed of the droplets. However, due to the miscibility of two droplets, the problem does not resemble the complexity of the problem discussed here. The goal of this paper is to investigate the film drainage between two partially engulfing immiscible droplets using a numerical study and to identify whether the immiscibility of droplets and the Marangoni effect between different interfaces affect the film drainage time. The observations from our numerical study that we report here show that the film drainage time during the partial engulfment of two immiscible droplets can be divided into three different phases of fast, intermediate and delayed film drainage and that this film drainage depends on the ratio of interfacial tension between the droplet and surrounding fluid to interfacial tension between two droplet fluids.

When two immiscible droplets coalesce, the final equilibrium state between the droplets depends on the three interfacial tensions γ ij (i ≠ j ≠ k = 1, 2, 3). Here, ‘2’ is the number designated for surrounding fluid. Torza and Mason (1969) indicated three different regimes, complete engulfment, partial engulfment and non-engulfment, between the immiscible droplets that depend on three spreading factors given as S i  = γ jk  − (γ ij  + γ ik ). They show that when three sets of values are such that S 1 < 0, S 2 < 0, S 3 < 0, the final equilibrium state of partial engulfment is reached. In this state, three interfacial tensions form a closed Neumann triangle along the interfacial line, as shown in Eq. 1 and Fig. 1a. The geometrical details of the resulting droplet depend on the interfacial tensions and the initial radius of droplets. The geometric details of the resulting droplet along with the Neumann triangle are shown in Fig. 1a.

$$\begin{gathered} \gamma_{13} + \gamma_{23} {\text{Cos}}\theta_{3} + \gamma_{12} {\text{Cos}}\theta_{1} = 0 \hfill \\ \gamma_{13} {\text{Cos}}\theta_{3} + \gamma_{23} + \gamma_{12} {\text{Cos}}\theta_{2} = 0 \hfill \\ \gamma_{13} {\text{Cos}}\theta_{1} + \gamma_{23} {\text{Cos}}\theta_{2} + \gamma_{12} = 0 \hfill \\ \end{gathered}$$
(1)
Fig. 1
figure 1

a Geometric details of two partially engulfed immiscible droplets and the Neumann’s triangle formation along the interface. b The simulation method that mimics the four mills technique. c The final steady state condition of the partially engulfed droplets depending on the interfacial tension ratios shown here. When the ratios of interfacial tensions are equal, the angles θ 1 and θ 3 are equal. When γ 12/γ 13 is greater than γ 23/γ 13, θ 1 is greater, and vice versa. d Phase diagram of film drainage time between two immiscible droplets based on our simulations. The partially engulfed region can be divided into three different regions of fast, intermediate and slow drainage (color online, please use 2 columns)

Full size image

In our numerical experiments, we employed the D3Q19 Gunstensen multi-component lattice Boltzmann model (Gunstensen et al. 1991) and extended it to three-fluid systems in order to simulate three immiscible fluids. The segregation between the individual fluids and surface tension generation scheme were employed following the method of Tolke et al. (2002). The multi-component lattice Boltzmann equation takes the following form:

$$f_{a}^{l} \left( {t + \Delta t,x + \xi_{a} \Delta t} \right) - f_{a}^{l} \left( {t,x} \right) = \Delta t\varOmega_{a}^{l} \left( {t,x} \right)\quad l = 1,2,3\quad a = 0, \ldots ,N - 1$$
(2)

where f l a is the probability of finding particles of species l at site x and time t, moving along the ath lattice direction defined by the discrete speeds c a . The left side of the equation represents molecular free-streaming, whereas the right side represents the collision function and consists of three parts:

$$\begin{aligned} &\varOmega_{a}^{l} = \varOmega_{a}^{l} 3\left( {\varOmega_{a}^{l} 1 + \varOmega_{a}^{l} 2} \right) \hfill \\ &{\text{where,}} \hfill \\ &\varOmega_{a}^{l} 1 = {\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} \tau }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\tau $}}_{l} \left( {f_{a}^{l} \left( {t,x} \right) - f_{a({\rm eq})}^{l} \left( {t,x} \right)} \right) \hfill \\ \end{aligned}$$
(3)

τ l is the relaxation time of the densities toward the equilibrium distribution function f l a (eq). The other two parts of the collision operator are the surface tension generation scheme (Ω l a 2) and segregation scheme (Ω l a 3)21. The relaxation time of each fluid is determined based on its kinematic viscosity (ν). Kinematic viscosity is calculated using the relaxation time as ν = (τ l  − 0.5)c 2 s ∆t. Here, c s is the speed of sound and is given as c s = ∆x/√3/∆t. ∆x and ∆t are the lattice spacing and lattice time, respectively, and are considered to be unity in LBM.

The equilibrium distribution function for each fluid is given by Schelke (1996) as

$$f_{{a, ( {\text{eq)}}}}^{l} = \rho^{l} \left( {\beta_{l} - \frac{1}{{2c^{2} }}\varvec{u}^{2} } \right),\quad {\text{for }}a = 0$$
(4a)
$$f_{{a, ( {\text{eq)}}}}^{l} = \rho^{l} \left( {\frac{1}{18}\left( {1 - \beta_{l} } \right) + \frac{1}{{6c^{2} }}\left( {\varvec{c}_{\varvec{a}} \cdot \varvec{u}} \right) + \frac{1}{{6c^{2} }}\left( {\varvec{c}_{\varvec{a}} \cdot \varvec{u}} \right)^{2} - \frac{1}{{12c^{2} }}\varvec{u}^{2} } \right),\quad {\text{for }}a = 1{\text{ to 6}}$$
(4b)
$$f_{{a, ( {\text{eq)}}}}^{l} = \rho^{l} \left( {\frac{1}{18}\left( {1 - \beta_{l} } \right) + \frac{1}{{12c^{2} }}\left( {\varvec{c}_{\varvec{a}} \cdot \varvec{u}} \right) + \frac{1}{{8c^{2} }}\left( {\varvec{c}_{\varvec{a}} \cdot \varvec{u}} \right)^{2} - \frac{1}{{24c^{2} }}\varvec{u}^{2} } \right),\quad {\text{for }}a\,=\,7{\text{ to 18}}$$
(4c)

Here, β l is an adjustable parameter set to be 1/5. ρ l and u are the macroscopic density and velocity, respectively, and are given as

$$\rho^{l} = \sum\limits_{a} {f_{a}^{l} } , \, \rho u = \sum\limits_{a} {c_{a} \left( {\sum\limits_{l} {f_{a}^{l} } } \right)}$$
(5)

In order to generate the surface tension across the interface, we modify the distribution functions using Ω l a 2, as shown in Eq. 3. The surface generator collision term is given by Tolke et al. (2002) as

$$\varOmega_{a}^{l} 2 = A\left| \varvec{C} \right|\left( {\frac{{\left( {c_{a} \cdot \varvec{C}} \right)^{2} }}{{\varvec{C}^{2} }} - \frac{5}{9}} \right)$$
(6)

where A is the free parameter that determines the surface tension between two fluids and C α is the color gradient between two fluids given as (for example between fluids 1 and 2)

$$C_{\alpha } = \frac{1}{\Delta tc}\sum\limits_{a} {c_{a\alpha } \left( {\rho^{1} \left( {t,\varvec{x} + \Delta t\varvec{c}_{\varvec{a}} } \right) - \rho^{2} \left( {t,\varvec{x} + \Delta t\varvec{c}_{\varvec{a}} } \right)} \right)}$$
(7)

The simulations were performed by mimicking a four-mill technique, as shown in Fig. 1b. The density and size of the droplets in the present simulations were set as 1,000 kg/m3 and 40 μm, respectively. The density ratio and viscosity ratio between the droplets and surrounding fluid were considered to be unity. The two immiscible droplets were kept very close to each other, and fluid was sent through the channel in horizontal directions and was collected out from the vertical directions. Using this method, the droplets were allowed to collide with each other. The Reynolds number of the flow, however, was kept very low (Re = 0.25) in order to reduce the effects of the external fluid source on the film drainage between the droplets. At equilibrium, the droplets experienced a partially engulfed state in which the geometries of the partially engulfed droplet followed Neumann’s triangle rule (Eq. 1). The structures of partially engulfed droplets were previously observed by Guzowski et al. (2010), and our structures closely matched theirs, as shown in Fig. 1c. Various morphologies of partially engulfed droplets are categorized in Fig. 1c based on the ratios of interfacial tensions γ 12/γ 13 and γ 23/γ 13.

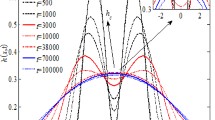
Several simulations were performed to study the film drainage by changing the ratios of interfacial tensions γ 12/γ 13 and γ 23/γ 13. The film drainage in the partially engulfed state can be divided into three regimes. Figure 2 shows the film drainage in all three regimes during the adherence of immiscible droplets. In Row A, where the interfacial tensions γ 12 and γ 23 are greater than γ 13, we observe fast film drainage. The time taken for a film to drain from its initial setup is τ = 0.607, where τ is the non-dimensional time equivalent to t/(ρR 3/γ 13)1/2. From the physics of our problem, we can surmise that the coalescence timescale is a function of three parameters: density (ρ), radius (R) and surface tension (γ). Thus, in order to non-dimensionalize our physical time, we used the characteristic time scale of (ρR 3/γ 13)1/2, which was also used in studies by Biance et al. (2004) and Blanchette (2010). Delayed film drainage is observed between the droplets when γ 12 and γ 23 are smaller than γ 13 (Row C). We observed intermediate film drainage when either γ 12 or γ 23 is greater than γ 13 and the other is smaller than γ 13 (Row B). The time taken for the film drainage in Rows B and C is almost 10 times greater than for the fast drainage case. In the present study, we categorize film drainage as fast or slow with respect to the time taken when the interfacial tension ratios are equal to 1 (i.e., γ 12/γ 13 = γ 23/γ 13 = 1). The film drainage time for this case is τ = 2.082 (not shown in Fig. 2). Figure 2 also shows the film drainage between two identical droplets (Row D). The film drainage between identical droplets is observed between the fast and intermediate drainage regimes. Qualitative observation of droplet deformations shows similarity between the droplets in the intermediate regime and identical droplets. However, the attractive forces among the identical droplets cause the droplets to drain out the surrounding film faster as the droplets approach each other.

Fig. 2
figure 2

The time taken for film drainage and adherence of two immiscible droplets for three different regions of drainage time is shown as Rows A, B and C. τ is the non-dimensional time given as t/(ρR 3/γ 13)1/2, where t is the physical time in the simulation. Row A is for the region of fast film drainage, Row B is for the region of intermediate film drainage and Row C is for the region of slow film drainage. The regions of fast, intermediate and slow film drainage depend on the interfacial tension ratios (γ 12/γ 13 and γ 23/γ 13), as shown here. For reference, film drainage between two identical droplets is shown in Row D (color online)

Full size image

Results for various interfacial tension ratios γ 12/γ 13 and γ 23/γ 13 are summarized using a phase diagram. The partially engulfed region can be split into three parts, as shown in Fig. 1d, depending on the ratio of interfacial tensions. When that ratio is greater than 1, we observed not only a fast drainage, but also that the time taken for film drainage was approximately the same irrespective of the difference in the interfacial tensions and their magnitudes. In the case of intermediate and delayed drainage regions, the film drainage time is observed to range in 1 magnitude of τ depending on the magnitudes of interfacial tensions.

In order to qualitatively analyze the reason for variation in film drainage time when the interfacial tension ratios between the droplets differ, we studied the additional hydrodynamic contributions that affect the film drainage process. Riegler and Lazar (2008) previously studied a change in pressure due to the Marangoni flow across the interface during the coalescence of miscible but different droplets. Following their model, in Fig. 3, we illustrate the Marangoni flow across the interfaces when the droplets are very close to each other. Due to the variation in interfacial tension of two droplets, the droplets have a Laplace pressure difference, which causes the film between the droplets to eject quickly. However, the interfacial tension formed between droplet interfaces can also cause the surrounding fluid to either flow into the film or out of the film depending on the magnitudes of respective interfacial tensions. For example, if γ 12 and γ 23 are less than γ 13, the surrounding fluid flows into the film region due to the Marangoni effect. We plotted the velocity vectors in the film drainage region before the adherence of droplets and found that the velocity of fluid moving in or out of the film is based on the region into which the interfacial tension ratios fall. In the case of slow and intermediate drainage, we observe fluid flowing into the film due to the presence of larger interfacial tension γ 13 (Fig. 4). In the case of the fast drainage region or for droplets with equal interfacial tension ratios, fluid flows out of the film region, which decreases the drainage time of the film.

Fig. 3
figure 3

a The effect of new interfacial tension formation due to the close affinity of the interfaces of droplets 1 and 3 on fluid flow in the film. b Surface flow speed due to the interfacial gradient is a function of ∆γ i /r, h and r. The amount of fluid influx into the film due to Marangoni flow is the product of surface flow speed and area of film thickness (color online)

Full size image
Fig. 4
figure 4

Velocity vectors and velocity slides are shown along with the droplet phases when the droplets are close to each other and about to adhere. The rectangular box in each portion of the figure signifies the film region affected by the surface tension gradient formation. a The region of slow drainage. The velocity vectors are directed into the film region due to the presence of a higher surface gradient at the center of the film. b The region of intermediate drainage. The velocity vectors near the droplet with interfacial tension ratio γ 12/γ 13 = 0.769 (right side droplet) are directed into the film region. c The ratio of interfacial tensions = 1, and due to the absence of surface tension gradients, the velocity vectors in the film are not small. d The region of fast drainage. Higher interfacial tension outside the film region directs the fluid in the film to flow out of the rectangular box as can be observed from the velocity vectors (color online)

Full size image

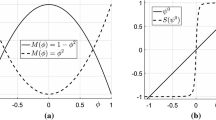
Theoretical understanding of these additional hydrodynamic contributions can be obtained by formulating the additional rate of change in film thickness in terms of hydrodynamic contributions of the above-mentioned Marangoni flow effects. The rate of change in film thickness (∂h/∂t) during the coalescence of two identical droplets can be obtained as ∂h/∂t = ∂Q/dz (Butt and Kappl 2010; Manor et al. 2008), where Q is the fluid flux into or out of the film. Using the theory, we can state that any additional change in the rate of film thickness is due to the addition or subtraction of fluid flux (Q) along the droplet interface (r). Loosely assuming a two-dimensional droplet interface, as shown in Fig. 3b, we formulate the additional rate of change in film thickness. If we assume that the length of the interface affected by the surface tension gradient is r, that the film thickness between the droplets is approximately constant at h(r,t) and that η is the fluid viscosity, then the additional velocity of fluid flowing into the film due to the presence of a surface tension gradient can be written as by Riegler and Lazar (2008):

$$\upsilon = \frac{{2\Delta \gamma_{i} }}{r}\frac{h}{\eta }$$
(8)

Here, ∆γ i  = γ 13 − γ i2 (i = 1 or 3). The velocity is the product of twice ∆γ i because the fluid flows from both the top and bottom halves of the interface. The influx or outflux of fluid into the film due to the presence of the surface gradient along two droplet interfaces is

$$Q = (\upsilon_{1} + \upsilon_{2} )\left( {\pi \frac{{h^{2} }}{6}} \right) = \frac{{\pi h^{3} }}{3r\eta }\left( {\Delta \gamma_{1} + \Delta \gamma_{3} } \right)$$
(9)

However, the presence of a difference in interfacial tensions among the droplets creates a Laplace pressure difference (∆P l), which is given as

$$\Delta P_{l} = \frac{2}{R}\left( {\left| {\gamma_{12} - \gamma_{32} } \right|} \right)$$
(10)

R is the radius of the droplets. Thus, velocity outflux from the film due to the Laplace pressure difference can be given as

$$\upsilon_{l} = 2\sqrt {\frac{{\left| {\gamma_{13} - \gamma_{23} } \right|}}{R\rho }}$$
(11)

Using Eqs. (9) and (11), the additional rate of change in film thickness (\(\hat{h}\)) due to the presence of surface tension gradients in immiscible droplets can be written as

$$\frac{{\partial \hat{h}}}{\partial t} = \frac{{\pi h^{3} }}{3r\eta }\left( {\Delta \gamma_{1} + \Delta \gamma_{2} } \right) - 2rh\sqrt {\frac{{\left| {\gamma_{13} - \gamma_{23} } \right|}}{R\rho }}$$
(12)

Qualitatively analyzing Eq. (12) reveals that when the interfacial tension ratios of droplets are equal to 1, the additional rate of change in film thickness is zero. When the droplets are in a region of slow drainage, the additional rate of change in film thickness shows an increase in film thickness, implying an increase in the film drainage time. When the droplets are in a fast drainage region (i.e., when γ i2/γ 13 > 1 for i = 1, 3), the first term of Eq. 12 can be rewritten as follows.

$$\frac{{\pi h^{3} }}{3r\eta }\left( {\Delta \gamma_{1} + \Delta \gamma_{2} } \right) = \frac{{\pi h^{3} \gamma_{13} }}{3r\eta }\left( {1 - \frac{{\gamma_{12} }}{{\gamma_{13} }} + 1 - \frac{{\gamma_{23} }}{{\gamma_{13} }}} \right)$$
(13)

If the ratio of surface tensions in Eq. 13 is greater than 1, then the additional rate of change in film thickness (Eq. 12) is always negative. Thus, the film drainage time in the region of fast drainage is faster than in the other two regions.

However, the formulation of change in the additional rate of film thickness given here is a loosely modeled approximation for the theoretical understanding of film drainage between two immiscible droplets. The actual rate of film drainage may vary due to instantaneous interfacial deformation and possible vortex formation in the film between two droplets.

In this study, we consider a novel problem of film drainage between two immiscible droplets, which shows a unique and interesting flow flux during the adherence of droplets. We suggest that the possible delay and fastening of adherence among the immiscible droplets when compared to identical droplets could be due to the presence of a difference in interfacial tension along the interface, which causes the fluid to either flow into or out of the film. This theory is validated by observing the velocity vectors in the film between two droplets, which bring us to the same conclusion. The problem studied here is not only of interest from a physics point of view, but also has significance in applications due to the ever growing study of immiscible droplets in the field of drug delivery, Janus droplets formation and the microfluidics approach of emulsion control.