1 Introduction

Microfluidic systems have far-reaching applications that are often far removed from the fluid physics that guides system design. Although computational fluid dynamics (CFD) can be used to design microfluidic networks, the knowledge of fluid mechanics, complex software packages, and, oftentimes, long solution times required to optimize systems can be time-consuming in a diverse microfluidics community (Oh et al. 2012). To assist the user base of microfluidics and to simplify system design, flow equations, which are mathematically analogous to those governing electrical circuits, are used to predict flow properties (Bruus 2008). Flow resistance in such systems is defined as the energy required to balancing the total shear stress in a flow with the energy driving the flow. It, in effect, relates the applied pressure gradient (voltage) with the resulting volumetric flow rate (current) (Kim et al. 2006; Vedel et al. 2010). In addition to electrical resistance, other basic phenomena can be related to electrical equivalents, e.g., channel compliance (capacitance) and inertia (inductance). Together, these electrical analogies have been used extensively to design microfluidic systems and optimize performance of a range of applications such as hydrodynamic particle trapping, viscosity measurement, and flow control (Zeitoun et al. 2010; Tan and Takeuchi 2007; Srivastava and Burns 2006; Cho et al. 2003; Saias et al. 2011; Fuerstman et al. 2003). Recently, electric analogies have been expanded to perform more complex functions like operation of fluid logic gates using pulsed air flow (Mosadegh et al. 2010; Leslie et al. 2009). But, despite widespread use and convenience, fluid models often fail to capture some of the many physical differences between electrical and fluidic systems like start-up effects, fluid–surface interactions, and thermodynamic considerations. These effects, if not properly assessed, can significantly impact their validity (Oh et al. 2012).

Flow resistance is best described by an energy balance in which an applied pressure gradient is equated to the energy required to overcome fluid frictional losses (Bruus 2008; Oh et al. 2012). Specifically, the pressure gradient acts to overcome shear stresses experienced by the bulk fluid during flow. Shear stress in a Newtonian, bounded pressure-driven flow arises from the flow’s parabolic velocity profile, which itself derives from a no-slip boundary condition at a channel wall. Shear stress in steady-state, fully developed flows is constant on a per distance basis, when the fluid travels within a conduit of constant cross section.

Macroscale flow systems have been shown to have flow rates lower than what would be predicted by flow resistance equations with respect to an increasing pressure gradient (Patience and Mehrotra 1989; Otis 1985). This is because flow resistance solely accounts for viscous losses. Realistically, the pressure gradient is balanced by both viscous shear stress and the start-up energy required to accelerate the flow and establish a kinetic head. In a channel with a fixed cross section, start-up becomes more significant with increasing flow velocity or with decreasing total shear stress (decreasing channel length). Although flow resistance in microfluidic channels is primarily dominated by viscous shear stress, owing to their small channel sizes, under certain conditions, start-up effects can be a significant and non-negligible source of fluidic resistance. Such effects are exaggerated in more complex microfluidic channel networks having several transient flow regimes where kinetic head must be repeatedly established. Also, complex microfluidic systems oftentimes contain many short channels that can be less than 1 mm in length while containing flow rates on the order from 1 to 100 mm/s (Yusuf et al. 2009; Dertinger et al. 2001; Gomez et al. 2007).

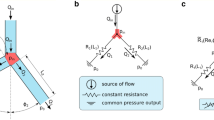
For example, a standard microfluidic element, such as a T-junction, can be modeled using a flow resistance model (Fig. 1). Since the flow resistance model assumes a constant fluidic resistance per distance traveled, the flow ratio out of the arms of a T-junction should be constant with respect to total flow rate (Fig. 1c). In this case, flow is accelerated to steady state at the inlet and at the split. Therefore, start-up effects, which are generally ignored, can lead to deviations from standard fluid-electrical analogies. By identifying the conditions where deviation from standard flow resistance equations arises and the consequences of start-up flow in microfluidic systems, microfluidic systems can be designed more accurately in an electrical analogy framework adding a simple design tool to the microfluidic researcher’s toolbox.

Fig. 1
figure 1

T-junction device performance. a Schematic of a sample microfluidic T-junction device. b Equivalent resistance model and performance of flow ratio with respect to overall flow rate. c Constant predicted flow rate

Full size image

Here, investigation is presented on (1) how the fluid resistance analogy can be appropriately modified to account for start-up flow with Newtonian fluids and (2) the flow implications that arise when start-up effects become significant in microfluidic systems. The influence of start-up flow is investigated by modulating total shear stress and flow’s kinetic energy. Therefore, start-up can be measured relative to viscous shear stress by comparing the flow rate ratio between varying channel lengths and flow rates. The implications of start-up flow on the performance of complex microfluidic channel networks are investigated in two-standard microfluidic systems: T-junctions are commonly used to split flow, mix, or converge flows, and serpentine channels are used to increase fluid resistance and residence time (Cho et al. 2003; Song and Ismagilov 2003). Finally, effects of this phenomenon are discussed with focus on passive methods toward changing baseline device flow behavior.

2 Materials and methods

2.1 Simulations

Simulations were performed using COMSOL Multiphysics v4.2, a finite-element method solver. In all cases, the Navier–Stokes equations were solved in 3-dimensional for laminar flow with COMSOL’s default general minimal residual solver (GMRES). The parametric solver was used to change inlet pressure conditions, and convergence residuals were set at 10−3. Outlet pressure was set to 0, while inlet pressure was set to a desired value with no inlet stress. Solutions were performed on free tetrahedral meshes. No inverted elements were used in simulations.

Flow rate was calculated by surface integration of the normal velocity from the channel exit. Boundary conditions were either wall no-slip (v = 0) on solid boundaries or symmetry (τ = 0) to reduce computation time. In the case of straight channels, two symmetry boundary conditions were used, and in the case of T-junction and serpentine simulations, only one symmetry condition was used. For most fluid simulations, a laminar flow model was used, which solves for the incompressible Navier–Stokes’ equations. Constant fluid properties (ρ = 1,000 kg/m3 and μ = 0.001 Pa s) were used for laminar flow studies. In cases where viscous dissipation was investigated, the non-isothermal laminar flow package was used with isopropanol material properties for the viscosity and density dependence on temperature.

Channel length was parameterized and varied between 1 and 5 mm. Channel heights were held constant at 80 μm (40 μm and a symmetry boundary condition). Depending on the simulation performed, channel width was either 80 or 100 μm. Inlet pressure was varied between 1 Pa and 100 kPa for simulations.

2.2 Flow rate calculations

Fluid flow rates were calculated using the variable flow resistance model (Eq. 4) in complex networks (like T-junctions) by solving the appropriate systems of equations. Flow in a T-junction has three arms: a common arm (c) splitting to the left arm (l) and right arm (r); Q l is flow rate out the left arm, and Q r is the flow rate out the right arm; P is the inlet pressure, and P’ is the pressure at the constriction. Setting up the equation as a circuit diagram (Fig. 3a). Equations 1a–c are the equations describing this system. R o and R 1 are described in Sect. 3.2.

$$P - P^{\prime } = R_{o} \left( {Q_{l} + Q_{r} } \right)^{2} + R_{1,c} \left( {Q_{l} + Q_{r} } \right)$$
(1a)
$$P^{\prime } = R_{o} Q_{l}^{2} + R_{1,l} Q_{l}$$
(1b)
$$P^{\prime } = R_{o} Q_{r}^{2} + R_{1,r} Q_{r}$$
(1c)

These three equations (Eq. 1a–c) are then solved using a multivariate Newton–Raphson iterative solver in MATLAB until residuals are less than 10−7. The dimensions and inlet pressures used are identical to those used for simulations.

2.3 Device construction and operation

Microfluidic devices were fabricated using standard soft-lithography practices. Briefly, bare silicon was spun with SU8-3150 following the manufacturers’ protocol for 80-μm thick resist. Patterns were exposed and developed and then treated using trichloro(1H,1H,2H,2H-perfluorooctyl)silane. Following overnight low-pressure exposure to the silane, poly(dimethylsiloxane) was mixed in a 10:1 base to cross-linker ratio and poured over the SU-8. After 1–2 h of degassing in a vacuum chamber, PDMS was cured in an oven at 60 °C for 1–2 h. Individual dies were excised with a razor blade, and access ports were made using a biopsy punch. Devices were irreversibly bonded to glass slides after a 40-s oxygen plasma treatment at 30 W followed by a 70 °C setting period for at least 1 h.

Fluid was driven using syringe pumps (Cole Parmer) with syringes connected to the device via silicone tubing (1/8″ ID), fittings (Harvard Apparatus) precision tips (EFD, 0.84″ ID), and accessing the biopsy openings. For outlets out of the syringe, tubing was identical length and was held at identical height to ensure equal pressure differentials between T-junction arms. A 0.2-μm syringe filter was used to remove particles prior to introducing fluid in the microchannel. 2-Propanol was used for all experiments. All devices were infused with solution overnight (Q v  = 5 μL/min) to equilibrate channels because PDMS swells from organic solvents. Flow rates were varied between 50 and 800 μL/min.

2.4 Fluid measurements

Effluent flow from devices was emptied into pre-weighed 1.5-mL microcentrifuge tubes. After fluid was flowed for a set time period, the tubes were capped to prevent further evaporation and weighed using a four point precision digital balance (Mettler Toledo). The ratio of weighed volumes, after considering evaporation, was used as the flow ratio. Each data point was taken from at least 0.3 mL of liquid (<1 % measurement weighing error) or a minimum of 2–3 min to reduce higher frequency noise, and the random error component was calculated from the standard deviation of 3 or 4 data points. Prior to measurement, flow rates were allowed to equilibrate from no flow rate for at least 5 min. For dimensionless calculations, the fluid properties of isopropanol were used (μ/ρ = 3.6 × 10−6 m2/s). Flow ratio was normalized by dividing a data set by the maximum flow ratio for the respective data set.

3 Results and discussion

3.1 Model verification

The integrity of the CFD simulation mesh was validated by comparing meshing parameters versus model results. Since channel dimensions were parameterized, the goal of this study was to generalize mesh parameters and not simply the minimum number elements and degrees of freedom. Choosing a correct mesh is a trade-off between fewer nodes (faster computational times) and model accuracy and quality. To determine basic mesh parameters to be used, flow rates were evaluated in three-dimensional straight channels as the mesh was improved. As the mesh was refined, flow rates asymptotically converge toward a fixed value. COMSOL’s default mesh parameters were used to build the mesh, and the mesh parameters are listed in Table 1. Flow rate versus meshing parameters was evaluated for a 1-mm channel length and is plotted in Fig. 2a. For cases where the minimum element size is 3.35 μm and the maximum element size is 13.4 μm, the simulation results appear to not significantly change. Therefore, these general parameters (Case II) were used to build meshes for the remainder of this work.

Table 1 Mesh settings used to build simulation meshes in square channel (L = 1 mm, h = 80 μm, w = 100 μm) with no-slip boundary conditions on two faces, and symmetry boundary conditions on appropriate faces
Full size table
Fig. 2
figure 2

COMSOL simulations of deviation from ideal flow at higher flow rates. a Flow rates in straight channels (L = 1 mm, h = 80 μm, w = 100 μm) under different mesh conditions. Detailed conditions are listed in Table 1. b Normalized pressure profile across the length of a rectangular channel (h = 80 μm, w = 100 μm). Pressure is taken at the centerline of the channel. c Simulated and derived flow rate versus inlet pressure at varying channel lengths in a rectangular channel (D = 80 μm). d Dimensionless plot of flow deviating from ideal flow rate parameterized with channel length

Full size image

COMSOL simulations were verified versus typical flow models for flow in a duct (Eq. 2) (Bruus 2008). Low-pressure gradients were chosen (under 1 kPa/mm) to model a linear flow resistance. Flow rate was calculated by the product of the cross-sectional area and average velocity. As seen by Fig. S1, the calculated results and simulation results closely agree suggesting the simulation appropriately captures the flow physics.

$$\frac{\Updelta P}{L} = 12\frac{\mu }{{h^{2} \left( {1 - .63h/w} \right)}}\bar{u}$$
(2)

3.2 Acceleration in laminar fluid flow

When start-up flow effects, like acceleration, comprise a substantial amount of energy with respect to viscous losses, then traditional analyses of flow resistance must be amended. Conceptually, this can occur at an abrupt constriction or at a 90-degree bend where fluid accelerates to steady state. By including a kinetic energy term needed to accelerate transient flow and establish kinetic head, flow in a square cross-section channel can be described by Eq. 3, which accounts for increased pressure drop (Patience and Mehrotra 1989).

$$\frac{\Updelta P}{L} = \frac{\rho }{2L}\bar{u}^{2} + 28.4\frac{\mu }{{D^{2} }}\bar{u}$$
(3)

In the above expression, the pressure gradient, ΔP/L, is equal to the sum of the intrinsic kinetic energy term, \(\frac{\rho }{2L}\bar{u}^{2} ,\) and the viscous shear stress term, \(28.4\frac{\mu }{{D^{2} }}\bar{u}.\) In Eq. 3, ρ is the fluid density, L is the channel length, μ is the viscosity, D is channel’s characteristic dimension (80 μm for a 80 × 80 μm square), and \(\bar{u}\) is the average velocity. For simplicity, shear stress in the developed region is assumed to be equal to shear stress effects in the entrance region. This is justified because the developing boundary layer asymptotically approaches fully developed flow. Realistically, the shear stress in the entrance region is approximately equal to shear stress in the developed flow (see Supplemental Information 1) (Wilkes 1999). By measuring the centerline pressure in a channel at a high- and low-pressure differential, a local pressure drop occurs for high-pressure differentials (105 Pa) which accounts for this start-up energy toward establishing kinetic head (Fig. 2b). At low pressures (P = 1 Pa), kinetic head does not comprise a significant amount of energy, and therefore, there is no local pressure drop. In addition, in the 1 mm channel, the start-up pressure drop is greater than the start-up pressure drop in 3 mm channel at 105 Pa. This is because in the 1 mm channel, flow is traveling faster than in the 3 mm channel, and kinetic head comprises more energy with respect to shear stress.

The modified fluid flow expression (Eq. 3) is modified to a form that is compatible with electrical analogies fluid resistance.

$${{\Updelta}}P = \left( {R_{o} Q_{v} + R_{1} } \right)Q_{v}$$
(4)

where R 1 is the traditional resistance based on shear stress and R o Q v is a flow resistance based on start-up flow. Q v is the product of average velocity and cross-sectional area. From Eqs. 3 and 4, it can be seen that R o Q v increases with respect to R 1 as the channel length, L, decreases, or as the flow rate is increased. It is also important to note that as the channel cross-section decreases, start-up effects are relatively less influential since the R 1 term has a D −2 dependence.

Both theory (Eq. 4) and simulation show that at low inlet pressures, flow rate scales linearly with inlet pressure (Fig. 2c). However, as pressure, ΔP, increases, flow rate decreases from the linear projection. In all cases, flow is still laminar with a Reynolds number less than 1,200. As seen in Fig. 2c, flow rate in shorter channels deviates more from the linear projection than long channels at identical inlet pressures. This is because as channel length decreases, total shear stress is lower. Also, at constant flow rates, kinetic head is constant for all channel lengths and therefore is more influential with shorter channel lengths. The nonlinear flow rate dependence on pressure gradient can be predicted by comparing the magnitudes of the two resistances in Eq. 4, or by comparing the kinetic energy and viscous dissipation. Comparing these two terms results in a dimensionless value, ξ (Eq. 5).

$$\xi = Re\frac{D}{L}$$
(5)

where Re is the Reynolds number which is the product of the velocity, hydraulic diameter (4A c /P w ) and inverse of the kinematic velocity. In the case of a rectangular cross section (Eq. 2), the aspect ratio correction will also appear in the numerator. By simulating channels of varying length, it is shown that the trend of actual simulated flow rate versus ideal viscous-only flow rate scales with respect to ξ (Fig. 2d). For values of ξ greater than 10−1, or as start-up energy is comparable to shear stress, flow rate decreases with respect to an ideally predicted flow rate. At values around 2, flow rate is about 90 % of ideal. Figure 2d also exhibits a slight deviation between curves of constant length. To correct for this, ξ could be modified to be dependent on (D/L)1/2 instead of D/L (Fig. S3). This could be caused by the model omitting differences in shear stress in the entrance region; however, since differences were slight, the dimensionless value was left as derived.

3.3 Theoretical flow splitting at a T-junction

The microfluidic T-junction is a standard microfluidic design used to separate and fractionalize flow. Transient flow rates at the T-junction make it susceptible to the effects of start-up flow. T-junction performance depends on upstream and downstream fluid resistance. Direct simulations require simulations of several channels, and therefore, optimization can be time intensive. In T-junctions, flow splits from a common channel into two arms. These two arms and the common channel have transient flow regimes at the entrance. Flow rates were modeled using the modified electric circuit equations in a T-junction (Fig. 3a) with the mathematical approach detailed in Sect. 2.2. Figure 3b shows model is in close agreement with simulations based on the design in Fig. 3a. This demonstrates that variable fluid resistance can assist quickly designing more accurate microfluidic systems than using simple constant resistance equations.

Fig. 3
figure 3

Behavior of flow at a T-junction. a Circuit layout of a T-junction with relevant dimensions labeled. b Simulations of flow rates to the T-junction example in Fig. 3a. Dotted lines are model solutions not considering start-up flow (Eq. 2), and straight lines are solutions considering start-up effects (Eq. 4). c Simulations and theory of the ratio of flow rates out of single straight channels of two different channel lengths. d T-junction comparison of model results and simulation results of the flow ratio from the circuit layout of Fig. 3a

Full size image

Fluid resistance downstream of a T-junction dictates the ratio of flow splitting. Neglecting start-up flow occurring in a T-junction by using standard fluidic resistance expressions results in overestimated flow splitting in a T-junction. For example, if a T-junction splits to a long channel (L = 3 mm) and a short channel (L = 1 mm) with a constant cross section, then traditional flow resistance theory would predict that three times the flow will exit the short channel with respect to the long channel. However, greater flow rates require more energy in the form of kinetic head for a fixed cross section, and the flow rate in the shorter channel will be reduced relative to that in the long channel. Simply comparing flow rates of two independent channels, the ratio of the channel’s flow rates, or flow ratio, decreases across the range of the pressures simulated, from 102 to 105 Pa (Fig. 3c). T-junction systems with straight asymmetric channels will asymptotically approach a flow ratio regardless of how flow ratio is defined.

By applying the modified fluid resistance model (Eq. 4), flow ratio convergence was accurately predicted. At inlet pressures of 105 Pa, simulations and theory with viscous and transient contributions begin to disagree (Fig. 3c). Simulations appear to predict an “evening out” of flow, while theory predicts flow ratio continues to decrease. This disagreement between theory and simulation could be the result of the entrance length of the developing flow approaching that of the channel length—a violation of the assumptions of the theory. Also, as the ratio between channel lengths decreases, the flow ratio deviates less from standard fluid resistance theory. This makes sense because if the channels have identical length, there is no difference in kinetic energy and no “driving force” changes flow ratio.

Interestingly, in the case of the T-junction in Fig. 3a, although the model predictions of flow rates appear quite accurate, there is discrepancy between the flow ratio of a directly simulated T-junction and model T-junction (Fig. 3d). First, the simulated T-junction never reaches a flow ratio of 3, as would be expected for flow rates where start-up effects are insignificant. Second, the predicted and simulated flow ratios appear to be exponentially shifted from one another. Although the overall trend is predicted, the listed discrepancies are likely due to minor losses that occur from the split, which were not considered in the model and are not typically mentioned in fluid–electrical analogies.

3.4 Experimental flow splitting at a T-junction

To experimentally verify the effect of start-up acceleration in a microfluidic system, flow splitting versus total flow rate was measured using a T-junction device. This device was split between 4.5 and 1.7 mm outlet channels so an unequal flow rate is expected out of each channel. Also, 2-propanol (IPA) was used for its high affinity for the PDMS channel walls compared to water in order to reduce the presence of large air bubbles that will adhere to the hydrophobic PDMS channel walls and increase flow resistance (Kang et al. 2008). IPA is a volatile substance and will evaporate when taking gravimetric measurements. Evaporation rate was determined by comparing total volume dispensed to collection vessels during each experiment to the syringe pump flow setting as shown in Eq. 6,

$$\frac{{{\text{d}}M}}{{{\text{d}}t}} = \rho AQ_{v} - \varepsilon$$
(6)

where ρ is the fluid density, A is the syringe volumetric flow rate per pump volumetric setting, ε is the mass evaporation rate, and ∂M/∂t is the change in mass with respect to time. A weighted least-squares analysis was used to determine evaporation rate and its associated error, which was factored into flow ratio calculations and was found to be substantial for some measured flow rates (Fig. 4a). Evaporation at low flow rates was more significant because a minimum volume of 0.3 mL was collected from each arm of every data point. It would take 24 min to collect 0.3 mL from flow rates around 50 μL/min when flow splits by ~3. Calculating evaporation by this method resulted in a value with no adjustable parameters.

Fig. 4
figure 4

Flow rate ratio. a Syringe pump flow setting versus flow rate. Weighted least-squares fit used to calculate evaporation rate. b Data in a T-junction device of the flow ratio versus dimensionless flow rate (L 1 = 1.7 mm, L 2 = 4.5 mm, h = 80 μm, w = 100 μm). c Schematic of flow ratio experiment. T-junction with variable length arm. d Nondimensional flow ratio data acquired from three devices (h = 80 μm, w = 100 μm)

Full size image

The predicted trend, where the flow ratio decreases with increasing flow rate, was experimentally observed in the T-junction device (Fig. 4b). At around a ξ = 0.2, this flow ratio begins to decrease, and the trend of the data is in agreement with simulations (Fig. 3c). Because the density-to-viscosity ratio of IPA is less than that of water, the range of ξ that was covered is less than that would be seen in systems using water. Also, to control for the pulsation of the stepper motor from the syringe pump, identical experiments were performed using three syringe cross-section sizes. For the same flow rate, small syringes experience less pulsation and a more constant pressure from a higher frequency of motor steps than larger syringes. No difference was observed between the syringes.

Experimentally collected data (Fig. 4b) have two interesting features that were not predicted by simulation. First, at low flow rates, it appears that the flow ratio decreases. This trend could be because low flow rates are accompanied by large evaporation errors mentioned earlier. Second, the maximum value of the flow ratio is higher than expected though the trend is the same. This could be caused by PDMS channel compliance or by microfabrication inhomogeneities and imperfections. One potential explanation considered was a variable viscosity from internal heating due to viscous dissipation. But, simulations (non-isothermal models) and theory suggest the heat generated would not cause an appreciable temperature change (ΔT ≪ 1 °C) (Deen 1998). Experiments setting the microfluidic device on an aluminum heat sink with conductive paste also showed no change in the trend at low velocities, although PDMS and glass are poor thermal conductors.

Systems with varying asymmetric arm lengths were studied to demonstrate generalizing non-dimensionalization of flow splitting from T-junctions. Three devices, each with one fixed arm (4.5 mm) and one variable arm (2.7, 1.7, and 0.7 mm), were studied over a range of flow rates between 50 and 800 μL/min (Fig. 4c). By non-dimensionalizing the parameters, all three devices are shown to collapse onto the same curve which closely follows the variable flow resistance model defined in Sect. 2.2 (Fig. 4d). In addition, the model slightly overestimates the experimental data, which is consistent with the results from Fig. 3d. Across the flow rate range, the device with a 2.7-mm variable arm had its flow ratio decrease by under 5 %, while the device with a 0.7 mm variable arm length had its flow ratio change by almost 15 % of the maximum. This is expected because higher flow ratios result in higher flow rates out the shorter channel for identical total flow rates. Additionally, the short channels have inherently less shear stress so the results are more dramatic. At higher flow rates, all of these devices should deviate from predicted performance because start-up energy in the longer fixed channel will become more influential.

3.5 Divergence from an equal flow ratio

Microfluidic systems often have complex geometries such as serpentine channels which are used, in some cases, to increase residence time improve mixing, or to increase fluidic resistance. The compounded energy required to establish kinetic head would be more dramatic in a serpentine channel, where flow changes direction many times. To demonstrate the effect of start-up on flow in a serpentine channel (which we define from hereon as channels with 180-degree turns), simulations of the ratio of flow rate in a straight channel versus flow rate in a serpentine channel of equal length were compared. The number of turns, N, was parameterized, and the total channel length was held constant at 8 mm. For example, in the case of N = 2 turns, each segment was 4 mm, and in the case of N = 16 turns, each segment was 0.5 mm. With increasing pressure, the flow rate of a serpentine channel decreases with respect to the straight channel. As the number of turns increases and segment size decreases, the divergence becomes larger for the same pressure drop (Fig. 5a). This can be justified by imagining the system is comprised of multiple straight channels in series. From previous results, the flow rate through the shorter channel deviates more from ideal conditions per pressure applied than in longer channels (Fig. 2b). Therefore, shorter channels in series should deviate from predicted flow rates more than a single straight channel. By modeling, these results as a set of channels connected in series a modified form of Eq. 3 can be arrived at in which the kinetic energy term is multiplied by the number of turns, N (Eq. 7). This modification matches the trend of the simulations, although the magnitude of influence of the serpentine channels was underestimated, likely because of additional minor losses at the 90-degree channel elbows (Fig. S4).

Fig. 5
figure 5

Serpentine channel data. a Normalized simulation of flow rate deviation versus ideal flow rate parameterized by the number of turns, for equal total channel length. b Flow ratio versus flow rate in a flow split with a serpentine channel (L = 1.25 mm). Inset: CAD drawing of the device. c Simulation of straight/serpentine and a surface plot of the velocity distribution. d Results for two different systems. One of which changes the majority of its flow, and the other diverges from a flow ratio of 1

Full size image
$$\frac{{{{\Updelta}}P}}{L} = N\frac{\rho }{2L}\bar{u}^{2} + 28.4\frac{\mu }{{D_{H}^{2} }}\bar{u}$$
(7)

Since start-up causes the flow rate in a serpentine channel to be lower than straight channels of the same length, this same idea can be used to design microfluidic T-junction systems to behave differently than two straight channels. In a T-junction with serpentine and straight arms, each arm should deviate from the ideal trend at different rates with the serpentine channel having greater deviation as seen in Fig. 5a. In the case of a device like that shown in Fig. 5b, if the change of flow rates between serpentine and straight channels decreases proportionally, then flow ratio is nearly constant at values greater than unity.

Microfluidic logic and switching elements based on passive fluid/channel interactions have garnered interest as a means to increase microfluidic device functionality while decreasing external infrastructure needed for control (Toepke et al. 2007). With this in mind, functions can be derived from the observation flow ratio can either diverge or converge flow ratio with respect to ideal behavior. For example, by properly tuning channel lengths, a T-junction can be made to change function from having a majority of the flow rate traveling through a serpentine channel at low pressures and a majority of flow rate flow through the straight channel at higher pressures (Fig. 5c, d). To illustrate this concept, a system was simulated which was comprised of a T-junction with a serpentine channel shorter than a longer straight channel. In this system (Fig. 5d), at low flow rates, a majority of flow travels through the serpentine channels, where at higher flow rates, a majority of flow travels through the straight channel. Furthermore, it is worth noting that dimensions can be tuned to meet specific flow demands. Fluidic logic devices may be assisted by systems whose ratio of pressure can be tuned depending on inlet pressures.

4 Conclusions

Fundamental physical differences between the flow of electricity and the flow of a fluid can limit the application of analogous modeling, particularly in complex microfluidic systems where energy used toward establishing kinetic head is non-negligible. But such differences can be corrected for through proper treatment of such start-up effects on flow rate. By connecting real performance with a physical basis through simple resistance equations, microfluidic system design can be performed by researchers without deep fluid mechanics backgrounds and systems can be designed without the use of fluid dynamics software packages. Although implicating start-up flow effects on flow rate more accurately predict microfluidic system performance, the effects of minor losses around bends must be included to fully model microfluidic systems. Further opportunities exist to understand why at low flow rates, experimentally the flow ratios initially rise, contrary to theory and simulation. In addition, it is also still unresolved as why ξ better scales by (D/L)1/2 and not D/L. The idea of converging and diverging flow has the potential to change system performance (such as what arm a majority of flow travels through) and can be further investigated for controlling system function or creating responsive microfluidic systems. Perhaps, systems with channels having more than just a simple split can be designed to have a sensitive response to flow conditions. Implications of start-up flow and other dismissed phenomena like surface interactions require further investigation to fully connect microfluidic systems performance to simple electrical analogy equations.