Liquid flow through a diverging microchannel

Abstract

In this work, experiments and three-dimensional numerical calculations of fluid flow through diverging microchannels were carried out with the aim of bringing out differences between flow in uniform and nonuniform passages. Deionized water was used as the working fluid in the experiments where the effects of mass flow rate (8.33 × 10⁻⁶ to 8.33 × 10⁻⁵ kg/s), microchannel hydraulic diameter (118–177 µm), length (10–30 mm) and divergence angle (4°–16°) on pressure drop were studied. The results are analyzed in detail with the help of numerical data. The pressure drop exhibits a linear dependence on the mass flow rate, whereas it is inversely proportional to the divergence angle and square of the hydraulic diameter. The pressure drop increases anomalously at 16°, suggesting that flow reversal occurs between 12° and 16°, which agrees with the corresponding value at the conventional scale. For the purpose of predicting pressure drop using straight microchannel theory, an equivalent hydraulic diameter was defined. It is observed that the equivalent hydraulic diameter, located at one-third of the diverging microchannel length from the inlet, becomes mostly independent of the mass flow rate, microchannel hydraulic diameter, length and divergence angle. The pressure drop for a diverging microchannel becomes equal to an equivalent hydraulic diameter uniform cross-section microchannel, suggesting that conventional correlations for straight microchannels can also be applied to diverging microchannels. The data presented in this work are of fundamental importance and can help in optimization of diffuser design used for example in valveless micropumps.

1 Introduction

Microscale and nanoscale passages are an intricate part of any microfluidic/nanofluidic device. These devices have potentially large applications in health-care, defense, electronic and agriculture industries. Therefore, fundamental study of flow through these passages is imperative in the development and advancement of knowledge on microfluidic and nanofluidic devices. Study of various aspects of uniform cross-section microchannel with both liquid and gas as working fluids have been in process since the last two decades (Gad-el-Hak 1999; Mala and Li 1999; Karniadakis et al. 2004; Barber and Emerson 2006; Verma et al. 2009a; Agrawal 2011). Researchers have studied numerically and experimentally the phenomenon of gas flow through microchannels of different shapes and sizes. Parametric studies have shown that new flow physics like rarefaction, velocity and temperature jump at the solid–fluid interface, and compressibility effect at low Mach numbers are present at micro-scale involving gas flow (Karniadakis et al. 2004; Agrawal 2011). Recent experiments by Demsis et al. (2009, 2010) have shown that the Nusselt number is anomalously low with gas flow, and that the available theoretical analyses are unable to correctly predict its value. A review of the experimental and numerical study of liquid flow through microchannel performed by Koo and Kleinstreuer (2003) reinforced that viscous forces were important at the microscale while wall slip is negligible.

Although flow through uniform cross-section microchannels has been largely understood, the fundamental phenomenon in varying cross-section microchannels, which may differ substantially from the uniform cross-section counterparts, has not received much attention. For example, a stability analysis by Sahu and Govindrajan (2005) has shown that the critical Reynolds number for onset of instability for a 3° diverging pipe is only 150, in contrast to infinity if the cross section is uniform. Varying cross-section microchannels are an integral part of microdevices such as valveless micropump and micromixer, and are likely to be employed in microchannels for reducing two-phase flow instability (Agrawal et al. 2012). It is therefore logical to investigate the flow properties in varying cross-section microchannel and to see if the flow behavior is size dependent; these issues provided the motivation for the present work.

Stemme and Stemme (1993) were the first to demonstrate a valveless micropump using a diffuser–nozzle arrangement, which are basically diverging/converging passages. This work led to several other designs utilizing the same principle as reviewed in Olsson et al. (1995) and Singhal et al. (2004), and renewed the interest involving flow in nonuniform passages. Recently, Wang et al. (2009, 2011) fabricated a valveless micropump for flow rectification driven by piston mechanism instead of actuated membrane. In most of these works, the performance of the pump has been studied in terms of the pumping efficiency and flow rectification efficiency. Verma et al. (2009b) integrated a modular valveless micropump with a printed circuit board for integrated electronic cooling. They achieved a maximum reduction of 57 % in the average surface temperature of the heat sink. However, very few researchers have studied the performance of the diffuser separately and the effect of diffuser geometry (like hydraulic diameter, divergence angle, length) on the performance of the device. Such a study is, however, important as it could lead to an improvement in the efficiency of the micropump; this lacunae is addressed in the present work.

Akbari et al. (2010a) performed numerical study on flow through series of converging–diverging microchannels and proposed an analytical model to calculate the flow resistance. In this study, the authors assumed a parabolic velocity profile in both the converging and diverging sections. Akbari et al. (2010b) carried out an experimental study on slowly varying cross-sectional tubes of arbitrary shape and proposed an analytical solution to determine the pressured drop of laminar flow in such a microchannel. Oliveira et al. (2007) studied experimentally and numerically the flow patterns in hyperbolic contraction microchannel for 1.28 < Re < 32.1 and found that the pressure drop was a linear function of Reynolds number. Lauga et al. (2004), based on analytical study, suggested that the flow is three dimensional in planar microchannel with varying cross-sectional area and curved side walls for Re < 100. Agrawal et al. (2005) and Tsai et al. (2007) performed numerical simulations to investigate the flow characteristics across a microchannel with a sudden expansion. Fu and Pan (2010) performed an experimental and theoretical investigation on the effect of microchannel axial cross section on mixing and chemical reaction of two fluids in microchannels. They reported that a diverging microchannel results in a better mixing efficiency. Lee and Pan (2008) employed a diverging microchannel to reduce flow instability during flow boiling in the microchannel. Runstadler et al. (1975) from the data of maximum diffuser performance for conventional scale suggest that the best conical diffuser is 10–80 % longer than the best flat-walled design.

As mentioned earlier, no clear understanding of the effect of various flow and geometric parameters on the flow in a diverging microchannel is available in the literature. Similarly, there appears to be uncertainty within the research community (see Stemme and Stemme 1993; Gerlach 1998; Lee and Pan 2008) about the characteristic scales to be employed for nondimensional purposes. The possible differences in flow characteristic at the macro- and microscales need to be documented. These issues provided the motivation for the present study. Here, a combined experimental and numerical study on liquid flow through diverging microchannel was carried out. The effects of hydraulic diameter, divergence angle, flow rate and microchannel length on flow have been studied in detail. The results are discussed with the help of the velocity profile, wall shear stress and forces acting on a fluid element. Flow reversal has been observed in microchannel with a diverging angle of 16°. A novel procedure is proposed to determine the characteristic length scale for the purpose of data reduction.

2 Experimental setup

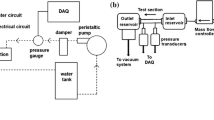
The schematic of the experimental setup used in the measurements is shown in Fig. 1, which is similar to that employed earlier by Singh et al. (2008). It consists of a deionized water reservoir, peristaltic pump, damper to reduce the pressure fluctuation from the pump, differential pressure gauge and a test section. All devices are connected in series using silicone tubing (from Master Flex). A pre-calibrated peristaltic pump (Master Flex) is used for metering and controlling the mass flow rate of water. A pre-calibrated digital pressure gauge (Keller) with a response time of 1 s and range of −1 to 3 bars is used to measure the pressure drop across the microchannel.

Fig. 1

a Schematic of experimental setup. b Microchannel geometry employed in the simulation

All the test sections are fabricated using in-house micro-fabrication facility. Single-sided polished, (100) p-type, 2′′ silicon wafers with resistivity 0.005–0.002 Ω are used for fabrication. The fabrication process [given in Singh et al. (2008)] can be divided mainly into RCA cleaning, wet oxidation, photolithography, and TMAH etching and bonding. Photolithography is used to transfer the pattern from hard to soft mask over the oxidized wafer. Silicone oxide then acts as the soft mask for TMAH etching where precise control of the process parameters decides the surface roughness. The characterization of the etched microchannel is done on a profilometer where the microchannel depth and surface roughness are determined. The surface roughness of all the microchannels is < 0.2 µm. Wafer bonding with quartz plate is an important step as it decides the maximum pressure at which the test section can work without leakage.

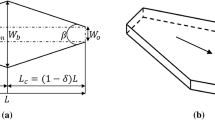
Detailed geometrical specifications are given in Tables 1, 2 and 3. The experimental work is categorized into three sets: study of the effect of diverging angle, hydraulic diameter and length of the microchannel. In the first set (Table 1), three test sections of different hydraulic diameters but same divergence angle and length are fabricated. In the second set (Table 2), four test sections of different divergence angle but same hydraulic diameter and length are fabricated. Finally, in the third set (Table 3), three microchannels of different length but same diverging angle and hydraulic diameter are fabricated. In the second set, the variation in hydraulic diameter owing to uncertainty in the wet etching process is ±3 %. The hydraulic diameters in Tables 1, 2 and 3 are calculated at the mean value of inlet and outlet widths, i.e., at the half-length of the microchannel; these values are only indicative. The length of all test sections in Tables 1 and 2 are maintained constant at 20 mm. The dimensions of the reservoirs at the two ends are 7 mm × 7 mm, with depth equal to the microchannel depth.

Table 1 Geometric specification of different hydraulic diameter with constant diverging angle and length of microchannel

Table 2 Geometrical specification of different divergence angles with constant hydraulic diameter and length of microchannel

Table 3 Geometrical specification of different length with constant hydraulic diameter and divergence angle of microchannel

The pressure gauge reading gives the pressure drop in test section including the losses inside the connecting tubes, fittings and entry/exit. The pressure drop across the tubing without the microchannel is also measured; this reading was validated against theory over the entire range of flow rate (0.5–5.0 ml/min). The net pressure drop across the test section was obtained by subtracting the pipe losses.

3 Experimental variation in pressure drop

For the test sections given in Tables 1, 2 and 3, the pressure drop was measured over the flow rate range of 0.5–5.0 ml/min (8.33 × 10⁻⁶ to 8.33 × 10⁻⁵ kg/s). The effect of hydraulic diameter, divergence angle and length on pressure drop has been studied and presented in this section.

3.1 Effect of mass flow rate and diverging angle

Figure 2 shows that the pressure drop varies linearly with mass flow rate, which is qualitatively similar to that for a uniform cross-sectional microchannel flow. In the latter case, under fully developed condition, the pressure force is exactly balanced by the viscous force, whereas in a diverging microchannel deceleration of the flow along with viscous and pressure forces are expected to be present. It is therefore somewhat unanticipated that for the flow range of 0.5–5.0 ml/min, these (and other) measurements in our study indicate that the pressure drop retains its linear variation with mass flow rate. The magnitude of the various forces involved is presented later in Sect. 4.2 in order to understand this linear variation better.

Fig. 2

Experimental pressure drop in different divergence angle microchannels with constant hydraulic diameter of 147 µm (±3 %) and length 20 mm

Figure 2 further shows that the overall pressure drop across the microchannel decreases with an increase in the divergence angle from 4° to 12°, whereas it increases beyond it (i.e., for divergence angle of 16°). Reversal of the flow at a higher degree of divergence is the reason for the larger pressure drop in the largest divergence angle microchannel. The appearance of a flow reversal region has been confirmed through numerical simulations (as shown later through Fig. 8). Therefore, 16° is the critical angle at which onset of flow reversal occurs; this value for a micro-diffuser is close to the angle of 15° mentioned in White (2008) for macro-conical diffuser. Knowledge of onset of flow reversal is of practical interest and should be taken into account while designing a micro-diffuser.

3.2 Effect of hydraulic diameter and length

Figure 3 shows the pressure drop variation for three different microchannels of hydraulic diameter 118, 147 and 177 µm over the flow rate range of 0.5–5.0 ml/min. The percentage difference in pressure drop is more between microchannels with hydraulic diameter of 118 and 147 µm than between 147 and 177 µm, although the difference in hydraulic diameter is constant at 30 µm. This is because the pressure drop is an inverse-function of the second power of the hydraulic diameter for trapezoidal/rectangular microchannels. This observation is qualitatively in line with that of uniform cross-section microchannels.

Fig. 3

Experimental pressure drop in different hydraulic diameter microchannels with constant angle of divergence 8° and length 20 mm

Along with the effect of hydraulic diameter and divergence angle, the effect of length of microchannel on pressure drop has also been experimentally studied. Three test sections of lengths 10, 20 and 30 mm with constant divergence angle 8° and hydraulic diameter 155 µm (±3 %) are fabricated. Figure 4 shows that the pressure drop increases with an increase in the length of the microchannel. The maximum percentage rise in pressure drop with increase in the length of microchannel is 25 % at high flow rate.

Fig. 4

Experimental pressure drop in different length microchannels with constant divergence angle 8  and mean hydraulic diameter 155 µm (±2.5 %)

The effect of divergence angle, hydraulic diameter and length on pressure drop is brought out by these measurements. The linear variation of pressure drop with flow rate and divergence angle noted in Sect. 3.1 is also confirmed for different values of hydraulic diameter and length of microchannel.

3.3 Variation in Poiseuille number

The mass flow rate and pressure drop are converted to nondimensional numbers (Reynolds number and Fanning friction factor, respectively) for the purpose of better comparison across various cases. The variation of Poiseuille number (f.Re) as a function of various governing parameters is plotted and discussed in this section.

The Fanning friction factor (f) is calculated as

$$ f = \frac{\Updelta P}{{2\rho \overline{U}^{2} \left( {\frac{L}{{D_{\text{h}} }}} \right)}} $$

(1)

The Reynolds Number (Re) is defined as

$$ Re = \frac{{\rho \overline{U} D_{\text{h}} }}{\mu } $$

(2)

Therefore,

$$ f.Re = \left( {\frac{\rho }{{2\mu {\text{L}}}}} \right)\left( {\frac{\Updelta P}{{\dot{m}}}} \right)(D_{\text{h}}^{2} A) $$

(3)

where D _h, A and $\overline{U}$ are, respectively, the hydraulic diameter, cross-sectional area and average velocity taken provisionally at the half-length of the microchannel, that is,

$$ D_{\text{h}} = \left. {D_{\text{h}} } \right|_{L/2}. $$

(4)

$\Updelta P$ and $\dot{m}$ are the experimental pressure drop and mass flow rate, respectively. The theoretical values were calculated using the correlation proposed by Morini (2004):

$$ f.Re = 24 - 42.267\gamma + 64.272\gamma^{2} - 118.42\gamma^{3} + 242.12\gamma^{4} - 178.79\gamma^{5} $$

(5)

where γ is the aspect ratio defined as the ratio of microchannel depth to width (average of top and bottom width) at the specified location. The above equation is applicable to 0 < γ < 0.707.

Figure 5 shows that the Poiseuille number is almost invariant with Reynolds number, but the value shows deviation from the corresponding value for uniform microchannels. Note that the f.Re values for uniform microchannels are calculated using aspect ratio at midpoint of the microchannel length in Eq. 5. The theoretical f.Re values for all the cases deviate by only 3 % from their average value owing to slight difference in the aspect ratio; therefore, the theoretical f.Re is represented by a single line in the figure. Figure 5a shows the comparison of the f.Re value for three different hydraulic diameters. The calculated f.Re (using Eq. 3) is higher for a smaller hydraulic diameter microchannel as compared to a larger hydraulic diameter. Also at lower Reynolds number, f.Re values deviate somewhat from their respective mean value.

Fig. 5

f.Re value in diverging microchannel for various cases studied: a different hydraulic diameter (Table 1); b different divergence angle (Table 2); c different length (Table 3)

Figure 5b shows that the f.Re value tends toward the value for uniform cross-section microchannel with decreasing divergence angle as expected. Note that the f.Re value remains constant with Reynolds number for lower divergence angle, whereas it varies substantially for higher divergence angle. Figure 5c shows that f.Re for 30-mm length microchannel is up to 25 % more as compared to 10-mm microchannel.

4 Results from numerical simulation

Three-dimensional numerical simulations were carried out on the test section presented in Table 2 using commercially available software (Fluent) with the aim of understanding the experimental results. Model geometry employed in the simulations is shown in Fig. 1b. All faces of the microchannel were divided into quadrilateral elements. The microchannel volume was discretised into 400,000 hexahedral elements. A grid independence study was carried out as shown in Table 4, which showed that this grid size was adequate for the calculations. Figure 1b shows the boundary conditions used for the present study (mass flow inlet, pressure outlet and wall with no-slip conditions). A pressure-based solver with SIMPLE algorithm for pressure–velocity coupling was employed. A direct comparison of numerical and experimental data at various flow rates suggests that the overall pressure drop compares within 5–12 %. The slight difference is attributed to experimental uncertainty (uncertainty about microchannel dimension and measurement of pressure drop) along with possible differences in the inlet condition. The variations in local velocity, pressure, wall shear stress and forces acting on a control volume were analyzed from the numerical data.

Table 4 Grid independent study for numerical simulations

4.1 Pressure and velocity distribution

Figure 6 shows the nondimensional streamwise velocity distribution along the flow direction, with 5 ml/min flow rate in 4°, 8°, 12° and 16° divergence angle microchannels. A nonlinear velocity distribution is observed; the entire microchannel can be divided into two regions depending upon the slope, as suggested by the figure. The flow decelerates rapidly between 0 < x/L < 0.4 and becomes approximately constant for the range 0.4 < x/L < 1. The centerline velocity is less for a larger divergence angle microchannel, as expected (Fig. 6). The rate of deceleration increases with the divergence angle, indicating that pressure recovery is more for the larger divergence angle than the smaller one. Therefore, the pressure drop decreases with an increase in the divergence angle as pointed out earlier in Sect. 3.1.

Fig. 6

Nondimensional streamwise velocity distribution along the flow direction in diverging microchannels of different divergence angles at a flow rate of 5 ml/min (U _c and U _in are centerline velocity and inlet velocity, respectively. L is the length of the microchannel)

The pressure and velocity contour for one case (12° microchannel) are presented in Fig. 7. Both pressure and velocity decrease nonlinearly from the inlet to the outlet. Deviation from linearity decreases with a decrease in the divergence angle (not shown). On increasing the divergence angle to 16°, a region of flow reversal near the wall is evident from Fig. 8; the size of the flow reversal region increases with the downstream distance.

Fig. 7

Pressure and velocity contours for 12° microchannel

Fig. 8

(a) Velocity vector along the flow direction, (b) zoomed view exhibiting flow reversal near the wall, for 16° microchannel

Figure 9a, b shows the wall shear stress distribution along the centerline of the top and side walls for the smallest (4°) and largest (16°) divergence angle microchannels, respectively. For the smaller divergence angle of 4°, the wall shear stress at the top and side wall drops from the inlet to outlet, as shown in Fig. 9a. This graph indicates a continuous variation in the lateral gradient of streamwise velocity at the wall. For the other case of 16°, the absolute wall shear stress drops along the top wall until half of the microchannel length and becomes almost constant further downstream (Fig. 9b). The shear stress remains constant with a small value throughout the microchannel length along the side wall. The larger shear stress for the 4° microchannel is evidently due to larger velocity for this case as compared to 16° microchannel.

Fig. 9

Side wall and top wall shear stress in diverging microchannels of divergence angle a 4° and b 16°

4.2 Force balance

The pressure, and viscous and inertial forces are expected to be important in this problem; however, their relative magnitudes vary with position in the microchannel. To understand the regions where each of these would dominate, a force balance as given through Eq. 6 has been undertaken from the numerical data. The forces over a small control volume (control volume extending over the entire cross section and unit increment along the streamwise direction) can be calculated as:

$$ \mathop {\rho u^{2} \text{d}A}\limits_{\begin{subarray}{l} {\text{inertial}} \\ {\text{force}} \end{subarray} } = \mathop {d(PA)}\limits_{\begin{subarray}{l} {\text{pressure}} \\ {\text{force}} \end{subarray} } + \mathop {\tau_{\text{w}} \text{d}A_{\text{s}} }\limits_{\begin{subarray}{l} {\text{shear}} \\ {\text{force}} \end{subarray} } $$

(6)

where ρ is the density of the fluid (kg/m³), u is the streamwise velocity (m/s), P is the pressure (N/m²), A is the cross-sectional area (m²), τ _w is the wall shear stress (N/m²), and A _s is the surface area (m²).

The magnitude of the three forces for a 12° diverging microchannel is shown in Fig. 10. It shows that at the inlet, the pressure force is positive (favorable) and of the same sign as the viscous force, resulting in a large positive inertial force (i.e., acceleration of the fluid). Fluid enters inside the microchannel from a virtually stagnant reservoir; therefore, positive inertia (i.e., acceleration of the fluid) is obtained near the entrance. Because of the maximum average velocity at entry, the streamwise velocity gradient in the lateral direction at the wall is also maximum; therefore, the fluid experiences the largest shear force at the microchannel entry.

Fig. 10

Streamwise variation of forces in a 12° diverging microchannel

After x/L = 0.03, the pressure force reduces at a large rate and becomes negative as expected. Along with a (negative) viscous force, a net negative force is obtained; the flow therefore starts decelerating from this point onward. The negative pressure force becomes positive after 8 % of the microchannel length (x/L = 0.08). The flow decelerates till 30 % of the microchannel length (x/L = 0.3) and becomes almost zero for the remaining part of the microchannel. Thereafter, the pressure and viscous forces balance each other while the inertial force is negligibly small. The reason for the inertial force (which can be estimated from u du/dx where u is the streamwise velocity) being small is that both u and du/dx terms are small in the later part of the microchannel as shown earlier in Fig 6. It can therefore be concluded that for 12° angle, for the present set of conditions, the diffuser effect is limited to the first 30 % of the microchannel length. Based on this, we would think that the inertial terms should be small in a large length diffuser; however, the position beyond which it occurs would be case specific. Because the viscous forces dominate over the inertial forces for a large part of the microchannel, the pressure drop versus mass flow rate curve exhibits a linear variation, as evident from Figs. 2, 3 and 4.

5 Characteristic length scale for diverging microchannel

Nondimensional Poiseuille number has been calculated for each test section for comparing the pressure drops of diverging and uniform cross-section microchannels. The value of hydraulic diameter (which is a measure of the characteristic length scale in the flow) is however needed for data reduction. In this section, different methods to define this length scale are explored. It is noted that ways employed in the literature for defining the characteristic length scale for this problem may not be adequate. A novel method for determining the characteristic hydraulic diameter is therefore proposed.

For noncircular cross-section microchannel, hydraulic diameter—the ratio of four times the cross-sectional area to the perimeter of the microchannel—is usually defined for the purpose of pressure drop calculations. The hydraulic diameter remains constant if the cross-sectional area is invariant. However for nonuniform cross-section (diverging) microchannel encountered here, the hydraulic diameter is a nonlinear function of position, as apparent from Fig. 11. Previously, Stemme and Stemme (1993) and Gerlach (1998) based the characteristic length scale (i.e., equivalent hydraulic diameter) of their nonuniform cross-section microchannel on the dimensions at the inlet:

Fig. 11

Hydraulic diameter variation along the flow direction. The calculations are for a divergence angle of 8° (refer test section IInd in Table 1)

$$ D_{\text{h}} = D_{\text{h(inlet)}} . $$

(7)

This parameter is however not satisfactory because it does not carry information of the divergence angle. Our calculations indicate that the uniform cross-section microchannel having hydraulic diameter calculated at the inlet of a diverging microchannel yields about 650 % higher pressure drop as compared to the pressure drop in corresponding diverging microchannels. In view of the fact that researchers have glossed over this important issue, sufficient emphasis has been given in this work for calculation of the characteristic length scale. The characteristic length scale is termed as equivalent hydraulic diameter because it establishes the equivalence of friction factor in diverging and corresponding uniform cross-section microchannels.

5.1 Theoretical calculation of hydraulic diameter

Besides Eqs. 4 and 7, the hydraulic diameter of a diverging microchannel can provisionally be defined as the average of the inlet ($D_{\text{h(inlet)}}$) and outlet ($D_{\text{h(outlet)}}$) hydraulic diameters. This is termed herein as “end point average hydraulic diameter”:

$$ D_{\text{h}} = \frac{{D_{\text{h(inlet)}} + D_{\text{h(outlet)}} }}{2}. $$

(8)

As per this definition, the hydraulic diameter is located at 1/13th part of the length (i.e., at about 7 % of the total microchannel length from the inlet), marked by a circle in Fig. 11. By comparing the pressure drop in uniform cross-section microchannel using hydraulic diameter given by Eq. 8 against the experimental data (in Fig. 2, curve for 8° microchannel), the theoretical pressure drop is found to be 193 % greater. This suggests that Eq. 8 is also not a representative length scale for this problem.

Alternatively, the equivalent hydraulic diameter can be defined as the average of the hydraulic diameters calculated along the profile. We term this as “mean integral value”:

$$ D_{\text{h}} = \frac{1}{L}\int\limits_{0}^{L} {D_{\text{h}} (x)\text{d}x} . $$

(9)

The location of this hydraulic diameter is at 1/3.3th part of the total microchannel length from the inlet (marked with square on curve in Fig. 11). The theoretical pressure drop in uniform cross-section microchannel with hydraulic diameter given by Eq. 9 is only 4 % greater than the experimental data (in Fig. 2, curve for 8° microchannel). This marks a substantial improvement as compared to the previous definitions (Eqs. 4, 7 and 8). An empirical procedure to arrive at an appropriate length scale is discussed next.

5.2 Empirical method

It is proposed that the f.Re value obtained from the experimental data should be compared with the f.Re value obtained from Morini’s correlation (Eq. 5). Accordingly, a procedure to calculate the equivalent hydraulic diameter has been suggested in this section.

An algorithm (illustrated in Fig. 12) is used to calculate the equivalent hydraulic diameter for all test sections using the experimental pressure drop values. The algorithm shows the comparison of experimental and theoretical f.Re values. Experimental f.Re value is obtained using experimental pressure drop and use of Eq. 10, whereas theoretical f.Re value is obtained from Morini’s correlation (Eq. 5). Eq. 3 can be rewritten as,

Fig. 12

Algorithm for calculating the location of equivalent hydraulic diameter (f.Re _P and f.Re _T are the experimental and theoretical Poiseuille numbers, respectively)

$$ fRe = c_{1} \left( {\frac{\Updelta P}{{\dot{m}}}} \right)c_{2} $$

(10)

where $c_{1} = \left( {\frac{\rho }{2\mu L}} \right)$,

$$ c_{2} = (D_{\text{h}}^{2} A) = \left( \frac{4A}{P} \right)^{2} A. $$

(11)

Note that c ₁ = constant for incompressible and isothermal flow. In the above equations, A and P are the cross-sectional area and perimeter of trapezoidal microchannels, respectively. These are calculated as

$$ A = \frac{1}{2}\left( {w_{\text{c}} + w_{\text{b}} } \right)H , $$

(12)

$$ P = (w_{\text{c}} + w_{\text{b}} + 2H_{\text{s}} ) , $$

(13)

where w _c is the top characteristic width of the microchannel, H is the height of the microchannel, and H _s is the slant height: $H_{\text{s}} = H/\sin (\alpha )$, and $\alpha$ is the angle between slant height and top width of trapezoidal cross section, which is equals to 54.5°. Substituting the above equations in Eq. 11 yields,

$$ c_{2} = \frac{{2[(2w_{\text{c}} - 1.414H)H]^{3} }}{{(2w_{\text{c}} + 1.042H)^{2} }}. $$

(14)

The algorithm provides the location, as a fraction of the microchannel length, from the microchannel inlet where the equivalent hydraulic diameter can be calculated.

The above procedure was applied to the entire experimental data except for 16° divergence angle (80 data points in total). The reason for excluding the data for 16° is that flow reversal is encountered for higher angle as already discussed. The results are compiled in Fig. 13. The figure shows that the location of equivalent hydraulic diameter lies within 2/5th to 1/4th part of the total length for all the cases under study, with a mean value of 1/3. It is noted that the locations are independent of Reynolds number.

Fig. 13

Location of equivalent hydraulic diameter as a function of Reynolds number. (nth part refers to the divisor of total length, i.e., L/n)

The suggested value of 1/3rd from the above analysis was chosen for further test. Upon shifting the location for calculation of the equivalent hydraulic diameter to the above-mentioned point, f.Re values lies within an absolute average error of 13.7 % compared to the value suggested by Morini’s correlation, as evident from Fig. 14a–c. Notice from Fig. 6 that the velocity calculated at this new location (termed as the characteristic velocity) is dependent on the divergence angle.

Fig. 14

a f.Re value in diverging microchannel with different hydraulic diameters; b f.Re value in diverging microchannel with different divergence angles; c f.Re value in diverging microchannel with different lengths [Symbols experimental value, solid lines theoretical value (Morini)]

5.3 Confirmation through numerical data

The proposition of employing equivalent hydraulic diameter calculated at 1/3rd location from microchannel inlet has been further verified through numerical simulations. Three cases containing five microchannels (0°, 4°, 8°, 12° and 16°) each are simulated at a constant flow rate (8.33 × 10⁻⁵ kg/s). For case I, the hydraulic diameter is calculated at the midpoint of the microchannel length and kept constant for all the microchannels. In case II, the hydraulic diameter calculated at the inlet of the microchannel is kept constant across all the microchannels. Finally, in case III, the hydraulic diameter calculated at 1/3rd location from the microchannel inlet is kept constant. Figure 15 shows that for cases I and II, the pressure drop increases upon increasing the divergence angle from 0° to 4°, and decreases beyond it. However, after employing the hydraulic diameter at the proposed location, it is observed that the pressure drop remains almost constant for all microchannels from 0º to 16º, as evident for case III from Fig. 15.

Fig. 15

Numerical pressure drop variation with divergence angle for three cases. (Case I: D _h at midpoint of the microchannel length with changing depth; Case II: D _h at the inlet of the microchannel, keeping inlet width and depth constant; Case III: D _h at 1/3rd location from the inlet of the microchannel, keeping width at 1/3rd location and depth constant)

Upon repeating the simulations for case III with a higher flow rate (of 2 × 10⁻⁴ kg/s), the drop in pressure from 0° to 4° becomes 8 % (not shown). Similarly, the increase in pressure drop from 12° to 16° (due to flow reversal) gets exaggerated to 21 %. These results further preclude the existence of a critical divergence angle exhibiting minima in pressure drop. The results in this section clearly bring out the difference in the trends that can be obtained by employing different length scales in the problem.

6 Discussion on the proposed approach

The equivalent hydraulic diameter should be such that the pressure drop in the diverging microchannel is the same as in a uniform cross-section microchannel of this hydraulic diameter. It then becomes possible to use the Hagen–Poiseuille formula (and its equivalent) to calculate the f.Re value for diverging microchannel, even though this formula is strictly used for fully developed flow through uniform cross-section microchannel. It would be ideal if the location as a percentage of the total length at which the equivalent hydraulic diameter is calculated is unique, i.e., independent of all the governing parameters—divergence angle, dimensions of the microchannel and flow rate. The quest to arrive at such a parameter was the primary motivation for this work.

To achieve this objective, we considered several methods: midpoint/half-length average (Eq. 4), inlet of diverging microchannel (Eq. 7), end point average (Eq. 8), mean integral value (Eq. 9) and empirically determined value. Most of these methods are being rigorously tested for the first time in this paper. As discussed in Sect. 5.1, the end point average method does not yield the representative location as it leads to 193 % (or almost three times) more theoretical pressure drop as compared to its experimental value. Alternatively, we have proposed the mean integral method to get the equivalent diameter which leads to 1/3rd position along the microchannel. However, there is no prior experimental validation available for this concept. We therefore validate this method and also develop a novel empirical method as discussed in Sects. 5.2 and 5.3.

The empirically obtained location of the equivalent hydraulic diameter lies within 2/5th to 1/4th part of the total length for all the cases (other than the diverging angle for which the flow gets reversed) with an average of 1/3. The f.Re values obtained with this equivalent hydraulic diameter and Morini’s correlation lie within an absolute average error of 13.7 % (Fig. 14), which indicates substantial improvement (the absolute average error for f.Re distribution presented in Fig. 5 is 37.5 %). The error is evidently owing to uncertainty in the experimental data; as the numerical data show that the pressure drop indeed becomes independent of the divergence angle (Fig. 15). Therefore, the location of equivalent hydraulic diameter for diverging microchannel can be taken at 1/3rd of the microchannel length, irrespective of the diverging angle, hydraulic diameter and length of the microchannel for the range of flow rate for which flow does not reverse its direction. This experimental finding can also be considered as a proof for the theoretical way of calculating the equivalent hydraulic diameter (via Eq. 9).

In summary, we propose the following correlation for calculation of the Poiseuille number for diverging microchannel of trapezoidal cross-sectional area:

$$ f.Re = \left( {\frac{\rho }{2\mu L}} \right)\left( {\frac{\Updelta P}{{\dot{m}}}} \right)\left( {\frac{{2[(2w_{\text{c}} - 1.414H)H]^{3} }}{{(2w_{\text{c}} + 1.042H)^{2} }}} \right). $$

(15)

The characteristic top width (w _c) of diverging microchannel in Eq. 15 at the new location can be expressed directly in terms of known geometrical parameters (refer Fig. 1b)—inlet top width (W _t(inlet)), length (L) and divergence angle (θ) of microchannel as

$$ w_{\text{c}} = W_{\text{t(inlet)}} + \frac{2}{3}L\tan \left( {\frac{\theta }{2}} \right). $$

(16)

The equivalent hydraulic diameter can finally be calculated in terms of known parameters as:

$$ D_{\text{h}} = \frac{{2(w_{\text{c}} - 0.707H)H}}{{(w_{\text{c}} + 0.524H)}} $$

(17)

Finally, we would like to remark that although Eq. 9 has been explicitly tested for a single case in this study, it is likely to be applicable to other geometries where the cross-sectional area is a function of the streamwise coordinate. This proposition, however, needs to be rigorously tested through future studies; nonetheless, the approach presented here would be a good starting point for such studies.

7 Conclusions

The study was conducted to bring out differences in flow characteristics in diverging microchannels with respect to uniform microchannels. There are a very large number of studies available for the latter geometry, but not for the former case. We also wanted to study the possible effects of scale on the flow—such as critical angle for appearance of secondary flow in a diverging microchannel. Both experimental and three-dimensional simulations have been employed in this work. Whereas pressure drop for various cases was experimentally determined, variation in velocity, shear stress and forces were obtained from three-dimensional computations. The experimental and numerical data for pressure drop compares within 5–12 %. Our results show that 16° divergence angle is the critical angle beyond which flow reversal occurs.

The equivalent hydraulic diameter calculated at 1/3th of the total length from the inlet is proposed as the characteristic length scale for this problem. This location is empirically obtained and also supported by theoretical considerations. The hydraulic diameter calculated at this location can be used to fabricate an equivalent uniform cross-section microchannel, such that the pressure drops in both diverging as well as uniform cross-section microchannel are same. The application of Hagen–Poiseuille formula to calculate f.Re value can thereby be extended to diverging microchannels using this concept of equivalent hydraulic diameter. It is further proposed that hydraulic diameter obtained by the mean integral method (Eq. 9) can be applied to other geometries with arbitrary variation in cross section. Our detailed results bring out the effect of flow rate, hydraulic diameter, length and divergence angle on flow in diverging microchannel, which have implications in the design of micro-diffusers and micropumps.