Electroosmotic flow in a nanofluidic channel coated with neutral polymers

Abstract

We use molecular dynamics simulations to investigate the control of electroosmotic flow by grafting polymers onto two parallel channel walls. The effects of the grafting density and the electric field strength on electroosmotic flow velocity, counterion distribution and conformational characteristics of grafted chains have been studied in detail for athermal, good, and poor solvent cases. The simulation results indicate that in the range of grafting densities investigated, increasing the grafting density induces a different change tendency of electroosmotic flow velocity for three different solvent qualities. These tendencies are demonstrated to be related to counterion distribution, polymer coverage, and interactions between monomers and solvent particles. It is found that counterions tend to move toward the interface between polymer layer and solvent as the grafting density increases. Especially in the poor solvent case, most of the counterions gather near the interface at high grafting densities. A similar behavior is also observed when enhancing the electric field strength at a fixed grafting density.

1 Introduction

The study of microfluidics has attracted considerable attention from many research communities because of its numerous applications in the fields of heat transfer, energy generation, biological analysis, and chemical process. It offers the possibility of solving outstanding system integration issues for biology and chemistry in miniaturizing plumbing and fluidic manipulation (Squires and Quake 2005). In general, microfluidic flow can be driven by an external electric field or a pressure gradient leading, respectively, to electroosmotic flow and pressure-driven flow. The bulk liquid in electroosmotic flow can be dragged by the mobile ions in the diffuse part of an electrical double layer (EDL) when an electric field is applied parallel to the channel walls. The thickness of EDL (Debye length) depends on the bulk ionic concentration and is commonly much smaller than the dimensions of the channel in most of the microfluidic applications. Thus, electroosmotic flow generally has a plug-like velocity profile leading to reduced dispersion of sample species, and scales more favorably compared to pressure-driven mode as the channel size decreases, especially down to microscale and nanoscale ranges. With the development of the lab-on-a-chip (LOC) technology, electroosmotic flow has been widely used as a pumping method in microfluidic and nanofluidic devices (Stone et al. 2004). Though the physics of electroosmosis is well understood, still many new challenges are presented to researchers, such as two-liquid electroosmotic flow (Gao et al. 2005; Lee and Li 2006), convective and absolute instability in electroosmotic convection (Chen et al. 2005), and effects of roughness on channel wall (Hu et al. 2003; Qiao 2007; Yang and Liu 2008).

Extensive attention has been paid to the modulation of electroosmotic flow by modifying the electrokinetic properties of surfaces (Krishnamoorthy et al. 2006; Wu et al. 2007; Paumier et al. 2008; Hickey et al. 2009; Wong and Ho 2009). In many ways of modulating electroosmosis, polymer coatings are often employed to control effectively the electroosmotic flow or minimize wall–analyte interactions (Paumier et al. 2008; Hickey et al. 2009), which is important for bio-molecule separations using electrophoresis technology. Experimentally, grafting polymer chains to a solid surface can be irreversible or reversible. For example, the polymer chains can be chemically bonded to the substrate or physically adsorbed onto the surface. Theoretical analysis of end-grafted polymers defines two regimes: the mushroom regime when grafted chains do not contact each other, and the brush regime where polymer chains are crowded and forced to stretch away from the surface to avoid overlapping. Obviously, the properties of the grafted polymer layer, such as the grafting density, the grafting method, the solvent quality, and the layer thickness, can influence critically the ion distribution in the EDL. Thus, compared to traditional electroosmosis, predicting quantitatively the behavior of electroosmotic flow controlled by polymer coatings is more difficult due to the coupling between polymer conformational dynamics and electrohydrodynamics. As a rule, polymer coatings tend to reduce the volume flux through the channel as a result of the viscous drag between the moving fluid particles and end-grafted polymer chains.

The structure of polymer layer has been investigated intensively under static (Alexander 1977; de Gennes 1980; Murat and Grest 1989; Grest 1994) and shear conditions (Lai and Binder 1993; Peters and Tildesley 1995; Kreer et al. 2001; Irfachsyad et al. 2002; Goujon et al. 2009). However, up to now, only a few relevant theoretical and numerical studies on electroosmotic flow in a channel coated with polymer layers (Harden et al. 2001; Qiao 2006; Tessier and Slater 2006; Qiao and He 2007; Hickey et al. 2009) are found in the literature. Theoretically, Harden et al. have obtained several important features of electroosmotic flow with end-grafted polymer chains using a scaling approach (Harden et al. 2001). Their theory, although was derived on basis of a scaling law (leading to that all prefactors are unknown) and at strong screening limit, can serve as a useful starting point to study further systems including the coupling of electrokinetic effects and polymer dynamics. Recently, Slater and co-workers have reported the results on electroosmotic flow in a nanoscopic pore modulated by neutral polymer coatings, using coarse-gained molecular dynamics simulations (Tessier and Slater 2006; Hickey et al. 2009). Their study further confirms some of scaling predictions of Harden et al. Moreover, their results were found to be in accordance with experimental observations (Doherty et al. 2002). Qiao and co-workers have studied electroosmotic flow confined between two apposing walls with grafted polymer layers using full scale molecular dynamics (Qiao 2006) and dissipative particle dynamics simulations (Qiao and He 2007). Their investigations give a good understanding of the mechanisms of electroosmotic transport modulated by neutral polymers. Although these studies provide insights into the role of polymer coatings in controlling electroosmotic flow, many open problems still remain to be addressed, such as effects of the solvent quality on electroosmotic transport and optimum design of polymer coating for improving bio-molecule separations.

In this study, through the employment of a coarse-gained molecular dynamics approach, we simulate the electroosmotic flow modulated by polymer coatings. The flow rate of electroosmosis is expected to be relevant to the strength of interactions between solvent particles and polymer monomers, which has not been considered in previous molecular simulations. Related numerical studies mainly focus on the athermal solvent case (Tessier and Slater 2006; Hickey et al. 2009), in which there is a purely repulsive pair interaction between moving particles and monomers. In most of the coarse-grained molecular simulation studies, solvent particles are not explicitly included. Moreover, most of the simulation studies are focused on the athermal solvent case. Recently, several simulation models explicitly including solvent molecules (or explicit solvent models) have been used to mimic polymer brushes in solvents of varying quality grafted onto cylindrical tubes (Adiga and Brenner 2005) and planar surfaces (Dimitrov et al. 2007). Compared to explicit solvent models, implicit solvent models, where the solvent is replaced by an effective interaction between the polymer monomers, have been extensively employed in different polymer systems to investigate the effect of solvent quality on the polymer conformation, such as polyelectrolyte solutions (Jeon and Dobrynin 2007), polymer brushes (Kreer et al. 2001), and self-assembly of polymers on surfaces (Chremos et al. 2009). Especially in dilute polymer solutions, the solvent molecules occupy most of the space, and generally one does not take into account their properties; thus, implicit solvent models can be used to improve the computational efficiency. Nevertheless, in some cases, the solvent properties are of interest, such as the solvent velocity profile and the influence of interplay between solvent and wall on boundary slippage in shear flow (Thompson and Robbins 1990). In this article, we use an explicit solvent model to simulate electroosmotic flow and perform a comparison of three cases with different solvent qualities at various grafting densities and electric field strengths. The remainder of this article is organized as follows. In the next section, we describe the model system and the simulation method. Following that, the results are presented and discussed. Finally, conclusions are given in Sect. 4.

2 Methodology

2.1 Molecular model

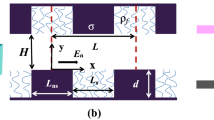
We used a coarse-grained model for the system consisting of two solid walls coated with polymer chains and a slab of ionic solution. Fluid particles are confined between two walls, each of which contains two layers of solid atoms arranged to form a (1 1 1) plane of an fcc crystal. One end of polymer chains with N monomers is fixed and arranged in a square lattice with the spacing $d = \rho_{\text{g}}^{ - 1/2}$, where ρ _g denotes the number of end-grafted chains per unit area. Surface charged particles are chosen from the wall atoms in the first layer. Grafted monomers of polymer chains lie initially on the same plane as the wall atoms in the first layer. They can be viewed as ghost particles that are fixed and do not interact with other particles. All wall particles are tethered to their initial positions by ideal harmonic springs with spring constant $400{{\varepsilon_{\text{LJ}} } \mathord{\left/ {\vphantom {{\varepsilon_{\text{LJ}} } {\sigma^{2} }}} \right. \kern-\nulldelimiterspace} {\sigma^{2} }}$. A snapshot of wall atoms and grafted beads at a certain simulation step is shown in Fig. 1d.

Fig. 1

Visual snapshots from molecular dynamics simulations of electroosmotic flow confined between two parallel planar surfaces at E/E* = 0.25 and $\rho_{\text{g}} \sigma^{2} = 0.2$. a–c Correspond to athermal, good and poor solvent cases, respectively. All the mobile particles including solvent particles, added salt ions and counterions are not shown for clarity. Color code in a–c: monomer beads, white; wall particles, dark grey. d Shows the arrangement of the wall particles and grafted monomer beads. The grafted monomer beads do not interact with other beads. Color code in d: grafted monomer beads, black; charged wall particles, grey; neutral wall particles, white

The short-range interaction between any two particles separated by a distance r is modeled by the truncated-shifted Lennard-Jones (LJ) potential.

$$ U_{\text{LJ}} (r) = 4\varepsilon_{\text{LJ}} \left[ {({\sigma \mathord{\left/ {\vphantom {\sigma r}} \right. \kern-\nulldelimiterspace} r})^{12} - ({\sigma \mathord{\left/ {\vphantom {\sigma r}} \right. \kern-\nulldelimiterspace} r})^{6} - ({\sigma \mathord{\left/ {\vphantom {\sigma {r_{\text{c}} }}} \right. \kern-\nulldelimiterspace} {r_{\text{c}} }})^{12} + ({\sigma \mathord{\left/ {\vphantom {\sigma {r_{\text{c}} }}} \right. \kern-\nulldelimiterspace} {r_{\text{c}} }})^{6} } \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r < r_{\text{c}} $$

(1)

where σ and ε _LJ are the Lennard-Jones parameters. Note that the choice of cut-off radius $r_{\text{c}} = 2^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-\nulldelimiterspace} 6}}} \sigma$ is corresponding to a purely repulsive interaction between the particles. In this article, σ, ε _LJ, and m are taken as the length, energy, and mass units, respectively. All the other units are derived from these basic units, such as time unit $({{m\sigma^{2} } \mathord{\left/ {\vphantom {{m\sigma^{2} } {\varepsilon_{\text{LJ}} }}} \right. \kern-\nulldelimiterspace} {\varepsilon_{\text{LJ}} }})^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$ and temperature unit ${{\varepsilon_{\text{LJ}} } \mathord{\left/ {\vphantom {{\varepsilon_{\text{LJ}} } {k_{\text{B}} }}} \right. \kern-\nulldelimiterspace} {k_{\text{B}} }}$ (k _B is Boltzmann constant).

The polymer chains are modeled using a widely utilized, coarse-grained bead-spring model. The beads are coupled by a finitely extendable nonlinear elastic (FENE) potential (Kremer and Grest 1990)

$$ U_{\text{bond}} (r) = - ({{kR_{0}^{2} } \mathord{\left/ {\vphantom {{kR_{0}^{2} } 2}} \right. \kern-\nulldelimiterspace} 2})\ln (1 - {{r^{2} } \mathord{\left/ {\vphantom {{r^{2} } {R_{0}^{2} }}} \right. \kern-\nulldelimiterspace} {R_{0}^{2} }}) $$

(2)

where the maximum bond length is $R_{0} = 1.5\sigma$ and the spring constant is given by $k = {{30\varepsilon_{\text{LJ}} } \mathord{\left/ {\vphantom {{30\varepsilon_{\text{LJ}} } {\sigma^{2} }}} \right. \kern-\nulldelimiterspace} {\sigma^{2} }}$. The choice of parameters gives an average bond length a = 0.98σ. The combination of LJ and FENE potentials ensures that the constituent chains cannot cross through one another.

The interaction between any two charged particles with charge valences Z _i and Z _j , and separated by a distance r _ij is modeled by the Coulomb potential

$$ U_{\text{Coul}} (r_{ij} ) = k_{\text{B}} TZ_{i} Z_{j} {\frac{{\lambda_{\text{B}} }}{{r_{ij} }}} $$

(3)

The Bjerrum length $\lambda_{\text{B}} = {{e^{2} } \mathord{\left/ {\vphantom {{e^{2} } {(4\pi \varepsilon_{0} \varepsilon_{\text{r}} k_{\text{B}} T)}}} \right. \kern-\nulldelimiterspace} {(4\pi \varepsilon_{0} \varepsilon_{\text{r}} k_{\text{B}} T)}}$ is defined as the distance, at which the electrostatic energy between two elementary charges is comparable in magnitude to the thermal energy $k_{\text{B}} T$. $\lambda_{\text{B}}$, is 0.71 nm for water at room temperature. ε₀ and ε_r are the vacuum permittivity and the dielectric constant of the solvent, respectively. The sum of all the long-ranged Coulomb interactions is calculated using the particle–particle/particle-mesh (PPPM) algorithm, which maps the charge to a 3D mesh and uses fast Fourier transforms (FFTs) to solve Poisson’s equation on the mesh (Hockney and Eastwood 1988). However, the original PPPM algorithm is used in periodic systems. In order to calculate the Coulomb interaction of the systems with a slab geometry which are periodic in the x- and y-directions and have a finite length in the z-direction, an empty volume with the height of nL _z is inserted along the z-direction. For all runs, n = 3 is taken. In addition, a correction term is also added to the modified PPPM method (Yeh and Berkowitz 1999).

2.2 Simulation details

All simulations are performed with the same mean fluid density $\rho_{\text{f}} = 0.81\sigma^{ - 3}$, the salt concentration $n_{0} = 0.025\sigma^{ - 3}$, the wall density $\rho_{\text{w}} = 1.0\sigma^{ - 3}$ and the surface charge density $\rho_{\text{c}} = - 0.1\sigma^{ - 2}$ (the surface charges are negative). The surface charges are negative, and thus the counterions are positive. The positive ions in the bulk fluid include the counterions and the positive added salt ions. The number of the counterions is equal to that of the surface charges to maintain overall electroneutrality. The length of each grafted chain is N = 10. In implicit solvent model, Kreer et al. have studied the features of friction between two polymer brushes under good and poor solvent conditions by varying the cutoff radius of monomer–monomer interactions (Kreer et al. 2001). We also use a similar approach to simulate three different solvent cases. In the poor solvent case, the cutoff radius for monomer–monomer pairs is set to $r_{\text{c}} = 2.5\sigma$, which introduces an attractive interaction between particle pairs, while other pair interactions are purely repulsive. In the good solvent case, the cutoff radius of $r_{\text{c}} = 2.5\sigma$ is assigned to solvent–monomer pairs, while a purely repulsive interaction potential is used with respect to other pair interactions. In the athermal solvent case, all pair interactions are purely repulsive. A detailed description as to how the solvent quality affects the chain conformation is given in their book by Rubinstein and Colby (2003). The dimensions of our simulation box are $L_{x} \times L_{y} \times h$, where $L_{x} = L_{y} = 22.2\sigma$, and $h = 24.3\sigma$. Periodic boundary conditions are applied in the x- and y-directions. A snapshot of the simulation system is present in Fig. 1 as an aid for describing our model in athermal, good, and poor solvent cases.

The system temperature is controlled by a dissipative particle dynamics (DPD) thermostat (Hoogerbrugge and Koelman 1992; Español and Warren 1995) with a friction coefficient $\gamma = 1.5\tau^{ - 1}$. For all our simulations, the desired temperature is set to $T = {{1.2\varepsilon_{\text{LJ}} } \mathord{\left/ {\vphantom {{1.2\varepsilon_{\text{LJ}} } {k_{\text{B}} }}} \right. \kern-\nulldelimiterspace} {k_{\text{B}} }}$ and the Bjerrum length is fixed at $\lambda_{\text{B}} = 2\sigma$. In order to mimic electroosmotic flow, we apply an electric field E parallel to the channel walls to induce translational motion of charged particles (Fig. 1a). The unit of electric field strength is taken as $E^{*} = {{\varepsilon_{\text{LJ}} \sigma^{ - 1} } \mathord{\left/ {\vphantom {{\varepsilon_{\text{LJ}} \sigma^{ - 1} } {\left( {4\pi \varepsilon_{0} \sigma \varepsilon_{\text{LJ}} } \right)^{1/2} }}} \right. \kern-\nulldelimiterspace} {\left( {4\pi \varepsilon_{0} \sigma \varepsilon_{\text{LJ}} } \right)^{1/2} }}$. In this study, the dimensionless electric field E/E ^* ranges from 0.1 to 1.75. If the system temperature is T = 300 K and the distance unit is $\sigma = 0.3\;{\text{nm}}$ which is the same as that given in Ref. (Tessier and Slater 2006), then the electric field E will vary from ${{0.11\;{\text{V}}} \mathord{\left/ {\vphantom {{0.11\;{\text{V}}} {\text{nm}}}} \right. \kern-\nulldelimiterspace} {\text{nm}}}$ to ${{1.88\;{\text{V}}} \mathord{\left/ {\vphantom {{1.88\;{\text{V}}} {\text{nm}}}} \right. \kern-\nulldelimiterspace} {\text{nm}}}$, corresponding to strong external electric field. The positions and velocities of the particles are calculated using the velocity Verlet algorithm. All simulations are conducted with a time step $\Updelta t = 0.005\tau$. The initial system is equilibrated for 4 × 10⁵ time steps, and then the production runs are performed. Each production run is from 5 × 10⁵ to 1 × 10⁶ time steps, depending on the strength of external electric field. In order to obtain the flow velocity profiles and the particle density ones, we divide the entire region into bins with the thickness $L_{\text{b}} = 0.2\sigma$ along the z-direction, and then perform an average over the velocity (along the x-direction) and the number of particles in each bin. Note that with respect to the flow velocity, the particles in bins include solvent particles, added salt ions and counterions, namely all the mobile particles in the bulk fluid.

3 Results and discussion

3.1 Influence of the grafting density

We first present simulation results obtained at different grafting densities and fixed electric field strength ${E \mathord{\left/ {\vphantom {E {E^{*} }}} \right. \kern-\nulldelimiterspace} {E^{*} }} = 1.0$. Figure 2 gives the electroosmotic velocity profiles at three grafting densities ($\rho_{\text{g}} \sigma^{2} = 0.032$, 0.1 and 0.4). Only half of the channel is shown because of the symmetry. One notes that the flow velocity at the center of the channel or maximum flow velocity u _max not only depends on the grafting density but also on the solvent quality. At the lowest grafting density $\rho_{\text{g}} \sigma^{2} = 0.032$, the flow velocity in the good solvent case is smaller than that in poor and athermal solvent cases due to attractive interactions between solvent particles and monomers, which induces larger viscous friction damping. Moreover, for athermal and poor solvent cases, two velocity profiles almost coincide. This indicates that at low grafting densities the flow velocity is mainly affected by polymer–solvent interaction, independently of polymer–polymer interaction. At an intermediate grafting density, $\rho_{\text{g}} \sigma^{2} = 0.1$, u _max under a poor solvent condition becomes larger. At the highest grafting density $\rho_{\text{g}} \sigma^{2} = 0.4$, u _max in the poor solvent case is remarkably larger than that in the other two cases and even exceeds that in the case without a polymer coating. In addition, the smallest u _max does not correspond to the good solvent case but to the athermal solvent case.

Fig. 2

Velocity profiles at three different grafting densities: a $\rho_{\text{g}} \sigma^{2} = 0.032$, b 0.1, and c 0.4, respectively, for athermal (squares), good (circles), and poor (triangles) solvent cases at E/E* = 1.0. The dotted line represents the case in absence of polymer coating

In order to more clearly observe the change of u _max, Fig. 3 gives the profiles of the maximum velocity in the channel center region as a function of the grafting density. Obviously, u _max varies nonlinearly as the grafting density increases. In the range of the grafting density studied, a monotonic decrease of u _max is observed for the athermal solvent case; however, there exists a minimum value of u _max in the intermediate regime of the grafting density for good and poor solvent cases, and u _max exhibits an ascending tendency at high grafting densities. In addition, for the athermal solvent case, u _max decreases rapidly at small grafting densities and at $\rho_{\text{g}} \sigma^{2} > 0.2$ it has a weak dependence on the grafting density. In the case where an attractive interaction exists between monomers and wall particles, when increasing the attractive strength, an increased monomer density can be observed near the wall, which forces the counterions away from the wall, further leading to increased bulk electroosmotic flow when the attractive strength is sufficiently high (Hickey et al. 2009). Similarly, we believe that the above features of u _max also may be related to the counterion distribution, especially for the poor solvent case, and that increasing the grafting density may lead to a significant decrease of counterion fraction near the wall due to the attraction between monomers. A detailed discussion about the counterion distribution follows below.

Fig. 3

Flow velocity u _max in the channel center region as a function of the grafting density at ${E \mathord{\left/ {\vphantom {E {E*}}} \right. \kern-\nulldelimiterspace} {E^*}} = 1.0$. The dashed line represents the case in absence of polymer coating

As seen from Fig. 4, the number of counterions inside the brush reduces as the grafting density increases. At a relatively high grafting density, i.e., $\rho_{\text{g}} \sigma^{2} = 0.4$, polymer chains in a poor solvent case condense together and form a compact polymer layer, so that the mobile particles are squeezed out from the layer. Thus, most of the counterions gather near the free end of the polymer layer and move along the interface between the polymer layer and solvent. In addition, a small fraction of counterions are still trapped inside the brush and adsorbed onto the wall surface due to the electrostatic attractive interaction. In the good solvent case, the strong attraction between solvent particles and monomers induce swelling of the brush. As a result, at high grafting densities, there are fewer counterions in the brush compared to the athermal solvent case because solvent molecules can more favorably enter into the brush region than counterions in a good solvent. Nevertheless, there is a higher density of counterions close to the wall compared to athermal and poor solvent cases. Clearly, these counterions adsorbed near the wall have little contribution to electroosmotic flow velocity. This is due to the fact that viscous drag exerted on the fluid via counterions near the wall is markedly screened by the polymer layer. As the grafting density decreases, more counterions can penetrate into the polymer layer. It is due to the fact that the increased distance between neighboring grafting points weakens the excluded-volume interaction between polymer chains or leads to more free volume in the polymer layer, which makes more counterions to be adsorbed on the wall surface. Thus, the screening of electroosmotic flow by polymer is enhanced with decreasing the grafting density. A similar feature is also observed under poor solvent conditions. As the grafting density decreases further, the effect of polymer layer on electroosmotic flow is weakened owing to a decreased drag force per unit area. One can note that under athermal solvent conditions, the screening of electroosmotic flow is enhanced monotonically with increasing the grafting density in the range of the grafting density investigated. The slow decrease of u _max at high grafting densities can be ascribed to an increased fraction of counterions outside the polymer layer.

Fig. 4

Density profiles of counterions for a athermal, b good, and c poor solvent cases at different grafting densities. Data are obtained at E/E* = 1.0. The arrows denote the average height of endpoints of the chains at $\rho_{\text{g}} \sigma^{2} = 0.4$

We also present the distribution of the negative ions for different solvent qualities (Fig. 5). At $\rho_{\text{g}} \sigma^{2} = 0.032$, and there are small density differences between different cases of solvent quality. Unlike the counterion distribution, the negative ion density becomes significantly low near the wall due to the repulsion between them and the surface charged particles. At the highest grafting density investigated, $\rho_{\text{g}} \sigma^{2} = 0.4$, the increased monomer density forces the negative ions toward the center of the channel. Especially in the good solvent case, almost all the negative ions distribute near the center of the channel and only occupy one-third of the channel volume.

Fig. 5

Density profiles of negative ions for athermal, good, and poor solvent cases at $\rho_{\text{g}} \sigma^{2} = 0.032$ and 0.4

Figure 6 gives the density profiles of monomers and solvent particles at $\rho_{\text{g}} \sigma^{2} = 0.4$. From the density profiles, it is clearly observed that a remarkable number of solvent particles are found in the polymer layer in a good solvent, whereas there are few solvent particles inside the polymer layer in a poor solvent except over a small region near the wall. It should be emphasized that the strong oscillation of the monomer density near the wall is mainly induced by the ordering layer structure of wall particles; nevertheless, the oscillation far away from wall ($z > 3.5\sigma$) is due to an effective increase in the rigidity of polymer chains in a good solvent. At a small grafting density $\rho_{\text{g}} \sigma^{2} = 0.1$, solvent particles have a larger density in the polymer layer for athermal and poor solvent cases due to the decreased polymer coverage (Fig. 7). In addition to the counterion distribution, the polymer coverage also plays an important role in controlling the electroosmotic flow, especially at low grafting densities or in the mushroom regime where increasing the grafting density can effectively enhance the local screening of flow. This is well supported by molecular dynamics simulations of electroosmotic flow in the nanopores coated with polymers in an athermal solvent (Tessier and Slater 2006).

Fig. 6

Density profiles of monomers (dashed line) and solvent particles (solid line) at $\rho_{\text{g}} \sigma^{2} = 0.4$ and E/E* = 1.0

Fig. 7

Density profiles of monomers (dashed line) and solvent particles (solid line) at $\rho_{\text{g}} \sigma^{2} = 0.1$ and E/E* = 1.0

In order to study quantitatively collapsed or swollen configuration of polymer layer, we calculate the average thickness h of polymer layer by taking the first moment of the monomer density profile

$$ h = {\frac{{\int_{0}^{{L_{\text{z}} }} {z\rho_{\text{m1}} \left( z \right)\;{\rm d}z} }}{{\int_{0}^{{L_{\text{z}} }} {\rho_{\text{m1}} \left( z \right)\;{\rm d}z} }}} $$

(4)

where ρ _ml is the monomer density of bottom polymer layer. h increases with increasing the grafting density (Fig. 8). A similar behavior is also observed for polymer brushes without charged particles (Binder 2002). It can be found that h for a good solvent system is evidently larger than that for the other two systems, revealing that polymer chains in a good solvent show a stretched conformation. A linear increase is found for the athermal solvent case in the entire range of the grafting density as well as for good and poor cases at small grafting densities. Under good solvent conditions, h increases slowly at high grafting densities due to the nonlinear elasticity of the chains. The increase of the layer thickness can diminish the size of channels and limit the volume flux. For the poor solvent case, the change of h at $\rho_{\text{g}} \sigma^{2} > 0.16$ may be related to the amount of fluid particles excluded from the polymer layer due to the inter-chain attraction. At $\rho_{\text{g}} \sigma^{2} > 0.16$, the number of interacting monomer pairs between the chains in a poor solvent increases more rapidly upon increasing the grafting density compared to cases of $\rho_{\text{g}} \sigma^{2} < 0.16$. Thus, increasing the grafting density leads to more fluid particles being squeezed out from the polymer layer at $\rho_{\text{g}} \sigma^{2} > 0.16$, which corresponds to a slower increase of the layer thickness; nevertheless, when $\rho_{\text{g}} \sigma^{2} > 0.3$, the layer thickness increases relatively rapidly due to a striking number decrease of the solvent particles which can be squeezed out from in the polymer layer. In the above discussion, we note that increasing the grafting density can change the counterion distribution along the direction normal to the channel wall and may result in an increase of electroosmotic velocity when varying the solvent quality. Thus, electroosmotic flow in channels coated with polymers is controlled by different mechanisms, making the fluid exhibit more complex flow characteristics. Moreover, in contrast to traditional electroosmotic flow, it is difficult to obtain several fundamental laws governing electroosmotic flow with polymer coating and the expression of counterion distribution.

Fig. 8

Thickness h of the polymer layer as a function of the grafting density at E/E* = 1.0

The effect of electroosmotic flow on the conformation of the chains can be well characterized by the inclination degree of polymer layer in the direction of the flow. Figure 9a gives the inclination angle θ at fixed electric field ${E \mathord{\left/ {\vphantom {E {E^{*} }}} \right. \kern-\nulldelimiterspace} {E^{*} }} = 1.0$ as a function of the grafting density, where θ is the angle between the unit vector X along the flow direction and the vector R _cm pointing to the mass center of a chain from its grafted end, namely, $\theta = \arccos \left( {{{{\mathbf R}_{\rm {cm}} \cdot {\mathbf x}} \mathord{\left/ {\vphantom {{R_{\rm {cm}} \cdot x} {R_{\rm {cm}} }}} \right. \kern-\nulldelimiterspace} {R_{\rm {cm}} }}} \right)$. The inclination angle is growing with the increase of the grafting density. We also compute the stretching length $L_{\text{s}} = \left\langle {\max \left( {x_{i} } \right) - \min \left( {x_{i} } \right)} \right\rangle$ as shown in Fig. 9b, where x _i is the position of polymer monomer i in the x-direction and $\left\langle \cdots \right\rangle$ denotes the ensemble average. At the smallest grafting density, the stretching length is approximately equal under different solvent quality conditions. Nevertheless, a large difference occurs with increase in the grafting density. For the good solvent case, polymer–solvent attraction can induce the stretching of polymer chains normal to the wall surface, and at the same time the extension in the flow direction will be restricted. Interestingly, when the grafting density is above a certain critical value, L _s for the poor solvent case exceeds that for the athermal solvent case, although there is a strong attractive interaction between the monomers of the chains in a poor solvent. We attribute this behavior to a relatively high shear rate at the interface between polymer layer and fluid for the poor solvent case. Note that at $0.2 < \rho_{\text{g}} \sigma^{2} < 0.3$ the inclination angle of the chains in a poor solvent almost holds constant, and L _s at $\rho_{\text{g}} \sigma^{2} = 0.3$ even becomes larger than that at $\rho_{\text{g}} \sigma^{2} = 0.2$. This peculiar feature is a consequence of the strongly enhanced electroosmotic flow as seen from Fig. 3.

Fig. 9

a Polymer inclination angle θ and b stretching length L_s along the flow direction as a function of the grafting density at E/E* = 1.0

3.2 Electroosmotic flow at different electric field strengths

In this section, we study the control of electroosmotic flow with grafted polymer chains by varying the electric field strength. An intermediate grafting density, $\rho_{g} \sigma^{2} = 0.2$, is taken in all the following simulations. Figure 10 shows the corresponding density profiles of counterions at four different electric fields (${E \mathord{\left/ {\vphantom {E {E^{*} }}} \right. \kern-\nulldelimiterspace} {E^{*} }} = 0.25$, 0.55, 1.0 and 1.75) for athermal, good and poor solvent cases. At weak electric field strengths, a significant amount of counterions are absorbed near the wall. As the applied electric field increases, the density profiles shift to larger distances along the direction normal to the wall. This may be caused by the fact that counterions avoid being confined within the polymer layer, and fluid transport is maximized. Such a phenomenon is also observed in the case of bare solid surface (Boroudjerdi et al. 2005). At high electric field strengths, most of the counterions are pulled out from the polymer layer, and the screening effect of polymer layer on flow is remarkably lowered.

Fig. 10

Density profiles of counterions for a athermal, b good, and c poor solvent cases at different electric field strengths. Data are obtained at $\rho_{\text{g}} \sigma^{2} = 0.2$. The arrows denote the average height of endpoints of the chains at ${E \mathord{\left/ {\vphantom {E {E*}}} \right. \kern-\nulldelimiterspace} {E^*}} = 1.75$

Figure 11 shows the maximum velocity u _max as a function of the electric field strength. As expected, the flow velocity increases with enhancement of the electric field. Moreover, u _max from large to small, in turn, corresponds to the poor, good, and athermal cases at each fixed electric field strength. Also, at low values of E, u _max increases slowly with the electric field strength; at high values of E, u _max exhibits a rapid increase as the electric field strength increases. This reveals that a considerable amount of counterions move away from the polymer layer at strong electric fields. Note that although at ${E \mathord{\left/ {\vphantom {E {E^{*} }}} \right. \kern-\nulldelimiterspace} {E^{*} }} = 1.75$ most of counterions are outside the polymer layer under a good solvent condition and there is a smaller effective channel height, the value of u _max is still lower than that under a poor solvent condition. This result confirms that viscous drag exerted on the fluid by the polymer chains has a noticeable contribution to electroosmotic flow velocity due to polymer–solvent attraction.

Fig. 11

Flow velocity u _max in the channel center region as a function of the electric field strength at $\rho_{\text{g}} \sigma^{2} = 0.2$. The inset zooms on the velocity profiles at low electric field strengths

In addition, we also present the velocity profiles of the fluid as a function of the z-coordinate for different values of E (Fig. 12). Clearly, the total flux is the highest in the flow direction for the poor solvent case as seen from the area under the velocity curves. The flow velocity of the fluid in the good solvent case is suppressed over a wide range ($z < 3.5\sigma$) of distances from the wall because of the swelling of the polymer layer. Under poor solvent conditions, the flow velocities near the wall ($z < 1.3\sigma$) at ${E \mathord{\left/ {\vphantom {E {E^{*} }}} \right. \kern-\nulldelimiterspace} {E^{*} }} = 0.75$ and 1.3 are larger than that at ${E \mathord{\left/ {\vphantom {E {E^{*} }}} \right. \kern-\nulldelimiterspace} {E^{*} }} = 1.75$. At ${E \mathord{\left/ {\vphantom {E {E^{*} }}} \right. \kern-\nulldelimiterspace} {E^{*} }} = 1.75$, the polymer layer becomes thinner and forms a more compact structure. Moreover, there is a smaller fraction of solvent particles in the layer (not shown here). Thus, in addition to the moving of counterions away from the layer, the mobility of fluid particles inside the layer is suppressed strongly, or mobile fluid particles shift away from the wall. The shape of velocity profiles in this study is different from that in theoretical studies (Harden et al. 2001) and dissipative particle dynamics simulations (Qiao and He 2007). In those studies, the maximum velocity occurs near the wall due to the assumption of the strong electrostatic screening limit, which leads to a much smaller thickness of double electric layer than the polymer layer.

Fig. 12

Velocity profiles for athermal (dashed lines), good (dotted lines), and poor (solid lines) solvent cases at $\rho_{\text{g}} \sigma^{2} = 0.2$. The clusters of data series are for electric field strengths of E/E* = 0.75, 1.3, and 1.75 from bottom to top

The dependence of the layer thickness on the electric field is shown in Fig. 13 for three different solvent qualities. It is found that increasing the electric field induces a thinning of the layer thickness. This result is clearly in line with previous simulations of shear flow carried out for neutral polymer chains grafted on cylindrical nanopores (Adiga and Brenner 2005) and planar surfaces (Irfachsyad et al. 2002; Pastorino et al. 2006). Irfachsyad et al. demonstrated that the shrinkage of two apposing polymer layers or polymer bilayer is caused by the shear and is independent of the separation between two layers in an athermal solvent (Irfachsyad et al. 2002). Furthermore, our results qualitatively agree with those obtained by Qiao and He (Qiao and He 2007). They also observed a decreased layer thickness. Note that polymer layer in a poor solvent has a small shrinkage with increase in the electric field. This is due to the fact that the layer has already collapsed to a compact state in the absence of flow. In addition, we find that the layer thickness exhibits a similar tendency for athermal and good solvent cases. That is, the layer thickness has a slow decrease when increasing the electric field, and a relatively rapid decrease is observed at high electric field.

Fig. 13

Thickness h of the polymer layer as a function of the electric field strength at $\rho_{\text{g}} \sigma^{2} = 0.2$

In Fig. 14a, the inclination angle θ is shown as a function of the electric field for athermal, good, and poor solvent cases. At the lowest electric field investigated, the configuration of polymer layer tends to be vertical to the channel wall, that is, the inclination angle approaches 90°. As we increase the electric field strength, the chains are forced to incline toward the flow direction. At low electric field strengths, the angle decreases approximately linearly with the electric field, and saturation effect becomes apparent with further enhancement of the electric field, especially for the athermal solvent case. The enhanced orientation ordering along the direction of the flow is also observed in molecular simulations for shear (Miao et al. 1996) and electroosmotic flows (Qiao and He 2007) with polymer coating. The inclination angle of grafted polymer layer in a good solvent decreases relatively slowly at low electric field strengths compared to that in an athermal and poor solvent. In addition, one can note that there is a small difference of the inclination angle between athermal and poor solvent cases.

Fig. 14

a Chain inclination angle θ, b stretching length L_s along the flow direction, and c transverse extension L_e normal to the flow direction as a function of the electric field strength at $\rho_{\text{g}} \sigma^{2} = 0.2$

Another important effect of the enhanced electroosmotic flow on polymer conformation is the stretching of polymer chains in the flow direction. As expected, polymer chains are elongated in the direction of the flow (Fig. 14b). We note that a faster stretching rate tends to appear in the intermediate regime of the electric field. At high electric field strengths, the chains are in a strongly stretched state, leading to the nonlinear elastic stretching of chains. At weak electric field strengths, a significant amount of counterions are condensed near the wall, and thus their mobility is reduced due to electrostatic attraction between the counterions and the charged wall particles. Just as discussed above, the polymer–solvent attraction reduces the angle of the vector R _cm of grafted chains in a good solvent with respect to the direction normal to the wall compared to other two cases. Thus, the chain extension along the flow direction is also suppressed. It is expected that the stretching of the chains can diminish the fluctuations perpendicular to the stretching direction. As seen in Fig. 14c, the transverse extension decreases upon increasing the electric field. The transverse extension is expressed as $L_{\text{e}} = \left\langle {\max \left( {y_{i} } \right) - \min \left( {y_{i} } \right)} \right\rangle$, where y _i is the position of polymer monomer i in the y-direction. In contrast to the stretching, there is a larger relative difference of L _e for good, athermal, and poor solvent cases at low electric field strengths, and this difference diminishes with increase in the electric field. Obviously, the stretching of the chains reduces their transverse fluctuations. Our simulation results indicate that the transverse extension is mainly related to the average end-to-end distance of the chains (not shown here), which exhibits an opposite tendency.

Finally, we present the shape factor $S = {{R_{\text{ee}}^{2} } \mathord{\left/ {\vphantom {{R_{\text{ee}}^{2} } {R_{\text{g}}^{2} }}} \right. \kern-\nulldelimiterspace} {R_{\text{g}}^{2} }}$ of grafted chains as a function of the electric field strength (Fig. 15), where $R_{\text{ee}}^{2}$ and $R_{\text{g}}^{2}$ are the average square end-to-end distance and the average radius of gyration squared, respectively. In a good solvent, polymer–solvent attraction induces a strong stretching of the chains. Thus, the enhanced electroosmotic flow has a small effect on the chain extension. It is concluded that the chain stretching along the flow direction is mainly affected by the inclination induced by the electroosmotic flow. A Gaussian chain and a rigid chain are corresponding to S = 6 and S = 12, respectively. Under athermal and poor solvent conditions, the shape factor shows an obvious increase, and S ≈ 9 is obtained at the highest electric field strength. This reveals that the chains undergo a conformational transition from coil state to stretched state.

Fig. 15

Shape factor S as a function of the electric field strength at $\rho_{\text{g}} \sigma^{2} = 0.2$

4 Conclusions

In summary, electroosmotic flow in a nanofluidic channel coated with polymers has been studied using molecular dynamics simulations. A comparison of polymer layer in athermal, poor, and good solvent was made at different grafting densities and electric field strengths. At a fixed electric field strength, our simulation results demonstrate that the maximum velocity u _max in the channel center region shows a significant dependence on the grafting density and the solvent quality. In the range of the grafting density investigated, u _max in the athermal solvent case decreases with increase in the grafting density; nevertheless, there is a minimum value of u _max at the intermediate grafting regime under poor and good solvent conditions. These features are mainly related to three different aspects: counterion distribution, polymer coverage, and viscous drag exerted on fluid by polymer. It should be emphasized that counterion distribution will play a significant role in determining the flow velocity with increase in the grafting density, especially for good and poor solvent cases. At low grafting densities, polymer–solvent attraction can induce a high viscous friction between fluid particles and polymer chains in a good solvent. We also find that in the poor solvent case, electroosmotic flow is enhanced prominently at high grafting densities and u _max even exceeds that in the case without polymer coating. With increasein in the electric field strength, counterions move toward the interface between polymer layer and fluid, and the screening of electroosmotic flow by polymer is weakened. At a chosen grafting density, u _max from high to low corresponds to the athermal, good, and poor solvent cases, respectively, which is independent of applied electric field strength. The investigations on the conformational characteristics of the chains show that in the good solvent case, the increase of the stretching length mainly depends on the increased inclination degree; however, it depends on the conformational transition of the chains in athermal and poor solvent cases from coil to stretch. In this study, the relation between the counterion distribution and the deformation of the chains has not been elucidated in detail, and it is not clear how u _max depends on the counterion distribution, which needs a precisely calculated fraction of counterions in the interface between polymer layer and solvent. These problems will be solved in a future study.