1 Introduction

The generation of monodisperse microdroplets is an important issue in many industrial domains and there are thus various techniques to produce such particles. They include for example, creating an emulsion by stirring the disperse phase into the continuous phase or pushing the disperse phase through a microporous membrane. However, these techniques all result in a fairly wide size distribution of the droplet population (Geerken et al. 2008). In some applications such as drug delivery or food engineering (Mc Clement et al. 2007), the formation of microdroplets is the first step for the preparation of microcapsules. The droplet size dispersion then leads to a dispersion in the capsule size and physical properties (e.g., membrane thickness) that can impair proper functioning of the capsules.

Recently, microfluidic devices have been investigated to prepare monodispersed microdroplets and microcapsules. The advantage of these devices lies in the possibility to produce micron size droplets in a confined geometry where the size of the microdroplets is controlled by the dimensions of the microchannels and by the flow rates of the dispersed and continuous phases. Some devices use a T junction geometry and different fluids phases such as oil/water (Thorsen et al. 2001; Anna et al. 2003), air–liquid (Stride et al. 2008) or liquid–liquid couples (Li et al. 2008). Models of the flow in a T junction have been proposed to predict the droplet formation (Stone et al. 2004; Garstecki et al. 2006; van der Graaf et al. 2006; Christopher and Anna 2007; Steegmans et al. 2009). In a second type of geometry, the droplets are created by injecting a central jet of liquid in another flowing liquid. In co-axial cylindrical jets, the mechanism of droplet formation is modeled by the Rayleigh Plateau theory (Guillot et al. 2007). However due to the microfabrication constraints, most of the flow focusing microfluidic devices consist of microchannels with square or rectangular sections rather than circular ones and the Rayleigh Plateau theory cannot be used to model microdroplet formation. The planar flow focusing microfluidic devices use either parallel or cross flows. Downstream of the junction, the inner fluid is submitted to the pressure and shear stress exerted by the outer fluid, and to interfacial tension. When those forces are balanced, the situation is unstable and a droplet breaks off. The droplet size is again controlled by the intersection geometry and by the flow rates of the inner and outer fluids (Christopher and Anna 2007; Lee et al. 2009).

The studies of droplet formation in microfluidic devices are mostly performed with model fluids such as oil (or air) and water with the objective of investigating the microscale physics of droplet generation. The model fluids have a large contrast in physicochemical properties such as viscosity or interfacial tension that facilitates droplet formation. However, in cosmetic or pharmaceutical applications the emulsions often consist of an aqueous protein solution dispersed in a fatty ester such as ethylhexyl 2-ethylhexanoate (Hurteaux et al. 2005), methyl laurate (Bouchemal et al. 2004), isopropyl myristate (Kogan and Garti 2006; Subramanian et al. 2005) or isopropyl palmitate (Kogan and Garti 2006). Such emulsions are then commonly used to produce microcapsules. The surface tension is small and the viscosity ratio between the two phases is of order unity. This makes microdroplet formation more difficult than for classical oil/water couples. To our knowledge, there has been no study of the formation of microdroplets in microfluidic devices for two immiscible liquid phases with low viscosity contrast and low surface tension as is the case in pharmaceutical formulations. It is thus the objective of this article to investigate the formation of albumin micro droplets in fatty esters by means of a microfluidic device. We have selected a Y junction flow focussing geometry, where the protein solution is injected in a central jet and the fatty esters are injected laterally through the two branches of the Y. This geometry has the advantage of keeping the protein solution centered in the channel downstream of the junction and of preventing protein adsorption on the channel wall (Boxshall et al. 2006), contrarily to T junctions geometries where the injected flow is squeezed near a wall before breaking. We investigate the conditions for droplet generation with this type of fluid couple in different channel geometries in order to clarify the governing parameters and scales controlling the process. We find that, depending on the central to lateral flow rate ratio, droplets are formed regularly (dripping regime) or a stratified flow situation prevails with a steady central albumin solution thread surrounded by the oil phase.

We first present the experimental set-up and procedures in Sect. 2. We discuss the different flow regimes and investigate the conditions for transition from stratified flow to dripping flow in Sect. 3.3. The drop size is then analysed as a function of geometry and flow conditions in Sect. 3.4. The results are discussed and compared to those obtained in a T junction in the last section.

2 Materials and methods

2.1 Fluid phases

The disperse phase consists of a 20% solution of Human serum albumin (HSA) in a pH 9.8 phosphate buffer, with dynamic viscosity μ = 3.3 mPa s at 25°C. The continuous phase is a biocompatible fatty ester. In most experiments, we used Dragoxat (2-ethylhexyl 2-ethylhexanoate, Symrise) with dynamic viscosity μ = 3.6 mPa s at 25°C (Viscometer,Thermo Haake) and surface tension with HSA γ = 0.006 N/m (tensiometer Kruss DSA10 Mk2). For comparison purposes, we have also run a few experiments using methyl laurate, with μ = 5.5 mPa s at 25°C and γ = 0.0093 N/m. It should be noted that albumin molecules tend to adsorb at the interface with the oil phase. A HSA-dodecane interface is saturated for a bulk HSA concentration of 10% (Chen et al. 1996). We can then expect the interface to be fully saturated (thus the low surface tension) so that Marangoni effects should not affect the drop formation process.

2.2 Micro-channels and experimental set-up

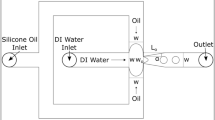
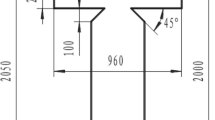
Polydimethylsiloxane (PDMS, Sylgard 184) microchannels are manufactured following a standard procedure (McDonald and Whitesides 2002). The mould master is made with a SU-8 photoresist material on a silicon wafer. The PDMS is poured, baked, peeled off the master and bound to a glass plate by air plasma. Four holes are drilled at the inlet and outlet of the microchannels for fluid perfusion or collection. As shown in Fig. 1, the microchip consists of a central channel (width W c) intersected at an angle α by two identical lateral channels (width W l). All channels of one system have a common depth h and a length of order 2 to 3 cm. The central channel ends in a reservoir with a gradual expansion, where the droplets are collected. The four parameters (W c, α, W l, h) determine the geometry of the Y junction microchip. The depth of the channel is equal to the master mould height which is measured by means of a surface profiler (Alpha Step IQ, TLA-Tencor). The width and depth of the microchannels are also checked by means of scanning electron microscope pictures.Three different geometries have been used where the ratios W c/W l and W c/h are varied. The geometrical properties of the microchannels are summarized in Table 1.

Fig. 1
figure 1

Schematics of the micro-channel

Full size image
Table 1 Geometrical parameters of the different systems, and corresponding symbol used in graphs
Full size table

2.3 Experimental procedure

The solutions are conserved at 4°C and heated to the room temperature of 25°C before use. The ester is introduced into the two lateral microchannels by means of a two-syringe pump (Bioblock, Illkirch, France) producing equal flow rates in each branch. The system is first flooded with Dragoxat. Then the HSA solution is introduced into the upper part of the central microchannel by means of another syringe pump. The flow rates in the central and in each lateral microchannel, respectively Q c and Q l, can thus be adjusted independently and can be varied between 2 and 120 μl/min, corresponding to velocities ranging between 3 and 180 mm/s in a 100 × 100 μm2 channel. The droplets, if any, are then formed at the junction and convected in the downstream part C down of the central channel. Flow visualisation at the junction is done by means of a high speed CDD camera (IF-865S) mounted on a conventional optical inverted microscope and connected to a computer (Matrox METEOR2-MC2 acquisition card). Data images are recorded with a resolution corresponding to 100 pixels per 250 μm. Image size was 350 × 344 pixels respectively in width × height. 750 images are recorded at a frequency of 150 images/s. The experiments are repeated at least three times (or more) using new micro-systems each time.

3 Results

All the experiments have been done with Dragoxat as the continuous phase, except in Sect. 3.5, where laurate is used in order to assess the effect of the ester physical properties. The experimental procedure consists in setting the value of Q l and then increasing Q c progressively.

3.1 Flow regimes

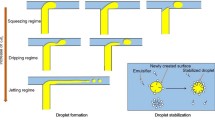
We observe three different flow regimes for increasing values of Q c, as reported repeatedly for different systems independent of the junction geometry (Anna et al. 2003; Husny and Cooper White 2008). For low values of Q c, there is an initial transient regime where the central microchannel is invaded by the Dragoxat while the HSA jet is squeezed. This situation is obviously unstable and small slugs of HSA are ejected periodically. This cannot be assimilated to droplet formation as the process is not quite repeatable and depends on the mechanical characteristics of the perfusion pumps and the compliance of the system. This regime persists until a threshold is reached that is a function of the pressure drop in the channels, and thus of the flow rate ratio and channel geometry. In our systems, we find that this threshold is of order Q c/Q l = 0.1 in systems 1 and 3 and of order 0.2 in system 2 where the pressure drop is larger for the same value of flow rate.

When this low threshold is exceeded, we reach a steady dripping regime where droplets are formed regularly at the channel junction as shown in Fig. 2. As the HSA jet reaches the junction, it is stretched by the Dragoxat flow and enters the downstream part of the central channel. Then capillary forces break the HSA jet and a droplet is formed. When Q c increases, the relative droplet size increases, as will be discussed in detail in the next section. The dripping regime persists until a higher limit is reached [Q l, Q c]high past which the HSA jet flows inside C down without breaking and a steady stratified two phase flow is observed as shown in Fig. 3. The confined geometry of the channel inhibits the the development of a capillary instability as studied in detail in (Humphry et al. 2009).

Fig. 2
figure 2

Successive phases of drop formation a in system 2, Q c/Q l = 0.3; b in system 3 Q c/Q l = 0.6

Full size image
Fig. 3
figure 3

Steady stratified flow with a central HSA liquid thread, Q c/Q l = 0.94, System 1

Full size image

The transition between the different regimes is difficult to get with precision. The reported values of [Q l, Q c]high are defined as the first value of Q c (Q l being fixed) for which the steady stratified flow is observed.

3.2 Stratified flow

When the threshold [Q l, Q c]high is exceeded, a steady central liquid thread of HSA is formed (Fig. 3) that is stable over the length of C down. The width L a of the thread depends on the channel geometry and on the values of Q c/Q l as shown in Fig. 5. The uniform axial velocity distribution u(y, z) in a rectangular duct can be found in a number of textbooks (see for example, Tabeling 2005):

$$ u(y,z)= {\frac{4h^2G}{\pi^3\mu}}\sum_n{\left[{\frac{1}{n^3}}-{\frac{\cosh n\pi y/h}{n^3\cosh n\pi W_{\rm c}/2h}}\right]\sin n\pi (z/h+1/2)},\quad n=1,3,\ldots $$
(1)

where G is the pressure gradient, and y and z the coordinates in a channel section (Fig. 4a). Since the two liquid viscosities are almost equal and surface tension is low, we assume that the axial velocity distribution u(y, z) in the duct is given by Eq. 1. We further assume that the HSA liquid thread is centred in the duct and has an elliptical cross section S with the same aspect ratio as the duct and thus with semi diameters L a and H = L a h/W c, (Fig. 4a). The flow rate of HSA is thus given by

$$ Q_{\rm c}=\int\int\limits_S{u(y,z){\text d}y {\text d}z}. $$
(2)

The inner integration over z is easily performed

$$ Q_{\rm c}= {\frac{-16h^3G}{\pi^4\mu}}\int\limits_0^{L_{\rm a}/2}\sum_n {\frac{1}{n^4}}\left[1-{\frac{\cosh n\pi y/h}{\cosh n\pi W_{\rm c}/2h}}\right]\cos\left[ n\pi\left({\frac{H}{h}}\sqrt{1-y^2/L^2_{\rm a}}+1/2\right)\right] {\text d}y, $$
(3)

The total flow rate Q t = Q c + 2Q l in the channel is given by

$$ Q_{\rm t}=4\int\limits_0^{W_{\rm c}/2}\int\limits_{0}^{h/2}{u(y,z){\text d}y {\text d}z} $$
(4)
$$ Q_{\rm t}={\frac{8h^3G W_{\rm c}}{\pi^4\mu}}\left[{\frac{\pi^4}{96}}-\sum_n{\frac{\tanh n\pi W_{\rm c}/2h}{n^5 \pi W_{\rm c}/2h}}\right]\quad n=1,3,\ldots $$
(5)

The numerical integration of (3) leads to a non-linear relation between Q c/Q l and L a/W c as shown in Fig. 5. For duct aspect ratios W c/h of order 2 or less, the relation between Q c/Q l and L a/W c does not depend much on the duct geometry. In the the range 0 < Q c/Q l < 2.5, the relation between central jet width and flow rate ratio can be approximated by

$$ L_{\rm a}/ W_{\rm c} \approx 0.4 \sqrt{Q_{\rm c} / Q_{\rm l}}+0.05,\quad R^2=0.98. $$
(6)
Fig. 4
figure 4

Schematics of the flow in a channel cross section. The HSA central thread has width L a and height L a h/W c

Full size image
Fig. 5
figure 5

Relation between the central jet width L a/W c and the flow rate ratio Q c/Q l for ducts with aspect ratio 1≤ h/W c <  2.2. Full line: exact solution; dashed line: linear correlation (6); symbols (defined in Table 1): experimental data in systems 1, 2, 3

Full size image

As shown in Fig. 5, the experimental measures of central thread width in Systems 1 and 3 correlate very well with either the exact solution or the approximate relation (6). The measurements for system 2 fall a little below the exact solution (by 6% at most). This may be due to the fact that in a rectangular duct with W c/h = 2, the hypothesis of an elliptical central thread is not quite accurate.

3.3 Transition from dripping to laminar flow

The transition from regular droplet flow to laminar flow depends on the geometry of the junction and of the the channels as well as on the flow dynamics, but we can make an order-of-magnitude estimate. We first note that the flow Reynolds number varies between 0.1 and 6, the highest value corresponding to a central flow rate Q c = 120 μl/min. This means that inertia effects are not very important can be neglected in a first approach. Consider the laminar flow in half the central channel (Fig. 4b). The HSA and Dragoxat film thicknesses are L a/2 and (W c − L a)/2, respectively, with corresponding mean velocities u c and u l. When a drop is forming, the surface tension stress is of order σcap = γ(2/h + 2/W c), where γ is the surface tension between the two phases and where we have assumed a longitudinal disturbance of order W c for the laminar jet. The viscous stress exerted by the external flow is of order σvisc = 2μu l/(W c − L a) with u l = 2Q l/h(W c − L a). We assume that droplets are formed when the capillary forces exceed viscous effects. This condition can be expressed in terms of a critical capillary number Ca:

$$ \frac{\sigma_{\text{visc}}}{\sigma_{\text{cap}}}\le {\text{Ca}} $$

Replacing the stresses by their order of magnitude, we find

$$ Q_{\rm l}\le \frac{\gamma {\text{Ca}}}{2\mu}(1+h/W_{\rm c}){W_{\rm c}}^2(1 -L_{\rm a}/W_{\rm c})^2. $$
(7)

Keeping in mind that L a/W c is smaller than unity and usually less than 0.5 in our experiments, we neglect quadratic terms and the constant term in (6)

$$ Q_{\rm l}\le A(1 -2L_{\rm a}/W_{\rm c}). $$
(8)

The constant A has the dimensions of a flow rate and is given by

$$ A={\frac{\gamma {\text{Ca}}}{2\mu}}(1+h/W_{\rm c}){W_{\rm c}}^2. $$
(9)

Finally, using the laminar flow correlation for the central jet width (6), we obtain the condition for droplet formation

$$ Q_{\rm c}\le 1.6 (Q_{\rm l} -2Q_{\rm l}^2/A+Q_{\rm l}^3/A^2), $$
(10)

As explained earlier, we have defined [Q l, Q c]high as the first couple of flow rate values for which a steady central thread of HSA occurred in C down. The experimental limiting values of Q c and Q l are shown in Fig. 6 together with a quadratic fit of each data set. We find, respectively,

$$ Q_{\rm c}= -0.0084 Q_{\rm l}^2 + 1.9 Q_{\rm l} -18,\quad\quad R^2=0.967\quad \hbox{for system 1}, $$
(11)
$$ Q_{\rm c}= -0.012 Q_{\rm l}^2 + 2.6 Q_{\rm l} -21,\quad\quad R^2=0.993\quad \hbox{for system 2}, $$
(12)

where the flow rates are expressed in μl/min. The coefficients of the Q 2l term give us the values of A for both systems. We find A 1 = 381 μl/min for system 1 and A 2 = 266 μl/min for system 2. The term Q 3l /A 2 is negligible in (10), because A is much larger than the experimental flow rates we used. The experimental value of the ratio A 1/A 2 = 1.45 is very near the one that can be estimated from (10), namely (1 + h 1/W c1)/(1 + h 2/W c2) = 1.33. The critical capillary number for which a droplet forms is found to be Ca ≈ 0.3, a value which is of the same order of magnitude that what is obtained for the breakup of liquid droplets freely suspended in an unbounded shear flow (Stone 1994). Note too, that the linear term in correlations (11) and (12) has a coefficient of order 2 when the analysis predicts a value of 1.6. Considering the difficulty of threshold detection and the approximations made in the transition analysis, the agreement can be considered as quite good. This means that the proper physical phenomenon has been accounted for.

Fig. 6
figure 6

High threshold values of Q c and Q l (in μl/min) where transition occurs from dripping to jetting. The system symbols are given in Table 1. The full lines represent quadratic fits

Full size image

3.4 Droplet flow

When droplets form regularly, the different phases of the process are depicted in Fig. 2a, b. There are two slightly different drop formation processes that depend on the size of the intersection. For a large intersection such that W l > W c, the HSA jet occupies the centre of the intersection as depicted in Fig. 2a. The tip of the jet extends under the effect of the continuous flow of HSA and of the Dragoxat elongational flow. The tip of the HSA jet enters the downstream channel, the elongational effect of the Dragoxat increases and the jet is broken, thus forming a droplet. For smaller intersections such that W l = W c, the process is different as shown in Fig. 2b. There is no steady HSA jet in the intersection, but the jet emerges from C up every time a droplet is formed. The jet then enters quickly C down and is broken in a fashion similar to that of the previous case.

We measure the length L g of the droplet flowing down C down. If the droplet moves too fast for the camera exposure time, it is blurred. In order to limit this phenomenon, we have used flow rates Q c and Q l in the range of 2–40 μl/min, corresponding to a maximum velocity of 60 mm/s in a 100 × 100 μm2 channel. The droplet length is measured with a precision of ±10 μm. The results presented in this section have been repeated with different systems fabricated from the same mould. The dispersion is due to small experimental errors in the pump setting, system compliance and the non linear dynamics of the dripping regime. For a given value of Q l, the droplet length increases with Q c, but for a given value of Q c, the droplet length decreases with Q l. This is in accordance with the experimental or numerical results obtained in T or planar flow-focussing geometries (Stone et al. 2004; Garstecki et al. 2006; Husny and Cooper White 2008; van der Graaf et al. 2006; Lee et al. 2009). For the range of tested values, the drop length normalized with the channel height increases linearly with the flow rate ratio Q c/Q l, provided it is larger than the lower limit mentioned in section 3.1 (Fig. 7). This result is qualitatively consistent with data reported in a T junction at low Capillary number (Stone et al. 2004). However, we find a significant effect of geometry. For example, it is interesting to note that the values obtained for systems 1 and 2 are nearly superimposed when L g is normalised with the system heights h that are in the ratio 2:1. The values obtained for system 3 with an intermediate height but a different intersection geometry are significantly higher. This shows that the geometry of the junction plays an important role.

Fig. 7
figure 7

Normalized drop length L g/h as a function of flow rate ratio Q c/Q l for HSA droplet in Dragoxat. Results for systems 1 (open square) and 2 (open circle) are superimposed although their heights h are in the ratio 2:1. System 3 (open triangle) has an intermediate height but a different intersection geometry

Full size image

The dripping hydrodynamic regime is unsteady, and the flow rates at the junction fluctuate with time. This dynamic process is very complicated as it involves the interplay of viscous and capillary forces. To our knowledge, there is no simple model of the two-phase flow in a Y junction, that can predict the dimensions of the droplets as a function of the system parameters such as geometry, flow rates and fluid physical properties. It is possible, however, to analyze the physics of the system and estimate how the droplet size should vary. The droplet volume V g is equal to Q cτ, where τ is the time of formation of a drop. Following Stone and co-workers (Stone et al. 2004; Garstecki et al. 2006), we estimate τ to be the time the external liquid takes to squeeze the HSA jet. It is proportional to W c/u l where u l is the velocity of the external liquid near the entrance to C down. The exact value of u l is not available as it depends on the two fluid configuration in the intersection, but it is proportional to the velocity Q l/(h W l) in a lateral channel. Consequently, we can expect the drop volume to be given by

$$ V_{\rm g}=L_{\rm g} W_{\rm c} h=K Q_{\rm c} \tau=K Q_{\rm c}{\frac{W_{\rm c}}{Q_{\rm l}/(h W_{\rm l})}}, $$
(13)

where K is a numerical constant that depends on the system geometry and physical properties such as viscosity contrast and capillary number. The droplet length is thus a linear function of the flow rate ratio as is indeed the case (Fig. 7). If we renormalize all the experimental drop lengths of Fig. 7 to account for the intersection geometry measured by W c/W l, we find that the results for the three systems fall approximately on the same line, as shown in Fig. 8. Consequently, from this experimental correlation, we find that for the HSA/Dragoxat fluid couple, the slug length is given by

$$ L_{\rm g} / h=4.1{\frac{ W_{\rm c}}{W_{\rm l}}}\,{\frac{ Q_{\rm c}}{Q_{\rm l}}}+1.9{\frac{ W_{\rm c}}{W_{\rm l}}}. $$
(14)

This correlation is valid for flow rate ratios between 0.1 and 1–1.4. Higher values of Q c/Q l leads to stratified flow situations as discussed in Sect. 3.2.

Fig. 8
figure 8

Drop length L g renormalized with hW c/W l as a function of flow rate ratio Q c/Q l for HSA droplet in Dragoxat. The symbols refer to the different systems as defined in Table 1. All data points fall approximately on the same linear correlation

Full size image

3.5 Effect of the continuous phase properties

In order to assess the effect of the fluids physical properties, we now replace Dragoxat with methyl laurate, another fatty acid also commonly used in pharmaceutical industry. The disperse phase is the same HSA solution. The continuous phase has now a viscosity that is 1.5 that of the disperse phase. We then study droplet size as a function of flow rates in systems 1, 2 and 3, but do not try to identify the high threshold for stratified flow. As shown in Fig. 9, we find again that L g/h varies linearly with Q c/Q l and that the results for systems 1 and 2 are superimposed. The correlation giving droplet length as a function of flow rate ratio and geometry is now

$$ L_{\rm g} / h=2.5{\frac{ W_{\rm c}}{W_{\rm l}}}\,{\frac{ Q_{\rm c}}{Q_{\rm l}}}+1.5{\frac{ W_{\rm c}}{W_{\rm l}}}. $$
(15)

We obtain a correlation that is different from (14) because the viscosity ratio between the continuous and disperse phase is now 1.5 instead of 1.

Fig. 9
figure 9

Drop length as a function of flow rate ratio in the three systems (symbols defined in Table 1) for two continuous phases with different viscosity. Open symbols: Dragoxat, filled symbols: laurate. The same linear trend is observed for the more viscous continuous phase, laurate

Full size image

However, if we plot the drop length as a function of the viscous stress ratio, measured by μc Q c/μl Q l, we find that the results from the Dragoxat and laurate superimpose as shown in Fig. 10. From this study, we may conclude that in the Y junction that we studied and for the HSA/fatty esters systems, the drop length is given by

$$ L_{\rm g}/h=4.1{\frac{Q_{\rm c}}{Q_{\rm l}}}\,{\frac{\mu_{\rm c}}{\mu_{\rm l}}}\,{\frac{W_{\rm c}}{W_{\rm l}}}+1.8{\frac{W_{\rm c}}{W_{\rm l}}}\quad R^2=0.81. $$
(16)

This relation is useful for controlling the droplet volume as a function of flow rate, system geometry and fluid properties.

Fig. 10
figure 10

Drop length L g renormalized with hW c/W l as a function of ratio μc Q c/μl Q l for HSA droplet in Dragoxat or laurate. The symbols refer to the different systems as defined in Table 1, open symbols: dragoxat, filled symbols: laurate. All data points fall approximately on the same linear correlation

Full size image

4 Discussion and conclusion

We have studied the formation of droplets for a specific two fluid system with low viscosity contrast in a geometry that differs from the classical T junction or planar flow focussing. The Y junction has been designed to avoid albumin adsorption on the PDMS walls. Furthermore, as we first fill the system with the oil phase and then inject the HSA solution, we assume that the oil coats the channel walls of the junction and of C down, and thus that the droplets are fully detached from the wall. We have also assumed that the droplets were centred in the channel due to lubrication forces. The drawback with using a Y junction is that there are yet no systematic studies of drop formation in this geometry like those one can find for T junctions or planar flow focussing systems.

Droplet formation of water in oil, inside microfluidic channels, has been extensively described in T shape microchannels (see the review Steegmans et al. 2009). In particular, Garstecki et al. (2006) found that the characteristic length of the droplet was proportional to flow rate ratio L g/W c = 1 + βQ c/Q l (in terms of our notations), where β is a parameter of order 1. This relation has been obtained when the external flow capillary number Cal = μl u l/γ was very small (Cal ∼0.01). For higher values Cal ≥ 1, the droplet length was reported to be a non linear function of Q c/Q l (Adzima and Velankar 2006; Xu et al. 2006). In our case, the capillary number in each lateral channel is Cal ∼0.01−0.1. This may explain why the correlation (16) is linear and similar to the one of Garstecki et al. If we normalise the drop length with the channel width rather than the depth, we find

$$ L_{\rm g}/W_{\rm c}=4.1{\frac{Q_{\rm c}}{Q_{\rm l}}}\,{\frac{\mu_{\rm c}}{\mu_{\rm l}}}\,{\frac{h}{W_{\rm l}}}+1.8{\frac{h}{W_{\rm l}}},\quad \hbox{for}\quad {\frac{Q_{\rm c}}{Q_{\rm l}}}> 0.1, $$
(17)

which shows how β depends on the channel geometry and fluid properties. It should be noted that the droplet size is determined by the smallest dimension (here, the depth) of the injection channel and that it is not possible to product droplets with a length smaller than h in this regime. This correlation is of course valid for a fluid system with a O(1) viscosity ratio in cross flow systems with geometrical properties in the range of those tested here, namely W c/h ∈ [1, 2] and W l/W c ∈ [1, 2]. For example, we have been unable to create droplets in channels with W c/h ≥ 4 using the full range of flow rates.

We cannot assess the effect of Cal in an unambiguous fashion with the two different fluid systems we used. One reason is that we do not have a wide enough range of values of Q l for a given Q c because we hit the high threshold rather quickly. We have used two different liquid phases with different viscosity and surface tension. However, for a given lateral flow velocity u l, we obtain the same value of capillary number for Dragoxat and laurate because the ratio μ/γ has almost the same value for the two liquid systems. Finally, for a system with a small viscosity contrast, it could well be that the inner capillary number plays an equally important role as the outer capillary number.

In conclusion, we find that a Y junction flow focussing microfluidic device allows to create droplets through a process that is similar to the one that occurs in T junction for low capillary numbers. In Y junction systems, droplet creation does not necessitate large lateral flow rates and can be achieved for flow rate ratios Q c/Q l of order unity or less. Another advantage is that the lateral fluid is brought in contact with the disperse phase in a symmetrical way. In the case where reagents are carried in the continuous phase, this may be beneficial as it leads to a better distribution of chemicals on the surface of the droplet.