1 Introduction

Realizing the effective mixing is an important issue in various microfluidic applications, since the mixing is mainly conducted through the diffusion process due to relevant laminar flows in the microfluidics (Teh et al. 2008; Gunther and Jensen 2006; Whitesides 2006; Squires and Quake 2005; Stone et al. 2004). There have been two strategies to enhance the mixing in microfluidics: active and passive methods. The active method utilizes external fields such as electric (Paik et al. 2003a, b; Pollack et al. 2002) or magnetic fields (Kang et al. 2007a, b; Rida and Gijs 2004). On the contrary, the passive method is concerned with the design of microchannel, for example, with geometrically curved units (Chen et al. 2009; Bringer et al. 2004), or with grooving walls in electro-osmosis flow (Johnson et al. 2002), or in pressure-driven flow (Stroock et al. 2002a, b). Elastic instability was also utilized to enhance mixing (Burghelea et al. 2004; Groisman and Steinberg 2004, 2001). Another promising method is to utilize viscous folding, which recently attracted much attention since it can be applied to enhance the mixing of two materials with large viscosity contrast (Cubaud and Mason 2008, 2007a, b, 2006a, b).

The viscous folding is observed in our daily life, for instance, when we pour honey, molten chocolate, or shampoo onto the flat surfaces, the fluids are piling upward with oscillatory folding or coiling. The macroscopic viscous folding problem has been extensively studied since the pioneering study by Taylor (1968). He recognized that a longitudinal compressive stress is a primary factor of the folding instability. A quasi one-dimensional analysis was developed for buckling of an axisymmetric (Tchavdarov et al. 1993; Yarin 1993; Entov and Yarin 1984; Cruickshank and Munson 1983, 1982b) and thin plane jets (Yarin and Tchavdarov 1996) and for both cases (Cruickshank 1988; Cruickshank and Munson 1982a). Cruickshank and Munson (1982a) reported that the compressive stress associated with fluid buckling was related with energy loss which was experimentally determined for the axisymmetric and the plane jets. According to the perturbation analysis (Cruickshank 1988), the slenderness ratio of the viscous thread was found to determine the onset of buckling, where the slenderness can be defined as the ratio of the thickness and height of the thread. In the experimental data on the buckling of both plane and axisymmetric jets falling onto the free surface of the viscous fluids (Griffiths and Turner 1988), the buckling depended largely on the slenderness ratio of threads as well as density and viscosity difference across the interface. The folding process turned out to be a low Re phenomenon (Yarin and Tchavdarov 1996; Cruickshank 1988; Cruickshank and Munson 1981). Tome and McKee (1999) numerically predicted that low Re condition is a requisite for the buckling of viscous thread as well as the thinning of the thread. In brief, the viscous folding occurs due to three major factors: the compressive stress, the low thickness of the viscous thread, and low Re condition.

In recent times, the folding of the viscous thread in diverging microchannels was systematically investigated (Cubaud and Mason 2006a). The purpose of their study was to present the strategy to enhance the mixing by viscous folding. Motivated by their study (Cubaud and Mason 2006a), we investigated the effect of the change of kinematic history by changing channel design. We also studied the effects of the flow ratio and viscosity ratio between two fluids on the folding instability with numerical simulation. In addition to computer simulations, experiments were also carried out to support conclusions from the simulation results. To our knowledge, this study is the first attempt to simulate the viscous folding in microfluidics although the macroscopic approaches have been presented on the viscous folding phenomena (Tome et al. 2008; Kim et al. 2001; Tome and McKee 1999).

In the next section, we provide a brief description of numerical algorithm with channel geometries. In Sect. 3, we present experimental details on the viscous folding in microfluidics. Then, we investigate the effects of channel design, viscosity ratio, and flow ratio on the folding of the viscous thread. We will relate the folding phenomena with the thread width and kinematics in diverging channels. The experimental results are analyzed in terms of the numerical simulations. In the final section, we provide main conclusions and practical suggestions for relevant flows in microfluidics.

2 Numerical method

2.1 Governing equations

We consider 2D isothermal and incompressible two-phase flows. Momentum and continuity equations can be denoted as follows:

$$ \rho \left( {{\frac{{\partial {\mathbf{u}}}}{\partial t}} + {\mathbf{u}} \cdot \nabla {\mathbf{u}}} \right) = - \nabla p + \eta \nabla \cdot \left( {\nabla {\mathbf{u}} + \left( {\nabla {\mathbf{u}}} \right)^{T} } \right) + \sigma \kappa_{\text{l}} {\mathbf{n}}_{\text{l}} , $$
(1a)
$$ \nabla \cdot {\mathbf{u}}=0,$$
(1b)

where ρ is the fluid density, u the velocity vector, t the time, p the pressure, and η the fluid viscosity. The last term in Eq. 1a is a capillary force term, where σ is the interfacial tension between two fluids, κ l the interface curvature, and n l the outward normal vector of the interface. In this study, it is assumed that σ is negligible and that two fluids are immiscible since the time scale of diffusion is known to be larger than that of convection in microfluidic flows (Cubaud and Mason 2006a; Gunther and Jensen 2006). The cases considered in this study will be physically equivalent to high Peclet number (Pe = UL/D, where U is the characteristic fluid velocity, L the characteristic length, and D the diffusion coefficient) flows. According to our experimental study, the range of Pe is estimated as O(10) ~ O(103) since U is O(10−1) cm/s in downstream region, and D glycerol solution is 10−6 to 10−5 cm2/s (Ternstrom et al. 1996).

In this study, we employ the Finite Element–Front Tracking Method (Chung et al. 2008). The finite element method is employed to discretize the governing equations (1a, 1b), and the Adams-Bashforth second order method is used for time marching. The momentum and the continuity equations are formulated into the following weak form:

$$ \begin{aligned} & {\frac{\rho }{\Updelta t}}\left\langle {\psi ;{\mathbf{u}}^{n + 1} - {\mathbf{u}}^{n} } \right\rangle + \rho \left\langle {\psi ;{\frac{3}{2}}\,{\mathbf{u}}^{n} \cdot \nabla {\mathbf{u}}^{n} - {\frac{1}{2}}\,{\mathbf{u}}^{n - 1} \cdot \nabla {\mathbf{u}}^{n - 1} } \right\rangle \\ & \quad = - \left\langle {\nabla \psi ;p^{n + 1} {\mathbf{I}}} \right\rangle + \left\langle {\nabla \psi ;\eta \left( {\nabla {\mathbf{u}}^{n + 1} + \left( {\nabla {\mathbf{u}}^{n + 1} } \right)^{T} } \right)} \right\rangle - \left\{ {\bar{\psi };{\mathbf{t}}^{n + 1} } \right\}, \\ \end{aligned} $$
(2a)
$$ \left\langle {\phi ;\nabla \cdot {\mathbf{u}}^{n + 1} } \right\rangle = 0, $$
(2b)

where ϕ and ψ are the bilinear and biquadratic shape functions for spatial discretization in finite element method (Becker et al. 1981), respectively. 〈;〉 and {;} denote, respectively, domain integral and line integral along the finite element, \( \bar{\psi } \) is the 1D quadratic shape function, and the superscript n denotes time step. The pressure p is approximated in terms of bilinear shape function, while u is discretized with biquadratic shape function. Traction on the boundary is t n + 1 = T n + 1 · n d, where \( {\mathbf{T}}^{n + 1} = - p^{n + 1} {\mathbf{I}} + \eta \left( {\nabla {\mathbf{u}}^{n + 1} + \left( {\nabla {\mathbf{u}}^{n + 1} } \right)^{T} } \right),\) and n d is an outward normal vector from the boundary in the computational domain.

In the front tracking method, successive front elements comprise the interface, where each front element has two front particles. The position of front particle, x p , on the interface is convected with fluid velocity. The interface moves according to the following equation.

$$ {\frac{{{\text{d}}{\mathbf{x}}_{{p}} }}{{{\text{d}}t}}} = {\mathbf{u}}_{{p}} , $$
(3)

where u p is the particle velocity at position x p , which is interpolated with a biquadratic shape function. New position of the particle \( {\mathbf{x}}_{{p}}^{n + 1} \) is updated from the previous step \( {\mathbf{x}}_{{p}}^{n} \) using the Runge-Kutta second order method. Fluid viscosity (η i ) is defined in terms of the Heaviside function H(x) as follows:

$$ \eta_{i}({\mathbf{x}}) = \eta_{\text{m}} + \left( {\eta_{\text{d}} - \eta_{\text{m}} } \right)H({\mathbf{x}}), $$
(4)

where the subscript d and m denote the dispersed phase and medium phase, respectively. Compared to the previous study (Chung et al. 2008), different algorithm is employed to get the Heaviside function that is used to define the physical properties of two-phase fluids. In this study, we get Heaviside function based on a distance to the interface instead of solving the Poisson equation. The reader is referred to the Appendix or literature (Chung 2009) for details of the proposed algorithm.

2.2 Problem definition

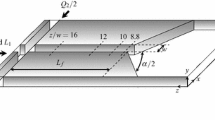
The computational domain is similar to the previous experimental study (Cubaud and Mason 2006a) as shown in Fig. 1. More viscous liquid (dispersed phase) flows into diverging channel from the center inlet along with less viscous liquid (medium phase) coming from two side inlets. The geometry is composed of two parts: flow focusing (y ≤ 5w c) and diverging regions (y ≥ 5w c). ρ d denotes the density of the dispersed phase, and ρ m is that of the medium phase. The mean velocity of the dispersed and medium phases is denoted as V d and V m, respectively, and the corresponding flow rates are Q d and Q m. The channel width in the flow focusing region is constant w c, the length of diverging region is 6w c, and the width of the outlet is 13w c. The proposed problem is concerned with unsteady flow, and the outlet boundary condition is also dynamically variable depending on flow conditions. In order to come up with this situation, the open boundary condition is imposed on the outlet which is known to be adaptable to dynamically variable outlet boundary condition (Park and Lee 1999; Papanastasiou et al. 1992).

Fig. 1
figure 1

Schematic diagram of viscous folding in diverging microchannel. Channels A and B have an abrupt angle (θ) of 90° and 45°, respectively. Channel C is designed as hyperbolic to get an approximately constant strain rate along the centerline

Full size image

Three important dimensionless numbers are defined as follows:

$$ \chi = {\frac{{\eta_{\text{d}} }}{{\eta_{\text{m}} }}}, $$
(5)
$$ \varphi = {\frac{{Q_{\rm d} }}{{Q_{\rm m}}}},$$
(6)
$$ Re={\frac{{\rho_{\rm m} LU}}{{\eta_{\rm m} }}} = {\frac{{\rho_{\rm m} \left( {0.5w_{\rm c} } \right)\left( {0.5V_{\text{m}} } \right)}}{{\eta_{\rm m}}}}.$$
(7)

The flow considered in this study is the creeping flow since Re is always less than 2.5 × 10−3. The characteristic length and velocity scales are L = 0.5w c and U = 0.5V m, respectively.

We designed the channel geometries with different diverging shapes at the exit region: channels A and B have the angle (θ) of 90° and 45°, respectively, with abrupt corners, and channel C is hyperbolic, which generates an approximately constant strain rate along the centerline (Kim and Doyle 2007; Randall et al. 2006). As for the mesh refinement, in the center region, where the viscous thread flows is more refined. More details on meshes including the number of elements and nodes, and the degree of freedom (DOF) are shown in Table 1. Δx min is the smallest mesh size in the refined region.

Table 1 Detailed information of meshes used in this study
Full size table

3 Experimental setup

3.1 Material

The experiments were conducted with aqueous glycerol solutions (purchased from Acros Organics). The solutions were Newtonian, and the viscosity was measured at different glycerol concentrations (e.g., η 10% = 1.3cp and η 86% = 89cp). The viscosity was measured using a controlled strain-type rheometer (ARES, TA Instruments) with parallel plate fixture at 25°C.

3.2 Channel fabrication and microscopy

Poly(dimethylsiloxane) (PDMS) microchannels were prepared using soft lithography method (McDonald et al. 2000). Both top and bottom walls were fabricated with PDMS to avoid wetting problem of the hydrophilic glycerol solutions. The width of the channel (w c) was 50 μm and the relevant length scales were the same as those in Fig. 1. The depth of the channel was 70 μm. The flow rates were controlled by syringe pumps (781100, KD Scientific; PHD4400, Harvard Apparatus), and the flow images were captured using a microscope (Olympus IX-71, 20X) and a high speed camera (Fastcam-ultima152, Photron). The images were analyzed with Photron Fastcam Viewer (Ver. 3).

4 Results and discussion

4.1 Numerical solutions

We performed numerical simulations by varying the viscosity ratios ( χ) and the flow ratios (φ) for three different channels. We could classify the flow patterns into three categories: “stable flow”, “folding”, and “chaotic flow”, where the “stable flow” is the case without viscous buckling, the “folding” corresponds to a periodic buckling, and the “chaotic flow” means irregular buckling which eventually results in numerical breakdown in the simulation. In Fig. 2, a “processing window” is provided as a function of three factors; χ, φ, and channel design. The unstable region (“folding” and “chaotic flow”) was the broadest in channel A. The flows were stable at high value of φ(= 0.5), independent of channel design. On the contrary, the unstable flow region could be generated at φ = 0.1 and 0.2 depending on χ. In the previous experimental study, it was reported that there exists a lower bound in χ for the generation of viscous folding, i.e., viscous folding is generated for χ > 15 (Cubaud and Mason 2006a). We also found that there exists a lower bound, e.g., we predict the viscous folding for χ ≥ 20 at φ = 0.1 for channel A. Interestingly, our numerical simulation predicts the existence of the upper bound of χ for viscous folding, e.g., the flow becomes stable for χ = 1,000 and φ = 0.1 in channel A, which has never been reported in the past. The existence of this upper bound may be attributed to thicker thread at high χ as will be explained in the next paragraph.

Fig. 2
figure 2

Processing window and flow patterns. The flow pattern depends on flow ratio (φ), viscosity ratio (χ), and channel design. filled circle stable flow, open circle folding, and times chaotic flow

Full size image

The viscous thread was always stable at φ = 0.5, which can be attributed to the fact that the thread becomes thicker as φ increases. We measured the thread thickness (w d) at the diverging point (y/w c = 5) as indicated in Fig. 1. The thread thickness, w d, monotonically increased with increasing φ as shown in Fig. 3a, where w d was nondimensionalized with L(= 0.5w c). w d also increased with increasing χ, which could be attributed to the fact that the liquid viscosity is considered as a resistance to the flow. The highly viscous thread spreads more in less viscous medium, consequently showing larger w d. The thicker width at high χ value results in flow stabilization as shown in Fig. 2, which accords with previous studies (Yarin and Tchavdarov 1996; Cruickshank 1988; Cruickshank and Munson 1981).

Fig. 3
figure 3

The width of viscous thread and the longitudinal stress as a function of flow ratio (φ) and viscosity ratio (χ). a The width of viscous thread depending on flow ratio (φ) and viscosity ratio (χ) for different channels. The large width for φ = 0.5 is related with stable flows as in Fig. 2. The thread width becomes larger with increasing χ for all φ. b Effect of channel design on the longitudinal stress along the centerline (φ = 0.1, χ = 1 (single phase)). The longitudinal stress (2η i u y /0.5w c) was nondimensionalized with 2η m0.5V m/0.5w c. In diverging region (y/w c ≥ 5), the magnitude of compressional stress becomes larger in the order of channel A > channel B > channel C. Channel C shows nearly constant stress since the hyperbolic channel is designed to induce constant strain rate along the centerline. c Effect of flow ratio on the longitudinal stress along the centerline (channel A, χ = 1 (single phase)). At low φ, the extensional stress and the compressional stress are highly developed

Full size image

The width of the thread (or central stream) was dependent upon the channel shape of the diverging region. In Fig. 3a, w d of channel C was notably smaller than that of other channels for the same φ and χ values. Nevertheless, the unstable region (“folding” and “chaotic flow” cases) was the smallest in channel C as shown in Fig. 2. Thus, there should be other factors for the occurrence of flow instability in addition to channel thickness w d. In order to elucidate the effect of channel design, we traced longitudinal extensional stress (2η i ∂u y /∂y) along the centerline for stable flow (χ = 1) as shown in Fig. 3b, where η i represents the fluid viscosity along the centerline. We notice that η i is a constant (= η d) along the centerline since no folding is reproduced in the case of χ = 1. The longitudinal extensional stress was nondimensionalized with 2η m U/L. As is expected, the flow kinematics strongly depended on the channel shape, where we simulated single-phase flow for comparison purpose. In the flow focusing region (y/w c < 5) where the flow is accelerated, there is no difference among the channels, in which positive extensional stress is predicted. However, the compressional stress was developed in the diverging region (y/w c > 5) in which the extent of compressional stress was dependent on the channel design. Channels A and B showed an abrupt increase of compressional stress in the entrance region of diverging channel, whereas the hyperbolic channel C showed a constant compressional stress with reduced level compared with other channels. Thus, the flow instability is directly related with kinematic history depending on the channel design. The higher the compressional stress, the more the viscous folding.

We also investigated the effect of φ on the compressional stress along the centerline. Fig. 3c shows that both extensional and compressional stress remarkably reduce as φ increases. Even in the single-phase flow (χ = 1), we notice that a different flow deformation (2∂u y /∂y) is induced by controlling φ with constant flow rate of the main stream (Q d). Furthermore, the thickness of a thread becomes larger with increasing φ as previously mentioned. Therefore, the viscous thread becomes stable at large φ.

The flow patterns are compared for three different channels at the same conditions of φ = 0.2 and χ = 20. In Fig. 4a, channel A shows folding, whereas other channels show stable flows. Contours of the extensional stress are presented in the figure, where the compressional stress is strongly developed near the entrance region of diverging channel in channels A and B (Fig. 4a, b). On the contrary, the stress is developed in broader region in channel C (Fig. 4c). When the longitudinal compressional stresses along the centerline are compared for three different channels as shown in Fig. 4d, channel C shows almost half of the compressional stress compared with other channels. The stress (2η i ∂u y /∂y) normalized with 2η m U/L in Fig. 4d is two orders of magnitude higher than the one in Fig. 3b and c since the flow deformation (2∂u y /∂y) becomes larger in case of higher χ(= η d/η m) compared to χ = 1.

Fig. 4
figure 4

Contours of the longitudinal stress (a–c) and the longitudinal stress along the centerline (2η i ∂u y /∂y) for φ = 0.2 and χ = 20. a Folding in channel A. b Stable flow in channel B. c Stable flow in channel C. d The longitudinal stress along the centerline. The level of compressional stress is highly developed as near −600 in channels A and B, whereas the lower value (~−300) is observed in channel C. The longitudinal stress (2η i u y /0.5w c) was nondimensionalized with 2η m U/L

Full size image

In recent experimental studies (Cubaud and Mason 2006a, b), a subfolding phenomenon was also reported, in which two or more folding frequencies were observed. It was considered as a transition from periodic to chaotic flows. In Fig. 5, a secondary folding similar to the subfolding phenomenon was predicted when φ = 0.1 and χ = 50 in channel B. In the early stage (Fig. 5a), the onset of folding was observed due to high compressional stress near the diverging point. As time elapsed, the secondary folding pattern was observed as shown in Fig. 5b, where the high compressional stresses under −200 (nondimensionalized with 2η m U/L) were developed at some points along the viscous thread (designated with red circles). Also, the breakup of the symmetry in the folding thread was observed as in Fig. 5c and d, where the high compressional stress was developed only near the diverging point (5 ≤ y/w c ≤ 6). Thus, it is concluded that the onset of secondary folding is originated due to the development of locally heterogeneous compressional stresses. The secondary folding seems to be a natural phenomenon which is related with the minimization of viscous dissipation by reducing the level of the compressional stresses exerted on the viscous thread.

Fig. 5
figure 5

Contours of the longitudinal stress (2η i ∂u y /∂y) and the flow structures for secondary folding in channel B (φ = 0.1, χ = 50). a Onset of folding (tV d/0.5w c = 30); b straight folding (tV d/0.5w c = 40); c secondary folding to the left (tV d/0.5w c = 50); d secondary folding to the right (tV d/0.5w c = 80). In the case of straight folding as shown in Fig. 5b, high compressional stress under −200 is developed at some points (designated with red circles) along the thread, while the relevant stress is developed only near the diverging point (5 ≤ y/w c ≤ 6) in other cases as shown in Fig. 5a, c and d

Full size image

For the three channels, we observe a power–law relation between the folding frequency (f) and the shear rate \( \left( {\dot{\gamma}} \right) \) as in Fig. 6a, although the number of data points may not be large enough to draw a clear conclusion. The folding frequency (f) is defined as an inverse of average period at which the same folding pattern repeats, and the shear rate \( \left( {\dot{\gamma }} \right) \) is defined as u y /0.5w c at the diverging point (y/w c = 5). In the experimental study (Cubaud and Mason 2006a), the power–law relation was suggested as \( f \sim \dot{\gamma }^{1} \) for channels A and B. Although the simulation data presented in this study predict \( f\sim \dot{\gamma }^{1.68} , \) we observe that channel C also shows a similar flow dynamics with abrupt channels. The discrepancy between simulation results and the experimental observation will be mainly attributed to the assumption of ignoring depth dimension in the simulation (2D simulation). Also, a small number of data points obtained in the narrow region make it difficult to derive a clear conclusion.

Fig. 6
figure 6

Folding frequency versus shear rate based on a simulation, and b experimental results. Shear rate \( \left( {\dot{\gamma }} \right) \) is defined as u y /0.5w c at the diverging point (y/w c = 5) in (a). Following the previous study (Cubaud and Mason 2006a), shear rate is defined as\( (Q_{\rm d} /\pi (0.5w_{\rm d} )^{2} )/0.5w_c\) at the diverging point in (b)

Full size image

4.2 Experimental results

As expected, based on the simulation results in the previous paragraph, we confirm that hyperbolic channels show the same flow dynamics \( \left( {f\sim \dot{\gamma }^{1} } \right) \) with abrupt channels (Cubaud and Mason 2006a), which means that the folding frequency itself is a function of the shear rate (or absolute flow rates) independent of channel shape as shown in Fig. 6b. Therefore, the present study is supportive of the previous experimental works (Cubaud and Mason 2006a).

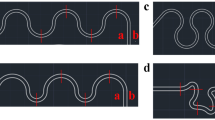
It is to be noted that the difference in folding pattern (frequency, amplitude, and the onset of folding) in each channel is related to the compressive stress when compared to the simulation results. The experimental results are shown in Fig. 7, in which the folding behavior is compared for different flow ratios and channels. We notice that the total flow rate (Q d + Q m) is O(100) ~ O(101) μl/min and the experimental conditions are considered to be creeping flows of Re ~ O(10−2). We took the average by carrying out three independent experiments for each channel. In channel C, the folding frequencies are smaller than in other channels, which could be attributed to lower compressive stress as in Fig. 4d. In the same manner, the amplitude (A) of the folding was remarkably reduced in channel C. In channel A, the folding frequency increased with decreasing φ as shown in Fig. 7a, d and g. As discussed in Fig. 3c, a thinner thread due to low φ showed higher compressional stress along the thread. Thus, the thinner thread showed higher frequency as in Fig. 7g. The delay of the onset of folding was also observed in channel C as in the simulation. The onset point was observed in channel C in more downstream region compared to other channels. It could be attributed to different development of compressive stresses along the centerline as discussed in Fig. 4a–c. Relatively weak compressive stress was expected to develop in broader region in channel C, whereas higher compressive stress was expected to develop at the entrance region (y/w c = 5) in channels A and B. In summary, the experimental results are all in accordance with the numerical prediction. Therefore, we conclude that the compressive stress developed at the entrance region plays a significant role on the onset of the viscous folding.

Fig. 7
figure 7

Experimental result. The folding frequency (f) is designated in the corresponding figures (± means the standard deviation). In Fig. 6i, the frequency could not be determined due to severe irregular folding (“chaotic flow”). χ = 68.5 (η d = 89cp; 86% glycerol solution, and η m = 1.3cp; 10% glycerol solution). Total flow rate (Q d + Q m) is O(100) ~ O(101)μl/ min. For a–c, φ = 0.5 (Q d = Q m = 1 μl/ min); for d–f, φ = 0.2 (Q d = 1 μl/ min, Q m = 5 μl/ min); for g–i, φ = 0.1 (Q d = 1 μl/ min, Q m = 10 μl/ min). In each channel, the folding frequency increases as φ decreases (w d decreases). Channel C gives lower frequency (f), lower amplitude (A), and a delay of onset of the folding due to lower compressive stress

Full size image

5 Concluding remarks

The viscous folding in diverging microchannels was investigated with direct numerical simulation. Microfluidic experiments were also carried out with the three different diverging channels to compare the folding patterns with those from numerical simulation. We showed that the compressive stress played a dominant role on the viscous folding. The hyperbolic channel generated relatively moderate flows (lower f and lower A) than other channels with abrupt corners. Thus, it was possible to control the mixing of two fluids in microfluidic flow not only by changing the flow ratio (φ) and viscosity ratio (χ) but also by different channel design. We suggest that the abrupt channels such as channel A or B should be exploited to enhance the mixing of the dispersed phase. On the contrary, a hyperbolic channel will be more appropriate for the stable flow in a diverging region. We hope this study will be helpful in getting more physical insights on viscous folding, solving mixing problems, and designing relevant experiments in microfluidic applications.