Electroosmotic control of width and position of liquid streams in hydrodynamic focusing

Abstract

This paper presents theoretical and experimental investigations on electroosmotic control of stream width in hydrodynamic focusing. In the experiments, three liquids (aqueous NaCl, aqueous glycerol and aqueous NaCl) are introduced by syringe pumps to flow side by side in a straight rectangular microchannel. External electric fields are applied on the two aqueous NaCl streams. Under the same inlet volumetric flow rates, the applied electric fields are varied to control the interface positions and consequently the width of the focused aqueous glycerol stream. The electroosmotic effect on the width of the aqueous glycerol is measured using fluorescence imaging technique. The electroosmotic effect under different flow rates, different viscosity, and aspect ratio are investigated. The results indicate that the electroosmotic effect on the pressure-driven flow becomes weaker with the increase in flow rates, viscosity ratio or aspect ratio of the channel. The measured results of the focused width of the non-conducting fluid agree well with the analytical model.

1 Introduction

Microfluidic systems have been studied extensively in recent years (Culbertson et al. 2000; Oleschuk and Harrison 2000; Sanders and Manz 2000). The Reynolds number in these systems is small, so the flows are always laminar. When two or more liquids flow in parallel within a single microchannel, laminar fluid interfaces are generated.

The interface and the width of a focused stream are important for sorting, separation, reaction and mixing in many applications. Controlling the interface leads to controlling the stream width, this is useful for focusing sample fluid or flow switching. Comparing with other controlling methods, the electroosmotic concepts (Besselink et al. 2004; Goranovic 2003; Kohlheyer et al. 2005) have many advantages. Interface control using electrokinetic was investigated previously. Its effectiveness and usefulness are demonstrated in many applications. Wang et al. (2005) demonstrated experimentally the concept of electroosmotic control of the interface location of a pressure driven two-fluid system in a microchannel. Adjusting the magnitude and direction of the electric field can control the interface position between the two liquids.

Gao et al. (2005) developed a numerical model to describe stratified two-fluid electroosmotic flow. The simulation results showed that the electroosmotic effect can control the interface location of a pressure-driven two-fluid system. By controlling the location of the interface between a microfluidic manometer and the test channel, Abkarian et al. (2006) presented a high-speed microfluidic differential manometer for cellular-scale hydrodynamics. Gao et al. (2007) presented theoretical and experimental results of electroosmotic control of the interface between two pressure-driven fluids.

Manipulating gases and liquids in a microfluidic network is crucial for applications such as bioassays, microreactors, chemical and biological sensing (Freemantle 1999). Zhao et al. (2001) showed that the maximum pressure at the interface between gas and fluid is determined by the surface free energy of the liquid, the advancing contact angle of the liquid on the hydrophobic regions, and the channel depth. Lee and Li (2006) presented the first experimental evidence on electroosmotic flow at a liquid–air interface, the results showed that the particle velocity at a liquid–air interface is significantly slower than the particle velocity in the bulk. Lee et al. (2006) studied the liquid velocity near a liquid–liquid interface, the experimental results showed that the liquid velocity near the liquid–liquid interface resembles a plug like profile for water phase of water–oil system.

Using “flow-rate-ratio” method, Blankenstein et al. (1996) presented a design for microfluidic flow switching. Wu and Nguyen (2005) theoretically studied the hydrodynamic focusing inside a rectangular microchannel, and the conclusions were verified by experiment. A fluidic oscillator employing a V-shaped fluidic circuit with feedback channel was demonstrated by Gebhard et al. (1997). A part of the output flow was fed back into the inlet region causing the main flow to be redirected to the other channel; the flow can then be switched between two outlets. The experiment reported by Blankenstein et al. (1996) showed that a stream can be guided to a desired outlet port using hydrodynamic force. Chein and Tsai (2004) presented two specific flow switches, one with a guided fluid flow to one of five desired outlets, and another with a guided fluid flow into one, two, or three equally distributed outlets.

Brotherton and Davis (2004) studied the couple effect of electroosmosis and pressure gradient, but it is on a single stream.

While most of the previous studies focus on interface control either by pressure-driven or by electroosmosis only, there are few investigations on the coupled effect between pressure-driven flow and electroosmosis flow for multi-fluid. This paper presents both theoretical and experimental results of the pressure-driven three-fluid flow in an H-shaped microchannel with electroosmotic effect. The first part of the paper presents the analytical model of the pressure-driven three-fluid flow in rectangular microchannel and coupled with electroosmotic effects, the width of the focused stream is investigated by fluorescence imaging technique. The results demonstrate an alternative solution for controlling the width and the position of the focused stream in a microchannel. The effect of parameters such as volumetric flow rate, electric field, viscosity ratio and channel aspect ratio are also discussed.

2 Theoretical model

2.1 Theoretical analysis

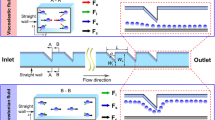
Figure 1 shows the model of a three-fluid flow system. The two sheath streams (fluid 1 and fluid 3) are electrically conducting with high electroosmotic mobility, while the focused stream (fluid 2) is non-conducting with a low electroosmotic mobility. At a given pressure gradient with electric fields applied along the conducting sheath streams, electroosmotic forces control the velocity of the conducting sheath streams. The velocity of the sheath streams depends on the directions and the strength of applied electric field. The fluid with low electroosmotic mobility is focused and delivered by the interfacial forces of the conducting fluids and the pressure gradient.

Fig. 1

Schematic of the phenomenon and coordinate system

The electric potentials in the conducting fluids due to the charged walls are taken as ψ ₁ and ψ ₃, respectively. The net charge densities in the two conducting fluids are ρ _q1 and ρ _q3. The length scale and velocity scale of the flow are taken as L _ref and U _ref, respectively, $L_{\text{ref}} = \frac{{h_{1} + 2h + h_{3} }}{2}$, $U_{\text{ref}} = \frac{{E_{x1} \varepsilon_{0} \varepsilon_{r} k_{b} T}}{{\mu_{\text{ref}} z_{0} }}.$The independent variable r and dependent variables u, p, ψ and ρ _q are expressed in terms of the corresponding dimensionless quantities (shown with an overbar) by

$$ \left\{ \begin{gathered} r = L_{\text{ref}} \bar{r} \hfill \\ u = U_{\text{ref}} \bar{u} \hfill \\ \psi = k_{b} T\bar{\psi }/(z_{0} e) \hfill \\ p = \rho_{\text{ref}} U_{\text{ref}}^{2} \bar{p} \hfill \\ \rho_{q} = 2n_{0} z_{0} e\bar{\rho }_{q} \hfill \\ \end{gathered} \right. $$

(1)

where ρ is the liquid density, k _b is Boltzmann constant, T is the absolute temperature, z ₀ is the valence of the ions, e is elementary charge, and n ₀ is the reference value of the ion concentration, ε _r is the relative permittivity of the conducting fluids, ε ₀ is the permittivity of vacuum, and E _x1 is the applied electric field.

In our model, the electric potentials in the conducting fluids are described by the Poisson–Boltzmann equation, using Debye–Hückel linear approximation, the distribution of electric potentials can be written in terms of dimensionless variables as

$$ ({\text{conducting}}\;{\text{fluid}}\;1)\;\;\;\nabla^{2} \bar{\psi }_{1} = K^{2} \bar{\psi }_{1} $$

(2)

$$ ({\text{conducting}}\;{\text{fluid}}\;3)\;\;\;\nabla^{2} \bar{\psi }_{3} = K^{2} \bar{\psi }_{3} $$

(3)

where K = L _refκ is the ratio of the length scale L _ref to the characteristic double layer thickness 1/κ where κ is the Debye–Hückel parameter

$$ \kappa = \left( {\frac{{2z_{0}^{2} e^{2} n_{0} }}{{\varepsilon_{r} \varepsilon_{0} k_{b} T}}} \right)^{{\frac{1}{2}}} $$

(4)

Using the separation of variables method, the electric potentials in the two sheath streams can be described as

$$ \begin{gathered} \bar{\psi }_{1} = \sum\limits_{j = 0}^{\infty } {\frac{{4\bar{\xi }_{1} }}{(2j + 1)\pi }( - 1)^{j + 1} \frac{{\sinh [(\bar{h} + \bar{y})]}}{{\sinh (B_{j} \bar{h}_{1} )}}\cos (\lambda_{j} \bar{z})} \hfill \\ \quad - \sum\limits_{j = 0}^{\infty } {\frac{{4\bar{\xi }_{3} }}{(2j + 1)\pi }( - 1)^{j + 1} \times \frac{{\sinh [B_{j} (\bar{h}_{1} + \bar{h} + \bar{y})]}}{{\sinh [B_{j} \bar{h}_{1} ]}}\cos (\lambda_{j} \bar{z})} \hfill \\ \quad + \sum\limits_{p = 1}^{\infty } {\frac{{2\bar{\xi }_{2} }}{j\pi }[( - 1)^{p} - 1]\frac{{\cosh (A_{p1} \bar{z})}}{{\cosh (A_{p1} \bar{w})}}\sin [\frac{p\pi }{{\bar{h}_{1} }}(\bar{y} + \bar{h})]} \hfill \\ \end{gathered} $$

(5)

$$ \begin{gathered} \bar{\psi }_{3} = - \sum\limits_{j = 0}^{\infty } {\frac{{4\bar{\xi }_{4} }}{(2j + 1)\pi } \times ( - 1)^{j + 1} \times \frac{{\sinh [B_{j} (\bar{y} - \bar{h})]}}{{\sinh (B_{j} \bar{h}_{3} )}}\cos (\lambda_{j} \bar{z})} \hfill \\ \quad + \sum\limits_{j = 0}^{\infty } {\frac{{4\bar{\xi }_{6} }}{(2j + 1)\pi } \times ( - 1)^{j + 1} \times \frac{{\sinh [B_{j} (\bar{y} - \bar{h}_{3} - \bar{h})]}}{{\sinh [B_{j} \bar{h}_{3} ]}}\cos (\lambda_{j} \bar{z})} \hfill \\ \quad - \sum\limits_{p = 1}^{\infty } {\frac{{2\bar{\xi }_{5} }}{p\pi }[( - 1)^{p} - 1]\frac{{\cosh (A_{p3} \bar{z})}}{{\cosh (A_{p3} \bar{w})}}\sin [\frac{p\pi }{{\bar{h}_{3} }}(\bar{y} - \bar{h})]} \hfill \\ \end{gathered} $$

(6)

where

$$ \left\{ \begin{gathered} \lambda_{j} = \frac{(2j - 1)\pi }{{2\bar{w}}} \hfill \\ B_{j} = \sqrt {K^{2} + \lambda_{j}^{2} } \hfill \\ A_{p1} = \sqrt {K^{2} + (\frac{p\pi }{{\bar{h}_{1} }})^{2} } \hfill \\ A_{p3} = \sqrt {K^{2} + (\frac{p\pi }{{\bar{h}_{3} }})^{2} } \hfill \\ \end{gathered} \right. $$

(7)

Once the electric potential distributions are known, the ionic net charge densities $\bar{\rho }_{q}$ can be obtained as

$$ ({\text{conducting}}\;{\text{fluid}}\;1)\;\;\;\bar{\rho }_{q1} = - \bar{\psi }_{1} (\bar{z},\bar{y}) $$

(8)

$$ ({\text{conducting}}\;{\text{fluid}}\;3)\;\;\;\bar{\rho }_{q3} = - \bar{\psi }_{3} (\bar{z},\bar{y}) $$

(9)

The dimensionless surface charge densities $\bar{\rho }_{q}^{s}$ at the liquid–liquid interfaces are

$$ ({\text{interface}}\;\text{1}{\text{--}}{\text{2}})\;\;\;\bar{\rho }_{q1}^{s} (\bar{z}) = - \frac{{\partial \bar{\psi }_{1} ( - \bar{h},\bar{z})}}{{\partial \bar{y}}} $$

(10)

$$ ({\text{interface}}\;\text{2}{\text{--}}{\text{3}})\;\;\;\bar{\rho }_{q3}^{s} (\bar{z}) = - \frac{{\partial \bar{\psi }_{3} (\bar{h},\bar{z})}}{{\partial \bar{y}}} $$

(11)

When external electric fields, $E_{x1}$ and $E_{x3}$, are applied to the conducting fluids 1 and 3, their interactions with the net charges within the electric double layers and create electroosmotic body forces on the bulk of the conducting liquids. We assume that

• (1) All the three liquids are Newtonian and incompressible.

• (2) The properties of the liquids are independent of local electric field and ion concentration. The electric field strength and ion concentration may affect the properties of the conducting fluids. In the current study, these effects are neglected (Dutta et al. 2002).

• (3) The liquid’s properties are independent of temperature. Joule heating is neglected for dilute electrolytes and low field strength (Tang et al. 2004).

  $$ \frac{{\partial \left( {\bar{\rho }\;\bar{v}} \right)}}{{\partial \bar{t}}} + \nabla \cdot \left( {\bar{\rho }\,\bar{v}\,\bar{v}} \right) = - \nabla \bar{p} + G\bar{\rho }_{q} + \frac{1}{\text{Re}}\bar{\mu }\nabla^{2} \bar{v} $$

  (12)

• (4) The flow is fully developed with the non-slip boundary condition. The second term on the left-hand side of Eq. (12), $\nabla \cdot (\bar{\rho }\bar{v}\,\bar{v})$, will be vanished.

• (5) The pressure gradient is assumed to be uniform along the channel, and the pressure gradients along y and z directions are both zero.

Then the momentum equation for the conducting fluid 1 is

$$ \frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{y}^{2} }} + \frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{z}^{2} }} = Re\frac{{\text{d}\bar{p}}}{{\text{d}\bar{x}}} - ReG_{x1} \bar{\rho }_{q1} $$

(13)

where ${{\text{d}\bar{p}} \mathord{\left/ {\vphantom {{\text{d}\bar{p}} {\text{d}\bar{x}}}} \right. \kern-\nulldelimiterspace} {\text{d}\bar{x}}}$ is the dimensionless pressure gradient of the three fluids in the fully developed state, $G_{x1}$ is a parameter, which measures the relative importance of the electrical force on the conducting fluid 1

$$ G_{x1} = \frac{{2z_{0} en_{0} L_{\text{ref}} E_{x1} }}{{\rho_{\text{ref}} U_{\text{ref}}^{2} }} $$

(14)

$$ {Re} = \frac{{\rho_{\text{ref}} U_{\text{ref}} L_{\text{ref}} }}{{\mu_{\text{ref}} }} $$

(15)

where $\mu_{\text{ref}} = \mu_{1}$.

The momentum equation of the non-conducting fluid 2 is

$$ \frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{y}^{2} }} + \frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{z}^{2} }} = \frac{Re}{{\beta_{2} }}\frac{{\text{d}\bar{p}}}{{\text{d}\bar{x}}} $$

(16)

where $\beta_{2} = {{\mu_{2} } \mathord{\left/ {\vphantom {{\mu_{2} } {\mu_{1} }}} \right. \kern-\nulldelimiterspace} {\mu_{1} }}$ is the ratio of the dynamic viscosities of fluid 2 and fluid 1.

The momentum equation of the conducting fluid 3 is

$$ \frac{{\partial^{2} \bar{u}_{3} }}{{\partial \bar{y}^{2} }} + \frac{{\partial^{2} \bar{u}_{3} }}{{\partial \bar{z}^{2} }} = \frac{Re}{{\beta_{3} }}\frac{{\text{d}\bar{p}}}{{\text{d}\bar{x}}} - ReG_{x3} \bar{\rho }_{q3} $$

(17)

where $\beta_{3} = {{\mu_{3} } \mathord{\left/ {\vphantom {{\mu_{3} } {\mu_{1} }}} \right. \kern-\nulldelimiterspace} {\mu_{1} }}$, $G_{x3} = \frac{{2z_{0} en_{0} L_{\text{ref}} E_{x3} }}{{\rho_{\text{ref}} U_{\text{ref}}^{2} }}$.

No-slip boundary conditions are applied at the channel walls. In addition, the matching conditions at the interfaces such as continuity of velocities and force balance should be warranted (Gao et al. 2007).

The continuity conditions of the velocities at the liquid–liquid interfaces are:

$$ \bar{u}_{1} = \bar{u}_{2} ,\;\quad {\text{at}}\quad \bar{y} = - \bar{h}\quad ({\text{interface}}\;\text{1}{\text{--}}{\text{2}}) $$

(18)

$$ \bar{u}_{2} = \bar{u}_{3} ,\quad \,{\text{at}}\quad \bar{y} = \bar{h}\quad ({\text{interface}}\;\text{2}{\text{--}}{\text{3}}) $$

(19)

The shear stress balances that jump abruptly at the interface due to the presence of a given surface charge density are

$$ \bar{\mu }_{1} \frac{{\partial \bar{u}_{1} }}{\partial n} + M_{1} \bar{\rho }_{q}^{s} = \bar{\mu }_{2} \frac{{\partial \bar{u}_{2} }}{\partial n},\quad {\text{at}}\quad \bar{y} = - \bar{h}\quad ({\text{interface}}\;\text{1}{\text{--}}{\text{2}}) $$

(20)

$$ \bar{\mu }_{3} \frac{{\partial \bar{u}_{3} }}{\partial n} + M_{3} \bar{\rho }_{q}^{s} = \bar{\mu }_{2} \frac{{\partial \bar{u}_{2} }}{\partial n},\quad {\text{at}}\quad \bar{y} = \bar{h}\quad ({\text{interface}}\;\text{2}{\text{--}}{\text{3}}) $$

(21)

where $\bar{\mu }_{1} = \frac{{\mu_{1} }}{{\mu_{ref} }} = \frac{{\mu_{1} }}{{\mu_{1} }},$ $\bar{\mu }_{2} = \frac{{\mu_{2} }}{{\mu_{1} }},$ $\bar{\mu }_{3} = \frac{{\mu_{3} }}{{\mu_{1} }},$

$$ M_{1} = \frac{{\varepsilon k_{b} TE_{x1} }}{{z_{0} eU_{\text{ref}} \mu_{\text{ref}} }} $$

and

$$ M_{3} = \frac{{\varepsilon k_{b} TE_{x3} }}{{z_{0} eU_{\text{ref}} \mu_{\text{ref}} }} .$$

Because of the linearity of the governing equations, the velocity fields can be decomposed into two parts,

$$ \left\{ \begin{gathered} \bar{u}_{1} = \bar{u}_{1}^{p} + \bar{u}_{1}^{E} \hfill \\ \bar{u}_{2} = \bar{u}_{2}^{p} + \bar{u}_{2}^{E} \hfill \\ \bar{u}_{3} = \bar{u}_{3}^{p} + \bar{u}_{3}^{E} \hfill \\ \end{gathered} \right. $$

(22)

where the superscript E denotes velocity components caused by electroosmotic forces, the superscript p denotes velocity components caused by the pressure gradient. These velocity components can be obtained using the separation of variables method.

With the known velocity distributions of $\bar{u}_{1}^{E}$, $\bar{u}_{1}^{p}$, $\bar{u}_{2}^{E}$, $\bar{u}_{2}^{p}$, $\bar{u}_{3}^{E}$ and $\bar{u}_{3}^{p}$, the dimensionless flow rates are given as

$$ \bar{q}_{1}^{E} = 2\int\limits_{{ - \bar{h}}}^{{ - \bar{h} - \bar{h}_{1} }} {\int\limits_{0}^{{\bar{w}}} {\bar{u}_{1}^{E} \left( {\bar{y},\bar{z}} \right)\text{d}\bar{z}} } \text{d}\bar{y} $$

(23)

$$ \bar{q}_{1}^{p} = 2\int\limits_{{ - \bar{h} - \bar{h}_{1} }}^{{ - \bar{h}}} {\int\limits_{0}^{{\bar{w}}} {\bar{u}_{1}^{p} (\bar{y},\bar{z})\text{d}\bar{z}} } \text{d}\bar{y} $$

(24)

$$ \bar{q}_{2}^{E} = 2\int\limits_{{ - \bar{h}}}^{{\bar{h}}} {\int\limits_{0}^{{\bar{w}}} {\bar{u}_{2}^{E} \left( {\bar{y},\bar{z}} \right)\text{d}\bar{z}} } \text{d}\bar{y} $$

(25)

$$ \bar{q}_{2}^{p} = 2\int\limits_{{ - \bar{h}}}^{{\bar{h}}} {\int\limits_{0}^{{\bar{w}}} {\bar{u}_{2}^{p} \left( {\bar{y},\bar{z}} \right)\text{d}\bar{z}} } \text{d}\bar{y} $$

(26)

$$ \bar{q}_{3}^{E} = 2\int\limits_{{\bar{h}}}^{{\bar{h} + \bar{h}_{3} }} {\int\limits_{0}^{{\bar{w}}} {\bar{u}_{3}^{E} \left( {\bar{y},\bar{z}} \right)\text{d}\bar{z}} } \text{d}\bar{y} $$

(27)

$$ \bar{q}_{3}^{p} = 2\int\limits_{{\bar{h}}}^{{\bar{h} + \bar{h}_{3} }} {\int\limits_{0}^{{\bar{w}}} {\bar{u}_{3}^{p} \left( {\bar{y},\bar{z}} \right)\text{d}\bar{z}} } \text{d}\bar{y} $$

(28)

3 Experiment

3.1 Materials and fabrication

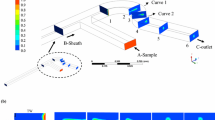
Figure 2 shows the H-shaped microchannel used in the experiment. The adhesive lamination technique (Wu et al. 2004) is used to fabricate the microchannel. In this method, two polymethylmethacrylate (PMMA) plates (50 mm × 25 mm) are bonded by one or multiple layers of a double-sided adhesive tape. First, two PMMA plates are cut using a CO₂ laser. Fluidic access holes and alignment holes are laser-machined into the PMMA substrate. Second, a double-sided adhesive sheet (Adhesives Research Inc., Arclad 8102 transfer adhesive) is cut to form the intermediate layer with the channel structures. The adhesive layer thickness of 50 μm defines the channel’s height. The three layers are positioned with the alignment holes and pressed for bounding.

Fig. 2

H-shaped microchannel a the fabricated device used in the experiment; b schematic representation of the three-fluid microchannel

Using this technique, a microchannel with a cross section of 1 mm × 50 μm and a length of 2 cm is fabricated. As shown in Fig. 2, the three fluids flow side by side in the straight microchannel in the direction from left to right. The flows at the inlets A, B and C are driven by syringe pumps. The outlets D, E and F are connected to a waste reservoir. Electric fields are applied by inserting two pairs of platinum electrodes into A, D and C, F, respectively.

3.2 Experimental setup

Figure 3 shows a schematic of the experimental setup. Fluorescence imaging technique is used in our experiments. The setup consists of four main components: an illumination system, an optical system, a coupled charge device (CCD) camera and a personal computer (PC) base control system. A mercury lamp is used as the illumination source for the fluorescence measurement, the wavelength of this mercury lamp is 540 nm.

Fig. 3

Schematic of the experimental setup for fluorescence imaging

The optical system is a Nikon inverted microscope (Model ECLIPSE TE2000-S) with a set of epi-fluorescent attachments. The filter cube consists of three optical elements: excitation filter, dichroic mirror and emission filter. Emission filters are used in the measurement to select the specific emission wavelength of the sample and to remove traces of excitation light.

An interline transfer CCD camera (Sony ICX 084) is used for recording the images. The resolution of the camera is 640 × 480 pixels with 12 bits grayscale. The active area of the CCD sensor is 6.3 mm × 4.8 mm. The exposure time for recording the images is 7 ×  10⁴ μs. To ensure that the CCD camera is working at its optimum temperature of −15°C, a cooling system is integrated into the CCD camera. In the mode of double exposure in double frames, the camera can record two frames of the flow fields and then digitizes them in the same image buffer.

Three identical syringes (5 ml gastight, Hamilton) are driven by a single syringe pump (Cole-Parmer, 74900-05, 0.2 μl/h–500 l/h, accuracy of 0.5%). A high voltage power supply (Model PS350, Stanford Research System, Inc) is used to provide the controlling electric fields. The power supply is capable of producing up to 5,000 V and changing the polarity of the voltage.

4 Results and discussion

4.1 Fluorescence imaging measurement

Rhodamine B (C₂₈H₃₁N₂O₃Cl) is used as the fluorescent dye in our experiment. Rhodamine B is neutrally charged, and it does not affect the ion concentration and the electroosmotic effect. For the purpose of image collection, the fluorescent dye is added to the NaCl solution. Rhodamine B is a water–solute fluorescent dye, which can be excited by green light (the excitation wavelength is 540 nm) and emit red light (the maximum emission wavelength is 610 nm), the fluorescent image is recorded by an epi-fluorescent attachment of type Nikon G-2E/C. The interface positions between the three fluids are determined using the recorded images and a customized image processing program written in MATLAB (Wu et al. 2004). The program cancels the noise in the collected images with an adaptive noise-removal filter. The program also determines the pixel intensity values across the channel, which is normalized using $I^{*} = \frac{{I - I_{\min } }}{{I_{\max } - I_{\min } }},$ where I _max and I _min are the maximum and minimum intensity values, respectively.

A linear relationship between the light intensity and the concentration of the fluorescent dye is assumed (Sato et al. 2003). Because of the mixing effect, an inter-diffusion region exists at the interface. This paper assumes that the inner diffusion of dye between the two fluids is a Gaussian distribution. A MATLAB program develops to determine the interface position. The program calculates the position (y) basing on the derivative of concentration c with respect to the distance y, dc/dy can be taken by the formula of${{(c_{2} - c_{1} )} \mathord{\left/ {\vphantom {{(c_{2} - c_{1} )} {(y_{2} - y_{1} )}}} \right. \kern-\nulldelimiterspace} {(y_{2} - y_{1} )}}$. The interface position is taken as the position where dc/dy its maximum value has.

Figure 4 shows the flow images at a flow rate of 0.05 ml/h when $E_{x1} = E_{x3} = 200\;{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}}$ and $E_{x1} = E_{x3} = - 200\;{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}}$, respectively. The corresponding normalized concentration profiles for different electric fields are shown in Fig. 5. A planar interface between NaCl solution and aqueous glycerol is assumed. Figure 6 shows the cross sectional view of the three fluids in the microchannel, h ₁, 2h and h ₃ are denoted as the width of NaCl solution, aqueous glycerol and NaCl solution, respectively. The dimensionless widths of NaCl solution are

Fig. 4

Measurement results at a flow rate of $q_{1} = q_{2} = q_{3} = 0.05{{\;{\text{ml}}} \mathord{\left/ {\vphantom {{\;{\text{ml}}} {\text{h}}}} \right. \kern-\nulldelimiterspace} {\text{h}}}:$ a $E_{x1} = E_{x3} = 200\;{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}} ,$ b $E_{x1} = E_{x3} = -200\;{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}}$

Fig. 5

Normalized concentration distribution of the fluorescent dye across the channel width under different applied voltages at a flow rate of $q_{1} = q_{2} = q_{3} = 0.05{{\;{\text{ml}}} \mathord{\left/ {\vphantom {{\;{\text{ml}}} {\text{h}}}} \right. \kern-\nulldelimiterspace} {\text{h}}}$: a $E_{x1} = E_{x3} = 200{{\;\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}} ,$ b $E_{x1} = E_{x3} = - 200{{\;\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}}$

Fig. 6

Cross sectional view of the three fluids in the main channel

$$ \begin{gathered} e_{1} = \frac{{h_{1} }}{{h_{1} + 2h + h_{3} }} \hfill \\ e_{3} = \frac{{h_{3} }}{{h_{1} + 2h + h_{3} }} \hfill \\ \end{gathered} $$

(29)

The dimensionless width of aqueous glycerol is

$$ e_{2} = \frac{2h}{{h_{1} + 2h + h_{3} }} $$

(30)

The aspect ratio, $\chi$ _, is defined as (Gao et al. 2007)

$$ \chi = \frac{{(2h + h_{1} + h_{3} )}}{w} $$

(31)

The negative wall potential affects the distribution of free ions in the NaCl solution and the electrical double layers (EDL) near the wall. An EDL can hardly form in the glycerol solution because only few free ions are available (Hunter 1981). This fact is reflected in the conductivity of the NaCl solution of 86.6 μs/cm and the conductivity of pure glycerol of 0.064 μs/cm (Yaws 2003). Thus, the electroosmosis has little effect on the aqueous glycerol flow. If two positive electric fields are applied between A and D, and between C and F (A and C are the positive electrodes, D and F are the negative electrodes), the NaCl solution is dragged in the same direction as the pressure-driven flow. When two negative electric fields are applied between A and D, and between C and F (A and C are the negative electrodes, D and F are the positive electrodes), the NaCl solution is dragged in the opposite direction as the pressure-driven flow.

4.2 Interface control and flow focusing

Three liquids (two conducting liquids with NaCl and aqueous glycerol as the non-conducting liquid with viscosity ratio β ₁ = β ₃ = 1 and β ₂ ≈ 1.46) are introduced through the inlets by the syringe pump. The volumetric flow rates of all three liquids are maintained at the same value.

When no electric field is applied, the flow is simply driven by a pressure gradient. As the aqueous glycerol ($\mu_{2} = 1.2 4\times 10^{- 3} \;{{\text{Ns}} \mathord{\left/ {\vphantom {{\text{Ns}} {{\text{m}}^{ 2} }}} \right. \kern-\nulldelimiterspace} {{\text{m}}^{ 2} }}$, $\rho_{2} = {\text{1,050}} \;{\text{kg/m}}^{3}$) is more viscous than the NaCl solution ($\mu_{1,3} = 0.8 5\times 10^ {-3} \;{{\text{Ns}} \mathord{\left/ {\vphantom {{\text{Ns}} {{\text{m}}^{ 2} }}} \right. \kern-\nulldelimiterspace} {{\text{m}}^{ 2} }}$, $\rho_{1,3} = 996\;{\text{kg/m}}^{3}$), the NaCl solutions occupy two smaller portions of the channel, Fig. 7a. When negative electric fields are applied along the conducting liquids, the electroosmotic flows act against the pressure-driven flow. Consequently, the NaCl solutions encounter a larger resistance. The NaCl solutions appear to be more “viscous” due to the electroosmotic effect. Due to the same pressure drop along the microchannel and the same volumetric flow rate forced by the syringe pump, the more viscous fluid has to spread over a larger area, thus occupy a larger portion of the channel. Figure 7b shows that when $E_{x1} = E_{x3} = - 200\,{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}} ,$ the dimensionless widths of NaCl increase symmetrically, e _1 =  e ₃. e ₁ and e ₃ increase with the increase of the negative electric fields. At different electric fields ($E_{x1} = - 50\;{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}} ,\;\;E_{x3} = - 200\;{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}}$), e ₁ and e ₃ increase differently, Fig. 7c. If positive electric fields ($E_{x1} = 200\;{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}} ,\;\;E_{x3} = 200\;{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}}$) are applied to the sheath flows, e ₁ and e ₃ decrease, Fig. 7d. Since the electroosmotic flow is in the same direction as the pressure-driven flow, the NaCl solutions flow faster. When a positive electric field ($E_{x1} = 50\;{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}}$) and a negative electric field ($E_{x3} = - 200\;{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{cm}}}} \right. \kern-\nulldelimiterspace} {\text{cm}}}$) are applied, e ₁ decreases, and e ₃ increases, as shown in Fig. 7e. The above results show that the location of the two interfaces can be controlled by applying different electric fields on the sheath flows.

Fig. 7

Interface control and flow focusing of three-fluid flow ($q_{1} = q_{2} = q_{3} = 0.05\;{\text{ml/h}}$) a purely hydrodynamic focusing, b combined electroosmotic/hydrodynamic focusing, c focusing and switching to the bottom, d combined electroosmotic/hydrodynamic extension, c extension and switching to the bottom

4.3 Comparison between theoretical analysis and experiment

Figure 8 compares the measured and analytical results under different applied electric field strengths. A reasonable agreement is obtained. A reference velocity of $U_{\text{ref}} = 1.77 \times 10^{ - 3} {{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}},$ a reference length of $L_{\text{ref}} = \; 1\,{\text{mm,}}$ and the viscosities of the NaCl solution and aqueous glycerol of $0.85\; \times 10^{ - 3}$ and $1. 2 4\times 1 0^ {-3} \;{\text{Nsm}}^ {-2} ,$ are taken, respectively. Under these conditions, the dimensionless flow rates are 0.019, 0.057, 0.095, and 0.19 for 0.1, 0.3, 0.5 and 1 ml/h, respectively. The zeta potential at the PMMA channel and NaCl solution is −24.4 mV as measured by the electroosmotic mobility method (Yan et al. 2006). The zeta potential at the interface between the aqueous glycerol and the NaCl solution is taken as 0 mV.

Fig. 8

Relationship between focused width e ₂ and the applied voltage for different flow rates ($\beta_{1} = \beta_{3} = 1$, $\beta_{2} = {{1.24} \mathord{\left/ {\vphantom {{1.24} {0.85}}} \right. \kern-\nulldelimiterspace} {0.85}} \approx 1.46$ and χ = 20)

Figure 8 shows the relationship between the focused width e ₂ and the applied voltage for the same volumetric flow rates of the three fluids. Figure 8 indicates that the focused width e ₂ changes according to the magnitude and the polarity of the electric field. When no electric field is applied along the channel, the flow is simply a pressure-driven three-fluid flow where the more viscous glycerol occupies a larger portion of the channel. Without electric field, the dimensionless width e ₂ is about 0.53.

The experimental results of Fig. 8 also show that the electroosmotic effect on the pressure-driven flow becomes weaker with the increase of the flow rates of the three-fluids. At a flow rate of 0.1 ml/h, the focused width e ₂ increases from 0.4 to 0.75, if the voltage varies from −1,200 to 1,200 V. At a flow rate of 1 ml/h, this dimensionless focused width increases from 0.51 to 0.537.

Figure 9 shows the ability of manipulating the interface position by the externally applied electric field for different viscosity ratios. In these cases, $q_{1} = q_{2} = q_{3} = 0.1\;{\text{ml/h,}}$ $\beta_{1} = \beta_{3} = 1,$ and χ = 20 are used. The experimental results show that, the lower the viscosity ratio β ₂, i.e. as β ₂ = 1.46, the larger is the focused width e ₂ for the same range of applied electric fields. Comparing the experiment results of different β ₂ and the theoretical analysis, a reasonable agreement is obtained.

Fig. 9

Relationship between the focused width e ₂ and the applied voltage for different viscosity ratios ($\beta_{1} = \beta_{3} = 1,\,q_{1} = q_{2} = q_{3} = 0. 1\;{\text{ml/h}}$, and χ = 20)

Figure 10 shows the variation of the focused width e ₂ with the applied electric fields for different aspect ratios when $q_{1} = q_{2} = q_{3} = 0.1\;{\text{ml/h,}}$ and $\beta_{2} = 1.46,$ $\beta_{1} = \beta_{3} = 1.$ The results show that the rate of change with applied electric field of the focused width e ₂ is higher at lower aspect ratios. An increase of e ₂ from 0.4 to 0.75 is successfully obtained for χ = 20 The comparison of measured data and theoretical results for different aspect ratios shows that the proposed model is capable of predicting the experimental results reasonably well, the average percentage difference is about 5%.

Fig. 10

Relationship between e ₂ and the applied voltage for different aspect ratio χ when $q_{1} = q_{2} = q_{3} = 0. 1\;{\text{ml/h,}}\,\beta_{1} = \beta_{3} = 1,\,\beta_{2} = {{1.24} \mathord{\left/ {\vphantom {{1.24} {0.85}}} \right. \kern-\nulldelimiterspace} {0.85}} \approx 1.46$

5 Conclusions

This paper reports a new technique for focusing a non-conducting fluid using two conducting fluids in a microchannel by combining both pressure gradient and electroosmosis. The dimensionless width of the non-conducting liquid can be controlled using the electroosmotic effect, rather than the conventional “flow-rate-ratio” method. By applying electric fields along the microchannel, the electroosmotic effect retards or adds the flow of the non-conducting fluid, so that the dimensionless width of the non-conducting fluid can be adjusted. Quantitatively, the dimensionless width of the non-conducting fluid under pressure and electroosmotic effect is measured by fluorescence imaging technique. The electroosmotic effect under different flow rates, different viscosities of the non-conducting fluid, and different aspect ratio is investigated. The results indicate that the electroosmotic effect on the pressure-driven flow becomes weaker with the increase of the flow rates, viscosity ratio of β ₂, and the aspect ratio χ.

The comparison of the dimensionless width of non-conducting fluid between the measured data and the analytical models shows good agreement. The dimensionless widths of the three-fluid stratified flows in a rectangular microchannel can be precisely controlled using the electroosmotic effect.