1 Introduction

The miniaturization of many appliances in biomedic, chemical and computer technology has brought with it increased demands for space-efficient high-performance heat dissipation and catalytic devices. Though much research on microscale level has already been done in recent years in the relevant fields, especially as regards hydrodynamic and heat transfer characterization, there is still much diversion of results to be discerned in the various experimental and numerical reports. The diversion occurs in different contexts: fluid drag of laminar, transient and turbulent single-phase flows, heat transfer of liquid and gas flows, and two-phase flow in adiabatic and heated microchannels; each with a vast class of problems relating to fluid type, phase or compressibility, channel shape and aspect ratio, surface properties and diabatic conditions.

In the numerous experimental and theoretical investigations done over the past years, a number of contradictory conclusions have been drawn, but lately most inconsistencies seem proved to originate from the difficulty of experimental conditions and high sensitivity of models to measurement errors.

One of the first studies on microscale heat transfer was done by Wu and Little (1984), where Nitrogen flowing through rectangular channels of 134–164 μm hydraulic diameter was investigated, both in laminar as in turbulent conditions. The authors found Nusselt numbers to be higher than predicted by conventional theory, and dependent on channel roughness. A new correlation was proposed with a stronger dependence on Reynolds number.

Peng and Peterson (1996) also worked on steel rectangular channels, using water as a working fluid, and found a dependence of the Nusselt number on Reynolds and Prandtl numbers even in laminar flow. The overall magnitude was lower than theoretical predictions however.

Channels of circular cross-section were examined by (Adams et al. 1998). Though the diameters studied were on the large size of the microscale (0.76–1.09 mm) they found a distinct increase of the turbulent Nusselt number in the smaller tube of up to 2.5 times the value predicted by the Gnielinski correlation. A corrective factor taking into account channel diameter was proposed.

Kandlikar et al. (2003) also restricted themselves to larger diameters (0.62–1.03 mm), though they investigated the effect of tube wall roughness. In the laminar regime they found a net increase and a dependence of the Nusselt number on roughness at diameters smaller than 1 mm and Ra/D values larger than 0.3%.

Hetsroni et al. (2004), on the other hand, observed a sharp decrease in the fully developed Nusselt number at Reynolds numbers below 100, doing experiments on a 1.07 mm smooth tube. For Re > 400 the heat transfer number tended towards the theoretical value; this evidenced a clear effect of axial conduction along the channel wall, which is amplified at lower fluid mass fluxes.

Owhaib and Palm (2004) validated the (unmodified) Gnielinski correlation for turbulent heat transfer in smooth mini-tubes between 0.8 and 1.7 mm using R-134a. Though Reynolds numbers below 2,300 were investigated (down to Re 1,000), no comment was made on the laminar heat transfer characteristics.

The smaller diameter range was studied by (Lelea et al. 2004): 125 < d < 500 μm. Their tubes were made of steel and therefore probably characterised by a non-negligible roughness, but no values of this quantity were given. They found, in the laminar regime (50 < Re < 800), a perfectly classical behaviour of the fluid (water), with well-identified thermal entrance region and a constant value (4.36 ± 10%) of the local Nusselt number for uniformly heated walls in the fully developed section.

Finally, Grohmann (2005) performed a numerical and experimental investigation of single-phase heat transfer using liquefied Argon (T < 120 K) in constant temperature boundary conditions. The Nusselt number found was higher than dictated by conventional correlations, but was nevertheless explained to be consistent with them if the wall roughness was taken into account, which was modelled with a new roughness parameter.

As the previous survey indicates, reporting on single-phase heat transfer in microducts is divided into laminar, turbulent and geometric characteristics of the channel-fluid system. For channel diameters around and above the unit-millimetre range, behaviour seems to be acceptably ‘normal’. The influence of roughness appears frequently in the literature, and especially at low diameters it seems to increase the Nusselt number. Entrance effects will also enhance this value, which is an important phenomenon in relatively short channels. Finally, so-called conjugate heat transfer can be a major disturbing factor in thick-walled microducts, distorting the conditions of experimentation. This paper aims to address these issues, and serves as a continuation and completion of the article published on laminar single-phase heat transfer (Celata et al. 2006).

2 Theoretical background

In this chapter the theory on fluid flow behaviour in single-phase diabatic conditions, used as reference, is set out. Also, an outline will be given of two physical mechanisms typical of single-phase heat transfer in ducts, which are of particular interest in the microscale experimental conditions studied.

2.1 Correlations for single-phase heat transfer in ducts

Conventional theory regarding heat transfer in closed (circular) channels is over 100 years old, and has been found to predict fluid behaviour in diabatic conditions very well for large-scale applications. The two regimes of flow that are defined by the transitional Reynolds number (Re) have different characteristics in heat transfer conditions. For smooth tubes with fully developed laminar flow (Re < 2,300) the Nusselt number (Nu), that describes the convective heat transfer performance with respect to the heat conduction in the fluid, is constant: 3.66 in the case of constant temperature boundary conditions, 4.36 in the case of a uniformly heated wall. For transitional and turbulent flow (Re > 2,300) the description of the Nusselt number is more complex. In this study reference will be made to the Gnielinski correlation (Gnielinski 1998), which is accepted as the most accurate:

$$ Nu = \frac{{{\left( {\raise0.7ex\hbox{$f$} \!\mathord{\left/ {\vphantom {f 8}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$8$}} \right)}{\left( {Re - 1000} \right)}Pr}} {{1 + 12.7{\left( {\raise0.7ex\hbox{$f$} \!\mathord{\left/ {\vphantom {f 8}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$8$}} \right)}^{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}} {\left( {Pr^{{\raise0.5ex\hbox{$\scriptstyle 2$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}} - 1} \right)}}} $$
(1)

where:

$$ f = {\left( {1.82\log {\left( {Re} \right)} - 1.64} \right)}^{{ - 2}} $$

This equation is generally valid for both types of boundary conditions.

2.2 Thermal entrance length

The thermal entrance length is a transitory region where flow at uniform temperature develops under influence of uniformly-heated walls to a steady-state profile of temperature that is dependent on fluid velocity and conductivity. Just like it is the case for the physics of flow in the hydrodynamic entrance region, the mechanism of heat transfer is rather different in the thermal entrance length—see Fig. 1.

Fig. 1
figure 1

Thermal entrance length and developing temperature profile

Full size image

Fluid with uniform temperature enters the heated section of a pipe (in our case, the velocity profile is already fully developed at this stage), and as the heat input is absorbed, the temperature of the fluid at the wall starts to rise. Through conduction across the fluid layers of the laminar flow, the temperature profile then develops over the entire cross-section. Superposition of the convective force then creates the thermal developing length (from z = 0 to z T in Fig. 1). Whether a heated flow has reached this semi-steady thermal state (the bulk temperature will of course be increasing steadily), can be deduced from the value of the Graetz number:

$$ Gz = RePr\frac{d} {z} $$
(2)

A thermally fully developed profile is achieved when Gz < 10, so the longer the distance z along the channel axis and the less force of convection Re, the more chance there is of obtaining a thermally fully developed profile.

The effect of a thermal entrance region is to increase the Nusselt number compared to that of the thermally fully developed region—see also (Shah and London 1978). The generalized Hausen correlation describes the mean Nusselt number as the sum of two terms: a fully developed value of the Nusselt number, and a term taking into account the effects of the thermal entrance region:

$$ < Nu > = Nu_{\infty } + K_{1} \frac{{Gz}} {{{\left( {1 + K_{2} Gz^{b} } \right)}}} $$
(3)

Here the Graetz number is taken over the entire length of channel, and in the case of constant wall heat flux and fully developed velocity profile, for circular ducts: K 1 = 0.023, K 2 = 0.0012 and b = 1 (Rohsenow and Choi 1961).

2.3 Axial conduction in the walls

For low values of the Reynolds number, the mean value of the Nusselt number quickly coincides with the fully developed value, because the entrance region is very short and (microscale) effects of viscous heating are not important in this regime of flow. On the contrary, at low Reynolds numbers the effects of conjugate heat transfer on the mean value of the Nusselt number may become very important because conduction along the channel walls becomes a competitive mechanism of heat transfer with respect to internal convection. (Maranzana et al. 2004) evidenced through numerical simulation that when the effects of conjugate heat transfer are predominant, the temperature distribution along the microchannel is not linear at all, but convex, even if the heat input is uniformly distributed. If nevertheless one were to assume the temperature profile as linear, this would result in an underestimation of the mean value of the bulk temperature along the microchannel, \( \ifmmode\expandafter\bar\else\expandafter\=\fi{T}_{f} \), leading to an underestimation of the mean heat transfer coefficient:

$$ < h > = \frac{{q\prime\prime}} {{{\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{T}_{{\text{w}}} - \ifmmode\expandafter\bar\else\expandafter\=\fi{T}_{{\text{f}}} } \right)}}} $$
(4)

This could also be an explanation for the dependence of the Nusselt number on the Reynolds number which is found in many experiments, as this effect of underestimation will become less as the convective term of heat transfer (∼Re) increases with respect to the conductive term in the channel wall. The temperature distribution along the tube axis will then approach a linear tendency (although the effects of thermal development would increase, see Eq. 1).

Chiou (1980) defined a parameter of axial conduction in the walls in the (conjugated) heat transfer problem, converted to a criterion by Maranzana (op. cit.) and used by (Morini 2005). For a circular tube it calculates as:

$$ {\left( {\frac{{k_{{\text{w}}} }} {{k_{{\text{f}}} }}} \right)}{\left( {\frac{{D^{2} - d^{2} }} {{dL}}} \right)}\frac{1} {{RePr}} > 10^{{ - 2}} . $$
(5)

The dimensionless quantity at the l.h.s. of Eq 4, the M number, allows the comparison of heat transfer by axial conduction in the wall with the convective heat transfer in the flow.

3 Experimental procedure

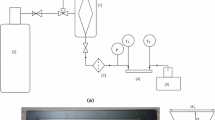
The test rig used for the experiments is schematised in Fig. 2.

Fig. 2
figure 2

Schematic of the experimental set-up

Full size image

The working fluid is demineralised water, which is degassed by passing through a very small, but continuous quantity of Helium. Being insoluble in water, an atmosphere of only Helium is created above the liquid level, so that all dissolved gases are driven out by their respective partial pressures in the water. A gear pump (Ismatec MCP-Z, for low pressure requirements, larger diameters) or a piston pump (Gilson 305, for large pressure drop, smaller diameters) is used to drive the flow, which passes through a 10 μm filter and is controlled with a microvalve regulator, before entering the test section.

The microtube under investigation is mounted inside a stainless steel capsule which is vacated by a turbo-molecular vacuum pump (Alcatel ATS-100) to create an environment free of natural convection. To this effect, the level of vacuum must be less than 10−3 mbar. The level obtained in our set-up is 2 × 10−4 mbar (Edwards Penning Gauge Model 6), so that we can consider the heat loss to the surroundings through convection inexistent.

The heat loss due to radiation is evaluated by considering the formula for two concentric cylindrical surfaces, simplified for the limiting case where the surface of the internal body (OD of the test section is 0.9 mm) is much smaller than the external, concave surface (ID of the vacuum chamber is 100 mm):

$$ q'_{{{\text{rad}}}} L = \sigma A_{{\text{i}}} \varepsilon _{{\text{i}}} {\left( {T_{{\text{i}}} ^{4} - T_{{\text{e}}} ^{4} } \right)}. $$
(6)

The entity of this loss is of the order of 0.01% in the case of the highest measured temperature difference between the two bodies, and thus considered negligible.

The only heat loss term of any importance would then be conduction through connecting wires, leads and tubing. The entity of this loss is difficultly quantifiable, inasmuch as it depends on the mass, conductivity and temperature of the various materials in contact with the test section. It will be seen that this disturbance is more important than expected.

A 250 μm K-type thermocouple measures the fluid temperature on entrance into the test section, and pressure transducers on either side of the microtube investigated allow the pressure drop over the channel to be established (Druck PTX100/IS, 0–35 bar; Transamerica 0–160 bar); also a differential manometer is mounted parallel to the transducers for extra precise differential pressure measurements.

A constant power DC supply is used to heat the test section, which is fitted with Gas Chromatography fittings (Upchurch Scientific) resistant to high temperature and pressure.

At the outlet of the channel, a 50 μm K-Type thermocouple is made to be inserted inside the (Near-Zero) dead volume of the fitting so that the fluid exit temperature (a critical quantity) is measured as closely as possible. The mass flow rate is measured with a high precision scale.

3.1 Tubes tested

Two types of capillaries were taken under consideration in this study: glass and stainless steel (see e.g. Fig.  3a, b). The glass tubes of varying inner diameter were manufactured in-house, and coated with a uniform, 100 nm layer of Chromium–Molybdenum (through sputtering technology) to materialise 35 mm of heating length. The outer diameter of the glass capillaries is practically constant (∼0.9 mm).

Fig. 3
figure 3

SEM images of a glass capillary, 259 μm ID (left) and a stainless steel capillary, 280 μm ID (right)

Full size image

The inner and outer diameters were measured by super-imposing a best-fitting circle over the respective circumferences in the SEM image. An overview of all the parameters of the tested tubes is given in Table 1.

Table 1 Experimental parameters
Full size table

As can be seen from Fig.  3 a, b, the internal roughness of the steel capillary is considerably larger than for the glass tube, which can be considered practically smooth (Ra < 0.01 μm). The value of this roughness is estimated by mapping a section of a transversely cut capillary with an electronic profilometer (ZYGO NewView 5000).

3.2 Calculation of the heat transfer coefficient

To determine the local heat transfer coefficient, it is necessary to know the inner wall temperature at that location, but as it is impossible to measure this value directly without altering the conditions of flow, due to the geometry, size and material of the channels, the outer wall temperature is measured instead. This is achieved by attaching 50 μm K-type thermocouple wires to the outer wall with cyanacrylic adhesive at first and subsequently fixing them with a non-conductive epoxy resin (see Fig. 4). This ensures in addition to a quick and reliable response, that there is no electrical conductance to disturb the temperature measurement.

Fig. 4
figure 4

Fitted test section with thermocouples attached to outer wall

Full size image

The local heat transfer coefficient, expressed in terms of measurable quantities only, is as follows:

$$ h(z) = {\left[ {\frac{{\pi dL_{{{\text{ht}}}} {\left( {T_{{\text{w}}} {\left( z \right)} - T_{{\text{f}}} {\left( z \right)}} \right)}}} {{\Gamma c_{{\text{p}}} \Delta T_{{\text{f}}} }} - \Lambda } \right]}^{{ - 1}} $$
(7)

with T w (z) the outer wall temperature at the thermocouple axial position z, as mentioned.

The heat flux is evaluated from the enthalpy rise of the fluid (Γc p ΔT f). For the determination of the local fluid temperature T f (z) a linear temperature rise is assumed along the heated length of tube.

In Eq. 6, represents the radial temperature distribution linked to the conduction across the tube wall. This term varies according to the method of heat input: in the case of heat input through the thin-film deposit on the outer surface of the glass tubes, it is as in Eq. 8:

$$ \Lambda = \frac{d} {{2k_{{\text{w}}} }}\ln {\left( {\frac{D} {d}} \right)} $$
(8)

In the case of the stainless steel tubes, the entire wall thickness is heated through Joule-effect, and the conductive term becomes (Isachenko et al. 1974):

$$ \Lambda = \frac{{D^{2} d}} {{16{\left( {D^{2} - d^{2} } \right)}k_{{\text{w}}} }}{\left[ {2\ln {\left( {\frac{D} {d}} \right)} + {\left( {\frac{d} {D}} \right)}^{2} - 1} \right]} $$
(9)

4 Results and discussion

First the laminar behaviour will be discussed. The results will be presented in the form of local Nusselt number vs. Reynolds number graphs for each channel diameter class, comparing the smooth glass tubes with the rough steel ones (Figs. 5, 6, 7). The local values are obtained at three axial positions (see Table 2). The reference value of the Nusselt number for thermally fully developed laminar flow (Nu = 4.36) is always given as a reference.

Fig. 5
figure 5

Glass versus stainless steel tubes (∼1/2 mm)—Local Nusselt versus Reynolds numbers at three axial locations

Full size image
Fig. 6
figure 6

Glass versus stainless steel tubes (∼1/4 mm)—Local Nusselt versus Reynolds numbers at three axial locations

Full size image
Fig. 7
figure 7

Glass versus stainless steel tubes (∼1/8 mm)—Local Nusselt versus Reynolds numbers at three axial locations

Full size image
Table 2 Test section characteristics, positioning of the three thermocouples
Full size table

For a closer evaluation of the turbulent regime, the experimental Nusselt number normalized with the Gnielinski correlation Nusselt number is plotted for the three stainless steel tubes. To conclude, an overview plot of global Nusselt versus global Reynolds numbers is presented for all diameters, with a reference correlation included for comparison (Eq. 2).

The error bars in the figures are the result of the uncertainty analysis that is given at the end of this chapter.

4.1 Laminar flow

To begin with the largest class of diameter (∼1/2 mm), the results depicted in Fig. 5 are clearly indicative of thermally developing flow. There is a considerable axial dependence of the heat transfer coefficient, especially for the glass tube, with higher Nusselt numbers nearer to the channel inlet. In fact, as is known from classical theory, the less thermal development, the stronger the drive for heat exchange [the factor is quantified in Shah and London (1978) as an incremental heat transfer number]. As we can see from the table of experimental conditions, at 528 μm ID (due to the relatively short length of heated tube) the flow is nearly always in thermal development (Gz > 10). Therefore only nearest to the exit and at low Reynolds numbers do we approach the thermally developed state corresponding to the constant value for the Nusselt number, 4.36.

It is interesting to note that the local temperature measurements at z 35 diameters—corresponding for both the glass (smooth) and the stainless steel (rough) pipe—show a behaviour of the Nusselt number which is practically identical, confirming the lack of influence of increased roughness in the latter type of tube. For the two axial locations on the steel microtube further downstream (z = 134d and z = 200d), the development effects can be seen to have disappeared, as the Nusselt numbers are overlaying for all Reynolds numbers, and tending to the fully developed value, as is also the case for the glass tube (with a slight undershoot though).

The advent of turbulence and its increased heat transfer efficiency can be individuated where the curves turn sharply upwards at Re 2,300.

In Fig 6, the experimental data of the ∼1/4 mm ID tubes can be seen. We notice with respect to the larger diameter duct a decrease of the local Nusselt numbers for the smooth glass tube, whereas the steel channel manifests comparable behaviour. The thermocouple closest to the inlet of the latter channel yields distinctly higher heat transfer values because of its extreme proximity to the start of the heated section (z = 16d), and therefore in full stage of thermal development. The other two axial locations indicate coherence with the fully developed Nusselt number for Re < 700. In fact, the corresponding global Graetz number drops below 10 here (see Sect. 2.2). For the glass channels the axial dependence is reduced (more fully developed heat transfer due to the relatively larger heated length) but especially the considerable decrease of the Nusselt numbers—below the fully developed value in laminar regime—catches the eye.

The trend that was already observed for the glass pipes is continued for the 120 μm tube as regards the lowering of the local Nusselt numbers and the decrease in axial dependence (Fig. 7). In fact, at this diameter the heated length is relatively much larger so that the flow reaches thermal development well inside the test section and no more axial dependence is expected. We can see from Table 1 that the Graetz number is still mainly above 10, but compared to the larger tubes the order of magnitude is distinctly lower.

There is still a distinct dependence on Reynolds number present, however. This could be due—at this small proportion of inner to outer diameter—to an incipience of the phenomenon of conduction along the walls and in the other materials attached to the test section. At very small diameters, the mass flow of fluid becomes itself extremely reduced compared to the mass of connected auxiliaries. Thus, to bring the entire system to a stable temperature means to distribute excessively the little heat convected by the fluid so that large losses and long settling times are the consequence. In fact, if we look at the criterion given for the heat conductance number (Eq. 4), we find that the values of this number for all experiments carried out here (see Table 1) are well below the limit suggested for the occurrence of significant axial conduction. This fact seems to point therefore rather at disturbances (heat sinks) that lie outside the system boundary of the channel strictly, like, e.g. thermocouples, fittings and connected tubing.

At higher Reynolds numbers, where the advected heat by the fluid could be larger, the limit on the outer wall temperature (set at 100°C) allowed a heating of the fluid—in the case of the glass microtubes—which was only of a couple of degrees, thereby augmenting the relative error of the temperature rise measurement. Again the cumbersome heat resistance in the vitreous material, and contributes significantly to the experimental error also at high Reynolds numbers.

This conclusion is fortified by observing the behaviour of the stainless steel tube of similar inner diameter, but smaller outer diameter (and therefore thinner wall). This channel maintains the general level of Nusselt numbers as was observed for the larger tubes of the same material: with an improving heat transfer at high (laminar) Reynolds numbers, but, importantly, tending to the fully developed value at lower Re, without dropping below. Evidently, the heat put in electrically is absorbed more efficiently by the water flow, both because of the thinner wall with better conductivity, as because of the fact that the entire wall thickness is heated as opposed to a thin layer deposited on the tube outer surface. Therefore, it is not so much a question of increased axial conduction in the thick glass wall that distorts the heat transfer coefficient measurements, but rather a question of inhibited radial conduction, causing the heat put in to disperse more easily to peripheral mass. The outer wall temperature measurements are true in both cases, but the generated heat that causes these temperatures is underestimated in the case of the thick-walled glass tubes because of the deficient enthalpic temperature rise of the water. This translates in lower Nusselt numbers, and this effect is stronger as the convective force (∼Re) of the fluid diminishes, increasing the relative contribution of the conductive losses to peripheral mass.

Let us try to describe the situation mathematically.

In Fig. 8 the hypothetical temperature profiles of a typical experiment are sketched, assuming there is a significant amount of the heat applied at the wall that is not absorbed by the fluid. Thus, the temperature profile of the wall (T wall) is given—assuming for now that the wall is uniform—and the temperature of the fluid is divided into the actual measured value (T f_meas) and the ideal value it would acquire if no dispersion took place (T f_ideal).

Fig. 8
figure 8

Schematic of the axial temperature profiles in a heat transfer test where significant peripheral heat dispersion takes place (e.g. in a thick-walled glass capillary)

Full size image

Now, the heat transfer equations are derived from (7):

$$ \left\{ \begin{aligned}{} & q_{{{\text{ideal}}}} = \Gamma c_{{\text{p}}} \Delta T_{{{\text{f\_ideal}}}} = h_{{{\text{ideal}}}} {\left( {T_{{{\text{wall}}}} - T_{{{\text{f\_ideal}}}} } \right)}A_{{{\text{ht}}}} \\ & q_{{{\text{meas}}}} = \Gamma c_{{\text{p}}} \Delta T_{{{\text{f\_meas}}}} = h_{{{\text{meas}}}} {\left( {T_{{{\text{wall}}}} - T_{{{\text{f\_meas}}}} } \right)}A_{{{\text{ht}}}} \\ \end{aligned} \right. $$
(10)

We want to find out what the effect on the measured heat transfer coefficient is (compared to the ideal value) of an underestimation of the exit bulk fluid temperature, as depicted in Fig 8.

Let us define an underestimation factor a on the ideal fluid temperature rise (0 < a < 1). Thus, T f_meas = a T f_ideal. Also, let us scale all temperatures with the fluid inlet temperature (which equates to stating T f_in = 0) since we are only interested in a qualitative analysis of the temperature differences between the wall and the fluid. This means that at each point z TC along the microtube—since the assumed profile is linear between inlet and outlet—the measured fluid temperature is underestimated by the same factor: T f_meas  = aT f_ideal.

Inserting these corrections in the second of equations (10):

$$ h_{{{\text{meas}}}} = \frac{{\Gamma c_{{\text{p}}} a\Delta T_{{{\text{f\_ideal}}}} }} {{A_{{{\text{ht}}}} {\left( {T_{{{\text{wall}}}} - aT_{{{\text{f\_ideal}}}} } \right)}}} $$
(11)

The effect on the heat transfer coefficient is strengthened therefore: if a is reduced (or: a larger error is made on the fluid temperature rise) the numerator decreases and the denominator increases. The underestimation of the heat transfer coefficient is therefore even larger.

This translates in lower Nusselt numbers, and the effect is stronger as the convective force (∼Re) of the fluid diminishes, because the relative contribution of conductive losses to peripheral mass will increase (in the example above, this would correspond to a smaller value of a).

A similar effect was also found recently in rectangular channels by Bavière et al. (2006).

4.2 Turbulent flow

Taking a closer look at the turbulent regime, we wish to confront the experimental data with the tried-and-tested Gnielinski correlation, Eq. 1. As was mentioned in the Introduction, this correlation has been validated for tubes down to 1 mm in diameter: the objective is to verify whether this validity holds for the genuine microscale. The influence of roughness, if any, should be to increase heat transfer performance with respect to smooth tubes in the same conditions. Therefore, the turbulence experiments were carried out first on the rough, stainless steel tubes, assuming—in the case of adherence to the unmodified Gnielinski correlation—that for smooth tubes the same behaviour would hold. The results of the experimental evaluation of the Nusselt numbers for the three sizes of tubes are normalized with the Nusselt numbers obtained with the Gnielinski correlation and presented in Fig. 9.

Fig. 9
figure 9

Ratio of experimental to Gnielinski Nusselt number versus Reynolds number—stainless steel tubes

Full size image

As can be seen, convergence with the Gnielinski correlation occurs for Re > 3,000; unstable transition effects scatter experimental data in the immediate post-laminar regime, but close adherence to conventional turbulent heat transfer behaviour is rapidly achieved:

  • for the 440 μm tube 90% of the data above Re = 3,000 lie within ±13% of the corresponding Gnielinski values,

  • for the 280 μm tube 90% of the data above Re = 3,300 lie within ±13% of the corresponding Gnielinski values,

  • for the 146 μm tube 90% of the data above Re = 3,000 lie within ±14% of the corresponding Gnielinski values.

It is to be expected that agreement is maintained at higher Reynolds numbers (a regime which is difficult to test because of the extremely high pressure drops involved), as also in the case of using perfectly smooth tubes.

4.3 Uncertainty analysis

The variable of interest in our study is the heat transfer coefficient h, as described by Eq. 7. In order to evaluate the influence of experimental parameters on this quantity, it is convenient to perform an uncertainty analysis. The analysis will give an indication as to the degree of reliability of the value of the heat transfer coefficient found, as well as shed light on the weight of the different parameters in the (im)precision of measurement. This can be useful for clarifying the difference of the wall influence hypothesised in the discussion of the laminar results.

Following classic methodology set out in, e.g. (Holman 1978), one arrives at a definition of the relative experimental error as a function of the uncertainty on each of the measured quantities. (Due to the intricate composition of the equation that results, it is not reported here.)

Taking two representative experiments, one for the 120 μm ID glass tube and one for the 146 μm ID stainless steel tube (see Table 3), we can arrive at a comparison of the errors.

Table 3 Comparison of a glass and a stainless steel microtube in similar diabatic conditions
Full size table

The total experimental error in the last column consists of the relative weights of each of the parameters in Eq. 7. If, for the working point under consideration, we plot these weights (the sum of which will always be 100, which corresponds to the total experimental error e h/h) as a function of the variance in, e.g. the wall conductivity k w, we can get an idea of the contribution of each variable to the total experimental uncertainty.

In Fig. 10 this is done for the glass tube in experimental conditions as in Table 3. If we compare this plot with the graph for the stainless steel tube in similar conditions (Fig. 11), we notice a clear difference. Observe the graphs at the respective working values of the conductivity parameter k w (1.18 for glass, 16.3 for stainless steel). First of all, it can be noted how the weight of k w to the total experimental error is higher in the case of the glass tube (35% compared to 0.6%). Furthermore, around the working value, the sensitivity of the total error is much lower for the stainless steel tube (practically stable distribution of the variables’ weights). This goes to strengthen the hypothesis that the manifest difference in diabatic behaviour between the two types of tubes (in laminar flow) is tied to the wall thermal resistance rather than, e.g. the roughness.

Fig. 10
figure 10

Weight of each variable in Eq. 7 on total relative experimental error e h/h—glass tube in experimental conditions of Table 3

Full size image
Fig. 11
figure 11

Weight of each variable in Eq. 7 on total relative experimental error e h/h—stainless steel tube in experimental conditions of Table 3

Full size image

5 Conclusions

Experiments were carried out on two types of microtubes, respectively made of smooth glass and rough stainless steel. The comparable diameters varied from ∼1/2 mm down to ∼1/8 mm. Both laminar and turbulent regimes were studied.

In turbulent flow, the experimental Nusselt number showed no appreciable difference to the corresponding values obtained from the classical Gnielinski correlation for all diameters.

In laminar flow, the stainless steel tubes evidenced fairly classical behaviour in that the local Nusselt numbers approached the fully developed constant for uniformly heated tubes as the Reynolds number decreased. For higher Reynolds numbers and positions closer to the inlet of the heated section, the region of thermal development increases in importance, augmenting heat transfer (and therefore Nusselt number). The dependence of Nusselt on Reynolds number is especially explained by this phenomenon.

For the smooth glass tubes, the anomalous overall decrease in Nusselt number well below the fully developed constant, for diminishing Reynolds number, is most probably due to the dispersion of the heat generated in the outer surface thin film through peripheral attachments rather than through conduction across the thick, poorly conducting wall to the fluid interface. (The steel tubes were heated over the entire wall thickness.) This means that the outer wall temperature measurements do not correspond exactly to the fluid temperature rise in the channel. An underestimation of the Nusselt number is the result, amplified as the convective force of the fluid is diminished (increasing the relative dispersion of heat through peripheral attachments like wires and thermocouples). It is expected that for thin-walled smooth (glass) tubes where this distorting effect can be avoided, heat transfer behaviour should be similar to the behaviour in the rough steel tubes, though no quantitative affirmation to this effect can be made with the presented data.