Introduction

Ultrasound imaging can be employed to characterize soft tissues. It can be repeatedly applied owing to the high level of safety and low cost [1,2,3,4,5]. Therefore, it is very useful in the diagnosis of various diseases, including cardiovascular diseases [6].

Linear and sector array probes are often used in ultrasound imaging. In conventional in vivo ultrasound imaging methods, the sound velocity in a tissue is typically assumed to be constant in the delay-and-sum beam-forming (in many cases, it is assumed to be 1540 m/s) [7]. However, when the sound velocity of a tissue is inhomogeneous in a clinical condition, the spatial resolution of a conventional beamformer deteriorates [8,9,10]. This issue is particularly conspicuous in the diagnosis of obese patients [11, 12], as the average sound velocity of fat (1450 m/s) is different from that of other soft tissues (1540 m/s). This problem is also present in the diagnosis of breast diseases [13, 14].

Determination of the sound velocity distribution in a tissue not only improves the image quality but can also be used for discrimination between normal and abnormal tissues for a diagnosis of various diseases. For example, the sound velocity of the normal liver decreases when the liver contains fat [15, 16]. Therefore, it is possible to diagnose fatty liver by estimating the sound velocity distribution.

Many studies have been performed to correct the time delay caused by tissue inhomogeneity. The cross-correlation technique is one of the most common methods for phase aberration correction [17, 18]. This method is highly accurate in the correction of the time delay caused by inhomogeneity [19]; however, it is susceptible to noise and its computational load is high [12, 20]. In addition, studies have been performed to estimate the optimal sound velocity for beam-forming to improve image quality. Methods have been developed to estimate the optimal sound velocity for imaging from the focusing quality [12, 21, 22]. The crossed beam method [23] has also been proposed as a method for estimating the local sound velocity in the living body. However, it is necessary to know the sound velocity between the ultrasonic probe and the region of interest (ROI) when estimating the local sound velocity. There is a large variation in the estimated sound velocity.

In this study, a new method was developed to estimate the sound velocity distribution from the time delay values in the radio-frequency (RF) signals received at 96 elements of an ultrasonic probe. This method utilizes the curvature set of the time delay, which depends on the average sound velocity distribution along the propagation path, yielding an estimated sound velocity distribution in the tissue. The performance of the proposed method was evaluated through experiments.

Methods

Estimation of sound velocity using time delay

The sound velocity distribution is estimated from the time delay set of the RF signals received at multiple elements of an ultrasonic probe, as follows. Let us assume that there are N (n = 1, 2,…, N) regions with different sound velocities {cn} in the beam direction. \( R_{n} \) is defined as the sound-velocity-estimation region where the depth is \( l_{n} \); cn in Rn is assumed to be constant.

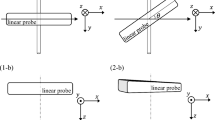
An array probe transmits an ultrasound beam with an incidence angle of \( \theta_{1} \) to a scatterer in the shallowest region R1, as shown in Fig. 1, where \( r_{1} \) is the distance from the central element to the strong target, and \( \theta_{1} \) is the direction angle of the target with respect to the central element (\( x_{k} = 0 \)). First, for the RF signal received at the central element, the arrival time of the echo returning from the strong target is determined. Second, the time delay of the echo at each element, with respect to the arrival time of the echo at the central element, is obtained using the cross-correlation function. The time delay \( T(x_{k} ) \) at the \( k \)th element is

$$ T_{1} (x_{k} ) = \frac{1}{{c_{1} }}\left\{ {r_{1} + \sqrt {x_{k}^{2} - 2r_{1} \sin \theta_{1} \times x_{k} + r_{1}^{2} } } \right\} ,\quad \left( { - K \Delta x \le x_{k} \le K \Delta x} \right), $$
(1)

where \( \Delta x \) is the element pitch, \( x_{k} =k \Delta x \) is the lateral position of the \( k \)th element, and \( \left( {2K + 1} \right) \) is the number of receiving elements \( \left( {k = - K, \ldots ,K} \right) \). As the forward path from the central element to the target coincides with its backward path (from the target to the central element), i.e., \( T_{1} \left( 0 \right) = 2r_{1} /c_{1} \), the time delay \( T_{{{\text{R}}_{1} }} (x_{k} ) \) at the \( k \)th element with respect to the central element is

$$ \begin{aligned} T_{{{\text{R}}_{1}}} \left( {x_{k} } \right) & = T\left( {x_{k} } \right) - \frac{T\left( 0 \right)}{2} \\ & = \frac{1}{c}\sqrt {x_{k}^{2} - 2r_{1} \sin \theta_{1} \times x_{k} + r_{1}^{2} } . \\ \end{aligned} $$
(2)
Fig. 1
figure 1

Schematic of the system setup with an ultrasonic probe and target scatterer

Full size image

Similarly, the time delay \( T_{{R_{n} }} \left( {x_{k} } \right) \) from the scatterer in the nth region is

$$ T_{{{\text{R}}_{n} }} \left( {x_{k} } \right) = \left( {\mathop \sum \limits_{i = 1}^{n - 1} \frac{{l_{i} }}{{c_{i} }} + \frac{{r_{n} \cos \theta_{n} - \mathop \sum \nolimits_{i = 1}^{n - 1} l_{i} }}{{{\text{c}}_{n} }} } \right) \times \frac{1}{{r_{n} \cos \theta_{n} }}\sqrt {x_{k}^{2} - 2r_{n} \sin \theta_{n} \times x_{k} + r_{n}^{2} } , $$
(3)

where {\( r_{n} \)} and {\( \theta_{n} \)} are the distance and beam angle from the central element to the target point in the region {Rn}, respectively. Here, the influence of refraction when the signal is incident on regions with different sound velocities is ignored. In addition, the influence of the heterogeneous sound velocity distribution in the lateral direction is also ignored. For example, in the liver, there is uniform sound velocity in the lateral direction in almost every case. It is also possible to suppress the influence by confirming and discriminating the inhomogeneity region using the ultrasound B-mode image. The square of Eq. (3) becomes a quadratic function \( f_{n} \left( {x_{k} } \right) \)

$$ \begin{aligned} f_{n} \left( {x_{k} } \right) & = T_{{{\text{R}}_{n} }}^{2} \left( {x_{k} } \right) \\ & = \left( {\mathop \sum \limits_{i = 1}^{n - 1} \frac{{l_{i} }}{{c_{i} }} + \frac{{r_{n} \cos \theta_{n} - \mathop \sum \nolimits_{i = 1}^{n - 1} l_{i} }}{{{\text{c}}_{n} }} } \right)^{2} \times \frac{1}{{r_{n}^{2} \cos^{2} \theta_{n} }}\left( {x_{k}^{2} - 2r_{n} \sin \theta_{n} \times x_{k} + r_{n}^{2} } \right) \\ & = a_{2} x_{k}^{2} + a_{1} x_{k} + a_{0} . \\ \end{aligned} $$
(4)

The coefficients \( a_{2} , a_{1} , \) and \( a_{0} \) are determined by fitting \( T_{{{\text{R}}_{n} }}^{2} \left( {x_{k} } \right) \) measured for the scatterer in each region to the quadratic function of Eq. (4) using the weighted least square method; {cn}, {rn}, and {θn} can be obtained using a2, a1, and a0.

This estimation process is applied to selected strong targets in each ROI. The propagation times in Eq. (4) include information not only about the sound velocity in the nth region but also about those up to the (n − 1)th region. Therefore, the sound velocities from the first to the nth region can be simultaneously estimated by fitting the propagation times from the scatterers in regions one to n to their propagation-time theoretical equations. The amplitude of the received signal is large at the element above the target, and decreases with the increase of the distance from the element, owing to the different distance and direction from the scatterer to each element of the ultrasonic probe. A weighting function determined by the amplitude of the received signal at each element was applied to the above fitting. Therefore, it is possible to estimate the sound velocity distribution along the beam direction, as shown in Fig. 2.

Fig. 2
figure 2

Measurement grids aligned vertically in an ROI to estimate the sound velocity distribution

Full size image

Beam-forming of the received signal using the estimated sound velocity

The delay time calculated using the velocity distributions obtained in “Estimation of sound velocity using time delay” is added to the received signal at each element. The received beams are then compounded. When the amplitude A(P) of the RF signal is estimated by forming the received beam at the point of interest P, the delay time to be applied to the received signal at each element is calculated as follows. Assuming that a linear probe is used, the ultrasonic wave is transmitted vertically to the probe surface, and the center of the transmitted beam (x = 0) is set as the origin in the direction parallel to the probe surface. The point of interest P is located at a distance r from the center of the ultrasonic probe, in the sound-velocity-estimation region \( {\text{R}}_{n} \); the local sound velocity estimated in that region is denoted as \( c_{n} \).

Figure 3 shows a schematic of the ultrasonic propagation path. The propagation time \( t_{k} \left( {\text{P}} \right) \) of the ultrasonic wave transmitted at x = 0, scattered at the point P, and received at the element k with a lateral position \( x_{k} \) is calculated as follows. The length in the region Rn of the forward path from the central element to the point P is \( r - \sum\nolimits_{i = 1}^{n - 1} {l_{i} } \), while that of the return path from the point P to the element k is \( \left( {r - \mathop \sum \nolimits_{i = 1}^{n - 1} l_{i} } \right)\sqrt {r^{2} + x_{k}^{2} } /r \).

Fig. 3
figure 3

Schematic of the ultrasonic propagation path

Full size image

In the sound-velocity-estimation regions \( {\text{R}}_{1} \) to \( {\text{R}}_{n - 1} \), the lengths of the forward path are \( \left\{ {l_{i} } \right\} \), while those of the return path are \( \left( {l_{i} /r} \right)\sqrt {r^{2} + x_{k}^{2} } \). The ultrasonic propagation time in each region can be obtained by dividing the propagation path by the local sound velocity of the region. \( t_{k} \left( {\text{P}} \right) \) can be obtained by adding up the round-trip propagation times from the probe surface to the region \( {\text{R}}_{n} \):

$$ \begin{aligned} t_{k} (P) & = \sum\limits_{i = 1}^{n - 1} {\frac{1}{{c_{i} }}} \left( {l_{i} + \frac{{l_{i} }}{r}\sqrt {r^{2} + x_{k}^{2} } } \right) + \frac{1}{{c_{n} }}\left\{ {\left( {r - \sum\limits_{i = 1}^{n - 1} {l_{i} } } \right) + \frac{{r - \sum\nolimits_{i = 1}^{n - 1} {l_{i} } }}{r}\sqrt {r^{2} + x_{k}^{2} } } \right\} \\ & = \left( {\sum\limits_{i = 1}^{n - 1} {\frac{{l_{i} }}{{c_{i} }}} + \frac{{r - \sum\nolimits_{i = 1}^{n - 1} {l_{i} } }}{{c_{n} }}} \right)\left( {1 + \frac{{\sqrt {r^{2} + x_{k}^{2} } }}{r}} \right). \\ \end{aligned} $$
(5)

If the sound velocities are equal in all regions, i.e., \( c_{i} = c_{0} \), Eq. (5) corresponds to Eq. (1) with \( \left\{ {\theta_{n} } \right\} = 0 \). Assuming the ultrasound is transmitted at \( t = 0 \), and the received RF signal at the element \( k \) is \( g_{k} \left( t \right) \), the amplitude corresponding to the point P of the RF signal after the formation of the reception beam is \( g_{k} \{{t_k({\text{P}})}\} \). By adding them for all elements of the probe, the reception beam RF signal can be formed. Therefore, A(P) can be expressed as

$$ A\left( {\text{P}} \right) = \mathop \sum \limits_{k = - K}^{K} g_{k} \left\{ {t_{k} \left( {\text{P}} \right)} \right\}. $$
(6)

Results and discussion

We demonstrated the usefulness of the proposed method through a basic experiment using a phantom including strong targets. Figure 4 shows the experimental system. An ultrasonic diagnostic unit (ProSound α10, Aloka) with a linear probe (UST-5412), whose center frequency is 10 MHz, was used with a transmission frequency of 7.5 MHz. The probe contained 192 elements, with a pitch of 0.2 mm. A total of 96 elements around the center were used to transmit and receive signals. The sampling frequency to obtain the RF signal in each element was 40 MHz. The temperature of the water was 16 °C, and the sound velocity was 1469 m/s in the water [24]. The sound velocity was 1540 m/s in the silicone phantom.

Fig. 4
figure 4

Experimental setup of the phantom experiment and B-mode image

Full size image

Two molybdenum wires with a diameter of 50 µm were installed in the water. Two nylon wires with a diameter of 100 µm were embedded in the silicone phantom to serve as target points. Four estimation regions were provided; the lengths l1, l2, l3, and l4 in the depth direction of the grid were 16.0, 17.0, 10.0, and 10.0 mm, respectively. The region size was assumed to be judged from the B-mode image for the target organ. Therefore, the length of each region was selected as above. As a linear probe was used in this experiment, the beam angles {θn}, introduced above, were assumed to be \( 0^\circ \). Four focused beams with different focus points set at the targets were transmitted. The measurements were repeated eight times.

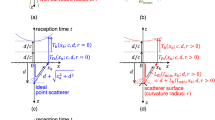
The delay-time distributions from the target at each region and parabolic approximations are shown with blue dots and red curves in Fig. 5, respectively. The maximum differences of the propagation times from the target in the deep region are smaller than those in the shallow region. The propagation times could not be obtained as a smooth curve for a part of the results from the target in the deep region.

Fig. 5
figure 5

Delay-time distributions from the target at each region (blue dots) and parabolic approximations (red curves)

Full size image

The estimated sound velocity and distance to the target in each region are compared with the true values in Fig. 6. Table 1 summarizes the local sound velocity in each region, its estimation error, and standard deviation. Table 2 shows the depth to the target. The estimated local sound velocity in each region was close to the true value. The estimated sound velocities of healthy persons and patients with hepatic steatosis were significantly different by about 10–40 m/s in the liver [25]. Therefore, we aimed for an accuracy of ± 10 m/s in sound velocity estimation by this proposed method. The error of 10 m/s did not significantly affect the resolution of the received beam. The standard deviations in the deeper region were larger than those in the shallower region, owing to the following three possible factors. The first factor is attributed to the maximum difference in propagation times, which is small in the deep region, as shown in Fig. 5, leading to a worse estimation accuracy. The second factor is attributed to the decreases in the amplitudes of the reflected signals and resultant reductions in the signal-to-noise ratio owing to the large attenuation along the large propagation distance from the deep region. The third factor is attributed to the parabolic approximation in the deep region, which is performed using the local sound velocities obtained in the shallow region; a slight difference from the true value in the shallow region would affect the sound velocity estimation in the deeper region.

Fig. 6
figure 6

Estimation results of the sound velocity distribution

Full size image
Table 1 Estimated local sound velocities in each region, estimation errors, and standard deviations in the phantom experiment
Full size table
Table 2 Estimated depths in the phantom experiment
Full size table

Furthermore, the received beam was formed using the estimated sound velocities. Figure 7 shows the lateral profile of the received beam composed of the signals from the wires in the third region. A sharp peak was obtained, and the peak amplitude was improved by 3.1 dB and 1.3 dB, compared with the profiles beam-formed with the assumed sound velocities of 1540 m/s (widely used in ultrasonic diagnostic units) and 1469.0 m/s (sound velocity in water), respectively. The nominal sound velocity of the silicone phantom (CIRS 054 GS) from the product information was treated as the true value. The full-width-at-half-maximum of the amplitude was also improved to 0.61 mm, from 0.92 mm with 1540.0 m/s and 0.76 mm with 1469.0 m/s. Regarding the imaging, tomograms obtained with the assumed velocities of 1540 m/s and 1469.0 m/s, and those with the estimated velocities, are shown in Fig. 8. Figure 9 shows the envelope amplitude of the beam direction formed using the assumed and estimated sound velocities. The results showed that the peak was slightly sharp in beam-forming using the estimated sound velocities. From these results, we confirmed improvements in the resolution in both the lateral and beam directions on the received beam using the sound velocities estimated by the proposed method. The blurring of the wire image became smaller using the estimated sound velocity, and the improvement in the image quality of the tomogram was confirmed by the proposed method.

Fig. 7
figure 7

Lateral beam profiles obtained using the a assumed sound velocity of 1540 m/s, b assumed sound velocity of 1469.0 m/s (sound velocity in water), and c estimated sound velocity

Full size image
Fig. 8
figure 8

Images obtained by the conventional method with velocities of a 1540 m/s and b 1496.0 m/s, and c estimated sound velocity

Full size image
Fig. 9
figure 9

In the beam direction, beam profiles obtained using the a assumed sound velocity of 1540 m/s, b assumed sound velocity of 1469.0 m/s (sound velocity in water), and c estimated sound velocity

Full size image

In the conventional method, the average sound velocity from the ultrasonic probe to the ROI is estimated to obtain a high-resolution ultrasonic tomographic image in the ROI. On the other hand, the proposed method estimates the sound velocity in each region along the beam direction from the probe. As a result, it is possible to realize a high-resolution ultrasonic tomographic image in the entire region by beam-forming of the received signal. For example, if the sound velocity distribution inside the organ is obtained, it is possible to estimate the local fat content and others, and early detection of the lesion can be expected.

In the phantom experiment, the sound velocities estimated by the proposed method were close to the true values as well as those estimated by the conventional method. In addition, since the procedure of this method is composed of only (1) calculation of the cross-correlation function between the elements of the received signals and (2) parabolic approximation by the least squares method, the computational effort is very small. On the other hand, in the conventional method, for example, the method [12, 21, 22] for estimating the optimum sound velocity using the focusing quality requires more computational cost because the focusing quality has to be calculated for the beam-formed data while changing the sound velocity from 1400 m/s to 1600 m/s in steps of 5 m/s.

Conclusions

We proposed a method to estimate the sound velocity and depth of a target in a ROI using the time delays of the signals received by each element of the array probe. In the phantom experiment, the local sound velocity in each region could be estimated, which was close to the true value. The usefulness of the proposed method was confirmed by improvement in the blurring of the wire image. In this study, a stationary phantom and wires were used as objects in the experiment. Clutter suppression [26] would be necessary in in vivo application and should be studied in the future. In future studies, we aim to investigate estimation methods using the plane boundary such as artery and estimate the sound speed using reflection from strong scatterers present in living bodies. There are high-intensity scatterers such as microvessels in the B-mode image of the liver [27]. We confirmed the propagation time distribution from a strong target in the liver by measuring with the same experimental setting in the present study. In the future, estimation of the sound velocity distribution in the liver by this method will be examined. After confirming the usefulness of this method in the liver, we plan to expand the application to the other organs including the breast.