Introduction

Long runout rock avalanches are large masses of rock debris, i.e. more than one million cubic metres that move rapidly down a mountain slope, sweeping everything in their path. Their stabilization is almost impossible and the only way to prevent fatalities and damages is to define areas that could be affected by their occurrence. For this reason, it is necessary to understand and model the propagation mechanisms involved in these destructive phenomena, which are still for most part unknown.

Several theories have been proposed to explain rock avalanche great mobility, but even if some of the mechanisms proposed could play an important role for some specific cases, it is difficult to decide which the most significant one is and how it controls the dynamics of the flow (Hungr 1990). Davies et al. (1999) identified two processes in the propagation of a rock mass, i.e. translation, mainly guided by basal friction, and deformation, affected by internal friction, and they classified the different theories proposed in literature according to whether or not they involve one of these processes. According to this distinction, theories are separated here between:

  1. 1)

    the ones considering mainly the translation process, implying a reduction of the friction at the base that could be due to different causes such as: a cushion of trapped air (Shreve 1968); the change from sliding to intermittent collisions caused by mechanical fluidization (Heim 1932; Scheiddeger 1973; Davies 1982; Campbell 1989); the layer of fine particles that fluidizes the coarser ones (Hsü 1975); the heat generated from friction between stationary and moved material (Erismann 1979); the liquefaction of the water saturated base (Heim 1882, supported afterwards by Abele 1974, 1994; Sassa 1988; Hungr 1990, 2002; Voight and Sousa 1994; Legros 2002, 2006);

  2. 2)

    the ones considering mainly the deformation process, implying a reduction of the friction within the mass that could be due to different causes such as: the entrapped and compressed air (Kent 1966); the steam generated by vaporization of ground water (Goguel 1978); volcanic gases (Voight et al. 1983); high-frequency acoustic vibrations due to the rapid shear of the granular material (Melosh 1979);

  3. 3)

    theories that imply other mechanisms such as an acceleration of the front blocks caused by the increase in the frequency of collisions (Okura et al. 2000a, b) or the transfer of momentum between the rear and the front parts of the mass flowing (Van Gassen and Cruden 1989 and also earlier Heim 1932); the simple spreading of a coherent mass, where its centre travels with a normal sliding friction law (Davies and McSaveney 1999); a decrease of the deceleration of the front part caused by an isotropic dispersive stress throughout the moving mass produced by fragmentation (Davies et al. 1999, 2010; Davies and McSaveney 2009).

Most of these theories have been translated into empirical, analytical and numerical formulations to try to improve the modelling of rock avalanche propagation.

As described in Manzella and Labiouse (2009, 2010) several authors have resorted to laboratory tests to validate their models or to have a data set for developing empirical formulations and to understand the behaviour of granular flows and the important parameters in their propagation.

Davies (1982) and Davies and McSaveney (1999, 2003) carried out tests that consisted in unconstrained dry granular flows of 0.1–1000 l of sand on a plane inclined at 35° or 45°. To carry out the analysis and to compare results to data coming from real events they defined some non-dimensional variables: the normalised longitudinal extent of the deposit R h/h*, where R h is the deposit length and h* is the cubic root of the volume; the normalised vertical fall height (h v/h*), where h v is the height of the centre of mass before release and represents as well the initial potential energy of the mass. R h/h* is called normalised runout by Davies and McSaveney (1999) although it is a measure of the longitudinal spreading of the final deposit. This is in contrast to the common use of the term in literature, where runout is usually defined as the total travel distance of the mass from the head scarp till the distal end of the final deposit. Anyway, their way of representing the results came out to be very effective to compare and analyse experimental and field data because normalising extension values with the volume of the considered events (experimental or real), scales them with respect to their size, bringing them to a common comparable framework.

An extensive experimental study of dry unconstrained granular and small brick flows has been carried out at the rock mechanics laboratory of the Ecole Polytechnique Fédérale de Lausanne (EPFL, Switzerland) to better understand mechanisms involved in rock avalanches and to improve the state of the art in assessing their propagation by means of analysis of the tests and comparison with existing theories and real cases. This research is the object of two PhD theses at the EPFL (Manzella 2008 and Sauthier in progress).

The experimental set-up and part of the results have already been presented in details in Manzella and Labiouse (2008a, 2009, 2010). This article focuses on the empirical analysis of the results based on the aforementioned non-dimensional factors used by Davies and McSaveney (1999) and on the comparison with an analytical sled block model.

Experiments

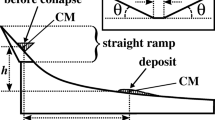
Experiments consist in releasing a dry mass of gravel or small bricks on a slope ending with a horizontal accumulation area. As shown in Fig. 1 and described in details in Manzella and Labiouse (2009, 2010), several factors were changed such as material, i.e. gravel (Gr2) and bricks (Br), volume (V), fall height (h), slope angle (37.5° and 45°), disposition of the bricks before release, i.e. piled orderly one on top of the other (BrP) or randomly poured into the released container (BrR), and panel covering, i.e. a wood and a plastic sheet (i.e. forex) were used to have different basal friction. In Table 1 the characteristics of the materials used and the corresponding friction angles are summarized. The height of the centre of mass before release (h v, as defined by Davies and McSaveney 1999) has not been the object here of a systematic study but has been considered as one of the factors since it changes along with the fall height and it will be used in the following to analyse the data.

Fig. 1
figure 1

Factors varied (written in grey); measurements and measuring tools (written in black): a set-up longitudinal and horizontal sections, b change in the slope break

Full size image
Table 1 Granular material characteristics: size, unit weight, static and dynamic friction angles of gravel, random and piled bricks (from Manzella and Labiouse 2009)
Full size table

According to the results of Manzella and Labiouse (2009), some series of tests have been carried out to verify whether the sharp discontinuity at the toe of the slope could have an influence on propagation introducing a slightly curved slope break. For the 45° slope, the sharp angular slope break between the two panels has been replaced by a smooth curve as shown in Fig. 1b. The radius of the arc is of approximately 0.5 m.

In Table 2 all tests considered in the present article are listed with the corresponding characteristics.

Table 2 Test series considered in the present article
Full size table

As shown in Fig. 1, for each test, the deposit length (R h) has been measured manually, the distance travelled by the mass front (mass front runout) and the apparent angle of friction (ϕap) have been then calculated; the apparent angle of friction, i.e. the angle of reach as defined by Corominas (1996), represents the slope of the straight line connecting the head scarp with the distal end of the final deposit. The mass front velocity has been obtained by high-speed film analysis, and an optical technique, called fringe projection method, has been used to recover the height information, the morphology and the position of the centre of mass of the final deposit. This allows computing the travel angle of the centre of mass (ϕCM) which gives an idea of the dissipated energy along the flow, i.e. the higher the travel angle, the higher is the energy dissipation. The fringe projection method consists in projecting alternate lines of dark and light (fringes) on the deposit surface. When fringes are projected on a planar surface, they are straight and equally spaced, whereas on an uneven surface they are distorted and this distortion is related to the thickness of the object. This information is contained in the object optical print (phase map) which can be computed using different algorithms based on the intensity of the image pixel. The obtained phase is directly proportional to the height of the object by a factor which has been computed as the ratio of the maximum height of the deposit and the maximum value of the phase. For further information on the fringe projection method and on how it has been applied to the present tests, see Desmangles (2003), Manzella (2008) and Manzella and Labiouse (2008b).

Analysis of the results

Dimensional considerations

For the dimensional analysis of small-scale granular flows, two important works have been carried out. The one of Denlinger and Iverson (Iverson and Denlinger 2001; Denlinger and Iverson 2001; Iverson et al. 2004) and the one of Massey (1983) as reported by Davies and McSaveney (1999).

Among them Denlinger and Iverson arrived at the conclusions that large geophysical flows, where fluid effects are significant, can exhibit dynamics not evident at laboratory scale (especially miniature ones), where additionally there could be the presence of electrostatic phenomena which can bedevil results. On the other hand, if fluid effects are negligible, which is one of the hypotheses at the base of the present study, the model is simplified and the dynamics of “ideal granular avalanches” (sensu Iverson and Denlinger 2001) can be reproduced at small scale since it is controlled only by the geometry of the path and by the internal and the basal friction coefficients (Iverson and Denlinger 2001). Nonetheless the scale must be large enough to satisfy the continuum assumption and to minimize the effects of microscopic forces.

Davies and McSaveney (1999) report more or less the same conclusions. They affirm that granular avalanches at small scale can realistically reproduce the major features of large-scale rock avalanches with the exception of some phenomena like rock fragmentation, the ground shaking due to the impact of the avalanche at the foot of the fall slope or the presence of a saturated substrate.

Drake (1991) comes also to similar conclusions regarding flow scale and limitations imposed by material properties. He affirms that the use of smaller particles satisfies the continuum hypothesis that suggests that particle diameter must be at least one tenth of the flow depth, but he states as well that it increases the effects due to air drag and electrostaticity which strongly influence collisional properties, inducing a behaviour which differs from large scale events. In the present case, particles are large enough to avoid air drag and electrostatic effects. For what concerns the continuum hypothesis, it should be satisfied both for gravel and bricks. As a matter of fact, in tests with 40 l of piled bricks, 9,680 elements of 0.8 × 3.1 × 1.5 cm are disposed in 22 elements height × 11 elements width × 40 elements length in the reservoir of 20 cm height × 40 cm width × 65 cm length with the longest dimension of the bricks (3.1 cm) perpendicular to the dip slope direction, whereas the larger surface (1.5 × 3.1 cm) is positioned parallel to the slope plane. With this initial disposition, the flow depth is in the order of ten elements height, i.e. around 8 cm, so the continuum hypothesis should be satisfied. Therefore it can be said that, when the phenomena mentioned by Davies and McSaveney (1999) and reported above are negligible, present experiments can contribute in understanding propagation mechanisms and factors of influence of large scale granular avalanches.

Empirical analysis of the results

As aforementioned the formulation of Davies and McSaveney (1999) resulted to be effective and as a consequence test results are represented taking inspiration from it, i.e. as shown in Figs. 2 and 3, the results are represented comparing the apparent friction angle (ϕap), the travel angle of the centre of mass (ϕCM), the normalised length (R h/h*) and the normalised total runout of the front mass (mass front runout/h*), in relation with the normalised vertical fall height of the centre of mass (h v/h*).

Fig. 2
figure 2

Plots of the normalised vertical fall height of the centre of mass (h v/h*) against ϕ ap, ϕ CM, normalised deposit length (R h/h*) and normalised mass front runout for series A1–A2 with gravel, on forex, 45° slope, sharp slope break: 20 l, 1 m fall height (light grey empty square); 40 l, 1 m fall height (black filled square); 20 l, 1.5 m fall height (light grey empty triangle); 40 l, 1.5 m fall height (black filled triangle)

Full size image
Fig. 3
figure 3

Plots of h v/h* against ϕ ap, ϕ CM, R h/h* and mass front runout/h*. a Gravel, 45° slope, sharp slope break, on: wood (Gr2 wood, series B1–B2) and forex (Gr2 forex, series A1–A2). b 45° slope, sharp slope break, on forex with: gravel (Gr2, series A1–A2), random bricks (BrR, series D1–D2), piled bricks (BrP, series E1–E2). c Gravel, on forex with different slope and slope break: 45° sharp (Gr2 45°, series A1–A2); 37.5° sharp (Gr2 37.5°, series C1–C2); curved (Gr2 curve, series F1–F2)

Full size image

In Fig. 2, results of tests with gravel on forex, 45° slope, with a sharp slope break at the toe (series A1–A2 in Table 2) are presented to highlight the influence of volume and fall height. These tests are used in the following as a reference to better understand the influence of each factor considered.

Figure 3 gives a general overview of the results through a series of plots disposed in three rows and four columns: i.e. looking at the plots along a row, it is possible to see the influence of a single factor specified in the legend in the first plot of the row, e.g. the use of wood or forex as basal surface, on all the parameters, i.e. ϕap, ϕCM, R h/h* and mass front runout/h*; looking at the plots along each column allows comparing the effects of all the different factors varied, i.e. basal surface, material used and slope break variation, on a single parameter specified at the bottom, e.g. ϕap. In Fig. 3a, results of experiments with gravel on wood and on forex with a sharp slope break and a 45° slope are presented (series A1–A2 and B1–B2 in Table 2). In Fig. 3b, results of experiments with the different types of material on forex with a sharp slope break and a 45° slope are presented (series A1–A2, D1–D2 and E1–E2 in Table 2). In Fig. 3c, results of experiments with gravel on forex for different slope angles and for a curved slope break are presented (series A1–A2, C1–C2 and F1–F2 in Table 2).

Lateral cross sections of the final deposits, the front mass runouts and the initial conditions of some representative tests are shown in Figs. 4, 5, 6 and 7 to better highlight the influence of the different factors changed, i.e. respectively fall height and volume, basal friction, material used and disposition of the bricks, slope and slope break.

Fig. 4
figure 4

Mass front runout and longitudinal section of tests of series A1–A2 with gravel, on forex, 45° slope, sharp slope break: a 20 l, 1 m fall height; b 40 l, 1 m fall height; c 20 l, 1.5 m fall height; d 40 l, 1.5 m fall height; the material at start is represented schematically as a dark grey rectangle at the top of the slope

Full size image
Fig. 5
figure 5

Mass front runout and longitudinal section of tests with 40 l, gravel, 1 m fall height on a 45° slope and sharp slope break on: a wood (series B1); b forex (series A1); the material at start is represented schematically as a dark grey rectangle at the top of the slope

Full size image
Fig. 6
figure 6

Mass front runout and longitudinal section of tests with 40 l, 1 m fall height on forex, 45° slope and sharp slope break with: a gravel (series A1); b random bricks (series D1); c piled bricks (series E1); the pictures in the rectangle at the top of the slope represent schematically the material used in the tests and how it is disposed in the container

Full size image
Fig. 7
figure 7

Mass front runout and longitudinal section of tests with 40 l, gravel, 1 m fall height, on forex and different slope and slope break: a 45°, curved (series F1); b 45°, sharp (series A1); c 37.5°, sharp (series C1); the material at start is represented schematically as a dark grey rectangle at the top of the slope

Full size image

In the case analysed in Fig. 2, it is possible to notice that ϕap, ϕCM and R h do not vary significantly when the height varies. Observing the plot of the mass front runout/h*, it is interesting to notice that normalising the value by h*, the scaled value of the mass front runout for 20 l is bigger than the one of 40 l even if the absolute value is actually smaller, respectively 1.73 and 1.84 m for 1 m fall height, 2.38 and 2.56 m for 1.5 m fall height (as can be seen in Fig. 4). This occurs because the increase in the front propagation is lower compared to the increase of the cubic root of the volume, inducing a general decrease of the normalised mass front runout. If experiments with 20 and 40 l are considered separately, the normalised mass front runout increases when the height increases.

In Fig. 3a, it is possible to observe how the basal friction angle influences the parameters studied. A higher friction angle (set-up covered by a wood panel, see Table 1) induces a general decrease in the mobility of the flow, i.e. higher apparent angles of friction and higher energy dissipation along the flow, i.e. higher travel angles of the centre of mass. The normalised length of the deposit diminishes compared with experiments with lower friction angle but it remains constant with the normalised height. The mass front runout/h* also diminishes, but a similar behaviour is observed, i.e. trendlines with similar slope.

In Fig. 3b, it is possible to observe how the use of different materials influences the parameters studied. When gravel (Gr2) and random bricks (BrR) are used, values of apparent friction angle, travel angle of the centre of mass and of the normalised mass front runout almost overlap. On the other hand, values of R h/h* are higher with random bricks; as shown in Fig. 6a, b, this is not due to a higher longitudinal spreading towards the front but in the rear part of the deposit, where few bricks pile up on the slope. Things are different when a more structured material at start is used: the use of piled bricks induces a higher mobility, i.e. lower apparent friction angles; a lower dissipation of energy along the slope, i.e. lower travel angles of the centre of mass; a higher longitudinal spreading, i.e. higher R h/h*, and higher normalised mass front runout. In this case, the higher values of R h/h* are due to a higher spreading towards the front as can be seen in Fig. 6. It has to be said here that even if the volume is equal to 40 l for all these tests, the mass varies significantly because of the difference in density in the random bricks and in the piled bricks configurations (see the different bulk unit weights in Table 1). For this reason, a higher number of bricks are used for the latter case and this could have also an effect on propagation. On the other hand, the factor considered here as important to measure the size of an event is the volume and not the mass, in agreement with most studies of rock avalanche propagation.

In Fig. 3c, it is possible to observe how a gentler slope and a curved slope break influence the parameters studied. As a matter of fact using a lower slope angle and a curved slope break, the topography of the pathway becomes smoother and smoother and more and more regular. This leads to a higher mobility, i.e. lower apparent friction angles, and a lower dissipation of energy along the pathway, i.e. lower travel angles of the centre of mass and higher normalised mass front runout. Also in the case of a curved slope break between the panels the relationship between the normalised mass front runout and the normalised fall height is clearly linear, but the slope of the three trendlines changes putting into evidence an influence of the topography on the mass propagation. This is probably related with the changes in the total initial potential energy, i.e. changes in fall height, and the different amount of energy required overcoming the different type of slope break.

Values of R h/h* for experiments with 45° and 37.5° slope and a sharp slope break overlap and are equal to around 2.5. Even if the longitudinal spreading is similar, the mass travels in total a longer distance on the 37.5° slope than on the 45° slope, as it can be observed in Fig. 7, showing a higher mobility. As pointed out in Manzella and Labiouse (2009) for tests carried out with different slope angles but a sharp slope break, “ϕCM would be predicted as constant if a simple frictional model is assumed for the energy dissipation (i.e. straight energy line model). Instead, ϕCM decreases (40° → 35°) when the slope angle decreases (45° → 37.5°).” A possible explanation could be that when the slope is gentler, there is lower energy dissipation when the mass flows on the smoother transition between the slope and the horizontal accumulation zone, suggesting that the energy line depends also on the set-up geometry. As a confirmation to that, when a curved slope break is used the mass shows an even higher mobility (ϕCM of around 32°–33°) and a longer longitudinal spreading (R h/h* around 3.2). Observing Fig. 8, it is possible to observe more in details how the change from a sharp into a curved slope break leads to longer runout of the front and of the centre of mass and to a higher mass front velocity on the horizontal panel.

Fig. 8
figure 8

Tests with 40 l, gravel, 1 m fall height, on forex and different slope break: curved (series F1, curve, black) versus sharp angular (series A1, sharp, grey). Horizontal (a) and longitudinal (b) deposit cross sections; front mass velocity on the horizontal panel (c)

Full size image

If Fig. 3 is read along a column of plots, the effect of all the factors considered on each parameter is highlighted. In this way, it is possible to see how the apparent friction angle, the travel angle of the centre of mass and the normalised longitudinal spreading are independent from the normalised fall height. On the other hand, a rather linear dependency is observed between the normalised front runout and the normalised fall height. It can be said though that the use of a more structured material before release, i.e. BrP, is the factor inducing a larger effect on the longitudinal spreading of the mass, i.e. higher values of R h/h*. A smoother slope break is the factor which induces the higher mobility of both the front and the centre of the mass, i.e. the lowest values of both the apparent friction angle and the travel angle of the centre of mass, and the highest values of the normalised front runout. The combined influence of both factors, i.e. structure of the material before release and type of slope break, is presented in the following section.

Influence of the structure of the material before release and of the type of slope break

Comparing series E1 and G1 of Table 2 (see Fig. 9), both performed with 40 l of piled bricks respectively with a sharp and a curved transition between the panels, it is possible to study the combined effect of the structure of the material before release and of the type of slope break. In the case of a curved slope break, the morphology of the mass is evidently more elongated and the mass, its front and its centre, but not its rear, travel much further than in the case of a sharp discontinuity. In Fig. 10, it is possible to observe how when the mass flows on a curved slope break, it still travels a certain distance on the horizontal panel with a limited lateral spreading and with a structure still kept at a certain degree. This reveals that, as the transition has been smoothed, the initial block arrangement is more preserved than in other tests with piled bricks. Tests of this series show also an even longer propagation and a higher mobility of both the front and the centre of the mass than all the other tests, i.e. the apparent friction angle is in average 23° and the travel angle of the centre of mass 28°. In addition several piles of bricks, which kept the initial structure, have been detected in the final deposit (see Fig. 11), which confirms that the shattering of the mass is less important with a curved slope break.

Fig. 9
figure 9

Tests with piled bricks, 40 l, 1 m fall height, 45° slope, on forex with: sharp slope break (series E1, grey) versus curved slope break (series G1, black). Longitudinal (a) and horizontal (b) deposit cross sections; the noise on the right boarder of the section is caused by the fact that the projector used for the fringe projection cannot cover more than 2 m length

Full size image
Fig. 10
figure 10

Images taken each 1/6 s of test with piled bricks, 40 l, 1 m fall height, 45° slope, on forex with: a sharp slope break (series E1); b curved slope break (series G1); c overlap of the mass contours at the different instants, grey line for the test with a sharp slope break and black line for the one with a curved one. The rectangle in light grey in b and c underlines the curved part, the dashed line in c indicates the sharp slope break

Full size image
Fig. 11
figure 11

Evidence of the initial structure in the final deposit of a test of 40 l of piled bricks with a curved slope break

Full size image

Lumped mass model and centripetal acceleration

The sled block model represents the first attempt to describe the rock avalanche propagation (Heim 1932). This is a rather simplistic representation of a rock avalanche but it is often recalled in literature and it constitutes the base of most existing models. According to Hungr et al. 2005, the flowing material is considered as a dimensionless point of mass M, the centre of mass, sliding along a path inclined of β, characterised by a constant Coulomb friction angle ϕ. The equations of motion can be derived from the work energy theorem, i.e. the change in kinetic energy of the block equals the work of the net force acting on the block. The simplest frictional model considers the net force as the difference between the gravity driving force and the frictional resistance and leads to the following equation for the acceleration of the centre of mass along the path:

$$ a = g \cdot \left( {\sin \beta - \tan \varphi \cdot \cos \beta } \right) $$
(1)

Where a is the acceleration of the centre of mass in the direction of the flow (Lagrangian system), g the acceleration of gravity, β the slope angle and ϕ the dynamic friction angle.

According to McDougall and Hungr (2004), a mass flowing on an irregular 3D terrain experiences centripetal acceleration due to the curvature of the path. In the case of present experiments with a curved slope break this acceleration could play an important role and should then be considered in the calculation of the net force. As a consequence, an attempt is made here to verify whether it is possible to reproduce the propagation of some tests carried out with a curved slope break (series F1–F2 of Table 2) with a sled block model which takes into account the centripetal acceleration. In this case, the Eq. 1 becomes:

$$ a = g \cdot (\sin \beta - \tan \phi \cdot \cos \beta - \frac{{{v^2} \cdot \tan \phi }}{{r \cdot g}}) $$
(2)

Where a and v are respectively the acceleration and the velocity of the centre of mass in the direction of the flow (Lagrangian system) and r is the radius of curvature.

The term accounting for the centripetal effect goes against the flow, i.e. as this term increases, the acceleration decreases, as do the velocity and the propagation. The acceleration a goes as −1/r, meaning that the smoother is the curvature, the larger is the radius r, the smaller the term is and the less this effect influences the acceleration of the block.

For the simulations of the experiments, only the longitudinal cross section has been considered. To simulate the 2D geometry of the experimental set-up, the path has been divided in three zones as shown in Fig. 12: the inclined slope at 45° before the curve, the curved part and the horizontal accumulation part. In the first and last parts, the centrifugal forces are equal to zero (r is infinite) and the equations of motion are derived from Eq. 1. For the curved part the calculations have been divided in steps of Δt and the slope has been updated of β − δ(t) for each time step, where δ(t) is the angle covered by the centre of mass along the curvature at time t (see Fig.12). The centre of mass is considered as being the centre of the rectangle representing schematically the mass at start in the releasing container. To simplify the calculation, the velocity v in Eq. 2 of the term counting the centripetal effect has been considered for each time step as the velocity v(t) of the previous integration step, leading to the following equations of motion:

$$ \begin{array}{*{20}{c}} {a\left( {t + \Delta t} \right) = g \cdot (\sin \left( {\beta - \delta (t)} \right) - \tan \phi \cdot \cos \left( {\beta - \delta (t)} \right) - \frac{{v{{(t)}^2} \cdot \tan \phi }}{{r \cdot g}})} \hfill \\ {v\left( {t + \Delta t} \right) = \left[ {g \cdot (\sin \left( {\beta - \delta (t)} \right) - \tan \phi \cdot \cos \left( {\beta - \delta (t)} \right) - \frac{{v{{(t)}^2} \cdot \tan \phi }}{{r \cdot g}})} \right] \cdot \Delta t + v(t)} \hfill \\ {s\left( {t + \Delta t} \right) = \left[ {\frac{g}{2} \cdot (\sin \left( {\beta - \delta (t)} \right) - \tan \phi \cdot \cos \left( {\beta - \delta (t)} \right) - \frac{{v{{(t)}^2} \cdot \tan \phi }}{{r \cdot g}})} \right] \cdot \Delta {t^2} + v(t) \cdot \Delta t + s(t)} \hfill \\ \end{array} $$
(3)

Where s is the displacement of the centre of mass in the direction of the flow (Lagrangian system) as shown in Fig. 12.

Fig. 12
figure 12

Simulation parameters of the topography with the curved slope break, r is the radius and s the displacement of the centre of mass in the direction of the flow (Lagrangian system)

Full size image

Tests with a curved slope break of series F1, F2 have been back analysed using the Eq. 3. Results of the computations and of the tests are listed in Table 3 and shown in Fig. 13. The average measured values on all the tests of the same series are reported. As for the computations, the dynamic friction angle ϕ at the base has been varied till the location of the centre of mass predicted by the sled block model matches the final deposit one measured in the tests, i.e. X CM in Fig.13. A similar value of the back-analysed dynamic friction angle, equal to ∼24.5°, has been obtained for the four tests considered. It is rather close to the ∼23.5° measured in laboratory tilting tests (see Table 1).

Table 3 Test conditions, measured and computed data (with and without taking into account centripetal acceleration)
Full size table
Fig. 13
figure 13

Longitudinal sections, measured and back-analysed data of tests with gravel on forex with a curved slope break (series F1, F2) with: a 40 l, from 1 m fall height; b 40 l, from 1.5 m fall height; c 20 l, from 1 m fall height; d 20 l, from 1.5 m fall height. The energy line given by the measured travel angle of the centre of mass ϕ CM is indicated by a dashed black line, the energy line accounting for the centripetal acceleration is indicated by a filled grey line; the path of the centre of mass in the case of the block model is indicated with a black dashed-dot line; experiment cross sections are of one test for each series considered

Full size image

The difference between the travel angle of the centre of mass measured in the experiments ϕ CM (∼33.5°) and the back-analysed value of the dynamic friction angle at the base ϕ C≠0 (∼24.5°) results from the increase of energy loss by friction in the curved transition due to the centripetal acceleration, as clearly pointed out in Fig. 13. Neglecting this term in the analysis, i.e. using Eq. 1 instead of Eq. 2, would have led to much higher values of the back-analysed dynamic friction angle, ϕ C=0 around 32°. This emphasises the importance of considering the centripetal forces in the propagation of masses on an irregular topography.

The difference of about 2° between ϕ CM and ϕ C=0 back analysed without centripetal acceleration comes from the small difference in height Δh CM of around 9 cm between the centre of mass of the model and the one of the experimental deposit (Fig. 13). This difference in height is related to the fact that the mass cannot deform in the idealized sled block model, thus the height of the centre of mass is constant all along the path as shown in Fig. 13 (dashed-dot line indicating the path followed by the block).

Discussion

Rock avalanches are very rapid flow characterised by long runout. Mechanisms and factors inducing this high mobility are not yet completely understood and for this reason, starting from the pioneer work of Heim (1932), researches in this field are continuously carried out. In particular, granular flow experiments have been largely used to better investigate mechanisms and characteristics of this phenomenon.

As aforementioned, Davies and McSaveney (1999) carried out unconstrained dry granular flow tests on a 45° slope and using the normalised R h/h* they could compare their results with real events. In particular they chose two events that can be considered as unconstrained flow on an average 45° slope in order to have similar characteristics to the ones of the tests they carried. The two events, i.e. the Elm (Switzerland, 1881) and Frank (Canada, 1903) rock avalanches, involved respectively a 10 million and a 37 million cubic metres volume. R h/h* values of the tests and of data from these two rock avalanches differed significantly and as a consequence they considered that “between volumes of about 105 m3 and 107 m3 the mechanism of deposit emplacement changes significantly from that seen in the laboratory” (Davies and McSaveney 1999). Finally they suggested that this difference could be caused by some conditions that cannot be reproduced at laboratory scale such as rock fragmentation or the presence of saturated sub-strata and the spreading of a coherent mass.

Although, as also stated by Friedmann et al. (2006), it is generally not possible to obtain long runout in laboratory granular flow tests, some of the present experiments gave particularly long longitudinal spreading, i.e. as shown in Fig. 14 high values of R h/h* are observed, ranging between 5.1 and 5.6, which are comparable to the data of the Elm and Frank rock avalanches. These experiments (marked by a star in Fig. 14) were carried out with piled bricks and a curved slope break putting into evidence the strong influence on the propagation of granular flows of these two factors combined together, namely the initial block arrangement and the regularity of the pathway.

Fig. 14
figure 14

Normalised (R h/h*) plotted against normalised vertical fall height (h v/h*) of: the experiments by Davies and McSaveney (1999) (empty hexagons) and Manzella (2008) (filled spheres, squares, ellipsoids and stars) and of two real events Elm (filled rhomb) and Frank (filled triangle) as reported by Davies and McSaveney (1999)

Full size image

The importance of the topography of the slope on runout has been already pointed out by Heim (1932), i.e. the dynamics of rock avalanches is governed by topographic features of their paths (Pudasaini and Hutter 2007). Friedmann et al. (2006) carried out experiments with a smooth transition at the slope break and they also concluded that this type of slope transition enhances the runout since less energy dissipation takes place at the toe of the slope and confirmed the importance of the changes in the flow geometry in the propagation. However, since the material used was sand, the initial block arrangement was obviously not considered. As a matter of fact, only few previous records (Okura et al. 2000a, b; Yang et al. 2011) have been found in literature where tests have been carried out with blocks instead of sand in the study of rock avalanche propagation; this is almost certainly due to the practical difficulty of performing these experiments. Nonetheless, small bricks represent better the dimensions of the blocks relative to small topographic irregularities in real events and they allow taking into account also the arrangement of the blocks before failure. Therefore they contributed to analyse phenomena which cannot be observed for gravel or sand flow at laboratory scale and consequently they could improve the understanding of the mechanisms involved in propagation.

Drake (1990, 1991), studying the behaviour of plastic spheres of 6 mm diameter down a narrow channel, could identify two main regimes in the flow:

  • Frictional regime: where momentum transfer is predominantly affected by persistent frictional interactions. This regime is characterized by a quasi-static zone just over the bed and an overlying block-gliding zone, in which coherent blocks of grains move parallel to the bed.

  • Collisional regime: where momentum transfer is predominantly affected by collisions. In this regime, three zones are observed: a lower grain-layer-gliding zone, in which grains slide one over another; a middle chaotic zone, in which grain motions are highly random; an overlying zone, even more chaotic in which grains trace long curved paths.

In present experiments, piled brick flows are characterized by a predominance of the frictional regime during the flow on the inclined board, where energy is consequently mainly dissipated through friction at the base. Only after the impact with the horizontal panel, when the slope break is sharp, the mass shatters inducing an increase in importance of the collisional regime. When the slope break is curved, the frictional regime remains important also on the horizontal panel since the impact and the shattering are limited due to the smoother transition. Energy dissipation is then reduced compared to experiments with a more irregular topography causing longer propagation and higher mobility of the mass. This behaviour gives credit to the theory of Davies (1982) and Davies and McSaveney (1999) of the spreading of a coherent mass, i.e. the long runouts are due to the shattering and spreading of the initially structured block masses. Finally, several columns of piled bricks, which underwent shear at the base, but preserved their initial structure, have been observed in the final deposit of experiments with a curved slope break (see Fig. 11). This evidence confirms the fact that in this case collisions within the mass between the bricks are limited and that the frictional regime is predominant also during the accumulation process. This is also relevant because the preservation of the stratigraphic order has been often identified as a characteristic of rock avalanche deposits where the mass, even if disintegrated into fragments, shows a surprising congruence of the sequential order it had before failure (Erismann 1979).

According to what suggested by McDougall and Hungr (2004), a sled block model taking into account centripetal acceleration has been used to back analyse the experiments with a curved slope break. Results highlight the fact that in the case of a simple geometry, such as the one of the present experiments, this model improves the estimation of the longitudinal propagation of the centre of mass compared to a lumped mass model where the centripetal acceleration is not considered. As a matter of fact the term related to the centripetal effect allows taking into account at some extent the influence of the topography of the pathway, i.e. the smoother is a slope break, the higher is its radius, the lower is the centripetal term and the lesser is the energy dissipated by friction at the base. On the other hand, even if small, a difference still exists between the values of the measured and back-analysed friction angles at the base and between the heights of the centres of mass of the final deposit. This demonstrates that additional energy dissipation phenomena take place along the flow. As highlighted by the empirical analysis of the present experiments, these phenomena are related to the internal deformation of the mass and its associated energy dissipation (Mcdougall 2006) through friction and collisions between particles.

In conclusion, the numerical modelling of the propagation of granular masses along an irregular path with a sled block model that takes into account the role of centripetal acceleration can be useful to back analyse the dynamic basal friction angle of past events and to make a rough estimation of the propagation of the centre of mass of potential ones. However, since the mass is treated as a lumped mass and only the 1D propagation of the centre of mass is considered, no lateral and longitudinal spreading is taken into account, thus this model cannot be used to estimate the mass front runout which has a major importance in a hazard assessment perspective in the field of rock avalanches.

Conclusions

The present article focuses on the empirical analysis of dry unconstrained gravel and block experiments to investigate rock avalanche propagation. Factors such as volume, fall height, basal friction angle, material used, structure of the material before release and type of slope break are considered and their influence on apparent friction angle, travel angle of the centre of mass, normalised deposit length and normalised front runout is analysed.

Results highlight that the granular mass shows a higher mobility of the distal end and of the centre of mass when the basal friction angle decreases, when the material is structured before release and when the slope break is smoother, i.e. lower slope angle or curved slope break. In general, when the other experimental conditions are kept identical, the normalised longitudinal spreading of the mass is independent from the normalised vertical fall height, whereas the normalised front runout is linearly dependent from this factor.

Interesting information about possible mechanisms of propagation and deposition comes out from the observation of the experiments with an initial structured block arrangement and with a difference in the topography regularity: when the mass is structured at the beginning and the slope break is curved instead of sharp, less shearing (friction) and collisions are developed within the sliding mass as it changes its flow direction. A certain coherence of the mass is preserved along the path and the regime seems to remain mainly frictional also during the accumulation process, as a consequence less energy is dissipated within the mass and the mobility of the granular flow is higher.

Finally back analyses with a sled-block model of experiments with a curved slope break contributed in putting into evidence the important role of centripetal acceleration in determining the propagation of the centre of mass of a granular flow on an irregular path. On the other hand, this kind of model does not take into account the spreading of the mass and the energy dissipation within the mass, which, as underlined by the experiments, are crucial phenomena in the assessment of the total runout of rock avalanches.