Wave Propagation in Graphene Platelet-Reinforced Piezoelectric Sandwich Composite Nanoplates with Nonlocal Strain Gradient Effects

Abstract

This research develops an analytical approach to explore the wave propagation problem of piezoelectric sandwich nanoplates. The core of the sandwich nanoplates is a nanocomposite layer reinforced with graphene platelets, which is integrated by two piezoelectric layers exposed to electric field. The material properties of nanocomposite layer are obtained by the Halpin–Tsai model and the rule of mixtures. The Euler–Lagrange equations of nanoplates are derived from Hamilton’s principle. By using the nonlocal strain gradient theory, the nonlocal governing equations are presented. Finally, numerical studies are conducted to demonstrate the influences of propagation angle, small-scale and external loads on wave frequency. The results reveal that the frequency changes periodically with the propagation angle and can be reduced by increasing voltage, temperature and the thickness of graphene platelets.

1 Introduction

In comparison with electromechanical systems, nano-electromechanical systems face greater challenges in manufacturing and application. Hence, designers must grasp reliable and useful information related to the mechanical performance of small-scale structures. The scale effects cannot be ignored when analyzing the nano-mechanical performance, which is not considered in classical continuity theory. Therefore, the size-dependent theories, including the nonlocal elastic theory (NET) [1,2,3], strain gradient [4], and coupled stress [5, 6], are used to study the scale effects in wave propagation problems. Many scholars have made important contributions in this regard. Wang et al. [7] made a breakthrough in wave propagation in elastic media considering size effect. The NET was used to quantify the contributions of small-scale parameters to the axial wave propagation of nanoplates [8]. The wave propagation was investigated using the size-dependent model in the micro-nano-beam structure [9]. Moreover, Zhang et al. [10] extended the above work to the field of piezoelectricity. The propagation characteristics of flexural waves were investigated for functionally graded piezoelectric nanobeams considering thermal and surface effects [11]. However, the NET cannot predict the stiffness hardening effect due to the lack of length scale parameters (LSP). Thus, Lim et al. [12] creatively proposed the nonlocal strain gradient theory (NLSGT) to solve the wave propagation problem of size-dependent structures. The same theory was also used to investigate the dispersion characteristics of waves in anisotropic doubly curved nanoshells [13] and the dispersion problem of functionally graded triclinic nanoplates [14].

Composites of a lightweight nature have become viable substitutes for conventional materials. Many scholars have focused on the propagation behavior of waves in laminated composite structures at various scales, such as wave dispersion characteristics of thin and medium-thick composite plates [15], propagation of waves in infinitely laminated composite plates [16], and wave dispersion characteristics of layered composite plates [17]. However, the structures mentioned above are not smart enough.

Newly designed systems often consist of multi-tasking units, composed of intelligent electromechanical materials. The wave propagation in piezoelectric structures becomes popular due to the well-known coupling between deformation and electrical excitation [18,19,20]. Ezzin et al. [21] proposed the dynamic solutions to the wave propagation in the piezoelectric laminate. Li et al. [22] studied the effect of the middle soft layer on the Love wave propagating in the layered piezoelectric system.

Currently, the graphene-reinforced composite materials have attracted the interest of many scholars due to their excellent electromechanical properties [23, 24]. Yang et al. [25] revealed that the graphene platelet (GPL) could enhance the post-buckling behavior of functionally graded nanocomposite beams. Graphene sheets were found to be able to boost the nonlinear bending characteristics of multilayer composite beams, which were less sensitive to higher GPL specific gravity and symmetrical distribution [26].

Although many studies have been focused on the vibration and buckling problems of graphene-reinforced piezoelectric composite nanoplates, or wave propagation in piezoelectric laminates considering small-scale effects, there still exist research gaps in the wave propagation problem of graphene platelet-reinforced piezoelectric sandwich composite nanoplates (GPL-RPSCN) using NLSGT. The motivation of this study is to use the NLSGT to investigate the scopes of the softening effect of nonlocal parameters (NLP) and the hardening effect of LSP. In addition, the effects of graphene’s size, voltage and temperature variation on frequency are also discussed.

Fig. 1

Schematic figure of graphene platelet-reinforced piezoelectric sandwich structure

2 Theory and Formulation

2.1 Problem Definition

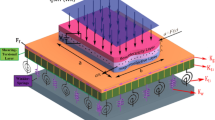
A schematic configuration of a piezoelectric sandwich structure is shown in Fig. 1. The origin of the Cartesian coordinate system (x, y, z) is taken as the reference in the mid-plane of the sandwich nanoplates. As can be seen, the composite layer with the thickness of $h_\mathrm{c} =10$ nm is covered by two piezoelectric layers, each with the thicknesses of $h_\mathrm{p} =5$ nm. The geometric parameters of the nanoplates are: length a and width $b=100$ nm. It is assumed that there is no slipping between the piezoelectric layers and the composite layer, and the electric fields are applied to the piezoelectric layers. The upper and lower face layers are used as the actuator and the sensor, respectively. In the rest of this paper, the subscripts or superscripts a and s represent the actuator and the sensor, respectively. In addition, the superscripts c and comp represent the composites layers, and the superscripts p and piezo represent the piezoelectric layers.

2.2 Constitutive Equations

The equivalent modulus of graphene platelet-reinforced composite (GPL-RC) is described by the Halpin–Tsai model [23]. Then, the relationship between volume fraction $V_{G}$ and graphene’s weight fraction $W_{G}$ can be written as

$$\begin{aligned} V_{G} =\frac{W_{G} }{W_{G} +\left( {\rho _{G} /\rho _{M} } \right) \left( {1-W_{G} } \right) } \end{aligned}$$

(1)

The mass densities of GPL and polymer matrix are denoted by $\rho _{G}$ and $\rho _{M}$, respectively. The equivalent elastic modulus of GPL-RC is obtained as

$$\begin{aligned} E_{C} =\frac{3}{8}\left( {\frac{1+2\left( {a_{G} /h_{G} } \right) \frac{\left( {E_{G} /E_{M} } \right) -1}{\left( {E_{G} /E_{M} } \right) +2\left( {a_{G} /h_{G} } \right) }V_{G} }{1-\frac{\left( {E_{G} /E_{M} } \right) -1}{\left( {E_{G} /E_{M} } \right) +2\left( {a_{G} /h_{G} } \right) }V_{G} }E_{M} } \right) +\frac{5}{8}\left( {\frac{1+2\left( {b_{G} /h_{G} } \right) \frac{\left( {E_{G} /E_{M} } \right) -1}{\left( {E_{G} /E_{M} } \right) +2\left( {b_{G} /h_{G} } \right) }V_{G} }{1-\frac{\left( {E_{G} /E_{M} } \right) -1}{\left( {E_{G} /E_{M} } \right) +2\left( {b_{G} /h_{G} } \right) }V_{G} }E_{M} } \right) \nonumber \\ \end{aligned}$$

(2)

The length, width and thickness of GPL are expressed by $a_{G}$, $b_{G}$ and $h_{G}$, respectively. Following the rule of mixtures, the expressions of mass density, Poisson’s ratio and thermal expansion coefficient of the nanocomposite are given by

$$\begin{aligned} \rho _{C} =\rho _{G} V_{G} +\rho _{M} V_{M} ,\quad \nu _{C} =\nu _{G} V_{G} +\nu _{M} V_{M} ,\quad \alpha _{C} =\alpha _{G} V_{G} +\alpha _{M} V_{M} \end{aligned}$$

(3)

The stress–strain relationship of the composite core is obtained by the classical plate theory (CPT) as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \sigma _{{xx} }^{\text {comp}} \\ \sigma _{{yy} }^{\text {comp}} \\ \sigma _{{xy} }^{\text {comp}} \\ \end{array}} \right\} =\left[ {{\begin{array}{*{20}c} {p_{11} } &{}\quad {p_{12} } &{}\quad 0 \\ {p_{21} } &{}\quad {p_{22} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {2p_{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{l} \varepsilon _{{xx} }^{\text {c}} \\ \varepsilon _{{yy} }^{\text {c}} \\ \varepsilon _{{xy} }^{\text {c}} \\ \end{array}} \right\} -\left\{ {\begin{array}{l} \alpha _\mathrm{c} \\ \alpha _\mathrm{c} \\ 0 \\ \end{array}} \right\} \Delta T \end{aligned}$$

(4)

For a piezoelectric layer under plane stress, the relationship between its stress and strain is derived as follows [3]:

$$\begin{aligned} \left\{ {\begin{array}{l} \sigma _{{xx} }^{\text {piezo}} \\ \sigma _{{yy} }^{\text {piezo}} \\ \sigma _{{xy} }^{\text {piezo}} \\ \end{array}} \right\} =\left[ {{\begin{array}{*{20}c} {\bar{{c}}_{11} } &{}\quad {\bar{{c}}_{12} } &{}\quad 0 \\ {\bar{{c}}_{12} } &{}\quad {\bar{{c}}_{11} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {2\bar{{c}}_{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{l} \varepsilon _{{xx} }^{\text {p}} \\ \varepsilon _{{yy} }^{\text {p}} \\ \varepsilon _{{xy} }^{\text {p}} \\ \end{array}} \right\} -\left[ {{\begin{array}{*{20}c} 0 &{}\quad 0 &{}\quad {\bar{{e}}_{31} } \\ 0 &{}\quad 0 &{}\quad {\bar{{e}}_{31} } \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} }} \right] \left\{ {\begin{array}{l} E_{x} \\ E_{y} \\ E_{z} \\ \end{array}} \right\} -\left\{ {\begin{array}{l} \bar{{\beta }}_{1} \\ \bar{{\beta }}_{1} \\ 0 \\ \end{array}} \right\} \Delta T \end{aligned}$$

(5)

$$\begin{aligned} \left\{ {\begin{array}{l} D_{x} \\ D_{y} \\ D_{z} \\ \end{array}} \right\} =\left[ {{\begin{array}{*{20}c} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ {\bar{{e}}_{31} } &{}\quad {\bar{{e}}_{31} } &{}\quad 0 \\ \end{array} }} \right] \left\{ {\begin{array}{l} \varepsilon _{{xx} }^{\text {p}} \\ \varepsilon _{{yy} }^{\text {p}} \\ \varepsilon _{{xy} }^{\text {p}} \\ \end{array}} \right\} +\left[ {{\begin{array}{*{20}c} {\bar{{s}}_{11} } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {\bar{{s}}_{11} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {\bar{{s}}_{33} } \\ \end{array} }} \right] \left\{ {\begin{array}{l} E_{x} \\ E_{y} \\ E_{z} \\ \end{array}} \right\} +\left\{ {\begin{array}{l} \bar{{p}}_{1} \\ \bar{{p}}_{1} \\ \bar{{p}}_{3} \\ \end{array}} \right\} \Delta T \end{aligned}$$

(6)

The piezoelectric, pyroelectric, dielectric constants, elastic and thermal moduli are denoted by $\bar{{e}}_{ij}$, $\bar{{p}}_{i}$, $\bar{{s}}_{ij}$, $\bar{{c}}_{ij}$ and $\bar{{\beta }}_{i}$, respectively.

The electric potential distribution of the piezoelectric layer, which satisfies Maxwell’s equations, is written as [18]

$$\begin{aligned} \bar{{\bar{{\varphi }}}}_{a} =\sin \left[ {\frac{\pi }{h_\mathrm{p} }\left( {z-\frac{h_\mathrm{c} }{2}} \right) } \right] \bar{{\varphi }}_{a} +\frac{z-\frac{h_\mathrm{c} }{2}}{h_\mathrm{p} }V_{0} ,\quad \bar{{\bar{{\varphi }}}}_{s} =\sin \left[ {\frac{\pi }{h_\mathrm{p} }\left( {-z-\frac{h_\mathrm{c} }{2}} \right) } \right] \bar{{\varphi }}_{s} \end{aligned}$$

(7)

where $\bar{{\varphi }}_{a}$ and $\bar{{\varphi }}_{s}$ are spatial electric potential distributions of the actuator layer and the sensor layer, respectively; and $V_{0}$ represents the external voltage. The electric field strength is calculated as $E_{n}^{m} =-\nabla \bar{{\bar{{\varphi }}}}_{m}$, where $m=a,s$ and $n=x,y,z$.

The displacement field obtained by CPT can be expressed as [19]

$$\begin{aligned} \bar{{u}}_{x} =u-z\frac{\partial w}{\partial x},\quad \bar{{u}}_{y} =v-z\frac{\partial w}{\partial y},\quad \bar{{u}}_{z} =w \end{aligned}$$

(8)

In the above formulas, displacements in the horizontal and vertical directions are represented by u and v, respectively, and the bending deflection is indicated by w. Therefore, the strain of the composite layer and the piezoelectric layer can be defined as

$$\begin{aligned} \left\{ {\begin{array}{l} \varepsilon _{xx}^{\text {c, p}} \\ \varepsilon _{yy}^{\text {c, p}} \\ \varepsilon _{xy}^{\text {c, p}} \\ \end{array}} \right\} =\left\{ {\begin{array}{c} \frac{\partial u}{\partial x} \\ \frac{\partial v}{\partial y} \\ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \\ \end{array}} \right\} +z\left\{ {\begin{array}{c} -\frac{\partial ^{2}w}{\partial x^{2}} \\ -\frac{\partial ^{2}w}{\partial y^{2}} \\ -2\frac{\partial ^{2}w}{\partial x\partial y} \\ \end{array}} \right\} \end{aligned}$$

(9)

2.3 Derivation of Euler–Lagrange Equations

According to Hamilton’s principle, the following expression can be obtained

$$\begin{aligned} {\int _{0}^t} {{\mathrm{\delta }}\left( {S-K+W} \right) {\mathrm{d}}t} =0 \end{aligned}$$

(10)

Strain energy, kinetic energy and external work are represented by S, K and W, respectively. Now, variations in the strain energy for the composite layer and the piezoelectric layer can be written as

$$\begin{aligned} {\mathrm{\delta }}S=\int _0^a {\left\{ {\begin{array}{l} \left( {N_{xx}^{\text {comp}} +N_{xx}^{\text {piezo}} } \right) \left( {{\mathrm{\delta }}\frac{\partial u}{\partial x}} \right) +\left( {M_{xx}^{\text {comp}} +M_{xx}^{\text {piezo}} } \right) \left[ {{\mathrm{\delta }}\left( {-\frac{\partial ^{2}w}{\partial x^{2}}} \right) } \right] \\ \quad + \left( {N_{yy}^{\text {comp}} +N_{yy}^{\text {piezo}} } \right) \left( {{\mathrm{\delta } }\frac{\partial v}{\partial y}} \right) +\left( {M_{yy}^{\text {comp}} +M_{yy}^{\text {piezo}} } \right) \left[ {{\mathrm{\delta } }\left( {-\frac{\partial ^{2}w}{\partial y^{2}}} \right) } \right] \\ \quad + \left( {N_{xy}^{\text {comp}} +N_{xy}^{\text {piezo}} } \right) \left[ {{\mathrm{\delta } }\left( {\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}} \right) } \right] +\left( {M_{xy}^{\text {comp}} +M_{xy}^{\text {piezo}} } \right) \left[ {{\mathrm{\delta } }\left( {-2\frac{\partial ^{2}w}{\partial x\partial y}} \right) } \right] \\ \quad + \int \limits _{Aa} {\left( {-D_{{x} }^{a} \delta E_{{x} }^{a} -D_{{y} }^{a} \delta E_{{y} }^{a} -D_{{z} }^{a} \delta E_{{z} }^{a} } \right) \text {d}A} +\int \limits _{As} {\left( {-D_{{x} }^{s} \delta E_{{x} }^{s} -D_{{y} }^{s} \delta E_{{y} }^{s} -D_{{z} }^{s} \delta E_{{z} }^{s} } \right) \text {d}A} \\ \end{array}} \right\} } \text {d}x\nonumber \\ \end{aligned}$$

(11)

where subscripts Aa and As represent integrations of the actuator and the sensor, respectively.

The expressions of axial force and bending moment are as follows:

$$\begin{aligned} \left( {N_{ij}^{\text {comp}} ,M_{ij}^{\text {comp}} } \right)= & {} \int _{-\frac{h_\mathrm{c} }{2}}^{\frac{h_\mathrm{c} }{2}} {\int _0^b {\left( {1,z} \right) } } \sigma _{ij}^{\text {comp}} {\mathrm {d}}y\text {d}z,\left( {N_{ij}^{\text {piezo}} ,M_{ij}^{\text {piezo}} } \right) =\int _{-h_\mathrm{c} /2-h_\mathrm{p} }^{-\frac{h_\mathrm{c} }{2}} {\int _0^b {\left( {1,z} \right) } } \sigma _{ij}^{\text {piezo}} \text {d}y{\mathrm {d}}z\nonumber \\&+\int _{\frac{h_\mathrm{c} }{2}}^{h_\mathrm{c} /2+h_\mathrm{p} } {\int _0^b {\left( {1,z} \right) } } \sigma _{ij}^{\text {piezo}} \text {d}y{\mathrm {d}}z \end{aligned}$$

(12)

In the above equations, i and j have the same value, and they can both get x and y. In addition, the expression of kinetic energy is stated as

$$\begin{aligned} {\mathrm{\delta }}K=\int _0^a {\left[ {\begin{array}{l} I_{0} \left( {\frac{\partial u}{\partial t}\frac{\partial {\mathrm{\delta } }u}{\partial t}+\frac{\partial v}{\partial t}\frac{\partial {\mathrm{\delta } }v}{\partial t}+\frac{\partial w}{\partial t}\frac{\partial {\mathrm{\delta } }w}{\partial t}} \right) +I_{2} \left( {\frac{\partial ^{2}w}{\partial x\partial t}\frac{\partial ^{2}{\mathrm{\delta } }w}{\partial x\partial t}+\frac{\partial ^{2}w}{\partial y\partial t}\frac{\partial ^{2}{\mathrm{\delta } }w}{\partial y\partial t}} \right) \\ -I_{1} \left( {\frac{\partial u}{\partial t}\frac{\partial ^{2}{\mathrm{\delta } }w}{\partial x\partial t}+\frac{\partial ^{2}w}{\partial x\partial t}\frac{\partial {\mathrm{\delta } }u}{\partial t}+\frac{\partial v}{\partial t}\frac{\partial ^{2}{\mathrm{\delta } }w}{\partial y\partial t}+\frac{\partial ^{2}w}{\partial y\partial t}\frac{\partial {\mathrm{\delta } }v}{\partial t}} \right) \\ \end{array}} \right] } \text {d}x \end{aligned}$$

(13)

in which the mass moments of inertia can be expressed as

$$\begin{aligned} I_{0} =b\left( {\rho _\mathrm{c} h_\mathrm{c} +2\rho _\mathrm{p} h_\mathrm{p} } \right) ,\quad I_{1} =0,\quad I_{2} =\frac{1}{12}\rho _\mathrm{c} bh_\mathrm{c}^{3}+\rho _\mathrm{p} bh_\mathrm{p} \left( {\frac{1}{2}h_\mathrm{c}^{2}+h_\mathrm{c} h_\mathrm{p} +\frac{2}{3}h_\mathrm{p} ^{2}} \right) \end{aligned}$$

(14)

The corresponding densities of the composite layer and the piezoelectric layer are $\rho _\mathrm{c}$ and $\rho _\mathrm{p}$, respectively. Then, the variation of the external work can be formulated as

$$\begin{aligned} {\mathrm{\delta } }W=-\int _0^a {\left[ {\left( {N_{x}^{E} +N_{y}^{T} } \right) \frac{\partial w}{\partial x}\frac{\partial {\mathrm{\delta } }w}{\partial x}+\left( {N_{y}^{E} +N_{y}^{T} } \right) \frac{\partial w}{\partial y}\frac{\partial {\mathrm{\delta } }w}{\partial y}+2{\mathrm{\delta } }\left( {N_{xy}^{E} +N_{xy}^{T} } \right) \frac{\partial w}{\partial x}\frac{\partial w}{\partial y}} \right] } \text {d}x \end{aligned}$$

(15)

The normal force caused by the electric field and temperature load in the equation can be defined as [18]

$$\begin{aligned} N_{x}^{E} =N_{y}^{E} =-\bar{{e}}_{31} V_{0} b,\quad N_{x\text {y}}^{E} =0,\quad N_{x}^{T} =N_{y}^{T} =\left( {a_\mathrm{c} h_\mathrm{c} +2\bar{{\beta }}_{1} h_\mathrm{p} } \right) b\Delta T,\quad N_{x\text {y}}^{T} =0 \end{aligned}$$

(16)

Note that the temperature of the nanoplates increases uniformly through the entire thickness, that is $T\left( z \right) =\Delta T$.

Assuming that the coefficients of ${\mathrm{\delta } }u$, ${\mathrm{\delta } }v$, ${\mathrm{\delta } }w$, ${\mathrm{\delta } }\bar{{\varphi }}_{a}$, ${\mathrm{\delta } }\bar{{\varphi }}_{s}$ are zero, the Euler–Lagrange equations for GPL-RPSCN are written as

$$\begin{aligned}&\frac{\partial N_{xx} }{\partial x}+\frac{\partial N_{xy} }{\partial y}=I_{0} \frac{\partial ^{2}u}{\partial t^{2}} \end{aligned}$$

(17)

$$\begin{aligned}&\frac{\partial N_{yy} }{\partial y}+\frac{\partial N_{xy} }{\partial x}=I_{0} \frac{\partial ^{2}v}{\partial t^{2}} \end{aligned}$$

(18)

$$\begin{aligned}&\frac{\partial ^{2}M_{xx} }{\partial x^{2}}+2\frac{\partial ^{2}M_{xy} }{\partial x\partial y}+\frac{\partial ^{2}M_{yy} }{\partial y^{2}}-\left( {N_{x}^{E} +N_{x}^{T} } \right) \frac{\partial ^{2}w}{\partial x^{2}}-\left( {N_{y}^{E} +N_{y}^{T} } \right) \frac{\partial ^{2}w}{\partial y^{2}}=I_{0} \frac{\partial ^{2}w}{\partial t^{2}}-I_{2} \nabla ^{2}\frac{\partial ^{2}w}{\partial t^{2}}\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned}&\int \limits _{Aa} {-\frac{\partial D_{{x} }^{a} }{\partial x}\sin \left[ {\beta \left( {z-\frac{h_\mathrm{c} }{2}} \right) } \right] -\frac{\partial D_{{y} }^{a} }{\partial y}\sin \left[ {\beta \left( {z-\frac{h_\mathrm{c} }{2}} \right) } \right] +D_{{z} }^{a} \beta \cos \left[ {\beta \left( {z-\frac{h_\mathrm{c} }{2}} \right) } \right] \text {d}A} =0 \end{aligned}$$

(20)

$$\begin{aligned}&\int \limits _{As} {-\frac{\partial D_{{x} }^{s} }{\partial x}\sin \left[ {\beta \left( {-z-\frac{h_\mathrm{c} }{2}} \right) } \right] -\frac{\partial D_{{y} }^{s} }{\partial y}\sin \left[ {\beta \left( {-z-\frac{h_\mathrm{c} }{2}} \right) } \right] -D_{{z} }^{s} \beta \cos \left[ {\beta \left( {-z-\frac{h_\mathrm{c} }{2}} \right) } \right] \text {d}A} =0\nonumber \\ \end{aligned}$$

(21)

2.4 Nonlocal Strain Gradient Theory

The constitutive equations of NLSGT are shown as follows [19]:

$$\begin{aligned} \begin{array}{l} \left[ {1-\left( {e_{1} a} \right) ^{2}\nabla ^{2}} \right] \left[ {1-\left( {e_{0} a} \right) ^{2}\nabla ^{2}} \right] \sigma _{ij} =\left\{ {\left[ {1-\left( {e_{1} a} \right) ^{2}\nabla ^{2}} \right] -l^{2}\left[ {1-\left( {e_{0} a} \right) ^{2}\nabla ^{2}} \right] \nabla ^{2}} \right\} \left( {c_{ijkl} \varepsilon _{kl} -e_{mij} E_{m} -\beta _{ij} \Delta T} \right) \\ \left[ {1-\left( {e_{1} a} \right) ^{2}\nabla ^{2}} \right] \left[ {1-\left( {e_{0} a} \right) ^{2}\nabla ^{2}} \right] D_{i} =\left\{ {\left[ {1-\left( {e_{1} a} \right) ^{2}\nabla ^{2}} \right] -l^{2}\left[ {1-\left( {e_{0} a} \right) ^{2}\nabla ^{2}} \right] \nabla ^{2}} \right\} \left( {e_{ikl} \varepsilon _{kl} +s_{im} E_{m} -p_{i} \Delta T} \right) \\ \end{array} \end{aligned}$$

(22)

Regardless of the terms of order $0\left( {\nabla ^{2}} \right)$ and $e_{1} =e_{0} =e$, the Laplace operator can be written as $\nabla ^{2}={\partial ^{2}}/ {\partial x^{2}}+{\partial ^{2}} / {\partial y^{2}}$. Then, the constitutive relationship is abbreviated as

$$\begin{aligned} \left( {1-\mu \nabla ^{2}} \right) \sigma _{ij}= & {} \left( {1-\eta \nabla ^{2}} \right) \left( {c_{ijkl} \varepsilon _{kl} -e_{mij} E_{m} -\beta _{ij} \Delta T} \right) \nonumber \\ \left( {1-\mu \nabla ^{2}} \right) D_{i}= & {} \left( {1-\eta \nabla ^{2}} \right) \left( {e_{ikl} \varepsilon _{kl} +s_{im} E_{m} -p_{i} \Delta T} \right) \end{aligned}$$

(23)

where $\mu =\left( {ea} \right) ^{2}$ and $\eta =l^{2}$ represent NLP and LSP, respectively. Accordingly, the force and moment equations of nanoplates are as follows:

$$\begin{aligned}&\left( {1-\mu \nabla ^{2}} \right) \left\{ {\begin{array}{l} N_{xx} \\ N_{yy} \\ N_{xy} \\ \end{array}} \right\} =\left( {1-\eta \nabla ^{2}} \right) \left\{ \left[ {{\begin{array}{*{20}c} {A_{11} } &{}\quad {A_{12} } &{}\quad 0 \\ {A_{21} } &{}\quad {A_{22} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {A_{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{c} \frac{\partial u}{\partial x} \\ \frac{\partial v}{\partial y} \\ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \\ \end{array}} \right\} \right. \nonumber \\&\quad +\left[ {{\begin{array}{*{20}c} {B_{11} } &{}\quad {B_{12} } &{}\quad 0 \\ {B_{21} } &{}\quad {B_{22} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {B_{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{c} -\frac{\partial ^{2}w}{\partial x^{2}} \\ -\frac{\partial ^{2}w}{\partial y^{2}} \\ -2\frac{\partial ^{2}w}{\partial x\partial y} \\ \end{array}} \right\} \nonumber \\&\quad \left. +\left[ {{\begin{array}{*{20}c} {A_{31}^{s} } &{}\quad {A_{31}^{a} } \\ {A_{31}^{s} } &{}\quad {A_{31}^{a} } \\ 0 &{} 0 \\ \end{array} }} \right] \left\{ {\begin{array}{l} {\bar{\varphi }}_{s} \\ {\bar{\varphi }}_{a} \\ \end{array}} \right\} -\left\{ {\begin{array}{c} N_{x}^{E} +N_{x}^{T} \\ N_{y}^{E} +N_{y}^{T} \\ 0 \\ \end{array}} \right\} \right\} \end{aligned}$$

(24)

$$\begin{aligned}&\left( {1-\mu \nabla ^{2}} \right) \left\{ {\begin{array}{l} M_{xx} \\ M_{yy} \\ M_{xy} \\ \end{array}} \right\} =\left( {1-\eta \nabla ^{2}} \right) \left\{ \left[ {{\begin{array}{*{20}c} {B_{11} } &{}\quad {B_{12} } &{}\quad 0 \\ {B_{21} } &{}\quad {B_{22} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {B_{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{c} \frac{\partial u}{\partial x} \\ \frac{\partial v}{\partial y} \\ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \\ \end{array}} \right\} \right. \nonumber \\&\quad +\left[ {{\begin{array}{*{20}c} {D_{11} } &{}\quad {D_{12} } &{}\quad 0 \\ {D_{21} } &{}\quad {D_{22} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {D_{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{c} -\frac{\partial ^{2}w}{\partial x^{2}} \\ -\frac{\partial ^{2}w}{\partial y^{2}} \\ -2\frac{\partial ^{2}w}{\partial x\partial y} \\ \end{array}} \right\} \nonumber \\&\quad \left. +\left[ {{\begin{array}{*{20}c} {E_{31}^{s} } &{}\quad {E_{31}^{a} } \\ {E_{31}^{s} } &{}\quad {E_{31}^{a} } \\ 0 &{}\quad 0 \\ \end{array} }} \right] \left\{ {\begin{array}{l} {\bar{\varphi }}_{s} \\ {\bar{\varphi }}_{a} \\ \end{array}} \right\} \right. \nonumber \\&\quad \left. -\left\{ {\begin{array}{c} M_{x}^{E} +M_{x}^{T} \\ M_{y}^{E} +M_{y}^{T} \\ 0 \\ \end{array}} \right\} \right\} \end{aligned}$$

(25)

$$\begin{aligned}&\begin{array}{l} \left( {1-\mu \nabla ^{2}} \right) \int \limits _{Aa} {\left\{ {\left\{ {\begin{array}{l} D_{{x} }^{a} \\ D_{{y} }^{a} \\ \end{array}} \right\} \sin \left[ {\beta \left( {z-\frac{h_\mathrm{c} }{2}} \right) } \right] } \right\} } \text {d}A=\left( {1-\eta \nabla ^{2}} \right) \left( {-F_{11}^{a} \left\{ {\begin{array}{l} \frac{\partial {\bar{\varphi }}_{a} }{\partial x} \\ \frac{\partial {\bar{\varphi }}_{a} }{\partial y} \\ \end{array}} \right\} } \right) \\ \left( {1-\mu \nabla ^{2}} \right) \int \limits _{Aa} {D_{{z} }^{a} \beta \cos \left[ {\beta \left( {z-\frac{h_\mathrm{c} }{2}} \right) } \right] } \text {d}A=\left( {1-\eta \nabla ^{2}} \right) \left[ {A_{31}^{a} \left( {\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}} \right) -E_{31}^{a} \nabla ^{2}w-F_{33}^{a} {\bar{\varphi }}_{a} } \right] \\ \end{array} \end{aligned}$$

(26)

$$\begin{aligned}&\begin{array}{l} \left( {1-\mu \nabla ^{2}} \right) \int \limits _{As} {\left\{ {\left\{ {\begin{array}{l} D_{{x} }^{s} \\ D_{{y} }^{s} \\ \end{array}} \right\} \sin \left[ {\beta \left( {-z-\frac{h_\mathrm{c} }{2}} \right) } \right] } \right\} } \text {d}A=\left( {1-\eta \nabla ^{2}} \right) \left( {-F_{11}^{s} \left\{ {\begin{array}{l} \frac{\partial {\bar{\varphi }}_{s} }{\partial x} \\ \frac{\partial {\bar{\varphi }}_{s} }{\partial y} \\ \end{array}} \right\} } \right) \\ \left( {1-\mu \nabla ^{2}} \right) \int \limits _{As} {D_{{z} }^{s} \beta \cos \left[ {\beta \left( {-z-\frac{h_\mathrm{c} }{2}} \right) } \right] } \text {d}A=\left( {1-\eta \nabla ^{2}} \right) \left[ {A_{31}^{s} \left( {\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}} \right) -E_{31}^{s} \nabla ^{2}w+F_{33}^{s} {\bar{\varphi }}_{s} } \right] \\ \end{array} \end{aligned}$$

(27)

Substituting Eqs. (24)–(27) into Eqs. (17)–(21), the nonlocal governing equations of nanoplates can be obtained by the following formulas:

$$\begin{aligned}&\left( {1-\eta \nabla ^{2}} \right) \left[ {A_{11} \frac{\partial ^{2}u}{\partial x^{2}}+A_{66} \frac{\partial ^{2}u}{\partial y^{2}}+\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}v}{\partial x\partial y}-B_{11} \frac{\partial ^{3}w}{\partial x^{3}}-\left( {B_{12} +2B_{66} } \right) \frac{\partial ^{3}w}{\partial x\partial y^{2}}+A_{31}^{a} \frac{\partial \bar{{\varphi }}_{a} }{\partial x}+A_{31}^{s} \frac{\partial \bar{{\varphi }}_{s} }{\partial x}} \right] \nonumber \\&\quad -\left( {1-u\nabla ^{2}} \right) I_{0} \frac{\partial ^{2}u}{\partial t^{2}}=0 \end{aligned}$$

(28)

$$\begin{aligned}&\left( {1-\eta \nabla ^{2}} \right) \left[ {\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}u}{\partial x\partial y}+A_{22} \frac{\partial ^{2}v}{\partial y^{2}}+A_{66} \frac{\partial ^{2}v}{\partial x^{2}}-B_{22} \frac{\partial ^{3}w}{\partial y^{3}}-\left( {B_{12} +2B_{66} } \right) \frac{\partial ^{3}w}{\partial x^{2}\partial y}+A_{31}^{a} \frac{\partial \bar{{\varphi }}_{a} }{\partial y}+A_{31}^{s} \frac{\partial \bar{{\varphi }}_{s} }{\partial y}} \right] \nonumber \\&\quad -\left( {1-u\nabla ^{2}} \right) I_{0} \frac{\partial ^{2}v}{\partial t^{2}}=0 \end{aligned}$$

(29)

$$\begin{aligned}&\begin{array}{l} \left( {1-\eta \nabla ^{2}} \right) \left[ {\begin{array}{l} B_{11} \frac{\partial ^{3}u}{\partial x^{3}}+\left( {B_{12} +2B_{66} } \right) \frac{\partial ^{3}u}{\partial x\partial y^{2}}+B_{22} \frac{\partial ^{3}v}{\partial y^{3}}+\left( {B_{12} +2B_{66} } \right) \frac{\partial ^{3}v}{\partial x^{2}\partial y} \\ -D_{11} \frac{\partial ^{4}w}{\partial x^{4}}-2\left( {D_{12} +2D_{66} } \right) \frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}-D_{22} \frac{\partial ^{4}w}{\partial y^{4}}+E_{31}^{a} \left( {\frac{\partial ^{2}\bar{{\varphi }}_{a} }{\partial x^{2}}+\frac{\partial ^{2}\bar{{\varphi }}_{a} }{\partial y^{2}}} \right) +E_{31}^{s} \left( {\frac{\partial ^{2}\bar{{\varphi }}_{s} }{\partial x^{2}}+\frac{\partial ^{2}\bar{{\varphi }}_{s} }{\partial y^{2}}} \right) \\ \end{array}} \right] \\ \quad +\left( {1-u\nabla ^{2}} \right) \left[ {-I_{0} \frac{\partial ^{2}w}{\partial t^{2}}+I_{2} \nabla ^{2}\frac{\partial ^{2}w}{\partial t^{2}}-\left( {N_{x}^{E} +N_{x}^{T} } \right) \frac{\partial ^{2}w}{\partial x^{2}}-\left( {N_{y}^{E} +N_{y}^{T} } \right) \frac{\partial ^{2}w}{\partial y^{2}}} \right] =0 \\ \end{array} \end{aligned}$$

(30)

$$\begin{aligned}&\left( {1-\eta \nabla ^{2}} \right) \left( {A_{31}^{a} \frac{\partial u}{\partial x}+A_{31}^{a} \frac{\partial v}{\partial y}-E_{31}^{a} \nabla ^{2}w+F_{11}^{a} \nabla ^{2}\bar{{\varphi }}_{a} -F_{33}^{a} \bar{{\varphi }}_{a} } \right) =0 \end{aligned}$$

(31)

$$\begin{aligned}&\left( {1-\eta \nabla ^{2}} \right) \left( {A_{31}^{s} \frac{\partial u}{\partial x}+A_{31}^{s} \frac{\partial v}{\partial y}-E_{31}^{s} \nabla ^{2}w-F_{11}^{s} \nabla ^{2}\bar{{\varphi }}_{s} +F_{33}^{s} \bar{{\varphi }}_{s} } \right) =0 \end{aligned}$$

(32)

The solution is assumed to be described as an exponential displacement field in the following:

$$\begin{aligned} d\left( {x,y,t} \right) =d_{0} \mathrm{e}^{\mathrm{i}\left( {k_{1} x+k_{2} y-\omega t} \right) },\,\,d_{0} =u_{0} ,v_{0} ,w_{0} ,\bar{{\varphi }}_{a0} ,\bar{{\varphi }}_{s0} \end{aligned}$$

(33)

where the displacement vector, system frequency, and wave numbers along the horizontal and vertical axes are expressed as $d_{0}$, $\omega$, and $k_{1}$, $k_{2}$, respectively. The harmonics propagate along the positive x-axis in the direction of the azimuth angle $\alpha$. Here, $k_{1} =k\cos \alpha$, and $k_{2} =k\sin \alpha$. Substituting Eq. (33) into Eqs. (28)–(32), we can obtain that

$$\begin{aligned} \left\{ {\left[ {{{\varvec{K}}}} \right] _{5\times 5} -\omega ^{2}\left[ {{{\varvec{M}}}} \right] _{5\times 5} } \right\} \left[ {{{\varvec{d}}}_{{{\varvec{0}}}} } \right] _{5\times 1} =\left[ {{\mathbf {0}}} \right] _{5\times 1} \end{aligned}$$

(34)

The wave’s angular frequencies of the first five natural modes can be calculated via solving the obtained equation for $\omega$. The solution to wave frequency, which includes the frequency corresponding to the first natural mode, can be ascertained by the formula $f=\frac{\omega }{2\pi }$. Here, the imaginary part of the complex frequency is ignored

3 Results and Discussion

3.1 Comparison Study

Currently, little research has been conducted on wave dispersion analysis of GPL-RPSCN, which means that our present model is hard to be verified directly, not to mention that there are very few reports on the experiments and molecular dynamic simulations of piezoelectric composite nanoplate models. To solve this problem, our model is conducted on a single piezoelectric layer and a graphene composite layer to compare with the results obtained by Ma et al. [3] and Ebrahimi et al. [24], respectively. The material properties of the graphene sheet are $E_{G}=1010$ GPa, $\nu _{G}=0.186$, $\rho _{G}=1.0625\times 10^{{3}}$ kg/m$^{{3}}$, $\alpha _{G}= 5.0\times 10 ^{{-6}}$ K$^{{-1}}$, $a_{G}=5.0$ nm, $b_{G}=2.5$ nm and $h_{G}=0.3$ nm. The material properties of the epoxy are $E_{M}=3.0$ GPa, $\nu _{M}=0.34$, $\rho _{M}= 1.200\times 10^{{3}}$ kg/m$^{{3}}$ and $\alpha _{M}= 60.0\times 10^{{-6}}$ K$^{{-1}}$ [23]. The piezoelectric material is PZT-4 and its thermoelectric elastic properties are given in Ref. [3].

As shown in Fig. 2, the results from the present model agree well with those in the literature. Moreover, when the wave number is constant, the frequency in Case 2 is higher than that in Case 1. The wave frequency decreases as the NLP increases, which indicates a softening phenomenon. These comparisons not only validate the present analytical model, but also show its potential in wave dispersion analysis of GPL-RPSCN.

Fig. 2

Influence of NLP on the dispersion curve of nanoplates for the two cases (Case 1: without piezoelectric layers ($h_\mathrm{p} =0$); Case 2: without composite layer ($h_\mathrm{c} =0$))

3.2 Wave Propagation Analysis

Figure 3 demonstrates that the dispersion relationship changes periodically with the azimuth angle, with a period of $\pi$/2. This is due to the symmetry of the material, where the wave number is set as $5\times 10^{{8}}$. The frequency reaches its maximum and minimum values when the azimuth angle is $\pi$/4 and $\pi$/2, respectively. This result is beneficial to the design of wave devices. In addition, with a fixed azimuth angle, the frequency decreases as the NLP increase. In the rest of this paper, the azimuth angle’s value is set as $\pi$/4.

Fig. 3

Influence of propagation angle and NLP on the GPL-RPSCN frequency

Without considering the strain gradient scale parameters, the influence of NLP on the dispersion relationship nanoplates is shown in Fig. 4, which could not be ignored. At a fixed wave number, the frequency decreases as $\mu$ increases. Moreover, the frequency values in all these three cases are smaller than the one in the classical case ($\mu =0$, $\eta =0$). In addition, when the NLP is nonzero, the stiffness softening effect caused by the NLP can be observed, which becomes more significant when the wave number is larger than $2\times 10^{{8}}$.

Fig. 4

Influence of NLP on the dispersion relationship of nanoplates ignoring the strain gradient scale parameters

Fig. 5

Influence of the strain gradient LSP on the dispersion relation of nanoplates without considering nonlocal parameters

Fig. 6

Influence of $\mu$ and $\eta$ on the dispersion relationship of nanoplates ($\mu \ne \eta )$

As shown in Fig. 5, the relationship between wave frequency and wave number is studied with different values of $\eta$. Compared with the classical case ($\mu =0$, $\eta =0$), the frequency increases faster with the wave number, which indicates that the LSP has a hardening effect, not from nonlocal elasticity, on the wave frequency of nanoplates. To be specific, the wave frequency increases as the LSP increases, which means that the stiffness enhancement effect becomes more significant. Particularly, when the wave number is larger than $2\times 10^{{8}}$, this hardening effect is more remarkable.

Figure 6 shows that the frequency is smaller than the one in the classical case when NLP is positive and $\mu > \eta$, where the softening effect occurs. However, the opposite trend indicates that the hardening effect occurs when the LSP is positive and $\mu <\eta$. Both of these effects become more pronounced when the wave number is larger than $2\times 10^{{8}}$.

From Figs. 4, 5 and 6, we can also find that the frequency of the wave increases almost linearly with the increase in the wave number when the size effect is not considered ($\mu =0$, $\eta =0$). Otherwise, the frequency of the wave will decrease as $\mu$ increases, and the frequency will increase as $\eta$ increases. At the same time, this softening and hardening effect becomes more obvious when the wave number becomes larger. In other words, when the wave number gets larger, the influence of the size effect on the dynamic behavior of the composite nanoplate is more significant.

Fig. 7

Dispersion curve of nanoplates when external voltage is applied

Fig. 8

Wave propagation behavior affected by temperature variation

Figure 7 shows the effect of applied voltage on the dispersion characteristics of nanoplates. Clearly, the applied voltage has a slight influence on wave frequency. Within a certain range of wave number, the frequency decreases with the increase in voltage. The reason is that the applied negative and positive voltages exert compressive and tensile forces on the nanoplates.

The effect of temperature variation on wave propagation behavior is investigated, as shown in Fig. 8. It can be found that the wave frequency is insensitive to the temperature change. However, the temperature rise causes the frequency to decrease, since the structure becomes softer. Consequently, lowering the temperature in a certain range is beneficial to the increase in frequency.

Figure 9 shows that the nanoplate thickness ($h=h_{\mathrm {c}}+2h_{\mathrm {p}})$ has a slight effect on wave frequency. Here, the thickness of the composite layer remains unchanged. The increase in the thickness of the nanoplate is achieved by increasing the thickness of the piezoelectric layer. As the thickness increases, the wave frequency increases. In addition, the results show that the wave frequency decreases as the NLP increases, which is much more obvious when the NLP is relatively small.

Fig. 9

Influence of nanoplate thickness on wave frequency

Fig. 10

Influence of weight fraction and size of graphene platelet on wave frequency

Figure 10 shows that the wave frequency gradually increases as the weight fraction of graphene platelet increases, which is closely related to the size of graphene platelet. It is not difficult to find that the increase in the length or width of the graphene platelet can increase the wave frequency. However, the length and width of the graphene platelet have different effects on wave frequency. The increase in the width of graphene platelet is more conducive to the increase in wave frequency, while the increase in thickness causes the wave frequency to decrease. In conclusion, adjusting the weight fraction and size of graphene platelet can change the stiffness of the composite nanoplate, which, in turn, affects the wave frequency.

4 Conclusion

This study analyzes the wave dispersion behavior of GPL-RPSCN. The main conclusions are as follows:

• 1. The wave frequency changes periodically as the azimuth angle changes, with a period of $\pi$/2, the maximum value of which occurs at $\pi$/4.

• 2. Once the NLP has a nonzero value, the stiffness softening effect can be observed. The LSP has the same degree of hardening effect.

• 3. Within a certain range, the frequency can be reduced by increasing the voltage, temperature, or thickness of the graphene platelets.

• 4. The frequency increases as the graphene’s weight fraction, length, width, or nanoplate thickness increases.