Estimation of LEO-GPS receiver differential code bias based on inequality constrained least square and multi-layer mapping function

Abstract

The differential code bias (DCB) of the global navigation satellite system (GNSS) receiver onboard a low earth orbit (LEO) satellite is one of the crucial hardware error sources in ionospheric estimation. In common practice, LEO DCBs are considered as constant within a single day. However, since such receivers are installed on moving platforms, they are subjected to the ever-changing space environment, and thus, LEO DCBs are prone to more frequent fluctuations than receiver DCBs of ground GNSS stations. We estimate the LEO GPS receiver DCBs and plasmaspheric vertical total electron content by using inequality constrained least square and a multi-layer mapping function (MF) approach to minimize mapping errors. The GPS receiver DCBs onboard constellation observing system for meteorology, ionosphere, and climate satellites (COSMIC) is investigated and analyzed during the January 2008 period. The results show that in most cases the multi-layer MF approach performs better than the commonly used single-layer MF. The mapping error from an inaccurately fixed single-layer height can be considerably reduced. Meanwhile, with the help of a multi-layer MF, the mean deviations of DCBs for five receivers compared with those based on a geometric MF at 1400 km are significantly decreased by 59%, 15%, 26%, 47%, and 22%, respectively.

Introduction

The inter-frequency differential code bias (DCB) is one of the most important error sources that affect the accuracy of slant total electron content (TEC) estimation from ground- as well as space-based GNSS measurements (Jin et al. 2017, 2019, 2020). It is a common practice to consider GNSS satellite and receiver DCBs as constant during a single day (Mannucci et al. 1998; Sardón et al. 1994; Yue et al. 2011). Over the last two decades, significant research concerning GPS DCB variability has been conducted (Zhang et al. 2014; Zhong et al. 2016a; Sardón and Zarraoa 1997). Different DCB estimation methods are reported, which include least squares-based estimation (Jin et al. 2012; Li et al. 2019) as well as estimation based on searching for the true value with a constraint condition through minimizing the standard deviation (Arikan et al. 2008). The performances of different GNSS systems besides GPS are also evaluated based on different GNSS networks by Jin et al. (2016) and Wang et al. (2020).

However, the mapping functions (MFs) such as the single-layer MF and modified single-layer MF used in most of the previous researches are usually based on the single-layer assumption of the earth’s ionosphere. The performance of the thin-shell MF degrades in areas with high spatial gradients, especially at low elevation angles, and is affected by an inaccurate single-layer height. Studies have been conducted to examine the applicability of three MFs for LEO-based GNSS observations (Zhong et al. 2016b). Ohashi et al. (2013) and Hoque and Jakowski (2013) compared the single-layer VTEC estimation method and multi-layer VTEC estimation method. Moreover, when compared with the satellite DCBs, which are rather stable, the instrumental delays of receivers on LEO satellites may fluctuate more significantly. When estimating the GPS receiver bias onboard LEOs, the method usually used for the ground-based GPS receiver is not applicable. This can also challenge the generally used assumption of constant DCB within a day used in the LEO DCB estimation. Jin et al. (2016) tried to use ground-based observations such as global ionospheric map (GIM) to reduce the amount of calculation and complexity when estimating the DCBs of GNSS satellites. Due to the sparse global distribution of LEO satellites and corresponding measurements, making use of ground-based observations to complement the lack of information about ionospheric horizontal gradients is important for reducing mapping errors.

In addition, Zhang and Tang (2014) applied a least square fit method to estimate the 4-h global VTEC maps in the geographic reference frame above COSMIC orbit and daily DCBs together. The result shows good consistency with similar products from University Corporation for Atmospheric Research (UCAR). However, they did not provide any description of the VTEC result that is solved with the DCBs together in their research, which is as important as DCB estimations. Furthermore, the DCB estimations might be affected by the assumption of single-layer height used in the MF. Lin et al. (2010) tried to estimate approximate DCB values by first finding the minimal value at first and then applying a threshold on VTEC values to mitigate the uncertainty caused by the spherical symmetric ionosphere assumption. The results showed that the receiver DCBs onboard COSMIC satellites are more stable and consistent with official products than receiver DCBs onboard a CHAMP satellite. The reason is that due to the lower altitude of CHAMP orbit and the corresponding higher ionospheric contribution above the orbit height, the systematic error in IPP height assumption is crucial. Li et al. (2019) estimated the receiver DCB onboard FengYun-3C satellites recently but still based on a single-layer height assumption and the MF.

In this work, the LEO DCBs are estimated by using the least square technique with an empirical inequality constraint on topside ionospheric and plasmaspheric VTEC, which can considerably improve the accuracy of daily DCB estimations. On the other hand, we apply a multi-layer MF to reduce the error caused by the inaccurate assumption of the single-layer height. In the following, LEO DCB estimation methods are presented. The performance of ICLS methods is analyzed as well as MF effect and validation of satellite DCB estimates. Finally, conclusions are given.

LEO DCB estimation methods

Constellation observing system for meteorology, ionosphere, and climate (COSMIC) is a joint mission of the USA and Taiwan, China, which includes six satellites with an inclination of 72°. Each satellite is equipped with four GPS antennas, two of which are used for radio occultation. The other two antennas are used for precision orbit determination (POD) and high-level ionospheric detection with a data sampling rate of 1 Hz (Schreiner et al. 2007). Using the dual-frequency GPS carrier phase and code pseudorange observations, the total electron content (TEC) of the ionosphere along the GPS signal propagation path can be estimated.

Here, we computed the DCBs of COSMIC receivers in January 2008 under stable solar activity conditions. The observation data include COSMIC podTEC products provided by UCAR/CDACC. Moreover, we need ground-based observations such as the Global Ionosphere Map (GIM) provided by the Center for Orbit Determination in Europe (CODE) and information about solar activities such as the F10.7 index when applying the multi-layer MF. The F10.7 (https://sepc.ac.cn/) and ap index (https://isgi.unistra.fr/data_download.php) variations are shown in Fig. 1. Figure 2 shows a scheme of COSMIC topside observation distributions, i.e., the orbit trajectory.

Fig. 1

Solar flux F10.7 (black line) and geomagnetic ap (red line) indices during January 2008

Fig. 2

A scheme of COSMIC position where COSMIC satellites provided available topside observation in the Earth-Centered-Earth-Fixed reference frame on January 1, 2008

The GPS receivers record signals transmitted at two L-band frequencies, namely $f_{1}$ at 1575.42 MHz and $f_{2}$ at 1227.60 MHz. The code pseudoranges at the $f_{1}$ and $f_{2}$ frequencies are recorded as $P_{1}$ and $P_{2}$, respectively, and the carrier phase delay measurements at the $f_{1}$ and $f_{2}$ frequencies are $L_{1}$ and $L_{2}$, respectively (Arikan et al. 2008). The pseudorange and phase measurements are recorded in a special format called receiver independent exchange format (RINEX). The time delay of signals is converted to pseudorange values, and the phase shifts are recorded as phase delays in the receiver. The standard observation equations of pseudorange and phase measurements for dual frequencies $f_{1}$ and $f_{2}$ are expressed as follows (Jin et al. 2015):

$$\begin{array}{*{20}c} {P_{i,u}^{m} = p_{u}^{m} + c\left( {\delta t_{u} - \delta t^{m} } \right) + d_{{{\text{trop}},u}}^{m} + d_{{{\text{ion}}\,i,u}}^{m} + c\left( {{\text{DCB}}^{s} + E_{r} } \right)} \\ \end{array}$$

(1)

$$ \begin{aligned}\begin{array}{*{20}c} &{L_{i,u}^{m} = p_{u}^{m} + c\left( {\delta t_{u} - \delta t^{m} } \right) + \lambda_{i} \varphi_{{{\text{trop}},u}}^{m} + \lambda_{i} \varphi_{{{\text{ion}}\,i,u}}^{m} }\\&{- c\left( {{\text{DCB}}^{s} + {\text{DCB}}_{r} } \right) + \lambda_{i} N_{i}^{m} } \\ \end{array}\end{aligned} $$

(2)

where the subscript $u$ denotes the receiver, the superscript $m$ denotes the satellite, the subscript $i$ denotes the frequency, $p$ is the actual range between satellite and receiver, $\delta t_{u}$ and $\delta t^{m}$ are the clock errors for the receiver and satellite, respectively, $d_{{{\text{trop}},u}}^{m}$ denotes the troposphere group delay, $d_{{{\text{ion}} i,u}}^{m}$ denotes the ionospheric delay, c is the speed of light in vacuum, ${\text{DCB}}^{s}$ denotes the satellite differential code bias (DCB), ${\text{DCB}}_{r}$ denotes the receiver DCB, $\lambda_{i}$ denotes the wavelength, $\varphi_{{{\text{trop}},u}}^{m}$ denotes the phase shift due to the troposphere, $\varphi_{{{\text{ion}} i,u}}^{m}$ denotes the phase shift due to the ionosphere, and $N_{i}^{m}$ denotes the initial phase ambiguity.

A relatively accurate TEC value can be obtained by a carrier phase smoothing pseudorange method,

$${\text{STEC}} = k \cdot \left( {L_{1} - L_{2} - \overline{N} + c \cdot \left( {{\text{DCB}}_{r} + {\text{DCB}}_{s} } \right)} \right)$$

(3)

$$\begin{array}{*{20}c} {k = \frac{{f_{1}^{2} f_{2}^{2} }}{{40.3\left( {f_{1}^{2} - f_{2}^{2} } \right)}}} \\ \end{array}$$

(4)

where ${\text{STEC}}$ is the slant total electron content, and $\overline{N}$ is the average ambiguity in a connected phase arc.

The combinations of the absolute STEC values and corresponding DCB values provided by UCAR in podTEC data are calculated as observations, i.e., ${\text{STEC}}_{{{\text{absolute}}}} - {\text{DCB}}_{{{\text{UCAR}}}}$. For more detailed data processing strategies, please refer to Table 1.

Table 1 Data processing strategies for parameterizing plasmaspheric VTEC

Due to the strong latitude and local time dependence of ionospheric TEC, we apply a spherical harmonic expansion (SHE) in the geomagnetic reference frame (geomagnetic latitude and local magnetic time MLT) when parameterizing VTEC above LEO orbit. We must note that the distribution of GNSS observations aboard LEO is not sufficient for global topside ionospheric VTEC modeling. Therefore, we are forced to use the inequality constrained least square (ICLS) technique when solving the topside ionospheric VTEC model together with LEO DCB. We adopt the most widely used single-layer MF, namely F&K geometric MF proposed by Foelsche and Kirchengast (2002). The F&K geometric MF can be expressed as follows:

$${\text{MF}}_{{{\text{geometric}}}} = \frac{{\sin \theta + \sqrt {R^{ - 2} - \cos^{2} \theta } }}{{1 + R^{ - 1} }}$$

(5)

$$R = \frac{{R_{{\text{e}}} + H_{{{\text{LEO}}}} }}{{R_{{\text{e}}} + H_{{{\text{ion}}}} }}$$

(6)

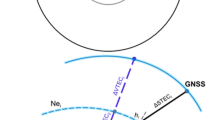
where $\theta$ is the elevation angle, $R_{{\text{e}}}$ is the average radius of the earth, $H_{{{\text{LEO}}}}$ is the altitude of LEO orbit, and $H_{{{\text{ion}}}}$ is the altitude of the ionospheric single layer. Figure 3 illustrates a simple geometry for the single-layer MF.

Fig. 3

Sketch of single-layer ionosphere assumption. Earth’s center is the center of the earth. $R_{{\text{e}}}$ is the average radius of the earth, h represents the height of the satellite, and $R_{x}$, $T_{x}$, and ${\text{IPP}}$ represent the location of the LEO satellite, GNSS satellite, and ionospheric pierce point, respectively

The VTEC parameterization approach is as follows:

$${\text{VTEC}}\left( {\varphi ,s} \right) = \mathop \sum \limits_{n = 0}^{N} \mathop \sum \limits_{m = 0}^{n} \tilde{P}_{nm} \left( {\sin \varphi } \right)\left( {C_{nm} \cos \left( {{\text{ms}}} \right) + S_{nm} \sin \left( {{\text{ms}}} \right)} \right)$$

(7)

$$\Lambda = \sqrt {\frac{{2\left( {2n + 1} \right)\left( {n - m} \right)!}}{{\left( {1 + \delta_{nm} } \right)\left( {n + m} \right)!}}}$$

(8)

$$\delta_{nm} = \begin{array}{*{20}c} 0 &\quad {n \ne m} \\ 1 & \quad{n = m} \\ \end{array}$$

(9)

$$I_{t} = {\text{MF}} \cdot \mathop \sum \limits_{n = 0}^{N} \mathop \sum \limits_{m = 0}^{n} \tilde{P}_{nm} \left( {\sin \varphi } \right)\left( {C_{nm} \cos \left( {{\text{ms}}} \right) + S_{nm} \sin \left( {{\text{ms}}} \right)} \right) - B_{r}$$

(10)

where ${\text{VTEC}}$ is the vertical total electron content, $\varphi$ is the latitude of the pierce point, s is the longitude of the pierce point, $\tilde{P}_{nm}$ is the normalized Legendre polynomials, $C_{nm}$ and $S_{nm}$ are the spherical harmonic coefficients, $\Lambda$ is the normalization factor used in $\tilde{P}_{nm} = \Lambda \left( {n,m} \right)P_{nm}$, $\delta_{nm}$ is the Kronecker delta, $I_{t}$ is the observation vector, and ${\text{MF}}$ is the mapping function. Here, we set the SHE degree as 15, while the spatial resolution is 2.5° in latitude and 5° in longitude. The receiver DCBs are regarded as a constant during one single day, and VTEC parameterization is done based on daily topside observations accordingly.

Finally, we solve the following least square equations with an empirical inequality constraint to estimate the SHE coefficients and DCBs at the same time. Note that the reason why we use an empirical constraint here is not only to avoid the anomaly of the VTEC map which is caused by insufficient global observation coverage but also to make the DCB estimation more rational. The main idea of solving the ICLS problems is to transform the least square equations to a corresponding linear complementarity problem (LCP):

$$y = B\beta + \varepsilon$$

(11)

$$G\beta \ge c$$

(12)

$$G\beta - c = h$$

(13)

Thus, the cost function can be extended as:

$$f(x) = \frac{1}{2}\left( {y - B\beta } \right)^{{{T}}} P\left( {y - B\beta } \right) - q^{{{T}}} \left( {G\beta - c - h} \right)$$

(14)

Kuhn–Tucker condition (Boyd et al. 2004):

$$q,\;h \ge 0,\;q^{T} h = 0$$

(15)

where $y$ is the observation vector, $B$ is the observation matrix, $\beta$ is the parameter vector to be determined, $P$ is the inverse of the covariance matrix, which is set to be an identity matrix here, $\varepsilon$ is the error vector, $G$ is a constraint matrix which is set as a matrix with 5184 (72 × 72) rows and 256 (16 × 16) columns, $c$ is a constant vector, and $f(x)$ is the extended cost function; both vectors to be determined, $q$ and $h$, satisfy the Kuhn–Tucker condition. Note that (12) is the inequality constraint.

The constraint can come from an empirical background model; the Neustrelitz plasmasphere model (NPSM) (Jakowski and Hoque 2018) was selected here. Because of the strong magnetic local time (MLT) dependency of topside ionospheric VTEC, we introduce a spatial–temporal constraint here, globally for each grid,

$${\text{VTEC}} \in \begin{array}{*{20}l} {\left( {0,4} \right]\quad {\text{High}}\;{\text{latitude}}} \hfill \\ {\left( {2,6} \right] \quad {\text{Mid}}\;{\text{latitude}}} \hfill \\ {\left( {5,10} \right]\quad {\text{Low }}\;{\text{lat}}\;{\text{day}}} \hfill \\ {\left( {2,6} \right]\quad {\text{Low}}\;{\text{lat}}\;{\text{night}}} \hfill \\ \end{array}$$

(16)

The admissible ranges for global VTEC are presented in (16). According to ionospheric TEC models, daytime here refers to the time period from 8 to 20 MLT, while nighttime represents the time period from 20 to 8 MLT.

Set the gradient of the extended cost function to 0,

$$\nabla_{\beta } f\left( x \right) = B^{{{T}}} PB\beta - B^{{{T}}} Py - G^{{{T}}} q = 0$$

(17)

Therefore, the optimal solution satisfies,

$$\hat{\beta } = \left( {B^{{{T}}} PB} \right)^{ - 1} \left( {B^{{{T}}} Py + G^{{{T}}} q} \right)$$

(18)

When we substitute (18) into $G\hat{\beta } - c = h$, we derive

$$h - Mq = w,\;{\text{where}}\;\left\{ {\begin{array}{ll} {w = G\hat{\beta }_{0} - c} \\ {M = G\left( {B^{T} PB} \right)^{ - 1} G^{T} } \\ \end{array} } \right.$$

(19)

where q and h are two unknown vectors in the Kuhn–Tucker condition, $\hat{\beta }_{0}$ is the optimal solution without any constraint, and $M$ and $w$ can be calculated from the known parameters.

After transformation from ICLS to LCP, we then apply the Lemke algorithm (Cottle et al. 1992) to solve the LCP that is equivalent to the original ICLS problem. As soon as we get h and q, the optimal solution can be easily derived with (18). The Lemke algorithm is known as an iterative process designed specifically for solving LCP within finite steps. In brief, the procedure used in the Lemke algorithm is as follows:

• 1. If w is positive, one of the optimal solutions should be $\left\{ {h = w,\;q = 0} \right\}$.

• 2. Otherwise, we additionally introduce a new vector $e \cdot q_{0}$, which may satisfy $h - Mq - eq_{0} = w$. e denotes a unit column vector of n dimension, and n is the dimension of h

  The strategy used to determine $q_{0}$ is

  $$q_{0} = \max \left\{ { - q_{i} } \right\}$$

  (20)

  Because w is replaced by $w = w - e \cdot q_{0}$, which is positive, now one of the optimal solutions should be $\left\{ {h = w,\;q = 0,\;q_{0} } \right\}$. Please refer to Table 2 for more details on the initial state of the Lemke algorithm.

  Table 2 Initial state of the Lemke algorithm

• 3. Then we start an iterative process in order to eliminate $q_{0}$ in the optimal solutions. The element to be eliminated next is called $y_{s}$. In the first step, $y_{s}$ becomes $q_{0}$ and the column number s becomes the same number as the column of the maximum value of $\left\{ { - q_{i} } \right\}$. The elements with the coefficient value that is equal to 1 are so-called basic elements. Obviously, in the beginning, the basic elements include all elements of h except $h_{s}$ and $q_{0}$.

• 4. In order to keep w positive, we need to find the row number r that satisfies

  $$\frac{{q_{i} }}{{d_{is} }} = \min \left\{ {\left. {\frac{{q_{i} }}{{d_{is} }}} \right|d_{is} > 0} \right\}$$

  (21)

  $d_{is}$ is the coefficient column vector of $y_{s}$. After this, we eliminate principal components with an element in the same column as $y_{s}$ and row of r. If the element eliminated in this step is $h_{l}$, ${\text{ then}}\; y_{s}$ should be $q_{l}$ in the next step. Otherwise, $y_{s}$ should be $h_{l}$ in the next step. Then go back to step (3).

• 5. If the element eliminated in this step is $q_{0}$, one of the optimal solutions can be obtained with the basic elements excluding the auxiliary element $q_{0}$.

Performance analysis of ICLS methods

In order to evaluate the performance of the ICLS technique, the RMS and STD are required to evaluate the errors with respect to UCAR and self-consistency, respectively,

$$\begin{aligned} {\text{RMS}} & = \sqrt {\frac{{\sum {\left( {{\text{DCB}}_{{{\text{ICLS}}}} - {\text{DCB}}_{{{\text{UCAR}}}} } \right)^{2} } }}{N}} \\ {\text{STD}} & = \sqrt {\frac{{\sum {\left( {{\text{DCB}}_{{{\text{ICLS}}}} - \overline{{DCB}} _{{{\text{ICLS}}}} } \right)^{2} } }}{{N - 1}}} \\ \end{aligned}$$

(22)

where ${\text{DCB}}_{{{\text{ICLS}}}}$ is the DCB estimated based on ICLS, $\overline{{{\text{DCB}}}}_{{{\text{ICLS}}}}$ is the corresponding monthly average DCB value, and $N$ is the number of days, i.e., 31.

Figure 4 shows the monthly series of DCBs of six COSMIC receivers that provide most of the topside observations during January 2008. Corresponding RMS values are given in Tables 3 and 4 for IPP at 1000 km and 1400 km, respectively. After changing the single-layer height to 1400 km, the RMS values of the six selected receivers decreased by 42.2%, 9.8%, 20.7%, 40.9%, 31.9%, and 10.3%, respectively, which implies that the performance of the F&K geometric MF is better at 1400 km than at 1000 km. From the monthly series of COSMIC DCBs, we can see that at an SLM height of 1000 km, DCB values based on ICLS are generally higher than UCAR DCB products. After trying to change the SLM height, we find a strong DCB dependence on single-layer height under the same constraints, which can be seen in Fig. 4. When changing the single-layer height from 1000 to 1400 km, DCBs estimated based on ICLS become considerably lower and much closer to UCAR products. It can be concluded that the single-layer height plays an important role in receiver DCB estimates based on the ICLS method and single-layer MF. Therefore, errors from the uncertainty of the single-layer height need to be mitigated. Another characteristic that can be concluded from Fig. 4 is that there is a generally upward (positive) drift between DCB estimated by ICLS and UCAR products.

Fig. 4

Comparisons of the monthly series of six COSMIC receiver DCBs during January 2008 based on ICLS-1000 km, ICLS-1400 km, and UCAR (unit: TECU)

Table 3 Monthly LEO DCB estimation errors with respect to UCAR using ICLS with a geometric MF (1000 km single-layer height) for different COSMIC POD receivers during January 2008

Table 4 Monthly LEO DCB estimation errors with respect to UCAR using ICLS with a geometric MF (1400 km single-layer height) for different COSMIC POD receivers during January 2008

For COSMIC-1 POD receiver 1, the DCBs estimated from ICLS are very consistent with UCAR products during the first 7 days in January 2008. Nevertheless, the DCBs estimated both before and after changing the single-layer height are not very consistent with UCAR products, especially after January 8, 2008. We find that there are a lot of negative STEC values in the podTEC products provided by UCAR during this period, which may partially result from the local spherical symmetric assumption in UCAR data processing. Here, due to the plasmaspheric VTEC constraints, DCB values estimated from ICLS for COSMIC-1 are expected to be higher than UCAR products for keeping the VTEC values positive. The reason for the existence of many negative values may be the underestimation of LEO receiver DCBs when using the UCAR method. When using ICLS, the number of abnormal STEC values can be dramatically decreased, which is shown in Fig. 5.

Fig. 5

Number of negative STEC values using ICLS with a multi-layer MF (green) and from UCAR products (black)

Mapping function effects

By fixing the shell height at a certain value, the thin-shell MF is only dependent on the ray path elevation angle. It ignores the vertical structure of the ionosphere as well as the horizontal gradients of the ionosphere. As already mentioned, we apply a multi-layer MF approach here in order to mitigate the mapping errors.

The MF or obliquity factor is computed for each LEO-GPS ray path using Global Ionosphere Maps (GIM) and a multi-layer ionosphere assumption. Since GIMs provide two-dimensional (2D) TEC maps, the common practice is to use single-layer MF from slant to the vertical conversion. Instead of collapsing the vertical structure of the ionosphere into a thin shell, we consider that the ionosphere is composed of numerous thin shells in between of which the vertical structure is modeled by a Chapman profile (Rishbeth and Garriott 1969) and a superposed exponential decay function for describing the topside ionosphere and plasmasphere. Thus, the ionosphere and plasmasphere is modeled by

$$n_{{\text{e}}}^{I} \left( h \right) = N_{m} \exp \left( {\frac{1}{2}\left( {1 - z - \exp \left( { - z} \right)} \right)} \right)$$

(23)

$$n_{{\text{e}}}^{P} \left( h \right) = n_{{\text{p}}} \exp \left( { - \frac{h}{{H_{{\text{p}}} }}} \right)$$

(24)

where N_m is the peak electron density observed at the altitude h_m, $z = \frac{{h - h_{m} }}{H}$, and H is the atmospheric scale height. The quantity n_p is the plasmaspheric basic density of electrons, and H_P (10,000 km) is the mean scale height of the plasma density.

In the approach, the MF is defined by

$${\text{MF}}_{{\text{multi } - \text{ layer}}} = \frac{{{\text{STEC}}_{{{\text{model}}}} }}{{{\text{VTEC}}_{{{\text{model}}}} }}$$

(25)

where STEC_model is the slant TEC along the LEO-GPS path and VTEC_model is the corresponding VTEC. The VTEC is defined as the VTEC from the LEO orbit height up to the GPS orbit height for which the measurement point is considered to be the IPP location at 1000 km height along the slant path. The MF is computed for each LEO-GPS path using the 2D TEC map together with the multi-layer ionosphere and plasmasphere model, as described below.

The ionosphere is considered to be composed of numerous thin shells. A slant path intersects each ionospheric shell characterized by shell heights of h₁… h_n (see Fig. 6 for illustration). The intersection points are projected at a 2D thin-shell surface where corresponding vertical TECs are computed from a TEC map as VTEC_IPP1, VTEC_IPP2 … VTEC_IPPi. In the present investigation, the thin-shell height is set to 450 km since the CODE TEC maps used are optimized for this height.

Fig. 6

Slant path intersects ionospheric layers at different shell heights

The incremental STEC, namely ΔSTEC₁, ΔSTEC₂ … ΔSTEC_i, is computed along the ray path, multiplying the VTEC_IPP1, VTEC_IPP2 … VTEC_IPPi by the corresponding obliquity factors determined from the Chapman layer function by Hoque and Jakowski (2013)

$$F_{i} \left( {h_{i} ,\beta } \right) \approx \frac{1}{{\sqrt {1 - \left( {\frac{{\left( {h_{i} + R_{{\text{e}}} } \right)\cos \left( {\theta_{i} } \right)}}{{h_{{m{\text{IPP}}i}} + R_{{\text{e}}} }}} \right)^{2} } }}\left[ {{\text{erf}}\left( { - \frac{{\exp \left( { - \frac{{h_{i} - h_{{m{\text{IPP}}i}} }}{{H_{{m{\text{IPP}}i}} }}} \right)}}{\sqrt 2 },} \right)} \right]_{{h_{i} }}^{{h_{i + 1} }}$$

(26)

where erf is the error function (see https://en.wikipedia.org/wiki/Error_function for more details), $h_{i}$ and $h_{i + 1}$ are the lower and upper shell heights of the ith layer along the ray, respectively, $\theta_{i}$ is the elevation angle at the lower shell height, ${\text{erf}}$ is the error function, $h_{{m{\text{IPP}}i}}$ is the peak ionization height, $H_{{m{\text{IPP}}i}}$ is the atmospheric scale height, and $R_{{\text{e}}}$ is the average radius of earth.

Finally, STEC is computed by summing all the ΔSTEC values. This represents STEC_model in (25). Similarly, VTEC_model in (25) is computed by taking the intersection points along the vertical direction at the IPP location, which is considered to be at a height of 1000 km along the LEO-GPS path. In this case, although VTEC_IPP1, VTEC_IPP2 … VTEC_IPPi obtained from the CODE TEC map are the same, and the obliquity factors are not the same, the obliquity factors are determined by (26) and multiplied by the VTEC_IPP value. Thus, when both STEC_model and VTEC_model are computed, finally MF_multi-layer is computed in a final step using (25). It should be noted that the height of the pierce point that affects the latitude and longitude of the pierce point does not significantly influence the performance of the multi-layer MF, which is shown in Fig. 7.

Fig. 7

A comparison example illustrating the multi-layer MF (blue and red lines) and the other two commonly used MFs (black and orange lines), as well as the change of azimuth (green line). Note that the pierce point height here, where the VTEC is computed, is 1000 km

For the present analysis, the parameters such as peak ionization height hm_IPPi and atmospheric scale height H_IPPi are kept constant at 350 km and 70 km, respectively (i.e., fixed parameters). Results could be improved by knowing their actual values, e.g., from supplementary measurements. The slant distance between consecutive shells is kept constant at a height of 100 km up to 2000 km and then 2000 km up to the GNSS satellite height of approximately 20,200 km. Alternatively, the peak height hmF2 can be derived from the Neustrelitz Peak Height Model (Hoque and Jakowski 2012) and the scale height H can be derived from NTCM together with the Neustrelitz Peak Density Model (Hoque and Jakowski 2011) via slab thickness estimation and Chapman layer assumption. The mapping results using model-derived values or fixed values are shown as mod and fix in Fig. 7, respectively.

Figure 7 shows a comparison example illustrating three different MFs, i.e., multi-layer MF, cosine MF, F&K geometric MF, as well as the variation of the azimuth angle. Note that multi-layer MF includes two different versions: model and fixed parameter. As mentioned above, we can see from the figure that these three MFs are generally fairly consistent in variation, but the values for the multi-layer functions are smaller, especially in the case of lower elevations. Note that in the case of IPP crossing the equatorial region, the multi-layer MF decreases slightly, probably due to the horizontal gradient provided by GIM. Two important parameters to be determined in multi-layer MF include ionospheric electron density peak height hmF2 and atmospheric scale height H, which can be estimated from NPHM, NTCM, and NPDM as already mentioned. Here, we use the multi-layer MF, utilizing these models rather than fixed parameters, which means that hmF2 is derived from the NPHM model.

Figure 8 shows comparisons of the monthly series of six COSMIC receiver DCBs based on different MFs during January 2008. As we can see from this figure, there is no big difference before and after changing the pierce point height. This implies that the utilization of multi-layer MF can mitigate the uncertainty from the single-layer height. Comparing Tables 2, 3, 4, and 5, we see that the accuracy of DCB values, except C6 POD1, estimated by ICLS is considerably improved after replacing the geometric MF with the multi-layer MF. For C6 POD1, the RMS and mean deviation of DCB values based on multi-layer MF are slightly larger than those based on the single-layer MF. The reason why the DCB accuracy of the COSMIC 6 POD 1 receiver somehow decreased is complicated. There are several reasons, such as errors from GIM, ionospheric modeling, inequality constraint, and the UCAR products itself. One of the possible reasons is that the DCB of C6 POD1 is one of the most variant DCBs of COSMIC receivers. Another possible reason is that most of the topside observations from the COSMIC 6 satellite occurred during 6–8 and 18–20 MLT when the Chapman layer may not exist. Figures 9 and 10 illustrate the daily absolute deviation and monthly mean deviation, respectively. From these figures, we can conclude that the first five of the receiver DCBs based on ICLS and the multi-layer MF are improved compared with those based on ICLS and the single-layer MF. In the case of COSMIC 6 POD1, the mean deviations for these three MF variations are similar. With the help of the multi-layer MF, the mean deviations of DCBs for the first five receivers compared with those based on the geometric MF at 1000 km (red column) decrease by 75%, 23%, 44%, 69%, and 49%, respectively. The mean deviations of DCBs for the first five receivers compared with those based on the geometric MF at 1400 km (black column) decrease by 59%, 15%, 26%, 47%, and 22%, respectively.

Fig. 8

Comparisons of the monthly series of six COSMIC receiver DCBs during January 2008 based on ML-1000 km, ML-1400 km, and UCAR (unit: TECU)

Table 5 Monthly LEO DCB estimation errors using ICLS with the multi-layer MF for different COSMIC POD receivers during January 2008

Fig. 9

Daily absolute deviations between UCAR products and DCB values based on ICLS using single-layer (geometric) MF at 1000 km (red) and 1400 km (black) and the multi-layer MF (green) during January 2008. The unit is TECU

Fig. 10

Mean deviations between COSMIC DCB values based on ICLS and UCAR products during January 2008

Figure 11 illustrates a plasmaspheric VTEC map above 800 km, modeled in the geomagnetic frame on Jan 1, 2008. After applying the empirical inequality constraints, not only are there no abnormal values on the VTEC map, but it also shows reasonable MLT and a seasonal feature, which, in turn, also validates the DCB estimations. As is shown above, if we were able to get more accurate information on the topside ionosphere, the accuracy of VTEC modeling and LEO DCB would be improved simultaneously.

Fig. 11

VTEC map above 800 km up to GPS height modeled based on the multi-layer MF in the geomagnetic reference frame on Jan 1, 2018

Further validation by satellite DCB estimates

In order to enhance the illustration of the feasibility of the ICLS method, we present a comparison between our results and the CODE DCB product. The strategy to estimate the satellite DCBs is similar to the ICLS method and multi-layer MF mentioned earlier, which means that the satellite DCBs are to be solved as an independent parameter and separated from receiver DCBs based on a zero-mean condition rather than using the CODE DCB product. However, during the period of interest, there were some GPS satellites that did not provide any topside observations. The information on these satellites is presented in Table 6. Furthermore, this fact forces us to adopt the corresponding satellite DCB from the CODE DCB product to maintain the stability of the other satellite DCB estimates when some of the satellites were not working correctly. The results of satellite DCB estimates are presented in Fig. 12; the results of PRN 07 were omitted due to its frequent malfunctions. It is necessary to note that because there is no satellite DCB of PRN 07 available in the CODE DCB product after January 16, 2008, we do not present the satellite DCB estimates for the second half of January 2008. The stabilities of the DCB time series based on the COSMIC constellation and ICLS method and comparisons between our DCB estimates and the CODE DCB product are shown in Fig. 13. According to the stability analysis and comparison to the CODE DCB product, it can be concluded that the STD and RMS with respect to the CODE product of all DCB estimates vary between 0.16 and 0.09 ns (with a median value of 0.12 ns) and between 0.42 and 0.08 ns (with a median value of 0.16 ns), which shows a similar stability compared with the results by other researchers (Lin et al. 2016). The comparison between the satellite DCB based on COSMIC topside observations and ICLS method and CODE DCB product also provides substantial validation of the method mentioned above.

Table 6 Information on satellites that did not provide any topside observations with COSMIC constellation

Fig. 12

Time series of all GPS satellite DCB estimates except for PRN 07 based on the COSMIC constellation and ICLS method during the first half of January 2008

Fig. 13

Standard deviations for the DCB time series based on the COSMIC constellation and the ICLS method and root-mean-square error with respect to the CODE DCB product

Conclusion

We applied an empirical inequality constraint on the traditional least square processes and multi-layer MF to estimate the LEO DCB with a VTEC map together in the geomagnetic reference frame. The most important improvements obtained include the following:

• 1. COSMIC GPS receiver DCBs based on ICLS show significant consistency with UCAR products. The RMS values when applying a multi-layer MF compared to UCAR products are within 0.9 TECU (0.31 ns). The corresponding STD values are below 0.5 TECU (0.17 ns).

• 2. The performances of estimated DCBs based on ICLS strongly depend on the accuracy of the MFs and single-layer height in the widely used MFs such as geometric mapping.

• 3. The multi-layer MF can effectively mitigate the influence of the uncertainty with respect to the single-layer height. Meanwhile, with the help of the multi-layer MF, the mean deviations of DCBs for the first five receivers compared with those based on the geometric MF at 1400 km were decreased by 59%, 15%, 26%, 47%, and 22%, respectively.

• 4. LEO GPS receiver DCBs based on ICLS can decrease the amount of negative STEC observations, which helps to make plasmaspheric observations, such as slant TEC observations, more rational.

• 5. The feasibility of the ICLS method and multi-layer MF approach is validated by comparing the satellite DCB based on COSMIC topside observations and ICLS method and CODE DCB product. The median values of STD and RMS with respect to the CODE DCB product are 0.12 and 0.16 ns, respectively.

In addition, this approach relies on the accuracy of information about the topside ionosphere and plasmasphere. With the launch of more LEO satellites such as Swarm and COSMIC-2, more and more observations on the plasmasphere are available, which facilitates an accurate estimation of the required topside ionosphere and plasmasphere information so that we can estimate the DCB as well as plasmaspheric VTEC more precisely in the future.