Introduction

Global navigation satellite systems (GNSSs) constitute a vital infrastructure for positioning, navigation and timing (PNT). However, GNSSs are severely limited in environments with strong attenuation, such as in dense cities and indoors, where they can easily suffer from jamming and spoofing due to their weak signals. Additionally, without augmentation from a densely distributed regional reference network, precise point positioning (PPP) and long-baseline real-time kinematic positioning always take a long time to obtain an ambiguity-fixed solution. In response to the emergence of proposals for megascale low earth orbit (LEO) broadband constellations presented by several internationally renowned companies, such as OneWeb, SpaceX and Boeing, since 2014, Reid et al. (2016) explored the feasibility of using these commercial constellations as complements to GNSSs for navigation based on a full system architecture. Not only for the fully deployed Iridium NEXT constellation but also for China’s future Hongyan and Hongyun constellations, the integration of communication and navigation has been considered (Meng et al. 2018). Compared to GNSS satellites in medium earth orbit (MEO), geostationary earth orbit (GEO) or inclined geosynchronous orbit, LEO satellites are closer to the earth, thus experiencing less free space loss and providing approximately 30 dB higher strength for a 1.5 GHz signal (Enge et al. 2012), which also means better antijamming and antispoofing performance. In addition, LEO satellites can be used as space-based monitor stations by incorporating their onboard data into precise GNSS orbit determination to augment the orbital accuracy of both GNSS and LEO satellites (Zhu et al. 2004). Moreover, a LEO satellite travels overhead more quickly than a MEO satellite, passing in minutes instead of hours. This gives rise to more multipath rejection because reflections are no longer static over the shorter averaging time. Their faster motion also contributes to rapid changes in spatial geometry, allowing for rapid convergence and initialization of ambiguity in LEO-augmented GNSS precise positioning (Rabinowitz et al. 1998). The performance of navigation augmentation has been found to be positively related to the number of visible LEO satellites and to be uneven along the north–south direction for a single polar-orbit constellation, as fewer satellites can be observed in low-latitude regions (Li et al. 2019). As a result, constellation design is a critical task for a LEO-based navigation augmentation system.

The aim of a constellation design is to distribute multiple satellites with similar types of functions into similar or complementary orbits to accomplish specific tasks under shared control. Related to the goal of continuous coverage, conventional constellation design usually relies on analytical methods, such as the streets of coverage method (Lüders 1961), the Walker approach (Walker 1970) or the orthogonal circular-orbit method (Wu and Wu 2008). Another method for hybrid multitiered constellation design with variations in orbital altitude and inclination but an equal regression rate for ascending nodes has been proposed by Razoumny et al. (2014). The basic idea is to reduce redundant coverage by dividing the earth’s surface into several latitudinal belts that can be collaboratively addressed by subconstellations adopting different pairs of orbital altitude and inclination, allowing for more even coverage, minimized revisit time or a reduced number of satellites. Note that the LEO constellations announced by SpaceX and Telesat are both hybrid in nature; details are given in Table 1 (del Portillo et al. 2019). The coverage performance of a given hybrid Walker/Walker or polar-orbit/Walker LEO constellation has also been compared with that of a single constellation by Yang et al. (2016). Regarding the optimization of a combined Walker constellation, Xue and Yang (2015) deduced a conditional equation for determining the optimal inclination combination, which varies with the number of satellites in each subconstellation, to minimize the geometric dilution of precision (GDOP) at the geocenter. Notably, however, this equation is suitable only for MEO constellations and not for LEO constellations because most LEO satellites are invisible from the earth’s surface; thus, there is a considerable distinction between surficial GDOP optimization and geocentric GDOP optimization (Xue 2018). He and Hugentobler (2018) used an enumeration method to determine the optimal combinations of inclinations and orbital altitudes for a given hybrid Walker/Walker LEO constellation to obtain a more even distribution of the number of visible satellites along the north–south direction for positioning. However, this method becomes ineffective when solving more complex multivariable and multiobjective optimization problems. Hence, genetic algorithms (GAs) have been introduced as a robust technique for obtaining a globally optimal solution through stochastic and heuristic search strategies.

Table 1 Summary of commercial LEO constellations proposed by SpaceX and Telesat
Full size table

A GA for constellation design was initially proposed to obtain an optimal satellite constellation geometry with discontinuous global coverage (Frayssinhes 1996; George 1997). Later, Asvial et al. (2003) proposed an approach for designing hybrid LEO/MEO, LEO/GEO and MEO/GEO constellations based on a GA. The results showed that 100% availability of dual satellite diversity was achieved, thus providing highly reliable satellite communication services. For regional positioning, a LEO constellation design method using a GA and gradient-based optimization was developed by Shtark and Gurfil (2018), and the generated constellation was fine-tuned to minimize the GDOP at a desired geodetic coordinate. For global navigation, Pan et al. (2018) established a LEO constellation optimization model using a GA with unevenly distributed right ascension of the ascending nodes (RAAN), aiming at GDOP optimization for several important cities worldwide with minimization of the cost of construction. However, GNSSs are the mainstream means of offering PNT services, and the total number of corresponding satellites is anticipated to reach 120 by 2020. Therefore, it is necessary to establish not another stand-alone navigation system with an optimized GDOP but rather a LEO-based navigation augmentation system that takes advantage of orbital diversity to improve availability, robustness and convergence. Our previous simulations have shown that the convergence time for full operational capability multi-GNSS PPP can be significantly shortened from 9.6 min to 7.0, 3.2, 2.1 or 1.3 min through augmentation with 2.4, 3.1, 6.3 or 9.5 visible LEO satellites, respectively (Li et al. 2019). In addition, to achieve more even augmentation performance around the world, a hybrid-type constellation is preferred.

We propose several hybrid LEO-augmented constellations optimized with a GA for rapid, precise positioning based on two objectives. The first objective (O1) is to allocate a limited number of LEO satellites, e.g., 100 satellites, to a proper hybrid constellation such that the average number of visible satellites is as large and as evenly distributed worldwide as possible. The second objective (O2) is to determine the required number of LEO satellites to enable globally even coverage with different elevation mask angles and different levels of satellite visibility.

Typical constellations

Polar-orbit constellations and Walker constellations are typically employed in communication and navigation systems. Also, an orthogonal circular-orbit constellation is a modification of the polar-orbit constellation type. Thus, we describe the characteristics and coverage performance of these typical constellations, and all hybrid constellations considered in this study can be decomposed into two of these types.

Polar-orbit constellation

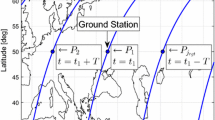
A polar orbit is an orbit in which a satellite travels in the north–south direction over both poles of the earth, i.e., the orbital inclination is 90°. Several polar-orbit planes with the same number of satellites, the same orbital altitude and specific spatial-phase relationships constitute a polar-orbit constellation. Such a constellation is always designed based on the streets of coverage method, in which multiple satellites in the same plane form a continuous coverage strip due to overlap and multiple strips associated with different planes enable continuous global or zonal coverage. As illustrated in Fig. 1, the angular radius \( \alpha \) with respect to the geocenter between the subsatellite point and the edge of coverage is expressed as

$$ \alpha = \arccos \left( {\frac{{R_{ \oplus } }}{{h + R_{ \oplus } }} \cdot \cos \varepsilon } \right) - \varepsilon $$
(1)

where \( R_{ \oplus } \) is the radius of the earth, i.e., 6378.137 km, h is the orbital altitude and \( \varepsilon \) is the elevation mask angle. The half-width c of the continuous coverage strip (green) can be calculated in accordance with the following formula from spherical trigonometry:

$$ c = \arccos \left[ {\frac{\cos \alpha }{{\cos \left( {{\pi \mathord{\left/ {\vphantom {\pi {S_{\text{p}} }}} \right. \kern-0pt} {S_{\text{p}} }}} \right)}}} \right] $$
(2)

where Sp is the number of polar-orbit satellites per plane. The left plot illustrates corotating orbits, between which the longitude difference \( \Delta_{ 1} \) is expressed as

$$ \Delta_{1} = \left( {\alpha + c} \right)\eta $$
(3)

where \( \eta \) is a scale factor and is no larger than 1. Moreover, the phase difference between satellites in adjacent corotating orbits is \( {\pi \mathord{\left/ {\vphantom {\pi {S_{\text{p}} }}} \right. \kern-0pt} {S_{\text{p}} }} \) and remains constant. The right plot illustrates counterrotating orbits. Due to the time-varying phase difference, the corresponding longitude difference \( \Delta_{2} \) must be smaller; it is given by

$$ \Delta_{2} = 2c\eta $$
(4)
Fig. 1
figure 1

Coverage of satellites in adjacent corotating (left) and counterrotating (right) orbits. The red arrows indicate the travel directions of the satellites. The black dots and circles denote the subsatellite points and edges of coverage, respectively. The green strips and black dotted lines represent the continuous coverage areas

Full size image

A top view of a polar-orbit constellation is shown in Fig. 2. The largest orbital spacing appears at the equator. Hence, global coverage can be guaranteed if continuous coverage is achieved in the equatorial region, i.e., the condition for continuous global coverage with one visible satellite is expressed as

$$ \left( {P_{\text{p}} - 1} \right)\Delta_{1} + \Delta_{2} = \left[ {\left( {P_{\text{p}} - 1} \right)\alpha + \left( {P_{\text{p}} + 1} \right)c} \right]\eta = \pi $$
(5)

where Pp is the number of polar-orbit planes. If we apply (1) and (2) to (5), Pp and Sp can be determined with integer constraints for a given orbital altitude and elevation mask angle.

Fig. 2
figure 2

Top view of a polar-orbit constellation

Full size image

Orthogonal circular-orbit constellation

To compensate for the sparse coverage of a polar-orbit constellation in the equatorial region, Wu and Wu (2008) introduced an equatorial orbit, thus forming an orthogonal circular-orbit constellation. The overlaps of the equatorial satellites constitute a continuous coverage strip with its edge reaching a latitude of

$$ \varphi = \arccos \left[ {\frac{\cos \alpha }{{\cos \left( {{\pi \mathord{\left/ {\vphantom {\pi {S_{\text{e}} }}} \right. \kern-0pt} {S_{\text{e}} }}} \right)}}} \right] $$
(6)

where Se is the number of equatorial satellites. This modification also relaxes the condition for continuous global coverage as we need to consider only the coverage of the spherical cap beyond this latitude; therefore, (5) can be adjusted as follows:

$$ \left[ {\left( {P_{\text{p}} - 1} \right) \cdot \arcsin \left( {\frac{\sin \alpha }{\cos \varphi }} \right) + \left( {P_{\text{p}} + 1} \right) \cdot \arcsin \left( {\frac{\sin c}{\cos \varphi }} \right)} \right]\eta = \pi $$
(7)

By substituting (6) into (7) and rearranging the equation, we can obtain the following expression:

$$ \left\{ {\left( {P_{\text{p}} - 1} \right) \cdot \arcsin \left[ {\tan \alpha \cdot \cos \left( {{\pi \mathord{\left/ {\vphantom {\pi {S_{\text{e}} }}} \right. \kern-0pt} {S_{\text{e}} }}} \right)} \right] + \left( {P_{\text{p}} + 1} \right) \cdot \arcsin \left[ {\frac{{\sin c \cdot \cos \left( {{\pi \mathord{\left/ {\vphantom {\pi {S_{\text{e}} }}} \right. \kern-0pt} {S_{\text{e}} }}} \right)}}{\cos \alpha }} \right]} \right\}\eta = \pi $$
(8)

Based on (1), (2), (3), (4) and (8), we can determine the configuration of an orthogonal circular-orbit constellation.

Walker constellation

The most symmetric and famous constellation type is the Walker constellation, which comprises several circular orbits of the same altitude and inclination. The RAAN of each orbital plane is evenly distributed in the reference plane, e.g., the equatorial plane, and all satellites are evenly distributed in orbital planes. Because of this evenness, the Walker constellation provides regular global or zonal coverage. Note that with a single Walker constellation in LEO, it is difficult to realize global coverage with the RAAN spread angle of 360° (Yang et al. 2016).

The geometry of a specific Walker constellation can be represented by three parameters Tw/Pw/Fw, where Tw denotes the total number of satellites, Pw is the number of planes and Fw denotes the phase difference between satellites in adjacent planes. Assuming that Sw is the number of satellites per plane, we have Tw = PwSw. To determine the angle between satellites in adjacent planes, we multiply the parameter Fw by 360°/Tw.

We define the first satellite in the first orbital plane as the nominal satellite. The orbital elements for the jth satellite in the ith plane of a Walker constellation can be expressed as

$$ \left\{ {\begin{array}{*{20}l} {a_{ij} = a_{0} } \hfill \\ {e_{ij} = e_{0} } \hfill \\ {I_{ij} = I_{0} } \hfill \\ {\varOmega_{ij} = \varOmega_{0} + \frac{360^\circ }{{P_{\text{w}} }} \cdot \left( {i - 1} \right)} \hfill \\ {\omega_{ij} = \omega_{0} } \hfill \\ {\mathcal{M}_{ij} = \mathcal{M}_{0} + \frac{360^\circ }{{P_{\text{w}} S_{\text{w}} }}F_{\text{w}} \cdot \left( {i - 1} \right) + \frac{{360^{ \circ } }}{{S_{\text{w}} }} \cdot \left( {j - 1} \right)} \hfill \\ \end{array} } \right. $$
(9)

where \( a_{0} \), \( e_{0} \), \( I_{0} \), \( \varOmega_{0} \), \( \omega_{0} \) and \( \mathcal{M}_{0} \) represent the semimajor axis, eccentricity, inclination, RAAN, argument of perigee and mean anomaly, respectively, of the nominal satellite at the initial epoch.

Once the initial orbital elements of all satellites have been obtained, it is always possible to uniquely calculate the position and velocity vectors as described in an earth-centered inertial frame, regardless of the constellation type (Montenbruck and Gill 2000). Then, by means of the orbit integration technique, we can generate the orbits for an entire regression period in order to evaluate the coverage performance of the constellation.

Constellation design

To narrow the scope of optimization and increase efficiency, we first fix part of the constellation configuration. Then, we propose several schemes for hybrid LEO constellations and use a GA to optimize them. Finally, the complete optimization procedure is described in detail.

Fixing part of the constellation configuration

Depending on their eccentricity, orbits can be divided into two types: circular orbits and highly elliptical orbits. An elliptical-orbit satellite travels slowly near the apogee and rapidly near the perigee. In addition, to make the perigee stable under actual gravity-disturbed conditions, a critical inclination of 63.4° is always employed; thus, the coverage in high-latitude regions is much wider than that in mid- to low-latitude regions. This unevenness in velocity and coverage is unfavorable for navigation augmentation. Moreover, circular orbits with the same inclination favor similar behavior of the satellites under orbital perturbations and minimize the dynamic distortions of the constellation. Therefore, only circular orbits are considered in the following, and both the eccentricity and argument of perigee are ideally set to 0.

To determine the orbital altitude, many factors, including the distribution of space objects, the radiation environment, the regression period, the coverage and the atmospheric drag effect, must be considered. Figure 3 shows the distribution of space objects in LEO until March 31, 2019, based on data from the Web site of the Air Force Space Command (https://www.space-track.org/#ssr). We prefer not to choose an altitude between 500 and 1000 km, where most operating satellites and space debris are concentrated, to avoid collisions. The total ionizing dose in silicon over a 5-year mission is also presented in Fig. 3. This result was produced using the SPace ENVironment Information System (SPENVIS) (https://www.spenvis.oma.be/models.php), which is sponsored by the European Space Agency (ESA). The radiation models used are the AE-8 trapped electron model (Vette 1991) for the solar maximum and the AP-8 trapped proton model (Sawyer and Vette 1976) for the solar minimum as well as long-term solar particle fluences and galactic cosmic ray fluxes. It is found that all LEO objects should remain below 2000 km to avoid radiation from the inner Van Allen belt. In addition, a chip-scale atomic clock (CSAC), a navigation payload that may be piggybacked on an LEO satellite, can survive a dose of 50 krad (Si). The target altitude should be below 1300 km but should not be too low to avoid small coverage and a large atmospheric drag effect to ensure its availability at different inclinations. Thus, an ideal altitude would be between 1000 and 1300 km. To facilitate orbit control and ensure periodic coverage of the earth, we consider a regressive orbit, of which the distinctive characteristic is that the track of the subsatellite point is duplicated with a certain time gap, meaning that the satellite passes through the space above a specific region at regular and fixed times. Suppose that the orbital period is Ts and satisfies the following condition with certain positive integers k and m:

$$ T_{s} = \frac{k}{m}T_{ \oplus } $$
(10)

where \( T_{ \oplus } \) is the period of the earth’s rotation, i.e., a sidereal day of 86,164 s. Then, the satellite will pass through m circles around the earth in k days, following which the ground track of the satellite will begin to be duplicated. k is called the regression period. Once the orbital period has been determined, the altitude h can be calculated as follows:

$$ h = \sqrt[3]{{\mu \left( {\frac{{T_{s} }}{2\pi }} \right)^{2} }} - R_{ \oplus } $$
(11)

where μ is the geocentric gravitational constant, i.e., 398,600.4418 km3/s2. To make the regression period as short as possible, k and m are set to 1 and 13, respectively, and the target altitude is accordingly fixed at 1248.171 km, thereby determining the semimajor axis. Thereafter, for a polar-orbit or orthogonal circular-orbit constellation, certain parameters of the configuration are fixed; for example, the numbers of satellites and planes can be derived based on (5) and (8), respectively. However, for a Walker constellation, these parameters cannot be determined directly but rather must be considered as variables to be optimized. Additionally, to avoid rotation of the entire constellation, we provide a spatial datum by fixing both the RAAN and the initial mean anomaly of the first nominal satellite to 0.

Fig. 3
figure 3

Number and distribution of objects in LEO and radiation dosage in silicon over a 5-year mission as functions of orbital altitude and inclination

Full size image

Optimization with a GA

Since the navigation augmentation system of interest relies on the platform of emerging LEO broadband constellations, which are being established with the intent of providing high-speed Internet connectivity to people everywhere around the world, the premise of the constellation design is to ensure 100% global coverage. On this basis, we optimize the constellation to the greatest possible extent for navigation augmentation.

As mentioned above, we are interested in two objectives. For O1, three kinds of hybrid constellations are designed by combining a low-inclination Walker constellation with either a polar-orbit constellation, an orthogonal circular-orbit constellation or a high-inclination Walker constellation, corresponding to scheme 3 (S3), scheme 4 (S4) and scheme 5 (S5), respectively. We also present scheme 1 (S1) and scheme 2 (S2), which employ a single polar-orbit constellation and an orthogonal circular-orbit constellation, respectively, for reference. For O2, the constellation type is fixed to a hybrid orthogonal circular-orbit/Walker constellation. Scheme 6 (S6), scheme 7 (S7) and scheme 8 (S8) are presented to investigate the number of LEO satellites required to enable globally even coverage with six visible satellites and elevation mask angles of 7°, 15° and 20°, respectively. Scheme 9 (S9) and scheme 10 (S10), together with scheme 6 (S6), are considered to determine how many LEO satellites are needed to realize globally even coverage with four, five and six visible satellites, respectively. All these schemes are summarized in Table 2.

Table 2 Summary of schemes proposed for constellation design and optimization
Full size table

Because every proposed hybrid constellation contains at least one Walker subconstellation, it is critical to determine the optimal integer parameters Pw, Sw and Fw as well as the real-valued variables I0, \( \varOmega_{0} \) and \( \mathcal{M}_{0} \). Even small variations in the parameters Pw, Sw and Fw can result in large performance gaps without any workable logic. This is particularly true of the phase difference Fw, to which the constellation performance is extremely sensitive; depending on Fw, either very good or very bad performance may be exhibited even by constellations with the same numbers of satellites and planes. To solve this problem, we suggest using a GA.

A GA is a stochastic heuristic search algorithm that simulates natural selection and natural genetic mechanisms. The basic idea originates from Darwinism and Mendelism. Each feasible solution of the problem to be optimized is regarded as an individual of a population and is encoded. Each code for a solution is called a chromosome, and the elements of each chromosome are called genes. Then, in accordance with the optimization target, a fitness function or an objective function is defined to evaluate all chromosomes and determine which ones are fit for survival with a certain probability. The surviving chromosomes are selected to form the initial population to be used for reproducing the next generation. A new generation is obtained through the mating of the parent chromosomes, i.e., through chromosomal crossover as well as genetic mutation with a certain probability. This process will result in the offspring being more competitive than their parents since they have inherited good genes. After several rounds of reproduction and evolution, the optimal individual in the last generation is decoded to obtain the approximate optimal solution to the problem (Goldberg 1989).

Decision variables and search ranges

The parameters to be optimized are called decision variables, and a set x of specific values of these parameters, i.e., an individual, is given by

$$ {\mathbf{x = }}\left[ {\begin{array}{*{20}c} {P_{\text{w}}^{n} } & {S_{\text{w}}^{n} } & {F_{\text{w}}^{n} } & {\begin{array}{*{20}c} {I_{0}^{n} } & {\varOmega_{0}^{n} } & {\mathcal{M}_{0}^{n} } \\ \end{array} } \\ \end{array} } \right]^{\text{T}} $$
(12)

where n is the index of the Walker subconstellation. The proper search ranges for the decision variables not only should include the globally optimal solution but also should not be so large as to unnecessarily increase the search burden. As shown in Table 3, the search ranges for \( P_{\text{w}}^{n} \) and \( S_{\text{w}}^{n} \) are larger for S7 and S8 than for the other schemes because S7 and S8 require more satellites with higher elevation mask angles. The upper limit of \( F_{\text{w}}^{n} \) is always smaller than that of \( P_{\text{w}}^{n} \), and the lower limit of \( F_{\text{w}}^{n} \) is 0. When setting the search range for \( I_{0}^{n} \), we consider larger upper limits for schemes with an orthogonal circular-orbit subconstellation because the coverage in the low-latitude region is already compensated by the equatorial-orbit satellites. With regard to S5, the range for \( I_{0}^{n} \) is considered to be 0°–45° for the low-inclination Walker subconstellation and 45°–90° for the high-inclination subconstellation. The range for \( \varOmega_{0}^{n} \) is assumed to be 0°–45° because the first subconstellation has at least four orbital planes. The range for \( \mathcal{M}_{0}^{n} \) is assumed to be 0°–90° because there are at least four satellites per plane in the Walker subconstellation. After selecting the search ranges, we encode the decision variables to form a chromosome using the binary coding technique. The length of the chromosome is determined by the precision levels of all variables. The precision is 1 for the integer variables \( P_{\text{w}} \), \( S_{\text{w}} \) and \( F_{\text{w}} \) and is 0.1° for the real-valued variables \( I_{0}^{n} \), \( \varOmega_{0}^{n} \) and \( \mathcal{M}_{0}^{n} \).

Table 3 Search ranges of the decision variables for the optimization of different schemes
Full size table

Objective functions and constraints

Before defining the objective functions, we first select ground points of interest. Since the coverage performance over an entire regression period is symmetric for the northern and southern hemispheres as well as for the eastern and western hemispheres, as shown in Fig. 4, for convenience, we select only 19 ground points, which are evenly located along the 0° longitude line from 0° to 90°N with a resolution of 5° in latitude. For any individual x, the average number of visible LEO satellites at one ground point over an entire regression period is denoted by \( v\left( {\mathbf{x}} \right) \). The interval between two epochs is 60 s. Then, we define the objective function as a trade-off between the mean and standard deviation (STD) of \( v\left( {\mathbf{x}} \right) \) at all 19 ground points. For O1, the expression is

$$ f\left( {\mathbf{x}} \right) = \hbox{min} \left\{ {w_{ 1} \cdot \varvec{E}\left[ {v\left( {\mathbf{x}} \right)} \right] + w_{2} \cdot \sqrt {\varvec{D}\left[ {v\left( {\mathbf{x}} \right)} \right]} } \right\} $$
(13)

where w1 and w2 are weighting factors, different combinations of which will result in different solutions. In this work, we assume that w1 = − 0.3 and w2 = 0.7, respectively. The absolute value of w2 is larger than that of w1 because we are more concerned with evenness than with the absolute number of visible satellites. w1 has a negative value, whereas w2 has a positive value. This is because the larger the mean value and the smaller the STD are, the better the fitness. Additionally, the optimization process is subject to certain constraints:

$$ \left\{ {\begin{array}{*{20}l} {\delta \left( {\mathbf{x}} \right) = 100\% } \hfill \\ {P_{\text{p}} S_{\text{p}} + S_{\text{e}} + \sum\nolimits_{n = 1}^{N} {P_{\text{w}}^{n} S_{\text{w}}^{n} } \le \gamma } \hfill \\ {F_{\text{w}} \le P_{\text{w}} - 1} \hfill \\ {P_{\text{w}} \in {\mathbf{Z}}} \hfill \\ {S_{\text{w}} \in {\mathbf{Z}}} \hfill \\ {F_{\text{w}} \in {\mathbf{Z}}} \hfill \\ \end{array} } \right. $$
(14)

where \( \delta \left( {\mathbf{x}} \right) \) represents the coverage availability of one visible satellite at all epochs and all target points, N is the number of Walker subconstellations and \( \gamma \) is the maximum allowable number of satellites, e.g., 100 satellites.

Fig. 4
figure 4

Distribution of the ground target points used to evaluate the coverage performance

Full size image

For O2, the objective function is given as

$$ f\left( {\mathbf{x}} \right) = \hbox{min} \left\{ {w_{ 1} \cdot \left| {\varvec{E}\left[ {v\left( {\mathbf{x}} \right)} \right] - \xi } \right| + w_{2} \cdot \sqrt {\varvec{D}\left[ {v\left( {\mathbf{x}} \right)} \right]} } \right\} $$
(15)

where \( \xi \) is the expected average number of visible satellites. Here, weighting factors of w1 = 0.3 and w2 = 0.7 are assumed. The optimization process is subject to the following constraints:

$$ \left\{ {\begin{array}{*{20}l} {\delta \left( {\mathbf{x}} \right) = 100\% } \hfill \\ {F_{\text{w}} \le P_{\text{w}} - 1} \hfill \\ {P_{\text{w}} \in {\mathbf{Z}}} \hfill \\ {S_{\text{w}} \in {\mathbf{Z}}} \hfill \\ {F_{\text{w}} \in {\mathbf{Z}}} \hfill \\ \end{array} } \right. $$
(16)

These constraints are looser than those for the previous objective function because of the lack of limitation on the total number of satellites.

GA settings

The GA toolbox in the MathWorks MATLAB 2018b software suite is used for data processing. The input parameters of the GA are set as follows: the population size is 500, and the initial population is created using a uniform creation operator for all schemes except S5, for which the initial population is instead evolved from an earlier population by means of a GA with an objective of maximum coverage availability for one visible satellite to improve efficiency in obtaining an optimal solution. This is because all schemes except S5 involve either a polar-orbit or an orthogonal circular-orbit subconstellation, thus ensuring 100% global coverage. For the reproduction and evolution process, the elite count, i.e., the number of best individuals that survive to the next generation without any change, is set to 15. Moreover, to solve the mixed-integer constrained optimization problem, the core subroutine for mixed-integer nonlinear programming (MINLP) is used, adopting modified operators such as tournament selection, Laplace crossover and power mutation as well as the truncation procedure for integer restrictions and the constraint-handling technique (Deep et al. 2009). The probabilities of crossover and mutation are 0.8 and 0.194, respectively. To evaluate the score of each chromosome, a penalty function is used internally instead of the objective function due to the presence of the constraints. The penalty value is equal to the objective value for a feasible individual, while it is equal to the sum of the objective value of the worst feasible individual plus the violation score for an infeasible individual. Additionally, the optimization procedure is set to not terminate until the end of the 40th generation.

Results and analyses

The optimized results are presented in this section. First, we compare the coverage performance of the different types of hybrid constellations. Second, the constellation type is fixed to investigate the required numbers of satellites for different elevation mask angles. Finally, we also consider the required numbers of satellites for different levels of visibility.

O1: allocation of a limited number of satellites to different types of hybrid constellations

Figure 5 shows the 40-generation traces of the mean and best penalty values for S3, S4 and S5. It is found that as reproduction and evolution progress, the population becomes more competitive. The corresponding penalty values decrease and eventually converge. In terms of the mean penalty value, S5 performs worse than S3 and S4 because some individuals in S5 cannot satisfy the requirement of 100% coverage availability with at least one visible satellite, thus resulting in poor scores. In terms of the best penalty value in the last generation, with which we are most concerned, S4 performs the best, followed by S5, and S3 performs the worst. The optimal solutions for these schemes are presented in “Appendix,” and the three-dimensional (3D) structures of the constellations are shown in Fig. 6. S3 comprises a polar-orbit subconstellation and a Walker 60/6/4 (\( {{T_{\text{w}} } \mathord{\left/ {\vphantom {{T_{\text{w}} } {{{P_{\text{w}} } \mathord{\left/ {\vphantom {{P_{\text{w}} } {F_{\text{w}} }}} \right. \kern-0pt} {F_{\text{w}} }}}}} \right. \kern-0pt} {{{P_{\text{w}} } \mathord{\left/ {\vphantom {{P_{\text{w}} } {F_{\text{w}} }}} \right. \kern-0pt} {F_{\text{w}} }}}} \)) subconstellation, S4 comprises an orthogonal circular-orbit subconstellation and a Walker 55/5/3 subconstellation, and S5 comprises a Walker 30/5/0 subconstellation and a Walker 70/7/4 subconstellation. The total number of LEO satellites for every hybrid constellation is 100, meaning that the available satellite resources are fully utilized.

Fig. 5
figure 5

Traces of the penalty values for S3, S4 and S5

Full size image
Fig. 6
figure 6

3D structures of the optimized hybrid LEO constellations for S3 (left), S4 (middle) and S5 (right). The red, green and yellow lines represent high-, low- and zero-inclination orbits, respectively

Full size image

Figure 7 shows the average and minimum numbers of visible LEO satellites for S3, S4 and S5 as well as those for S1 and S2 for comparison. By comparing S2 with S1, we find that the coverage performance in low-latitude regions is improved due to the presence of the equatorial-orbit satellites in the orthogonal circular-orbit constellation, while the number of visible satellites in mid- to high-latitude regions is slightly reduced. Comparisons of S3 with S1 and of S4 with S2 reveal that the coverage performance in mid- to low-latitude regions is significantly improved by introducing a proper Walker constellation. Furthermore, the distributions of the average number of visible satellites are quite even along the north–south direction for S3, S4 and S5. The bottom plot shows that S1 and S2 can provide 100% coverage availability with at least one visible satellite, while S3, S4 and S5 can provide 100% coverage availability with at least two visible satellites. For S3 and S4 in particular, at least three satellites are visible at all latitudes except 60°. To determine which scheme is the best for O1, we give the statistics at all 19 ground points in Table 4. The mean values are 3.03, 3.07, 5.49, 5.44 and 5.47 for S1, S2, S3, S4 and S5, respectively, and the corresponding STDs are 1.82, 1.40, 0.44, 0.18 and 0.28. S4 achieves the lowest STD, i.e., S4 provides the most even coverage worldwide; although its mean value is slightly lower than those of S3 and S5, it obtains the lowest overall penalty value due to the higher weight of the STD. Additionally, for the deployment of an actual hybrid LEO constellation based on S4, two steps are suggested: first, the orthogonal circular-orbit subconstellation should be deployed to realize 100% coverage availability with at least one visible satellite within a short time, and then, the proper Walker subconstellation can be subsequently deployed to realize globally even coverage.

Fig. 7
figure 7

Variation in the number of visible satellites with latitude for S1, S2, S3, S4 and S5

Full size image
Table 4 Statistics for S1, S2, S3, S4 and S5
Full size table

O2: required numbers of satellites for different elevation mask angles

For LEO constellation design, the elevation mask angle sometimes needs to be set relatively high, such as the angles of 20° for Telesat, 40° for SpaceX and 55° for OneWeb (del Portillo et al. 2019), not only to reduce transmission loss but also to reduce the aperture of the satellites or the number of point beams. In this section, we fix the constellation type to a hybrid orthogonal circular-orbit/Walker constellation and aim to determine the required number of LEO satellites to realize globally even coverage with six visible satellites for different elevation mask angles of 7°, 15° and 20°. The traces of the penalty values are shown in Fig. 8. S6 achieves the lowest value, followed by S7, and S8 achieves the highest value. The optimal solutions are also presented in “Appendix,” and the 3D structures of the constellations are shown in Fig. 9. We find that the higher the elevation mask angle is, the smaller the area a satellite covers. Moreover, S6, S7 and S8, respectively, comprise 45-, 68- and 91-satellite orthogonal circular-orbit subconstellations and Walker 64/8/0, 104/13/3 and 130/13/5 subconstellations. As a result, the optimized numbers of satellites for S6, S7 and S8 are 109, 172 and 221, respectively.

Fig. 8
figure 8

Traces of the penalty values for S6, S7 and S8

Full size image
Fig. 9
figure 9

3D structures of the optimized hybrid LEO constellations for S6 (left), S7 (middle) and S8 (right). The shaded circles represent the coverage of the nominal satellite

Full size image

Figure 10 shows the numbers of visible LEO satellites for S6, S7 and S8, and the corresponding statistics are given in Table 5. The distributions of the average number of visible satellites for S7 and S8 are not as even as that for S6. This is because many polar-orbit satellites are observed beyond 75° for S7 and S8, which makes it difficult to obtain a small STD while guaranteeing coverage with six visible satellites simultaneously. The mean values of the number of visible satellites are 5.87, 6.00 and 6.00 for S6, S7 and S8, respectively. All of them achieve the expected levels of satellite visibility. In addition, S6, S7 and S8 can provide 100% coverage availability with three, two and two visible satellites, respectively.

Fig. 10
figure 10

Variation in the number of visible satellites with latitude for S6, S7 and S8

Full size image
Table 5 Statistics for S6, S7 and S8
Full size table

O2: required numbers of satellites for different levels of visibility

Since different users may have different requirements in terms of even satellite visibility, we consider S9, S10 and S6 as examples, obtained by setting the expectation \( \xi \) in (15) to 4, 5 and 6, respectively. Figure 11 shows the traces of the corresponding penalty values. The mean penalty values usually converge by the tenth generation, while the series of best penalty values show only minor changes. The optimal solutions are presented in “Appendix,” and the 3D structures of the constellations are shown in Fig. 12. The same orthogonal circular-orbit subconstellation is adopted in each of these schemes, combined with Walker 45/9/8, 48/6/2 and 64/8/0 subconstellations in S9, S10 and S6, respectively. As a result, 90, 93 and 109 satellites are required to achieve globally even coverage with four, five and six visible satellites, respectively.

Fig. 11
figure 11

Traces of the penalty values for S9, S10 and S6

Full size image
Fig. 12
figure 12

3D structures of the optimized hybrid LEO constellations for S9 (left), S10 (middle) and S6 (right)

Full size image

Figure 13 shows the numbers of visible LEO satellites for S9, S10 and S6, and the corresponding statistics are given in Table 6. The distributions of the average number of visible satellites are generally even. The mean values are 4.98, 5.12 and 5.87 for S9, S10 and S6, respectively, and the corresponding STDs are 0.26, 0.20 and 0.31. For S9 in particular, although the expected satellite visibility is 4, the result obtained is 4.98 to ensure a smaller STD. If the expected value is of greater concern, either the value of the weighting factor w1 in (15) can be increased, or the ground points beyond 75° can be excluded before starting the optimization process. In addition, S9, S10 and S6 can provide 100% coverage availability with one, two and three visible satellites, respectively.

Fig. 13
figure 13

Variation in the number of visible satellites with latitude for S9, S10 and S6

Full size image
Table 6 Statistics for S9, S10 and S6
Full size table

Conclusions and outlook

We present several options for hybrid LEO constellations optimized with a GA for a LEO-based navigation augmentation system. First, three typical constellations are selected as the basis for constructing hybrid constellations. Then, the constellation design is conducted. For increased efficiency, part of the constellation configuration is predetermined. After that, all experimental schemes and the complete procedure for constellation optimization using a GA are described in detail. Finally, the results are analyzed.

Regarding O1, the coverage performance of S1 and S2 in mid- to low-latitude regions can be significantly improved by adding a proper Walker subconstellation. The distributions of the average number of visible satellites are quite even along the north–south direction for S3, S4 and S5. The mean values are 5.49, 5.44 and 5.47, with STDs of 0.44, 0.18 and 0.28. The best penalty values in the last generation are − 1.34, − 1.51 and − 1.45, indicating that the coverage performance of the hybrid orthogonal circular-orbit/Walker constellation is better than that of the hybrid polar-orbit/Walker or the Walker/Walker constellation for a given number of 100 LEO satellites.

Regarding O2, the constellation type is fixed to a hybrid orthogonal circular-orbit/Walker constellation, and there is no limitation on the total number of satellites. We find that when the elevation mask angles are set to 7°, 15° and 20°, the higher the elevation mask angle is, the smaller the area a satellite covers, and 109, 172 and 221 satellites, respectively, are required to realize globally even coverage with six visible satellites. If the elevation mask angle is fixed to 7°, the numbers of satellites required to achieve globally even coverage with four and five visible satellites are 90 and 93, respectively.

Overall, all optimized schemes can achieve globally even coverage for navigation augmentation while guaranteeing 100% coverage availability with one to three visible satellites for broadband Internet access. Nevertheless, when constructing these constellations in practice, some adjustments should also be considered; e.g., the inclination of the polar orbits should not be strictly equal to 90°, and the orbital altitudes of the different subconstellations should slightly vary to avoid collisions between satellites. Future research will address the multitiered constellation design for communication, navigation, remote sensing, radio occultation and reflectometry. It would also be interesting to investigate how this GA method compares to other satellite constellation optimization methods as far as performance and efficiency are concerned.