An optimal linear combination model to accelerate PPP convergence using multi-frequency multi-GNSS measurements

Abstract

We propose an optimal ionospheric-free linear combination (LC) model for dual- and triple-frequency PPP which can accelerate carrier phase ambiguity and decrease the position solution convergence time. To reduce computational complexity, a near-optimal LC model for triple-frequency PPP is also proposed. The uncombined observation (UC) model estimating ionospheric delay gives the best performance, because all information contained within the observations are kept. The proposed optimal and near-optimal LC models are compared with the UC model, using both simulated and real data from five GNSS stations in Australia over 30 consecutive days in 2017. We determine a necessary and sufficient condition for a combination operator matrix which can eliminate the first-order ionospheric component to obtain the optimal LC model for dual- and triple-frequency PPP. Numerical results show that the proposed LC model is identical to the UC model. In addition, the proposed near-optimal LC model even outperforms the current LC models. Ambiguity resolution (AR) is faster and positioning accuracy is improved using the optimal triple-frequency LC model compared to using the optimal dual-frequency LC model. An average time-to-first-fix of 10 min with a fixing success rate of 95% can be achieved with triple-frequency AR.

Introduction

Precise point positioning (PPP) with ambiguity resolution (AR) can provide centimeter- to millimeter-level positioning accuracy using a single GNSS receiver. Recent research results have shown that the extra-wide-lane (EWL) and wide-lane (WL) ambiguities can be estimated instantaneously, or with very few epochs, in triple- and dual-frequency PPP-AR. However, resolving the narrow-lane (NL) ambiguity rapidly and reliably remains a challenge. Tens of minutes are still required for dual-frequency PPP NL-AR (Collins and Bisnath 2011; Ge et al. 2008; Geng et al. 2010; Laurichesse et al. 2009, 2010). Utilization of next-generation GNSS satellites transmitting on three signal frequencies could improve PPP-NL integer AR compared to the dual-frequency case (Duong et al. 2016; El-Mowafy et al. 2016; Geng and Bock 2013; Laurichesse and Blot 2016; Li et al. 2013). As of the time of writing (March 2019), there are more than 14 GNSS satellites transmitting 3 signals visible in the Asia–Pacific region, including GPS L1–L2–L5, Galileo E1–E5a–E5b and BeiDou B1–B2–B3 signals.

For both dual- and triple-frequency PPP, the ionospheric-free linear combination (LC) eliminating the first-order ionospheric delay and the uncombined observations (UC) estimating the ionospheric delay are commonly used. Teunissen and Khodabandeh (2014) stated that the UC model provides the best performance if an external ionosphere model is applied. They also stated that the LC models are relatively weak with respect to their AR capabilities. However, the UC model contains more equations and variables than the LC model, hence the UC model is computationally more intensive. In addition, the ionospheric delay needs to be estimated in the UC model, hence the model is sensitive to ionospheric phenomena such as geomagnetic storms and solar flares. The LC models on the other hand can be used to eliminate the ionospheric delay, and given its long wavelengths and minimal combined noise properties, the LC models are commonly used for precise positioning (Cocard et al. 2008; Feng 2008; Wang and Rothacher 2013). However, few efforts have been made to compare the performance of the LC models with the UC model.

We propose an optimal LC model for dual- and triple-frequency PPP which has comparable performance to the UC model. The proposed optimal LC model will be assessed against current LC and UC models based on theoretical analysis, numerical simulations and using real GNSS measurements. First, the current LC models used in PPP are described and evaluated. Next, a necessary and sufficient condition to obtain an optimal set of LC models for dual- and triple-frequency PPP is derived. In addition, a near-optimal geometry-based (GB) code and phase LC model for the triple-frequency GNSS case is proposed. The evaluation is based on the theoretical variance–covariance matrix of the geometric terms and ambiguity estimation after applying the weighted least-squares estimator. Results show that current LC models are suboptimal. Finally, the results of the comparison between the performance of the proposed LC models (including optimal and near-optimal LC models), current LC models and the UC model using real GNSS data is presented.

Dual- and triple-frequency PPP NL ambiguity resolution

The mathematical model for multi-frequency multi-constellation GNSS PPP will be first presented using the single-difference between-satellite observable model where the receiver clock error, as well as the receiver phase and code biases were eliminated via differencing. Next we introduce two methods to resolve multi-frequency multi-GNSS NL ambiguities. In the first method, the UC model including the geometric terms, the ambiguity term, and the ionospheric delay are estimated in the PPP solution, whereas in the case of the second method using the LC model, the ionospheric delay will be excluded from the PPP estimation. It is to note that henceforth the phrase “uncombined observation models” or UC implies that no ionospheric-free LC of measurements were created and that the ionospheric delay was estimated along with the other parameters using the single-difference measurements. The phrase “linear combination models” or LC, on the other hand, means that the ionospheric-free LC was used to eliminate the ionospheric delay. Single-difference measurements were used in both cases. To combine GPS, Galileo and BeiDou measurements in a triple-frequency PPP with ambiguity resolution (PPP-AR) model, one satellite from each constellation will be selected as the reference satellite for that GNSS, to form intra-system single-difference ambiguities. In addition, for PPP-AR using the ionospheric-free code–carrier phase combination, the code elevation-dependent biases need to be corrected for BeiDou measurements (Wanninger and Beer 2015).

Single-difference between-satellite model

The functional PPP models of single-difference between-satellite code and phase measurements on the i^th frequency are denoted as (Leick et al. 2015):

$${P_i}=\rho +ct+\frac{{f_{1}^{2}}}{{f_{i}^{2}}}{I_1}+T+{b_i}+{\nu _i}$$

(1)

$${L_i}=\rho +ct - \frac{{f_{1}^{2}}}{{f_{i}^{2}}}{I_1}+T+{\lambda _i}{B_i}+{\lambda _i}{N_i}+{\varepsilon _i}$$

(2)

where ${L_i}$ and ${P_i}$ are the phase and code measurements on the ith frequency (in units of meters), respectively; $\rho$ is the geometric distance as a function of receiver and satellite coordinates (m); $c$ is the speed of light in vacuum (m); $t$ is the single-differenced satellite clock error (s); ${\lambda _i}$ is the wavelength of the carrier phase on the ith frequency (m); ${f_i}$ is the ith frequency (MHz); ${I_1}$ is the first-order ionospheric delay on the first frequency (m); $T$ is the tropospheric delay (m); ${b_i}$ is the code observable-dependent satellite bias (m); ${\lambda _i}{B_i}$ are the phase observable-dependent satellite bias (m); ${N_i}$ is the integer ambiguity on the ith frequency (cycles); and ${\nu _i}$ and ${\varepsilon _i}$ denote the remaining unmodeled errors, such as multipath effects on the code and phase measurements, respectively. The receiver clock errors, as well as the receiver phase and code biases, are excluded using (1) and (2).

In the case of dual-frequency PPP-AR, there are two main steps: the Hatch–Melbourne–Wubbena WL integer AR (Hatch 1983; Melbourne 1985; Wubbena 1985), and the ionospheric-free NL integer AR. With triple-frequency measurements, three steps are normally required, for EWL, WL and NL integer AR. Before resolving the NL $({\text{or}}\,{N_1})$ ambiguity, the procedure for dual- and triple-frequency PPP NL-AR based on the UC or LC model requires correct AR of the EWL and WL carrier phase observables, which are ${N_{{\text{ew}}}}({N_{23}}={N_2} - {N_3})$ and ${N_{{\text{wl}}}}({N_{12}}={N_1} - {N_2})$. The EWL ambiguities can be resolved instantaneously due to their long wavelengths (5.86 m for GPS, 9.77 m for Galileo and 4.88 m for BeiDou). However, several minutes of data are required to resolve the WL ambiguities correctly. The procedure for resolving those ambiguities has been well documented in the literature (see for example Leick et al. 2015). It is assumed that there is a very small chance of incorrect fixing of EWL and WL. As soon as the EWL and WL ambiguities are resolved, attention is shifted to the NL ${\text{ }}({N_1})$ integer AR.

Uncombined observation models

When the satellite errors such as clocks, orbits, code and phase biases for L1–L2–L5, E1–E5a–E5b or B1–B2–B3 measurements are corrected for, using for example, correction products provided by service providers, and the EWL and WL ambiguities are resolved, then (1) and (2) are rearranged for dual- and triple-frequency measurements as:

$$l=\left[ {\begin{array}{*{20}{c}} {{{\bar {P}}_1}} \\ \begin{gathered} {{\bar {P}}_2} \hfill \\ {{\bar {L}}_1} \hfill \\ {{\bar {L}}_2} \hfill \\ \end{gathered} \end{array}} \right]=\left[ {\begin{array}{*{20}{l}} {{P_1} - ct - {b_1}} \\ {{P_2} - ct - {b_2}} \\ {{L_1} - ct - {\lambda _1}{B_1}} \\ {{L_2} - ct - {\lambda _2}{B_2}+{\lambda _2}{N_{{\text{wl}}}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} 1&0 \\ 1&0 \\ 1&{{\lambda _1}} \\ 1&{{\lambda _2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \Re \\ {{N_1}} \end{array}} \right]+\left[ {\begin{array}{*{20}{c}} 1 \\ {{\mu _1}} \\ { - 1} \\ { - {\mu _1}} \end{array}} \right][{I_1}]+\left[ {\begin{array}{*{20}{c}} {{v_1}} \\ \begin{gathered} {v_2} \hfill \\ {\varepsilon _1} \hfill \\ {\varepsilon _2} \hfill \\ \end{gathered} \end{array}} \right]\,~({\text{dual}})$$

(3)

$$l=\left[ {\begin{array}{*{20}{c}} {{{\bar {P}}_1}} \\ \begin{gathered} {{\bar {P}}_2} \hfill \\ {{\bar {P}}_3} \hfill \\ {{\bar {L}}_1} \hfill \\ {{\bar {L}}_2} \hfill \\ {{\bar {L}}_3} \hfill \\ \end{gathered} \end{array}} \right]=\left[ {\begin{array}{*{20}{l}} {{P_1} - ct - {b_1}} \\ {{P_2} - ct - {b_2}} \\ {{P_3} - ct - {b_3}} \\ {{L_1} - ct - {\lambda _1}{B_1}} \\ {{L_2} - ct - {\lambda _2}{B_2}+{\lambda _2}{N_{{\text{wl}}}}} \\ {{L_3} - ct - {\lambda _3}{B_3}+{\lambda _3}({N_{{\text{wl}}}}+{N_{{\text{ew}}}})} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} 1&0 \\ \begin{gathered} 1 \hfill \\ 1 \hfill \\ \end{gathered} &\begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \\ 1&{{\lambda _1}} \\ \begin{gathered} 1 \hfill \\ 1 \hfill \\ \end{gathered} &\begin{gathered} {\lambda _2} \hfill \\ {\lambda _3} \hfill \\ \end{gathered} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \Re \\ {{N_1}} \end{array}} \right]+\left[ {\begin{array}{*{20}{c}} 1 \\ \begin{gathered} {\mu _1} \hfill \\ {\mu _2} \hfill \\ \end{gathered} \\ { - 1} \\ \begin{gathered} - {\mu _1} \hfill \\ - {\mu _2} \hfill \\ \end{gathered} \end{array}} \right][{I_1}]+\left[ {\begin{array}{*{20}{c}} {{v_1}} \\ \begin{gathered} {v_2} \hfill \\ {v_3} \hfill \\ {\varepsilon _1} \hfill \\ {\varepsilon _2} \hfill \\ {\varepsilon _3} \hfill \\ \end{gathered} \end{array}} \right]\,({\text{triple}})$$

(4)

On the right-hand side of (3) and (4), $\Re =\rho +T$ is the geometric term containing the topocentric satellite distance and the tropospheric delay. The goal of GB AR is to estimate the integer ambiguities first and then estimate the position coordinates. Hence, the topocentric satellite distance $\rho$ is not parameterized in terms of coordinates. ${\mu _1}=\frac{{f_{1}^{2}}}{{f_{2}^{2}}}$ and ${\mu _2}=\frac{{f_{1}^{2}}}{{f_{3}^{2}}}$ are the ionosphere coefficients. If a regional or global ionosphere model is not available, the PPP NL-AR will rely on the geometric terms $(\Re )$ and the NL ambiguity $({N_1})$, which is constant as long as there is no cycle slip, and the ionospheric delay on the first frequency $({I_1})$. Assuming that the geometric and ambiguity parts are grouped together as $\xi ={[\begin{array}{*{20}{c}} \Re &{{N_1}} \end{array}]^\text{T}}$, the functional model of UC, i.e., equations (3) and (4) can be written in a simplified and linear form:

$$l=Ax+\upsilon ={A_1}\xi +{A_2}{I_1}+\upsilon$$

(5)

where $l[n \times 1]$ is the vector of measurements, and $A[n \times u]$ is the design matrix comprising two submatrices ${A_1}$ and ${A_2}$. ${A_1}$ is the design matrix corresponding to the geometric part and ambiguity term, ${A_2}$ is the ionospheric part of the design matrix. $x[u \times 1]$ is the vector of unknown parameters. $\upsilon [n \times 1]$ is the vector of the unmodeled errors for code and phase measurement. The values of $(n,{\text{ }}u)$ are (4, 3) and (6, 3) for dual- and triple-frequency case, respectively. Measurement noise and uncertainty are assumed to be Gaussian normally distributed with zero mean. The stochastic model (3) and (4) also denoted as $D[l]=\sigma _{o}^{2}{Q_l}$ where a priori variance of unit weight $\sigma _{o}^{2}$ is often assumed to be 1, and ${Q_l}$ corresponds to the cofactor matrix. Its inverse is the weight matrix ${P_l}=Q_{l}^{{ - 1}}$.

The strategy to solve (5) is to minimize the sum of the squares of the residuals using a weighted least-squares adjustment (Hofmann-Wellenhof et al. 2008). The variance–covariance matrix of the unknown parameter vector $({Q_{\hat {x}}})$ can be obtained by applying the variance–covariance propagation law:

$${Q_{\hat {x}}}={({A^{\text{T}}}{P_l}A)^{ - 1}}=\left[ {\begin{array}{*{20}{c}} {\operatorname{var} (\Re )}&{\operatorname{cov} (\Re ,{N_1})}&{\operatorname{cov} (\Re ,{I_1})} \\ {\operatorname{cov} (\Re ,{N_1})}&{\operatorname{var} ({N_1})}&{\operatorname{cov} ({N_1},{I_1})} \\ {\operatorname{cov} (\Re ,{I_1})}&{\operatorname{cov} ({N_1},{I_1})}&{\operatorname{var} ({I_1})} \end{array}} \right]$$

(6)

To resolve the unknown parameters rapidly and enhance the PPP NL-AR capabilities, the smaller the diagonal values of the variance–covariance matrix (6), the better. More specifically, the smaller the geometric variance $\operatorname{var} (\Re )$, the better the position solution; while the smaller the ambiguity variance $\operatorname{var} ({N_1})$, the larger the corresponding probability of correct integer estimation (or faster AR).

Current linear combination models

The benefit of using the LC model is to eliminate nuisance parameters (here those corresponding to the ionospheric effect). In general, the LC model uses a combination operator matrix $(C)$ which can eliminate the first-order ionospheric component and keep the geometric terms in the UC models. Then

$${Cl}=C{A_1}\xi +C{A_2}{I_1}+C\upsilon {\text{ }} \Leftrightarrow {\text{ }}{l_{\text{c}}}={A_{\text{c}}}\xi +0{I_1}+{\upsilon _{\text{c}}}$$

(7)

where ${l_{\text{c}}}={Cl}$, ${A_{\text{c}}}=C{A_1}$, $C{A_2}=0$ and ${\upsilon _{\text{c}}}=C\upsilon.$ ${P_{{\text{lc}}}}=Q_{{{\text{lc}}}}^{{ - 1}}={(CP_{{\text{l}}}^{{ - 1}}{C^{\text{T}}})^{ - 1}}$ is the weight of the combined observables. The general forms of the matrix $C$ for dual- and triple-frequency are:

$${C_{({\text{No.LC}} \times 4)}}={\left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}&{{c_{13}}}&{{c_{14}}} \\ {{c_{21}}}&{{c_{22}}}&{{c_{23}}}&{{c_{24}}} \\ \vdots & \vdots & \vdots & \vdots \end{array}} \right]_{{\text{(dual)}}}}\,{\text{or }}\,{C_{({\text{No.LC}} \times 6)}}={\left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}&{{c_{13}}}&{{c_{14}}}&{{c_{15}}}&{{c_{16}}} \\ {{c_{21}}}&{{c_{22}}}&{{c_{23}}}&{{c_{24}}}&{{c_{25}}}&{{c_{26}}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \end{array}} \right]_{({\text{triple}})}}$$

(8)

where each row contains the ${c_{ij}}$ coefficients of $C$ that correspond to one LC, and ${\text{No.LC}}$ is the total number of GB-IF LCs used. The number of columns $(n)$ of $C$ is 4 or 6 for dual- and triple-frequency measurements, respectively. In the following section, the current ionospheric-free LC models for the dual- and triple-frequency cases, and how $C$-matrices are applied to the vector of measurements $l[n \times 1]$ will be described.

Dual-frequency case

The standard ionospheric-free code and phase observation equations can be written in matrix form (Hofmann-Wellenhof et al. 2008, Equation 6.25) as:

$$\left[ {\begin{array}{*{20}{c}} {{\text{PC2F}}} \\ {{\text{LC2F}}} \end{array}} \right]={\left[ {\begin{array}{*{20}{c}} {{\alpha _o}}&{{\beta _o}}&0&0 \\ 0&0&{{\alpha _o}}&{{\beta _o}} \end{array}} \right]_{C(2 \times 4)}}{\left[ {\begin{array}{*{20}{c}} {{{\bar {P}}_1}} \\ {{{\bar {P}}_2}} \\ {{{\bar {L}}_1}} \\ {{{\bar {L}}_2}} \end{array}} \right]_{l(4 \times 1)}}=\left[ {\begin{array}{*{20}{c}} 1&0 \\ 1&{{\lambda _{{\text{LC2F}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \Re \\ {{N_1}} \end{array}} \right]+{v_{2{\text{F}}}}$$

(9)

where the combinations for dual-frequency code and phase measurements are ${\text{PC2F}}$ and ${\text{LC2F}}$, respectively; ${\alpha _{\text{o}}}=\frac{{f_{1}^{2}}}{{f_{1}^{2} - f_{2}^{2}}}$ and ${\beta _{\text{o}}}= - \frac{{f_{2}^{2}}}{{f_{1}^{2} - f_{2}^{2}}}$ are ionospheric-free coefficients; and the dual-frequency combined wavelength is ${\lambda _{{\text{LC2F}}}}=\frac{c}{{{f_1}+{f_2}}}$. Table 1 lists the coefficients along with noise amplification factors of the dual-frequency LC for code and phase measurements (${\sigma _{{\text{PC2F}}}}$ and ${\sigma _{{\text{LC2F}}}}$) for GPS, Galileo and BeiDou. Note that standard deviations of combined (between-satellite differences) code and carrier phase measurement denoted as ${\sigma _{\text{P}}}$ and ${\sigma _{\text{L}}}$ are assumed to be identical (in units of meters) for all frequencies.

Table 1 Dual-frequency linear combination of code and phase measurements coefficients and noise amplification factors for three GNSS constellations

Triple-frequency case

Li et al. (2013) introduced a code LC that has minimal measurement noise, is GB, and is ionospheric free:

$$\left[ {\begin{array}{*{20}{c}} {{\text{PC3F}}} \\ {{\text{LC3F}}} \end{array}} \right]={\left[ {\begin{array}{*{20}{c}} {{\alpha _1}}&{{\beta _1}}&{{\gamma _1}}&0&0&0 \\ 0&0&0&{{\alpha _1}}&{{\beta _1}}&{{\gamma _1}} \end{array}} \right]_{C(2 \times 6)}}{\left[ {\begin{array}{*{20}{c}} {{{\bar {P}}_1}} \\ \begin{gathered} {{\bar {P}}_2} \hfill \\ {{\bar {P}}_3} \hfill \\ {{\bar {L}}_1} \hfill \\ {{\bar {L}}_2} \hfill \\ {{\bar {L}}_3} \hfill \\ \end{gathered} \end{array}} \right]_{l(6 \times 1)}}=\left[ {\begin{array}{*{20}{c}} 1&0 \\ 1&{{\lambda _{{\text{LC3F}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \Re \\ {{N_1}} \end{array}} \right]+{v_{{\text{3F}}}}$$

(10)

where the functions for triple-frequency code and phase measurements are ${\text{PC3F}}$ and ${\text{LC3F}}$ respectively; and the triple-frequency combined wavelength is ${\lambda _{{\text{LC3F}}}}={\alpha _1}{\lambda _1}+{\beta _1}{\lambda _2}+{\gamma _1}{\lambda _3}$. If the three scaling factors for the triple-frequency measurement noises are chosen as 1, the three ionospheric-free coefficients $({\alpha _1},{\beta _1},{\gamma _1})$ and noise amplification factors of the triple-frequency LC of code and phase measurements (${\sigma _{{\text{PC3F}}}}$ and ${\sigma _{{\text{LC3F}}}}$) in (10) fulfill the conditions:

$$\left\{ {\begin{array}{*{20}{l}} {{\alpha _1}+{\beta _1}+{\gamma _1}=1} \\ {{\alpha _1}+\frac{{f_{1}^{2}}}{{f_{2}^{2}}}{\beta _1}+\frac{{f_{1}^{2}}}{{f_{3}^{2}}}{\gamma _1}=0} \\ {\sigma _{{{\text{PC3F}}}}^{2}=(\alpha _{1}^{2}+\beta _{1}^{2}+\gamma _{1}^{2})\sigma _{P}^{2}=\hbox{min} ,\,{\text{or}}\,\sigma _{{\text{LC3F}}}^{2}=(\alpha _{1}^{2}+\beta _{1}^{2}+\gamma _{1}^{2})\sigma _{{\text{L}}}^{2}=\hbox{min} } \end{array}} \right.$$

(11)

To solve this equation, the first and second variable (${\alpha _1}$, ${\beta _1}$) can be expressed as functions of the third one $F({\gamma _1})$. Then, they should be substituted into the minimization of the third condition of (11). Solving the quadratic equation by setting the first derivative equal to zero $\left( {\frac{{{\text{d}}F}}{{{\text{d}}{\gamma _1}}}=0} \right)$ (finding critical points of ${\gamma _1}$) and considering the sign of the second derivative (finding when a critical point of ${\gamma _1}$ is a local maximum or a local minimum), one can find ${\gamma _1}$ first. Back substitution is required to find (${\alpha _1}$, ${\beta _1}$). The three coefficients $({\alpha _1},{\beta _1},{\gamma _1})$ in (11) and the combined wavelength in (10) are determined, and listed in Table 2.

Table 2 Triple-frequency linear combination of code and phase measurements coefficients and noise amplification factors for three GNSS constellations

Note that the noise levels in Table 2 are slightly smaller than those in Table 1, while the newly constructed long wavelengths in Table 2 are slightly longer than those in Table 1. Therefore, the NL-AR using triple-frequency LC observable is expected to be quicker than that for the dual-frequency case. Although the noise amplification is slightly reduced when using the triple-frequency LC observable, the combined triple-frequency code noise in model (10) is still large and needs to be reduced.

Li et al. (2013) have proposed LC models, with EWL and WL ambiguities resolved, based on triple-frequency phase measurements only:

$$\left[ {\begin{array}{*{20}{c}} {{\text{LC3}}{{\text{F}}_{\text{w}}}} \\ {{\text{LC3F}}} \end{array}} \right]={\left[ {\begin{array}{*{20}{c}} 0&0&0&x&y&z \\ 0&0&0&{{\alpha _1}}&{{\beta _1}}&{{\gamma _1}} \end{array}} \right]_{C(2 \times 6)}}{\left[ {\begin{array}{*{20}{c}} {{{\bar {P}}_1}} \\ \begin{gathered} {{\bar {P}}_2} \hfill \\ {{\bar {P}}_3} \hfill \\ {{\bar {L}}_1} \hfill \\ {{\bar {L}}_2} \hfill \\ {{\bar {L}}_3} \hfill \\ \end{gathered} \end{array}} \right]_{l(6x1)}}=\left[ {\begin{array}{*{20}{c}} 1&0 \\ 1&{{\lambda _{{\text{LC3F}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \Re \\ {{N_1}} \end{array}} \right]+{v_{{\text{3F}}}}$$

(12)

In (12), the combination for triple-frequency phase measurements ${\text{(LC3F)}}$ is the same as in model (10). The ${\text{PC3F}}$ part will now be replaced by an ambiguity-resolved combination $({\text{LC3}}{{\text{F}}_{\text{w}}})$, which can be determined using the following three conditions:

$$\left\{ {\begin{array}{*{20}{l}} {x+y+z=1} \\ {x+\frac{{f_{1}^{2}}}{{f_{2}^{2}}}y+\frac{{f_{1}^{2}}}{{f_{3}^{2}}}z=0} \\ {{\lambda _1}x+{\lambda _2}y+{\lambda _3}z=0} \end{array}} \right.$$

(13)

The first two equations of (13) fulfill the conditions of GB and ionospheric free, while the last condition is derived from the triple-frequency ambiguity term expressed as ${\lambda _1}x{N_1}+{\lambda _2}y{N_2}+{\lambda _3}z{N_3}=({\lambda _1}x+{\lambda _2}y+{\lambda _3}z){N_1} - ({\lambda _2}y+{\lambda _3}z){N_{{\text{wl}}}} - {\lambda _3}z{N_{{\text{ew}}}}$. When the EWL integer ambiguities are resolved beforehand, the third condition of (13) can be generated if the term ${\lambda _1}x+{\lambda _2}y+{\lambda _3}z$ equals to 0. Solving (13), the $x, y\,{\text{and}}\,z$ are listed in Table 3. The newly formulated ${\lambda _{{\text{LC3}}{{\text{F}}_{\text{w}}}}}= - ({\lambda _2}y+{\lambda _3}z)=\frac{{{f_1}}}{{{f_1} - {f_3}}}.\frac{c}{{{f_1} - {f_2}}}$ is the corresponding WL wavelength.

Table 3 Triple-frequency linear combination of phase measurement coefficients and noise amplification factors for three GNSS constellations

The noise level of the proposed WL in the last column in Table 3 is amplified to more than an about $110{\sigma _{\text{L}}}$ for each constellation. The WL wavelength of the LC is more than 3.2 m, longer than in the standard dual-frequency case for GPS of about 0.86 m. As a result, this WL combination can be resolved with just several minutes of measurements. If the combined phase-only measurement noise ${\sigma _{{\text{LC3}}{{\text{F}}_{\text{w}}}}}$ in (12) is smaller than the combined code measurement noise ${\sigma _{{\text{PC3F}}}}$ in (10), it can be used for the NL-AR, because it is also GB and ionosphere free. As can be seen from the last column of Tables 2 and 3, ${\sigma _{{\text{PC3F}}}}>{\sigma _{{\text{LC3F}}}}$ $({\text{or}}\,2.51{\sigma _{\text{P}}}>109.98{\sigma _{\text{L}}})$ if the ratio of ${\sigma _{\text{P}}}/{\sigma _{\text{L}}}$ is larger than 43.13 for GPS (L1 + L2 + L5) system. Similarly, the ratio values required are 68.65 for Galileo (E1 + E5a + E5b) and 39.86 for BeiDou (B1 + B2 + B3). In fact, (12) is recommended because in GNSS data processing the ratio is empirically chosen to be around 100 or 150 (Li et al. 2013; Teunissen et al. 1999; Verhagen and Teunissen 2013). Furthermore, the experimental results have shown that the actual ${\sigma _{\text{P}}}/{\sigma _{\text{L}}}$ is greater than 150 for GNSS systems (Brack 2017; Cai et al. 2016; Teunissen and de Bakker 2013). Table 4 summarizes the coefficients for the matrix $C$ in (9), (10) and (12).

Table 4 Combination operator matrix $(C)$ used in (9), (10) and (12)

Equivalence between an optimal LC model and the UC model

In this section, we will answer the key question which one is confronted with when the estimations of $\hat {\xi }$ and its variance–covariance matrix ${Q_{\hat {\xi }}}$ from the LC models of (7) coincide with the ones from the UC model of (5) according to the weighted least-squares adjustment. In addition, as can be seen in (7), the LC models are transformed from the UC model using combination operator matrices $(C)$, with the condition $C{A_2}=0$. Therefore, it is necessary to investigate which conditions of the $C$ matrices result in identical solutions from the two models.

To derive $\hat {\xi }$ and ${Q_{\hat {\xi }}}$ from (5), one can execute the standard elimination of ${\hat {I}_1}$ from the normal equations for $\hat {x}={[\begin{array}{*{20}{c}} {\hat {\xi }}&{{{\hat {I}}_1}} \end{array}]^{\text{T}}}$. We first write the normal equations in partitioned form:

$$\left[ {\begin{array}{*{20}{c}} {A_{1}^{{\text{T}}}{P_l}{A_1}}&{A_{1}^{{\text{T}}}{P_l}{A_2}} \\ {A_{2}^{{\text{T}}}{P_l}{A_1}}&{A_{2}^{{\text{T}}}{P_l}{A_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\hat {\xi }} \\ {{{\hat {I}}_1}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {A_{1}^{{\text{T}}}{P_l}l} \\ {A_{2}^{{\text{T}}}{P_l}l} \end{array}} \right]$$

(14)

Multiply row 2 by $A_{1}^{\text{T}}{P_l}{A_2}{(A_{2}^{\text{T}}{P_l}{A_2})^{ - 1}}$and subtract from row 1 in (14), this produces a zero block in row 1, column 2. It leaves an equation for $\hat {\xi }$ alone

$$\left[ {\begin{array}{*{20}{c}} {A_{1}^{{\text{T}}}{P_l}{A_1} - A_{1}^{{\text{T}}}{P_l}{A_2}{{(A_{2}^{{\text{T}}}{P_l}{A_2})}^{ - 1}}A_{2}^{{\text{T}}}{P_l}{A_1}}&0 \\ {A_{2}^{{\text{T}}}{P_l}{A_1}}&{A_{2}^{{\text{T}}}{P_l}{A_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\hat {\xi }} \\ {{{\hat {I}}_1}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {A_{1}^{{\text{T}}}{P_l}l - A_{1}^{{\text{T}}}{P_l}{A_2}{{(A_{2}^{{\text{T}}}{P_l}{A_2})}^{ - 1}}A_{2}^{{\text{T}}}{P_l}l} \\ {A_{2}^{{\text{T}}}{P_l}l} \end{array}} \right]$$

(15)

After executing the ionospheric-free elimination, the estimated parameters and its variance–covariance matrix in the UC model are expressed by:

$${\hat {\xi }_{{\text{UC}}}}={(A_{1}^{{\text{T}}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{l}^{{{\text{UC}}}}{A_1})^{ - 1}}(A_{1}^{{\text{T}}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{l}^{{{\text{UC}}}}l)$$

(16)

$${Q_{{{\hat {\xi }}_{{\text{UC}}}}}}={(A_{1}^{{\text{T}}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{l}^{{{\text{UC}}}}{A_1})^{ - 1}}$$

(17)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{l}^{{{\text{UC}}}}={P_l} - {P_l}{A_2}{(A_{2}^{{\text{T}}}{P_l}{A_2})^{ - 1}}A_{2}^{{\text{T}}}{P_l}$ represents a modified weight matrix for the UC model.

From (7), the estimated parameters and the variance–covariance matrix can be derived as:

$${\hat {\xi }_{{\text{LC}}}}={(A_{{\text{c}}}^{{\text{T}}}{P_{{\text{lc}}}}{A_{\text{c}}})^{ - 1}}(A_{{\text{c}}}^{{\text{T}}}{P_{{\text{lc}}}}{l_{\text{c}}})={(A_{{\text{1}}}^{{\text{T}}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{l}^{{{\text{LC}}}}{A_1})^{ - 1}}(A_{{\text{1}}}^{{\text{T}}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{l}^{{{\text{LC}}}}l)$$

(18)

$${Q_{{{\hat {\xi }}_{{\text{LC}}}}}}={(A_{{\text{c}}}^{{\text{T}}}{P_{{\text{lc}}}}{A_{\text{c}}})^{ - 1}}={(A_{1}^{{\text{T}}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{l}^{{{\text{LC}}}}{A_1})^{ - 1}}$$

(19)

with $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P}_{l}^{{{\text{LC}}}}={C^{\text{T}}}{(CP_{l}^{{ - 1}}{C^{\text{T}}})^{ - 1}}C$ being a modified weight matrix for the LC models.

As can be seen from (16) to (19), the two approaches, the UC and LC models in (5) and (7) using the least-squares principle, result in identical $\hat {\xi }$ and ${Q_{\hat {\xi }}}$, if and only if the two modified weight matrices are equal, that is:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{l}^{{{\text{UC}}}}=\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{l}^{{{\text{LC}}}}\,{\text{or}}\,{P_l}[{I_n} - {A_2}{(A_{2}^{{\text{T}}}{P_l}{A_2})^{ - 1}}A_{2}^{{\text{T}}}{P_l}]={C^{\text{T}}}{(CP_{l}^{{ - 1}}{C^{\text{T}}})^{ - 1}}C$$

(20)

where ${I_n}$ denotes the ${\text{ }}\left[ {n \times n} \right]$ identity matrix, $n$ is the number of measurements, which has a value of 4 and 6 for the dual- and triple-frequency case, respectively.

Next, we have to answer the second question concerning which conditions on $C$ make the left- and right-hand side of (20) equal. The theory of nuisance parameter elimination presented by Schaffrin and Grafarend (1986) can be used. Basically, a theorem and two corollaries in that study are only applied for a differencing matrix constructed for single, double and triple differencing to eliminate biases (i.e., satellite–receiver clock errors, ambiguity unknowns). We will, however, apply this theory for eliminating the ionospheric delay which is usually the main purpose of using the LC models. Schaffrin and Grafarend (1986, Equation 1.3) has introduced a transformed matrix $R$ of full column rank (here it is referred to $C$ with full row rank) such that

$$\left\{ \begin{gathered} C{A_2}=0 \hfill \\ {\text{rank}}(C)=n - {\text{rank}}({A_2}) \hfill \\ \end{gathered} \right.$$

(21)

The first condition of (21) shows that the columns of ${C^{\text{T}}}$ construct a basis of the nullspace of $A_{2}^{{\text{T}}}$ (or every row containing ${c_{ij}}$ coefficients of $C$ is perpendicular to vector ${A_2}$), while the second condition is the number of independent rows (LCs). Once we have a certain solution of the first condition of (21) at hand, say ${C_{\text{o}}}$ with ${\text{rank}}(C)={\text{rank}}({C_{\text{o}}})$, Schaffrin and Grafarend (1986, Equation 1.5a, b) then introduced the general class of admissible matrices given by

$$\begin{aligned} C & = KP_{{\text{l}}}^{{ - 1}} C_{{\text{o}}}^{{\text{T}}} (C_{{\text{o}}} P_{{\text{l}}}^{{ - 1}} C_{{\text{o}}}^{{\text{T}}} )^{{ - 1}} C_{{\text{o}}} \\ & = K\left[ {I_{{\text{n}}} - A_{2} (A_{2}^{{\text{T}}} P_{{\text{l}}} A_{2} )^{{ - 1}} A_{2}^{{\text{T}}} P_{{\text{l}}} } \right] \\ \end{aligned}$$

(22)

with the additional requirement of $KP_{l}^{{ - 1}}C_{{\text{o}}}^{{\text{T}}}$ being regular for any otherwise arbitrarily chosen $[(n - {\text{rank}}({A_2})) \times n]$ matrix. The second part of (22) characterizes the whole class of admissible matrices $C$ as a linear form in the rows of the singular projection matrix $\left[ {{I_n} - {A_2}{{(A_{2}^{{\text{T}}}{P_l}{A_2})}^{ - 1}}A_{2}^{{\text{T}}}{P_l}} \right]$. Schaffrin and Grafarend (1986, Corollary 1.2) has stated and proved that $\hat {\xi }$ and ${Q_{\hat {\xi }}}$ in the original (UC) model and any transformed (LC) models coincide if $C$ fulfills (21) and is chosen out of class (22). In fact, the correctness of Schaffrin’s corollary 1.2 can be validated by multiplying $P_{l}^{{ - 1}}$ to both sides of (20), which results in the singular projection matrices, $[{I_n} - {A_2}{(A_{2}^{{\text{T}}}{P_l}{A_2})^{ - 1}}A_{2}^{{\text{T}}}{P_l}]\,{\text{and}}\,P_{l}^{{ - 1}}{C^{\text{T}}}{(CP_{l}^{{ - 1}}{C^{\text{T}}})^{ - 1}}C$, on both sides of (20). These singular projection matrices are identical, as shown in the first and second part of (22). Therefore, with $C$ arbitrarily chosen out of class (22), an optimal LC model for dual- and triple-frequency must satisfy the following conditions:

For dual frequency:

$$\left\{ \begin{gathered} C{A_2}=0{\text{ (a}}\,{\text{necessary}}\,{\text{condition ) }} \hfill \\ {\text{rank}}(C)=3\,({\text{a}}\,{\text{sufficient}}\,{\text{condition)}} \hfill \\ \end{gathered} \right.$$

(23)

For triple frequency:

$$\left\{ \begin{gathered} C{A_2}=0{\text{ (a}}\,{\text{necessary}}\,{\text{condition) }} \hfill \\ {\text{rank}}(C)=5{\text{ (a}}\,{\text{sufficient}}\,{\text{condition)}} \hfill \\ \end{gathered} \right.$$

(24)

When we start with dual- and triple-frequency code and phase, we have four and six observations $(n=4\,{\text{or}}\,{\text{6)}}$, respectively, as shown in (3) and (4). Then, we eliminate one unknown parameter from the model $({\text{rank}}({A_2})=1)$, namely ionospheric delay (${I_1}$), and we should formally be left with three and five independent LCs, respectively. In fact, in the dual-frequency case, only two LCs are traditionally formed based on code and carrier phase measurements. The ionospheric delay is eliminated twice (in other words, we estimate the ionospheric delay once from the code measurements and once from the carrier phase measurements) (Van Der Marel and De Bakker 2012). Shen (2002) and Xiang et al. (2017) demonstrated that an observation model with three independent LCs had a smaller noise level and slightly fast convergence time than the traditional model with two LCs.

Near-optimal LC models for triple-frequency GNSS measurements

In terms of computational complexity, that is multiplication and inversion for matrices using a least-squares adjustment, an optimal LC model with five sets of triple-frequency LC measurements provides a small improvement of computing speed compared to the UC model with six observables. Therefore, it is necessary to find the operator matrix $C$ with rank of only four or even three to further reduce the computational burden, which still ensures the near-optimal performance for triple-frequency GNSS measurements.

The near-optimal LC models with four and three set triple-frequency LCs can be written as:

$${C_{(4 \times 6)}}=\left[ {\begin{array}{*{20}{c}} {{\alpha _1}}&{{\beta _1}}&{{\gamma _1}}&0&0&0 \\ 0&0&0&{{\alpha _o}}&{{\beta _o}}&0 \\ 0&0&0&x&y&z \\ {{\kappa _1}}&{{\kappa _2}}&{{\kappa _3}}&{{\kappa _4}}&{{\kappa _5}}&{{\kappa _6}} \end{array}} \right]$$

(25)

$${C_{(3 \times 6)}}=\left[ {\begin{array}{*{20}{c}} 0&0&0&{{\alpha _1}}&{{\beta _1}}&{{\gamma _1}} \\ 0&0&0&{{\alpha _o}}&{{\beta _o}}&0 \\ {{\kappa _1}}&{{\kappa _2}}&{{\kappa _3}}&{{\kappa _4}}&{{\kappa _5}}&{{\kappa _6}} \end{array}} \right]$$

(26)

where the first row (or the first LC) in ${C_{(4 \times 6)}}$ and ${C_{(3 \times 6)}}$ is the same as the coefficients of the combined triple-frequency code and phase measurements [${\text{PC3F}}$ and ${\text{LC3F}}$ in (10)]. The second row in ${C_{(4 \times 6)}}$ and ${C_{(3 \times 6)}}$ represents the coefficients of the combined dual-frequency phase measurements [${\text{LC2F}}$ in (9)]. The third in ${C_{(4 \times 6)}}$ contains the coefficients of the ambiguity-resolved combination [${\text{LC3}}{{\text{F}}_{\text{w}}}$ in (12)]; and ${\kappa _i}(i=1 \ldots 6)$ in the last row of ${C_{(4 \times 6)}}$ and ${C_{(3 \times 6)}}$ represent the weighting coefficients of the three code and three phase measurements in the triple-frequency vector $l$ of (4). Apart from that, those six coefficients must satisfy a general condition for code and carrier phase measurements based on GB, ionospheric-free (IF) and minimal noise amplification of the LC:

$$\left\{ \begin{gathered} {\kappa _1}+{\kappa _2}+{\kappa _3}+{\kappa _4}+{\kappa _5}+{\kappa _6}=1 \hfill \\ {\kappa _1}+{\mu _1}{\kappa _2}+{\mu _2}{\kappa _3} - {\kappa _4} - {\mu _1}{\kappa _5} - {\mu _2}{\kappa _6}=0 \hfill \\ \sigma _{{({\text{PL}})}}^{2}=(\kappa _{1}^{2}+\kappa _{2}^{2}+\kappa _{3}^{2})\sigma _{{\text{P}}}^{2}+(\kappa _{4}^{2}+\kappa _{5}^{2}+\kappa _{6}^{2})\sigma _{{\text{L}}}^{2}=\hbox{min} \hfill \\ \end{gathered} \right.$$

(27)

The first two conditions in (27) are the GB and IF conditions, while the last condition is the optimal noise for linear code and phase combinations. ${\sigma _{\text{P}}}$ and ${\sigma _{\text{L}}}$ are again assumed to be identical for all three frequencies. The resulting integer ambiguity terms on the ith frequency in the general condition for code and carrier phase measurements can be grouped as:

$${\kappa _4}{\lambda _1}{N_1}+{\kappa _5}{\lambda _2}{N_2}+{\kappa _6}{\lambda _3}{N_3}={\lambda _{{\text{LC,(GB}} - {\text{IF}})}}({n_1}{N_1}+{n_2}{N_2}+{n_3}{N_3})={\lambda _{{\text{LC,(GB}} - {\text{IF}})}}{N_{({n_1},{n_2},{n_3})}}$$

(28)

with ${\lambda _{{\text{LC,(GB}} - {\text{IF}})}}$ and ${f_{{\text{LC,(GB}} - {\text{IF}})}}$ being the combined wavelength and frequency, respectively; ${n_1}$, ${n_2}$ and ${n_3}$ are three integer coefficients for the three frequencies. As a result of (28) we obtain the following relations between the weighting coefficients ${\kappa _4}$, ${\kappa _5}$ and ${\kappa _6}$, and the integer coefficients ${n_1}$, ${n_2}$ and ${n_3}$:

$$\left\{ \begin{gathered} {\kappa _4}={n_1}\frac{{{f_1}}}{{{f_{{\text{LC,(GB}} - {\text{IF}})}}}} \hfill \\ {\kappa _5}={n_2}\frac{{{f_2}}}{{{f_{{\text{LC,(GB}} - {\text{IF}})}}}} \hfill \\ {\kappa _6}={n_3}\frac{{{f_3}}}{{{f_{{\text{LC,(GB}} - {\text{IF}})}}}} \hfill \\ {f_{{\text{LC,(GB}} - {\text{IF}})}}={n_1}{f_1}+{n_2}{f_2}+{n_3}{f_3} \hfill \\ \end{gathered} \right.$$

(29)

This combination has the advantage of being more general and not losing any degrees of freedom. In addition, the weighting coefficients ${\kappa _1}$, ${\kappa _2}$ and ${\kappa _3}$ of the code observations do not have to have the same form as those of the phase observations [see (10)]. Wang and Rothacher (2013) have described a procedure to solve the six weighting coefficients (${\kappa _{i=1,6}}$) in (27) and (29), but applied it to the geometry-free $\left( {\sum\nolimits_{{i=1}}^{6} {{\kappa _{i=1,6}}} =0} \right)$ and ionospheric-free case. A similar approach can be applied in the GB context. The six coefficients will be based on three integer coefficients ${n_1}$, ${n_2}$, ${n_3}$ and the three frequencies. Next, the three integer coefficients ${n_1}$, ${n_2}$ and ${n_3}$ are varied in magnitude in the range − 20 to + 20. ${\sigma _{\text{P}}}$ and ${\sigma _{\text{L}}}$ can be arbitrarily chosen as 1.00 m and 0.01 m, respectively. The most suitable three integer coefficients for the NL LC are (4, 0, − 3), (4, − 2, − 1) and (4, − 5, 2) for GPS (L1, L2, L5), Galileo (E1, E5a, E5b) and BeiDou (B1, B2, B3). In general, the most suitable three integer coefficients (${n_1}$, ${n_2}$ and ${n_3}$) will be selected based on the highest ratio of combined wavelength and associated noise amplification factor $({\lambda _{{\text{LC,(GB}} - {\text{IF}})}}/{\sigma _{({\text{PL}})}})$.

Numerical analysis

As mentioned above, the smaller the diagonal values of the variance–covariance matrix (6), the more accurate the float solution will be. The optimal LC model is determined when the variance of $\Re$ and ${N_1}$ in (6) is the smallest. Note that both EWL and WL ambiguities are fixed beforehand with high confidence to given values. In fact, the impact of fixed EWL and WL ambiguities (denoted as a vector $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N}$) on the values of a grouped vector $\xi ={[\begin{array}{*{20}{c}} \Re &{{N_1}} \end{array}]^{\text{T}}}$ and its corresponding variance can be added back into the NL float solution as $\tilde {\xi }=\xi - {Q_{\xi \hat {N}}}Q_{{\hat {N}\hat {N}}}^{{ - 1}}(\hat {N} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N} )$ and ${Q_{\tilde {\xi }\tilde {\xi }}}={Q_{\xi \xi }} - {Q_{\xi \hat {N}}}Q_{{\hat {N}\hat {N}}}^{{ - 1}}{Q_{\hat {N}\xi }}$. Interestingly, although incorrect fixing EWL and WL will significantly affect the values of $\Re$ and ${N_1}$, it will not affect the variances of $\Re$ and ${N_1}$. Hence, the correctness of the derived models (23) and (24) will be verified using a numerical test based on a standard least-squares adjustment for both the UC [see (3) and (4)] and LC models [see (9), (10) and (12)]. Assume that the code and phase noises are ${\sigma _{\text{P}}}=1.00$ m and ${\sigma _{\text{L}}}=0.01$ m, respectively. The combination operator matrix $(C)$ is given in Table 5.

Table 5 Combination operator matrix $(C)$ for the optimal LC models of (23) and (24)

Tables 6 and 7 compare the variances of the ambiguity and the geometric terms of the optimal, the near-optimal and the current LC models with that of the UC model for both the dual- and triple-frequency GNSS cases. Note that the performance of the UC models without using the ionosphere models is the best (Teunissen and Khodabandeh 2014), thus the variance–covariance matrix obtained from the UC solutions is used as reference to evaluate the current LC models. The first thing to note is that the UC and the optimal LC results are identical, since the variance differences of the ambiguity term and geometric terms are zeros. As a result, the optimal LC models [(23) and (24)] are expected to have the same performance with the UC models providing the best performance amongst all cases. As can be seen from Table 6, the near-optimal LC models [(25) and (26)] have significantly lower variances and thus outperform the LC models proposed by Li et al. (2013) [see (10) and (12)]. Amongst the triple-frequency combinations tested, the Galileo E1 + E5a + E6 has the best performance. However, the dual-frequency combination of L1 + L5 for GPS and E1 + E5a for Galileo give the best performance.

Table 6 Variances of the ambiguity and geometric terms for the triple-frequency GNSS UC model [model (4)] and the differences in variance between the UC model with the proposed optimal LC model (24), the near-optimal LC models (25) and (26), and the current LC models (10) and (12)

Table 7 Variances of the ambiguity and geometric terms for the dual-frequency GNSS UC model [model (3)] and the differences in variance between the UC model with the proposed optimal LC model (23) and the current LC model (9)

To assess the potential improvement in positioning accuracy and ensure fast AR using triple-frequency measurements, the ratio between the standard deviation (square root of the variance) of the dual- and triple-frequency LC model is listed in Tables 6 and 7. The results are summarized in Table 8. The triple-frequency results of GPS (L1 + L2 + L5), Galileo (E1 + E5a + E5b) and BeiDou (B1 + B2 + B3) are compared to the dual-frequency results of GPS (L1 + L2), Galileo (E1 + E5a) and BeiDou (B1 + B2). In kinematic PPP processing, the receiver’s estimable position coordinates are not accumulated over time and thus the positioning accuracy is assumed to be proportional to the geometric accuracy and the position dilution of precision (PDOP) as ${\sigma _{\text{POS}}}={\text{PDOP}}{\sigma _{\hat {\Re }}}$. According to Table 8, when using triple-frequency measurements, the positioning accuracy and the ambiguity variance can be improved by 2.9, 1.8 and 2.6 times for GPS, Galileo and BeiDou, respectively (the fourth and fifth column).

Table 8 Ratios between the standard deviation of the optimal dual- and triple-frequency GNSS models for geometric terms, ambiguity term, positioning accuracy

GNSS data test

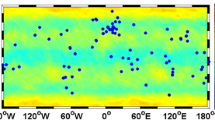
To validate the performance of the proposed optimal and near-optimal LC models for dual- and triple-frequency PPP, real measurements were collected from 5 GNSS stations within the Australian Regional GNSS Network (ARGN) over 30 consecutive days, July 10–August 09, 2017 (DOY 191–221). The reference stations were selected based on two criteria: (1) the receiver must track three frequencies and three constellations (GPS, Galileo and BeiDou) simultaneously, and (2) the selected stations should be well distributed across the Australian continent. Figure 1 shows the locations of the selected GNSS stations. For each station, an average of six 1-h sessions in a day were selected, on the basis that they contain the maximum number of triple-frequency satellites in view for all three constellations. A total 883 datasets were analyzed.

Fig. 1

Distribution of the selected GNSS stations tracking GPS, Galileo and BeiDou satellites

Seven different models (or test cases), listed in Table 9, were evaluated: (1) the triple-frequency UC model (UNCB3F), (2) the proposed optimal triple-frequency LC model (OPTM3F), (3) the proposed near-optimal triple-frequency LC model with the rank of operator matrix being four (NOPTM1), (4) the proposed near-optimal triple-frequency LC model with the rank of operator matrix being three (NOPTM2), (5) the triple-frequency LC model proposed by Li et al. (2013) (CURR3F), (6) the proposed optimal dual-frequency LC model (OPTM2F), and (7) the standard dual-frequency LC model (STND2F). It should, however, be pointed out that the number of GNSS satellites transmitting three frequencies were limited during certain periods in a day. Therefore, the triple-frequency PPP results were based on a combination of dual- and triple-frequency measurements. Although the Galileo E1 + E5a + E6 signal combination gives the best performance, as indicated by the numerical analysis, the satellite correction products (i.e., code and phase biases) for the Galileo E6 signal are not yet publicly available. Hence, only the Galileo E1 + E5a + E5b was used in this analysis.

Table 9 Seven different models evaluated in kinematic PPP NL data analysis

A modified version of the RTKLIB software (Takasu 2013) was used to stream GNSS measurements and output-corrected observables free from the effects listed in Table 10. The table also outlines the processing strategy used. A MATLAB-based GNSS PPP software with a Kalman filter estimator was developed to process the corrected observables using the dual- and triple-frequency UC and LC models for GPS, Galileo and BeiDou. Since the orbit and clock products for Galileo and BeiDou have poorer quality than for GPS (Guo et al. 2017; Laurichesse and Blot 2016; Montenbruck et al. 2017), it is difficult to fix a full set of float NL ambiguities. Hence the partial ambiguity resolution (PAR) technique, based on LAMBDA decorrelation (Brack 2017; Odijk et al. 2014; Teunissen 1994, 2001; Verhagen and Li 2012), was implemented in the GNSS software to resolve ambiguities. To fix a subset of decorrelated ambiguities with high confidence, both success rate and ratio test were applied in a modified PAR method based on an iterative procedure. For the LC models, the receiver coordinates, tropospheric delay and ambiguity parameters were estimated within the Kalman filter. For the UC model, in addition to the receiver coordinates, tropospheric delay and ambiguity parameters, the slant ionospheric delay for each satellite was also estimated (and treated as a random walk process). The commonly used variance function, depending on the satellite elevation angle $e$, is:

Table 10 Triple-frequency multi-GNSS PPP NL processing strategy

$${\sigma ^2}=\left( {{d^2 _0}+\frac{{{d^2 _1}}}{{{{\sin }^2}e}}} \right),$$

(30)

where $d _0$ and $d_1$ were chosen to have the value of 3 mm, and ${\sigma _{\text{P}}}/{\sigma _{\text{L}}}$ is selected as 100. These are the default values in the RTKLIB software (Takasu 2013).

The performance of the seven different models was compared based on the root mean square (RMS) error for the horizontal and vertical position estimates, the NL ambiguity fixing rate and the time-to-first-fix (TTFF). The RMS errors were computed from the differences between the estimated PPP solutions and the “known” coordinates of the GNSS reference stations. Figure 2 shows the horizontal and vertical RMS as a function of time for the seven models. Depending on the model used, the horizontal and vertical position solutions require at least 6–9 min and 10–18 min to converge to within 0.1 m, respectively. As anticipated, the UNCB3F, OPTM3F, NOPTM1 and NOPTM2 models gave the best positioning accuracy and had the shortest convergence time. When compared to the standard dual-frequency STND2F model, the UNCB3F, OPTM3F and even NOPTM1 or NOPTM2 models provide slightly improved convergence times of 4 min. Once the solution converged to 0.1 m, the results from the seven models are comparable. A 5 cm horizontal positioning accuracy can be achieved after 15 min, and 8 cm vertical positioning accuracy after 20 min.

Fig. 2

Time series of the horizontal (top) and vertical (bottom) RMS errors based on the seven different UC and LC models used for PPP NL ambiguity resolution

Figure 3 shows the overall NL ambiguity fixing rates (as a percentage) for the seven test cases. In general, the average ambiguity fixing success rate of using the triple-frequency UNCB3F and OPTM3F or even NOPTM1 and NOPTM2 models is about 15% higher than the standard dual-frequency STND2F model. This confirms that the proposed optimal (OPTM3F) or near-optimal (NOPTM1 and NOPTM2) triple-frequency LC model results in improved ambiguity fixing success rates. All seven models achieve a 95% ambiguity fixing rate after 10–13 min.

Fig. 3

Narrow-lane ambiguity fixing rate in percentage when using different UC and LC models

Table 11 lists the average TTFF for the seven cases. The TTFF for the UNCB3F, OPTM3F, NOPTM1, and NOPTM2 models are generally lower than for the other cases. Again, this highlights the equivalence of the uncombined UNCB3F model with the proposed optimal OPTM3F model. The TTFF using the OPTM3F and UNCB3F models is 302 s compared to 490 s using the CURR3F model. In addition, the proposed NOPTM1 and NOPTM1 models even outperform the CURR3F model, having shorter TTFF values. The UNCB3F and OPTM3F models provide an improvement of 38% compared to the CURR3F and 46% compared to the STND2F. This is reasonable since the UNCB3F and OPTM3F models have minimal noises (variances) for geometry and ambiguity terms, as shown in Tables 6 and 7. Hence, the UC and optimal LC models are expected to be more reliable compared to the current LC models.

Table 11 TTFF (in seconds) for the seven different UC and LC models

It is worth mentioning that the UNCB3F results agreed with the OPTM3F results for all criteria, and they always outperformed the current standard dual- and triple-frequency LC models STND2F and CURR3F. The NOPTM1 and NOPTM1 results are comparable with the OPTM3F results, and outperform the current standard dual- and triple-frequency LC models STND2F and CURR3F. These results have verified the correctness and efficiency of the proposed optimal and near-optimal LC model for PPP NL-AR. It should be noted that the performance of the triple-frequency PPP using real measurements may not be as good as the results of the numerical analysis presented in Table 8 due to an insufficient number of triple-frequency GNSS satellites at certain periods in a day.

Concluding remarks

Multi-frequency multi-constellation GNSS offers additional signal frequencies and measurements, which allows for the creation of a variety of LCs of measurements for fixed ambiguity PPP. In this contribution, we have proposed an optimal LC model to improve the narrow-lane ambiguity resolution (NL-AR) and time-to-first-fix (TTFF) by shortening the solution convergence time. The performance of triple-frequency multi-constellation GPS + Galileo + BeiDou NL-AR based on the uncombined (UC) and the LC PPP models was assessed. To constrain the NL phase ambiguity vector, several LC models for dual- and triple-frequency measurements with minimal measurement noise and longer wavelength were studied. The performance of seven different UC and LC models using real triple-frequency multi-constellation GNSS measurements was evaluated. The findings can be summarized as follows. First, the equivalence of mathematical forms between the UC and LC models was derived. The optimal LC models for dual- and triple-frequency measurements were developed, and these models were derived from mathematical relations between the UC and LC models. Furthermore, the near-optimal LC models with four and three sets of LCs for the triple-frequency case were also proposed to reduce computational complexity. Second, numerical analysis has confirmed that the proposed LC models under certain constraints are identical to the UC model. In fact, the current LC models for dual- and triple-frequency are not optimal compared to the UC model and the proposed LC models. Third, in both the numerical analysis and the kinematic test using real GNSS measurements, the performance of the proposed LC models in terms of position accuracy, NL ambiguity fixing success rate and solution TTFF, was always identical to those using the UC model. It also outperformed the current LC models. In particular, due to significantly lower variances and better performance in all criteria, the near-optimal LC models even outperformed the LC models proposed by Li et al. (2013). Numerical results show that the ambiguity variance using triple-frequency measurements can be smaller, being 2.9, 1.8 and 2.6 times compared to that using dual-frequency measurements for GPS, Galileo and BeiDou, respectively. Moreover, using triple-frequency GNSS measurements, the positioning accuracy can be improved by 2.9, 1.8 and 2.6 times for GPS, Galileo and BeiDou, respectively. With respect to the convergence time in the kinematic test, triple-frequency multi-GNSS measurements can shorten the solution convergence time by an average of 4 min when compared to dual-frequency multi-GNSS PPP cases. Moreover, an average TTFF of 10 min with a fixing success rate of 95% was achieved for the triple-frequency LC model in kinematic mode. Compared to the dual-frequency approach, the average fixing rate in PPP-AR using triple frequency was increased by 15% in the first 5 min. This confirms that the proposed triple-frequency LC model can accelerate the PPP NL solution. It is envisaged that with an improved accuracy of correction products such as satellite clocks, phase center offset and variation, code and phase biases (i.e., E6 phase bias), as well as increased availability of triple-frequency GNSS satellites in the near future, the performance of PPP NL-AR could be improved even further.