Introduction

Multi-antenna-based GPS real-time kinematic (RTK) has been widely applied for precise positioning and attitude determination. Besides its high cost and complex operation, the position and attitude accuracies gained with this technique are sensitive to observation environments (Scherzinger 2000) and the baseline length of multi-antenna (Vander Kuylen et al. 2006). To achieve positioning solutions of high accuracy at low cost, Zumberge et al. (1997) proposed the precise point positioning (PPP) mode based on undifferenced GPS code and phase observations, which has been proven effective for providing high-accuracy positions for a stand-alone receiver, especially after dramatic improvements in the accuracy of satellite orbits and clocks (Kouba and Héroux 2001; Kouba 2009) and significant developments of PPP models (Gao and Shen 2002; Ge et al. 2008; Tu et al. 2013).

However, in addition to the requirement of a minimum number of available satellites for positioning with global navigation satellite systems (GNSS), Zhang and Li (2012) showed that additionally continuous signal tracking is required to prevent re-initialization in GNSS precise positioning. According to the previous work, the PPP performance can be improved by using undifferenced ambiguity resolution (Ge et al. 2008) together with multi-constellation GNSS, thereby yielding more observations and smaller position dilution of precision (PDOP) (Li et al. 2015; Lou et al. 2016; Quan et al. 2016; Montenbruck et al. 2017). Currently, the GNSSs, namely GPS, GLONASS, BDS, and Galileo, can be used (Montenbruck et al. 2017). Nevertheless, neither single- nor multi-GNSS can be employed when the number of available satellites is smaller than the minimum required, which, for example, is four in the case of GPS.

Fortunately, according to Cox (1978), GNSS positioning performance can be clearly improved, especially in challenging environments by integrating GNSS with an inertial navigation system (INS). In recent years, along with the significant developments of PPP, its related technologies and satellite orbit and clock products, PPP/INS integration has been treated as a promising technique for precise positioning and attitude determination. Previous researches have proven that the positioning accuracy, reliability, and re-convergence time of PPP can be discernibly improved by INS. Roesler and Martell (2009) found that the PPP positioning accuracy can be visibly improved by using PPP/INS tight integration; this was validated by using different-grade inertial sensor measurements and GPS observations with different cutoff angles. Rabbou and El-Rabbany (2015) confirmed that PPP/INS tight integration based on inter-satellite single-differenced mode can provide higher positioning accuracies than that using undifferenced observations, which was validated by a set of GPS and low-cost inertial measurement unit (IMU) data. Also, Gao et al. (2015) introduced ionospheric delay constraints and receiver hardware time delay constraint into the PPP mode, based on which the uncombined and undifferenced PPP/INS tight integration mode was proposed and validated by an airborne test and a vehicular test using tactical-grade IMU measurements. However, the solutions from the low-cost IMU-based GNSS/INS integration system may diverge rapidly in the case of GNSS outages because of rapidly time-increasing IMU errors.

In order to overcome IMU drifts during partial and complete GNSS signal outages, we introduced an odometer, which is a self-contained and largely unsusceptible to interference, into the uncombined and undifferenced multi-GNSS PPP/INS tightly coupled integration system. Then, a set of test data from a land-borne vehicle including four-GNSS observations, low-cost IMU outputs, and odometer data are analyzed to indicate the enhancements of the odometer and IMU on positioning and attitude determination in both open-sky and challenging environments.

Mathematical model

Currently, PPP as such disposes of a mature technology (Teunissen and Khodabandeh 2015). PPP models are not introduced here, and only the model of the INS- and odometer-enhanced four-GNSS PPP using uncombined and undifferenced observations is investigated.

Observational and state functions

According to Mohamed and Schwarz (1999), the extended Kalman filter (EKF) (Brown and Hwang 1992) can be applied to our integration system with the measurement function of

$$ \varvec{Z}_{k} = \varvec{H}_{k} \varvec{X}_{k} +\varvec{\upsilon}_{k} ,\varvec{\upsilon}_{k} \sim\,N(0,\varvec{R}_{k} ) $$
(1)

and the corresponding state function of

$$ \varvec{X}_{k} =\varvec{\varPhi}_{k,k - 1} \varvec{X}_{k - 1} +\varvec{\eta}_{k - 1} ,\varvec{\eta}_{k - 1} \sim\,N(0,\varvec{Q}_{j - 1} ) $$
(2)

where Zk is the innovation vector at epoch k; \( \varvec{H}_{k} \) represents the design coefficient matrix for state parameter vector (\( \varvec{X}_{k} \)); \( \varvec{\varPhi}_{k,k - 1} \) denotes the state transition matrix from epoch k − 1 to k; \( \varvec{\upsilon}_{k} \) stands for the observation noise vector with zero mean and variance \( \varvec{R}_{k} \); \( \varvec{\eta}_{k - 1} \) is the state noise vector with variance \( \varvec{Q}_{k - 1} \).

INS-aided four-GNSS PPP observational model

The innovation vector Zk of INS tightly aided PPP model is generated by using the differences between the pseudorange, carrier phase, and Doppler predicted by INS (OINS,k) and those observed by receiver (OGNSS,k), which can be expressed as

$$ \varvec{Z}_{k} = \varvec{O}_{{{\text{INS}},k}} - \varvec{O}_{{{\text{GNSS}},k}} $$
(3)

For the GPS + BDS + Galileo + GLONASS case, we have

$$ \varvec{O}_{{{\text{GNSS}},k}} = \left[ {\begin{array}{*{20}c} {\varvec{P}_{{{\text{GNSS}},j}} } & {\varvec{L}_{{{\text{GNSS}},j}} } & {\varvec{D}_{{{\text{GNSS}},j}} } \\ \end{array} } \right]^{\text{T}} $$
(4)

where \( \varvec{P}_{{{\text{GNSS}},j}} = \left[ {\begin{array}{*{20}c} {\varvec{P}_{j}^{G} } & {\varvec{P}_{j}^{B} } & {\varvec{P}_{j}^{E} } & {\varvec{P}_{j}^{R} } \\ \end{array} } \right]^{\text{T}} \), \( \varvec{L}_{{{\text{GNSS}},j}} = \left[ {\begin{array}{*{20}c} {\varvec{L}_{j}^{G} } & {\varvec{L}_{j}^{B} } & {\varvec{L}_{j}^{E} } & {\varvec{L}_{j}^{R} } \\ \end{array} } \right]^{\text{T}} \), and \( \varvec{D}_{{{\text{GNSS}},j}} = \left[ {\begin{array}{*{20}c} {\varvec{D}_{j}^{G} } & {\varvec{D}_{j}^{B} } & {\varvec{D}_{j}^{E} } & {\varvec{D}_{j}^{R} } \\ \end{array} } \right]^{\text{T}} \); P, L, and D represent GNSS pseudorange, carrier phase, and Doppler at j frequency, wherein the frequencies used are L1 and L2 of GPS (G), B1 and B2 of BDS (B), E1 and E5b of Galileo (E), and R1 and R2 of GLONASS (R), respectively.

Since the GNSS observations in (4) contain errors, the correction models should be added to the INS-predicted vector OINS,k, which can be written as

$$ \begin{aligned} \varvec{O}_{{{\text{INS}},k}} & = \left[ {\begin{array}{*{20}c} {\varvec{P}_{{{\text{INS}},j}} } \\ {\varvec{L}_{{{\text{INS}},j}} } \\ {\varvec{D}_{{{\text{INS}},j}} } \\ \end{array} } \right] \\ & { = }\,\left[ {\begin{array}{*{20}l} { |\varvec{p}_{{{\text{INS}},{\text{r}}}} - \, \varvec{p}^{\text{s}} |+ T_{\text{r}}^{\text{s}} + I_{{j,{\text{r}}}}^{\text{s}} + c(t_{\text{r}} - t^{\text{s}} ) + d_{{{\text{r}},j}} - d_{j}^{\text{s}} + \Delta P_{{{\text{r}},j}}^{\text{s}} } \hfill \\ { |\varvec{p}_{{{\text{INS}},{\text{r}}}} - \, \varvec{p}^{\text{s}} |+ T_{r}^{s} - I_{{j,{\text{r}}}}^{\text{s}} + c(t_{\text{r}} - t^{\text{s}} ) + \lambda_{j} \tilde{N}_{j} + \, \Delta L_{{{\text{r}},j}}^{\text{s}} } \hfill \\ {( |\varvec{v}_{{{\text{INS}},{\text{r}}}} - \, \varvec{v}^{\text{s}} |+ c(\dot{t}_{\text{r}} - \dot{t}^{\text{s}} ))/\lambda_{j} } \hfill \\ \end{array} } \right] \\ \end{aligned} $$
(5)

where \( \varvec{p}_{{{\text{INS}},{\text{r}}}} \) and \( \varvec{v}_{{{\text{INS}},{\text{r}}}} \) are the position and velocity of the GNSS receiver calculated by INS mechanization (Shin 2005) in earth-centered and earth-fixed (e) frame; \( \varvec{p}^{\text{s}} \) and \( \varvec{v}^{\text{s}} \) are the satellite position and velocity computed from IGS precise orbital products; \( \mathop {()}\limits^{ \cdot } \) and | | depict the differential and the modular operation; I sr, j and T sr denote slant ionospheric delay and slant tropospheric delay; \( t_{\text{r}} \) and \( t^{\text{s}} \) indicate clock offsets of GNSS receiver and satellite; c is the light velocity in vacuum; λj and \( \tilde{N}_{j} \) represent carrier phase wavelength and float ambiguity; dr,j and d s j are pseudorange hardware delays on receiver and satellite (Tu et al. 2013), respectively; \( \Delta L_{{{\text{r}},j}}^{\text{s}} \) and \( \Delta P_{{{\text{r}},j}}^{\text{s}} \) indicate the sum of corrections of relativity effect, earth rotation effect, phase center offset, phase center variation, and phase windup for pseudorange and carrier phase, respectively (Witchayangkoon 2000).

System offset between GNSS receiver and IMU

To predict carrier phase, pseudorange, and Doppler, the INS-updated receiver position and velocity are needed, which can be obtained by processing the error-compensated IMU data in INS mechanization (Shin 2005; Roesler and Martell 2009; Gao et al. 2015; Rabbou and El-Rabbany 2015). However, the INS-predicted position and velocity have reference points different to those of GNSS observations, which lead to lever-arm system offsets. Therefore, a correction model should be applied to eliminate such system offsets before calculating the innovation vector in (3). In general, two major methods can be adopted to remove the impact of lever-arm offsets on GNSS/INS integration. Tang et al. (2009) proposed a method to parameterize such offsets as random constants and estimate them together with other parameters in EKF, obtaining estimate accuracies of several centimeters in horizontal direction and decimeter in vertical component. To get precise corrections, the other method is typically adopted, in which such system offsets are accurately measured before the test and then corrected using the measured values in the test data processing. In the navigation frame (n), the correction applied to the INS-predicted position and velocity can be written as (Shin 2005; Gao et al. 2017)

$$ \left[ {\begin{array}{*{20}c} {\varvec{p}_{{{\text{INS}},{\text{r}}}}^{n} } \\ {\varvec{v}_{{{\text{INS}},{\text{r}}}}^{n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varvec{p}_{\text{INS}}^{n} } \\ {\varvec{v}_{\text{INS}}^{n} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\varvec{D}^{ - 1} \varvec{C}_{b}^{n}\varvec{\iota}^{b} } \\ { - (\varvec{\omega}_{in}^{n} \times )\varvec{C}_{b}^{n}\varvec{\iota}^{b} - \varvec{C}_{b}^{n} (\varvec{\iota}^{b} \times )\varvec{\omega}_{ib}^{b} } \\ \end{array} } \right] $$
(6)

where \( \varvec{ p}_{{{\text{INS}},{\text{r}}}}^{n} \) and \( \varvec{v}_{{{\text{INS}},{\text{r}}}}^{n} \) are the receiver position in geodetic form (latitude, longitude, and height) and receiver velocity in n-frame at GNSS receiver antenna phase center; and \( \varvec{p}_{\text{INS}}^{n} \) and \( \varvec{v}_{\text{INS}}^{n} \) are the INS-predicted receiver position and velocity; \( \varvec{C}_{b}^{n} \) is the transition matrix from the body frame (b) to the n-frame; \( \varvec{\omega}_{in}^{n} \) is the rotation angular rate of n-frame with respect to inertial frame (i) projected in n-frame; \( \varvec{D}^{ - 1} = {\mathbf{diag}}\left[ {1/\left( {R_{M} + h} \right), 1/\left( {\left( {R_{N} + h} \right){ \cos }\left( B \right)} \right), - 1} \right] \) is the diagonal matrix to transform the lever-arm values (\( \varvec{\iota}^{b} \)) to geodetic form. Here, diag refers to diagonal matrix; RM and RN are the meridian radius of curvature and the radius of curvature in the prime vertical; B and h denote geodetic latitude and height.

Ionospheric delay compensation

Due to frequency dependency, the ionospheric delays are frequency correlated; hence, the ionospheric delay at f2 frequency can be expressed by that at f1 frequency as

$$ I_{{{\text{r}},2}}^{\text{s}} = I_{{{\text{r}},1}}^{\text{s}} \cdot f_{1}^{2} /f_{2}^{2} $$
(7)

with a random walk process

$$ I_{{{\text{r}},1,k}}^{\text{s}} = I_{{{\text{r}},1,k - 1}}^{\text{s}} + \omega_{{I_{{{\text{r}},1,k}}^{\text{s}} }} ,\omega_{{I_{{{\text{r}},1,k}}^{\text{s}} }} \sim\,N(0,\sigma_{I,k}^{2} ) $$
(8)

where σ 2 I, k is the priori variance of ionospheric variation noise, and the satellite elevation angle-dependent model (Gendt et al. 2003) is utilized to calculate the corresponding values. Also, in order to strengthen the estimability of ionospheric parameters, the ionospheric information from an existing ionospheric model can be introduced as a pseudo-observation as:

$$ \begin{aligned} I_{{{\text{r}},1}}^{\text{s}} & = 40.28 \cdot {\text{VTEC}}_{m} /\left( {f_{1}^{2} \cos \left( {Z_{\theta } } \right)} \right) \\ & \quad + \,\mu_{{{\text{r}},1,m}}^{\text{s}} ,\mu_{{{\text{r}},1,m}}^{\text{s}} \sim\,N(0,\sigma_{m}^{2} ) \\ \end{aligned} $$
(9)

where VTECm is vertical total electronic content that can be computed from an priori ionospheric models (Schaer et al. 1998; Chen and Gao 2005); Zθ denotes zenith angle at ionospheric pierce point; σ 2 m represents the priori variance which can be described by Tu et al. (2013)

$$ \sigma_{m}^{2} = \left\{ {\begin{array}{*{20}l} {\sigma_{{{\text{I}},0}}^{2} /{ \sin }^{2} \left( E \right),} \hfill & {\quad t < 8||20 < t||B > \pi /3} \hfill \\ {\left( {\sigma_{{{\text{I}},0}}^{2} + \sigma_{{{\text{I}},1}}^{2} \cos \left( B \right)\cos \left( {\frac{t - 14}{12}\pi } \right)} \right)/{ \sin }^{2} \left( E \right),} \hfill & {\quad {\text{other}}} \hfill \\ \end{array} } \right. $$
(10)

where σI,0 and σI,1 represent the ionospheric model accuracy under stationary state and the ionospheric changes error under non-stationary state.

Hardware time delays of four-GNSS systems

For the GPS + BDS + Galileo + GLONASS case, the pseudorange and carrier phase prediction functions are expressed as

$$ \begin{aligned} \varvec{P}_{{{\text{INS}},j}} & = \left[ {\begin{array}{*{20}c} {P_{{{\text{INS}},j}}^{G} } \\ {P_{{{\text{INS}},j}}^{B} } \\ {P_{{{\text{INS}},j}}^{E} } \\ {P_{{{\text{INS}},j}}^{R} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} { |\varvec{p}_{{{\text{INS}},{\text{r}}}} - \varvec{p}^{G} |+ T_{\text{r}} + I_{{j,{\text{r}}}}^{G} + c(t_{\text{r}}^{G} - t^{G} ) + d_{{{\text{r}},j}}^{G} - d_{j}^{G} + \Delta P_{{{\text{r}},j}}^{G} } \\ { |\varvec{p}_{\text{INS,r}} - \varvec{p}^{B} |+ T_{\text{r}} + I_{{j,{\text{r}}}}^{B} + c(t_{\text{r}}^{B} - t^{B} ) + d_{{{\text{r}},j}}^{B} - d_{j}^{B} + \Delta P_{{{\text{r}},j}}^{B} } \\ { |\varvec{p}_{\text{INS,r}} - \varvec{p}^{E} |+ T_{\text{r}} + I_{{j,{\text{r}}}}^{E} + c(t_{\text{r}}^{E} - t^{E} ) + d_{{{\text{r}},j}}^{E} - d_{j}^{E} + \Delta P_{{{\text{r}},j}}^{E} } \\ { |\varvec{p}_{\text{INS,r}} - \varvec{p}^{R} |+ T_{\text{r}} + I_{{j,{\text{r}}}}^{R} + c(t_{\text{r}}^{R} - t^{R} ) + d_{{{\text{r}},j}}^{R} - d_{j}^{R} + \Delta P_{{{\text{r}},j}}^{R} } \\ \end{array} } \right] \\ \end{aligned} $$
(11)
$$ \begin{aligned} \varvec{L}_{{{\text{INS}},j}} & = \left[ {\begin{array}{*{20}c} {L_{{{\text{INS}},j}}^{G} } \\ {L_{{{\text{INS}},j}}^{B} } \\ {L_{{{\text{INS}},j}}^{E} } \\ {L_{{{\text{INS}},j}}^{R} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} { |\varvec{p}_{{{\text{INS}},{\text{r}}}} - \varvec{p}^{G} |+ T_{\text{r}} - I_{{j,{\text{r}}}}^{G} + c(t_{\text{r}}^{G} - t^{G} ) + \lambda_{j}^{G} \tilde{N}_{j}^{G} + \Delta L_{r,j}^{G} } \\ { |\varvec{p}_{{{\text{INS}},{\text{r}}}} - \varvec{p}^{B} |+ T_{\text{r}} - I_{{j,{\text{r}}}}^{B} + c(t_{\text{r}}^{B} - t^{B} ) + \lambda_{j}^{B} \tilde{N}_{j}^{B} + \Delta L_{r,j}^{B} } \\ { |\varvec{p}_{\text{INS,r}} - \varvec{p}^{E} |+ T_{\text{r}} - I_{{j,{\text{r}}}}^{E} + c(t_{\text{r}}^{E} - t^{E} ) + \lambda_{j}^{E} \tilde{N}_{j}^{E} + \Delta L_{r,j}^{E} } \\ { |\varvec{p}_{\text{INS,r}} - \varvec{p}^{R} |+ T_{\text{r}} - I_{{j,{\text{r}}}}^{R} + c(t_{\text{r}}^{R} - t^{R} ) + \lambda_{j}^{R} \tilde{N}_{j}^{R} + \Delta L_{r,j}^{R} } \\ \end{array} } \right] \\ \end{aligned} $$
(12)

where d G j ,d B j ,d E j , and d R j are satellite hardware time delays of GPS, BDS, Galileo, and GLONASS, d Gr, j , d Br, j , \( d_{{{\text{r}},j}}^{E} \), and d Rr, j denote the corresponding receiver hardware time delays, and t Gr , d Br , d Er , and d Rr represent receiver clock offsets. Usually, the hardware time delays on carrier phase are un-calibrated phase delays (UPDs) (Ge et al. 2008) and those on pseudorange are un-calibrated code delays (UCDs) (Schönemann et al. 2011). It should be pointed out that UPDs, UCDs, and receiver clocks of different GNSS systems are not the same because of the specific signal structures and frequencies, time and coordinate frame characteristics of the particular GNSS system. In the uncombined and undifferenced float PPP model, UPDs can be absorbed by the associated ambiguity, whereas UCDs could be compensated by differential code bias (DCB) (Tu et al. 2013). According to Li et al. (2015), the differences between each the UCDs of two satellite systems can be expressed as

$$ \varvec{d}_{\text{DUCD}} = \left[ {\begin{array}{*{20}c} {d_{\text{DUCD}}^{G,B} } \\ {d_{\text{DUCD}}^{G,E} } \\ {d_{\text{DUCD}}^{G,R} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \,1} & 1 & 0 & 0 \\ { - \,1} & 0 & 1 & 0 \\ { - \,1} & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {d_{r,j}^{G} } \\ {d_{r,j}^{B} } \\ {d_{r,j}^{E} } \\ {d_{r,j}^{R} } \\ \end{array} } \right] $$
(13)

For GLONASS, the UCDs of each satellite are different due to the frequency division multiple access (FDMA) technique being applied. Hence, \( d_{\text{DUCD}}^{G,R} \, = \,[d_{{{\text{DUCD}},0}}^{G,R} ,d_{{{\text{DUCD}},1}}^{G,R} \cdots d_{{{\text{DUCD}},m}}^{G,R} ] \), where \( d_{{{\text{DUCD}},0}}^{G,R} \) and \( d_{{{\text{DUCD}},m}}^{G,R} \) are the basic UCD at reference frequency with respect to GPS and the mth UCD with respect to reference frequency. The differences between each two receiver clock offsets

$$ \varvec{d}_{\text{ISB}} = \left[ {\begin{array}{*{20}c} {d_{\text{ISB}}^{G,B} } \\ {d_{\text{ISB}}^{G,E} } \\ {d_{\text{ISB}}^{G,R} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \,1} & 1 & 0 & 0 \\ { - \,1} & 0 & 1 & 0 \\ { - \,1} & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {t_{r}^{G} } \\ {t_{r}^{B} } \\ {t_{r}^{E} } \\ {t_{r}^{R} } \\ \end{array} } \right] $$
(14)

are called the inter-system biases (ISB).

Currently, the UCDs on ionospheric-free combination pseudorange of each individual GNSS system will be absorbed by clock parameters and be defined as zero because of the current clock determination method. Hence, the UCDs at different frequency in (13) can be achieved from

$$ \left\{ {\begin{array}{*{20}c} {d_{{{\text{r}},1}}^{\text{s}} = - {\text{DCB}}_{{{\text{r}},1{ - }2}}^{\text{s}} f_{2}^{2} /(f_{1}^{2} - f_{2}^{2} )} \\ {d_{{{\text{r}},2}}^{\text{s}} = - {\text{DCB}}_{{{\text{r}},1{ - }2}}^{\text{s}} f_{1}^{2} /(f_{1}^{2} - f_{2}^{2} )} \\ \end{array} } \right. $$
(15)

with

$$ {\text{DCB}}_{{{\text{r}},1 - 2,k}} = {\text{DCB}}_{{{\text{r}},1 - 2,k - 1}} + \omega_{{{\text{DCB}}_{k} }} ,\omega_{{{\text{DCB}}_{k} }} \sim\,N\left( {0,\sigma_{\text{DCB}}^{2} } \right) $$
(16)

where \( {\text{DCB}}_{{{\text{r}},1 - 2}}^{\text{s}} \) is the receiver DCB between pseudoranges P1 and P2, and σ 2DCB is the priori variance of receiver DCB.

Odometer-aided PPP/INS integration system

When the vehicle moves on the ground, the velocities in lateral and vertical components would be close to zero if no side slipping or jump happens (Sukkarieh 2000). The forward velocity can be measured by the odometer. Accordingly, the observational vector of odometer can be written as

$$ \varvec{v}_{\text{od}} \approx \left[ {\begin{array}{*{20}c} {v_{\text{od}}^{\text{v}} /\left( {1 + S_{\text{od}} } \right)} & 0 & 0 \\ \end{array} } \right]^{\text{T}} $$
(17)

where v vod is odometer-measured velocity in forward direction in the vehicle frame (v), which is influenced also by the scale factor (Sod), and can be modeled as a random walk process. By applying (17), the observability of velocity is increased, which can enhance the estimation of velocity and IMU sensor errors according to Shin (2005, pp. 74–75).

However, the v-frame cannot be completely aligned with the b-frame. Thus, a rotation matrix based on misalignment angles between b-frame and v-frame should be calculated before applying (17). Then, the innovation equation (\( \varvec{Z}_{\text{od}} \)) for the odometer-aided PPP/INS integration model can be obtained as

$$ \begin{aligned} \varvec{Z}_{\text{od}} & = \varvec{v}_{\text{od}}^{v} - \varvec{C}_{b}^{v} \varvec{v}_{\text{INS}}^{b} \approx \left[ {\begin{array}{*{20}c} {v_{\text{od}}^{v} /\left( {1 + S_{\text{od}} } \right)} \\ 0 \\ 0 \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {v_{\text{INS}}^{F} } \\ {v_{\text{INS}}^{R} } \\ {v_{\text{INS}}^{D} } \\ \end{array} } \right] \\ & \quad + \,\eta ,\eta \sim\,N(0,\sigma_{\text{od}}^{2} ) \\ \end{aligned} $$
(18)

where \( \varvec{C}_{b}^{v} \) denotes the rotation matrix from b-frame to v-frame; F, R, and D indicate forward–right–down direction; \( \varvec{\eta} \) is the noise of odometer innovation function with the priori variance of \( \varvec{\sigma}_{\text{od}}^{2} \). In addition, there are also system offsets between odometer and IMU center. Therefore, we measured such offsets in the b-frame before the test and the corresponding correction method described in Shin (2005, pp. 74–75) was applied. As mentioned above, the INS solutions are in the n-frame and GNSS observations and products are in the e-frame. To make sure all of this information from different frames can be used in the same frame, the information must be transformed to n-frame, which will be introduced in the following section.

Linearization and parameter adjustment

According to the models above, the innovation vector for tightly coupled integration of odometer, INS, and GNSS PPP can be described as

$$ \varvec{Z}_{k} = \left[ {\begin{array}{*{20}c} {\varvec{P}_{{{\text{INS}},j}} - \varvec{P}_{{{\text{GNSS}},j}} } \\ {\varvec{L}_{{{\text{INS}},j}} - \varvec{L}_{{{\text{GNSS}},j}} } \\ {\varvec{D}_{{{\text{INS}},j}} - \varvec{D}_{{{\text{GNSS}},j}} } \\ {\varvec{I}_{{{\text{r}},1}}^{\text{s}} - \varvec{I}_{{{\text{r}},m}}^{\text{s}} } \\ {\varvec{v}_{\text{od}}^{\text{v}} - \varvec{C}_{b}^{\text{v}} \varvec{v}_{\text{INS}}^{b} } \\ \end{array} } \right] $$
(19)

with the corresponding linearization functions of

$$ \left[ {\begin{array}{*{20}c} {\partial \varvec{Z}_{P}^{\text{s}} } \\ {\partial \varvec{Z}_{L}^{\text{s}} } \\ {\partial \varvec{Z}_{D}^{\text{s}} } \\ {\partial \varvec{Z}_{I}^{\text{s}} } \\ {\partial \varvec{Z}_{{v_{\text{od}} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\varvec{u}^{\text{s}} \varvec{C}_{1} (\delta \varvec{p}_{\text{INS}}^{n} + (\varvec{C}_{b}^{n}\varvec{\iota}^{b} \times )\delta \theta ) + c\delta t_{\text{r}}^{\text{s}} - m_{w} \delta T_{{{\text{r}},w}} + \kappa_{j}^{\text{s}} \delta {\text{DCB}}_{\text{r}}^{\text{s}} - \gamma_{j}^{\text{s}} \delta I_{{{\text{r}},1}}^{\text{s}} } \hfill \\ {\varvec{u}^{s} \varvec{C}_{1} (\delta \varvec{p}_{\text{INS}}^{n} + (\varvec{C}_{b}^{n}\varvec{\iota}^{b} \times )\delta \theta ) + c\delta t_{\text{r}}^{\text{s}} - m_{w} \delta T_{{{\text{r}},w}} + \lambda_{j} \delta \tilde{N}_{j}^{\text{s}} + \gamma_{j}^{\text{s}} \delta I_{{{\text{r}},1}}^{\text{s}} } \hfill \\ {\varvec{u}^{s} \left[ {\varvec{C}_{2} \varvec{D}^{ - 1} \delta \varvec{p}_{\text{INS}}^{n} { + }\varvec{H}_{\theta } \delta \theta + \varvec{C}_{n}^{e} \left( {\delta \varvec{v}_{\text{INS}}^{n} + \varvec{C}_{b}^{n} \left( {\varvec{\iota}^{b} \times } \right)\delta\varvec{\omega}_{ib}^{b} } \right)} \right] + c\delta \dot{t}_{\text{r}}^{\text{s}} \delta I_{{{\text{r}},1}}^{\text{s}} } \hfill \\ {\varvec{v}_{\text{od}} \delta S_{\text{od}} - \varvec{C}_{b}^{\text{v}} \left( {\varvec{C}_{n}^{b} \delta \varvec{v}_{\text{INS}}^{n} - \varvec{C}_{n}^{b} (\varvec{v}_{\text{INS}}^{n} \times )\delta \theta - (\varvec{\iota}_{\text{od}}^{b} \times )\delta \varvec{B}_{g} - (\varvec{\iota}_{\text{od}}^{b} \times )\varvec{\omega}_{ib}^{b} \delta \varvec{S}_{g} } \right)} \hfill \\ \end{array} } \right] $$
(20)

after considering

$$ \left\{ {\begin{array}{*{20}l} {\delta \varvec{p}_{\text{r}}^{e} = \varvec{C}_{1} (\delta \varvec{p}_{\text{INS}}^{n} + (\varvec{C}_{b}^{n}\varvec{\iota}^{b} \times )\delta \theta )} \hfill \\ {\delta \varvec{v}_{\text{r}}^{e} = \varvec{C}_{2} \varvec{D}^{ - 1} \delta \varvec{p}_{\text{INS}}^{n} + \varvec{C}_{n}^{e} \left( {\delta \varvec{v}_{INS}^{n} - \varvec{H}_{\theta } \delta \theta + \varvec{C}_{b}^{n} \left( {\varvec{\iota}^{b} \times } \right)\delta\varvec{\omega}_{ib}^{b} } \right)} \hfill \\ \end{array} } \right. $$
(21)

where s refers to GNSS system and δ means the correction of the parameters following closely; \( \varvec{p}_{\text{r}}^{e} \) and \( \varvec{v}_{\text{r}}^{e} \) are position and velocity at receiver antenna phase center in the e-frame; \( \varvec{u} \) is the direction cosine matrix; \( \varvec{p}_{\text{INS}}^{n} \), \( \varvec{v}_{\text{INS}}^{n} \), and \( \varvec{\theta} \) denote position, velocity, and attitude at IMU center, respectively; \( \varvec{H}_{\theta } \) is the attitude coefficient that can be found in Gao et al. (2017); \( \varvec{C}_{1} \) is the matrix to transform position corrections in geodetic form to e-frame and projected in n-frame, and \( \varvec{C}_{2} \) is derived from \( \delta (\varvec{C}_{n}^{e} \varvec{v}_{\text{INS}}^{n} ) \) (Gao et al. 2017); \( \varvec{\iota}_{\text{od}}^{b} \) is the lever-arm between IMU center and odometer center measured in the b-frame; \( \delta\varvec{\omega}_{ib}^{b} \) denotes gyroscope errors including biases \( \delta \varvec{B}_{g} \) and scale factors \( \delta \varvec{S}_{g} \) (Niu et al. 2006, pp. 766–771). Also, biases and scale factor of accelerometers \( \delta \varvec{B}_{a} \) and \( \delta \varvec{S}_{a} \) should also be parameterized here.

Theoretically, the position prediction errors would also affect the accuracy of velocity estimation by forming the satellite-user unit vector in Doppler function. Hence, we added

$$ \partial \varvec{Z}_{D}^{\text{s}} { + } = \left( {\varvec{v}_{\text{r}}^{e} - \varvec{v}^{\text{s}} - \varvec{u}^{\text{s}} \varvec{D}_{{{\text{INS}},j}} \lambda_{j} } \right)\varvec{C}_{1} \left( {\delta \varvec{p}_{\text{INS}}^{n} { + }\delta \theta } \right)/\left( {\varvec{p}^{\text{s}} - \varvec{p}_{\text{r}}^{e} } \right) $$
(22)

to the Doppler functions in (20).

From (20) and (21), the parameter vector of odometer- and INS-aided four-GNSS uncombined and undifferenced PPP can be obtained as

$$ \varvec{X}_{k} = \left[ {\delta \varvec{p}_{\text{INS}}^{n} ,\delta \varvec{v}_{\text{INS}}^{n} ,\delta \theta ,\delta \varvec{B}_{g} ,\delta \varvec{B}_{a} ,\delta \varvec{S}_{g} ,\delta \varvec{S}_{a} ,\delta S_{\text{od}} ,\delta \varvec{t}_{\text{r}} ,\delta \varvec{DCB}_{\text{r}} ,\delta \dot{\varvec{t}}_{\text{r}} ,\delta T_{{{\text{r}},w}} ,\delta \tilde{\varvec{N}}_{1} ,\delta \tilde{\varvec{N}}_{2} ,\delta \varvec{I}_{{{\text{r}},1}} } \right]^{\text{T}} $$
(23)

Then, the designed matrix H can be obtained from (20) to (22), and finally, the parameter can be estimated by the EKF (Brown and Hwang 1992) as

$$ \left\{ {\begin{array}{*{20}l} {\varvec{X}_{k} =\varvec{\varPhi}_{k,k - 1} \varvec{X}_{k - 1} + \varvec{K}_{k} \left( {\varvec{Z}_{k} - \varvec{H}_{k}\varvec{\varPhi}_{k,k - 1} \varvec{X}_{k - 1} } \right)} \hfill \\ {\varvec{P}_{k} = ({\mathbf{I}} - \varvec{K}_{k} )\left( {\varvec{\varPhi}_{k,k - 1} \varvec{P}_{k - 1}\varvec{\varPhi}_{k,k - 1}^{\text{T}} + \varvec{Q}_{k - 1} } \right)({\mathbf{I}} - \varvec{K}_{k} )^{\text{T}} + \varvec{K}_{k} \varvec{R}_{k} \varvec{K}_{k}^{\text{T}} } \hfill \\ \end{array} } \right. $$
(24)

where \( {\mathbf{I}} \) is unit matrix. The elements in \( \varvec{\varPhi}_{k,k - 1} \) are determined strictly by the models in Table 1.

Table 1 State models adopted to describe the dynamic behavior of parameters
Full size table

Algorithm implementation

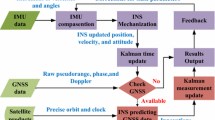
According to these mathematical models, the multi-sensor-augmented multi-GNSS PPP using uncombined and undifferenced observations can be implemented as depicted in Fig. 1. First, the INS mechanization is run based on the compensated velocity and angular increments from accelerometer and gyroscope after initialization. Then, the corresponding state parameter variance is calculated within the EKF time update. Afterward, time synchronization between INS and GNSS is started to match the high-rate IMU data with the low-rate GNSS observations. If no GNSS data are available at the current IMU epoch, the system checks whether there is odometer information. If there is, it runs the odometer-aided INS mode; otherwise, it goes to the next IMU epoch. When there are GNSS data, the INS tightly aided multi-GNSS PPP using uncombined and undifferenced observations will work. Similarly, odometer availability checking is also necessary before the close-loop feedback operation. Finally, the state parameters are fed to the IMU data in the next IMU epoch to restrain the divergence of the INS.

Fig. 1
figure 1

Implementation of odometer- and INS-augmented four-GNSS PPP using uncombined and undifferenced observations

Full size image

Evaluation and discussion

A test with a land-borne vehicle equipped with Trimble BD982, micro-electro-mechanical system (MEMS) IMU STIM300, and encoder/odometer SICK DFS60E, was arranged around Wuhan city, China, on October 19, 2016, as shown in Fig. 2, to evaluate the performance of multi-sensor-augmented four-GNSS PPP using uncombined and undifferenced observations. In this test, the sampling rates of the GNSS observations, INS measurements, and forward velocity of the platform were 1, 125, and 125 Hz, respectively. During the motion, the velocity in horizontal and vertical components was within ± 12 and ± 0.5 m/s. Because the vehicle moves almost along west–east and north–south directions on a flat road, the pitch and roll angles were within ± 2°, and heading angles were around 90°, 180°, 270°, 360° or 0°.

Fig. 2
figure 2

Trajectory of the land-borne vehicle experiment

Full size image

Data processing schemes

In the data processing phase, three schemes, namely (a) PPP, (b) INS tightly aided PPP (PPP/INS), and (c) odometer- and INS-aided PPP (PPP/INS/odometer), were employed whereby uncombined and undifferenced GNSS observations were used in all cases. In the analysis phase, the smoothed solutions from RTK/INS tight integration were employed as reference values for the positions and attitudes calculated by our methods (a, b, and c). To further evaluate the impacts of odometer and INS on the accuracy of positioning and attitude determination, ten partial and complete satellite signal outages were generated to simulate the frequent losses of GNSS signals in challenging dynamic environments.

GNSS availability

Satellite availability is one of the most important factors in GNSS precise positioning. Shown in Fig. 3 is the sky-plot distribution of the available GPS, BDS, Galileo, and GLONASS satellites. Significantly, unlike the almost uniform coverage of GPS and GLONASS, both BDS and Galileo suffer from irregularities due to the specific satellite constellation structure and the incomplete satellite constellation at present.

Fig. 3
figure 3

Sky plot of observed GPS, BDS, Galileo, and GLONASS satellites in the kinematic test performed around the pink pentagram

Full size image

Figure 4 shows the GNSS observabilities in terms of the number of available satellites and PDOP. Statistics show that the root-mean-square (RMS) of the number of available satellites of GPS, BDS, Galileo, and GLONASS is 7.4, 6.9, 3.3, and 5.1, respectively, and the PDOP of GPS, BDS, GLONASS is 2.7, 6.6, and 20.2, respectively. There is no PDOP for Galileo, because the number of tracked Galileo satellites was smaller than the minimal number for positioning during most of the experiment time. According to the works from Yang et al. (2011) and Quan et al. (2016), combinations of different GNSS systems can raise the number of available satellites and strengthen the user-satellite spatial geometry significantly. The availability and continuity of combined GNSS are presented in Fig. 4 (bottom) where G, R, B, and E stand for GPS, GLONASS, BDS, and Galileo, respectively. Compared to single-GNSS, the number of available satellites of G + R, G + B, G + E, G + B + R, G + E + R, and G + B + E + R is 12.4, 14.2, 10.7, 19.2, 15.8, and 22.5, respectively, and the corresponding PDOP is 1.9, 2.2, 2.4, 1.7, 1.8, and 1.6, respectively. Clearly, 1.5–3.0 times more available satellites can be observed while adopting the G + B + E + R combination compared to GPS-only.

Fig. 4
figure 4

Number of available satellites and the corresponding PDOP of single-GNSS (top) and multi-GNSS (bottom)

Full size image

INS-enhanced PPP positioning solutions

For comparison, the PPP solutions based on different GNSS data were also calculated as plotted in Fig. 5. The corresponding position RMSs are listed in Table 2, confirming visible enhancements from multi-GNSS as already shown in previous works (Li et al. 2015; Lou et al. 2016; Gao et al. 2017). GPS PPP solutions compared to those from combined GNSS PPP illustrate that the benefits from BDS and GLONASS manifest themselves mainly in the north and the vertical components, whereas all three components can be enhanced by Galileo. These differences are potentially caused by the specific spatial structure of each individual system.

Fig. 5
figure 5

Position offsets of uncombined and undifferenced PPP mode using single-GNSS data (top), two-GNSS data (middle), and three- and four-GNSS data (bottom)

Full size image
Table 2 RMSs of position errors of uncombined and undifferenced PPP (unit: m)
Full size table

The position differences of the low-cost INS tightly aided uncombined and undifferenced PPP are shown in Fig. 6. They are significantly improved in terms of stability, continuity, and accuracy compared to the PPP-only solutions in Fig. 5, especially for the solutions based on GLONASS and BDS. From the results in Table 3 and Fig. 7, the average position improvements obtained from low-cost INS are about 36.4, 38.7, and 31.3%, with maximum improvement of 65.9, 62.8, and 55.5%, respectively, in the north, east, and vertical components. The poorest GLONASS PPP solutions are improved from 1.4, 1.8, and 5.4 to 0.6, 0.8, and 3.9 m, and the best G + B + E + R PPP solutions are improved from 4.4, 25.8, and 19.8 to 2.8, 9.6, and 9.9. Such improvements are mainly due to the tight constraint of INS and the rigorous state dynamic function models (Table 1) adopted in the PPP/INS integration model (Gao et al. 2015, 2017). However, the influences of multi-GNSS on position accuracy of PPP/INS are similar to those on PPP.

Fig. 6
figure 6

Position differences of INS-aided PPP using different GNSS data

Full size image
Table 3 RMSs of position errors of INS-aided PPP (unit: m)
Full size table
Fig. 7
figure 7

PPP improvements from INS and odometer

Full size image

The differences between the solutions of PPP and those of INS-aided PPP are plotted in Fig. 8. Visibly, the results of the two modes are close to each other, while PPP can provide good solutions. Otherwise, there are large differences. These are due to (1) the absolute positioning accuracy of INS-aided PPP is mainly dependent on PPP; (2) INS can provide high-accuracy solutions during short-term GNSS signal losses; and (3) INS helps position-correlated parameters to be estimated more accurately, which can accelerate ambiguity re-convergence after signal losses.

Fig. 8
figure 8

Position differences between PPP and INS-aided PPP using single-GNSS data (top), two-GNSS data (middle), and three- and four-GNSS data (bottom)

Full size image

Odometer-upgraded PPP/INS positioning solutions

However, the performance of INS-aided PPP would be degraded with increasing GNSS outage time due to the time-increasing IMU drifts. Hence, the odometer is introduced into the INS-aided PPP to reduce such drifts. Figure 9 depicts the position differences of odometer-aided PPP/INS tight integration with respect to the reference solution. According to the position RMS in Table 4, the odometer can further improve the positioning accuracy of the PPP/INS tight integration. The enhancements from the odometer are shown in Fig. 10. Maximum improvements of about 25–50 cm in horizontal and 125 cm in vertical components occur in the solutions based on GLONASS and BDS, whereas very small position enhancements of about 0.5–1.0 cm in horizontal components and about 1.0–3.0 cm in altitude can be found when there are abundant GNSS observations. The latter is due to the fact that in such good GNSS conditions, the INS-updated velocity would be highly accurate leading \( \varvec{Z}_{\text{od}} \) in (18) to be close to zero; consequently, almost no position corrections can be obtained from the odometer. This matches the statistics results in Fig. 7 that the average position improvements from the odometer are only about 1.58, 0.35, and 4.32% in north, east, and vertical components. Somewhat surprisingly, the performance of land-borne PPP/INS tight integration can be further improved by using odometer in challenging environments.

Fig. 9
figure 9

Position differences of odometer-augmented PPP/INS tight integration using data of different GNSS combinations

Full size image
Table 4 RMSs of position differences of odometer-augmented PPP/INS tight integration with respect to the reference solutions (unit: m)
Full size table
Fig. 10
figure 10

Improvements in the positions of INS-aided PPP from the odometer

Full size image

PPP/INS attitude solutions enhanced by odometer

In Fig. 11, the attitude differences from INS-aided PPP and odometer-aided PPP/INS tight integration using data of different GNSSs are shown. According to Table 5, the average attitude RMSs of INS-aided PPP are 0.024°, 0.051°, and 0.191° in roll, pitch, and heading components. Compared to attitude solutions from the multi-antenna RTK attitude system with 3-m baselines (Vander Kuylen et al. 2006), INS-aided PPP can provide more precise roll and pitch angles, but is worse in heading components. Besides, due to the weak observability of gyroscope in the vertical direction, the attitude accuracy in the heading component is significantly worse than the other two directions. Meanwhile, the application of data using different GNSS combinations may also affect the attitude accuracy. In general, under open-sky conditions, RMS of attitude differences amounts to not more than 0.006°, 0.006°, and 0.023° in roll, pitch, and heading. In challenging environments (e.g., GLONASS-based solutions) in contrast, such differences amount to up to 27, 31, and 23% (0.008°, 0.021°, and 0.052°). These results illustrate that the low-cost INS-aided uncombined and undifferenced PPP can provide users attitudes with high accuracy.

Fig. 11
figure 11

Attitude differences of INS-aided PPP mode (top) and odometer-aided PPP/INS mode (bottom) using uncombined and undifferenced observations from different GNSS system combinations. Shifts of − 0.08°, − 0.06°, − 0.04°, − 0.02°, 0.02°, 0.04°, 0.06°, and 0.08° for roll/pitch, and shifts of − 0.20°, − 0.15°, − 0.10°, − 0.05°, 0.05°, 0.10°, 0.15°, and 0.20° for heading are added to the solutions using R, B, G, G + E, G + R, G + B, G + B + R, and G + E + R

Full size image
Table 5 RMS (°) of attitude differences of the INS-aided PPP using uncombined and undifferenced observations
Full size table

Attitude solutions from the odometer-enhanced uncombined and undifferenced PPP/INS mode are shown in Fig. 11 (bottom). The average attitude RMS values in Table 6 are 0.024°, 0.050°, and 0.094° for the three components. While the accuracies of roll and pitch angle are close to those from the multi-antenna RTK attitude system with 10-m baselines in Vander Kuylen et al. (2006), the heading solutions are close to those from the multi-antenna RTK attitude system with 3-m baselines, but of slightly poorer quality than those with 10-m baselines. Similarly, there are about 15, 12, and 9% differences in the RMS of roll, pitch, and heading, respectively, in the application of different GNSS combinations under open-sky conditions and about 17–29% differences in challenging environments. Besides, noticeable heading improvements appear after 21 and after 51 min, which is caused by abrupt changes of GNSS availability (as shown in Fig. 4).

Table 6 RMS (°) of the attitude differences of the odometer-aided PPP/INS tight integration
Full size table

Figure 12 shows a further contribution of the odometer on improving attitude accuracy. According to the statistics in Fig. 12, about 2.1, 1.4, and 50.6% average improvements in roll, pitch, and heading are obtained by using an odometer. In the meantime, the attitude enhancements of using GLONASS data have become slightly larger (3.1%) than those of other GNSS systems in pitch and heading angles. This means that an odometer would perform even more effective in weak GNSS availability environments. The absolute attitude differences of INS-aided uncombined and undifferenced PPP with and without odometer support are calculated and plotted in Fig. 13. Clearly, noticeable humps emerge, which are mainly due to the use of the odometer and can improve the observability of the vertical gyroscope. Statistically, maximum attitude improvements of 0.01–0.06° in roll/pitch and 0.1–0.6° in heading are observed by using the odometer. It is evidently possible to use odometer and INS to enhance multi-GNSS uncombined and undifferenced PPP to provide high-accuracy attitudes in land-borne applications.

Fig. 12
figure 12

Improvements in attitude of PPP/INS tight integration from the odometer

Full size image
Fig. 13
figure 13

Attitude differences between the solutions of INS-aided PPP and those of odometer-aided PPP/INS tight integration using different GNSS combinations

Full size image

INS solutions improved by odometer

To validate the capacity of odometer enhancements on PPP/INS tight integration during time periods of non-availability of GNSS satellites (only INS can be used), ten simulated complete GNSS outages, each lasting 30 s, were included with a 300-s step size in the calculations on original GNSS observations. The corresponding solutions of INS-only and odometer-aided INS mode are shown in Fig. 14. According to the statistics, the average RMSs are reduced from 2.24, 2.13, and 0.60 m for the position and 0.044°, 0.082°, and 0.038° for the attitude of INS mode to 0.57, 0.54, and 0.43 m and 0.028°, 0.056°, and 0.027° of the odometer-aided INS mode, respectively. This indicates that odometer-aided INS can discernibly enhance the performance of INS in cases of short-term GNSS outages because the major error in odometer measurements is due to the scale factor of the odometer sensor that varies slowly with time. This scale factor can be estimated accurately under open-sky GNSS conditions. When suffering from GNSS outages, the estimated scale factor would be highly precise for short-term periods, which would degrade the accuracy of the corrected odometer measurements insignificantly. Thus, by using such odometer information, the solutions from INS can be improved.

Fig. 14
figure 14

RMSs of the drifts of position (left) and attitude (right) from INS-only mode and odometer-augmented INS mode with GNSS outages on different scales

Full size image

Re-initialization of odometer-aided PPP/INS tight integration

Another important issue for dynamic PPP under GNSS outage conditions is the requirement of re-initialization after the recapture of satellite signals. To validate the impact of odometer on PPP/INS tight integration after a complete or partial GNSS outage (0–4 available satellites), the data with simulated GNSS outages are also processed in the three data processing schemes described above.

Figures 15, 16, and 17 show position solutions applying the three data processing schemes with simulated complete outages, while Figs. 18 and 19 illustrate those solutions with simulated partial outages. Significantly, both INS and odometer can shorten the re-initialization time and improve the positioning accuracy after a complete or partial GNSS outage. Actually, faster re-initialization of PPP leads to higher positioning accuracy, which means that the positioning accuracy can be indirectly indicative of the re-initialization performance. According to the statistics depicted in Fig. 20, the total position enhancements obtained from INS, odometer, and partially available GNSS satellites (as compared to uncombined and undifferenced PPP solutions) amount to 37.8, 31.6, and 46.9% in north, east, and down directions, respectively. At this, the impacts of INS account for 33.7, 26.9, and 41.6%, the effects of odometer for 2.3, 1.8, and 8.7%, and the influences of partially available GNSS for 6.4, 6.8, and 1.9%, respectively. The average position RMS of the three components is improved from 0.45, 0.32, and 1.32 m in the PPP mode to 0.28, 0.19, and 0.64 m in the odometer-augmented PPP/INS tight integration mode throughout the complete outage test. Further improvements, amounting to about 0.03, 0.02, and 0.02 m, can be obtained by using partially available satellites. Also, obvious rapid re-initialization procedures are being achieved when using odometer and INS in both complete and partial GNSS outage tests. These solutions indicate that the proposed fusion system has the potential for much stronger performance than current multi-GNSS PPP and PPP/INS tight integration approaches in land-borne dynamic applications.

Fig. 15
figure 15

Position differences of the uncombined and undifferenced PPP for data with 30-s complete GNSS outages at a step size of 300 s

Full size image
Fig. 16
figure 16

Position differences of the INS-aided uncombined and undifferenced PPP for data with 30-s complete GNSS outages at a step size of 300 s

Full size image
Fig. 17
figure 17

Position differences of the odometer-aided PPP/INS tight integration for data with 30-s complete GNSS outages at a step size of 300 s

Full size image
Fig. 18
figure 18

Position differences of the INS-aided uncombined and undifferenced PPP for data with 30-s partial outages at a step size of 300 s

Full size image
Fig. 19
figure 19

Position differences of the odometer-aided PPP/INS tight integration for data with 30-s partial outages at a step size of 300 s

Full size image
Fig. 20
figure 20

Improvements in the PPP position with the aid of various combinations of INS, odometer, and partially available GNSS satellites during the outages, which are marked as “INS,” “O” and “SN,” respectively

Full size image

Odometer-aided attitude determination under frequent GNSS outages

In order to analyze the impact of the odometer on attitude accuracy during GNSS outages, comparisons between attitude solutions containing no, partial, or complete outages were made. In Fig. 21, it can be summarized that (1) less attitude accuracy is lost when an odometer is used to aid the PPP/INS tight integration under both complete and partial outage situations (top-subfigure); (2) attitude accuracy losses can be further decreased when a small number of satellites are available, even if these satellites cannot be used for GNSS PPP calculation (bottom-subfigure). In general, the attitude accuracy losses due to complete GNSS outages amount on average for 14.4, 13.5, and 3.5% in INS-aided PPP mode and for about 5.8, 4.8, and 5.1% in odometer-aided PPP/INS tight integration mode. Using partially available GNSS data, accuracy losses further drop to 5.3, 6.2, and 3.3% in INS-aided PPP mode and to 4.1, 4.5, and 3.2% in odometer-aided PPP/INS tight integration mode. This means that the attitude accuracy can be significantly improved under challenging environments by applying odometer and partially available satellites.

Fig. 21
figure 21

Attitude accuracy losses in INS-aided PPP mode and odometer-aided PPP/INS tight integration mode in complete (top) and partial (bottom) GNSS outage tests

Full size image

Conclusions

A fusion system integrating multi-GNSS PPP using uncombined and undifferenced observations, low-cost IMU, and odometer is introduced in order to achieve positions and attitudes of better accuracy in dynamic land-borne applications. Our study yields the following conclusions.

  1. 1.

    With the aid of INS, i.e., PPP/INS tight integration, the position accuracy can be upgraded on average by more than 36.4, 38.7, and 31.3% in the north, east, and down components, respectively. Further position improvements can be obtained by introducing an odometer into the PPP/INS tight integration system, especially under conditions of poor satellite availability.

  2. 2.

    Attitude improvements of about 2.1, 1.4, and 50.6% can be obtained in roll, pitch, and heading directions, respectively, by using an odometer in the PPP/INS tight integration system.

  3. 3.

    During short-term GNSS outages, low-cost INS can retain accurate positions and attitudes, and the accuracy can be further improved by adding an odometer. Also, a limited number of available satellites in environments of frequent GNSS outages can be utilized to improve the accuracy of position and attitude.

  4. 4.

    By introducing odometer into the PPP/INS tight integration mode, the re-initialization time of PPP can be significantly shortened, especially under challenging GNSS conditions.

In conclusion, according to our research, the performance of multi-GNSS PPP using uncombined and undifferenced observations can be considerably improved by introducing an odometer and low-cost inertial sensors. The multi-sensor fusion system shows a great potential for precise positioning and attitude determination. Our future work will, therefore, focus on developing the fusion system into a real-time system with still more cost-effective inertial sensors.