Introduction

Precise point positioning (PPP) (Zumberge et al. 1997) can provide static and dynamic position estimates at millimeter- to centimeter-level accuracy, as verified by Wang (2013), with a single dual-frequency receiver. Hence, PPP is widely used in post-processing applications such as crustal deformation monitoring (Calais et al. 2006), ocean-tide measuring (King and Aoki 2003), and orbit determination of low earth orbiting satellites (Bock et al. 2003). It is also applied in near real-time areas, such as geohazard monitoring, early warning of earthquakes and tsunami, and GPS meteorology (Blewitt et al. 2006; Dousa and Vaclavovic 2014; Gendt et al. 2004). Precise satellite orbit and clock products are essential for obtaining high-precision results in PPP. The final orbit and clock products of the International Global Navigation Satellite System (GNSS) Service (IGS) offer the best performance regarding stability, reliability, completeness, and robustness in comparison with the products of any single analysis center. However, they are usually available only with a delay of at least 17 h (Kouba 2003). Since December 2012, the real-time service of the IGS and its associated analysis centers has been providing real-time (RT) orbit and clock products to the GNSS community, which has enabled PPP for RT applications.

Because the satellite motions are dynamically stable, the RT orbits are usually predicted based on products from batch analysis using the latest available observations. During eclipsing periods, the predicted IGS ultra-rapid orbits (IGU) for satellites of the Global Positioning System (GPS) reach an accuracy of 4–5 and 8–12 cm over the 9-h prediction period for the nominal situation and for old-type Block IIA GPS satellites, respectively (Douša 2010). Fortunately, the Block IIA GPS satellites have been replaced by newer satellite types; currently, there are no Block IIA satellites in operation according to the GPS constellation status (https://glonass-iac.ru/en/GPS/). Considering the relatively smaller magnitude of the orbit error, RT users can use the predicted orbits between the prediction period from 3 to 9 h (Springer and Hugentobler 2001). The impact of the IGU orbit errors on satellite clock estimation and PPP-based estimation has been analyzed in several previous studies. The radial component of predicted orbit errors can be absorbed by satellite clock corrections. This assimilation increases as the size of the network used for clock estimation decreases (Lou et al. 2014). The impact of orbit errors on PPP-based zenith total delay (ZTD) estimation causes errors in ZTDs estimates of < 1 cm, provided care is taken to remove occasional outlier orbits based on post-fit observation residuals (Douša 2010).

Compared with orbit products, satellite clock corrections are more critical in RT situations and must be updated more frequently because of their short-term fluctuations and relatively large magnitudes (Zhang et al. 2010). Techniques have been developed, such as undifferenced (UD), epoch-differenced (ED), and mixed-difference (MD) methods for precise satellite clock estimation (Ge et al. 2012; Hauschild and Montenbruck 2009; Laurichesse et al. 2009; Zhang et al. 2010). Experimental results based on simulated RT clocks, together with corresponding IGU orbit products, have shown that all RMS values of the Signal-in-Space Range Error are at the centimeter level (Zhang et al. 2010). The estimated clock corrections contain biases caused by hardware delays. In the dual-frequency case, hardware-specific biases cancel straightforwardly when the users employ the same observables as the clock providers. With the available of triple-frequency observable, a new time-variant phase hardware delay, i.e., temperature-dependent phase bias in triple-frequency observable, has been observed by Montenbruck et al. (2012). Pan et al. (2017) illustrated that the time-variant bias may originate from phase hardware delay of the satellite. But it is known that only constant code hardware delays are absorbed by dual-frequency clocks. Therefore, it is necessary to clarify the relation between the time-variant satellite phase delay and standard dual-frequency clocks. This is especially important for the development of multi-frequency PPP ambiguity resolution with original undifferenced observation (Gu et al. 2015). In this data processing model, the dual-frequency clocks are used for triple-frequency fractional cycle biases estimation, hence overlooking the time-variant phase bias in the clocks which might affect the characteristics of fractional cycle biases modeling.

Apart from the hardware delays, estimated clock corrections contain biases caused by inaccurate clock modeling. For example, the BeiDou pseudorange observable is affected by satellite code-carrier divergence (Wanninger and Beer 2015). The error cannot be precisely modeled for geostationary satellites, thus causing initial clock bias error. In real-time applications, the clock accuracy is affected by the quality and latency of real-time data streams in various operators. In addition, unavailable high-precision external troposphere corrections will also degrade the clock precision. Therefore, it is important to analyze the effects of the clock biases caused by the modeling factors and the aforementioned hardware-specific delays.

However, few reports have presented detailed analyses of impact of these biases on PPP-based estimations. Initial analysis related to the impacts of GPS time-variant phase hardware delays on kinematic positioning was conducted by Pan et al. (2017). Shi et al. (2015) also showed the impact of satellite clock modeling errors on GPS PPP-based ZTD estimations. The experimental results showed that the precision of the satellite clock products affects the PPP-based ZTD estimations more than does accuracy. However, their analyses concentrate on the impacts of a certain satellite bias on PPP. With the development of real-time multi-frequency PPP, the satellite-related errors, including clock errors, constant satellite code biases, and time-variant phase biases, can be corrected with products from different analysis centers. Hence, a comprehensive analysis is required to classify the biases and analyze their effects.

The objectives of this study are to illustrate the clock biases induced by different estimation models and to analyze the impacts of clock biases on PPP-based ZTD and coordinate estimations. We begin by presenting the mathematical derivations of clock estimation methods and analyze the clock biases induced by different models. The biases are classified, and their impacts are analyzed theoretically. We then present the validation strategies and data collection employed in the sample demonstration, and then the experimental analysis of the impact of the biases in satellite clocks. Finally, we summarize the main findings of this study.

Theoretical analysis

The generalized linearized ionospheric-free (IF) phase and range combinations for PPP between receiver \(r\) and satellite \(s\) at a particular epoch are:

$$\begin{aligned} v_{P,r}^{s} (i) &= u_{r}^{s} \delta x_{r} + \delta t_{r} (i) - \delta t^{s} (i) + b_{r}^{{}} (i) - b_{{}}^{s} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + l_{P,r}^{s} (i) \\ v_{L,r}^{s} (i) &= u_{r}^{s} \delta x_{r} + \delta t_{r} (i) - \delta t^{s} (i) + B_{r}^{{}} (i) - B_{{}}^{s} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + N_{r}^{s} + l_{L,r}^{s} (i) \\ \end{aligned}$$
(1)

where \(i\) is the epoch time, \(v_{P,r}^{s}\) and \(v_{L,r}^{s}\) are the residuals of the IF code and phase combinations, \(u_{r}^{s}\) is the unit vector from the satellite to the receiver, \(\delta x_{r}\) is the increment for the a priori receiver position vector, \(\delta t_{r}\) is the receiver clock offset, \(\delta t^{s}\) is the satellite clock offset, \(b_{r}^{{}}\), \(b_{{}}^{s}\), \(B_{r}^{{}}\), and \(B_{{}}^{s}\) are the IF combined pseudorange and carrier phase hardware delays (biases) for satellites and receivers, \(m_{r}^{s}\) and \(\delta T_{r}\) are the mapping function and ZTD parameter, \(N\) is the ionospheric-free ambiguity in meters, and \(l_{P,r}^{s}\) and \(l_{L,r}^{s}\) are the IF code and phase combination corrections. Only the fractional hardware delays are considered since their integer part is inseparable from ambiguities. Furthermore, hardware biases differ by measurement types and signal frequencies and vary slowly (Gabor 1999). Therefore, they are usually regarded as constants within time spans of 24 h. However, their temporal behavior can also be modeled by a random walk process (Wen et al. 2011). Because of the uncertainties of the temporal properties of hardware biases, they are divided into time-invariant and time-dependent parts when rigorously modeling their physical properties, i.e.,

$$\begin{aligned} & b_{r} (i) = \ell b_{r} + \delta b_{r} (i) \\ & b^{s} (i) = \ell b^{s} + \delta b^{s} (i) \\ & B_{r} (i) = \ell B_{r} + \delta B_{r} (i) \\ & B^{s} (i) = \ell B^{s} + \delta B^{s} (i) \\ \end{aligned}$$
(2)

where \(\ell b\) and \(\ell B\) denote the constant time-invariant offset, and \(\delta b\) and \(\delta B\) denote the time-dependent part. Considering that the satellite clocks are estimated on a daily basis, constant hardware delays are regarded stable enough over a period of 24 h.

Precise satellite clock estimation method considering the hardware delays

Assuming that station coordinates and satellite orbits are known and can be fixed in the clock estimation, the linearized observation Eq. (1) can be expressed as:

$$\begin{aligned} & v_{P,r}^{s} (i) = \delta t_{r} (i) - \delta t^{s} (i) + b_{r}^{{}} (i) - b_{{}}^{s} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + l_{P,r}^{s} (i) \\ & v_{L,r}^{s} (i) = \delta t_{r} (i) - \delta t^{s} (i) + B_{r}^{{}} (i) - B_{{}}^{s} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + N_{r}^{s} + l_{L,r}^{s} (i) \\ \end{aligned}$$
(3)

In (3), all unknown parameters except \(\delta T_{r}\) are linearly dependent, but only \(\delta t_{r}\), \(\delta t^{s}\), \(\delta T_{r}\), and \(N\) are taken as parameters requiring estimation in the precise satellite clock estimation procedure. Hence, the receiver and satellite hardware delays in the observation equations should be assimilated by the estimated parameters or otherwise remain as residuals (Geng et al. 2010). Such assimilation should satisfy the requirement of minimizing the weighted sum of the squares of residuals. Considering that different mathematical models can be used to estimate satellite clocks, the biases assimilated by the models are presented.

Undifferenced satellite clock estimation

In the undifferenced model, both pseudorange and carrier phase observations are used for the clock estimation. Because carrier phase measurements are ambiguous, the absolute clock biases are determined by pseudorange observations, while the epoch-wise clock variations are determined by carrier phase observations (Defraigne and Bruyninx 2007). Hence, the hardware delays \(\ell b^{s} { + }\delta B^{s} (i)\) and \(\ell b_{r}^{{}} + \delta B_{r} (i)\) will be absorbed by satellite and receiver clocks, respectively. However, the constant hardware delays \(\ell b_{r}^{{}}\) and \(\ell b^{s}\), contained in the clocks, and the phase constant hardware delays \(\ell B_{r}^{{}} - \ell B_{{}}^{s}\) will be assimilated into the ambiguities of the phase observations. For the pseudorange observations, the time-variant hardware delays induced by the clocks cannot be absorbed and thus remains in residuals. Following the described conventions, Eq. (3) can be rewritten as:

$$\begin{aligned} & \overline{v}_{P,r}^{s} (i) = \overline{{t_{r} }} (i) - \overline{{t_{{}}^{s} }} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i)\; + l_{P,r}^{s} \\ & v_{L,r}^{s} (i) = \overline{{t_{r} }} (i) - \overline{{t^{s} }} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + \overline{N}_{r}^{s} + l_{L,r}^{s} (i) \\ \end{aligned}$$
(4)

where

$$\begin{aligned} & \overline{{t_{r} }} (i) = \delta t_{r} (i) + \ell b_{r}^{{}} + \delta B_{r} (i) \\ & \overline{{t^{s} }} (i) = \delta t^{s} (i) + \ell b_{{}}^{s} + \delta B_{{}}^{s} (i) \\ & \overline{v}_{P,r}^{s} (i) = v_{P,r}^{s} (i) + \delta B_{r} (i) - \delta b_{r}^{{}} (i) + \delta b_{{}}^{s} (i) - \delta B_{{}}^{s} (i) \\ & \overline{N}_{r}^{s} = N_{r}^{s} - \ell b_{r}^{{}} + \ell B_{r}^{{}} + \ell b_{{}}^{s} - \ell B_{{}}^{s} \\ \end{aligned}$$
(5)

The reparameterized ambiguity parameter \(\overline{N}_{r}^{s}\) in (5) has lost the integer property due to absorbing the constant satellite and receiver dependent hardware delays. Moreover, the normal equation derived with (4) is singular. To obtain satellite clock corrections, a reference station should be selected to avoid rank deficiency. Then, the satellite clock biases, as well as ambiguities, can be estimated simultaneously using a least squares adjustment. The estimated satellite clock can be written as:

$$t_{\text{UD}}^{s} (i) = \delta t^{s} (i) + \ell b_{{}}^{s} + \delta B^{s} (i)$$
(6)

where subscript UD indicates the satellite clock estimated using the undifferenced method.

Mixed-differenced clock estimation

To improve the efficiency of the undifferenced satellite clock estimation method, Ge et al. (2012) proposed the mixed-differenced clock estimation method. It combines the epoch-differenced phase observations and the undifferenced range observations for clock estimation. They reported that absolute clock corrections at epoch \(i\) could be written as:

$$\delta t^{s} (i) = \delta t^{s} (i_{0} ) + \sum\limits_{{j = i_{0} + 1}}^{i} {\Delta \delta t^{s} (j)}$$
(7)

where \(\Delta\) is the difference operator between two adjacent epochs, \(\Delta \delta t^{s}\) is the epoch-differenced clock variation, and \(\delta t^{s} (i_{0} )\) is the initial clock at the starting epoch \(i_{0}\). However, the phase and pseudorange hardware delays are not shown in their derivation.

If we look at hardware delays, the epoch-differenced phase observations based on (3) can be written as:

$$v_{\Delta L,r}^{s} (i) = \Delta \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{t}_{r} (i) - \Delta \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{t}^{s} (i)\,+\,\Delta m_{r}^{s} (i) \cdot \delta T_{r} (i) + \Delta l_{L,r}^{s} (i)$$
(8)

where \(\Delta\) is the difference operator between two adjacent epochs if there is no cycle slip between epochs, and \(\Delta \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{t}_{r} = \Delta \delta t_{r} + \Delta \delta B_{r}^{{}}\), \(\Delta \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{t}^{s} = \Delta \delta t^{s} + \Delta \delta B_{{}}^{s}\). Because the receiver and satellite clocks are both part of (8), one singularity has to be dealt with. We introduce a zero-mean condition over all estimated satellite clocks, i.e., the sum the epoch-differenced clock estimates is set to zero. Alternatively, one station with hydrogen master clocks could be chosen as references to avoid the singularity. It should be noted that using a reference clock introduces bias to the satellite clock estimates; fortunately, this bias is identical for all satellites and is absorbed by the receiver clock.

Similarly, considering the hardware delays the undifferenced range observation in (3) can be written as:

$$v_{P,r}^{s} (i) = \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}_{r} (i) - \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}^{s} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + l_{P,r}^{s} (i)$$
(9)

where \(\delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}_{r} = \delta t_{r} + b_{r}^{{}}\) and \(\delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}^{s} = \delta t^{s} + b_{{}}^{s}\). The satellite clock corrections at epoch \(i\) in (9) can be decomposed into:

$$\begin{aligned} \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}^{s} (i) & = \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}^{s} (i_{0} ) + \sum\limits_{{j = i_{0} + 1}}^{i} {\Delta \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}^{s} (j)} \\ & = \delta t^{s} (i_{0} ) + b_{{}}^{s} (i_{0} ) + \sum\limits_{{j = i_{0} + 1}}^{i} {\Delta \delta t^{s} (j)} + \sum\limits_{{j = i_{0} + 1}}^{i} {\Delta b_{{}}^{s} (j)} \\ & = \delta t^{s} (i_{0} ) + b_{{}}^{s} (i) + \sum\limits_{{j = i_{0} + 1}}^{i} {\Delta \delta t^{s} (j)} \\ \end{aligned}$$
(10)

If substituting \(\delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}^{s} (i)\) into (9) using (10), and fixing the epoch-differenced satellite clock and ZTD to the epoch-differenced phase estimation, we obtain:

$$v_{P,r}^{s} (i) = \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}_{r} (i) - \left( {\delta t^{s} (i_{0} ){ + }b_{{}}^{s} (i) - \sum\limits_{{j = i_{0} + 1}}^{i} {\Delta \delta B^{s} (j)} } \right) + \overline{l}_{P,r}^{s} (i)\;\;\;$$
(11)

where \(\overline{l}_{P,r}^{s}\) is the reparameterized pseudorange correction:

$$\overline{l}_{P,r}^{s} (i)\; = l_{P,r}^{s} (i)\; + m_{r}^{s} (i) \cdot \delta T_{r} (i)\; - \sum\limits_{{j = i_{0} + 1}}^{i} {\Delta \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{t}^{s} (j)}$$
(12)

Since only one initial clock parameter is estimated for each satellite, the constant satellite clock biases should be accumulated to the initial clock parameter; whereas the time-variant biases are absorbed by the residuals. Then, Eq. (11) can be rewritten as:

$$\tilde{v}_{P,r}^{s} (i)\; = \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}_{r} (i) - \delta \tilde{t}^{s} (i_{0} ) + l_{P,r}^{s} (i)$$
(13)

where \(\delta \tilde{t}^{s} (i_{0} )\) is the actual estimated initial clock and \(\tilde{v}_{P,r}^{s} (i)\) is the corresponding residual with:

$$\begin{aligned} & \delta \tilde{t}^{s} (i_{0} ) = \delta t^{s} (i_{0} ) + \ell b_{{}}^{s} + \delta B^{s} (i_{0} ) \\ & \tilde{v}_{P,r}^{s} (i) = v_{P,r}^{s} (i) + \delta b_{{}}^{s} (i) - \delta B^{s} (i) \\ \end{aligned}$$
(14)

The receiver clock \(\delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t}_{r} (i)\) and initial satellite clock \(\delta \tilde{t}^{s} (i_{0} )\) are simultaneously estimated in (13), which will lead to a rank deficiency. The singularity can be eliminated by using the same method as (8). Alternatively, this study forms the difference between satellites to remove receiver clock parameters and selects a reference satellite as the clock datum. The datum is common for all estimated satellite clocks, thus being absorbed by receiver clocks without affecting the PPP results. The initial clock is then estimated if it has converged to an accuracy comparable to the range accuracy.

Combining the undifferenced initial clock estimated with (13) and the epoch-differenced clock estimated with (8), the satellite clock corrections obtained can be written as:

$$\begin{aligned} t_{\text{MD}}^{s} (i) & = \delta \tilde{t}^{s} (i_{0} ) + \sum\limits_{{j = i_{0} + 1}}^{i} {\Delta \delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{t}^{s} (j)} \\ & = \delta t^{s} (i_{0} ) + \ell b_{{}}^{s} + \delta B^{s} (i_{0} ) + \sum\limits_{{j = i_{0} + 1}}^{i} {(\Delta \delta t^{s} (j) + \Delta \delta B_{{}}^{s} (j))} \\ & = \delta t^{s} (i) + \ell b_{{}}^{s} + \delta B^{s} (i) \\ \end{aligned}$$
(15)

where the subscript \({\text{MD}}\) indicates the satellite clock estimated using the mixed-differenced method.

Compared with the clock corrections (7) developed by Ge et al. (2012), the time-dependent phase hardware bias \(\delta B^{s} (i)\) is introduced additionally. Furthermore, it can be observed from (6) and (15) that the satellite clock products retrieved from the undifferenced and mixed-differenced methods are identical. This proves the theoretical equivalence of the two clock estimation methods.

It should be noted that \(\ell b_{{}}^{s}\) and \(\delta B^{s} (i)\) are hardware-dependent biases, whereas \(\delta t^{s} (i_{0} )\) and \(\sum\nolimits_{{j = i_{0} + 1}}^{i} {\Delta \delta t^{s} (j)}\) are estimated clock variations which are affected by the clock modeling errors. To analyze the impact of satellite clock corrections on PPP positioning, the time-invariant biases \(\delta t^{s} (i_{0} )\) and \(\ell b_{{}}^{s}\) introduced by pseudorange observations are denoted as initial clock biases (ICBs), whereas the time-variant biases \(\delta B^{s} (i)\) and \(\sum\nolimits_{{j = i_{0} + 1}}^{i} {\Delta \delta t^{s} (j)}\) determined by carrier phase observations are denoted as time-dependent biases (TDBs). In addition, \(\ell b_{{}}^{s}\) and \(\delta B^{s} (i)\) are described as the hardware-dependent parts of the ICBs and TDBs. In the following, the mixed-differenced clock products are used to analyze the effects of the biases, but the derived conclusions are also relevant to the undifferenced clock products.

Impacts of biases in satellite clocks on PPP

For conventional PPP processing, the orbits and clocks are fixed to the precise products. The observation model for PPP can be expressed as:

$$\begin{aligned} v_{P,r}^{s} (i) &= u_{r}^{s} \delta x_{r} + \delta t_{r} (i) + b_{r}^{{}} (i) - b_{{}}^{s} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + l_{P,r}^{s} (i) + t_{\text{MD}}^{s} (i) \\ v_{L,r}^{s} (i) &= u_{r}^{s} \delta x_{r} + \delta t_{r} (i) + B_{r}^{{}} (i) - B_{{}}^{s} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + N_{r}^{s} + l_{L,r}^{s} (i) + t_{\text{MD}}^{s} (i) \\ \end{aligned}$$
(16)

Given that receiver hardware delays can be separated into parts that are temporally variable and parts that are stable, the observation equation can be rewritten as:

$$\begin{aligned} & v_{P,r}^{s} (i) = u_{r}^{s} \delta x_{r} + \delta \overline{t}_{r} (i) - b^{s} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + \left( {l_{P,r}^{s} (i) + t_{\text{MD}}^{s} (i)} \right) \\ & v_{L,r}^{s} (i) = u_{r}^{s} \delta x_{r} + \delta \overline{t}_{r} (i) - B^{s} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + \overline{N}_{r}^{s} + \left( {l_{L,r}^{s} (i) + t_{\text{MD}}^{s} (i)} \right) \\ \end{aligned}$$
(17)

where \(\delta \bar{t}_{r}\) and \(\overline{N}\) represent the reparameterized receiver clocks and float ambiguities, respectively, where

$$\begin{aligned} & \delta \bar{t}_{r} (i) = \delta t_{r} (i) + \ell b_{r}^{{}} + \delta B_{r} (i) \\ & \overline{N}_{r}^{s} = N_{r}^{s} - \ell b_{r}^{{}} + \ell B_{r}^{{}} \\ \end{aligned}$$
(18)

Considering the impact of ICBs and TDBs in satellite clock corrections, the pseudorange measurements in (17) can be rewritten as:

$$v_{P,r}^{s} (i) = u_{r}^{s} \delta x_{r} + \delta \bar{t}_{r} (i) + m_{r}^{s} (i) \cdot \delta T_{r} (i) + l_{P,r}^{s} (i) + \delta t^{s} (i_{0} ) + \sum\limits_{{j = i_{0} + 1}}^{i} {\Delta \delta t^{s} (j)}$$
(19)

Compared to the precision of pseudoranges, the magnitudes of the errors caused by time-variant biases are relatively small and can, therefore, be ignored for pseudorange observations. The constant code hardware delays cancel straightforwardly when the users employ the same observables as those used by clock providers. Otherwise, the constant hardware delays, along with the ICBs, introduce a constant offset to the pseudorange observations. Hence, they might degrade the accuracy of the pseudorange measurements if not accurately estimated.

Pseudorange measurements are used mainly to separate the clocks and the ambiguities; hence, a single difference between satellites can be applied to (17) to avoid considering the receiver clocks. The reparameterized phase observation in (17) can be written as:

$$v_{L,r}^{{s,s_{0} }} (i) =\,u_{r}^{{s,s_{0} }} \delta x_{r} - B_{{}}^{{s,s_{0} }} (i) + m_{r}^{{s,s_{0} }} (i) \cdot \delta T_{r} (i) + \overline{N}_{r}^{{s,s_{0} }} + l_{L,r}^{{s,s_{0} }} (i) + \sum\limits_{{j = i_{0} + 1}}^{i} {\Delta \delta t^{{s,s_{0} }} (j)}$$
(20)

where the superscript “\(s,s_{0}\)” denotes the difference between the satellite \(s\) and the reference satellite \(s_{0}\), and \(\bar{N}_{r}^{{s,s_{0} }}\) donates the new ambiguities, which can be expressed as:

$$\bar{N}_{r}^{{s,s_{0} }} = N_{r}^{{s,s_{0} }} + \ell b_{{}}^{{s,s_{0} }} - \ell B_{{}}^{{s,s_{0} }} { + }\delta t^{s} (i_{0} )$$
(21)

As can be seen from (20) and (21), the TDBs in the satellite clocks affect the precision of the phase observation equation, whereas the ICBs are absorbed by the ambiguities. It should be noted that the phase-specific hardware delays in TDBs cancel since the same phase combination is used in PPP and in the clock estimation. But for triple-frequency applications, the hardware-specific delays in TDBs cannot be canceled. Therefore, analyzing the effects of the biases is significant for multi-frequency applications.

Experimental strategy and data description

The precise clock product contains a single correction for a satellite, without distinguishing the TDBs and ICBs. Hence, the effects of ICBs and TDBs on PPP are usually not identified. To identify separately the impact of satellite bias on PPP solutions, the mixed-differenced method (Ge et al. 2012) is used for clock estimation. Three clock products retrieved using different processing strategies are detailed in Table 1. The ICBs in the ESTBRD strategy are fixed to the broadcast clock, whereas the ICBs are fixed to CODE final clock for strategy ESTCOD. Since only a constant offset is added to the phase clock estimates, a comparison of results of the two strategies can illustrate the impact of ICBs. Since the hardware-dependent parts of TDBs cannot be separated from real clock variation in dual-frequency case, the troposphere is usually fixed to improve the overall modeling precision of the TDB estimates. Therefore, to illustrate the impact of TDBs, the troposphere in strategy ESTTROP is fixed to the IGS troposphere products, whereas the ICBs remain the same as in strategy ESTCOD. To retain consistency between the orbit products in the different processing strategies, the CODE final satellite orbits and earth rotation parameters were used (Dach et al. 2009). We note that the use of CODE satellite products, rather than IGS products, is to avoid the incorporation of possible inhomogeneities in the IGS final products, which could degrade the PPP quality (Teferle et al. 2007).

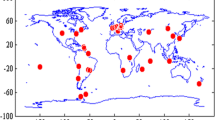
Table 1 Experimental processing strategies for different clock products
Full size table

Daily GPS data from DOY 158–164, 2015, from 107 globally distributed reference stations were used to study the effects of ICBs. The applied tracking network is shown in Fig. 1. General settings adopted for the PPP validation are provided in Table 2.

Fig. 1
figure 1

Tracking network for experimental validation

Full size image
Table 2 Data modeling strategies for satellite clock estimation and PPP
Full size table

Validation and analysis

An initial comparison of the estimated satellite clocks using the different strategies with the CODE final clocks is presented. Then, globally distributed stations are used for both static and simulated kinematic PPP tests to verify the effects of biases on PPP. Furthermore, the results of a vehicle-borne experiment to assess the impacts of biases in real dynamic situations are discussed.

Assessment of clock products employing different strategies

Recall that accuracy describes the deviation of estimated parameters from the true value, whereas the precision refers to the spread from the mean. The problem in determining the accuracy is that most of the time the true value is unknown. Therefore, one approach is to compare our results with those of other processing centers, assuming the results of the other labs are accurate. The CODE final clock products were selected as the reference to describe the quality of the estimated clock corrections. To eliminate the effects of the clock datum, an arbitrary satellite should be first selected as the reference satellite. Then, the difference between each of the satellite and reference satellite is calculated for the estimated and reference products, respectively. The accuracy and precision are calculated based on the differenced clocks. The accuracy can be measured by the root mean square (RMS):

$${\text{RMS}} = \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {({\Delta}_{i} \cdot {\Delta}_{i} )} } \right)^{{\frac{1}{2}}}$$
(22)

where \({\Delta}_{i}\) is the difference between the estimated clock and CODE final clock at epoch \(i\).

According to (15), the RMS of the clock corrections contains the effects of both ICBs and TDBs. Since the standard deviations (STDs) are computed by removing the mean bias, the STDs reflect the precisions of TDBs, which can be calculated with:

$${\text{STD}} = \left( {\frac{1}{n - 1}\sum\limits_{i = 1}^{n} {\left( {{\varDelta}_{i} - \bar{\varDelta}} \right)\left( {{\varDelta}_{i} - \bar{\varDelta}} \right)} } \right)^{{\frac{1}{2}}}$$
(23)

where \(\bar{\varDelta}\) is the average bias, and n refers to the number of epochs. Equation (23) indicates statistical precision of TDBs.

The mean values of the STD and RMS of the clock differences were calculated and they are depicted in Fig. 2. No results were obtained for PRN 01 because it was selected as the reference for clock assessment. The results for PRN 08 are absent because these are not available in the CODE final clock products. It is clear from the figure that the STDs of the ESTCOD and ESTBRD strategies are identical, whereas the RMSs of the ESTBRD strategy are larger than the ESTCOD strategy. Since the troposphere is fixed to estimate the clocks for strategy ESTTROP, the STD is relatively small compared with the other two strategies, and the RMS is comparable with that of the ESTCOD strategy.

Fig. 2
figure 2

Mean standard deviation (STD) and root mean square (RMS) of all the satellite clocks over the experimental session

Full size image

Impacts of biases on coordinate estimates

In this study, all data were processed both in kinematic mode, i.e., estimating coordinates for each epoch independently, and in static mode, i.e., estimating coordinates as a single set of parameters during the processing period. Assessing the position differences with the IGS weekly solutions can directly illustrate the impact of the clock products on positioning accuracy. To ensure convergence, the coordinate solutions of the first 4 h were excluded. Furthermore, the last 15 min is excluded to avoid the orbit extrapolation error. In addition, stations with data gaps and frequent re-convergence were excluded from the statistics. Out of the 749 stations observing over the 7 days, data from 528 and 701 stations were used for the kinematic and static PPP experiments, respectively.

We calculated the RMS values of the kinematic and static PPP solutions for all the selected days using the different processing strategies. The statistical results for the North, East, and Up components are shown in Table 3. In this table, the horizontal RMS statistics of all stations are at centimeter level, they are smaller than 2.2 cm for the kinematic mode, and smaller than 1.2 cm for the static mode. The Up RMS statistics are smaller than 5 cm for the kinematic mode and smaller than 2 cm for the static mode. The RMS difference between the North, East, and Up components for strategies ESTCOD and ESTBRD in the kinematic and static modes are almost all less than 0.1 mm. These statistics are well below the normal precisions of IGS weekly solutions (Altamimi and Collilieux 2009), which indicate that ICBs do not affect the positioning estimates. However, the RMS of the ESTTROP strategy is better than that for the other two strategies; the improvement for the static PPP experiment is more significant. These statistics indicate that the accuracy of PPP after convergence is unaffected by ICBs, whereas it is affected by TDBs.

Table 3 RMS statistics of position residuals of estimates against the IGS weekly solutions
Full size table

Of those stations excluded from the computation of the accuracy statistics shown in Table 3, the kinematic PPP results for stations CHUR and GLPS, and stations MANA and CAS1 are compared in Fig. 3 as a typical example. The figure clearly indicates for stations CHUR and GLPS that the positioning results of the two strategies are consistent after the convergence period, although frequent re-convergence is observed for GLPS. A discontinuity in the coordinate series can be observed for station MANA near the eighth hour; the results of the two strategies suffer from the same jump, which is a result of undetected cycle slips in PRN 25.

Fig. 3
figure 3

Differences between estimated and reference coordinates for four typical examples

Full size image

Figure 4 shows the corresponding coordinate series after the removal of PRN 25. It is evident that the coordinate series of the two processing strategies correspond well. Furthermore, large differences for station CAS1 are observed during the period of 14–20 h without re-convergence. Our analysis shows that this was due to a failure of the cycle slip detection method for this station. Six satellites were marked with cycle slip with the default slip threshold of 0.05, leading to the re-convergence. The results achieved after resetting the slip threshold to 0.15 and reprocessing the station data are shown in the figure. Similar results were obtained for the other stations not included in the accuracy statistics.

Fig. 4
figure 4

Differences in coordinates after removal of satellite PRN 25 (MANA) and the resetting of the slip threshold (CAS1)

Full size image

There are occasions when the stations used for computing accuracy statistics suffer from cycle slips, which could lead to positioning differences. As can be observed in Fig. 5 for station ALRT, the coordinate series conforms well after the initial period of convergence. However, during the period 17–21 h, larger coordinate differences are observed in the North and East components. These are also attributable to the imperfect cycle slip processing strategies implemented in the RTKLIB software, which is the principal contributing factor to the minor coordinate differences shown in Table 3.

Fig. 5
figure 5

Coordinate differences for station ALRT

Full size image

Impacts of biases on tropospheric estimates

All extracted ZTDs were compared with respect to the IGS (Byram et al. 2011) final tropospheric products. Figure 6 depicts the STDs and mean biases for the ESTCOD strategy at each station, showing that the STDs of the ZTD estimates for most stations are < 1 cm and that the mean biases are all within 1 cm. This fulfills the threshold requirements for operational numerical weather prediction (Huang et al. 2003). Also, we can exploit the fact that the variability of the tropospheric STD and mean bias is independent of geographic latitude.

Fig. 6
figure 6

Standard deviations and biases of zenith total delay in static mode (top row) and kinematic mode (bottom row) for strategy ESTCOD

Full size image

Figure 7 depicts the STDs and mean biases at different stations, irrespective of their location. Note that a zero value indicates that the precise troposphere product was not available for the station. Statistics shows that the bias and STD differences between the ESTBRD and ESTCOD strategies are < 1 mm at all stations. However, the differences between the ESTCOD and ESTTROP strategies are relatively large. The bias difference is within 10 and 1.5 mm for the static and kinematic modes, respectively, whereas the STD difference is within 1 and 0.5 mm over all stations. This demonstrates that while the ICBs do not affect PPP-based tropospheric estimations, the TDBs do. Furthermore, the tropospheric and coordinate estimates in the static mode are more susceptible to TDBs. This might be due to the re-initialization of the variance of coordinate parameters at each epoch in the kinematic mode, and therefore, the estimates can absorb a part of the TDBs effects. However, the TDBs are accumulated in static mode and thus affect the troposphere and coordinate estimates significantly.

Fig. 7
figure 7

Standard deviations and mean biases of zenith total delay in static mode (top row) and kinematic mode (bottom row) for different stations

Full size image

Impacts of ICBs on permanent stations

Since satellite clocks are estimated on a daily basis, the ICBs suffer from daily re-convergence. For post-processing of the clock products, it is possible to determine ICBs with relatively high accuracy based on data analyzed in daily batches. However, for real-time satellite clock estimations, the ICBs can only be retrieved from broadcast ephemeris before the ICB estimates have converged to an accuracy comparable to the quality of the range. Hence, it is necessary to investigate the overall impact of ICBs retrieved from broadcast navigation information on the PPP convergence period. It should be noted that the “ground truth” of the ICBs cannot be retrieved; hence, IGS final clocks are used as the reference, and the ICBs in the final clocks are regarded as zero, although this is not actually the case.

The broadcast ephemeris and the IGS final 30 s clocks from January 1, 2015, to April 1, 2016 (DOY 001, 2015–DOY 092, 2016) were used to analysis the magnitudes of the ICBs. The temporal resolution of the comparison used in this study was set to 900 s, and the outliers in the broadcast messages were excluded from the comparison. The mean and STD of the broadcast ICBs with respect to the IGS final clock ICBs are detailed in Fig. 8. As can be observed, the mean bias of all satellites is mostly within 3 ns, with only a few satellites exceeding 3 ns. Furthermore, the STD of most satellites is < 2 ns, with only a few satellites exceeding 4 ns.

Fig. 8
figure 8

Mean bias and standard deviation of the broadcast initial clock biases with respect to the IGS final clock from January 1, 2015, to April 1, 2016

Full size image

To investigate the maximum impact of ICBs, the threshold of the ICBs was set to the mean value of the ICBs, plus or minus three STDs of the bias. Using the simulated maximum values, we calculated the prolonged convergence time for static and kinematic PPP on a daily basis. The distribution of the prolonged convergence time for kinematic PPP is shown in Fig. 9. In most cases, the impact of the ICBs on the convergence time is < 20 min, and the reduced time retains a slightly larger proportion than the prolonged convergence time. However, there are no statistically significant differences in the proportions of the prolonged and reduced convergence times.

Fig. 9
figure 9

Distribution of prolonged convergence time for kinematic precise point positioning; upper panel (mean plus three standard deviations); lower panel (mean minus three standard deviations)

Full size image

We selected four globally distributed stations as typical examples with which to detail the impact of the ICBs. Figure 10 shows that the ICBs affect the convergence period, but that the magnitude of the impact depends on stations and different coordinate components. This is because the convergence time is affected by the satellite distribution, quality of the observations, and magnitudes of the ICBs. According to our analysis, pseudorange observation quality is the primary factor that affects the convergence time of PPP solutions because the globally distributed GPS satellites can always guarantee good geometric strength. When the quality of the observation is good (stations ABPO and NRMD), the ICBs will not affect the convergence time significantly. However, when the observation quality is poor, such as at stations HOLM and RESO, the impacts of ICBs are more obvious.

Fig. 10
figure 10

Comparisons of kinematic positioning performance with clocks fixed to different initial clock biases on June 8, 2015 (DOY 159)

Full size image

Impacts of ICBs on vehicle-borne station

The vehicle-borne experiment was performed in Wuhan on April 21, 2015 (DOY 111). The data collection frequency is 1 Hz, and the cutoff elevation angle is 10°; the total number of observation epochs 3370. In this test, a base station was installed near the mission area to allow quantitative assessment of the PPP results. The reference position of the base station was calculated by conducting static PPP, whereas the North/East/Up components of the baseline were calculated using GrafNav® software. The distance between the base and rover receivers is < 1.3 km; hence, the ambiguity was reliably fixed in the double-difference (DD) processing. Figure 11 shows the trajectory of the moving carrier, while the observed number of satellites and Position Dilution of Precision (PDOP) are plotted in Fig. 12. Satellite clocks with different ICBs were estimated; the consistency between the PPP and DD solutions is shown in Fig. 13. The solutions of the ESTCOD and ESTTROP strategies show good agreement. This is considered reasonable, since we have shown in the permanent station experiments that the TDBs have only a minor effect on kinematic positioning. The solution for the ESTBRD strategy converges more slowly, and it shows poorer agreement with the DD results, particularly in the East and Up directions. These results agree with the theoretical analysis and indicate that the ICBs also affect the convergence period for real kinematic PPP.

Fig. 11
figure 11

Trajectory of the vehicle-borne experiment on April 21, 2015 (DOY 111)

Full size image
Fig. 12
figure 12

Number of satellites and PDOP for kinematic data on April 21, 2015 (DOY 111)

Full size image
Fig. 13
figure 13

Kinematic positioning errors for different processing strategies on April 21, 2015 (DOY 111)

Full size image

Conclusions

Precise satellite orbit and clock products are critical prerequisites for PPP. Considering the stability of satellite motion and the assimilation of orbit errors by clocks, the predicted orbits of ultra-rapid products can be applied to RT applications with sufficiently high accuracy. Hence, having high-accuracy satellite clock corrections is important for PPP service because of poor short-term clock stability.

Since satellite clocks can assimilate frequency related code and phase biases, the biases induced by different mathematical models were presented. Analysis shows that the clock biases derived using the undifferenced and mixed-difference methods are equivalent. Depending on their relation to hardware or real clock variations, the biases were grouped into TDBs and ICBs according to their impact on PPP. Then, the impact of the biases on PPP was analyzed in detail. The results show that ICBs contained in the clock corrections are absorbed by the phase ambiguities, and thus do not affect PPP estimates. Instead, the ICBs introduce a constant error to the pseudorange observations. If ICBs are not accurately estimated, they might degrade the quality of pseudorange observations. Furthermore, the TDBs are found to affect both the coordinate and the troposphere estimates.

We validated the impact of biases on the estimation of coordinates and tropospheric delay. Three satellite clock products were estimated. The precision of the clock products with respect to the CODE final clock product was assessed. Then, a network of 107 globally distributed reference stations from the IGS in 2015 was used to study the impact of biases on the estimated tropospheric ZTD and coordinate series. The validation for kinematic and static solutions shows that the ICBs of the satellite clock products do not affect PPP solutions, although they might cause small errors if the cycle slips are handled incorrectly. However, TDBs do affect PPP estimates; their impact on static PPP is more significant. The impact of ICBs on the convergence period of PPP was validated. We tested the impact of the biases on the convergence period using IGS permanent stations and a vehicle-borne station. The results show that the ICBs affect the convergence period but that their magnitudes differ by stations and coordinate components.

Whereas the experiments analyzed the effects of TDBs and ICBs biases caused by the modeling errors, the results also illustrate the impacts of real-time clock corrections that are susceptible to modeling errors. In triple-frequency PPP, time-variant satellite phase hardware delays and the constant satellite code delays cannot be ignored. The two types of biases can be classified as TDBs and ICBs; therefore, the conclusions are applicable for the impacts of the biases. Future research should focus on investigating the effects of time-variant hardware delays in dual-frequency clocks on PPP fractional cycle biases estimation and ambiguity resolution with the undifferenced observation model.