Introduction

The error sources in GNSS, such as clock errors, ephemeris errors, tropospheric propagation delay, and multipath, could degrade the positioning performance of GNSS. Many of the errors are constant for all GNSS receivers in a given small area and can be removed or reduced by using the popular differential technique. However, due to the difference in geographical location between reference station and the receiver, the multipath environment always differs. Thus, differential technique cannot eliminate the multipath error. Many studies have shown that multipath interference will lead to a pseudorange error which impacts the reliability and accuracy of GNSS. Therefore, multipath interference mitigation has been a hot topic in the field of satellite navigation receiver design.

The term multipath is derived from the fact that a signal transmitted from a GNSS satellite can follow a multiple number of propagation paths to the receiving antenna. This is possible because the signal can be reflected back to the antenna from surrounding objects, e.g., buildings, vehicles, and the surface of the earth. The multipath interference and the LOS signal reach the receiver simultaneously, causing a phase distortion in the tracking loops. The phase distortion caused by multipath interference results in serious tracking and positioning errors (Braasch 2001; Kalyanaraman et al. 2006).

There have been many studies on the multipath effect on GNSS. Multipath interference mitigation techniques are mainly based on antenna technique and signal processing algorithms. By mounting the antenna in a well-designed place based on the multipath environment, the performances of multipath interference mitigation for different antennas were compared in Maqsood et al. (2013). Some other multipath mitigation algorithms using measurements from different antennas to estimate multipath based on antenna array were proposed in Counselman (1998), Ray et al. (2001), and Lopez (2010). However, the special antenna-based technique can only suppress the multipath coming from the ground below the antenna, e.g., choke ring antenna. This property is useless for the multipath interference signal reflected by the objects above the antenna (Counselman 1998).

Narrow correlator has been adopted widely in multipath interference mitigation, and the improved performance is obtained by decreasing the early–late correlator spacing (Dierendonck et al. 1992; Van Nee 1992; Michael 1996). However, the infinite bandwidth assumption in the narrow correlator is invalid in practice. Thus, the tracking error cannot be further decreased by reducing the early–late correlator spacing when it is less than the reciprocal of the channel bandwidth (Cannon et al. 1994). The double delta correlator is a general term for a special class of code discriminator. These techniques use two pairs of correlators to describe the shape of the correlation curve near the correlation peak, which is then used to establish a reasonable discrimination function. Strobe correlator and high-resolution correlator are the varieties of this technique (Garin et al. 1996; McGraw et al. 1999). The performance of these techniques has been improved compared to the conventional and narrow correlators. However, they can only decrease the pseudorange error to some extent. The carrier phase tracking error cannot be mitigated.

MEDLL (Multipath Estimated Delay Locked Loop) is a multipath mitigation technology proposed by NovAtel (van Nee 1992), which can detect and eliminate the multipath interference (Townsend et al. 1995). It is based on statistical estimation theory. Both the code phase error and the carrier phase error can be greatly reduced by MEDLL. However, it requires higher sampling rate and more correlators. The improved version of MEDLL with structure simplification includes MMT (Weill 2002) and vision correlator (Jones and Fenton 2005). Another category technique is the CADLL (Coupled Amplitude Delay Lock Loop) and its improved version ECADLL (Enhanced CADLL) (Chen et al. 2010, 2013). It has been proven that the CADLL algorithms deserve even better anti-noise performances; however, the structure of these algorithms is also complex. The CADLL needs a batch of tracking units, and each tracking unit consists of a traditional code delay locked loop to track the code phase, and the two ALL (Amplitude Lock Loops) to track the signal amplitude of the Q and I branches. Every ALL contains an estimator, a loop filter, and an integrator. Hence, the complexity of CADLL is obvious. In addition, both MEDLL and CADLL need the carrier tracking loop to provide a fine carrier frequency.

The RELAX (RELAXation) algorithm was proposed for mixed spectrum estimation (Li and Stoica 1996) and also for angle and waveform estimation of narrowband plane waves arriving at a uniform linear array (Li et al. 1997). RELAX mainly requires a sequence of FFTs (fast Fourier transform); hence, it is both conceptually and computationally simple. The RELAX algorithm has also been extended to high-resolution time-delay estimation (referred to as WRELAX for short, which is weighted RELAX) (Li and Wu 1998; Wu and Li 1998, Wu et al. 1999, 2015; Li et al. 2012). It joints amplitude and time-delay estimation and outperforms other existing algorithms in estimation accuracy. Considering the superiority of WRELAX, two algorithms are proposed to mitigate multipath in GNSS. The proposed algorithms have the following advantages: First, there is no need of any correlators. Second, the parameters are estimated by FFT operation, which can be easily implemented and have a fine estimation performance. Third, there is no need of an extra carrier tracking loop, because the carrier frequency can be obtained by a simple estimation process as proposed in (Li et al. 2011). Theoretical analysis and numerical simulation results are given to demonstrate the performances of the proposed algorithms compared to the state-of-art technique.

Multipath data model

GNSS signal can be divided into three parts: the carrier, the ranging codes, and the navigation data. Here, GPS is taken as an example to facilitate the presentation. However, the proposed algorithms are also suitable to other GNSS system.

Suppose the transmitted signal of GNSS satellites can be given by

$$x(t) = d(t)c(t)\cos \left( {\omega_{c} t} \right)$$
(1)

where d(t) denotes the navigation data and c(t) represents the C/A code in GPS. Suppose there are P multiple reflections in addition to the LOS signal. The received data can be written as

$${\overline{\overline {y}}}(t) = \sum\limits_{p = 0}^{P} {\alpha_{p}^{{\prime }} } d(t - \tau_{p} )c(t - \tau_{p} )\cos \left( {\omega_{c} \left( {t - \tau_{p} } \right) + \varphi_{p} } \right) + e(t)$$
(2)

The symbol e(t) represents the thermal noise. The amplitude, code delay, and initial phase of the signal from the pth path are denoted as α p ′, τ p , φ p , respectively. Here, p = 0 represents the LOS signal.

As is known, the navigation code length is much longer than the repeated cycle of C/A code. Also, only several periods of the C/A code, e.g., one period, is used in the code delay estimation; hence, the navigation data jump can be neglected in our discussion. Here, the navigation data, which equals to +1 or −1, is combined with the amplitude α p ′ together and denoted as α p . Then, (2) can also be given by

$${\overline{\overline {y}}} \left( t \right) = \sum\limits_{p = 0}^{P} {\alpha_{p} } c\left( {t - \tau_{p} } \right)\cos \left( {\omega_{c} \left( {t - \tau_{p} } \right) + \varphi_{p} } \right) + e\left( t \right)$$
(3)

The Doppler frequency of the pth path can be obtained by

$$\omega_{dp} = \frac{{{\text{d}}\phi_{p} }}{{{\text{d}}t}} = \frac{{{\text{d}}\left( {\omega_{c} \tau_{p} } \right)}}{{{\text{d}}t}} = \frac{{{\text{d}}\left( {\omega_{c} \left( {{{R_{p} \left( t \right)} \mathord{\left/ {\vphantom {{R_{p} \left( t \right)} c}} \right. \kern-0pt} c}} \right)} \right)}}{{{\text{d}}t}}$$
(4)

Assume the radial velocity of the receiver to the satellite is v, then the propagation range can be given by

$$R_{p} \left( t \right) = R_{0} + vt + \Delta R_{p} \left( t \right)$$
(5)

where R 0 denotes the range between receiver and satellite in the initial moment. The symbol ΔR p (t) stands for the propagation range difference between the LOS signal and the reflected multipath from the pth path. The range difference ΔR p is much smaller than R 0; hence, ΔR p (t) can be considered as constant in the short integration time. Further insert (5) into (4), we can obtain

$$\omega_{dp} = \frac{{{\text{d}}\phi_{p} }}{{{\text{d}}t}} \approx 2\pi \frac{v}{\lambda }$$
(6)

It can be noted that the LOS signal and reflect signal approximately share the same Doppler shift, which is termed as ω d in the following. Inserting (6) into (3), then we can get

$${\overline{\overline {y}}}(t) = \sum\limits_{p = 0}^{P} {\alpha_{p} } c\left( {t - \tau_{p} } \right)\cos \left( {\omega_{d} t + \varphi_{p} } \right) + e(t)$$
(7)

where ω d  = ω d0 + ω c . The symbols φ 0 = R 0/λ and φ p  = φ 0 + Δφ p are the phase of the LOS signal and the reflected ones, respectively, with Δφ p  = 2πΔR p /λ an extra phase caused by the extra propagation range ΔR p .

Take Hilbert transform to (7), and then, we can get

$$\bar{y}(t) = \sum\limits_{p = 0}^{P} {\alpha_{p} } c\left( {t - \tau_{p} } \right)e^{{j\omega_{d} t}} e^{{j\varphi_{p} }} + e(t)$$
(8)

Assume the Doppler frequency can be obtained accurately, then the complex phase \(e^{{j\omega_{d} t}}\) can be compensated after down-conversion. Hence, Eq. (8) can be written as

$$y(t) = \sum\limits_{p = 0}^{P} {\alpha_{p} } c\left( {t - \tau_{p} } \right)\cos \left( {\varphi_{p} } \right) + e(t)$$
(9)

The data in (9) are used by the code tracking loop to obtain the code phase. The following descriptions are all based on (9).

MEDLL

MEDLL is a multipath mitigation technique build upon statistical estimation theory. The multiple correlation samples obtained with MEDLL are used in an iterative step based on ML (maximum likelihood) theory; hence, it can obtain better performance than the narrow correlator. The detail of MEDLL is given as follows.

Define the following ML function

$$L\left( {\xi \left( t \right)} \right) = \int_{0}^{T} {\left[ {y(t) - \xi \left( t \right)} \right]}^{2} dt$$
(10)

where ξ(t) is the reconstruct signal by the estimated parameters, which can be given by

$$\xi (t) = \sum\limits_{p = 0}^{P} {\hat{\alpha }_{p} c\left( {t - \hat{\tau }_{p} } \right)\exp \left( {j\hat{\varphi }_{p} } \right)}$$
(11)

where \(\hat{\alpha }_{p} ,\hat{\tau }_{p} ,\hat{\varphi }_{p}\) are the amplitude, code delay and phase estimation of the pth path. In practice, a summation can be used to take the place of the integral in (10) for simplification.

Because of the unknown parameters (α p , τ p , φ p ) in (10), the ML function L(ξ(t)) can be represented as L(α p , τ p , φ p ). By setting the partial derivation of L(α p , τ p , φ p ) to zero, which means \(\frac{{\partial L\left( {\hat{\alpha },\hat{\tau },\hat{\varphi }} \right)}}{{\partial \hat{\alpha }}} = 0,\frac{{\partial L\left( {\hat{\alpha },\hat{\tau },\hat{\varphi }} \right)}}{{\partial \hat{\tau }}} = 0,\frac{{\partial L\left( {\hat{\alpha },\hat{\tau },\hat{\varphi }} \right)}}{{\partial \hat{\varphi }}} = 0,\) then we can get

$$\hat{\tau }_{p} = \mathop {\arg \hbox{max} }\limits_{\tau } \left\{ {\text{Re} \left\{ {\left[ {R_{x} (\tau ) - \sum\limits_{\begin{subarray}{l} k = 0 \\ k \ne p \end{subarray} }^{P} {\hat{\alpha }_{k} R\left( {\tau - \hat{\tau }_{k} } \right)\exp \left( {j\hat{\varphi }_{k} } \right)} } \right]} \right\}\exp \left( { - j\hat{\varphi }_{p} } \right)} \right\}$$
(12)
$$\hat{\alpha }_{p} = \text{Re} \left\{ {\left[ {R_{x} \left( {\hat{\tau }_{p} } \right) - \sum\limits_{\begin{subarray}{l} k = 0 \\ k \ne p \end{subarray} }^{P} {\hat{\alpha }_{k} R\left( {\hat{\tau }_{p} - \hat{\tau }_{k} } \right)} \exp \left( {j\hat{\varphi }_{k} } \right)} \right]\exp \left( { - j\hat{\varphi }_{p} } \right)} \right\}$$
(13)
$$\hat{\varphi }_{p} = {\text{angle}}\left[ {R_{x} \left( {\hat{\tau }_{p} } \right) - \sum\limits_{\begin{subarray}{l} k = 0 \\ k \ne p \end{subarray} }^{P} {\hat{\alpha }_{k} R\left( {\hat{\tau }_{p} - \hat{\tau }_{k} } \right)} \exp \left( {j\hat{\varphi }_{k} } \right)} \right]$$
(14)

where R(τ) is the autocorrelation of the local C/A code, with the normalized maximum value equal to 1 and the relative code delay equal to 0. The function R(τ) is taken as the reference autocorrelation function. The cross-correlation of the received data and the local C/A code is denoted as R x (τ). For the coupling of the unknown parameters from (12) to (14), MEDLL is solved by an iterative way.

Step 1. Assume there is only the LOS signal in the received data, namely y(t) = ξ 0(t), then the correlation function can be taken as \(\hat{R}_{0} \left( \tau \right) = R_{x} \left( \tau \right)\). Insert \(\hat{R}_{0} \left( \tau \right)\) into the parameter estimation modular to obtain a set of estimates \(\left( {\hat{\alpha }_{0} ,\hat{\tau }_{0} ,\hat{\varphi }_{0} } \right)\). By using the estimates and the reference autocorrelation function, the autocorrelation of ξ 0(t) can be constructed from \(\hat{R}_{0} \left( \tau \right) = \hat{\alpha }_{0} R\left( {\tau - \hat{\tau }_{0} } \right)\exp \left( {j\hat{\varphi }_{0} } \right)\).

Step 2. Subtract the constructed correlation \(\hat{R}_{0} (\tau )\) from R x (τ), and the difference is \(\hat{R}_{1} (\tau ) = R_{x} (\tau ) - \hat{R}_{0} (\tau )\), which can be treated as the correlation function of ξ 1(t). Send \(\hat{R}_{1} (\tau )\) to the parameter estimation modular to estimate \(\left( {\hat{\alpha }_{1} ,\hat{\tau }_{1} ,\hat{\varphi }_{1} } \right)\). Similarly, the correlation function of ξ 1(t) can be constructed from \(\left( {\hat{\alpha }_{1} ,\hat{\tau }_{1} ,\hat{\varphi }_{1} } \right)\) by \(\hat{R}_{1} (\tau ) = \hat{\alpha }_{1} R\left( {\tau - \hat{\tau }_{1} } \right)\exp \left( {j\hat{\varphi }_{1} } \right)\).

Step 3. Subtract the constructed correlation function \(\hat{R}_{1} (\tau )\) from R x (τ), and the difference is \(\hat{R}_{0} \left( \tau \right) = R_{x} \left( \tau \right) - \hat{R}_{1} \left( \tau \right)\), which can be thought as the correlation function of ξ 0(t). Then, a new set of estimates \(\left( {\hat{\alpha }_{0} ,\hat{\tau }_{0} ,\hat{\varphi }_{0} } \right)\) can be obtained. After that, the correlation function of ξ 0(t) can be reconstructed.

Step 4. Iterate the previous two steps until “practical convergence” is achieved.

Remaining Steps: Continue similarly until P is equal to the desired or estimated number of signals.

Here we discuss how to obtain the estimates \(\left( {\hat{\alpha }_{p} ,\hat{\tau }_{p} ,\hat{\varphi }_{p} } \right)\) in MEDLL. First, the maximum value of R p (τ) is searched, which is equivalent to find the location of the peak value of \(\text{Re}^{2} [R_{p} \left( \tau \right)] + \text{Im}^{2} [R_{p} \left( \tau \right)]\). The corresponding code delay of the peak value is the estimated code delay, which can be stated as follows

$$\tau_{\hbox{max} } = \mathop {\hbox{max} }\limits_{\tau } \left\{ {\left[ {\text{Re} \left( {R_{p} \left( \tau \right)} \right)} \right]^{2} + \left[ {\text{Im} \left( {R_{p} \left( \tau \right)} \right)} \right]^{2} } \right\}$$
(15)

The phase \(\hat{\varphi }_{p}\) can be obtained by

$$\begin{aligned} \hat{\varphi }_{p} = {\text{atan}}\left( {\frac{{\text{Im} \left[ {R_{p} \left( {\tau_{\hbox{max} } } \right)} \right]}}{{\text{Re} \left[ {R_{p} \left( {\tau_{\hbox{max} } } \right)} \right]}}} \right),\quad {\text{if}}\quad \text{Re} \left[ {R_{p} \left( {\tau_{\hbox{max} } } \right)} \right] > 0 \hfill \\ \hat{\varphi }_{p} = {\text{atan}}\left[ {\frac{{\text{Im} \left[ {R_{p} \left( {\tau_{\hbox{max} } } \right)} \right]}}{{\text{Re} \left[ {R_{p} \left( {\tau_{\hbox{max} } } \right)} \right]}}} \right] + \pi ,\quad {\text{if}}\quad \text{Re} \left[ {R_{p} \left( {\tau_{\hbox{max} } } \right)} \right] > 0 \hfill \\ \hat{\varphi }_{p} = \, \frac{\pi }{2},\quad {\text{if }}\text{Re} \left[ {R_{p} \left( {\tau_{\hbox{max} } } \right)} \right] = 0\quad {\text{and}}\quad \text{Im} \left[ {R_{p} \left( {\tau_{\hbox{max} } } \right)} \right] > 0 \hfill \\ \hat{\varphi }_{p} = - \frac{\pi }{2},\quad {\text{if }}\text{Re} \left[ {R_{p} \left( {\tau_{\hbox{max} } } \right)} \right] = 0\quad {\text{and}}\quad \text{Im} \left[ {R_{p} \left( {\tau_{\hbox{max} } } \right)} \right] < 0 \hfill \\ \end{aligned}$$
(16)

By using the estimated \(\hat{\varphi }_{p}\), the correlation function after phase demodulation can be given by

$$R^{\prime}_{p} \left( \tau \right) = \text{Re} \left[ {R_{p} \left( \tau \right)} \right]\cos \left( {\hat{\varphi }_{p} } \right) + \text{Im} \left[ {R_{p} \left( \tau \right)} \right]\sin \left( {\hat{\varphi }_{p} } \right)$$
(17)

The demodulated correlation function R′ p (τ) is real valued, which can be used to estimate the delay and amplitude.

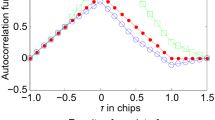
In most cases, the code delay is not the integral multiple of the correlator space; hence, the real maximum value of R(τ) is not included in the samples, as in Fig. 1. If A and B are the first two maximum point of R(τ), which is nearest to the real maximum location, the corresponding code delay of A and B is τ a and τ b , with the correlator space Δτ = τ b  − τ a . The actual code delay τ 0 = τ c  + τ x , with τ x , is the unknown parameter to be determined.

Fig. 1
figure 1

Multiple correlator sampling of the correlation function

Full size image

Using the reference autocorrelation function R(τ), a discrimination function f(τ x ) can be built in the following way

$$f\left( {\tau_{x} } \right) = \frac{{R\left( {\tau_{0} - \tau_{x} - \frac{1}{2}\Delta \tau } \right) - R\left( {\tau_{0} - \tau_{x} + \frac{1}{2}\Delta \tau } \right)}}{{\left| {R\left( {\tau_{0} - \tau_{x} - \frac{1}{2}\Delta \tau } \right)} \right| + \left| {R\left( {\tau_{0} - \tau_{x} + \frac{1}{2}\Delta \tau } \right)} \right|}}$$
(18)

The obtained f(τ x ) can be used as a reference discrimination function. As shown in Fig. 1, \(\tau_{a} = \tau_{0} - \tau_{x} - \frac{\Delta \tau }{2}\) and \(\tau_{b} = \tau_{0} - \tau_{x} + \frac{\Delta \tau }{2}\). By assuming τ 0 is known prior, the range of τ x can be determined as \(\tau_{0} - \frac{\Delta \tau }{2} \le \tau_{x} \le \tau_{0} + \frac{\Delta \tau }{2}\), and then, the corresponding τ a , τ b and further the value of f(τ x ) can be calculated and stored for reference.

It is said beforehand that estimating the code delay only by finding the correlation peak will lead to serious error, because the actual code delay is not always the integral times of the correlator space. Therefore, the phase discriminate function built from the real correlation function R p (τ′) can be given by

$$f^{{\prime }} \left( {\tau_{x}^{{\prime }} } \right) = \frac{{R_{p} \left( {\tau_{a}^{{\prime }} } \right) - R_{p} \left( {\tau_{b}^{{\prime }} } \right)}}{{\left| {R_{p} \left( {\tau_{a}^{{\prime }} } \right)} \right| + \left| {R_{p} \left( {\tau_{b}^{{\prime }} } \right)} \right|}}$$
(19)

where τ′ a and τ′ b are the corresponding value of τ a and τ b in f(τ x ). Comparing each value of f(τ x ′) with f(τ x ), the code delay can be obtained when \({\text{abs}}\left[ {f\left( {\tau_{x} } \right) - f^{{\prime }} \left( {\tau_{x}^{{\prime }} } \right)} \right]\) gets its minimum.

In the phase estimation process, the code delay τ max that corresponding to the peak value was obtained, which can be used to get the amplitude estimation by \(\hat{a}_{p} = R_{p}^{{\prime }} \left( {\tau_{\hbox{max} } } \right)\). This amplitude estimation has high accuracy in the case of narrower correlator space. Alternatively, the amplitude can be obtained also by (13) (Townsend et al. 1995).

Correlation domain WRELAX algorithm

In this section, the time-delay estimation problem is first formulated as a NLS problem in the correlation domain. Then, WRELAX is taken to minimize the complicated multidimensional NLS cost function. The reason for choosing the WRELAX algorithm is its striking feature that it decouples the multidimensional optimization problem into a sequence of 1 − D optimization problems in a conceptually and computationally simple way. Compared with other existing algorithms, WRELAX is more systematic and efficient, and also it has fewer limitations on the signal shapes. Based on these properties, WRELAX is used here to estimate code delay and amplitude of the LOS signal and the multipath for the purpose of multipath mitigation in GNSS.

After sampling, the data in (8) can be written as

$$y\left( {nT_{s} } \right) = \sum\limits_{p = 0}^{P} {\alpha_{p} } c\left( {nT_{s} - \tau_{p} } \right)\exp \left( {j\varphi_{p} } \right) + e\left( {nT_{s} } \right)\quad n = 1,2,{ \ldots },N$$
(20)

where T s is the sampling interval and N is the total number of samples. Furthermore, we combine exp (jφ p ) and α p together as a new complex variable denoted as β p , and then, (20) can be rewritten as

$$y\left( {nT_{s} } \right) = \sum\limits_{p = 0}^{P} {\beta_{p} } c\left( {nT_{s} - \tau_{p} } \right) + e\left( {nT_{s} } \right)$$
(21)

The received satellite signal in (22) can be used to obtain the correlation function with the reference signal c(nT s ), which can be formulated by

$$r\left( {nT_{s} } \right) = {\text{corr}}\left( {c\left( {nT_{s} } \right),y\left( {nT_{s} } \right)} \right)$$
(22)

where \({\text{corr}}\left( {} \right)\) represents the cross-correlation operation. Owing to the uncorrelated characteristic between the noise and the signal, Eq. (22) can be expressed as

$$r\left( {nT_{s} } \right) = \sum\limits_{p = 0}^{P} {\beta_{p} } r^{s} \left( {nT_{s} - \tau_{p} } \right) + w\left( {nT_{s} } \right)$$
(23)

where r s(nT s ) is the autocorrelation of c(nT s ) and \(w\left( {nT_{s} } \right) = {\text{corr}}\left( {c\left( {nT_{s} } \right),e\left( {nT_{s} } \right)} \right)\) can still be treated the same as e(n). Apply the discrete Fourier transform (DFT) to (23)

$$p_{f} (k) = r_{f}^{s} (k)\sum\limits_{p = 0}^{P} {\beta_{p} e^{{j\omega_{p} k}} + } w_{f} (k)$$
(24)

where p f (k), r s f (k) and w f (k) are the DFT of r(nT s ), r s(nT s ) and w(nT s ), respectively, ω p  = −2πτ p /(NT s ) with T s standing for the sampling interval. Therefore, the code delay estimation is turned into the estimation of the angular frequency, and the code delay can be further obtained by τ p  = −ω p NT s /2π.

In fact, p f (k) can also be obtained in the following way to further decrease the computation complexity. First, apply DFT to (21) we can get

$$y_{f} (k) = s_{f} (k)\sum\limits_{p = 0}^{P} {\beta_{p} } e^{{j\omega_{p} k}} + e_{f} (k),\quad - N/2 \le k \le N/2 - 1$$
(25)

where y f (k), c f (k) and e f (k) are the DFT of y(nT s ), c(nT s ) and e(nT s ), respectively. Further, the DFT of the correlation function p f (k) can be obtained by

$$p_{f} (k) = y_{f} (k)c_{f}^{*} (k)$$
(26)

The correlation obtained from (24) and (26) is the same, but (26) is much easier to calculate.

Define a NLS cost function in the following way

$$C_{1} \left( {\omega_{p} ,\alpha_{p} } \right) = \sum\limits_{k = - N/2}^{N/2} {\left\| {p_{f} (k) - r_{f}^{s} (k)\sum\limits_{p = 0}^{P} {\alpha_{p} e^{{j\omega_{p} k}} } } \right\|^{2} } ,\quad p = 0,1,{ \ldots },P$$
(27)

By minimizing C 1({ω p , α p }), the unknown parameters {ω p , α p }, p = 0, 1, …, P can be estimated. In order to solve the NLS problem, a multidimensional space searching is required, which is complicated. Hence, WRELAX is utilized here to reduce the complexity. First, define the following quantities

$${\mathbf{a}}\left( {\omega_{p} } \right) = \left[ {e^{{j\omega_{p} ( - N/2)}} ,e^{{j\omega_{p} ( - N/2 + 1)}} ,{ \ldots },e^{{j\omega_{p} (N/2 - 1)}} } \right]^{\text{T}}$$
(28)
$${\mathbf{p}}_{f} = \left[ {p_{f} ( - N/2),p_{f} ( - N/2 + 1),{ \ldots },p_{f} (N/2 - 1)} \right]^{\text{T}}$$
(29)
$${\mathbf{R}}_{f} = diag\left\{ {r_{f}^{s} ( - N/2),r_{f}^{s} ( - N/2 + 1),{ \ldots },r_{f}^{s} (N/2 - 1)} \right\}$$
(30)

Insert the above quantities into (27) to obtain

$$C_{1} \left( {\omega_{p} ,\alpha_{p} } \right) = \left\| {{\mathbf{p}}_{f} - \sum\limits_{p = 0}^{P} {\beta_{p} } {\mathbf{R}}_{f} {\mathbf{a}}(\omega_{p} )} \right\|^{2} ,\quad p = 0,1,{ \ldots },P$$
(31)

Further, we assume \(\{ \hat{\omega }_{q} ,\hat{\beta }_{q} \} \left( {p = 0,1,{ \ldots },P{\text{ and }}p \ne q} \right)\) have been estimated, then

$${\mathbf{p}}_{fp} = {\mathbf{p}}_{f} - \sum\limits_{\begin{subarray}{l} q = 0 \\ q \ne p \end{subarray} }^{P} {\hat{\beta }_{q} [{\mathbf{R}}_{f} {\mathbf{a}}(\hat{\omega }_{p} )]}$$
(32)

Inserting (32) into (31), we have

$$C_{2} \left( {\omega_{p} ,\beta_{p} } \right) = \left\| {{\mathbf{p}}_{fp} - \beta_{p} {\mathbf{R}}_{f} {\mathbf{a}}(\omega_{p} )} \right\|^{2} ,\quad p = 0,1,{ \ldots },P$$
(33)

The estimation \(\hat{\omega }_{p}\) and \(\hat{\beta }_{p}\) can be obtained by minimizing the above cost function as

$$\hat{\omega }_{p} = \arg \mathop {\hbox{max} }\limits_{{\omega_{p} }} \left| {{\mathbf{a}}^{\rm H} (\omega_{p} )\left( {{\mathbf{R}}_{f}^{ * } {\mathbf{p}}_{fp} } \right)} \right|^{2}$$
(34)

and

$$\hat{\beta }_{p} = \left. {\frac{{{\mathbf{a}}^{\rm H} (\omega_{p} )\left( {{\mathbf{R}}_{f}^{ * } {\mathbf{p}}_{fp} } \right)}}{{\left\| {{\mathbf{R}}_{f}^{{}} } \right\|_{F}^{2} }}} \right|_{{\omega_{p} = \hat{\omega }_{p} }}$$
(35)

where ∥·∥ F stands for the Frobenius norm. Hence, \(\hat{\omega }_{p}\) can be obtained as the location of the dominant peak of the periodogram \(\left| {{\mathbf{a}}^{\rm H} (\omega_{p} )\left( {{\mathbf{R}}_{f}^{ * } {\mathbf{p}}_{fp} } \right)} \right|^{2}\), which can be computed efficiently by applying FFT with the data sequence \({\mathbf{R}}_{f}^{ * } {\mathbf{p}}_{fp}\). Note that zero padding of FFT is used to determine \(\hat{\omega }_{p}\) with more accuracy. Then, \(\hat{\beta }_{p}\) can be obtained by calculating the complex height of the peak of \({{{\mathbf{a}}^{\rm H} (\hat{\omega }_{p} )\left( {{\mathbf{R}}_{f}^{ * } {\mathbf{p}}_{fp} } \right)} \mathord{\left/ {\vphantom {{{\mathbf{a}}^{\rm H} (\hat{\omega }_{p} )\left( {{\mathbf{R}}_{f}^{ * } {\mathbf{p}}_{fp} } \right)} {\left\| {{\mathbf{R}}_{f}^{{}} } \right\|_{F}^{2} }}} \right. \kern-0pt} {\left\| {{\mathbf{R}}_{f}^{{}} } \right\|_{F}^{2} }}\).

The diagram of the correlation domain algorithm is shown in Fig. 2. The following steps are given to further explain the minimization of the NLS cost function in the proposed algorithm.

Fig. 2
figure 2

Diagram of the correlation domain algorithm

Full size image

Step (1): Assume p = 0 (there is only the LOS signal). Obtain \(\{ \hat{\omega }_{0} ,\hat{\beta }_{0} \}\) from (34) and (35).

Step (2): Assume p = 1 (the LOS signal with a multipath interference). Compute \({\mathbf{p}}_{f1}\) with (32) by using \(\{ \hat{\omega }_{0} ,\hat{\beta }_{0} \}\) obtained in Step (1). Estimate \(\{ \hat{\omega }_{1} ,\hat{\beta }_{1} \}\) from \({\mathbf{p}}_{f1}\) as described in (34) and (35).

Next, compute \({\mathbf{p}}_{f0}\) with (32) by the obtained \(\{ \hat{\omega }_{1} ,\hat{\beta }_{1} \}\) and redetermine \(\{ \hat{\omega }_{0} ,\hat{\beta }_{0} \}\) from \({\mathbf{p}}_{f0}\) as in (34) and (35) above.

Iterate the previous two substeps until “practical convergence” is achieved, and then \(\{ \hat{\omega }_{p} ,\hat{\beta }_{p} \}_{p = 0}^{1}\) can be obtained. Furthermore, by using the relation, \(\hat{\omega }_{p} = {{ - 2\pi \hat{\tau }_{p} } \mathord{\left/ {\vphantom {{ - 2\pi \hat{\tau }_{p} } {NT_{s} }}} \right. \kern-0pt} {NT_{s} }}\) the code delay \(\hat{\tau }_{p} ,p = 0,1\) can be obtained.

Remaining steps: Continue similarly until P is equal to the desired or estimated number of paths. In the case that P is unknown, it can be estimated by using the generalized AIC rules. See, also Li and Stoica (1996).

Data domain WRELAX algorithm

Different from the correlation domain algorithm, the unknown parameters {β p , τ p } (p = 0, 1, …, P) can also be estimated directly in the data domain. The detail of the data domain algorithm can be described as follows.

Again, the frequency down-converted signal is given here

$$y(nT_{s} ) = \sum\limits_{p = 0}^{P} {\beta_{p} } c(nT_{s} - \tau_{p} ) + e(nT_{s} )$$
(36)

In order to obtain the unknown parameters {β p , τ p } (p = 0, 1, …, P) in (37), DFT is first applied to the received data,

$$y_{f} (k) = c_{f} (k)\sum\limits_{p = 0}^{P} {\beta_{p} } e^{{j\omega_{p} k}} + e_{f} (k)\quad - N/2 \le k \le N/2 - 1$$
(37)

where y f (k), c f (k) and e f (k) are the DFT of y(nT s ), c(nT s ) and e(nT s ), respectively. Until now, the code delay estimation is again transformed into the estimation of the angular frequency ω p , after that τ p can be obtained by the relation τ p  = −ω p N/2πf s .

Define the following NLS cost function

$$Q_{1} \left( {\beta_{p} ,\omega_{p} } \right) = \sum\limits_{k = - N/2}^{N/2 - 1} {\left| {y_{f} (k) - c_{f} (k)\sum\limits_{p = 0}^{P} {\beta_{p} } e^{{j\omega_{p} k}} } \right|}^{2} ,\quad p = 0,1,{ \ldots },P$$
(38)

The above cost function is similar to (27), which can also be solved by WRELAX. Now define the following quantities

$${\mathbf{C}}_{f} = diag\left[ {c_{f} \left( { - N/2} \right),c_{f} \left( { - N/2 + 1} \right),{ \ldots },c_{f} \left( {N/2 - 1} \right)} \right]$$
(39)
$${\mathbf{y}}_{f} = \left[ {y_{f} \left( { - N/2} \right),y_{f} \left( { - N/2 + 1} \right),{ \ldots }y_{f} \left( {N/2 - 1} \right)} \right]^{\text{T}}$$
(40)
$${\mathbf{a}}(\omega_{p} ) = \left[ {e^{{j\omega_{p} \left( { - N/2} \right)}} ,e^{{j\omega_{p} \left( { - N/2 + 1} \right)}} ,{ \ldots },e^{{j\omega_{p} \left( {N/2 - 1} \right)}} } \right]^{\text{T}}$$
(41)

By inserting (39) to (41) into (38), then minimizing the cost function in (38) is equivalent to minimizing

$$Q_{2} \left( {\beta_{p} ,\omega_{p} } \right) = \left\| {{\mathbf{y}}_{f} - \sum\limits_{p = 0}^{P} {\beta_{p} {\mathbf{C}}_{f} {\mathbf{a}}\left( {\omega_{p} } \right)} } \right\|^{2}$$
(42)

Assume \(\left\{ {\hat{\beta }_{q} ,\hat{\omega }_{q} } \right\},\left( {q = 0,1,q \ne p} \right)\) is known prior or has been estimated, then we have

$${\mathbf{y}}_{fp} = {\mathbf{y}}_{f} - \sum\limits_{\begin{subarray}{l} q = 0 \\ q \ne p \end{subarray} }^{P} {\hat{\beta }_{q} } \left[ {{\mathbf{C}}_{f} {\mathbf{a}}\left( {\hat{\omega }_{q} } \right)} \right]$$
(43)

Substitute (43) into (42)

$$Q_{2} \left( {\beta_{p} ,\omega_{p} } \right) = \left\| {{\mathbf{y}}_{fp} - \beta_{p} {\mathbf{C}}_{f} {\mathbf{a}}\left( {\omega_{p} } \right)} \right\|^{2}$$
(44)

Equation (44) achieves minimum when \({\mathbf{y}}_{fp} = \beta_{p} {\mathbf{C}}_{f} {\mathbf{a}}\left( {\omega_{p} } \right)\), and then, the estimation of \(\hat{\omega }_{p}\) and \(\hat{\beta }_{p}\) can be obtained by

$$\hat{\omega }_{p} = \arg \mathop {\hbox{max} }\limits_{{\omega_{p} }} \left| {{\mathbf{a}}^{\text{H}} (\omega_{p} )\left( {{\mathbf{C}}_{f}^{ * } {\mathbf{y}}_{fp} } \right)} \right|^{2}$$
(45)

and

$$\hat{\beta }_{p} = \left. {\frac{{{\mathbf{a}}^{\text{H}} \left( {\omega_{p} } \right)\left( {{\mathbf{C}}_{f}^{ * } {\mathbf{y}}_{fp} } \right)}}{{\left\| {{\mathbf{C}}_{f} } \right\|_{F}^{2} }}} \right|_{{\omega_{p} = \hat{\omega }_{p} }}$$
(46)

It is clearly from (45) that \(\hat{\omega }_{p}\) can be obtained as the maximum location of the periodogram \(\left| {{\mathbf{a}}^{H} (\omega )\left( {{\mathbf{C}}_{f}^{*} {\mathbf{y}}_{fp} } \right)} \right|^{2}\), which can be efficiently computed by applying FFT to the data sequence \({\mathbf{C}}_{f}^{*} {\mathbf{y}}_{fp}\) with zero padding. Then, \(\hat{\beta }_{p}\) can be easily obtained by the complex height of the peak of \({{{\mathbf{a}}^{H} \left( {\omega_{p} } \right)\left( {{\mathbf{C}}_{f}^{*} {\mathbf{y}}_{fp} } \right)} \mathord{\left/ {\vphantom {{{\mathbf{a}}^{H} \left( {\omega_{p} } \right)\left( {{\mathbf{C}}_{f}^{*} {\mathbf{y}}_{fp} } \right)} {\left\| {{\mathbf{C}}_{f} } \right\|_{F}^{2} }}} \right. \kern-0pt} {\left\| {{\mathbf{C}}_{f} } \right\|_{F}^{2} }}\).

The diagram of the process is given in Fig. 3. With the above simple preparations, the data domain WRELAX algorithm can be concluded as the following steps.

Fig. 3
figure 3

Diagram of the data domain algorithm

Full size image

Step (1): Assume p = 0. Obtain \(\{ \hat{\omega }_{0} ,\hat{\beta }_{0} \}\) from (45) and (46).

Step (2): Assume p = 1. Compute \({\mathbf{p}}_{f1}\) with (43) by using the \(\{ \hat{\omega }_{0} ,\hat{\beta }_{0} \}\) obtained in Step (1). Obtain \(\{ \hat{\omega }_{1} ,\hat{\beta }_{1} \}\) from \({\mathbf{p}}_{f1}\) described above.

Next, compute \({\mathbf{p}}_{f0}\) with (43) by \(\{ \hat{\omega }_{1} ,\hat{\beta }_{1} \}\) and redetermine \(\{ \hat{\omega }_{0} ,\hat{\beta }_{0} \}\) from \({\mathbf{p}}_{f0}\) as in (45) and (46) above.

Iterate the previous two substeps until “practical convergence” is achieved. Furthermore, the code delay \(\hat{\tau }_{p} ,p = 0,1\) can be obtained by the relation \(\hat{\omega }_{p} = {{ - 2\pi \hat{\tau }_{p} } \mathord{\left/ {\vphantom {{ - 2\pi \hat{\tau }_{p} } {NT_{s} }}} \right. \kern-0pt} {NT_{s} }}\).

Remaining Steps: Continue similarly until P is equal to the desired or estimated number of signals.

Comparison of the three algorithms

All the three algorithms described above mitigated the multipath by estimating the delay of the LOS signal first. It is interested to know the complexity and the performance of them for further study and practical application. Hence, the computation complexity and the estimation performance are compared in this part.

Computational complexity comparison

MEDLL is an estimation algorithm based on ML, which can be solved by nonlinear curve fitting, by finding a set of reference correlation function with the best fit of the input signal in amplitude, phase, and delay. Hence, MEDLL can reduce the code and carrier tracking error greatly. Essentially, MEDLL is similar to the classic DLL in the traditional receiver, but the classic DLL is only for one path (LOS signal). In the multipath environment, the excellent performance of MEDLL is obtained by increasing the number of signals to be estimated. Hence, the multipath interference can be estimated and further be subtracted from the received data. In practical, MEDLL needs more correlators to obtain better performance.

It can be noted from the previous sections that by exploiting the correlation characteristic of the C/A code, the correlation function is constructed for the iterative refine step to obtain better estimation. Hence, the correlation domain WRELAX algorithm has a comparable complexity with MEDLL, whereas the data domain algorithm directly use the peculiarity of the C/A code, which can avoid not only the calculation of the cross-correlation function of the received data and the reference one, but also the autocorrelation function of the reference signal. Hence, by assuming that the number of the iteration is the same, the data domain algorithm owns much less computation complexity. Besides, the two WRELAX algorithms obtain the delay estimation by using FFT, which has more accurate estimation performance compared with the cure fitting used in MEDLL.

Subsequently, the cost functions of the three algorithms are compared. Continue the analysis in the previous sections. If we define

$${\mathbf{c}}_{f} = \left[ {c_{f} \left( { - N/2} \right),c_{f} \left( { - N/2 + 1} \right),{ \ldots },c_{f} \left( {N/2 - 1} \right)} \right]^{T}$$
(47)

then

$${\mathbf{R}}_{fs} = {\mathbf{c}}_{f} {\mathbf{c}}_{f}^{H}$$
(48)

and

$${\mathbf{p}}_{fp} = \alpha_{p} {\mathbf{R}}_{fs} {\mathbf{a}}\left( {\omega_{p} } \right)$$
(49)

Therefore, by inserting (47)–(49) into the correlation domain cost function, the estimating of ω p in (34) can further be represented as

$$\begin{aligned} \hat{\omega }_{p} & = \arg \mathop {\hbox{max} }\limits_{{\omega_{p} }} \left| {{\mathbf{a}}^{H} (\omega_{p} ){\mathbf{R}}_{fs}^{ * } {\mathbf{p}}_{fp} } \right|^{2} \\ & = \arg \mathop {\hbox{max} }\limits_{{\omega_{p} }} \left| {{\mathbf{a}}^{H} (\omega_{p} )\left[ {{\mathbf{R}}_{fs}^{ * } {\mathbf{R}}_{fs} } \right]\left( {\alpha_{p} {\mathbf{a}}(\omega_{p} )} \right)} \right|^{2} \\ \end{aligned}$$
(50)

It can be noted that (50) can be considered as the convolution of \({\text{FFT}}\left( {\alpha_{p} {\mathbf{a}}(\omega_{p} )} \right)\) with \(\text{FFT} \left( {{\mathbf{R}}_{fs}^{ * } {\mathbf{R}}_{fs} } \right)\).

Meanwhile, the cost function of the data domain WRELAX algorithm can be further denoted as

$$\begin{aligned} \hat{\omega }_{p} = & \arg \mathop {\hbox{max} }\limits_{{\omega_{p} }} \left| {{\mathbf{a}}^{\text{H}} \left( {\omega_{p} } \right){\mathbf{C}}_{f}^{*} {\mathbf{Y}}_{p} } \right|^{2} \\ = & \arg \mathop {\hbox{max} }\limits_{{\omega_{p} }} \left| {{\mathbf{a}}^{\text{H}} \left( {\omega_{p} } \right){\mathbf{R}}_{fs} \left( {\alpha_{p} {\mathbf{a}}\left( {\omega_{p} } \right)} \right)} \right|^{2} \\ \end{aligned}$$
(51)

The above equation can be regarded as the convolution of \({\text{FFT}}\left( {\alpha_{p} {\mathbf{a}}(\omega_{p} )} \right)\) with \(\text{FFT} \left( {{\mathbf{R}}_{fs} } \right)\). In fact, as the data length N → ∞, \({\text{FFT}}\left[ {\alpha_{p} {\mathbf{a}}(\omega_{p} )} \right]\) becomes an impulse signal, convolving with \(\text{FFT} \left( {{\mathbf{R}}_{fs} } \right)\) will be the delayed replica of \(\text{FFT} \left( {{\mathbf{R}}_{fs} } \right)\), where the delay is the parameter to be estimated. Comparing \(\text{FFT} \left( {{\mathbf{R}}_{fs} } \right)\) with \(\text{FFT} \left( {{\mathbf{R}}_{fs}^{ * } {\mathbf{R}}_{fs} } \right)\), it can be noted that \(\text{FFT} \left( {{\mathbf{R}}_{fs} } \right)\) is narrower than \(\text{FFT} \left( {{\mathbf{R}}_{fs}^{ * } {\mathbf{R}}_{fs} } \right)\), as in Fig. 4. Hence, from this point of view, the data domain algorithm performs better than the correlation domain algorithm. The cost function of MEDLL is also given in Fig. 4, since MEDLL works just as the classic DLL in its every iteration, the cost function of which is much broader.

Fig. 4
figure 4

Comparison of the cost function

Full size image

Performance comparison

The performance of the proposed algorithms in the presence of multipath is given in this section by simulation experiments. The code delay estimation error is given as the relative delay changes. As explained in Kos et al. (2010), the maximum and minimum errors occur when the multipath signal is in-phase Δφ = 0° or out-of-phase Δφ = ±180° with the LOS signal. The curve of the maximum and minimum errors is regarded as the error envelopes, which is always utilized to evaluate the multipath mitigation performance. The sampling frequency used in all the experiments is 5.714 MHz.

Consider the situation that there is only one reflected multipath signal combined with the LOS signal, which usually occurs in practice. The noise and the receiver bandwidth are not considered in this experiment. The amplitude ratio of the LOS signal and the reflected multipath interference is α 2/α 1 = 0.5. The relative code delay Δτ = τ 2 − τ 1 is varied from 0 to 1.5 chips. The error is calculated at the maximum points when the multipath signal is at 0° in phase with respect to the LOS signal. The results are shown in Fig. 5.

Fig. 5
figure 5

Comparison of the error envelopes with DMR = 0.5

Full size image

In Fig. 5, DLL denotes the error envelope of the classical tracking loop, and narrow correlator denotes the error envelope of the narrow correlator with spacing d = 0.1 chip. Both the classical DLL and the narrow correlator were calculated by solving the DLL equations. The curve MEDLL, correlation domain, and data domain denote the code delay estimation error of MEDLL, proposed correlation domain algorithm and data domain algorithm, respectively. The results indicate that in the presence of multipath, the classical DLL results in a large tracking error. The tracking error is reduced greatly by the narrow correlator. However, its tracking error is nearly constant when the correlator space is less than 0.1 chip. The tracking error is greatly reduced by the proposed algorithms and MEDLL. The improved performance can be of great help in critical GPS applications, where the multipath errors of the conventional receivers might exceed the accuracy requirements. The results in the top panel are also magnified in the bottom panel to further illustrate the detail performance of the two proposed algorithms and MEDLL. It is clear that the proposed two algorithms have a more favorable performance than MEDLL. Furthermore, the proposed data domain algorithm is superior to the correlation domain algorithm, which is consistent with the conclusion above. In order to obtain a universal suitable conclusion, the simulation results in different direct-to-multipath ratio (DMR) are given in Fig. 6.

Fig. 6
figure 6

Comparison of the error envelopes in different DMRs: DMR = 0.1 (top left), DMR = 0.2 (top right), DMR = 0.5 (bottom left), and DMR = 0.7 (bottom right)

Full size image

As the GNSS LOS signal and multipath interference are all drowned in the noise in practice, we now verify the performance of the proposed WRELAX algorithms and MEDLL in a noise environment. Suppose there is only one reflected multipath combined with the LOS signal. The relative amplitude of the LOS signal and the reflected multipath interference is α 2/α 1 = 0.5. The relative code delay is Δτ = 0.18T c . The error is calculated when the multipath signal is at 0° in phase. The longitudinal axis stands for the root-mean-square estimation error (RMSE) obtained by Monte Carlo experiments. The additive Gauss white noise is added into the simulated data with signal-to-noise ratio (SNR) that changes from −25 to −15 dB (the corresponding carrier-to-noise-density ratio is 38–48 dB-Hz). The experiment result is given in Fig. 7.

Fig. 7
figure 7

Code delay estimation performance in noise environment with different SNRs

Full size image

From Fig. 7, we can see that the delay estimation performance of the two proposed WRELAX algorithms is better than MEDLL in the noise environment except that the correlation domain WRELAX has a bad estimation performance, while the SNR is below −23 dB. As is known, the SNR of GNSS signal is about −20 dB, so the performance loss below −23 dB can be ignored.

We now give the estimation performance in the noise environment with the relative delay changes. Suppose there is only one reflected multipath combined with the LOS signal. The relative amplitude of the LOS signal and the reflected multipath interference is α 2/α 1 = 0.5. The error is calculated when the multipath signal is in phase with the LOS signal. The longitudinal axis stands for the absolute estimation error as in Fig. 5; here, the estimation error is also obtained by Monte Carlo experiments. The additive Gauss white noise is added into the simulated data with signal-to-noise ratio (SNR) −25 dB. The experiment result is given in Fig. 8. From the figure, we can see that the delay estimation performance of the two proposed WRELAX algorithms is better than that of MEDLL as the relative delay changes.

Fig. 8
figure 8

Code delay estimation performance in noise environment with different relative delays

Full size image

Conclusion

Two WRELAX-based algorithms for multipath mitigation in GNSS are presented and assessed. WRELAX was first proposed for the time-delay estimation problem in radar system, which possesses low computation burden and high estimation accuracy. By applying WRELAX to the multipath mitigation problem in GNSS, the receiver tracking loop is replaced by an open-loop parameter estimation process. The correlation domain WRELAX algorithm obtains the parameters first by correlating the received data with the local reference data, and the data domain algorithm estimates the parameters directly using the received data. Both of the algorithms estimate the code delay by solving NLS equations, which can be further solved by WRELAX by using FFT operation. However, the data domain algorithm possesses even less computation burden as there is no need of the correlate operation. Compared with the state-of-art algorithms, the proposed two algorithms perform a better performance with lower computation burden.