Introduction

Multipath is difficult to reduce in satellite navigation applications. In case of large multipath reflections from buildings or the ground, the resulting carrier phase and pseudorange measurement errors might not be acceptable. Ground stations can be constructed at places where there are fewer reflections by objects. Therefore, the major problem is multipath reflection from the ground. Multipath can be reduced by signal receiving techniques and signal processing techniques. Signal receiving techniques reject multipath corrupted signals. Signal processing techniques use mitigation technologies such as narrow correlation, estimation based on the slope, and double-delta multiple correlators. However, these techniques are not effective for short delay multipath. Multipath reflected by the ground is short delay multipath, and it cannot be reduced by these signal processing multipath mitigation technologies. We adopt a receiving antenna array and reject multipath by beamforming and array signal processing.

A ground-planeless, three element vertical array with fixed beamforming has been reported to reject multipath interference better than a conventional, 0.5-m-diameter, ground plane antenna for precise differential GPS applications (Counselman 1999). The ground antenna of the Local area augmentation system (LAAS) in America is composed of the High-Zenith antenna (HZA) and the multipath limiting antenna (MLA) (Dickman et al. 2003). Fourteen or sixteen elements MLA with fixed beamforming can satisfy Category I accuracy requirements for the LAAS (Mohammad and Daniel 2006). Simulation results of phase delay and group delay after beamforming, placing nulls in various directions, indicate that the phase delay in the useful signal direction varies (Mohammad and Daniel 2006). The phase center variation (PCV) introduced by beamforming will cause extra carrier phase measurement errors. The phase delay and the group delay corrections of the MLA is complex. Therefore, research on beamforming with steady phase center is necessary.

When the angle of incidence is the Brewster angle, the ground reflected multipath is horizontally polarized. The reflections in one side of the Brewster angle are right circular polarized, and the reflections in the other side of the Brewster angle are left circular polarized (Sun 2011). Considering the polarization characteristics of the multipath reflected by the ground, the direction of the multipath, and the direction of the satellite signal, we mitigate multipath based on a vertical linear array which is composed of vertically polarized dipole antennas. Compared to right circular polarized (RCP) elements, the linear polarized elements can reduce multipath effectively in the polarization field, especially the vertical polarized elements can reject multipath reflected by the ground at the Brewster angle. The vertical linear array beamforming discussed places nulls in the multipath directions, points at the direction of the satellite signal, and the phase is not changed during the vector weighting method.

Antenna array receiving model

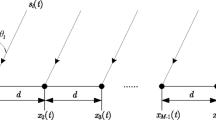
The high-performance multipath limiting antenna array is a vertical linear array composed of vertically polarized dipole antennas. The sensor spacing along the Z-axis is half the wavelength of the signal transmitted. The vertical linear array and the directions of arrival are shown in Fig. 1.

Fig. 1
figure 1

Vertical linear array and the directions of arrival

Full size image

The angle between the positive Z-axis and the direction of the incident signal is defined as DOA (direction of arrival). The DOA of the satellite signal is θ, and the DOA of the multipath reflected by the ground is 180°-θ.

If the ground has some inclined ramp, there might be more than one multipath signal. The multipath limiting antenna array, including the algorithm we discuss, allow more than one multipath with different amplitudes and delays, as well as phase shifts for multipath signals. The model of the receiving environment considered here includes the satellite signal and two multipath signals reflected by the ground,

$$ X(t) = S_{s} (t) + S_{m} (t) + N(t) $$
(1)

where

$$ N(t) = \left[ {n_{0} (t),n_{1} (t), \ldots ,n_{N - 1} (t)} \right]^{\,T} $$
(2)
$$ S_{s} (t) = e^{{j\frac{2\pi }{\lambda }r_{z} k_{s} }} e^{j2\pi ft} $$
(3)
$$ S_{m} (t) = (e^{{j\frac{2\pi }{\lambda }r_{z} k_{m1} }} + e^{{j\frac{2\pi }{\lambda }r_{z} k_{m2} }} )e^{j2\pi ft} $$
(4)

and

$$ k_{s} = - (a_{x} \sin \theta_{s} \cos \phi_{s} + a_{y} \sin \theta_{s} \sin \phi_{s} + a_{z} \cos \theta_{s} ) $$
(5)
$$ k_{{m_{1} }} = - (a_{x} \sin \theta_{{m_{1} }} \cos \phi_{{m_{1} }} + a_{y} \sin \theta_{{m_{1} }} \sin \phi_{{m_{1} }} + a_{z} \cos \theta_{{m_{1} }} ) $$
(6)
$$ k_{{m_{2} }} = - (a_{x} \sin \theta_{{m_{2} }} \cos \phi_{{m_{2} }} + a_{y} \sin \theta_{{m_{2} }} \sin \phi_{{m_{2} }} + a_{z} \cos \theta_{{m_{2} }} ) $$
(7)
$$ r_{z} = nda_{z} $$
(8)

with \( n = (0,1,2, \ldots ,N - 1) \), and d denoting the sensor spacing. The steering vector of the satellite signal is k s, where a x , a y , and a z are unit vectors along the coordinate axis. The steering vectors of the multipath signals reflected by the ground are k m1 and k m2. The wavelength of the signal transmitted is λ. The symbol N(t) denotes the Gaussian white noise added to the antenna elements.

Beam forming algorithm

The DOA estimation of the coherent signals adopts the forward–backward spatial smoothing technique and the MUSIC (multiple signal classification) algorithm. Based on the estimated DOA, the improved minimum variance distortionless response (MVDR) beamforming algorithm works. Details are given below.

DOA estimation of the coherent signals

The covariance matrix of the array receiving data can be estimated by (1) as

$$ R = E\left[ {XX^{H} } \right] = \frac{1}{K}\sum\limits_{k = 1}^{K} {X(t_{k} } )X^{H} (t_{k} ) $$
(9)

where E[·] denotes the mathematical expectation, (·)H denotes the complex conjugate transpose, and \( k = 1,2 \ldots ,K \), with K denoting the number of sampling.

Divide the vertical linear array in Fig. 1 into H subarrays. Each subarray has L elements. So H = N−L + 1, where N is the total number of the array elements. Adopting the forward–backward spatial smoothing technique (Williams et al. 1988; Zhang 2002), the spatial smoothing covariance matrix is

$$ R_{FB} = \frac{1}{H}\sum\limits_{h = 1}^{H} {\frac{1}{2}(R_{h} + JR_{h}^{*} J)} $$
(10)

where (·)* denotes the complex conjugate, R h is the covariance matrix of the h-th (h = 1,2,…,H) subarray with L × L dimensions, and J is the permutation matrix with L × L dimensions,

$$ J = \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 & 1 \\ 0 & 0 & \cdots & 1 & 0 \\ \vdots & {} & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & {} & \vdots \\ 0 & 1 & \cdots & 0 & 0 \\ 1 & 0 & \cdots & 0 & 0 \\ \end{array} } \right] $$
(11)

The MUSIC algorithm eigenvalue decomposition of (10) is

$$ \tilde{R}_{FB} = \sum\limits_{i = 1}^{L} {\lambda_{i} } v_{i} v_{i}^{H} $$
(12)

where λ 1  ≥ λ 2  ≥ … ≥ λ L  ≥ 0. The noise subspace is

$$ \prod_{N} = \sum\limits_{i = 4}^{L} {v_{i} } v_{i}^{H} $$
(13)

where v i are the eigenvectors corresponding to the noise eigenvalues.

The DOA estimation of the MUSIC algorithm (Jin et al. 2006; Miron et al. 2005; Schmidt 1986) spatial spectrum is

$$ MUSIC(\theta ) = \frac{1}{{\left\| {\prod_{N} S(\theta )} \right\|}} $$
(14)

where

$$ S(\theta ) = e^{{ - j\frac{2\pi }{\lambda }nda_{z} [a_{x} \sin \theta \cos \phi ,a_{y} \sin \theta \sin \phi ,a_{z} \cos \theta ]^{T} }} $$
(15)

with \( n = \left( {0,1, \ldots ,L} \right) \), \( \theta = \left( {0,x,2x,3x, \ldots ,180} \right) \), S(θ) scans the space by a certain angle (x degrees) interval.

In the computer simulation, the total elements of the vertical linear array is ten, thus N = 10. The number of the subarrays is three, thus H = 3. Each subarray contains eight elements, thus L = 8. The first subarray contains elements 0…7 of the vertical linear array in Fig. 1, the second subarray contains elements 1…8 of the vertical linear array, and the third subarray contains elements 2…9 of the vertical linear array. Assume the antenna elements are ideal point sources. The noise added to the antenna elements and the channels are Gaussian white noise. The C/No of the satellite signal is about 45 dB-Hz, and the integration time is 1 ms in the receiver. The signal-to-noise ratio on each antenna array element is 15 dB. The DOA of the satellite signal is θ s  = 30°, the DOA of its multipath reflected by the ground is θ m1  = 150°, and the DOA of another multipath is assumed to be θ m2  = 140°. The simulation parameters discussed here apply to all cases in this study.

The DOA estimation result of the three coherent signals is shown in Fig. 2. The X-axis is the elevation angle and the Y-axis is the MUSIC spatial spectrum of (14). The three peaks indicate three estimated direction of arrival of coherent signals. The estimated values are θ se  = 30°, θ m1e  = 150°, and θ m2e  = 140°. The estimated elevation angle that the antenna array null is steered to has almost no error. The estimation accuracy of the MUSIC algorithm is related to the number of array elements. As the array element number increases, the estimation accuracy improves.

Fig. 2
figure 2

DOA estimation result of coherent signals

Full size image

Improved MVDR beamforming algorithm

In the MVDR algorithm, one minimizes the output power of the antenna array conditionally to insure that the antenna array gain toward the desired signal is kept constant, in other words, the antenna array insures a distortionless response in the direction of the desired signal. This is accomplished by

$$ \mathop {\hbox{min} }\limits_{w} \left\{ {w^{H} Rw} \right\} $$
(16)

subject to the condition \( w^{H} v_{s} = 1 \). The symbol R denotes the covariance matrix of the array receiving data, and v s is the steering vector of the useful signal. Thus, the MVDR weighting vector becomes (Haykin 1996; Puska et al. 2007)

$$ w = \frac{{R^{ - 1} v_{s} }}{{v_{s}^{H} R^{ - 1} v_{s} }} $$
(17)

Based on the estimated DOA, generate the array steering vectors of the multipath directions using (4), (6), (7), and (8). Then, construct the null-steering vector signal as

$$ X_{m} (t) = e^{{j\frac{2\pi }{\lambda }r_{z} k_{m1} }} e^{{j2\pi f_{1} t}} + e^{{j\frac{2\pi }{\lambda }r_{z} k_{m2} }} e^{{j2\pi f_{2} t}} + N(t) $$
(18)

The covariance matrix R MM of the constructed null-steering vector signal can be estimated from (18) and (9), and the inverse of the matrix R MM can be computed. Substitute it in (17), and then, the weighting vector is obtained.

A standard tool for analyzing the performance of a beamforming algorithm is the response for a given weighting vector w as a function of angle θ, known as the beam response. This response is computed by applying the beamforming weighting vector w to a set of array steering vectors in the space,

$$ B(\theta ) = w^{H} S(\theta ) $$
(19)

where S(θ) is given by (15), with \( \theta = \left( {0,y,2y,3y, \ldots ,180} \right) \). S(θ) scans the space by a certain angle (y degrees) interval.

The gain radiation pattern of the beam response of the improved MVDR beamforming algorithm is shown in Fig. 3 in three dimension. Antenna array beamforming places nulls in the multipath direction and points at the satellite signal direction. The antenna array gain toward elevation 30° is six times that of the arrived signal power.

Fig. 3
figure 3

Gain radiation pattern of the improved MVDR

Full size image

The gain radiation pattern in dB of the beam response is shown in Fig. 4 in two dimension. The X-axis is the elevation angle and the Y-axis is the antenna array beamforming gain in dB. The antenna array nulls are steered to multipath. The antenna array gain toward elevation 150° is −85 dB, and the antenna array gain toward elevation 140° is −84 dB.

Fig. 4
figure 4

Gain radiation pattern in dB of the improved MVDR

Full size image

The phase radiation pattern of the beam response of the improved MVDR beamforming algorithm is shown in Fig. 5. The X-axis is the elevation angle and the Y-axis is the phase center variation of antenna array beamforming. The phase center of the beam response in the direction of elevation 30° is zero degrees.

Fig. 5
figure 5

Phase radiation pattern of the improved MVDR

Full size image

The gain radiation pattern of the improved MVDR algorithm points at the direction of the satellite signal θ s  = 30°, places nulls in the direction of multipath reflection by the ground θ m1 = 150°, and the direction of another multipath θ m2 = 140°. And the phase center does not change in the direction of the satellite signal θ s  = 30°.

Comparison of beamforming algorithms

We compare the MVDR and improved MVDR algorithms with the DFB (deterministic beamforming) and PI (power inversion) algorithms. Typically, the DBF method is used to augment the satellite signal, and PI is used to limit large power interference. The DBF obtains the weighting vector from the steering vector of the useful signal. Thus, the DBF weighting vector becomes

$$ w_{DBF} = v_{s}^{{}} $$
(20)

where v s is the steering vector of the useful signal. In the PI algorithm, select one channel as the reference signal and keep it while minimizing the output power of the antenna array. This is accomplished by

$$ \mathop {\hbox{min} }\limits_{w} \left\{ {w^{H} Rw} \right\} $$
(21)

subject to the condition \( w^{H} b = 1 \). The symbol R denotes the covariance matrix of the array receiving data, and vector b is the restrict matrix, \( b = [1,0, \ldots ,0]^{T} \). Thus, the PI weighting vector becomes (Compton 1979)

$$ w_{PI} = \frac{{R^{ - 1} b}}{{b_{{}}^{H} R^{ - 1} b}} $$
(22)

Figure 6 shows a comparison of the gain radiation patterns for the improved MVDR algorithm, the MVDR algorithm, the DBF method, and the PI beamforming algorithm. The MVDR and the PI beamforming algorithms place nulls in the direction of multipath interferences, but also place a null in the direction of the useful signal. The DBF beamforming points at the direction of the useful signal, but cannot place nulls in the direction of the multipath. The improved MVDR beamforming algorithm points at the direction of the useful signal and places nulls in the directions of the multipath.

Fig. 6
figure 6

Comparison of gain radiation patterns

Full size image

The comparison of the phase radiation patterns is given in Fig. 7. The phase is changed during the vector weighting method in the PI beamforming algorithm, and the phase changing in the direction of the useful signal varies when the weighting vector is different. In the improved MVDR beamforming algorithm, the phase is not changed in the direction of the useful signal.

Fig. 7
figure 7

Comparison of phase radiation patterns

Full size image

The improved MVDR beamforming algorithm has advantages in multipath mitigation due to placing nulls in the direction of multipath interferences, and obtaining high gain in the direction of the satellite signal. In addition, the phase in the satellite signal direction is not changed during the vector weighting method.

Conclusions

We described the generation and the polarization characteristics of multipath interference and then designed the antenna array mode accordingly. Finally, the multipath was greatly reduced in the array signal processing. The multipath limiting antenna array presented rejects the multipath interference in the space field severely, solves the problem of the short delay multipath mitigation, and can provide support for the high-performance satellite navigation system such as LAAS.