Introduction

A global positioning system (GPS) receiver needs to acquire and track signals from satellites in order to calculate trustworthy positioning solutions. The two main factors that affect the performance of acquisition and tracking are the signal strength and dynamics of the receiver platform. A receiver requires the received signal from satellites to be above a certain power level which is usually referred to as signal-to-noise ratio (SNR) or carrier-to-noise spectral density ratio (C/N 0). However, it is not always possible to ensure high C/N 0 values such as the applications in urban unmanned aerial vehicles (UAVs), aeronautic/astronautic aircrafts and precision-guided weapons. Under these conditions, due to the operating environments induced interferences including line-of-sight (LOS) obstruction, multipath fading, and unintentional and intentional jamming, the GPS signal can be easily attenuated below the normal acquisition and tracking thresholds (Kaplan and Hegarty 2006). This makes it impractical for a normal receiver to derive trustworthy positioning solutions.

The research on new techniques to ensure a receiver works in lower C/N 0 [also known as high-sensitivity (HS) receiver] has attracted growing attention (Petovello et al. 2008; Ziedan and Garrion 2004; Gao and Lachapelle 2008; van Grass et al. 2009). Until now, the feasible HS-tracking methods for weak signals mainly include vector tracking, Strapdown Inertial Navigation System (SINS)-aided tracking and fast Fourier transform (FFT)-based frequency-domain tracking. Vector tracking is the most common unaided method for weak signal tracking. This method performs the data fusion of all tracking channels with an extended Kalman filter (Psiaki and Jung 2002; Ziedan and Garrion 2004; Lashley et al. 2009; Salem et al. 2012). It allows a receiver to track weaker signals by taking advantage of the presence of relatively stronger ones. The primary drawback is that processed data from all satellites are intimately correlated. Any error in one channel could potentially corrupt other channels. SINS-aided GPS tracking (Alban et al. 2003; Razavi et al. 2008; Gao and Lachapelle 2008; Yu et al. 2010) utilizes the SINS-derived Doppler as aiding information to reduce the dynamics required for a receiver tracking loop, and subsequently reduce the noise level by narrowing the loop filter bandwidth. The performance of SINS aiding depends on the grade of inertial sensors and the aiding modes (closed loop/open loop). A closed aiding loop is normally used where SINS errors need to be continuously corrected by GPS. With strong GPS signals, this works well. However, in weak signal conditions, the receiver performance is degraded. The closed aiding loop may diverge resulting in loss of lock (Wang and Li 2012). Therefore, the SINS aiding normally operates in open-loop mode where SINS is in a free run when GPS performance is poor. Due to the nature of error growing over time in SINS, the open aiding loop can work only for short periods of time. The length of the period depends on the grade of inertial sensors. The FFT-based frequency-domain tracking (Yang 2003; Schamus et al. 2002; van Grass et al. 2009; Ba et al. 2009; Borio et al. 2008) is a new HS tracking method developed to perform an accurate frequency parameter estimate by processing the spectral peak line and adjacent lines. Compared with the conventional discriminator-based tracking, the FFT operation provides a more desirable way to obtain linear measurement and lower tracking SNR threshold (Palmer 1974). Therefore, in this HS carrier-tracking loop study, the FFT-based tracking method is selected to obtain a high tracking sensitivity for weak GPS signals.

The FFT-based tracking method needs long GPS data for FFT operation in order to enhance the spectral resolution. However, this type of approach increases the storage and calculation account, resulting in a slow response to receiver platform dynamics. In addition, frequency changes corresponding to receiver dynamics make the spectral peak diffuse to lots of spectral lines and sharply attenuate the SNR gain of FFT operation. Therefore, the existing FFT-based tracking methods are mainly applicable to the tracking of weak signals for static or low-dynamic applications (Ba et al. 2009; Borio et al. 2008). The FFT-based tracking accuracy and sensitivity of carrier frequency are degraded in high-dynamic conditions.

As above, the SINS-aided tracking loop works well in high-dynamic conditions with strong GPS signals. The FFT-based tracking has good performance in weak signal and static conditions. However, none of them can achieve good performance in both weak signal and high-dynamic conditions. We propose a novel HS carrier-tracking loop suitable for both weak signal and high-dynamic applications by integrating the SINS aiding and an improved FFT-based tracking. A dynamic-division FFT (DDFFT) is proposed to respond to the dynamics of the receiver platform while maintaining the capability of tracking weak signals.

Frequency-domain GPS carrier tracking

A system level functional block diagram of a generic GPS receiver is depicted in Fig. 1. For navigation purpose, a GPS receiver needs to fulfill several tasks to derive the raw measurements from the GPS radio frequency (RF) signals transmitted by the satellites. First, a well-designed antenna is necessary to receive the RF signals which are down-converted and digitized into intermediate frequency (IF) discrete signals by the front-end. Then, the IF signals are fed into the baseband processing section, which mainly conducts operations of acquisition, tracking and data demodulation. Acquisition is used to detect a signal and derive its initial code shift and Doppler estimates. The purposes of tracking and data demodulation are to continuously obtain the navigation message, the code phase measurements, carrier phase measurements and other relevant parameters such as C/N 0 and Doppler in variable environments. Finally, the navigation solution is computed.

Fig. 1
figure 1

Generic GPS receiver functional block diagram

Full size image

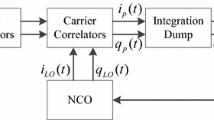
Since the particular vulnerability to noise, oscillator instability, dynamic stress etc., the carrier tracking is the weak link in a GPS receiver which needs an elaborate design. Figure 2 shows a typical Costas loop used for carrier tracking. The two sets of multipliers wipe off the carrier and code of the input IF signal. After that, the integration and dump (I&D) operation produces in-phase (I) and quadraphase (Q) measurements. A discriminator is therefore used to detect the frequency or phase error between the input and the local carrier signal. The output of the discriminator is then filtered and used as a feedback to the carrier numerically controlled oscillator (NCO), which adjusts the frequency of the local signal. The detection accuracy of the discriminator and the quality of NCO (Yin et al. 2013) are the dominant factors of the carrier-tracking performance. In weak signal conditions, the tracking loop may not be able to feedback correct information to the NCO, resulting in big frequency errors or may not be able to respond to changes in carrier frequency (Yu et al. 2006). In this case, there is no trustworthy solution from the receiver and the receiver needs a reacquisition process to capture the GPS signal.

Fig. 2
figure 2

Configuration of the Costas loop

Full size image

In order to extend the applications of GPS to a certain level of weak signal, a frequency-domain method is normally used. Figure 3 presents a generic configuration of the carrier loop based on the frequency-domain tracking method. Compared with the Costas loop, it utilizes FFT operation to detect the frequency error. With the FFT coherent integration processing, this approach can significantly improve the SNR. As a result, the FFT-based carrier loop can obtain an accurate detection of the frequency error and increase the tracking sensitivity.

Fig. 3
figure 3

Configuration of the frequency-domain carrier-tracking loop

Full size image

The IF signal from one satellite can be expressed as,

$$s_{\text{IF}} (n) = a_{c} D(n)C[(1 + {{f_{d} (n)} \mathord{\left/ {\vphantom {{f_{d} (n)} {f_{L} }}} \right. \kern-0pt} {f_{L} }})nt_{\text{s}} - \tau ]\cos \left\{ {2\pi [f_{\text{IF}} + f_{d} (n)]} \right.nt_{s} + \left. {\varphi_{0} } \right\} + n_{w} (n)$$
(1)

where a c is the signal amplitude, D is the navigation data, C[·] is the C/A code of a satellite, τ is the code propagation delay and t s is the sampling period. The symbols f L and f IF are the carrier transmitting and intermediate frequency, respectively, f d is the carrier Doppler frequency shift, φ 0 is the initial carrier phase and n w is the Gaussian noise.

As shown in Fig. 3, a navigation data wipeoff process is implemented after the I&D operation to eliminate the bit transition for the FFT operation (Ba et al. 2009). The resulting signal can be written as,

$$\begin{aligned} s_{c} (k) & = D_{L} (k) \otimes \left[ {I(k) + jQ(k)} \right] = A_{c} \cdot \{ \cos [\delta \varphi (k)] + j \cdot \sin [\delta \varphi (k)]\} + n_{k} \\ & = A_{c} \cdot \exp \left\{ {j \cdot \left[ {\delta \varphi {}_{0}(k) + 2\pi \delta f_{d}^{0} (k)T + \pi \dot{f}_{d} (k)T^{2} } \right]} \right\} + n_{k} \\ \end{aligned}$$
(2)

where \(A_{c} = a_{c} \cdot ({T \mathord{\left/ {\vphantom {T {2t_{\text{s}} }}} \right. \kern-0pt} {2t_{\text{s}} }})R[\delta \tau ]{ \sin }c\left[ {\delta f_{d} (k)\pi T} \right]\) is the signal amplitude after IF stage. The symbol T denotes the pre-detection integration time, k denotes the index of the pre-detection integration interval, D L is the locally stored navigation data, δφ is the mean value of the carrier phase error over the integration interval, δf 0 d is the initial carrier frequency error, \(\dot{f}_{d}\) is the change rate of the Doppler frequency (namely the carrier frequency dynamic), R c [·] is the autocorrelation function of C/A code and δτ is the code phase error. The symbol n k denotes the Gaussian noise term.

Figure 4 shows the distribution of the FFT spectrum with different carrier frequency dynamics \(\dot{f}_{d}\). It can be observed that the spectral peak gradually diffuses with the increase of \(\dot{f}_{d}\). Moreover, the increase of the FFT size N worsens this spectrum diffusion, which results in an attenuated SNR gain and an uncertain estimate of the frequency error δf d . For static applications, the Doppler in received signal is caused by the motion of the satellite only. The corresponding carrier frequency dynamic \(\dot{f}_{d}\) is relatively small over short time periods. Therefore, the FFT-based tracking has a good performance (close to the red line). It can also be seen that the FFT-based method has distorted peaks or no peak at all for high-dynamic applications (relatively big \(\dot{f}_{d}\)).

Fig. 4
figure 4

Spectrum distributions with different Doppler dynamics and different FFT sizes

Full size image

Dynamic-division FFT algorithm

In order to deal with the issues raised in last section, a dynamic-division FFT algorithm is proposed. This tracking method is based on the employment of SINS aiding. Figure 5 describes the block diagram of the DDFFT-based carrier-tracking method.

Fig. 5
figure 5

Block diagram of the carrier-tracking method based on dynamic-division FFT

Full size image

On the basis of SINS aiding, the signal in (2) can be rewritten as,

$$s_{a} (k) = A_{\text{aid}} \cdot \exp \left\{ {j \cdot \left[ {\delta \varphi_{0} (k) + 2\pi \delta f_{a}^{0} (k) \cdot T + \pi \delta \dot{f}_{a} (k) \cdot T^{2} } \right]} \right\} + n_{k}$$
(3)

where \(A_{\text{aid}} = a_{c} \cdot ({T \mathord{\left/ {\vphantom {T {2t_{\text{s}} }}} \right. \kern-0pt} {2t_{\text{s}} }})R[\delta \tau ]{ \sin }c\left[ {\delta f_{a} (k)\pi T} \right]\) is the signal amplitude. Here, δf a is the SINS aiding frequency error, δf 0 a is the initial aiding frequency error and \(\delta \dot{f}_{a}\) denotes the dynamic of the aiding frequency error.

It can be seen that through the SINS aiding, the DDFFT algorithm only needs to deal with the residual dynamic of the aiding frequency error, namely \(\delta \dot{f}_{a}\).

DDFFT implementation steps

The DDFFT algorithm is designed to estimate the error of SINS aiding frequency. Figure 6 shows the scheme of the DDFFT algorithm, and it is implemented by the following steps.

Fig. 6
figure 6

Scheme of the dynamic-division FFT algorithm

Full size image

  • Step 1 Frequency dynamic-division.

The change rate of the SINS aiding frequency error is assumed within the range from \(\delta \dot{f}_{a}^{\hbox{min} }\) to \(\delta \dot{f}_{a}^{\hbox{max} }\), and \(\delta \dot{f}_{a}^{\hbox{min} } = - \delta \dot{f}_{a}^{\hbox{max} }\). This range is equally divided into M steps. Each step can be expressed as,

$$\delta \dot{f}_{\text{step}} = {{\left( {\delta \dot{f}_{a}^{\hbox{max} } - \delta \dot{f}_{a}^{\hbox{min} } } \right)} \mathord{\left/ {\vphantom {{\left( {\delta \dot{f}_{a}^{\hbox{max} } - \delta \dot{f}_{a}^{\hbox{min} } } \right)} {(M - 1)}}} \right. \kern-0pt} {(M - 1)}}$$
(4)

  • Step 2 Carrier demodulation based on dynamic-division.

With the dynamic-division value \(\delta \dot{f}_{m}\), the signal s a can therefore be divided into M parts as expressed below,

$$s_{a}^{m} (k) = A_{\text{aid}} \cdot \exp \left\{ {j \cdot \left\{ {\delta \varphi_{0} (k) + 2\pi \delta f_{a}^{0} (k) \cdot T + \pi [\delta \dot{f}_{a} (k) - \delta \dot{f}_{m} ] \cdot T^{2} } \right\}} \right\} + n_{k}$$
(5)

where \(\delta \dot{f}_{m} = \delta \dot{f}_{a}^{\hbox{min} } + m \cdot \delta \dot{f}_{\text{step}}\) denotes the dynamic-division value of the m th part, and m = 0, 1, …, M − 1 is the index.

  • Step 3 FFT operation.

The FFT operation applied to the signal s m a results,

$$F(m,l) = \sum\limits_{k = 0}^{N - 1} {s_{a}^{m} (k) \cdot \exp \left( { - j \cdot \frac{2\pi k}{N} \cdot l} \right)}$$
(6)

where l = 0, 1, …, N − 1 denotes the frequency points of FFT operation, and k = 0, 1, …, N − 1 denotes the samples of signal s m a .

  • Step 4 Frequency parameter detection.

Equation (6) shows that each frequency dynamic value \(\delta \dot{f}_{m}\) yields N FFT frequency samples. Therefore, the M different frequency dynamic steps form a two-dimensional matrix \({\mathbf{F}}(m,l)\) of M × N. The peak detection is implemented to find the maximum absolute value of all elements in the matrix \({\mathbf{F}}(m,l)\). That is,

$$\begin{aligned} \left[ {m_{p} ,l_{p} } \right] & = \arg \mathop {\hbox{max} }\limits_{M,N} \left| {{\mathbf{F}}(m,l)} \right| \\ {\mathbf{F}}(m,l) & = \left[ {\begin{array}{*{20}c} {F(0,0)} & {F(0,1)} & \cdots & {F(0,N - 1)} \\ {F(1,0)} & {F(1,1)} & \cdots & {F(1,N - 1)} \\ \vdots & \vdots & \ddots & \vdots \\ {F(M - 1,0)} & {F(M - 1,1)} & \cdots & {F(M - 1,N - 1)} \\ \end{array} } \right] \\ \end{aligned}$$
(7)

Then, the change rate \(\delta \dot{f}_{a}\) of SINS aiding frequency error and the initial aiding frequency error δf 0 a can be calculated by the following formula,

$$\begin{aligned} \delta \hat{\dot{f}}_{a} & = [m_{p} - {{(M - 1)} \mathord{\left/ {\vphantom {{(M - 1)} 2}} \right. \kern-0pt} 2}] \cdot \delta \dot{f}_{\text{step}} \\ \delta \hat{f}_{a}^{0} & = {{l_{p} \cdot 1} \mathord{\left/ {\vphantom {{l_{p} \cdot 1} {(N \cdot T)\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} } & {l_{p} < {N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0pt} 2}} \\ \end{array} }}} \right. \kern-0pt} {(N \cdot T)\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} } & {l_{p} < {N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0pt} 2}} \\ \end{array} }} \\ \delta \hat{f}_{a}^{0} & = ({{l_{p} - M) \cdot 1} \mathord{\left/ {\vphantom {{l_{p} - M) \cdot 1} {(N \cdot T)\begin{array}{*{20}c} {} & {l_{p} \ge {N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0pt} 2}} \\ \end{array} }}} \right. \kern-0pt} {(N \cdot T)\begin{array}{*{20}c} {} & {l_{p} \ge {N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0pt} 2}} \\ \end{array} }} \\ \end{aligned}$$
(8)

where 1/(N · T) is the spectral resolution of N-point FFT operation, and the value of \(\delta \hat{f}_{a}^{0}\) is in the range [−1/(2T), 1/(2T)].

  • Step 5 Reconstruction of SINS aiding frequency error.

The SINS aiding frequency error δf a can therefore be reconstructed in the interval of (0, NT) (i.e., the FFT operation period) as,

$$\delta \hat{f}_{a} (k) = \delta \hat{f}_{a}^{0} + \delta \hat{\dot{f}}_{a} \cdot (k + {1 \mathord{\left/ {\vphantom {1 {2) \cdot }}} \right. \kern-0pt} {2) \cdot }}T\quad k \in \left[ {0, N - 1} \right]$$
(9)

where \(\delta \hat{f}_{a}^{0}\) and \(\delta \hat{\dot{f}}_{a}\) represent the initial aiding frequency error and the error change rate estimations, respectively.

DDFFT SNR gain

For weak GPS signal tracking, the SNR gain is an important factor. For the proposed DDFFT algorithm, the SNR gain is related to the C/A code de-spreading process and the FFT operation. It can be expressed as,

$${\text{SNR}}_{\text{out}} = {\text{SNR}}_{\text{in}} + G_{\text{CA}} + I_{\text{SNR}}$$
(10)

where SNRout denotes the SNR corresponding to the peak value of |F(m, l)|. The symbol SNRin denotes the SNR depending on the input C/N 0, G CA denotes the gain related to the C/A code dispreading process and I SNR denotes the gain related to the DDFFT operation.

The process gain G CA depends on the spread GPS signal bandwidth and the integration duration. Considering that the SINS aiding used is at a 100 Hz update rate, the integration duration is set to be 10 ms (i.e., T = 10 ms). Then, the process gain G CA can be expressed as,

$$G_{\text{CA}} = 10 \times \log_{10} \left( {{{{\text{BW}}_{{{{\text{C}} \mathord{\left/ {\vphantom {{\text{C}} {\text{A}}}} \right. \kern-0pt} {\text{A}}}}} } \mathord{\left/ {\vphantom {{{\text{BW}}_{{{{\text{C}} \mathord{\left/ {\vphantom {{\text{C}} {\text{A}}}} \right. \kern-0pt} {\text{A}}}}} } {{\text{BW}}_{\text{I,Q}} }}} \right. \kern-0pt} {{\text{BW}}_{\text{I,Q}} }}} \right) = 10 \times \log_{10} [{{2.046\;{\text{MHz}}} \mathord{\left/ {\vphantom {{2.046\;{\text{MHz}}} {({1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T})}}} \right. \kern-0pt} {({1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T})}}] = 43.1\;{\text{dB}}$$
(11)

The determination of the gain I SNR is not straightforward. The selection of coherent integration time must take into account the carrier frequency error. For the FFT-based tracking loop, the coherent integration time T I depends on the FFT size N and the pre-detection integration time T (T I  = N × T). For a given T (10 ms), if the residual frequency error caused by the uncompensated dynamic is not null (\(\Delta \dot{f}_{m} = \delta \dot{f}_{a} - \delta \dot{f}_{m} \ne 0\)), an important step needed is to analyze the optimal selection of the two parameters N and \(\delta \dot{f}_{\text{step}}\).

Assuming the frequency estimate of signal s m a corresponding to the FFT, spectral peak is \(\delta \hat{f}_{a}\). With a frequency shift operation on signal s m a by \(\delta \hat{f}_{a}\), the resulting signal y m can be expressed as,

$$\begin{aligned} y_{m} (k) & = s_{a}^{m} (k) \cdot \exp \left( { - j \cdot 2\pi \delta \hat{f}_{a} kT} \right) \\ & = A_{aid} \exp \left\{ {j \cdot \left[ {\delta \varphi_{0} + 2\pi (\delta f_{a}^{0} - \delta \hat{f}_{a}^{0} ) \cdot kT + \pi\Delta \dot{f}_{m} \cdot (kT)^{2} } \right]} \right\} + n_{k} \\ \end{aligned}$$
(12)

where \(\Delta \dot{f}_{m}\) is the uncompensated frequency dynamic, and n k denotes the Gaussian noise with a variance σ 2 m .

The initial phase error and the picket fence effect of FFT only introduce biases. They have little impact on the dynamics. Therefore, the result of an N-point coherent integration on the signal y m can be expressed below by assuming δφ 0 = 0 and \(\delta f_{a}^{0} = \delta \hat{f}_{a}^{0}\),

$$F_{s} = \sum\limits_{k = 0}^{N - 1} {y_{m} (k)} = A_{\text{aid}} \sum\limits_{k = 0}^{N - 1} {\exp [j \cdot \pi \cdot \Delta \dot{f}_{m} \cdot (kT)^{2} ]} + n^{{\prime }}$$
(13)

where n′ still denotes the Gaussian noise; however, the variance becomes Nσ 2 m . According to the signal F s , the SNR gain I SNR can then be written as,

$$I_{\text{SNR}} = 20\log_{10} \left| {\sum\limits_{k = 0}^{N - 1} {\exp [j \cdot \pi \cdot\Delta \dot{f}_{m} \cdot (kT)^{2} ]} } \right| - 10\log_{10} N$$
(14)

where the 10 log10 N term denotes the noise power increase caused by the N-point coherent integration.

The variation trends of I SNR are shown in Fig. 7 with different dynamic-division steps and different FFT sizes. It can be seen in the figure the I SNR does not grow linearly with the increase of FFT size when the residual frequency dynamic \(\Delta \dot{f}_{m}\) is nonzero (\(\Delta \dot{f}_{m}^{\hbox{max} } = {{\delta \dot{f}_{\text{step}} } \mathord{\left/ {\vphantom {{\delta \dot{f}_{\text{step}} } 2}} \right. \kern-0pt} 2}\)). The spectral resolution increases with the FFT size N; however, FFT SNR gain decreases, vice versa. Therefore, there is a trade-off in the selection of the FFT size N.

Fig. 7
figure 7

DDFFT SNR gain depending on the FFT size with different dynamic-division steps

Full size image

Table 1 shows the statistics of the values of I SNR calculated by simulated signals (the simulation parameters are listed in section “Dynamic test results and analysis”). For the low-grade inertial measurement unit (IMU), a 256-points FFT operation with a 0.2 Hz/s dynamic-division step is selected empirically taking into account the dynamic detection range of the error in SINS aiding and the spectrum resolution. It can be seen from Table 1 that the selected dynamic-division FFT operation can increase the SNR by 22.24 dB, which is only 1.73 dB lower than the value in static conditions.

Table 1 SNR gain (dB) for different dynamic-division steps and FFT sizes
Full size table

Probability of detection

The probability of detection is one of the most important factors to assess the performance of the proposed DDFFT. When the maximum search strategy is employed, a right detection is obtained when F(m t , l t ) assumes the maximum value of the matrix \({\mathbf{F}}(m,l)\) and it passes the threshold V th. Then, the probability of detection P D can be written as,

$$P_{D} (V_{\text{th}} ) = P\left( {F(m_{t} ,l_{t} ) = \mathop {\hbox{max} }\limits_{M,N} [{\mathbf{F}}(m,l)],F(m_{t} ,l_{t} ) \ge V_{\text{th}} } \right)$$
(15)

where F(m t , l t ) denotes the value of the cell corresponding to the true frequency parameters. By using the theorem of the total probability in the case of continuous random variables, P D can be expressed as,

$$\begin{aligned} P_{D} (V_{\text{th}} ) & = \int\limits_{{V_{\text{th}} }}^{ + \infty } {\prod\limits_{m = 0}^{M - 1} {\prod\limits_{l = 0}^{N - 1} {P\left( {\left. {F(m_{t} ,l_{t} ) \ge F(m,l)} \right|F(m_{t} ,l_{t} ) = x} \right)} } \cdot f_{s} (x){\text{d}}x} \\ & = \int\limits_{{V_{\text{th}} }}^{ + \infty } {[1 - P_{\text{fa}} (x)]^{M \cdot N - 1} \cdot f_{s} (x){\text{d}}x} \\ \end{aligned}$$
(16)

where P fa is the allowed single trial probability of false alarm and f s (x) is the probability density function of the absolute value of F(m t , l t ).

As the signal s m a has a Gaussian distribution (Yu et al. 2007), f s (x) is a Ricean distribution. For the given P fa(x), M and N, Eq. (16) can be rewritten as,

$$P_{D} (V_{\text{th}} ) = \left( {1 - P_{\text{fa}} } \right)^{M \cdot N - 1} \cdot \int\limits_{{V_{\text{th}} }}^{ + \infty } {f_{s} (x)} {\text{d}}x = \left( {1 - P_{\text{fa}} } \right)^{M \cdot N - 1} \cdot Q_{1} \left( {\sqrt {\frac{{p_{\text{out}} }}{{\sigma_{m}^{\prime 2} }}} ,\sqrt {\frac{{V_{\text{th}}^{2} }}{{\sigma_{m}^{\prime 2} }}} } \right)$$
(17)

where Q 1 is the generalized Marcum Q-function, p out is the signal power corresponding to the absolute value of F(m t , l t ) and σ ′2 m  = Nσ 2 m is the noise power after the DDFFT operation.

For the threshold V th, it can be defined in terms of the allowed single trial probability of false alarm and the measured 1-σ noise power (Kaplan and Hegarty 2006),

$$V_{\text{th}} = \sigma_{m}^{{\prime }} \sqrt { - 2\ln P_{fa} } = \sqrt N \sigma_{m} \cdot \sqrt { - 2\ln P_{\text{fa}} }$$
(18)

Combining (17) and (18), the probability of detection can be derived as,

$$\begin{gathered} P_{D} (V_{\text{th}} ) = \left( {1 - P_{\text{fa}} } \right)^{M \cdot N - 1} \cdot Q_{1} \left( {\sqrt {\frac{{p_{\text{out}} }}{{\sigma_{m}^{{{\prime }2}} }}} ,\sqrt {\frac{{V_{\text{th}}^{2} }}{{\sigma_{m}^{{{\prime }2}} }}} } \right) \\ = \left( {1 - P_{\text{fa}} } \right)^{M \cdot N - 1} \cdot Q_{1} \left( {\sqrt {{\text{SNR}}_{\text{out}} } ,\sqrt { - 2\ln P_{fa} } } \right) \\ \end{gathered}$$
(19)

where \({\text{SNR}}_{\text{out}} = 10^{{({{{\text{SNR}}_{\text{out}} } \mathord{\left/ {\vphantom {{{\text{SNR}}_{\text{out}} } {10}}} \right. \kern-0pt} {10}})}}\).

Figure 8 shows the curves of the probability of detection using proposed DDFFT method for different values of the probability of false alarm P fa . In this figure, the FFT size N is 256, the dynamic-division step \(\delta \dot{f}_{\text{step}}\) is 0.2 Hz/s and the pre-detection integration time T is 10 ms. For a given P fa equal to 10−5 and an input C/N 0 above 13 dB-Hz, the probability of detection is above 0.92. This demonstrates that the proposed algorithm is very reliable in the estimation of SINS aiding frequency error.

Fig. 8
figure 8

Probability of detection

Full size image

Optimization of GPS carrier-tracking loop design

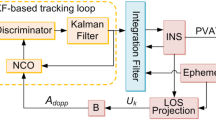
As addressed in the “Introduction” section, the performance of SINS aiding in strong signal conditions is good including the continuous calibration of inertial sensors. The proposed DDFFT method requires relatively large amount computation resources. However, the DDFFT results can be used to correct the output/aiding of SINS for high-dynamic applications in weak signal conditions. In addition to the DDFFT method, we also propose an automatic switch scheme between SINS-aided PLL [time domain (TD)] (Alban et al. 2003) and SINS-aided DDFFT [frequency-domain (FD)] as shown in Fig. 9. In order to achieve the best performance, the C/N 0 is used to control the switch.

Fig. 9
figure 9

SINS-aided carrier-tracking loop in time and frequency-domain

Full size image

The C/N 0 estimation is based on the power ratio method (PRM) (Sharawi et al. 2007). This method is a classic and low-complexity approach to estimate the C/N 0 in a software GPS receiver (Ma et al. 2004; Falletti et al. 2011). It can be defined as,

$$\begin{aligned} {C \mathord{\left/ {\vphantom {C {N_{0} }}} \right. \kern-0pt} {N_{0} }} & = 10\,\log_{10} \left( {\frac{{\bar{\mu }_{\text{NP}} - 1}}{{\mu - \bar{\mu }_{\text{NP}} }} \cdot \frac{1}{T}} \right) \\ \bar{\mu }_{\text{NP}} & = \frac{1}{H}\sum\limits_{h = 1}^{H} {{\text{NP}}_{h} } \\ {\text{NP}}_{h} & = \frac{{{\text{NBP}}_{h} }}{{{\text{WBP}}_{h} }} = {{\left[ {\left( {\sum\limits_{k = 1}^{\mu } {I_{k} } } \right)^{2} + \left( {\sum\limits_{k = 1}^{\mu } {Q_{k} } } \right)^{2} } \right]_{h} } \mathord{\left/ {\vphantom {{\left[ {\left( {\sum\limits_{k = 1}^{\mu } {I_{k} } } \right)^{2} + \left( {\sum\limits_{k = 1}^{\mu } {Q_{k} } } \right)^{2} } \right]_{h} } {\left[ {\sum\limits_{k = 1}^{\mu } {\left( {I_{k}^{2} + Q_{k}^{2} } \right)} } \right]_{h} }}} \right. \kern-0pt} {\left[ {\sum\limits_{k = 1}^{\mu } {\left( {I_{k}^{2} + Q_{k}^{2} } \right)} } \right]_{h} }} \\ \end{aligned}$$
(20)

where WBP h and NBP h are the wideband and narrowband power measurements, respectively, and \(\bar{\mu }_{\text{NP}}\) is the average ratio of the narrowband to wideband power.

Since the PRM estimator is based on averages of the samples I k and Q k , its result depends on the number of samples H · μ employed to compute the C/N 0 estimates. This fact also determines the refreshing rate of the estimates. In our case, for T = 10 ms and H · μ = 100, a new C/N 0 estimate is produced every T refr = 1 s. With the refreshing period T refr = 1 s, the estimation error can be bounded within ±0.75 dB in the range [20, 45] dB-Hz.

If the computed C/N 0 from (20) is lower than the threshold predetermined experimentally (i.e., 20 dB-Hz), the designed carrier loop will be switched to the FD tracking mode automatically. In the FD mode, the SINS aiding frequency error δ fa reconstructed from (9) is converted into the pseudo-range (PR) rate difference between SINS derived and GPS derived,

$$\begin{aligned} \delta \dot{\rho } & = [\dot{\rho }_{I} - \dot{\rho }_{G}^{f} ]_{4 \times 1} = \lambda_{L1} \cdot [f_{{I,{\text{dopp}}}} - f_{{G,{\text{dopp}}}} ]_{4 \times 1} = - \lambda_{L1} \delta f_{a,4 \times 1} \\ & = \lambda_{L1} \cdot G_{4 \times 3} \cdot C_{L}^{e} \cdot \left[ {\begin{array}{*{20}c} {\delta v_{E} } \\ {\delta v_{N} } \\ {\delta v_{U} } \\ \end{array} } \right] + \delta t_{ru,4 \times 1} + n_{{\dot{\rho },4 \times 1}} \\ \end{aligned}$$
(21)

where λ L1 is the wavelength of L 1 carrier, G 4×3 is formed by the LOS unit vectors from the receiver to the observed satellites, C e L is the direction cosine matrix (DCM) from the navigation east-north-up (ENU) frame to the Earth-centered Earth-fixed (ECEF) frame, [δv E , δv N , δv U ]T is the vector of velocity errors along ENU, δt ru,4×1 is the receiver clock drift, and \(n_{{\dot{\rho },4 \times 1}}\) is the measurement noise error.

The difference of pseudo-range rates \(\delta \dot{\rho }\) is then fed into the Integration Kalman Filter as observations (Yang 2008; Yu et al. 2010). This operation prevents the divergence of SINS navigation errors.

Simulation results and analysis

Static and dynamic tests are conducted to assess the performance of the DDFFT algorithm and the designed frequency-domain carrier-tracking loop aided by SINS. In a static test, a situation where the input signal C/N 0 is lower than 20 dB-Hz is simulated to show the tracking sensitivity of the DDFFT algorithm. In a dynamic test, a situation where a GPS receiver is tracking a low C/N 0 signal including dynamic effect is simulated to assess the performance of the designed SINS-aided carrier-tracking loop in frequency-domain. In both static and dynamic tests, the maximum search strategy described in section “Probability of detection” is utilized to detect the frequency estimates.

Static test results and analysis

In the static simulation, a noise interference was imposed to real GPS signals to simulate low C/N 0 conditions. The C/N 0 of the simulated input could be adjusted between 20 and 12 dB-Hz. For the static conditions, the maximal change rate of Doppler frequency caused by the satellite motion is about 1 Hz/s (Tsui 2000). Given the low dynamics in frequency, for demonstration purpose the SINS aiding was not used. The dynamic-division step is 0.2 Hz/s, the FFT size N is 256 and the pre-detection integration time T is 10 ms (the same as below).

Figure 10 shows the response of the DDFFT to weak signal and frequency dynamics. The C/N 0 of signal is about 18 dB-Hz and the dynamics of carrier frequency is 0.41 Hz/s (PRN15). It can be seen that the estimated \(\delta \dot{f}_{d}\) and δf 0 d where the FFT spectral peak are 0.4 Hz/s and 14.45 Hz, respectively. These values are much closer to the true values (\(\delta \dot{f}_{d} = 0. 4 1\) Hz/s, δf 0 d  = 14.31 Hz). This shows that the proposed algorithm can provide high accuracy estimates of the frequency errors.

Fig. 10
figure 10

Response of the dynamic-division FFT to the errors in carrier frequency

Full size image

In Fig. 11, the left-side y axis denotes the frequency tracking accuracy of the standard FFT- and DDFFT-based algorithms, whereas the right-side y axis denotes the C/N 0 of the input signal. The performance of standard FFT shows poorer tracking accuracy than DDFFT even with the signal between 20 dB-Hz and about 16.1 dB-Hz. For a C/N 0 lower than 16.1 dB-Hz, severe oscillations appear in the standard FFT tracking results. This is mainly because the standard FFT-based carrier loop is unable to simultaneously tackle incidents of noise interference and problems of frequency dynamics. In contrast, the DDFFT method can track signal as low as about 12.9 dB-Hz without obvious errors. This improves the tracking sensitivity by 3.2 dB-Hz.

Fig. 11
figure 11

Carrier frequency-tracking errors for standard FFT and dynamic-division FFT

Full size image

Dynamic test results and analysis

In the high-dynamic simulation, a GPS IF signal simulator was used to simulate signals. The Doppler shift was generated according to a simulated UAV flight trajectory and precise ephemeris data downloaded from International GNSS service (IGS) website. The duration of the simulation was 120 s. During the 0–10 s, the signal power was set to its normal level with the C/N 0 at 44 dB-Hz. A noise interference was introduced during 10–90 s resulting the C/N 0 reduced to 13 dB-Hz. In the last 20 s, the signal power was resumed to the normal. A low-grade IMU was used to simulate SINS. The gyroscope bias was 2.5°/h, and the scale factor error was 150 ppm. The accelerometer bias was 1 mg, and the scale factor error was 300 ppm. The random noise standard variations of gyroscope and accelerometer were 0.2°/h and 50 μg, respectively. The detailed parameters of the test GPS signal (PRN#15) are shown in Fig. 12.

Fig. 12
figure 12

Dynamics and C/N 0 in the simulation test

Full size image

For comparison purpose, the frequency tracking errors of SINS-aided PLL (TD mode) and the combined TD mode with proposed DDFFT (FD) are shown in Fig. 13. In the case of low C/N 0 (below 20 dB-Hz), the conventional SINS-aided PLL is running in an open-loop mode. The carrier frequency error dramatically increases over time (red line between 33 and 96 s). With the proposed method, the carrier loop switches to the FD tracking mode using the DDFFT algorithm to estimate and correct the frequency error in SINS aiding. This approach prevents the frequency error from growing over time. As a result, the proposed loop improves the tracking performance of GPS receivers for weak signals.

Fig. 13
figure 13

Tracking errors of carrier frequency in the dynamic test (PRN#15)

Full size image

Figure 14(top) shows the velocity errors of the receiver using the conventional SINS-aided PLL. With the decrement of C/N 0, the tracking loop is maintained by un-calibrated SINS. The up velocity error reaches a value as large as 4 m/s during the test period. Figure 14(bottom) shows the velocity errors of the optimized tracking loop (combined TD and FD). During the low C/N 0 period, the DDFFT-based tracking can maintain the velocity errors lower than 1.1 m/s.

Fig. 14
figure 14

Velocity errors using conventional SINS-aided PLL and optimized tracking loop. Top conventional SINS-aided PLL. Bottom optimized tracking loop

Full size image

Figure 15 shows the position errors of the receiver using the conventional SINS-aided PLL (top) and the position errors of the receiver using the optimized tracking loop (bottom). It can be seen that the position errors have the similar characteristics to those of velocity errors.

Fig. 15
figure 15

Position errors using conventional SINS-aided PLL and optimized tracking loop. Top conventional SINS-aided PLL. Bottom optimized tracking loop

Full size image

In addition, the performance of optimized tracking loop is based on the precondition that the GPS signal has already been acquired. In other HS receivers (Wang 2010; Xie 2011), it is still an issue to improve the acquisition/startup performance of the designed SINS/GPS integration system in low signal strength and high-dynamic conditions.

Conclusions

An optimized GPS carrier-tracking loop combining SINS aiding and dynamic-division FFT (DDFFT)-based tracking is proposed. It is designed to improve the tracking performance of GPS receivers in weak signal and high-dynamic conditions.

This design is based on conventional SINS aiding concept (time domain) and FFT-based signal processing for weak GPS signals. The time domain method has been proved to be one of the most efficient ways for high-dynamic applications with good GPS signals. The FFT processing has been proved to be the best method to increase the sensitivity for a low-dynamic receiver. We propose a DDFFT algorithm exploiting the complemented advantages of these two methods. The algorithm takes information from SINS to minimize the negative impact of dynamics on the FFT type algorithm. Meantime, the DDFFT estimates and compensates the error in aiding information derived from SINS in weak signal conditions. In order to fully exploit the advantages of existing and new methods to achieve the best performance, an optimized tracking loop is designed which can switch between the standalone SINS aiding mode and the DDFFT tracking mode depending on the signal quality (C/N 0).

Simulation results and theoretical analysis show that the DDFFT algorithm provides a 22.24 dB SNR gain by a 256-point FFT operation with a dynamic-division step \(\delta \dot{f}_{\text{step}} = 0. 2\,{\text{Hz}}/{\text{s}}\). The probability of detection for the true frequency parameters is above 92 % (C/N 0 ≥ 13 dB-Hz, T = 10 ms). Furthermore, with the DDFFT tracking algorithm in weak signal and high-dynamic conditions, the maximum position error in any direction is <5 m and the velocity error in any direction is <1.1 m/s. While the standalone SINS aiding has a position error up to 120 m and a velocity error up to 4 m/s.

These results demonstrate that the proposed method can significantly improve the carrier-tracking performance of a GPS receiver in both weak signal and high-dynamic conditions. Subsequently high performances of navigation solutions are achieved.