Multi-stage stochastic optimization: the distance between stochastic scenario processes

Abstract

Approximation techniques are challenging, important and very often irreplaceable solution methods for multi-stage stochastic optimization programs. Applications for scenario process approximation include financial and investment planning, inventory control, energy production and trading, electricity generation planning, pension fund management, supply chain management and similar fields. In multi-stage stochastic optimization problems the amount of stage-wise available information is crucial. While some authors deal with filtration distances, in this paper we consider the concepts of nested distributions and their distances which allows to keep the setup purely distributional but at the same time to introduce information and information constraints. Also we introduce the distance between stochastic process and a tree and we generalize the concept of nested distance for the case of infinite trees, i.e. for the case of two stochastic processes given by their continuous distributions. We are making a step towards to a new method for distribution quantization that is the most suitable for multi-stage stochastic optimization programs as it takes into account both the stochastic process and the stage-wise information.

1 Introduction

Suppose that a multi-stage stochastic optimization program (1) is given in the form

$$\begin{aligned} \max _{x}\{\mathcal{A }[H(x^0, \xi ^1, x^1, \xi ^2,\ldots ,x^{T-1}, \xi ^T); \mathcal{F }]: x\triangleleft \mathcal{F }, x\in \mathbb{X }\}, \end{aligned}$$

(1)

where

• $\xi =(\xi _1,\ldots ,\xi _T)$ is a stochastic process defined on the probability space $(\Omega , \mathcal{F }, P)$ and $\xi ^t=(\xi _1,\ldots ,\xi _t)$ is the history up to time $t$;

• $\mathcal{F }=(\mathcal{F }_1,\ldots ,\mathcal{F }_T)$ is a filtration on the $(\Omega , \mathcal{F }, P)$ to which the process $\xi$ is adapted (i.e. $\xi _t$ is measurable with respect to $\sigma$-algebra $\mathcal{F }_t,\; \forall t=1,\ldots ,T$): we denote it as $\xi \triangleleft \mathcal{F }$. The fact that filtration is defined only on a particular probability space leads to the question of how to introduce information and information constraints, keeping the setup purely distributional;

• We add the trivial $\sigma$-algebra $\mathcal{F }_0=\{\emptyset , \Omega \}$ as the first element of the filtration $\mathcal{F }$. A sequence of decisions $x=(x_0,\ldots ,x_{T-1})$ with history $x^t=(x_0,\ldots ,x_{t-1})$ must be adapted to $\mathcal{F }$: i.e. it must fulfill the non-anticipativity conditions $x\triangleleft \mathcal{F }$Pflug and Pichler (2012), that means only those decisions are feasible, which are based on the information available at the particular time;

• $H(\cdot )$ is the loss/profit function;

• $\mathbb{X }$ is the set of constraints other than the non-anticipativity constraints;

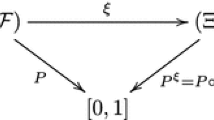
• $\mathcal{A }(\cdot ,\cdot )$ is a version-independent (also called law-invariant) multi-period acceptability functional (see Pflug 2010; Pflug and Römisch 2007), i.e. it is defined on the probability space $(\Omega , \mathcal{F }, P)$ and depends only on the distribution of the outcome variable.

Our goal is to solve this problem numerically by the approximation though it may be difficult to solve it explicitly due to its functional form. So the necessity of approximating of the initial problem with a solvable one (2) arises immediately:

$$\begin{aligned} \max _{x}\{\mathcal{A }[H(\widetilde{x}^0, \widetilde{\xi }^1, \widetilde{x}^1, \widetilde{\xi }^2,\ldots ,\widetilde{x}^{T-1}, \widetilde{\xi }^T); {\widetilde{\mathcal{F }}}]: \widetilde{x}\triangleleft {\widetilde{\mathcal{F }}}, \widetilde{x}\in \mathbb{X }\}, \end{aligned}$$

(2)

where the stochastic process $\xi$ is replaced by a scenario process with finite number of values $\widetilde{\xi }=(\widetilde{\xi }_1,\ldots ,\widetilde{\xi }_T)$ defined on a probability space $(\widetilde{\Omega }, \widetilde{\mathcal{F }}, \widetilde{P})$: it is not natural to construct approximations on the same probability space, because concrete decision problems of type (1) are given without reference to a probability space, they are given in distributional setups (Pflug 2010; Pflug and Römisch 2007).

Distance between problems (1) and (2) determines approximation error. Previously, distances between the initial problem (1) and its approximation (2) have been defined only if both processes $\xi$ and $\widetilde{\xi }$ and both filtrations $\mathcal F$ and $\widetilde{\mathcal{F }}$ are defined on the same probability space $(\Omega , \mathcal{F }, P)$. The introduction of the concept of nested distribution (Pflug 2010), which contains in one mathematical object the scenario values as well as the information structure under which decisions have to be made, has brought the problem to the purely distributional setup. The nested distance between these distributions is introduced in Pflug and Pichler (2011, 2012), and turns out to be a generalization of the well-known Kantorovich distance for single-stage problems (see Pflug and Pichler 2012, 2011; Villani 2003 for more details).

The main problems that are considered in this paper are:

• Scenario generation: When dealing with scenario generation for the multi-stage stochastic optimization problem, the natural question that arises is how to approximate (to quantize) the continuous distribution of the stochastic process in such a way, that the nested distance between the initial distribution and its approximation is minimized. The stage-wise minimization of the Kantorovich distance gives us a well-known result for the optimal quantizers of the distributions at each stage (Villani 2003). However, this result does not mean that the nested distance between initial and approximate problems is minimized. The aim of this article is to show that the quantizers received by the minimization of the nested distance are better (in the sense of minimal distance) than the quantizers received by the stage-wise minimization of the Kantorovich distance.

• Computational efficiency: When dealing with numerical calculation of the nested distance the question of the computational efficiency is of interest. It is necessary to understand how many values should the scenario process have at each stage in order to make the computational time small and at the same time to make the approximation good (i.e. to make the approximation error small). The compromise for this should be found.

• Applications: Stochastic programming offers a huge variety of applications. In this paper we would like to focus on the applications in the field of natural hazards risk-management.

The article is organized as follows:

Section 2 of the article gives some basic insight into the problem and reminds the reader of the distances between measures as well as of the nested distances between trees. In Sect. 3 we construct a distance between stochastic process and a tree and a distance between two stochastic processes. Section 4 introduces numerical algorithms for one-dimensional and multi-dimensional distributional quantization based on the minimization of the distance between measures, while Sect. 5 shows that the minimization of the nested distance between stochastic process and a tree may lead to a better quantization result than the minimization of the distance between measures. Section 6 is devoted to the applications of the developed algorithms.

2 Preliminaries

Consider stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$. The $\sigma$-algebra generated by the random variable $\xi _t$ is denoted by $\sigma (\xi _t)$, the filtration generated by the process $(\xi _1,\ldots ,\xi _T)$ is denoted by $\sigma (\xi )=(\sigma (\xi _1),\sigma (\xi _1,\xi _2),\ldots ,\sigma (\xi _1,\xi _2,\ldots ,\xi _T)).$

If random variable $\xi _t$ is measurable w.r.t. a $\sigma$-algebra, we write $\xi _t\triangleleft \mathcal{F }_t$. The similar notation $\xi \triangleleft \mathcal{F }$ we use to indicate that the process $\xi =(\xi _1,\ldots ,\xi _T)$ is adapted to the filtration $\mathcal{F }=(\mathcal{F }_1,\ldots ,\mathcal{F }_T)$.

In our distributional setup, there is no predefined probability space and therefore there is no room for introducing other filtration than those which is generated by the random process itself. Hence, we can make the following assumption:

At time $t$, no other information is available to the decision-maker rather than the values of the scenario process $\xi _s,\; s\le t,\; \forall t=1,\ldots ,T$. In different words we assume that the decision $x_t$ is measurable with respect to $\sigma$-algebra $\mathcal{F }_t$, which is the one generated by $(\xi _1,\ldots ,\xi _T)$.

Definition 2.1

(Tree process) (Pflug 2010) A stochastic process $\nu =(\nu _1,\ldots ,\nu _T)$ is called a tree process, if $\sigma (\nu _1), \sigma (\nu _2),\ldots ,\sigma (\nu _T)$ is a filtration.

The random component $\xi =(\xi _1,\ldots ,\xi _T)$ of the decision problem (1) is described by the continuous distribution function, while the random component $\widetilde{\xi }=(\widetilde{\xi }_1,\ldots ,\widetilde{\xi }_T)$ of the approximate decision problem (2) is discrete, i.e. it takes finite (and in fact few) number of values. Since every finitely valued stochastic process $(\widetilde{\xi }_1,\ldots ,\widetilde{\xi }_T)$ is representable as a tree, we deal with tree approximation of stochastic processes (Heitsch and Römisch 2009; Mirkov and Pflug 2007). The tree that represents the finitely valued stochastic process $(\widetilde{\xi }_1,\ldots ,\widetilde{\xi }_T)$ we call finitely valued tree.

To solve the approximate problem (2) numerically we should represent the stochastic process $\widetilde{\xi }$ as a finitely valued tree. The tree can be determined by its graph structure, the scenario probabilities and by the values sitting on the nodes. The structure of the tree could be given by the vector of predecessors or in the simplest case by the bushiness vector of the tree at each stage.

Definition 2.2

(Bushiness of the tree) Consider a finitely valued stochastic process $\widetilde{\xi }=(\widetilde{\xi }_1,\ldots ,\widetilde{\xi }_T)$ that is represented by the tree with the same number of successors $b_t$ for each node at the stage $t,\; \forall t=1,\ldots ,T$. The vector $bush=(b_1,\ldots ,b_{T})$ is a bushiness vector of the tree.

Figure 1 shows two trees with different bushiness (the bushiness vector of the left-hand side tree is [5 5 5], the bushiness vector of the right-hand side tree is [2 2 2]).

Fig. 1

Comparison of the trees with different bushiness

In this article we distinguish between two types of scenario trees:

• Tree 1: is a tree with a given treestructure (that is given either by the vector of predecessors or by the bushiness vector). If Tree 1 is given, we are not going to change its treestructure, it is fixed for a particular problem;

• Tree 2: is a tree with changeable treestructure. This tree type is going to be used for a better approximation of the stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$ by the tree. The structure of Tree 2 is described by the bushiness vector $bush$ that may change.

2.1 Distance between scenario trees

Consider a distance $d(P, \widetilde{P})$ between probability measures $P$ and $\widetilde{P}$ which concept initially arises in the Monge Transportation Problem (Rachev 1991) and is developed by Kantorovich in the later works (Rachev 1991; Villani 2003). If $P$ and $\widetilde{P}$ are two Borel probability measures given on separable metric spaces $(\Omega , d_{\Omega })$ and $(\widetilde{\Omega }, d_{\widetilde{\Omega }})$ respectively and $\pi$ is a Borel probability measure on $\Omega \times \widetilde{\Omega }$ with fixed marginals $P(\cdot )=\pi (\cdot , \widetilde{\Omega })$ and $\widetilde{P}(\cdot )=\pi (\Omega , \cdot )$, the Kantorovich distance can be defined for random variables from probability spaces $(\Omega , \mathcal{F }, P)$ and $(\widetilde{\Omega }, {\widetilde{\mathcal{F }}}, \widetilde{P})$:

Definition 2.3

(The Kantorovich distance) (Villani 2003)

$$\begin{aligned} d(P,\widetilde{P})&= \inf _{\pi }\left\{ \int _{\Omega \times \widetilde{\Omega }} d(w, \widetilde{w})\pi [dw, d\widetilde{w}]\right\} ,\nonumber \\ \pi (\cdot , \widetilde{\Omega })&= P(\cdot ),\nonumber \\ \pi (\Omega , \cdot )&= \widetilde{P}(\cdot ). \end{aligned}$$

(3)

Theorem 2.1

Suppose that $N$-dimensional distribution $P$ has a density $f$ with $\int |u|^{1+\delta }f(u)du< \infty$ for some $\delta >0$ and suppose that

$$\begin{aligned} \left[ \int f(x_t|x_1,\ldots ,x_{t-1})^{\frac{N}{N+1}}dx_t\right] ^{\frac{N+1}{N}}\le c,\; \forall t \end{aligned}$$

where $c$ is some constant.

Then

$$\begin{aligned} d\left( P, \widetilde{P}^{n}\right) \le cn^{-\frac{1}{N}}, \end{aligned}$$

where we denote by $\widetilde{P}^{n}$ a discrete approximation of $P$ that sits on $n$ points, and for $n\rightarrow \infty$

$$\begin{aligned} d\left( P, \widetilde{P}^{n}\right) \rightarrow 0. \end{aligned}$$

Proof

The result of the theorem obviously follows from Zador-Gersho formula (see Graf and Luschgy 2000; Pflug and Pichler 2011).$\square$

Considering the stochastic process together with the gradually increasing information, provided by the filtrations, the Kantorovich distance is generalized for the multi-stage case in the works of Pflug, Römisch and Pichler (Pflug 2010; Pflug and Pichler 2012, 2011).

Definition 2.4

(Scenario process-and-information structure) If $\nu$ is a tree process and $\mathcal{F }=\sigma (\nu )$, then any process $\xi$ adapted to $\mathcal{F }$ can be written as $\xi _{t}=f_t(\nu _t)$ for some measurable function $f_t$. We call a pair consisting of a scenario process $\xi$ and a tree process, such that $\xi \vartriangleleft \sigma (\nu )$, a scenario process-and-information structure. We denote it as $(\Omega , \mathcal{F }, P, \xi )$.

The distribution of such a process-and-information structure is called a nested distribution $\mathbb{P }$. This concept is explained in Pflug (2010), Pflug and Pichler (2012), Pflug and Pichler (2011). The nested distributions are defined in a pure distributional concept. The relation between the nested distribution $\mathbb P$ and the process-and-information-structure $(\Omega , \mathcal{F }, P, \xi )$ is comparable to the relation between a probability measure $P$ on $\mathbb{R }^k$ and a $\mathbb{R }^k$-valued random variable $\xi$ with distribution $P$.

We may alternatively consider either the nested distribution $\mathbb P$ or its realization with $\Omega$ being a tree, $\mathcal F$ an information and $\xi$ a process. We symbolize this fact by $\mathbb{P }\sim (\Omega , \mathcal{F }, P, \xi )$.

To generalize the Kantorovich distance for the multi-stage case it is necessary to consider two process-and-information structures

$$\begin{aligned} \mathbb{P }\sim (\Omega , \mathcal{F }, P, \xi )\; and\; {\widetilde{\mathbb{P }}}\sim \left( \widetilde{\Omega }, {\widetilde{\mathcal{F }}}, \widetilde{P}, \widetilde{\xi }\right) \end{aligned}$$

and to minimize the effort or costs that have to be taken into account when passing from one process-and-information structure to another Pflug and Pichler (2012, 2011).

Definition 2.5

(The multi-stage (nested) distance) (Pflug and Pichler 2012) The multi-stage distance of two process-and-information structures is

$$\begin{aligned} \begin{aligned} d(\mathbb{P }, {\widetilde{\mathbb{P }}})&=\inf _{\pi }\left( \int d(w, \widetilde{w})\pi (dw, d\widetilde{w})\right) , \\ \mathbb{P }&\sim (\Omega , \mathcal{F }, P, \xi ),\; {\widetilde{\mathbb{P }}}\sim (\widetilde{\Omega }, {\widetilde{\mathcal{F }}}, \widetilde{P}, \widetilde{\xi }) \\ \pi \left[ A\times \widetilde{\Omega }| \mathcal{F }_t\otimes \widetilde{\mathcal{F _t}}\right] (w, \widetilde{w})&=P(A|\mathcal{F }_t)(w),\; (A\in \mathcal{F }_T, 1\le t\le T),\\ \pi \left[ \Omega \times B| \mathcal{F }_t\otimes {\widetilde{\mathcal{F }}}_t\right] (w, \widetilde{w})&=\widetilde{P}(B|{\widetilde{\mathcal{F }}}_t)(\widetilde{w}),\; (B\in {\widetilde{\mathcal{F }}}_T, 1\le t\le T), \end{aligned} \end{aligned}$$

(4)

where we use the distance $d(w, \widetilde{w})=\sum _{t=0}^Td_t(\xi _t(w_t), \widetilde{\xi }_t(\widetilde{w}_t))$ on the sample space $\Omega \times \widetilde{\Omega }$ and $d_t$ is the distance available in the state space of the processes $\xi _t$ and $\widetilde{\xi }_t$; $w_t$ is a predecessor of $w$ that belongs to the stage $t$ of the tree $\forall t=1,\ldots ,T$ (in symbol we denote it $w_t=pred_t(w)$, where $w=w_T$).

To understand the relationship between the nested distance and the the multi-stage stochastic optimization program consider the optimization problem of the type

$$\begin{aligned} v(\mathbb{P })=\inf \left\{ \mathbb{E }_P[H(x, \xi )]: x\triangleleft \mathcal{F }, x\in \mathbb{X }\right\} =\inf \left\{ \int {H(x, \xi )dP: x\triangleleft \mathcal{F }, x\in \mathbb{X }}\right\} ,\nonumber \\ \end{aligned}$$

(5)

where the objective is an expectation.

The following theorem is the result to bound stochastic optimization problems by the nested distance.

Theorem 2.2

(Lipschitz property of the value function) (Pflug and Pichler 2012) Let $\mathbb P$ and ${\widetilde{\mathbb{P }}}$ be process-and-information structures. Assume $\mathbb X$ is convex, and profit function $H$ is convex in $x$ for any $\xi$ fixed,

$$\begin{aligned} H((1-\lambda )x_0+\lambda x_1, \xi )\le (1-\lambda )H(x_0, \xi )+\lambda H(x_1, \xi ). \end{aligned}$$

Moreover, let $H$ be uniformly Hölder continuous $(\beta \le 1)$ with constant $L_{\beta }$, that is

$$\begin{aligned} \left| H(x, \xi )-H(x, \widetilde{\xi })\right| \le L_{\beta }\left( \sum _{t\in T}d_t(\xi _t, \widetilde{\xi }_t)\right) ^{\beta } \end{aligned}$$

for all $x\in \mathbb{X }$.

Then the value function $v$ in (5) inherits the Hölder constant with respect to the multi-stage distance, that is $|v(\mathbb{P })-v({\widetilde{\mathbb{P }}})|\le L_{\beta }d(\mathbb{P }, {\widetilde{\mathbb{P }}})^{\beta }.$

That means the less the distance between two process-and-information structures the closer the solutions of the initial and approximate multi-stage stochastic optimization programs to each other.

So, if we would be able to minimize the distance $d(\mathbb{P }, {\widetilde{\mathbb{P }}})$ between stochastic process given by the continuous distribution function and a tree we would calculate the best upper bound for the difference between true and approximate solutions $|v(\mathbb{P })-v({\widetilde{\mathbb{P }}})|$.

3 Distance between stochastic scenario processes

Using the Kantorovich distance $d(P, \widetilde{P})$ (see definition 2.3) we are able to measure stage-wise the difference between continuous distribution function $P$ and its discrete approximation $\widetilde{P}$. We are not able, though, to measure the distance between stochastic process given by the continuous distribution function and the whole tree that contains all available information (incl. stage-wise information). The multi-stage distance (see definition 2.5) gives us an opportunity to measure the difference between two finite trees (${\widetilde{\mathbb{P }}}^{(1)}$ and ${\widetilde{\mathbb{P }}}^{(2)}$). But, in case one of the trees is infinite (i.e. in case of stochastic process given by the continuous distribution function) there is a numerical difficulty to find the shipping plan $\pi (dw, d\widetilde{w})$.

In this article we do not consider how the continuous distribution function of the stochastic process is obtained: we suppose that given the empirical data and using modeling methods of econometrics it is always possible to approximate the data by the continuous distribution function. Hence, we focus on the approximation of the continuous-state stochastic process by the scenario trees:

In this section we are going to introduce an approximation of the multi-stage distance between stochastic process given by its continuous distribution function, and a tree with given structure, probabilities and values (Tree 1, see Sect. 2).

Suppose that Tree 1 is given: we know the treestructure, the probabilities of the nodes $p_{n, i}$ and the values sitting on the nodes $y_{n, i}$, where every node of the tree is identified by two numbers $(n, i)$, where $n$ is the identification number of its predecessor and $1\le i\le s(n)$, where $s(n)$ is a total number of successors of $n$.

The stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$ is given by the joint distribution function $F$. We would like to find the distance between this stochastic process and the given tree.

Suppose that $\mathbb P$ is a nested distribution of the stochastic process $\xi ,\,{\widetilde{\mathbb{P }}}$ is a nested distribution of the given tree (Tree 1) and $\mathbb{P }^*$ is a nested distribution of the approximate stochastic process $\xi ^*$ (Tree 2).

We would like to calculate the distance $d(\mathbb{P }, {\widetilde{\mathbb{P }}})$ between stochastic process $\xi$ and the given tree (Tree 1) by the approximation of this stochastic process by a tree with high bushiness (Tree 2, see Sect. 2).

According to the triangle inequality that holds for the nested distance, we can write

$$\begin{aligned} d(\mathbb{P }, {\widetilde{\mathbb{P }}})\le d({\widetilde{\mathbb{P }}}, \mathbb{P }^*)+d(\mathbb{P }, \mathbb{P }^*). \end{aligned}$$

In order to approximate the distance $d(\mathbb{P }, {\widetilde{\mathbb{P }}})$ between stochastic process and Tree 1 by the distance $d({\widetilde{\mathbb{P }}}, \mathbb{P }^*)$ between Tree 1 and the process approximation (Tree 2) we should guarantee that the distance between stochastic process $\xi$ and its approximation (Tree 2) is small enough:

$$\begin{aligned} d(\mathbb{P }, \mathbb{P }^*)\le \varepsilon . \end{aligned}$$

(We do not say minimized as the minimum may be not obtained due to the computational error).

Let P be a probability on $\mathbb{R }^{NT}$, dissected into transition probabilities $P_1,\ldots ,P_T$. We say that $P$ has the $(K_2,\ldots ,K_T)$-Lipschitz property, if for $t=2,\ldots ,T$,

$$\begin{aligned} d(P_t(\cdot |u), P_t(\cdot |v))\le K_td(u, v). \end{aligned}$$

The following two statements hold for the multivariate distributions with Lipschitz property (this concept is explained in more details in Pflug and Pichler (2012).

Lemma 3.1

(Pflug and Pichler 2011) Let $\mathbb P$ be a nested distribution, $P$ its multivariate distribution, which is dissected into the chain $P=P_1\circ P_2 \ldots \circ P_T$ of conditional distributions. If $P$ has the $(K_2,\ldots , K_T)$-Lipschitz property, then

$$\begin{aligned} d\left( \mathbb{P }, {\widetilde{\mathbb{P }}}\right) \le \sum _{t=1}^Td\left( P_t, \widetilde{P}_t\right) \Pi _{s=t+1}^{T+1}(K_s+1). \end{aligned}$$

Theorem 3.1

(Pflug and Pichler 2011) Let $\mathbb P$ and ${\widetilde{\mathbb{P }}}$ be two nested distributions and let $P$ and $\widetilde{P}$ be the pertaining multivariate distribution respectively. Then

$$\begin{aligned} d\left( P, \widetilde{P}\right) \le d\left( \mathbb{P }, {\widetilde{\mathbb{P }}}\right) . \end{aligned}$$

Hence, for the multivariate distributions with Lipschitz property (for example, Gaussian distribution) we can find the following bounds for the distance between stochastic process and a tree:

$$\begin{aligned} L=d\left( P, \widetilde{P}\right) \le d\left( \mathbb{P }, {\widetilde{\mathbb{P }}}\right) \le \sum _{t=1}^Td\left( P_t, \widetilde{P}_t\right) \Pi _{s=t+1}^{T+1}(K_s+1)=U_1, \end{aligned}$$

(6)

and

$$\begin{aligned} d\left( \mathbb{P }, {\widetilde{\mathbb{P }}}\right) \le d\left( {\widetilde{\mathbb{P }}}, \mathbb{P }^*\right) +\sum _{t=1}^Td(P_t, {P}^*_t)\Pi _{s=t+1}^{T+1}(K_s+1)=U_2. \end{aligned}$$

(7)

Theorem 3.2

(Sufficient condition for the convergence) Suppose that the stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$ is approximated by the tree with bushiness vector $bush=[b_1,\ldots ,b_T]$ ($\mathbb P$ and ${\widetilde{\mathbb{P }}}$ are corresponding to the process and to the tree nested distributions). Suppose that the $(K_2,\ldots , K_T)$-Lipschitz property holds for the corresponding multivariate distribution $P$, that is dissected into the chain $P=P_1\circ P_2 \ldots \circ P_T$ of conditional distributions. If the bushiness factors $b_1,\ldots ,b_T$ are increasing and the conditions of the Theorem 2.1 are satisfied for each $P_t$, then the multi-stage distance $d(\mathbb{P }, {\widetilde{\mathbb{P }}})$ is converging to zero.

Proof

As the conditions of the Theorem 2.1 are satisfied for all $P_t,\,t=1,\ldots ,T$, then $d(P_t, \widetilde{P}_t^{b_t})\rightarrow 0\; \forall t=1,\ldots ,T$ if the bushiness factor $b_t\rightarrow \infty \; \forall t=1,\ldots ,T$. As the $(K_2,\ldots , K_T)$-Lipschitz property holds for $P$, that is dissected into the chain $P=P_1\circ P_2 \ldots \circ P_T$ of conditional distributions, then according to Lemma 3.1

$$\begin{aligned} d\left( \mathbb{P }, {\widetilde{\mathbb{P }}}\right) \le \sum _{t=1}^Td\left( P_t, \widetilde{P}^{b_t}_t\right) \Pi _{s=t+1}^{T+1}(K_s+1). \end{aligned}$$

This implies that the upper bound for the nested distance is converging to zero when the bushiness of the tree is increasing and, hence,

$$\begin{aligned} d\left( \mathbb{P }, {\widetilde{\mathbb{P }}}\right) \rightarrow 0. \end{aligned}$$

$\square$

The rate of the convergence depends on the method of scenario generation (Heitsch and Römisch 2009; Römisch 2010).

Figure 2 shows the convergence of the nested distance between normally distributed stochastic process and a tree with optimally generated scenarios (Fig. 2a, see Fort and Pagés 2002; Luschgy et al. 2010; Villani 2003 and Sect. 4 for the details) as well as with a tree with randomly generated scenarios (boxplot in the Fig. 2b, see Römisch 2010 and Sect. 4). As one can see in the Fig. 2b the convergence of the nested distance between the stochastic process and the tree with randomly generated scenarios holds in probability. The reason is that the conditions of the Theorem 2.1 are satisfied almost surely for the tree with randomly generated values sitting on it and, hence, the conditions of the Theorem 3.2 that implies the convergence are satisfied in probability for this case.

Fig. 2

Convergence of the nested distance to zero. a Optimal quantization. b Random generation

As soon as we are able to find the bounds (6) and (7) for the distance between stochastic process and a tree, we can generalize these bound for the case of two stochastic processes as the distance between two stochastic processes is the nested distance between two infinitely large trees (i.e. the trees with infinitely many nodes) (Pflug and Pichler 2012).

Suppose that $\mathbb{P }_1$ is a nested distribution of the stochastic process $\xi _1,\,\mathbb{P }_2$ is a nested distribution of the stochastic process $\xi _2,\,{\widetilde{\mathbb{P }}}_1$ is a nested distribution of the approximate stochastic process $\widetilde{\xi _1}$ and ${\widetilde{\mathbb{P }}}_2$ is a nested distribution of the approximate stochastic process $\widetilde{\xi _2}$.

We would like to calculate the distance $d(\mathbb{P }_1, \mathbb{P }_2)$ between two stochastic processes (i.e. infinitely large trees).

According to the triangle inequality that holds for the nested distance, we can claim $d(\mathbb{P }_1, \mathbb{P }_2)\le d(\mathbb{P }_1, {\widetilde{\mathbb{P }}}_1)+d(\mathbb{P }_2, {\widetilde{\mathbb{P }}}_1),$ and $d(\mathbb{P }_2, {\widetilde{\mathbb{P }}}_1)\le d({\widetilde{\mathbb{P }}}_1, {\widetilde{\mathbb{P }}}_2)+d(\mathbb{P }_2, {\widetilde{\mathbb{P }}}_2)$ and, then, $d(\mathbb{P }_1, \mathbb{P }_2)\le d(\mathbb{P }_1, {\widetilde{\mathbb{P }}}_1)+d(\mathbb{P }_2, {\widetilde{\mathbb{P }}}_2)+d({\widetilde{\mathbb{P }}}_1, {\widetilde{\mathbb{P }}}_2)$.

In order to calculate the distance $d(\mathbb{P }_1,\mathbb{P }_2)$ between two stochastic processes as a distance $d({\widetilde{\mathbb{P }}}_1,{\widetilde{\mathbb{P }}}_2)$ between two trees that approximate these stochastic processes, we should guarantee that the distance between stochastic process $\xi _1$ and its approximation is small enough (as well as the distance between stochastic process $\xi _2$ and its approximation): $d(\mathbb{P }_1, {\widetilde{\mathbb{P }}}_1)\le \varepsilon _1,$ and $d(\mathbb{P }_2, {\widetilde{\mathbb{P }}}_2)\le \varepsilon _2$.

For the multivariate distributions with $(K_2,\ldots , K_T)$-Lipschitz property it is easy receive the bounds similar to (6) and (7). Which upper bound is better ($U_1$ or $U_2$) depends on the bushiness of the approximate tree (Tree 2). Notice that upper bound $U_1$ for the distance does not depend on the bushiness of the tree, because it does not contain approximations of the stochastic process but just the continuous distribution function $P_t$. As it is for the case of the distance between stochastic process and a tree it is natural to guess that $U_1$ is better than $U_2$, i.e. $U_1\le U_2$, if the approximation tree of the stochastic process has low bushiness and $U_2$ is better than $U_1$ if the bushiness is high.

This means that the gap between the best upper and lower bounds $U$ and $L$ for the distance between stochastic process and a tree does not change while $U_1\le U_2$ and decreases as long as the upper bound $U_2$ decreases, i.e. as long as the bushiness of the tree increases.

Hence, one way to receive an approximation for the nested distance $d(\mathbb{P }_1, \mathbb{P }_2)$ between stochastic processes is to increase the bushiness of the tree that approximates these stochastic processes until the necessary level $\varepsilon$ of the gap between the lower $L$ and the upper bound $U_2$ is obtained (and, of course, $U_2\le U_1$):

$$\begin{aligned} d(\mathbb{P }_1, \mathbb{P }_2)=\lim _{bush\rightarrow \infty }d({\widetilde{\mathbb{P }}}_1, {\widetilde{\mathbb{P }}}_2). \end{aligned}$$

4 Optimal quantization based on the Kantorovich distance minimization

Consider stochastic process $\xi$ given by its continuous distribution function $F$ and suppose that we should approximate this distribution by a discrete one with at most $N$ values. Approximation of the random variable $\xi$ defined on $(\Omega , \mathcal{F }, P)$ by a measurable function with at most $N$ values can be done by:

• Monte-Carlo (random) generation: that chooses $N$ random points from the distribution $F$ and assigns equal probabilities to them (see Pflug and Römisch 2007; Pflug and Pichler 2011);

• Optimal quantization: that minimizes the Kantorovich distance between the continuous distribution and its discrete approximation. This type of quantization finds optimal supporting points $z_i,\,i=1,\ldots , N$ by the minimization of $D(z_1,\ldots , z_N)=\int \min _{i}d(x, z_i)P(dx)$ over $z_1,\ldots , z_N$. Then, given the supporting points $z_i$, we calculate their probabilities $p_i$ by the minimization of the Kantorovich distance $d(P, \sum _{i=1}^Np_i\delta _{z_i})$ (see Fort and Pagés 2002; Luschgy et al. 2010; Pflug and Pichler 2011; Rachev 1991; Römisch 2010).

Suppose now that the stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$ is given by the continuous distribution functions $F_t$ of each random variable $\xi _t\; \forall t=1,\ldots ,T$. We would like to approximate this stochastic process by the tree with $T$ stages and with known treestructure. As the treestructure is given, the number $N_t$ of nodes at each stage of the tree is known too. Hence, to approximate the stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$ by this tree we need to approximate each continuous $F_t$ by $N_t$ discrete points - that can be done either by Monte-Carlo generation or by optimal quantization. If we use optimal quantization to approximate the distribution functions, the Kantorovich distance between the distribution and its approximation at each stage of the tree is minimized (Fort and Pagés 2002; Luschgy et al. 2010; Villani 2003). Figure 3 compares stage-wise optimal quantization (Fig. 3a) with stage-wise random generation (Fig. 3b) for one-dimensional Gaussian distribution sitting on the tree with given treestructure (bush= [5 5 5]) (see Luschgy et al. (2010)).

Fig. 3

Optimal quantization and random generation for the normal distribution. a Optimal quantization. b Random generation

Such a stage-wise tree approximation of the stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$ can be described in the following algorithmic form:

• (1) At the root of the tree there is only one node (the root) which probability is one. Hence, either we know the value $\xi _1$ at the root for sure, or we can generate one from the given distribution and assign probability one to it;

• (2) Second stage of the tree has $N_2$ nodes (this number depends on the structure of the tree). All of them are dependent on the root. We should generate $N_2$ values of $\xi _2$ according to the conditional distribution of $\xi _2$ given $\xi _1$;

• (3) For each of the following stages $t=3,\ldots ,T$ we should generate $\xi _t$ according to the conditional distribution of $\xi _t$ conditional on the historical values of the random variables $\xi ^{t-1}$.

4.1 One-dimensional case

Till this point we have not specified the number of dimensions of the random variable $\xi _t$, which in general could have had several dimensions. Now, consider stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$ for which each random variable $\xi _t,\; t=1,\ldots ,T$ is one-dimensional and suppose that the joint probability distribution function $F_{\xi _1, \ldots , \xi _T}(u_1,\ldots ,u_T)$ of this stochastic process is known. We would like to show how to approximate this stochastic process by the tree with known probabilities $p_{n, i}$ of the nodes ($n$ is the predecessor number and $1\le i\le s(n)$, where $s(n)$ is a total number of successors of $n$).

Suppose that we have found the form of each of the conditional distributions $F_{\xi _t|\xi _1\ldots \xi _{t-1}}(u_t|u_1\ldots u_{t-1}),\; t=1,\ldots ,T$. Figure 4 shows how to construct and to approximate the conditional distributions at each stage of the tree based on the joint distribution function of $\xi =(\xi _1,\ldots ,\xi _T)$ for the case of Gaussian distribution.

Fig. 4

Stage-wise conditional distributions sitting on the tree (Gaussian case)

Given the probabilities $p_{n, i}$ we are able to calculate the intervals in which the realization of our stochastic process is lying for each of the nodes using the quantile function:

$$\begin{aligned} F^{-1}(p)=\inf \{u\in \mathbb{R }:\; p\le F(u)\}. \end{aligned}$$

Denote the bounds for the realization of the stochastic process by $b_{n, i-1}$ and $b_{n, i}$ for each node $(n, i)$ of the tree. Calculation of these bounds can be done in two steps:

• (1) Calculation at the root: Let $\overline{p}_{1,i}=\sum _{j=1}^ip_{1,j}$ then

  $$\begin{aligned} b_{1,0}&= -\infty ,\\ b_{1,i}&= F_1^{-1}(\overline{p}_{1,i}),\\ b_{1,s(1)}&= \infty . \end{aligned}$$

• (2) Calculation at other nodes: Now we calculate the bounds recursively: suppose all bounds at stage $t-1$ are calculated. For each node at the stage $t$ consider all its predecessors, denoting by $(1, n_2,\ldots , n_{t-1})$, and the corresponding intervals $[b_{1,i_1-1},b_{1,i_1}]$, $[b_{n_2,i_2-1},b_{n_2,i_1}]$,...,$[b_{n_{t-1},i_{t-1}-1},b_{n_{t-1},i_{t-1}}]$. Then let $\overline{p}_{n,i}=\sum _{j=1}^ip_{n,j}$. Now we can find

  $$\begin{aligned} b_{n,0}&= -\infty ,\\ b_{n,i}&= F_t^{-1}(b_{1,i_1-1},b_{1,i_1},\ldots ,b_{n_{t-1},i_{t-1}-1},b_{n_{t-1},i_{t-1}} ;\overline{p}_{n,i}), \\ b_{n,s(n)}&= \infty , \end{aligned}$$

  where the conditional distributions are

  $$\begin{aligned} F_t(u_1, v_1,\ldots ,u_{t-1}, v_{t-1}; \xi )=\frac{P(u_1\le \xi _1\le v_1,\ldots ,u_{t-1}\le \xi _{t-1}\le v_{t-1}; \xi _t\le \xi )}{P(u_1\le \xi _1\le v_1,\ldots ,u_{t-1}\le \xi _{t-1}\le v_{t-1})} \end{aligned}$$

  and their inverse functions $F_t^{-1}(u_1, v_1,\ldots ,u_{t-1}, v_{t-1}; p)$ are such that $F_t^{-1}(u_1, v_1,\ldots ,u_{t-1}, v_{t-1}; F_t(u_1, v_1,\ldots ,u_{t-1}, v_{t-1}; \xi ))=\xi$.

As soon as we have calculated the bounds for the stochastic process we can approximate the process by the midpoints of the obtained intervals.

Example (Gaussian distribution) Considering the treestructure with probabilities in the Fig. 5a, suppose that the stochastic process $(\xi _1,\dots , \xi _T)$ is distributed as multivariate normal variable with mean vector $(\mu _1,\dots , \mu _T)$ and non-singular covariance matrix $C = (c_{s,t})_{s,t=1,\ldots ,T}$. The value at the root is known and suppose that it is equal to 0.

Fig. 5

Approximation of a normal distribution using the bounds for the stochastic process sitting on given treestructure. a Given treestructure with probabilities. b Bounds for the Gaussian stochastic process. c Approximation of a normal distribution

From Lipster and Shiryayev (1978) we know that the conditional distributions at each stage are of the form¹

$$\begin{aligned} N\left( \mu _t + \left( \xi ^{t-1}-\mu ^{t-1}\right) C_{t-1}^{-1} c^t, c_{t,t} - (c^t)^\top C_{t-1}^{-1} c^t\right) , \end{aligned}$$

(8)

where the covariance matrix is dissected into

$$\begin{aligned} C_t =\left( \begin{array}{c|c} C_{t-1} &{} c^t\\ \hline (c^t)^\top &{} c_{t,t} \end{array} \right) , \end{aligned}$$

(9)

and $\mu ^t$ is the history of the mean values up to time $t$.

Using the quantile function for the conditional normal distribution (8) at each stage of the tree (Fig. 5a) we find lower and upper bounds at each node for the Gaussian distribution (for example, $b(1, 1)$ and $b(1, 2)$ for the stage $t=1$ as it is shown in the Fig. 5 b). Then we approximate the stochastic process by the midpoints of the obtained bounds (Fig. 5c).

At $t=1$: The bounds for the stochastic process are

$$\begin{aligned} (-\infty , F_1^{-1}(0.1)]\cup (F_1^{-1}(0.1), F_1^{-1}(0.7)]\cup (F_1^{-1}(0.7), \infty ), \end{aligned}$$

At $t=2$: The bounds are

$$\begin{aligned} (-\infty , F_2^{-1}(0.4)]\cup (F_1^{-1}(0.4), F_1^{-1}(0.7)]\cup (F_1^{-1}(0.7), \infty ),\\ (-\infty , F_2^{-1}(0.8)]\cup (F_1^{-1}(0.8), \infty ),\\ (-\infty , F_2^{-1}(0.5)]\cup (F_1^{-1}(0.5), \infty ). \end{aligned}$$

$\square$

Such an approximation method helps us to calculate the upper bound 6 of the nested distance between stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$ with Lipschitz property and a tree with values $y_{n,t}$ sitting on the nodes (with nested distributions $\mathbb P$ and ${\widetilde{\mathbb{P }}}$ respectively):

$$\begin{aligned} d\left( \mathbb{P },{\widetilde{\mathbb{P }}}\right) \le \sum _{t=1}^T\sum _{n\in \mathcal{N }_t} \mathbb{E }\left( |\xi _t-y_{n,t}|\;|\xi ^{t-1}\in \mathbb{B }^{t-1}\right) P\left( \xi ^t\in \mathbb{B }^t\right) \Pi _{s=t+1}^{T+1}(K_s+1), \end{aligned}$$

where $\mathbb{B }_t$ is the bounds in the form $\mathbb{B }_t=\{{\xi _t}: b_{n_{t},i_{t}(n)-1}\le {\xi _t}\le b_{n_{t},i_{t}(n)}\}$ ($\mathbb{B }^t$ is a history of all the bounds up to time $t$); $\mathcal{N }_t$ is a set of all node indexes $n$ at the stage $t$ of the tree.²

4.2 Multi-dimensional case

Suppose that the tree is given and that at each stage of this tree a multi-dimensional random variable $\xi _t,\; t=1,\ldots ,T$ with known continuous multi-variate distribution function $F_t$ is sitting. The same as for the one-dimensional random variable, we would like to approximate the stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$ by the given tree.

In case of one-dimensional random variable the problem is relaxed to the approximation based on the quantiles of the one-dimensional distribution. In case of multi-dimensional random variable the problem is more involved, as there is no quantile function for the multi-dimensional distribution $F_t$. The way to approximate the multi-dimensional distribution is to use the Voronoi diagram (read Voronoi (1907) for the details), that allows to divide the space into given number of regions and to approximate the distribution by the midpoints of these regions (Fig. 6). To assign probabilities to the approximate points we need to calculate the area of the regions in the Voronoi diagram: the way to do this is to generate $N$ random points from the distribution function $F_t$ and to calculate how many of them are in the specific region (suppose, $n$). The ration $\frac{n}{N}$ is the necessary probability $p$ (Fig. 6).

Fig. 6

Bivariate Gaussian distribution sitting on the Voronoi diagram

4.3 Numerical algorithms

Numerical algorithms for distributional quantization should solve the problem of finding $N$ points $z_1$,...,$z_N$ from a given distribution $F$, such that the Kantorovich distance between the given continuous distribution and the discrete distribution sitting on the obtained points is minimized (Fort and Pagés 2002; Heitsch and Römisch 2009; Pflug and Pichler 2011; Rachev 1991; Römisch 2010).

At first, consider $L_1$-distance $D(z_1,\dots , z_N) = \int \min _i (| x - z_i|) \, dF(x)$ to be minimized, where $F$ is a distribution function on $\mathbb{R }^N$.

We distinguish between one-dimensional and multi-dimensional cases:

• One-dimensional case: as soon as the solution of the quantization problem has been found, one can define the breakpoints $q_i = \frac{1}{2}(z_i+z_{i+1})$ for $i=1,\dots , N-1,\,q_0=-\infty$ and $q_N=\infty$, the intervals $I_i=[q_{i-1},q_i]$ for $i=1,\dots N$ and the probabilities $p_i = F(q_i) - F(q_{i-1})$. Then the following equations must hold: $z_i = F^{-1}(p_1 + \dots + p_{j-1} + \frac{p_i}{2})= F^{-1}(\frac{F(q_{i-1})+F(q_i)}{2}),$ i.e. $z_i$ is the conditional median within $I_i$;

• Multi-dimensional case: in case random variable is multi-dimensional, the quantile function cannot be used any more as there is no analogue for it in the multi-dimensional space. It is possible, thought, to use random number generation technique in order to calculate probabilities of the Voronoi cells (or regions) Voronoi (1907).

The following iterative algorithms solve the problem for one-dimensional and multi-dimensional cases (converges at least to local solution):

Secondly, consider $L_2$-distance $D(z_1, \dots , z_N) = \int \min _i ( x - z_i)^2 \, dF(x)$ to be minimized, where $F$ is the distribution function on $\mathbb{R }^N$. The following numerical algorithms work for the minimization of $D(z_1, \dots , z_N)$ for both one-dimensional and multi-dimensional cases:

5 Optimal quantization based on the nested distance minimization

Using the optimal quantization method on the stage-wise basis we minimize Kantorovich distance at each stage of the tree, but that does not mean that the nested distance between stochastic process and this tree is minimized. In this section we are going to study what minimization of the Kantorovich distance means for the minimization of the nested distance and to check if there is a better quantization of the distribution sitting on the tree than the quantization that minimizes the Kantorovich distance.

Let the stochastic process $(\xi _1, \dots , \xi _T)$ be distributed as a multivariate normal variable with mean vector $(\mu _1, \dots , \mu _T)$ and non-singular covariance matrix $C = (c_{s,t})_{s,t=1,\ldots ,T}$. Denote the conditional expectations and variances of $\xi _t$ given $\xi _{t-1}$ by $\mu _t(\xi _{t-1})$ and $\sigma ^2_t(\xi _{t-1})$ correspondingly. Consider the main submatrix of the covariance matrix and dissect it as it is shown in (9). Then the conditional distribution of $\xi _t$ given that $\xi ^{t-1}$ is a normal distribution $P(\cdot |\xi ^{t-1})$ of the form (8). We claim that

$$\begin{aligned} d\left( P_t\left( \cdot |\xi _1^{t-1}\right) , P_t\left( \cdot |\xi _2^{t-1}\right) \right) \le \left\| \left( \xi _1^{t-1}-\xi _2^{t-1}\right) C_{t-1}^{-1} c^t\right\| . \end{aligned}$$

Let $\xi \sim N(0, \sigma _t)$ and $\xi _1=a_1+\xi$ and $\xi _2=a_2+\xi$. Then $\xi _1\sim N(a_1, \sigma _t),\,\xi _2\sim N(a_2, \sigma _t)$ and therefore

$$\begin{aligned} d(N(a_1, \sigma _t), N(a_2, \sigma _t))\le \mathbb{E }(||\xi _1-\xi _2||)=||a_1-a_2||. \end{aligned}$$

Let $\mu ^t = (\mu _1, \dots , \mu _t)^\top$. Setting $a_1=\mu _t + (\xi _1^{t-1}-\mu ^{t-1}) C_{t-1}^{-1} c^t,\,a_2=\mu _t + (\xi _2^{t-1}-\mu ^{t-1}) C_{t-1}^{-1} c^t$ and $\sigma _t=c_{t,t} - (c^t)^\top C_{t-1}^{-1} c^t$ we obtain the result.

Using the Cauchy-Schwarz inequality we derive

$$\begin{aligned} d\left( P_t\left( \cdot |\xi _1^{t-1}\right) , P_t\left( \cdot |\xi _2^{t-1}\right) \right)&\le ||\left( \xi _1^{t-1}-\xi _2^{t-1}\right) C_{t-1}^{-1} c^t||\le \\&\le ||C_{t-1}^{-1} c^t||||\xi _1^{t-1}-\xi _2^{t-1}||. \end{aligned}$$

Hence, normal distribution has Lipschitz property with $K_t=||C_{t-1}^{-1} c^t||$.

Suppose now that the treestructure is given and let $\widetilde{P}^+_t$ be the solution of the minimization problem $\min _{\widetilde{P}_t} d(P_t, \widetilde{P}_t)$ on this treestructure for the case of normally distributed stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$. Let ${\widetilde{\mathbb{P }}}^+$ be the corresponding nested distribution and $\widetilde{P}^+$ be the corresponding joint distribution.

As normal distribution has Lipschitz property, bounds (6) hold for the stochastic process $\xi$. Using bounds (6) with $\widetilde{P}^+_t,\,{\widetilde{\mathbb{P }}}^+$ and $\widetilde{P}^+$ one can derive the bounds for the minimal nested distance between stochastic process and a tree:

$$\begin{aligned} d\left( \mathbb{P }, {\widetilde{\mathbb{P }}}^*\right) =\min _{{\widetilde{\mathbb{P }}}}d\left( \mathbb{P }, {\widetilde{\mathbb{P }}}\right) \le \sum _{t=1}^Td\left( P_t, \widetilde{P}^+_t\right) \Pi _{s=t+1}^{T+1}(K_s+1)=U^+, \end{aligned}$$

where ${\widetilde{\mathbb{P }}}^*$ denotes the solution of the minimization problem $\min _{{\widetilde{\mathbb{P }}}}d(\mathbb{P }, {\widetilde{\mathbb{P }}})$.

Numerical calculation of the true nested distance $d(\mathbb{P }, {\widetilde{\mathbb{P }}}^*)$ can be done by the finding of upper bound $U^*_2=d(\mathbb{P }^+, {\widetilde{\mathbb{P }}}^*)+\sum _{t=1}^Td(P_t, {P}^+_t)\Pi _{s=t+1}^{T+1}(K_s+1)$ between given tree and the approximate scenario tree, where $P_t^+$ is a solution of the minimization problem $\min _{{\widetilde{P}_t}}d(P_t, {\widetilde{P}}_t)$ and $\mathbb{P }^+$ is a corresponding nested distribution.

If the bushiness of the approximate tree is high enough, the error term converges to zero $(\sum _{t=1}^Td(P_t, {P}^+_t)\Pi _{s=t+1}^{T+1}(K_s+1)\rightarrow 0)$ and, hence, the distance $d(\mathbb{P }, {\widetilde{\mathbb{P }}}^*)$ can be calculated as $d(\mathbb{P }^+, {\widetilde{\mathbb{P }}}^*)$ (according to Theorem 3.2), i.e.

$$\begin{aligned} d\left( \mathbb{P }, {\widetilde{\mathbb{P }}}^*\right) =\lim _{bush\rightarrow \infty } d\left( \mathbb{P }^+, {\widetilde{\mathbb{P }}}^*\right) . \end{aligned}$$

The question of interest is the relationship between $d(\mathbb{P }, {\widetilde{\mathbb{P }}}^*),\,d(\mathbb{P }, {\widetilde{\mathbb{P }}}^+)$ and $d(P, \widetilde{P}^+)$. For the Gaussian process (which distribution can be described stage-wise by the formula (8) with covariance matrix independent on the previous values of the process) is experimentally shown that the upper bound $U^+$ (i.e. the minimal upper bound) gives a good approximation for the minimal nested distance. Figure 7 shows the behavior of the nested distance and the error term with respect to the minimal upper bound. Generating different possible tree scenarios and increasing the bushiness of the approximate tree we check if it is possible to obtain nested distance lower than the minimal upper bound: it comes out that the resulting nested distance does not appear to be lower than $U^+$ (Fig. 7a) and in the best case it is very close to the minimal upper bound (Fig. 7b).

Fig. 7

Behavior of the nested distance between stochastic process and a tree

Though the Kantorovich distance minimization can give a good approximation of the minimal nested distance for the case of Gaussian distribution, it is not clear if this property holds for other distribution functions. Let us, for example, check if the situation changes in case we include the dependence of the covariance on the previous values to the formula of the stage-wise normal distribution $N(\mu , \sigma )$ (8): $\sigma =c_{t,t} - (c^t)^\top C_{t-1}^{-1} c^t+\frac{1}{2}(\xi ^{t-1}-\mu ^{t-1})(\xi ^{t-1}-\mu ^{t-1})^T$.

Figure 8 shows that the minimal nested distance between stochastic process and the tree becomes sufficiently lower than the minimal upper bound in this case and it is not enough to find the minimal upper bound in order to approximate the stochastic process by the tree with given treestructure. Hence, other possible quantization methods based on the minimization of the nested distance between stochastic process and a tree rather than on the minimization of the Kantorovich distance should be developed.

Fig. 8

Minimal nested distance between stochastic process and the tree w.r.t. minimal upper bound

6 Applications

In the previous sections we have described algorithms for the approximation of continuous distribution function $F$ of the stochastic process $\xi =(\xi _1,\ldots ,\xi _T)$. In this section we would like to demonstrate some applications of the stage-wise approximation algorithms for the solution of multi-stage stochastic optimization programs. The algorithm for the numerical solution of the approximate problem (2) is:

• (1) Create a simple tree of the height $T$ and define it by the bushiness vector (Tree 2);

• (2) Generate the realization of the scenario process $\xi =(\xi _1,\ldots ,\xi _T)$ either randomly or optimally according to the known distribution function $F$;

• (3) Solve problem (2) with a use of any numerical method;

• (4) Increase the bushiness of Tree 2 and goto step 2;

• (5) Iterate until convergence.

The algorithm converges according to the Theorem 3.2.

6.1 Test example: multi-stage inventory control problem

Let us consider a multi-stage inventory control problem as an example for the multi-stage stochastic optimization program which has been deeply studied in Pflug and Römisch (2007) and for which the explicit solution is known. That gives us an opportunity to compare approximate solutions obtained by the developed algorithms with the true solution and, hence, to see the quality of the approximation.

The grocery shop has to place regular orders one period ahead.

• The random process $\xi _1, \ldots , \xi _T$ defines the demand for goods of the shop at times $t=1, \ldots , T$;

• $x_{t-1},\,t=1,\ldots ,T$ is an order of goods one period ahead; the cost for ordering one piece is one;

• Unsold goods may be stored in the inventory with a storage loss $1-l_t$;

• If the demand exceeds the inventory plus the newly arriving order, the demand has to be fulfilled by rapid orders (which are immediately delivered), for a price of $u_t>1$ per piece (the shop pays $u_t>1$ per piece);

• The selling price is $s_t\,(s_t>1)$ and the final inventory $K_T$ has a value $l_TK_T$.

Let $K_t$ be the inventory volume right after all sales have been effectuated at time $t$ with $K_0=0$ and $M_t$ be the shortage at time $t$. The problem is to maximize the expected profit:

$$\begin{aligned} \max _{x}\mathbb{E }[\sum _{t=1}^T(s_t\xi _t-x_{t-1}-u_tM_t)+l_TK_T,\\ x_t\triangleleft \mathcal{F }_t,\; t=1,\ldots ,T,\\ l_{t-1}K_{t-1}+x_{t-1}-\xi _t=K_t-M_t,\\ K_t\ge 0,\; M_t\ge 0. \end{aligned}$$

Let the demand $(\xi _1, \dots , \xi _T)$ in multi-inventory control problem be distributed as a multivariate normal variable with mean vector $(\mu _1, \dots , \mu _T)$ and non-singular covariance matrix $C = (c_{s,t})_{t=1,\ldots ,T; s=1,\ldots ,T}$, then the exact analytical solution of the problem is

$$\begin{aligned} m^*=-\sum _{t=1}^Tu_t\mu _t+\sum _{t=1}^T(u_t-1)\left\{ \mu _t-\frac{1}{\beta _t}\sqrt{\frac{c_{t,t} - (c^t)^\top C_{t-1}^{-1} c^t}{2\pi }}\Upsilon \right\} , \end{aligned}$$

where $\Upsilon =exp(-\frac{1}{2}[\Phi ^{-1}(min(\beta _t, 1-\beta _t))]^2)$ and $\beta _t=1-\alpha _t,\,0<\alpha _t<1$; $\mu _t(\xi _{t-1})$ and $\sigma ^2_t(\xi _{t-1})$ are conditional expectations and variances of $\xi _t$ given $\xi _{t-1}$. The filtration $\mathcal{F }_t=\sigma (\xi _1,\ldots ,\xi _T)$ is generated by the process $(\xi _1,\ldots ,\xi _T)$ [(see section 3.3.3 in Pflug and Römisch (2007)].

So, the optimal value for the normal case of the multi-stage inventory control problem depends only on the mean vector and the covariance matrix of the random process $\xi =(\xi _1,\ldots ,\xi _T)$.

As the inventory control problem can be solved explicitly we can use this advantage to check the approximation algorithms for the solution of the multi-stage stochastic optimization problem. We focus on two methods for the approximation of the distribution function: stage-wise random generation and stage-wise optimal quantization (i.e. minimization of the Kantorovich distance). For Gaussian distribution it was shown in Fig. 7 that the stage-wise minimization of the Kantorovich distance gives a good approximation for the minimal nested distance.

Figure 9 shows how the approximate optimal solutions obtained by random generation and optimal quantization behave with respect to the explicit solution. The solution received with a use of random generation technique allows to achieve the convergence in probability (boxplot in Fig. 9). The solution by optimal quantization, though, approaches the explicit solution pointwise (the convergence is in bushiness).

Fig. 9

Convergence of the approximate solution for the inventory-control problem

6.2 Test example: catastrophic risk-management

Now we consider a multi-stage stochastic optimization problem for which the explicit solution is unknown. Hence, we solve this problem only by approximation.

Consider a government (a policy-maker), which may lose a part of its stock $S_t$ at time $t=1,\ldots ,T$ because of the random natural hazard event of loss size $\xi _t$. The stock is depreciating in time. At each period the government has budget $B_t$ to spend and is going to take some decision about the budget allocation. To rise the stock to a new level the policy-maker invests in the next period (i.e. the stock is summed up of the depreciated stock and the investment). At the same time the government has an opportunity to be insured against some types of natural hazards and has a possibility to take debts from other governments in which case it also pays the debt service. Some money should be spent for the consumption as well. The decision about the amount of investment, insurance, consumption and debt should be the best possible for the maximization of the objective of the policy-maker, i.e. optimization problem arises (for more problems of this type see Ermoliev et al. 2010; Hochrainer and Pflug 2005):

• (1) At first stage the policy-maker consumes, insures and invests into the next period and has an opportunity to take a debt;

• (2) At all stages except the first and the last one the policy-maker invests, insures, consumes, loses some part of the stock and obtains the insurance in case of natural hazard event; there is an opportunity to take a debt and the government should return interests on all previously taken debts;

• (3) At the last stage the policy-maker consumes, loses some part of the stock and receives the insurance in case of natural hazard event. All taken debts should be returned.

Consider the following components of the model: $S_t$—stock quantity at period t; $r$—return on the stock; $B_t=rS_t$—available budget at period t; $\delta$-depreciation rate; $\xi _t$—random relative loss because of the natural hazard; $i_t$—interest rate of the debt; $V$—insurance load; $E_t$—loss expectation $E_t=\mathbb{E }(\xi _t)$ and the decision variables: $d_t$—debt that might be taken at each period t; $c_t$—consumption at period t; $z_t$—insured value of the stock; $x_t$—amount of investment.

The multi-stage stochastic optimization program of our consideration maximizes the expected governmental stock dependent on the possible losses after natural hazards taking into account stage-wise consumption:

$$\begin{aligned}&\displaystyle \max _{d_t, c_t, z_t,x_t}(1-\alpha )\sum _{t=1}^{T}\rho ^{-t}\mathbb{E }(u(c_t))+\alpha \mathbb{E }(u(S_T)), \\&\displaystyle x_t\triangleleft \mathcal{F }_t,\; z_t\triangleleft \mathcal{F }_t,\; t=1,\ldots ,T \; c_t\ge c,\;, d_t\le d,\; t=1,\ldots ,T,\\&\displaystyle rS_t-\sum _{j=1}^{t-1} d_ji_j\ge c_t+x_t+E_t(1+V)z_tS_t, t=1,\ldots ,T-1,\\& \qquad \qquad \qquad \displaystyle rS_T-\sum _{t=1}^Td_t\ge c_T,\\&\displaystyle S_{t+1}=[(1-\delta )S_t+x_t](1-\xi _t)+z_t\xi _tS_t+d_{t+1},\; t=1,\ldots ,T-2\\&\displaystyle S_{T}=[(1-\delta )S_{T-1}+x_{T-1}](1-\xi _T)+z_T\xi _TS_T. \end{aligned}$$

In this decision problem the attitude towards risk is introduced by the utility function $u(c)=\frac{c^{\gamma }-1}{\gamma }$ with a constant relative risk aversion $R=1-\gamma$. Changing $\gamma$ we can introduce risk-averse ($\gamma <1$), risk-neutral ($\gamma =1$) or risk-loving ($\gamma >1$) policy-maker.

The following pattern shows how the governmental stock develops over time:

Though this problem can hardly be solved analytically one can solve it numerically using the multi-stage stochastic optimization programming algorithms with scenario process $\xi =(\xi _1,\ldots ,\xi _T)$ that describes losses after natural hazard events. The scenario process is supposed to be distributed according to the estimated Pareto distribution that is usually used for the description of natural hazards.

Suppose that the policy-maker would like to solve the decision problem using the developed algorithms for the tree approximation. Increasing the bushiness of the approximate scenario tree, generating Pareto losses sitting on this tree either randomly or optimally and solving the optimization problem we obtain the convergence to its explicit solution according to the Theorem 3.2 (Fig. 10). The convergence holds both for random generation and for optimal quantization methods, though for the case of random generation the convergence is in probability (Fig. 10).

Fig. 10

Random generating v.s. Optimal quantization