Loads distributed in vivo among vertebrae, muscles, spinal ligaments, and intervertebral discs in a passively flexed lumbar spine

Abstract

The load distribution among lumbar spinal structures—still an unanswered question—has been in the focus of this hybrid experimental and simulation study. First, the overall passive resistive torque-angle characteristics of healthy subjects’ lumbar spines during flexion–extension cycles in the sagittal plane were determined experimentally by use of a custom-made trunk-bending machine. Second, a forward dynamic computer model of the human body that incorporates a detailed lumbar spine was used to (1) simulate the human–machine interaction in accordance with the experiments and (2) validate the modeled properties of the load-bearing structures. Third, the computer model was used to predict the load distribution in the experimental situation among the implemented lumbar spine structures: muscle–tendon units, ligaments, intervertebral discs, and facet joints. Nine female and 10 male volunteers were investigated. Lumbar kinematics were measured with a marker-based infrared device. The lumbar flexion resistance was measured by the trunk-bending machine through strain gauges on the axes of the machine’s torque motors. Any lumbar muscle activity was excluded by simultaneous sEMG monitoring. A mathematical model was used to describe the nonlinear flexion characteristics. The subsequent extension branch of a flexion–extension torque–angle characteristic could be significantly distinguished from its flexion branch by the zero-torque lordosis angle shifted to lower values. A side finding was that the model values of ligament and passive muscle stiffnesses, extracted from well-established literature sources, had to be distinctly reduced in order to approach our measured overall lumbar stiffness values. Even after such parameter adjustment, the computer model still predicts too stiff lumbar spines in most cases in comparison with experimental data. A review of literature data reveals a deficient documentation of anatomical and mechanical parameters of spinal ligaments. For instance, rest lengths of ligaments—a very sensitive parameter for simulations—and cross-sectional areas turned out to be documented at best incompletely. Yet by now, our model well reproduces the literature data of measured pressure values within the lumbar disc at level L4/5. Stretch of the lumbar dorsal (passive) muscle and ligament structures as an inescapable response to flexion can fully explain the pressure values in the lumbar disc. Any further external forces like gravity, or any muscle activities, further increase the compressive load on a vertebral disc. The impact of daily or sportive movements on the loads of the spinal structures other than the disc cannot be predicted ad hoc, because, for example, the load distribution itself crucially determines the structures’ current lever arms. In summary, compressive loads on the vertebral discs are not the major determinants, and very likely also not the key indicators, of the load scenario in the lumbar spine. All other structures should be considered at least equally relevant in the future. Likewise, load indicators other than disc compression are advisable to turn attention to. Further, lumbar flexion is a self-contained factor of lumbar load. It may be worthwhile, to take more consciously care of trunk flexion during daily activities, for instance, regarding long-term effects like lasting repetitive flexions or sedentary postures.

1 Introduction

Already during embryonal development, biological tissue is formed by mechanical loads [for a recent review, see Miller and Davidson (2013)]. The response of biological tissue to given mechanical loads depends both on the loads themselves and on the tissue’s susceptibility to damage (Ker 2002). In living biological tissue, repair processes counter potential damage caused by loads (Ker 2007). Of course, susceptibility to damage and effectiveness of repair depends, as all other biological processes, on genetic disposition. This article focuses on providing mechanical load data to enable the prediction of tissue responses in the lumbar spine.

A comprehensive, retrospective, cohort, twin study has demonstrated that degeneration of intervertebral discs (IVDs) is mainly determined by genetics (Battie et al. 1995, 2009; Videman et al. 1997). Degeneration can be seen as irreversibly accumulated damage. Beyond the cited observation for IVDs, in particular, and despite more than a century of research into mechanical loads on spinal structures (White III and Panjabi 1990; Panjabi and White III 2001), there is virtually blank space—hypotheses at best—instead of knowledge regarding the mechanisms of how mechanical loads may induce damage and eventually degeneration of spinal structures. One reason for this is still a lack of knowledge about the load distribution among all main structures of the spine—the vertebrae with their connecting facet joints (FACs), the muscles, the ligaments (LIGs), and the IVDs—in vivo and in motu.

For this to understand, a critical review on how load distributions in the lumbar spine have been computed until today is advisable, almost mandatory. A look back on the record of model development reveals that the computer-based calculation of spinal loads started at the end of the sixties, which has been nicely summarized by Chaffin (1969). In this paper, he also presented an example of a computer-based quantitative assessment of the compressive load in a pelvis–spine cross-section, performing an entirely inverse statics approach by use of a seven-segment whole-body model in the sagittal plane, with kinematic and human anthropometric data, as well as the lumped lever arm of all erector spinae muscle parts as an input. It took another decade to significantly increase sophistication—particularly introducing optimization techniques (Gracovetsky et al. 1977)—of computer-based calculations of the spine-internal loads.

In a study (Gracovetsky et al. 1981) that simulated trunk movements—in the sagittal plane—of one athlete subject who lifted weights of up to approximately 200 kg to hip height, with the trunk initially oriented almost parallel to the ground, the authors demonstrated then that the minimization of a combination of muscle stresses and squeezing torques as well as shear forces in the IVD joints validly predicts electromyographic (EMG) surface signals. For this, they assumed that EMG signals are a good representation of quasi-static muscle forces. They concluded that lifting work in this whole-body lifting movement seems to be mainly generated by hip extensors erecting the pelvis, rather than by the trunk muscles (Gracovetsky 1981, 1986). They also suggested that, when lifting the heaviest weights, the lumbar torques provided by the lumbar LIGs are approximately five times higher than what can be maximally generated by active lumbar muscles.

In a work almost contemporary to Gracovetsky et al. (1981), Schultz et al. (1983) computed, for a given external load on either the chest or the arms of an upright standing human, the static load distribution solely between the redundant set of the main muscles in the L3 level transversal plane, neglecting any LIG forces in conspicuous contradiction to a main finding by Gracovetsky et al. (1981). As in Gracovetsky et al. (1981), the muscles’ lines of action and their cross-sectional areas were used as input data. Without LIG forces, they found that the computing scheme minimizing the maximum stresses in all muscles gave the best correlation between calculated individual muscular pulling forces and their corresponding, measured EMG surface signals. The same model with a slightly modified static optimization criterion—minimizing both muscle stresses and spinal compression force—was then applied (Schultz et al. 1985) to calculate the muscle force distribution while statically holding a weight with a downward-flexed spine. Data compiled in a later study (McGill and Norman 1987, see their table 1) demonstrated that neglecting the LIGs as in Schultz (1983, 1985) comes at the cost of calculating muscle stresses that may be benevolently characterized as ‘at the upper boundary of published maximum values’ (tolerated maximum isometric stress values in the model in the range 30,$\ldots$,100 N cm$^{-2}$). In their later review about the cause of structural failure of spinal structures, Gracovetsky (1986) further demonstrated by measuring the EMG of them. erector spinae at L3 level during a slow, quasi-static 5-kg-weight lifting movement from the same flexed position as in Schultz et al. (1985) that back muscles are practically passive in the most flexed position (spine roughly parallelly aligned to the floor) and concluded that the LIGs must fully compensate the external load from upper body plus maybe a low additional weight. Thus they showed that low to vanishing external loads are very likely compensated solely by the spinal LIGs in significantly forward-bent trunk positions, with muscles increasingly switched on when approaching upright posture.

We would summarize the state of the art regarding lumbar spine loading in the mid-eighties as this: At least with only moderately flexed spines and low external loads, the spinal LIGs seem to be the main compensators for all-day-loads on the spine, and active muscle forces play only a secondary role. Quite the converse, McGill and Norman (1986) predicted in another study that, when (a) external loads of up to about body weight were lifted from the ground with the additional condition of (b) keeping the back distinctly flat, muscle force compensation should clearly dominate, whereas both LIG loads and IVD torsion would be neglectable. We are gravitated at this point to remark three main issues: (1) The viscoelastic properties of neither the IVDs, nor the facet joints, nor the LIGs, nor the passive muscle tissue had then been allowed to determine the load distribution. This statement holds notwithstanding their then one-time incorporation into a model in McGill and Norman (1986): Their calculations yielded vanishing contributions of LIG and IVD stress-strain relations. (2) Boundary conditions and optimization criteria determine the inferred muscle force distribution, while the criteria represent hypotheses, and the forces evidently depend on both the pre-selection of model structures and EMG signals measured. (3) The calibration between EMG signals and muscle forces is generally vague (De Luca 1997).

Next, McGill and Norman (1987) made another two clear points by using a four-segment (pelvis, L5, L4, L3), sagittal-plane lumbar model. First, predictions of shear force components transmitted between vertebrae are very sensitive to assumptions about the force directions routed by the anatomical structures, that is, the fiber directions of the sacrospinalis parts. Second, the erector spinae parts with lever arms of almost 10 cm enable, for one thing, the limiting of compressive IVD forces. For another thing, fully active muscles can probably well compensate torque requirements in bent trunks even if loaded externally with low weights. Both findings are principally not surprizing from a mechanical point of view. They set, however, the level of quantitative significance and sharpened the focus on structure-based modeling.

Next, Jäger and Luttmann (1989) were the first to consistently analyze the mechanical dynamics during weight lifting by taking inertia forces into account. In an inverse dynamics approach deploying an even three-dimensional, musculoskeletal, rigid-body model that included five lumbar segments, they prescribed segmental kinematics and inferred the driving muscular forces and, with this, the constraint forces in the lumbar joints. Their analysis allowed to see that an explosive initiation of the weight lift induces a doubled amplitude of the compressive force peak—solely originating from inertia effects—as compared to the use of a low-jerk lifting technique. As in all other studies by then, the consistency of movement generation by internal forces, which interact with inertia and external forces, and the resulting movement itself had not been in the focus. Full consistency is gained if all internal and external forces are modeled in dependence of parameters and state variables solely, that is, as force laws representing dynamic material properties. For example, neither the contribution of an IVD’s mechanical resistance and its geometric dimension to the joint torque generation in a lumbar cross section, nor the force and torque contributions of the facet joints, nor the dynamic contraction properties of muscle–tendon complexes, nor transversal forces from redirecting lines of action or muscle thickening had been taken into account.

Regarding modeling consistency, a salient strength of the study by Cholewicki and McGill (1996) was that they put a particular emphasis on checking the validity of their model predictions, referring back to basic validity reflections by Lewandowski (1982). Therefore, their rigid-body spine model (Cholewicki and McGill 1996) may still be considered a benchmark. It was introduced as a three-dimensional upgrade of its two-dimensional forerunner (McGill and Norman 1985), which had also been used for calculations in McGill and Norman (1987). The number of spinal elements (lumbar vertebrae: rigid bodies) increased up to five, connecting the pelvis to the cranially located remaining trunk by 18 rotational degrees of freedom, and the number of muscle threads interconnecting vertebrae and pelvis went up to 90. The torsional elastic resistance of all but muscle tissue (i.e., an IVD plus LIGs plus facet joints) connecting each two adjacent bodies was lumped into one rotational spring element nonlinearly depending on the three joint angles to generate three joint torque components. The one-time partitioning in McGill and Norman (1986) into elastic properties of individually modeled LIGs and IVDs had been relinquished again. Muscle forces were fed into the model by calculating their absolute values from measured EMG signals as an input to a Huxley-type muscle model (Ma and Zahalak 1991), modifying these first guesses by varying maximum muscle stress values as little as possible (optimization criterion), and applying the force vectors according to their anatomically based lines of action. The muscle model also calculated muscle stiffness values for the final purpose of the model application: predicting buckling stability of the spine. By analyzing seven different three-dimensional movement and loading situations, in which they assumed that statics is a reasonable approximation, they found that the hazard of buckling is particularly high in conditions of low local torque demand. In some of the analyzed situations, their model computed muscle stress values that approached the upper boundary of published maximum values (100 N cm$^{-2}$), however, a little less than in the studies (Schultz et al. 1983, 1985; McGill and Norman 1987) mentioned above.

Shortly after Cholewicki and McGill (1996) and Wilke et al. (1999) measured—by deploying refined sensor equipment as compared to pioneering work on intradiscal pressure measurement (Nachemson 1960, 1963, 1965, 1966; Nachemson and Morris 1964; Nachemson and Elfström 1970)—the pressure in a volunteer’s L4/5 IVD in vivo for 24 h during various movements and activities, as well as during night sleep. Typical pressure values were 0.5 MPa in upright stance and a pressure ‘recovery’, when lying in bed at night rest, from about 0.1 MPa at lay down to about 0.24 MPa at getting up. As an astonishing mnemonic, the latter value is very close to the theoretical one for L4/5 IVD compression by solely the weight of all body masses located cranially to this IVD (approximately 45 kg pressing on an IVD area of 18 cm$^{2}$). Combined with the volunteer’s anthropometrical data (Wilke et al. 2001), this mechanical data set of internal, in vivo loads on a well-defined spinal structure is to date the hardest available, thus, indeed unique and essential for validation of any current computer model.

Major enhancements of biomechanical spine models during the last two decades focused on incorporating more degrees of freedom as well as a more detailed and naturalistic representation of biological tissue properties, thus, a higher mathematical complexity. For calculating internal load distributions, near to all published model approaches have so far relied on the input variables and optimization criteria already formulated by Chaffin (1969) and Gracovetsky et al. (1977): as an input from measurements or assumptions, they use study-specifically weighted combinations of given kinematics, scenarios of external or partly local, internal load conditions, as well as EMG signals, and solve the mechanical equations of motion in static posture or quasi-static movement situations, usually applying one or multiple optimization criteria to resolve the redundancy of the load-carrying structures. In this, a widely used method is the finite-element (FE) modeling approach. The smallish selection Kiefer et al. (1997), Shirazi-Adl et al. (2002), Arjmand and Shirazi-Adl (2006), Mohammadi et al. (2015) and Ghezelbash et al. (2016) of exemplary papers maps the state of the art in spine FE modeling. From a nice review (Schmidt et al. 2013), it can be learned that FE modeling related to spinal structures goes back to the early seventies when an FE IVD model had been developed that assumed linear elastic properties for the annulus, and the nucleus being made of an ideal fluid. From Schmidt et al. (2013), it can also be learned that “$\ldots$ [FE models] cover nowadays a wide range of complex phenomena involving irregular geometries, nonlinearities, contacting bodies, remodeling, degradation, failure, and multi-physics couplings”.

The work by Christophy et al. (2012) is a recent exception from mainly using the FE method in modeling the spine: They developed a three-dimensional lumbar spine model with 238 Hill-type muscle fascicles using a software package (Delp et al. 2007) that implements a rigid-body model approach. Rigid-body solvers are made for integrating forward in time (solving) the ordinary differential equations of mechanical model dynamics. The software package (Delp et al. 2007) and thus any potential simulation of movements of the spine model by Christophy et al. (2012) relies on kinematics—or, more generally expressed: trajectories of variables like coordinates, EMG signals, or internal or external forces versus time—as input for driving the dynamics. In contrast, a recent study by Rupp et al. (2015), who employed a musculoskeletal rigid-body model with complexity similar to Christophy et al. (2012), did not use any trajectory-based knowledge or given loads as an input. Instead, all model muscles do only require modeled, event-based stimulation signals for their activation dynamics during movements, and all external loads (e.g., contact forces) are likewise modeled as parametrized force characteristics. With this approach, complete consistency of the entire force and kinematics scenario is guaranteed at any point in time, which allows, for example, simulating shock wave propagation along the body (Rupp et al. 2015, app. 8).

Now using a revised version of the model by Rupp et al. (2015), this paper aims at providing a scenario of the loads on and their distribution among the main internal structures of the human lumbar spine in the well-defined loading condition of the trunk being flexed passively. Due to ethical and principal reasons, this requires both experiments on humans and modeling them by a corresponding musculoskeletal model. The scenario is mechanically and biologically consistent since (1) experimental data acquisition and model calculations have been performed entirely independently and, (2) in the model, the mechanics of all deformable structures are represented by force characteristics which reflect their physiological properties. Issue (1) implies that it is just the boundary conditions that experiment and model have in common. Issue (2) implies that we have aimed at maximizing the degree of model validity by feeding no time-resolved data whatsoever from our (or other) experiments into the model. All this implies, for any single structure of the body including its contact to the environment and the neural input, using parameter information from literature solely. Hence, fully consistent scenarios of distributed external and internal structural loads result from letting physiologically based representations of the body-device contact interaction and the (passive) mechanical properties of all loaded spinal structures equilibrate dynamically, without imposing any optimization criterion for solution selection.

The experimental situation was designed to exclude any muscular stimulation: The spines of the subjects lying on their sides were gently passed through slow flexion–extension (bending) cycles of quasi-static spinal states, with the movements enforced by a strong torque engine of the test device.

Table 1 “Supra and interspinal ligament” data taken from Chazal et al. (1985, table 3): stiffness $k_{AB}$ = $\frac{F_{B}-F_{A}}{\varDelta L_{B} - \varDelta L_{A}}$ and Young’s modulus E = $k_{AB} \cdot \frac{L_{0}}{CSA_{0}}$ calculated therefrom; “origin” denotes whether a ligament is taken from a cadaver (“dcd”) or a living person (“liv”), “years” denotes the person’s age; $\varDelta L_{i}$ are elongations from rest length $L_{0}$; $F_{i}$ are resistive force values in the respective elongation state

Table 2 Parameter values for our model LIGs on lumbar level L4/5: elongation ($\varDelta L_{i}$) data are taken from Chazal et al. (1985, table 3), force data ($F_{i}$) likewise and then divided by three (see Sect. 3.2.1), and rest lengths $L_{0}$ are adjusted to our model geometry (see Sect. 2.5.8)

2 Methods

2.1 Subjects

Nineteen volunteers underwent measurement of passive spine mechanics (Table 3). All subjects had no current episode of low back pain, while the last event of low back pain had occurred at least 1 year ago. Exclusion criteria were known deformations of the spine (e.g. scoliosis), spinal instability, and inflammatory diseases of the spine. All subjects gave written informed consent under the terms of the Declaration of Helsinki. The experimental procedure was reviewed and approved by the local ethics commission (37826/2011/7).

Table 3 Age, body height, and body weight as mean (standard deviation) for all investigated subjects

2.2 Procedure

After consent, the subject was prepared for the measurements. In sitting position, landmarks of the spinous processes at levels L1 and L5 were marked. From these positions, bellies of lumbar spine muscles were located regarding the recommendations of SENIAM for the positioning of surface electromyographic (sEMG) electrodes (Hermens et al. 1999). Selected muscles were longissimus muscle on level L2 and multifidus muscle on lumbar level L4. sEMG recordings were collected from lumbar back muscles to monitor spinal muscle activation during measurements of passive spine mechanics.

For allowing sEMG normalization as an alternative to use of signals from submaximal contractions (see further below), the subject was asked to take a specific posture in which significant activation of the lumbar muscles was found. For this, the subject held the knees slightly bent in standing posture, with the trunk slightly forward-tilted and the lumbar spine held in pronounced lordosis. The subject was asked to keep this posture for a few seconds.

Then, the subject was placed in the testing machine, lying on the base table part on the right side of its body (Fig. 1). When lying relaxed, infrared light-emitting markers were placed over the spinous processes on level L1 and L5 to measure the curvature of the lumbar spine, and on spina iliaca posterior superior (SIPS) for position information of the subject.

Fig. 1

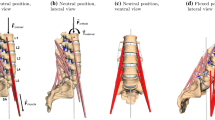
Principal construction of the trunk-bending machine with supporting tables for upper body (mobile table) and lower body (base table). Top view a: the machines rotational axes $\mathcal {A}$ (a strong motor driving flexion/extension), $\mathcal {B}$ (also motor-driven: regulation of subject-specific positions, mainly), and $\mathcal {S}$ below the tables are shown; furthermore, the corresponding angles $\phi _{\mathcal {A}}$, $\phi _{\mathcal {B}}$, $\phi _{\mathcal {A}\,\mathcal {S}}$, and $\phi _{\mathcal {S}}$ representing the machine’s geometry are measured by angle sensors integrated into the bending machine, which also determines the position $\mathcal {K}$ of the assumed point of force application at the shoulder cushion roll. Front view b: a subject positioned and fixed in the testing machine

Fig. 2

The global coordinate system (top right: fixed at the immobile base table) and the local joint coordinate system (top left) located within an IVD (as an example, here, between vertebrae L4 and L5). The position of its origin and its rotations are calculated as the arithmetic mean of the homogeneous $4\times 4$ matrices (Denavit and Hartenberg 2014; Hartenberg and Denavit 1964; Legnani et al. 1996a, b)—also termed “rototranslation” in Legnani et al. (1996a)—of the two constituting joint coordinate systems (top, left: red triads ‘TO’ and ‘FROM’). The angular orientation $\phi _{L\,i/i+1}$ of two vertebrae relative to each other (here: i = L4 and $i+1$ = L5) can be specified by projecting each their local x—(the dashed midlines of the adjacent vertebrae) or corresponding z-axes, respectively, onto the table (global x–y) plane and then calculating the angle between both projected lines. In the neutral (lordotic) lumbar posture (Sect. 2.5.3: lumbar angle $\phi _{neutral}\,=\,-25.6^{\circ }$), $\phi _{L4/5}$ = $\phi _{L5}$ - $\phi _{L4}\,=\,-7^{\circ }$ applies (Table 4, rightmost column; cf. Figs. 9,10), and the angular orientation of the two joint triads that define a joint is 0$^{\circ }$ in each lumbar joint, that is, the respective endplates of the two adjacent vertebrae are aligned (see bottom, left)

Table 4 Geometry of the neutral (lordotic) lumbar posture, according to Kitazaki and Griffin (1997), projected into the sagittal plane

After height adjustment of the upper body and the legs (to position the body non-twisted and straight in the frontal plane of the body), legs, pelvis, and shoulders were fixed in the testing machine by adjustable pads, cushions, and a saddle (see Sect. 2.3.1). The head was comfortably positioned on a pillow. Fixation of the subject was necessary to prevent rotation of the pelvis. With this, solely rotations of the spine in the sagittal plane of the body were possible. To prevent the body from passive scoliosis due to relaxation and for comfort reasons, thorax and the upper (left) leg were supported by cushions (Fig. 1). Finally, the left arm was positioned on the left hip to prevent shoulders and upper spine from distortion.

The experimental protocol was as follows: First, the machine was set to idle mode, in which the machine did not apply forces on the subject, while the subject was asked to relax. Then, the investigator iteratively rotated—with forces as low as possible—the mobile table part, with the subject’s trunk fastened to, into a subject-specific neutral posture in which the passive structures of the trunk generated near-zero resistance. Next, to provide a submaximal level of muscular activation for sEMG normalization, the subject was asked to contract the back muscles against the hereto fixed testing machine. For all following tests, the subject was asked to relax again. Next, the subject’s range of motion (ROM) of the lumbar spine was manually tested by the investigator with the testing machine once again in idle mode. Eventually, a cyclic flexion trial with up to 20 repetitions at 10$^{\circ }$ s$^{-1}$ angular velocity of the testing machine (lasting approximately 10 minutes) was carried out with an amplitude of 80% of the subject’s lumbar ROM. In case the investigator noticed an intermediate sEMG signal above resting level, the subject was asked to relax, and the experiment was restarted.

The flexion movements represent daily activities like bending or lifting low weights. All experimental procedures happened without any subject feeling pain. The combination of supported passiveness and slow-moving, long-lasting trial conditions actually relaxed the subjects such that most of them were near sleep at the end of the experimental protocol.

2.3 Biomechanical measurements

2.3.1 Trunk bending machine

In order to eliminate gravitational loads and enable sustained relaxation of the trunk muscles, a measurement position was chosen, in which the subject lay on the right side. Choosing this side further reduced body-weight-induced pressure on the cardio-vascular system. This is in line with other setups (McGill et al. 1994; Parkinson et al. 2004) measuring passive trunk stiffness. Impact of the moment of inertia was eliminated by measuring and analyzing data solely during conditions of constant angular velocity.

The trunk-bending machine (approximately 250 kg) that applies torques on a subject consists in fact of two separate tables (Fig. 1). The base table supports the legs and the pelvis, whereas the mobile table supports the upper body with thorax, shoulder/arms, and head. There is no support for the spine between pelvis and thorax in order to prevent any external force acting on the lumbar spine, that would bias mechanical analysis.

The mobile table is driven by two electric motors. The rotational axis of motor $\mathcal {A}$ applies flexion/extension on the subject and is positioned at the edge of the base table (Fig. 1), at which the subject’s spine extends from the base table. The rotational axis of motor $\mathcal {B}$ is used for subject-specific length adjustments and length changes during measurements. The right shoulder of the subject was positioned above rotational axis $\mathcal {S}$, which is a non-powered, frictionless hinge joint. The machine was designed based on the idea that the torque $M_{\mathcal {A}}$ around axis $\mathcal {A}$ controls as good as possible the joint torque transmitted between the structures that create the intervertebral joint flexion axis (angle $\phi _{L4/5}$) of the IVD on the level L4/5. Exerting the machine torque $M_{\mathcal {A}}$ on the subject is realized by applying the force $\mathbf {F}$ at the cushioned roll positioned on top of the scapula. As both axes do actually not coincide, we generally perform an inverse statics analysis (Sect. 2.3.3).

Each electric motor is equipped with a strain gauge for determining the torque around each driven axis of rotation ($\mathcal {A}$ and $\mathcal {B}$). Together with the three angle sensors for the axes $\mathcal {A}$, $\mathcal {B}$, and $\mathcal {S}$, the complete mechanical scenario of the machine (kinematics as well as internal and exerted load) is known and sampled at a frequency of 50 Hz.

A custom-made software was developed to provide measurement protocols for the machine. Two protocols were used: one for holding a static position to resist submaximal voluntary contractions and another for generating cyclic flexion at constant angular velocity. The trunk-bending machine was manufactured by Thumedi GmbH & Co KG, Jahnsbach, Germany.

2.3.2 Lumbar angle

The movements of skin markers nearby the spinous processes at lumbar levels L1 and L5 were measured by a 3-D infrared cine-metric device (Lukotronik, Laitronic, Innsbruck, Austria). We attached, on each level L1 and L5, two markers: one at the cranial and the other at the caudal edge of the tip of a vertebra’s spinous process.

From the coordinates of the two markers on each level, we calculated the angle $\phi$ between the projections of their respective difference vectors onto the x–y (cine-metric) plane of the global coordinate system (Fig. 2), with the x–y planes of the cine-metric and table systems tilted to each other by less than 15$^{\circ }$. The net curvature of the whole lumbar region in such a near-sagittal plane is quantified by this flexion angle $\phi$ that we concisely term ‘lumbar angle’ in the following. Our method of inferring vertebrae from skin marker kinematics in passive flexing movements has been validated earlier (Mörl and Blickhan 2006).

The method of calculating the lumbar angle $\phi$ reflects exactly what has been defined in literature as the clinical procedure to determine the ‘lumbar lordosis angle’ (Polly jr. et al. 1996): from lateral X-ray radiographical views of the spine, each a cranial and a caudal lumbar vertebra’s endplate orientation is measured as the respective projection into the very plane of the measuring device that is assumed to approximate the sagittal plane, and the difference of both projections is calculated.

Lordotic postures, being the anatomical norm, are characterized by negative values of our measure $\phi$, and decreasing lumbar angle values represent increasing lordosis. Vice versa, approaching more kyphotic postures is characterized by increasing lumbar angles and usually termed ‘spine flexion’.

2.3.3 Calculation of the joint torque acting on lumbar level L4/5

We also calculated the so-called joint torque $M_{L4/5}$ and the ‘joint force’ $F=|\mathbf {F}|$, respectively, at the intersection between lumbar levels L4 and L5. Data from three sources of information were used for this: (1) the sensor measuring the torque $M_{\mathcal {A}}$ acting around the bending machine joint $\mathcal {A}$, (2) the angle sensors measuring the current geometry of the machine (Fig. 1a), in particular, the position $\mathcal {K}$ of the shoulder cushion roll and the difference vector perpendicular to the axis $\mathcal {S}$ of the frictionless joint in the bending machine, Fig. 1a, and (3) the positions of the skin marker at L5 and another two markers at the pelvis. Based on $\mathcal {S}$ being frictionless and knowing that the subject is in static equilibrium, we calculated from (1) and (2) the absolute value $|\mathbf {F}|$ of the net external force $\mathbf {F}$ on the subject, assuming $\mathbf {F}$ to act at the roll $\mathcal {K}$ in the direction given by the line $\mathcal {K}$–$\mathcal {S}$.

Next, we used (3) to determine an intersection between L4 and L5, located within the IVD, in which the joint torque $M_{L4/5}$ as well as the joint force $\mathbf {F}$ are transmitted, again applying statics. For this, we calculated a plane on the subjects surface specified by skin markers on each the left and the right side of the spina iliaca superior posterior (SIPS) plus the cranial one at the spinous process L5. A perpendicular vector pointing from the arithmetic mean value of the three markers into the body was assumed to approximate the position of the point of force ($\mathbf {F}$) transmission in the L4/5 intersection. The length of the vector (i.e., the exact position of point of force transmission) was computed from the subject’s anthropometric dimensions.

This point of force ($\mathbf {F}$) transmission in the L4/5 intersection is represented in our computer model by the origin of the local IVD joint coordinate system [termed “virtual” in Rupp et al. (2015)] which is calculated as the arithmetic mean of the homogeneous $4\times 4$ [‘rototranslation’: (Legnani et al. 1996a)] matrices (Denavit and Hartenberg 2014; Legnani et al. 1996a, b) of the two constituting joint triads (Fig. 2).

Now, with the current lever arm $\mathbf {l}_{L4/5,F}$ from the assumed L4/5 joint centre to the point of external force application (cushioned roll), we find the net joint torque acting on lumbar level L4/5 as the cross-product

$$\begin{aligned} M_{L4/5} = \left( \mathbf {l}_{L4/5,F} \times \mathbf {F} \right) |_{z} \end{aligned}$$

(1)

Angle and torque data were processed by a Savitzky-Golay filter (first order, symmetric window, 51 data points for angle data, 21 data points for torque data).

2.3.4 Muscle activation

The PS11-UD long-term measuring device (Thumedi, Jahnsbach, Germany) was used to measure lumbar muscle activation (4–650 Hz, 4096 Hz, 688 nV per bit). Abrasive lotion was used to prepare the skin for bipolar sEMG and electrocardiogram (ECG) measurements. In case of sEMG-impairing hair growth, the subjects were shaved prior to skin preparation. After this, the skin was fumigated and dried. The electrodes used were Ag/AgCl-electrodes (H93SG, Kendall, Covidien, Germany) with a circular uptake area of 10 mm and an inter-electrode distance of 25 mm. The electrode positions of the four investigated muscles were in line with the recommendations of SENIAM. Cross talk due to the ECG signal at very low sEMG levels was suppressed by subtracting the ECG signal in each sEMG channel (Mörl et al. 2010).

Raw data were high-pass-filtered (16 Hz), low-pass-filtered (1 kHz), and band-pass-filtered (moving average multiplies of 50 Hz). The device calculates and stores the root-mean-square (RMS) at 8 Hz. All sEMG data were normalized to the data collected during submaximal voluntary contraction against the fixed trunk flexion machine, thus given in relRMS.

2.3.5 Data synchronization

The trunk flexion machine emits a rectangular hardware signal at the beginning of each measurement. For synchronizing the sampled data, this signal was read by the cine-metric and sEMG measurement devices via a bridge.

2.4 Experimental data analysis and statistics

2.4.1 The passive, nonlinear torque-angle characteristic for lumbar flexion on level L4/5

To describe the mechanical characteristic of the passively resisting torque $M_{L4/5}$ on lumbar level L4/5 as a function of the lumbar spine angle $\phi$, i.e., the passive L4/5 flexion characteristic (examples in Fig. 4), we used the ansatz

$$\begin{aligned} M_{L4/5}\big ( \phi (t) \big )= & {} C \cdot sign(\phi (t) -\phi _\mathrm{TP}) \cdot \left| \phi (t) -\phi _{TP} \right| ^{\nu } \nonumber \\&+\, k_\mathrm{TP} \cdot \big ( \phi (t) - \phi _\mathrm{TP} \big ) + M_\mathrm{TP} \end{aligned}$$

(2)

with $\phi _{TP}$ the lumbar angle at which the turning point (TP) of the nonlinear $M_{L4/5}\big (\phi \big )$ function occurs, and $M_\mathrm{TP}$ the torque value at the TP. The slope $k_\mathrm{TP}$ of the $M_{L4/5}\big (\phi \big )$ curve at the TP is either at its minimum in the analyzed angle range for $\nu >1$ or at its maximum for $\nu <1$. Optimal fit values of the five parameters C, $\nu$, $\varphi _\mathrm{TP}$, $M_\mathrm{TP}$, and $k_\mathrm{TP}$ were calculated for any single flexion and extension phase by using the routine ‘lsqcurvefit’ implemented in ‘GNU Octave’ (version 4.2.2), which is a nonlinear least-square-fit algorithm. Only fits (trials) that fulfilled the requirement of having changed in the final iteration step both the optimized parameter values and the summed residuals by less than 10$^{-10}$ (tolerance) were further considered.

We assessed the fitting quality of the nonlinear ansatz (Eq. (2)) by calculating the median residual value R of the absolute values of the data points’ residuals. Only trials fulfilling R < 0.6 N m were analyzed. For these trials, the distance of each of the five fitted parameter values to its, respectively, ‘allowed’ lower and upper boundary was additionally checked: ‘touching’ a boundary was detected if the absolute difference between value and boundary, normalized to the difference between upper and lower boundary values, was less than 0.001. We found that the lower C boundary was the only one that the fitting algorithm relied on, in about a third of the analyzed trials. With choosing 0.0001 N m $(^{\circ })^{-\nu }$ was the lowest C value allowed (in a possible second fitting run of a trial, see below), the nonlinear fits resulted in $\nu$ values not exceeding 5.1.

Lower and upper limits for C, $\phi _\mathrm{TP}$, $\nu$, $k_\mathrm{TP}$, and $M_\mathrm{TP}$ were set to

• $\left[ 0.001,\,\, 10 \cdot \overline{\frac{\varDelta M}{\varDelta \phi }} \right]$ N m $(^{\circ })^{-\nu }$,

• $\left[ min(\phi ) - \varDelta \phi ,\,\, min(\phi ) + \varDelta \phi \right]$,

• $\left[ 0,\,\, 10 \right]$,

• $\left[ 0,\,\, 10 \cdot \overline{\frac{\varDelta M}{\varDelta \phi }} \right]$, and

• $\left[ min(M) - 4 \cdot \varDelta M,\,\, min(M) + 4 \cdot \varDelta M \right]$,

respectively. The measured ranges of angles and torques are $\varDelta \phi = \hbox {max}(\phi ) - \hbox {min}(\phi )$ and $\varDelta M = \hbox {max}(M) - \hbox {min}(M)$, respectively.

Initial guesses for C, $\phi _\mathrm{TP}$, $\nu$, $k_\mathrm{TP}$, and $M_\mathrm{TP}$ were $\overline{\frac{\varDelta M}{\varDelta \phi }}$, $\overline{\phi }_{0}$, 1, $\overline{\frac{\varDelta M}{\varDelta \phi }}$, and 0, respectively. In order to fix these boundary and initial guess values for each trial, we first calculated the values of the two parameters $\overline{\frac{\varDelta M}{\varDelta \phi }}$ = $A_{0}$ and $\overline{\phi }_{0}$ = $-\frac{B_{0}}{A_{0}}$, which are the mean slope and the angle for zero torque, respectively, of the linear least-square-regression line $\mathbf {M}_{L4/5}(\mathbf {\phi }) = \left( A_{0} \,\, B_{0} \right) \cdot \left( \mathbf {\phi } \,\,\, \mathbf {1} \right)$ through the cloud of I measured sample pairs $M_{L4/5,i}(\phi _{i})$ in this trial, with i indicating the sample, and $\mathbf {M}_{L4/5}$, $\mathbf {\phi }$, and $\mathbf {1}$ being I-component column vectors of the $M_{L4/5,i}$, the $\phi _{i}$, and ones, respectively: this over-determined, linear system of i = 1 $\ldots$ I equations was solved for the vector $\left( A_{0} \,\, B_{0}\right)$ by ‘GNU Octave’ (version 4.2.2) using the operator ‘$\backslash$’.

If, in a first run of the fitting algorithm ‘lsqcurvefit’ for a trial, one of the parameter boundaries was ‘touched’, we widened the boundaries to

• $\left[ 0.0001,\,\, 10 \cdot isbv \right]$ N m $(^{\circ })^{-\nu }$,

• $\left[ isbv - 0.5 \cdot \varDelta \phi ,\,\, isb + 0.5 \cdot \varDelta \phi \right]$,

• $\left[ 10^{-12},\,\, 2 \cdot isbv \right]$,

• $\left[ 10^{-12},\,\, 10 \cdot isbv \right]$, and

• $\left[ isbv - 0.5 \cdot \varDelta M,\,\, isbv + 0.5 \cdot \varDelta M \right]$,

for C, $\phi _\mathrm{TP}$, $\nu$, $k_\mathrm{TP}$, and $M_\mathrm{TP}$, respectively, with isbv meaning ‘initially set boundary value’.

2.4.2 Statistics

Measurement parameters for the group of subjects or sub groups were given as mean (standard deviation). Due to the measurement data not being normally distributed, median and quartiles were used to represent measurement data, and the Mann-Whitney U test was used to test for differences from baseline. For paired samples (e.g., flexion vs. extension) the U test for paired samples was used.

2.5 Computer model of the human–machine interaction

Our computer simulation model of the human, which is used for calculating the load distribution among the lumbar structures, has been described in detail in Rupp et al. (2015). In this section, we give a summary with additionally accounting significant parameter value modifications. As the only essential structural enhancement, bidirectional linear spring–damper elements have been added for modeling FACs.

2.5.1 Anthropometry and model segments (bodies)

The human body model is made of three-dimensional rigid bodies. The bodies are actuated by Hill-type muscle–tendon units (MTUs) which are made of massless threads and apply internal forces on the respective rigid bodies at each their origins and insertions. The model’s anthropometry represents a male of 1.78 m body height and 68 kg body weight. The model consists of two legs each made of a foot, a shank, and a thigh body, which are connected to each other as well as to the pelvis body by hinge joints with parallel axes. The model was exposed to gravitational acceleration and lay on its side, contacting a model of the trunk bending machine in congruence with the subjects in the experiments. The single angular degree of freedom (DOF) in each leg (hinge) joint was sufficient to allow a realistic representation of both the restrictions imposed on the subjects being tightened to the machine and the compliant responses of the ramified chain legs–pelvis–spine induced by the bending movements of the machine in the model’s sagittal plane.

2.5.2 Joints and DOFs

Altogether, the model consists of 42 mechanical DOFs (six hinge joints and six 6-DOF joints: IVDs) plus 404 additional DOFs (first-order differential equations) representing the contraction (van Soest and Bobbert 1993; Günther et al. 2007; Mörl et al. 2012; Haeufle et al. 2014a) and activation (Hatze 1977, 1981; Rockenfeller et al. 2015; Rockenfeller and Günther 2018) dynamics of 202 Hill-type MTUs, of which 35 such threads are located in each leg, 84 surround the lumbar spine, and 48 represent abdominal muscles.

2.5.3 Neutral lumbar posture

Our lumbar spine geometry has been taken (Rupp et al. 2015) from Kitazaki and Griffin (1997). In the neutral (lordotic) lumbar posture, the lumbar angle (Sect. 2.3.2) is $-\,25.6^{\circ }$ (Table 4), and our model IVDs (Sect. 2.5.4) generate zero torques.

2.5.4 IVDs (6-DOF joints)

Cranially to the pelvis, an alternating sequence of six IVDs and five rigid bodies representing the lumbar vertebrae L5 to L1 is arranged. The most caudal vertebra L5 is connected via the first IVD to the vertebra S1 which is on its part rigidly linked to (i.e., an integral part of) the pelvis body. The most cranial lumbar vertebra (L1) is connected via the sixth IVD to the most cranial rigid body in our model, which represents the dimensions and masses of the upper trunk, the head, and the arms: the head–arms–upper trunk (HAUT) body. IVDs are modeled as three-dimensionally acting, nonlinear, viscoelastic force and torque elements (Rupp et al. 2015, sec. 2.3) in which most of the components are simplified limit cases of cubic polynomial characteristics derived from a finite-element model of an IVD (Karajan et al. 2013). The elastic contribution to each component depends on the respective displacement component of the two joint triads (each fixed to its parent body). Their displacement is measured in our current model by Cartesian coordinates for translations and by Cardan angles for rotations. The latter is demanded by the IVD model formulation in Karajan et al. (2013), which is employed here in a decoupled version that is comparable to Rupp et al. (2015, sec. 2.3) but again modified. Constituting the anatomical basis for the interaction between two vertebra, the (normal vector on a) vertebra’s endplate is assumed to be represented by the local z-direction of the respective IVD joint triad (Fig. 2, top left).

Deviating from Rupp et al. (2015, sec. 2.3), we have now assumed that both elastic ‘squeezing’ torque components (x- and y in the local joint coordinate system: Fig. 2) are parametrized according to the IVD’s nonlinear torque-angle characteristic of the y-component in Rupp et al. (2015, sec. 2.3), with their respective Cardan angle component as input. All other elastic force and the caudo-cranial (z: linear in its respective Cardan angle) torque components have been adopted from (Rupp et al. 2015). As a second deviation from Rupp et al. (2015, sec. 2.3), we have now neglected any damping in the IVD torque components, as (i) the analyzed movement was quasi-static and (ii) parametrizing damping in terms of elementary angular rotations like Cardan or Euler representations is very intransparent as it appears almost impossible to trace the corresponding model parameter values back to their physiological and structurally based sources. An improved mathematical model formulation for describing damping in the IVDs seems a research issue worthwhile to invest in. Notwithstanding, a damping contribution in analogy to Eq. (3) was added to all force components. Deviating from Rupp et al. (2015, sec. 2.3) the damping coefficient $d_{k,damp}$ of each single IVD force component k was assumed to depend on the compressive (caudal-cranial: z) elastic IVD force component $F_{z,elast}(D_{z})$. The same damping strength was chosen as in LIGs and FACs: $d_{k,damp}$ = $d_{IVD,damp}$ = 1 s m$^{-1}$.

To give a number for comparison to other models, an axial compression stiffness of approximately 5 $\cdot$ 10$^{5}$ N m$^{-1}$ (Rupp et al. 2015) and a shear stiffness of about a tenth of this value characterize the elastic IVD responses around an operating point that corresponds to the external load scenario in upright standing posture.

2.5.5 MTUs

Each MTU is made of four pulling force elements (Günther et al. 2007; Haeufle et al. 2014a) internally fulfilling static equilibrium: (1) a contractile element (CE) of Hill-type (hyperbolic force-velocity relation Hill (1938)), (2) an elastic element (PEE) in parallel to the CE representing connective tissue surrounding muscle fibers, (iii) a serial elastic element (SEE) representing tendon and aponeurosis material, and (iv) a serial damping element (SDE) representing low but ever-existing energy dissipation in the latter material.

CEs as part of MTUs (indicated by i) generate the internal driving forces of the body model. A CE’s chemical state $\tilde{c}_{i}$ represents the calcium ion concentration $[\text {Ca}^{2+}]$ in the sarcoplasma of the corresponding muscle fibers, normalized to its saturation value (Rockenfeller and Günther 2018), which translates into the normalized CE activity $q_{i}$ by a normalized nonlinear function $q_{i}(\tilde{c}_{i},l_{CE,i})$ (Rockenfeller and Günther 2018, equ. (A3)). The CE’s length $l_{CE,i}$ and its normalized concentration $\tilde{c}_{i}$ are the two state variables of an MTU, which determine by $F_{max,i}$ $\cdot$ $q_{i}$ $\cdot$ $F_{fo,i}$ the isometric force of the CE, with $F_{max,i}$ the maximum value and normalized $F_{fo,i}(l_{CE,i})$ quantifying the degree of filament overlap. Both state variables evolve from each a first-order ordinary differential equation for the contraction (Haeufle et al. 2014a) and activation (Hatze 1977, 1981; Rockenfeller et al. 2015; Rockenfeller and Günther 2018) dynamics, respectively. Their evolution is coupled to each other and the state of the mechanical system. The CE’s activation dynamics model the muscle fibers’ collective response to neuronal, electrical stimulation which is represented by input (control) parameter $u_{i}$. In our trunk-bending simulations, all CEs of all MTUs i were simply stimulated with the same fixed value $u_{i}$ = 0.02, chosen in accordance to measured activation levels (see Sect. 3.1.1) that indicate muscles being near ‘resting activation’ (practically inactive). Thus, dynamic properties of muscle activation are absent, whereas its steady-state (length-dependent) properties (Rockenfeller and Günther 2017, 2018) do matter very well. We have collected all generic MTU parameters in Table 5.

Table 5 Generic MTU parameters, that is, parameters that are identical for all MTUs implemented (compare Gũnther et al. (2007, tab. 2) and Mörl et al. (2012, tab. 1)

2.5.6 Revising the optimal CE lengths

As particularly the muscle parameter data and the whole spine model geometry have been collected (Rupp et al. 2015) from diverse sources, some process of making the set of all model parameters consistent is required. Our current study was an ideal test bed for guiding this process, at least regarding all geometric, passive, and elastic properties, because (1) the whole body was examined around and starting in a neutral posture during (2) slow, quasi-static movements with (3) almost no interference by gravity and (4) in the condition of all muscles being practically passive.

The lumbar posture in the sagittal plane, i.e., the flexion of the lumbar spine, is represented by an overall deflection measure of the entire region: the angle between the L1 and L5 vertebrae’s midplane normals (see Table 4) projected into the table plane (see Fig. 2). With the boundary conditions (1), (2), (3), (4) and the lumbar angle being $-\,25.6^{\circ }$ (Sect. 2.5.3) in the modeled, geometry-defined, neutral lumbar posture, plus given that our model IVDs generate zero torques in this posture, the LIGs, the FACs, and the passive MTUs will generally only equilibrate—even without any external torque applied—by all structures’ torque contributions being nonzero on the L4/5 level, like on any other lumbar level.

For then allowing reproducibly alterable model conditions, like potentially adjusting the neutral posture, we made modeled geometry and passive mechanical properties as consistent as possible. This applied likewise to revising the set of the LIGs’ rest lengths (see Sect. 2.5.8) and choosing a geometry of the FACs’ points of force application (spinal processes; see Sect. 2.5.9) both anatomically based and adapted to our lumbar spine geometry (Sect. 2.5.3).

Regarding our model muscles (MTUs), for gaining model consistency, we modified the heterogeneous set of optimal CE lengths $l_{CE,opt,i}$ of all 132 trunk MTUs (i.e., those crossing at least one IVD) as collected by Rupp et al. (2015) from the literature, while preserving the chosen rest lengths $l_{SEE,0,i}$ of these MTUs’ SEEs from the diverse sources: new $l_{CE,opt,i}$ values were calculated by subtracting an MTU’s SEE rest length $l_{SEE,0,i}$ from its length $l_{MTU,i}$ exactly in the neutral lumbar posture of $\phi _{lumb}\,=\,-\,25.6^{\circ }$ (Sect. 2.5.3), and multiplying this CE length by 1.05. Together with assuming in our MTU model that all the PEEs’ rest lengths are 0.95 $\cdot$ $l_{CE,opt,i}$ (0.95 being a generic parameter value in our MTU model; see Table 5), our revised default set of optimal trunk CE lengths is such that all these CEs are close to their PEEs just so non-slack.

2.5.7 Revising the CEs’ maximum isometric forces

The maximum isometric stress in macroscopic mammalian skeletal muscle is in the range $\sigma _{max}$ = 20$\ldots$35 N cm$^{-2}$ (Close 1972; McMahon 1984, tab. 9.7), (Weis-Fogh and Alexander 1977, p. 518: $p\cdot \sigma _{0}$), (Powell et al. 1984; Biewener et al. 1988; Biewener and Blickhan 1988; Reconditi 2006), (Christensen et al. 2017, suppl. mat.). For example, Weis-Fogh and Alexander (1977) suggested about 30 N cm$^{-2}$ for both slow and fast twitch fibers in rats and mice (the lower boundary in McGill and Norman (1987, tab. 1), see below), Biewener et al. (1988) measured about 20 N cm$^{-2}$ in Kangaroo rats’ ankle extensor muscles, and Christensen et al. (2017) measured about 27 N cm$^{-2}$ in rats’ gastrocnemius muscles.

Human spine muscles have not been examined in direct measurements. Values for human leg muscles have all been estimated on the basis of noninvasive methods. Best estimates of maximum isometric stresses available, from using mechanical measurements that capture multiple-muscle ankle or knee torques for humans lying of sitting in a dynamometer, have provided 24 N cm$^{-2}$ (Fukunaga et al. 1996) in ankle (dorsi-)flexors and between 20 N cm$^{-2}$ and 30 N cm$^{-2}$ Erskine et al. (2009, 2010) in knee extensors (quadriceps muscle). In running at 5 m s$^{-1}$, which implies some eccentric muscle force enhancement at midstance Seyfarth et al. (2000), the highest peak stress (around midstance) in the leg muscles has been calculated for the knee extensors: 28 N cm$^{-2}$ Thorpe et al. (1998). The spine muscle data implemented in our model so far (Rupp et al. 2015) apparently imply 46 N cm$^{-2}$ (Christophy et al. 2012), which might be traced back as far as (McGill and Norman 1987, tab. 1) who tolerated maximum isometric stress values in their model in the range 30$\ldots$100 N cm$^{-2}$. It seems thus that maximum isometric CE force parameter values ($F_{max,i}$) of the trunk MTUs in our model have been systematically too high so far, and accordingly also the PEE stiffnesses which directly scale with $F_{max,i}$ (Haeufle et al. 2014a; Günther et al. 2007, eq. 14). As compared to Rupp et al. (2015), we have therefore generally halved the $F_{max,i}$ values in all trunk MTUs of our human body model, now implying a more conservative average value of 23 N cm$^{-2}$ for the trunk muscles’ maximum isometric stress.

2.5.8 Revising the LIGs’ rest lengths

As the third crucial structures in addition to IVDs and MTUs, lumbar LIGs are incorporated into our model. As the real, anatomical LIGs are often rather sheet than string-like, we usually separated one anatomical structure into three model threads (Rupp et al. 2015) and implemented altogether 58 of them for representing the lumbar LIGs. A LIG’s force-length characteristic $F_{LIG,elast}(l_{LIG})$ is modeled by four parameters (Rupp et al. 2015) in full analogy to an SEE (Günther et al. 2007), with a nonlinear toe zone of force starting to rise from zero above a threshold (rest) length $l_{IVD,0}$ and an approximately linear continuation at further increasing lengths.

Energy dissipation in the LIG material is implemented as a damping force contribution

$$\begin{aligned} F_{k,damp} = d_{k,damp} \cdot F_{E,elast}(E) \cdot \frac{\hbox {d}D_{k}}{\hbox {d}t} \end{aligned}$$

(3)

which adds to the elastic force $F_{E,elast}(E)$ that resists some material deformation (elongation) component E. $\frac{\hbox {d}D_{k}}{\hbox {d}t}$ symbolizes the time rate of deformation (e.g., length) change of the material in direction k. In a general three-dimensional material, E represents a deformation component that may equal the deformation $D_{k}$ in the same direction k as the rate $\frac{\hbox {d}D_{k}}{\hbox {d}t}$ (e.g., in tendons or ligaments); however, it may also be a deformation component in another direction, e.g., determining the pressure in compressed material. It is thus assumed that the material’s damping coefficient $d_{k,damp} \cdot F_{E,elast}(E)$ itself goes in proportion to an elastic force by which the material is currently loaded, i.e., to a material’s force-deformation characteristic $F_{E,elast}(E)$. Examples are found in Eq. (4) for FACs, in Sect. 2.5.4 for IVDs, in Rupp et al. (2015) for LIGs, in Günther et al. (2007) for SEEs (modeling damping in tendons and aponeuroses), and in Scott and Winter (1993); Gerritsen et al. (1995); Günther and Ruder (2003) for modeling heel pad characteristics.

We use the same generic value $d_{LIG,damp}$ = 1 s m$^{-1}$ as in IVDs and FACs for the damping strength of all LIGs. The rest lengths $l_{LIG,0,i}$ of all LIGs is now chosen such that they equal their lengths in the neutral lumbar posture of $-\,25.6^{\circ }$ (Sect. 2.5.3). That is, in the neutral posture, all LIGs are close to being non-stretched.

2.5.9 FACs

In addition to our model as documented in (Rupp et al. 2015), we have now implemented an inexpensive representation of the forces transmitted at the FACs. There are two FACs in the dorsal part of a each vertebra. Each of the 12 FACs—which act mechanically in parallel to the respective IVD—is implemented as a nonlinear spring generating the elastic force

$$\begin{aligned} F_{FAC,elast} = C_{FAC} \cdot (l - l_{FAC,0})^{\nu _{FAC}} \end{aligned}$$

(4)

that connects the respective facet articular processes of two adjacent vertebrae. If the distance l of the coordinate systems of both spring triads is shorter than $l_{FAC,0}$, then $F_{FAC,elast}$ = 0. Common to all FACs, we chose a rest length $l_{FAC,0}$ = 2 mm, an exponent $\nu _{FAC}$ = 4, and a value $C_{FAC}$ = $1.0\cdot 10^{12}$ N m$^{-\nu _{FAC}}$ for the elastic coefficient. Damping in the FACs is modeled the same way as in IVDs and LIGs (Eq. (3)): with the damping coefficient in proportion to the elastic force, and the damping factor chosen alike ($d_{FAC,damp}$ = 1 s m$^{-1}$).

2.5.10 Body-table contact

The human body model contacts the machine model by point-to-plane contact elements (PPCEs) in which the plane is fixed to one body (from triad) and the point to the other one (to triad). The force is transmitted to both contacting bodies at the position of the point. In App. 1, we have compiled the description of the twenty PPCEs implemented in our computer model.

2.5.11 Initial conditions

The initial condition for the mechanical DOFs of the human body model was adopted from previous simulations (Rupp et al. 2015). There, the body model had generally been in conditions near upright stance, with earth-like gravitational acceleration acting along the long axis of the body model. Thus, to match the experimental situation examined here, the whole model was first rotated in space to lie perpendicularly to gravity on the model table, with the most protruding contact point at its right side (pelvis: Sect. 2.5.10) just so contacting the table’s surface plane.

Next, the initial posture of the lumbar spine was modified locally: Along the body cascade pelvis/S1-L5-L4-L3-L2-L1-HAUT, each of the six bodies was simply rotated relative to its predecessor by an angle in the sagittal plane, which accords to a (geometry-defined) neutral lumbar posture (Sect. 2.5.3). In this neutral posture, the lumbar angle is -25.6$^{\circ }$ and the initial sagittal torque component vanishes in all IVDs.

Rotating the mobile table to an angle $\phi _{\mathcal {A}}$ = -50$^{\circ }$, i.e., $\phi _{\mathcal {AS}}$ = 10$^{\circ }$ (see Fig. 1a: $\phi _{\mathcal {A}}$ = -60$^{\circ }$ would make line $\mathcal {A}$-$\mathcal {S}$ align with the global x-axis, i.e., $\phi _{\mathcal {AS}}$ = 0$^{\circ }$), allowed to start the simulation with the four contact points of the HAUT shoulder PPCEs falling within the ’railing’ gap of 1 cm, thus, none of the four ‘railing’ shoulder PPCEs of the HAUT segment was initially in contact with the modeled shoulder fixation by cushion roll and belt. This choice, together with the initial conditions of the force-bearing structures outlined in the next two paragraphs, allowed to start simulations nearby an equilibrium condition when lying on the side.

The CE’s of all MTUs were uniformly initialized to a chemical state value $\tilde{c}_{i}$ = 0.1. The CE length in each trunk MTU was initialized to the MTU length in neutral lumbar posture (i.e., the initial condition of all trunk segments) minus the rest length $l_{SEE,0,i}$ of its respective SEE. This adjustment of the initial conditions of the trunk MTUs to the above-exposed initial conditions of all mechanical DOFs (neutral lumbar posture and stance-like leg joint angles)—which imply a torque- and force-free state of all IVDs—was made possible by our homogenizing revision of the set of optimal trunk CE lengths $l_{CE,opt,i}$ (see Sect. 2.5.6), and enabled both the PEEs and the SEEs of the trunk MTUs to be just so non-stretched initially (in neutral lumbar posture). With the additionally initially just so non-stretched LIGs and the geometry of the facet articular processes chosen to enable vanishing forces in the FACs in neutral lumbar posture, the work done by the initially submaximally activated but almost unstimulated CEs plus the remaining potential energy initially stored in the PPCEs was dissipated during the first two seconds of the simulation, allowing the model to nearly equilibrate.

2.5.12 Simulation parameters and conditions

The model movements were simulated with in-house simulation code demoa (Rupp et al. 2015) using library SpaceLib (http://robotics.unibs.it/SpaceLib/ by Legnani et al. (1996b), Università degli Studi di Brescia, Italy) for matrix operations. Relative and absolute error tolerances of $10^{-6}$ were chosen for integrating the system of equations of motion with the Shampine-Gordon algorithm ‘de’ (Shampine and Gordon 1975) which has been slightly modified (Henze 2002) to allow event handling (root finding). Matrix inversions in demoa are realized by function ‘linear’ from SpaceLib, which combines the dual-pivot algorithm with Gaussian elimination. With the very low, uniform stimulation levels $u_{i}$ = 0.02, the model relaxed considerably during the first about 50 ms from the initial chemical state values $\tilde{c}_{i}$ = 0.1. The simulated physical time period was 7 s. During the first 2 s, the model (in particular its MTUs and PPCEs) was given time to equilibrate internally and against the external boundary conditions, with no torque ($M_{\mathcal {A}}$ = 0) acting around the machine’s hinge axis $\mathcal {A}$. Then, for the next 5 s, the trunk-bending movements were induced by driving the mobile table with $M_{\mathcal {A}}$ > 0 into rotation around the axis $\mathcal {A}$ fixed to the table. For this, the hinge joint torque $M_{\mathcal {A}}$ increased linearly with time t to 30 Nm at a rate of 6.0 Nm s$^{-1}$ starting from zero torque. During the 5-s bending period, an average angular velocity of approximately 9 $^{\circ }$ s$^{-1}$ resulted (Sect. 2.2: 10 $^{\circ }$ s$^{-1}$ in the experiment), with a corresponding deflection of the mobile against the fixed table of about $\varDelta \phi _{\mathcal {AS}}$ = 45 $^{\circ }$ and a final value of about $\phi _{\mathcal {AS}}$ = 60$^{\circ }$ (in the case of realistic LIG stiffnesses: see Sect. 3.2.1).

3 Results

3.1 Experimental findings

3.1.1 Resting activations of the subjects’ lumbar muscles

Resting activation of lumbar muscles was measured during all tests (Fig. 3, Table 6). The lower resolution limit of the measurement device is 1 $\mu$V. The median values of RMS activation signals were 6 $\mu$V for the longissimus and multifidus muscles. The maximum relRMS values among those subjects, for which sEMG was normalized to subMVC (see next paragraph), were 0.16 (m6) in the longissimus muscle and 0.17 (f1) in the multifidus muscle. Within the values normalized by subMVC, we found 0.06 as mean relRMS value.

Fig. 3

Data examples during two cyclic trunk flexion trials (left and right, respectively) with RMS (upper panel) of left multifidus muscle at lumbar level L4 and left longissimus muscle at lumbar level L2, as well as the corresponding lumbar angles (raw data: bottom panel) for subjects f9 (a) and m4 (b). Although distinct flexion of the lumbar spine, the lumbar muscle activation did not deviate from resting activation

Table 6 Summary of sEMG activation signals of left longissimus muscle $RMS_{LoL2}$ and multifidus muscle $RMS_{MuL4}$ during the trials, which are given as absolute numbers and normalized RMS as median (99th percentil)

The subjects were exposed to mechanical loads on submaximal level during the sEMG normalization (subMVC). This is because the machine resistance measured as the torque $M_{\mathcal {A}}$ around the machine axis $\mathcal {A}$—which is also a reasonable first estimate of lumbar joint torque $M_{L4/5}$—was set to maximally 80 Nm. According to Cholewicki and McGill (1996), the average maximum torque value is approximately $M_{L4/5}=217$ Nm. Thus, our measured relRMS levels divided by three may roughly approximate muscular activity ($q_{i}$ in the model), which is defined as normalized to the isometric MVC condition. As an estimate of muscle activation or stimulation $u_{i}$, respectively, in the model, we have therefore chosen $q_{i}$ $\approx$ $u_{i}$ = 0.06/3 = 0.02, which is assumed to apply at low activation.

3.1.2 Measured passive L4/5 flexion characteristics

About 20% of the 295 flexion–extension trials measured were removed from our analysis as their residual values R indicated deviations from the fitted nonlinear ansatz (Eq. (2)) that exceeded the chosen limit of R = 0.6 N (see Sect. 2.4.1). Reasons for poor fitting quality could have been a signal-to-noise ratio too low as well as unreproducible (Fig. 4e) or reproducible but unexplained subject-specific events or processes during flexion and extension (Fig. 4f). Such latter events occurred for all 20 trials of this specific subject and was entirely unrelated to any feedback of discomfort by the subject.

Fig. 4

Selected examples of experimentally determined passive L4/5 flexion characteristics $M_{L4/5}\left( \phi \right)$ (with respect to the global coordinate system) during flexion (black spheres) and extension (grey spheres). Associated parameter values of the fitted (by Eq. (2)) characteristics are given in the left upper corner for [flexion]/[extension], the courses of the fitted functions are depicted as thin, black and grey lines, respectively, in the depicted range of measured data. The number of the selected trial $n_{t}$ and the count of all trials of the subject are given in the lower right corner. For a summary of all fitted parameter values, see Tables 7, 8, and 9. In the upper four panels, the corresponding characteristic calculated by our model simulation (see particularly Sects. 2.5.11, 2.5.12; glance through Sects. 2.5.3–2.5.9 for parameter value choice) is depicted for comparison (green line here and in Fig. 11). The lower two panels depict examples of measured trials that have not been accepted, due to one of their two residues $R_{f}$, $R_{e}$ exceeding 0.6 N, to contribute to the data compilation given in Tables 7 and 8, which are used for statistical analysis (Table 9)

The parameter $\nu$ defines the overall shape of $M_{L4/5}(\phi )$, e.g., linear ($\nu =1$), root-like ($\nu <1$: concave), or near-quadratic ($\nu >1$: convex). The value of the parameter C in itself does not contain immediate information, as indicated by its unit depending on $\nu$ (Eq. (2)). Yet, for a given $\nu$ value, the slope of $M_{L4/5}(\phi )$ and thus local stiffnesses do directly increase with parameter C. To allow comparisons across loading situations and subjects, we calculated stiffness values at selected operating points: the slope $k_{M0} = \frac{d M_{L4/5}}{d \phi }(\phi =\phi _{M0})$ at the angle $\phi _{M0}$ of zero torque ($M_{L4/5}$ = 0), the parameter $k_{TP}$ of the five-parameter ansatz being the slope at the TP ($\phi _{TP}$, $M_{TP}$), $k_{TP+5} = \frac{d M_{L4/5}}{d \phi }(\phi =\phi _{TP}+5^{\circ })$, $k_{TP+15} = \frac{d M_{L4/5}}{d \phi }(\phi =\phi _{TP}+15^{\circ })$, and $k_{lin}$ as the linear (finite difference) estimation $\frac{\varDelta M_{L4/5}}{\varDelta \phi }$ between $\phi _{TP}$ and $\phi _{TP}+5^{\circ }$.

The shape of the fitted passive L4/5 flexion characteristics $M_{L4/5}(\phi )$ vary from slightly concave ($\nu <1$) in few cases (Fig. 4b; see, e.g., subjects ‘f3’ and ‘m2’ in Table 7 as well as ‘f4’ and ’m8’ in Table 8) to usually convex ($\nu >1$: Fig. 4; Tables 7, 8). The TP allowed by the nonlinear ansatz (Eq. (2)) occurs usually within the range of measured data (compare Table 9 with Fig. 4a–d). The angular positions of the fitted TP ($\phi _{TP}$) and the calculated zero torque point ($\phi _{M0}$) deviate on average by no more than 6.7$^{\circ }$ (Table 9: flexion$_{f}$).

Table 7 Passive L4/5 flexion characteristic $M_{L4/5}(\phi )$ during lumbar flexion: values of the parameters C, $\phi _\mathrm{TP}$, $\nu$, $k_\mathrm{TP}$, and $M_\mathrm{TP}$ resulting from least-square fits by Eq. (2) to measured data

Table 8 Passive L4/5 flexion characteristic $M_{L4/5}(\phi )$ during lumbar extension: values of the parameters C, $\phi _\mathrm{TP}$, $\nu$, $k_\mathrm{TP}$, and $M_\mathrm{TP}$ resulting from least-square fits by Eq. (2) to measured data

3.1.3 Hysteresis in passive flexion–extension cycles

Our main experimental finding is that, after a passive flexion of the lumbar spine, the extension branch of the passive L4/5 flexion characteristics $M_{L4/5}(\phi )$ is generally shifted to reduced lordosis: the zero-torque angle $\phi _{M0}$ is reduced on average by 8$^{\circ }$ in males and 6.5$^{\circ }$ in females (Table 9). This hysteresis phenomenon is likewise reflected in the TP angle $\phi _{TP}$ in males. These shifts of characteristic angles can be considered a general phenomenon as they likewise occur significantly when testing extension versus flexion for both sex groups as a whole (last column in Table 9: f+m).

Table 9 Comparison (median and quartiles) of the parameters C, $\phi _\mathrm{TP}$, $\nu$, $k_\mathrm{TP}$, and $M_\mathrm{TP}$ of the passive L4/5 flexion characteristics $M_{L4/5}(\phi )$ (Eq. (2)) in females and males during lumbar flexion and extension

Also for the f+m group as a whole, the overall curvature of the flexion characteristics decreases in subsequent extension: the $\nu$ value is reduced. From flexion to extension, two significant changes in local f+m stiffness values can be noticed: Whereas the linear approximation nearby the TP ($k_\mathrm{lin}$) is increased, stiffness values at higher deflections ($k_{TP+15}$) is decreased. This corresponds to decreased $\nu$ values. Analyzing each sex group separately, these change tendencies are dominated by males in case of $k_\mathrm{lin}$ and females in case of $k_{\mathrm{TP}+15}$. Using our analysis technique so far, the noticeable stiffness changes may be blurred as it depends sensitively on the TP angle $\phi _\mathrm{TP}$, which shows in some cases an extended difference between the flexion and extension branches (see, e.g., Fig. 4a).

3.1.4 Differences in females’ and males’ passive lumbar mechanics

A general finding is that females have a more pronounced lordosis, noticeable both in $\phi _{TP}$ and $\phi _{M0}$ (Table 9). The second general finding is that a male’s lumbar region is stiffer than a female’s: about twice as stiff on the flexion branch, and about 50%  stiffer on the extension branch (significant in $k_{TP+5}$ and $k_{M0}$, but also as a consistent tendency in all other stiffness measures).

3.2 Model calculations

3.2.1 Revised lumbar LIGs’ stiffnesses

One clear-cut result of model-experiment comparison in our study is that the initially chosen values of our model’s LIG stiffnesses, taken from Chazal et al. (1985), were too high. When using these ligament values plus maximum isometric forces—which directly scale the PEEs stiffnesses (Sect. 2.5.7)—initially taken from Christophy et al. (2012), that is, the whole model parameter setup used by Rupp et al. (2015), the overall lumbar stiffness calculated on L4/5 level in the trunk bending simulation was a factor of about two to four too high as compared to our experimental data: compare the mean measured values of $k_{TP+5}$ and $k_{TP+15}$ in Table 9, i.e., the slopes at the working points $\phi$ = $\phi _{TP}$ $+$ 5$^{\circ }$ and 15$^{\circ }$, respectively, to NET $k_{TP+15}$ in Table 10, left. Therefore, we have now generally scaled all lumbar LIGs’ stiffness values down by a factor of three.

Table 10 Passive L4/5 flexion characteristic $M_{L4/5}(\phi )$ during model simulations of lumbar flexion: values of the parameters C, $\phi _\mathrm{TP}$, $\nu$, $k_\mathrm{TP}$, and $M_\mathrm{TP}$ resulting from least-square fits by Eq. (2); compare to experimental data in Table 9

With this, the value of Young’s modulus E of supra- and interspinal ligaments (SSLs and ISLs, respectively) is now 9.8 times 10$^{6}$N m$^{-2}$ in our model. Measured in vitro values from older sources are, for example: 23.7 times 10$^{6}$N m$^{-2}$ (Shah et al. 1977, table 2), 29.4 times 10$^{6}$N m$^{-2}$ (see Table 1 based on Chazal et al. (1985)), and 8.5 $\times$ 17.8 $\times$ $10^{6}$N m$^{-2}$ (Yahia et al. 1991, table 7, right column), with all these data gained from measurements of overall (‘global’) ligament length and force as well as anatomical dimensions, rather than from methods that use specific sensors for measuring local strain or stress. In a more recent literature (Beaubien et al. 2016, table 3), a mean value of 17.5 times $10^{6}$N m$^{-2}$ was found for thoracal ligaments. Scaling this value with the ratio of thoracal to lumbar mean values in Table 1 (about 1.8), we end up with $9.7\,\times \,10^{6}$ N m$^{-2}$, which is practically the same as what we have used in our model as down-scaled SSL/ISL values from Chazal et al. (1985).

Using such down-scaled LIG stiffnesses, in combination with the PEE stiffnesses also reduced according to Sect. 2.5.7, we end up with what Fig. 4 provides as a quick overview: The model still exhibits slopes of its passive L4/5 flexion characteristic being usually higher than in the subjects. The quantitative comparison of $k_{TP+15}$ values between experimental and simulation data in Table 9 (measured) and Table 10, right (reduced LIG and PEE stiffnesses), respectively, reveals that the model is still almost a factor of two stiffer than the average male. It can be seen in Fig. 5 that the lumbar flexion characteristic is determined by the three contributions from IVDs, MTUs, and LIGs, with the net LIG stiffness increasingly dominating at higher flexions.

Fig. 5

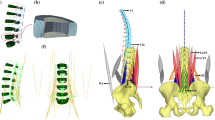
Net joint torque y-component computed by our model (grey, dashed line: ‘total’; same as Fig. 11, lilac) in the local joint coordinate system (see Fig. 2) at level L4/5, with the y-axis in this local and the z-axis in the global system directed nearly the same. Accordingly, its main course is very similar to $M_{L4/5}\left( \phi \right)$ (Fig. 4, green and Fig. 11, green: compare to Fig. 11, lilac). Furthermore, the predicted net contributions (sums) of all similar anatomical structures (muscles, IVDs, ligaments, and facet joints) to the net joint torque are plotted, which then again sum up to the latter. Thin black lines indicate fitted data by the five-parameter ansatz

3.2.2 Load distribution (overview): structural resolution of force and torque contributions at L4/5, and single LIGs’ strains and forces

With our current model using the generally reduced stiffness values, we look in more detail at the LIG loads on the L4/5 level. That is, we first break down the net force contributions of the structures MTU, LIG, IVD, and FAC to the net joint torque (Fig. 5) and to the compressive IVD force (Fig. 6). In Fig. 7, we then resolve the single contributions of the five implemented anatomical analoga of lumbar LIGs in our model to the compressive IVD load as given in Fig. 6. The circle in Fig. 7 indicates the condition in which the present simulation calculates the SSL to enter its region of plastic deformation, with the SSL here being the only LIG to reach this critical stretch level. In Fig. 8, the realized paths along all implemented LIGs’ force-length relations in this simulation are visualized. Among all single LIG model structures that are implemented on L4/5 level to contribute to the joint torque (Fig. 5) and IVD force (Fig. 6), the SSL responds by far most sensitive to strain. This leads to an anatomical–mechanical design issue with relevance for both the load distribution and further modeling steps, which is discussed in Sect. 4.1.

Fig. 6

Compressive force on the IVD (blue line) at level L4/5 predicted by our model, that is, the z-component (craniocaudal) in the local joint coordinate system. The value is negative, because the (pushing) force by the IVD acting on body L5 is depicted. Accordingly, the sums of the z-components of all similar anatomical structures other than the IVD are usually positive because they pull on L5 (accept for the low FAC forces in neutral lordosis). The sum of all four sub-structural forces is the net joint force (‘total’: black, dashed line) on L5, which is a slight pull (i.e., directed in cranial direction). As the system is near static force equilibrium, this net pulling force on vertebral body L5 is always nearly compensated by the net counter force exerted on vertebral body L4 on the other side of the IVD

3.2.3 Load distribution (specific example): structural resolution of lumbar craniocaudal forces identifies determinants of compressive IVD load

The dashed line in Fig. 6 shows the net joint force that is applied by vertebra L4 on vertebra L5 along the craniocaudal axis (i.e., the local IVD z-axis, see Fig. 2,top-left) during passive trunk flexion: if a skilled headsman would be able to rapidly cut in one strike through the modeled subject in its lumbar trunk region between these vertebrae, while the subject lies in the relaxed near-equilibrium initial condition according to the left side of Fig. 6, the cleft through the trunk would immediately widen because the net joint force acting on L5 is positive: initially, there is net pull (i.e., directed cranially) by L4 on L5 along the local IVD z-axis. The same applies during the whole flexion process. Already in the initial condition, mainly the dorsal MTUs are passively stretched. Their pulling force on L5 is higher than the net joint force, as both the IVD and the FACs partly counteract the MTUs by pushing on L5, whereas there are no LIG forces in this situation. Yet, the net effect by IVD and FACs does not fully compensate the MTUs’ pull. Static equilibrium in this condition can only be fulfilled because the pelvis and legs lie on and the shanks are ‘clamped’ to the base table, and the trunk lies on and is fastened to the mobile table. At a contact point, the corresponding body part usually sticks to the table surface, with possible intermediate slip phases, and the conjoint body-table contact interactions counter the net craniocaudal force. Increasing flexion comes along with increasing passive MTU forces, which are supported, starting from about $-\,20^{\circ }$ flexion, by likewise pulling forces of the dorsal LIGs. Accordingly, the IVDs do increasingly counteract by being compressed. In the final flexion posture, the compressive force on the IVD has reached a level that corresponds to about upper body weight, even though lying perpendicularly to gravity.

4 Discussion

The investigated lumbar back muscles showed very low or no activation near the resolution limit of the sEMG measuring device. Thus, no relevant active forces generated by backside muscles bias the determined lumbar torque which is assumed to be of solely passive origin. But other forces, not monitored in this study, may still impact the determined torque values. Such forces may be due to structures not implemented in our model. For example, we have not modeled any enveloped, liquid-containing structures like the entrails or the abdomen as a whole, which may also resist trunk bending.

Our model’s passive L4/5 flexion characteristic $M_{L4/5}(\phi )$ still, even after some literature-backed (e.g., Sect. 2.5.7) and precursory, inferred (Sect. 3.2.1) parameter modifications, indicates in most cases higher overall lumbar flexion stiffness than what we found in our experiments (Fig. 4). In the following Sect. 4.1, we reflect upon the potential sources of this stiffness overestimation by our current model. For three reasons, we first and foremost focus on the mechanical properties of the ligaments: (1) Fig. 5 indicates that the LIGs contribute most to the net lumbar flexion stiffness, and Fig. 7 predicts the SSL to be already overloaded in moderate flexion. (2) All parameters that determine the LIGs’ force–length relations have been extracted from in vitro studies. (3) There are simply no in situ data of LIG rest (slack, crimp) lengths. Yet, there are some recent in vitro data (Robertson et al. 2013) on rest lengths, which reveal an interesting fact that we start our discussion with in Sect. 4.1.

Fig. 7

Structural resolution of the (pulling) LIG forces on L5 at level L4/5, their sum at a given angle makes the orange line in Fig. 6: force components in z-direction of the local joint coordinate system are plotted for each implemented LIG crossing the L4/5 IVD. LIGs are supraspinal ligament (SSL), intraspinal ligament (ISL), ligamentum flavum (LF), posterior longitudinal ligament (PLL), and anterior longitudinal ligament (ALL). Note that we have collected the contributions of the three modeled sub-structures in each ISL, LF, and ALL into one curve. Due to the anatomy of these ligaments, each plotted force component does practically equal the absolute value of a LIGs pulling force. Accordingly, the model would predict, based on the current set of LIG input parameters (see, particularly, Sect. 3.2.1), the SSL to exceed the physiological limit (depicted by the open circle) into plastic deformation: the point $\varDelta L_{B}$, $F_{B}$ according to terminology (cf. Table 1) by Chazal et al. (1985). Eventually, also note that our current four-parameter LIG model (Rupp et al. 2015) simply extrapolates linearly beyond this point

4.1 Significance of LIG rest lengths for predicted lumbar loads

The relation between the change in length of a LIG and the change in angle of a joint crossed by the LIG is a direct measure of the LIG’s (functional) lever arm with respect to this joint. The LIGs’ anatomy—i.e., origins and insertions represented by lever arm values in Table 2—was chosen realistically as implemented in our model by identifying anatomical landmarks in the graphic representation of a human spine (Rupp et al. 2015, section 2.2). Terming the lever arm ‘functional’ owes to the fact that it is not only determined by the anatomy (including potential routing structures) but likewise by the entire load distribution of the surrounding structures. In Fig. 9, we have plotted the corresponding strain-angle relations of our LIGs on level L4/5, which can be directly compared to Panjabi et al. (1982, fig. 5) who had measured such in experiments on human cadavers. The functional lever arm of a LIG (sub-structure) is the slope of its strain–angle relation normalized to its rest length. At 3.5$^{\circ }$ L4/5 excursion, the LF strain is about 0.07 in Panjabi et al. (1982, fig. 5) and 0.08 in our simulation (Fig. 9). The model PLL is about double as strained as the experimental value (0.05). The big deviation between measured properties and our model implementation of SSL is also reflected in the strain-angle relation: Panjabi et al. (1982, fig. 5) have measured 0.15 at 3.5$^{\circ }$ excursion, whereas the model SSL is much less strained (0.09). Regarding the ISL, its measured strain equals that of the SSL (0.15), and our current model shows similar (0.18). Thus, combined only half the measured SSL strain response in the model with its calculated overload (Fig. 7), we would conclude, first of all, that our model SSL is too stiff.

Moreover, Adams et al. (1980, fig. 3), documented that after having cut the SSL/ISL it still takes about 3$^{\circ }$ flexion in a lumbar joint angle (e.g., $\phi _{L4/5}$, i.e., the abscissae in Figs. 9,10) before this cut has any impact on the overall resisting torque (e.g. $M_{L4/5}$). This implies: in initial (probably some neutral) posture, the ISL/SSL are slack, and their (torque) resistance starts not before about 3$^{\circ }$ flexion. This joint angle deflection corresponds, with a lever arm of 6 cm of the SSL (Table 2), to near 3 mm SSL lengthening, i.e., about 9% strain. Such slackness is not documented for SSL, ISL, LF, or PLL in Panjabi et al. (1982, Fig. 5), which is difficult to explain with their data presentation and analysis being not sufficiently traceable (e.g., ligament reference lengths not given). It is further conceivable that the successive onsets of strain resistances of the four layers of LIGs in physiological conditions occur at systematically higher deflection angles than determined in Adams, 1980: Due to their preparation conditions, some swelling of the lumbar joints or enhanced frictional inter-LIG force transmission might have occurred, and, by these superposing factors, an earlier recruitment of the LIGs in the bending cycle.

A more recent, direct experimental determination (Robertson et al. 2013) of slack lengths has yet clearly confirmed the above indication noticeable in Adams et al. (1980, Fig. 3): according to Robertson et al. (2013, table 1), lumbar SSLs were about 6% slack in the neutral posture. Their neutral posture was defined very similar to our model approach, namely, by a stress- and stiffness-minimal, near torque-free position of a spinal region. A level of 6% SSL slackness would correspond to almost half the maximum flexion in our experiments and simulations: according to Fig. 9 the SSL is maximally strained by about 14% for a joint angle deflection of about $\varDelta \phi _{L4/5}$ $\approx$ 6.5$^{\circ }$. This maximum angle deflection is then again comparable to about 6$^{\circ }$ in Adams et al. (1980, fig. 3) and 4.5$^{\circ }$ in Panjabi et al (1982, fig. 5).

As an obvious consequence of not having taken these indications into account, the rest length of the SSL in particular (and maybe the ISL) has been certainly chosen too short in our model so far. Although our modeled LIGs’ stiffness values seem now to having been chosen within physiological boundaries (Sect. 3.2.1), the SSL is then again predicted to be overloaded in moderate flexion (Fig. 7) in the present model simulations. The above strain check reveals in addition that the stiffness of our modeled SSL, at least, is still too high.

The rest length values delicately determine the LIG forces acting at any posture, including the neutral posture (i.e., the equilibrium state of the unloaded, passively lying rigid-body model) in which the LIGs usually operate within the nonlinear toe zone (Shah et al. 1977) of their respective force-length relation, i.e., at low strain, force, and stiffness values. As such low-energy equilibria are very often valuable in serving as initial conditions (also in this study), and specific body postures like the purely geometry-defined neutral lumbar posture are landmarks for equilibria, the LIG’s rest lengths and their reference to such postures need particular attention in the modeling process (Sect. 2.5.8). This implies that, when compiling rest length data, specific posture choices like a neutral posture (i.e., joint angle choices), and anatomical landmarks from different sources into a model, proper adjustment of rest lengths should be always handled with particular care and urgently asks for clear structural design ideas. Unfortunately, the association between rest lengths, angular conditions, and anatomical data are very rarely documented in the literature.

As a major consequence of this study, the LIG rest lengths will be accordingly adjusted in future model versions, and LIG stiffness values must be scrutinized again. We would suppose that the modeled passive L4/5 flexion characteristic $M_{L4/5}(\phi )$ (green lines in Fig. 4) immediately become more curved (nonlinear) and thus better match the experimentally determined curves.

4.2 Mechanical parameters behind the passive L4/5 flexion characteristic $M_{L4/5}(\phi )$

A LIG’s anatomical origin-insertion distance can provide both its reference length for scaling and a reasonable first guess of its rest length. The LIG parameters that crucially affect the passive L4/5 flexion characteristic $M_{L4/5}(\phi )$ are then its actual rest length, cross-sectional area, and Young’s modulus. It seems, however, that currently there are neither of these three parameter values reliably known for animal or all the more human in vivo conditions.

Regarding MTU parameters likewise crucial for $M_{L4/5}(\phi )$, the situation seems to be even more complicated, as it is the serial arrangement of muscle fiber, aponeurosis, and tendon material which is represented in relatively simple muscle models (Hill-type) like ours by the combination of PEE and SEE properties. Similar to the LIGs, the PEE rest lengths (here, generically set to 0.95 $\cdot$ $l_{CE,opt,i}$) are delicate parameters. Yet, the combined PEE-SEE rest length and stiffness from their serial arrangement can be much less delicately estimated realistically: the stiffness is guaranteed to be lower than what results from SEE stiffness, which can be estimated from pretty reliably known values of Young’s modulus (Alexander 2002; Ker 2007) and the anatomical dimensions of a tendon. And combined rest lengths can be determined from manipulating intact joints or whole muscle preparations. With given SEE stiffnesses, PEE stiffness values may then be estimated from directly measured values of Young’s modulus of a passive overall MTU. Since recently (Christensen et al. 2017), data of Young’s moduli of each active and passive muscle fiber material itself are also available, which in principle allows to estimate PEE stiffnesses from scaling by use of anatomical cross-sectional areas and lengths.

FACs are joints and thus structurally more complex than LIGs and MTUs: their force–displacement characteristics originate from, on the one hand, bony contacts and, on the other hand, strained connective tissue that surrounds the joint. Our simple, preliminary FAC implementations seems to indicate that these structures are of low relevance for flexion situations. However, for analysing loads during axial rotation, lumbar extension, and sagittal bending, an enhanced modeling is advisable that better reflects the structure of, e.g., the joint surfaces (Panjabi et al. 1993).

The force/torque-displacement characteristics of the IVDs are probably the most reliably known among the implemented passive model structures, as they are derived from a three-dimensional FE model (Karajan et al. 2013) that includes the major physical and physiological material properties spread across a realistic geometry of the IVD structure.

Any reduction in stiffness of a single structure (e.g., the SSL) of the functional spinal unit can not be expected to transfer proportionally into an overall lumbar stiffness as the reduction in resistance of the structure is usually nonlinearly compensated by structures acting mechanically in parallel, if these structures are not significantly more compliant. We have seen this in the revision process of our current model: as well the PEE stiffnesses had been about halved as the LIG stiffnesses had been reduced to a third, and yet the overall stiffness level has not even be halved. Single over-proportionately stiff structures, or deficiently modeled rest lengths, like the suspected SSL in our present model simulations, dominate overall lumbar and joint stiffnesses and can almost compensate for reducing stiffness of parallel structures.

4.3 The functional significance of the mechanical interplay of the lumbar structures for the regional (lumbar) and local (joint) characteristics

The mathematical analysis of experimental and model data by the five-parameter ansatz (see Eq. (2)) determines nonlinear $M_{L4/5}(\phi )$ characteristics in most subjects with usually ($\nu >1$) a low-slope-region (low $k_{TP}$) around the TP. This mathematical $M_{L4/5}(\phi )$ ansatz is a sum of a linear (parameters: $k_{TP}$, $\phi _{TP}$) and a nonlinear (parameters: C, $\nu$, $M_{TP}$) characteristic, thus, a minimal model for the superposition of mechanical properties originating from two structures. Introducing the parameters $\phi _{TP}$ and $M_{TP}$ this way allows to separate the zero crossings of the linear from that of the nonlinear contribution to the overall characteristic while avoiding any parameter redundancy. This minimal nonlinear model ansatz is also meant to help apprehending how the superposition of single structure (LIG, MTU, IVD, FAC) properties affects any $M_{Li/j}(\phi _{Li/j})$ on joint level, and the overall characteristic $M_{L4/5}(\phi )$ in substance. We can particularly see that $\phi _{TP}$ is the zero crossing of the nonlinear contribution, i.e., its rest angle, conceivably corresponding to a structural rest length. The slope $k_{TP}$ at the TP is the stiffness of the second, superposing contribution—here linearly modeled, representing all structures except the nonlinear contribution—at this very operating point of the nonlinear contribution which does not generate any torque here, combined with zero stiffness (i.e., showing a ‘toe zone’ around $\phi _{TP}$). In general, all structures are characterized by potentially distinctly different rest lengths as well as moderately divergent nonlinearities and local (at the TP) stiffnesses. Hence, they certainly contribute with different magnitude to the ‘background’ stiffness $k_{TP}$ at the TP. Altogether, the occurrence of a TP in the characteristic $M_{L4/5}(\phi )$, or $M_{L4/5}(\phi _{L4/5})$ on the more local joint level, in the physiological range of motion, may well be an indicator for the ‘toe zone’ of a lumbar structure, a single dominating one or a ‘package’ of similar ones like, e.g., the net LIG effect, located at the TP.

A structure that operates in the ‘toe zone’ region of its mechanical characteristic (see, e.g., Fig. 8) does neither generate significant forces/torques nor mechanical resistance against displacement (stiffness). If this ‘toe zone’ condition occurs within the common range of physiological operation, as, e.g., probably in IVDs and LIGs in the range of lumbar joint angles around the neutral lumbar posture (see Figs. 4a and 5), the question for the functional significance of such a ’toe zone’ design arises immediately. We suppose that a possible answer may be that this design facilitates recovery of the respective structure in load-free situations like the neutral lumbar posture, which would be sleep for IVDs (Botsford et al. 1994; Wilke et al. 1999). Regarding the arrangement of multiple LIGs, varying their joint angles of onset along with their rest length design (i.e., constructing an overall LIG ‘toe zone’) may be due to distributing the overall function of all LIGs across a range of motion extended as compared to what a single LIG can provide. When loaded externally, a joint, or even more a sequence of such, can only ‘afford’, in a mechanical sense, in an extended angular range such a potentially vulnerable overall ‘toe zone’ condition if other, parallel structures give support by force/torque and stiffness in this condition.

Fig. 8

LIG forces versus strain at level L4/5. The data of all modeled LIG sub-structures (see Table 2) are depicted, i.e., three lines for each ISL, LF, and ALL (always practically slack), and one line for each SSL and PLL (orange lines with symbols, as for the middle sub-structures of ISL, LF, and ALL). Looking at the LF, its left sub-structure (brown) is less strained than the right one (green), due to lying on the right side. The proximal (‘nearer’) ISL sub-structure (green) is less strained than the distal (‘further’) one (brown) due to their lever arms differing slightly. Their slopes differ, with identical stiffnesses (see again Table 2), along with their rest lengths

The superposition of a number of nonlinear structure characteristics with each a different angular location of their mechanically critical ‘toe zones’ has another advantage: the occurrence of an operating point of low stiffness $k_{TP}$ can be separated from the point of zero torque ($\phi _{M=0}$ or $\phi _{L4/5,M=0}$ with $M_{L4/5} = 0$) by passive design. The zero-torque point is a particularly critical one, because the response of a joint to a demanded change in torque direction should be provided as rapid as possible, which is best realized by passive mechanical responses due to significant stiffness (compare $k_{M0}$ to $k_{TP}$ in Tables 9 and 10) with practically vanishing delay.

Therefore, the separation of TP and zero torque condition is a protective mechanism for all lumbar structures, particularly for the IVD. The latter is definitely relieved of torque demands (see Fig. 5). IVDs may have thus been designed during evolution for first and foremost resisting force demands, certainly (high) compressive but maybe also shear forces based on rather elasticity (anulus fibrosus) than friction, as the latter can be expected to come with higher wear-out.

We have discussed seemingly somehow hand-waving, in one go, the emergence from structural contributions of the lumbar flexion characteristic $M_{L4/5}(\phi )$ and the analogue $M_{L4/5}(\phi _{L4/5})$ on single joint level. Measuring the regional angle $\phi$, instead of the more local joint angle $\phi _{L4/5}$, simply owes to the experimental challenge of acquiring as accurate and reliable lumbar angular deformation as possible, yet without using invasive methods, with reasonable time resolution, and applicable in near-natural movements rather than constraining the subjects by CT or MRI apparatuses. From a mechanical point of view, however, the regional degree of freedom $\phi$ is just a descriptive measure: It is the sum of four joint angles of which one is $\phi _{L4/5}$ and which are mechanically arranged in series in the spinal column.

The joint angles are structure-based degrees of freedom that have to be actuated, be it passively or actively, in a coordinated way during movement. Such a serial arrangement is a challenge for actuation because mechanical instabilities are lurking (Seyfarth et al. 2001) if loaded externally: There is a manifold of redundant joint angle combinations that can yield a given $\phi$ value, and, depending on the distribution of joint stiffnesses, local buckling of the chain of joints at critical deformations or loads, respectively, can occur if these joint stiffnesses are not adjusted to each other and the geometry of the chain (Seyfarth et al. 2001).

4.4 Knowing mechanical properties of all load-bearing structures well: toward calculating valid load distributions

Currently, neither in vivo functional lever arms, nor rest lengths, nor cross-sectional areas, nor Young’s moduli are reliably known for LIGs, which is reflected by the marked variability in their force-length relations as extractable from literature (Damm et al. 2019). Such lack in firm knowledge about basic mechanical LIG properties is only one example that highlights the urgent need to determine such and, with this, fulfil prerequisites that allow to disentangle the role of single players that contribute to the internal load distribution in the (lumbar) spine. In vivo experiments that probe for the lumbar angle—or even better: joint angle on each single lumbar level—at which the LIGs become slack (Fig. 9) are urgently needed, as are more accurate in vivo anatomical data, particularly of the LIGs’ cross-sectional areas (see above). The addressed data may principally be available via state of the art, noninvasive visualization techniques. Furthermore, such techniques should be used to directly measure in vivo strains from which, if related to the corresponding joint angular excursions, functional lever arm values can be easily calculated.

Fig. 9

LIG strains versus joint angle $\phi _{L4/5}$ between L4 and L5. The slope of such a characteristic is the functional lever arm of the LIG (sub-structure) normalized to its rest length

Fig. 10

Versus joint angle $\phi _{L4/5}$ between L4 and L5: the structural resolution of the contributions by LIG forces at level L4/5 to the y-component of the net joint torque in the local joint coordinate system. Their sum corresponds to the orange line in Fig. 5, but here plotted versus $\phi _{L4/5}$ instead of $\phi$. Note again that the y-axis in this local and the z-axis in the global system almost align, i.e., these $M_{y}\left( \phi _{L4/5}\right)$ curves are very good approximations of their contributions to net $M_{L4/5}\left( \phi _{L4/5}\right)$.

Second, the particular emphasis on the word ‘directly’ leads us to the general issue addressed in this section: knowledge on properties of isolated structures in the spine, or lumped characteristics of a combination of structures determined in specific lab situations, are not sufficient to calculate the load distributions in situations different from the lab. Continuing with the example of the LIGs’ functional lever arms, the sole assumption that the actual lumbar joint rotation centers can be accurately derived from anatomical data should be taken with great care. The actual joint rotation centers in vivo and in motu predictably depend—beyond anatomy only—on the local load distribution between them, which itself is determined by the combination of the mechanical properties of all surrounding spinal load-bearing structures and the external load scenario. Therefore, the functional lever arms, being basic mechanical determinants, and with them the overall force/torque–angle relations of the lumbar joints themselves are not independent of the load scenario, which makes unravelling the mechanical conditions within the spinal column a particular challenge.

It is thus not only the number of contributing anatomical structures and their abundance of degrees of freedom, combined with their diverse material properties and their highly redundant (parallel) anatomical arrangement yielding nonlinearly interwoven paths of mutual force transmission, that makes an analysis of the mechanical situation in the spine more intricate than in and around, e.g., a main human leg joint. The particular challenge is to take the tight and nonlinear mechanical coupling of all potentially load-bearing anatomical structures into account, which only then allows to reliably and validly quantify the relation between specific external and corresponding internal load scenarios.

4.5 Comparison of simulated and measured compressive IVD loads

As intended by decoupling, with the subjects lying on their sides, spinal flexion from upper body weight, the subjects’ trunk muscles have been checked by EMG electrodes to be in fact nearly inactive. Likewise, the immediate contribution of upper body weight to compressive IVD loads is ‘turned off’ in this experimental condition. Therefore, a minimum load condition for the spine has been well approximated. The corresponding spinal loads predicted by our model can now be compared to directly measured data, in particular, pressure values in IVDs.

Such pressure data within a human L4/5 IVD were measured in vivo by Wilke et al. (1999, 2001). This data set constitutes, until now, the most solid base for validating biomechanical spine models. From the data in Fig. 6, it is easy to estimate pressure values that correspond to compressive forces on our model’s L4/5 IVD. Assuming the radius of this IVD is about 1.5 cm, we get 0.07 MPa in the lying rest position (about 50 N at $\phi$ < -20$^{\circ }$) for which Wilke et al. (1999, table 1) have documented 0.12 MPa. The pressure increases up to 0.7 MPa (500 N) when the lumbar lordosis has almost disappeared ($\phi$ = -2$^{\circ }$). This flexed posture is comparable to unsupported sitting with maximum flexion for which Wilke et al. (1999) have reported 0.83 MPa. Despite considerable remaining uncertainty in the model parameters of the LIGs (e.g., rest lengths, see Sects. 3.2.1,4.1, and whole force-length relations (Damm et al. 2019)) and MTUs (mainly the PEEs’ rest lengths, see end of Sect. 2.5.6, and PEEs’ stiffnesses, see Sect. 2.5.7), the model well reproduces the measured compressive IVD loads.

Comparing the in vivo measured pressure data with our model calculations demonstrates the posture of the lumbar spine being a major determinant of IVD load. With having ‘turned off’ both the activity of all muscles and the immediate contribution of upper body weight to compressive IVD load, the model-predicted pressure values in the L4/5 IVD yet, for increasing flexion, go through the range of values measured (Wilke et al. 1999) in elbow-supported sitting (0.43 MPa), standing (0.5 MPa), and walking (0.53 $\ldots$ 0.65 MPa), with the latter two tasks being certainly accompanied by neutral, lordotic lumbar postures. Altogether, even when lying on the side, there is generally a basic, inescapable compressive load on the IVD that is determined by the degree of lumbar flexion. In contrast to a synovial joint, a joint in the lumbar spine can thus not be flexed in the sagittal plane without significantly loading the joint structures, particularly compressing the joint surfaces (IVD).

4.6 Muscle activity: loads and recovery

Any muscle activity, be this due to, e.g., compensating trunk weight in forward-bent situations, picking up some external load, performing other daily activities like closing up shoelaces, or any other movement task, will further increase the inescapable, passive flexion-induced minimum values of loads in the lumbar structures, which have been determined here in relaxed positions lying on the side. Even in seemingly static tasks like quiet upright stance, the spinal column must be actively balanced by fluctuating forces of the lumbar muscles. This is because the spinal column is an inverted multi-link chain that is basically unstable in gravity. Naturally, the same applies for the lumbar region. It seems that neither the whole spine nor the lumbar region in particular have so far been biomechanically analyzed during (dynamically balanced) quiet upright stance. It is yet very likely that the mean sagittal, horizontal positions of the HAUT COM and the hip joints deviate on average. Thus, a tonic tension basis of the lumbar muscles for quasi-statically maintaining the (sagittal, horizontal) position of the lumbar spine in addition above the pelvis, and also its lordosis, is expectably required, in addition to dynamically re-estabilising force fluctuations.

In humans, a unique feature of the lumbar spine is the arrangement of passive structures in parallel to the MTUs, namely LIGs, and their involvement in force generation during daily activities (Fig. 11). There are situations in which the activity of all trunk muscle forces are reduced to full quietness (Mork and Westgaard 2009; Mörl and Bradl 2013). Coming back to the above example of forward-bending, for then potentially closing shoelaces, the bending movement must be initiated by reducing muscle activity and then partially using gravity as a drive. The trunk muscles will accordingly have to mainly act as brakes. Yet, in bent or suspended intermediate postures, muscle activity would often not be required at all (Mörl and Bradl 2013). Accordingly, the gradual interplay between often passive (near ballistic) movement generation and an accent of active muscular braking of spine movements in humans, with their two, legged, upright posture and the main portion of body mass concentrated in the trunk, is certainly a peculiarity in animal movement actuation.

Fig. 11

Versus lumbar angle $\phi$: the torque $M_{\mathcal {A}}$ (blue line) generated by the machine around axis $\mathcal {A}$ (see Fig. 1a) and various calculations of the net joint torque component $M_{L4/5}$ in the direction of the normal vector of the table (z-direction in the global coordinate system, see Fig. 2, aligned with axis $\mathcal {A}$), which is transmitted at the junction between the modeled vertebrae (bodies) L4 and L5, as acting on L5. The associated point of torque analysis (force transmission) equals the origin of the local joint coordinate system which is calculated as the arithmetic mean of the two joint triads (compare Fig. 2): here, the ones on body L4 and body L5. A joint triads’ respective local x- and y-axes are in the plane of the respective modeled vertebra’s endplate, its local z-axis is the respective normal vector on the endplate. The y-direction in the local joint system is nearly aligned with the table normal (global z-axis; see again Fig. 2), both in the sideways lying subjects and the model, i.e., $M_{y}$ $\approx$ $M_{L4/5}$ (compare lilac and green lines). The line ‘torque assuming KS’ (orange) shows the result of a simplified static analysis, in which $M_{L4/5}$ is calculated from assuming that measured $M_{\mathcal {A}}$ acts by just one external force $\mathbf {F}$ on the subject, with the force being applied at the shoulder point $\mathcal {K}$ and directed to the axis $\mathcal {S}$ (see Fig. 1a), because (1) the latter is nearly friction less and (2) no frictional torque acts between trunk and mobile table part.

In essence, the obviously significant passive force generation of the lumbar structures for maintaining the lordosis will dynamically interplay with active muscle forces, already in quiet upright stance, with any muscle activity inevitably increasing at least the compressive loads on the IVD. The secondary impact of muscle activity on LIG loads is an open question. This applies likewise to the effect of transversal (Siebert et al. 2014, 2018) and shear (Huijing et al. 1998; Huijing and Baan 2008) forces of the muscles on LIG and IVD loads.

From a biomechanical point of view, the interplaying mechanism is very likely a basic energy saver. The mechanical design alternative to maintaining posture by muscle activity, which has probably been employed during evolution, is partly replacing active joint resistance by passive structures, at least in parts of a joint’s range of motion. For example, there is clear evidence from the theoretical side (Günther and Wagner 2016) that actively fluctuating muscle forces in an inverted multi-link chain enable to reduce the quasi-static (tonic) stiffness requirements in other joints of the chain by a factor of roughly two, which means reducing metabolic energy consumption by muscular co-contraction for maintaining basic background stiffness within the chain. Head, trunk, shoulders, and arms (HAUT) sum up to 65% of body weight. In upright position, HAUT COM is positioned in horizontal direction near the hips and only low forces of lumbar muscles (and also m. psoas, glutes and hamstrings) are required to provide torques for maintaining upright posture. For fulfilling the static torque requirements during excursions of the spine from upright posture, any lack of restoring support by passive structures accordingly induces metabolic costs of muscle activity.

Crouched sitting positions on the floor as observed in the habits of primitive people, like some sedentary positioning on chairs chosen by people in modern societies, may then serve the recovery of lumbar muscles. Though, recovery by unloading of passive structures and muscles at once seems only possible in lying positions. The idea behind is the following: as compared to the neutral lumbar posture ($\phi$ $\approx$ 25$^{\circ }$: Sect. 2.5.3), mean measured values of the zero-torque angle $\phi _{M0}$ are at reduced lordosis (Table 9, last row), which corresponds to slightly flexed spines in relaxed (inactive muscles) positions lying on the side. Neutral lumbar posture probably approximates the spine in upright posture, e.g., during quiet stance. Adopting relaxed, slightly flexed lying postures that correspond to $\phi _{M0}$ can thus be conceived a preferred sleeping condition around which any of the passive spinal structures is not far from its ‘toe zone’ of very low tension. This condition seems well be appropriate for a structure’s recovery. Accordingly, repeated changes in spinal posture during sleep might then be interpreted as providing all structures with significant recovery periods.

It seems, nature has also built into the passive mechanical properties of the spinal load-bearing structures, particularly their force/torque–deformation characteristics and their structural arrangement, that a sane spine can maintain its integrity in the range of functional movements with minimum active motor control effort (Haeufle et al. 2014b, 2020). The latter potentially comes along with a minimization of metabolic energy consumption (Niven et al. 2007). Due to its serial arrangement of many mechanical degrees of freedom and with a huge variety of conceivable load scenarios, the spinal column seems to be an exciting construct to study nature’s design principles for conflating diverse demands like load tolerance of many different anatomical materials and structures, mobility and flexibility, energy efficiency, mechanical stability, and control effort.

4.7 Dissipative properties of the LIGs

Any real world material dissipates energy when deformed. The underlying mechanisms and processes are termed ‘friction’ and the corresponding mechanical property is usually termed ‘damping’ because its effect can be observed as attenuating amplitudes in oscillations. Reliable knowledge about damping properties of (passive) biological materials like connective tissue or cartilage, which tendons, muscle sheaths, ligaments, intervertebral discs, and joint surfaces are made of, is utterly scarce. We have therefore implemented very low damping strengths of all corresponding model structures, such that the simulated bending movement is definitely underdamped here (see the very low hystereses, e.g., in Figs. 4,5, 6, 7 and 11).

We want to estimate two things now: (1) What is an approximated upper limit of strain rates of a lumbar LIG in human movement? Strain rate data can be estimated for high level sports, e.g., javelin throw (Best et al. 1993) and snatch in weight lifting (Liu et al. 2019). (2) How does in such a stretch situation the damping compare to the elastic LIG force? Ratios of a force and a stretch rate, at high values, are available for cervial spine ligaments (Panjabi et al. 1998). As an example, we do calculations for our model SSL at level L4/5 (Table 2), which is about 32 mm long, has a lever arm of about 60 mm with respect to the centre of its IVD, and can generate about 72 N when stretched by about 4 mm (an estimate of a high but physiological load).

Ad (1): As a rough guess, during the acceleration phase in javelin throw, which is defined as the time period from the final foot plant before the foul line and the javelin release from the throwing hand, the lumbar spine will go through a sequence of approximately neutral lumbar lordosis at foot plant, to pronounced lordosis—the hip moves intermediately faster than the body COM after foot plant, see Best et al. (1993, fig. 3)—, and finally to an estimated full release of lordosis ($\phi$ = 0$^{\circ }$) toward javelin release. Taking into account that the SSL is slightly slack in neutral lumbar posture (Sect. 4.1), we thus estimate that the SSL only begins to be stretched when lordosis is already slightly reduced in the second half of the acceleration phase. As we assume that the lordosis is reduced to about zero at javelin release, the SSL may experience loaded stretch during a final lumbar angle change of about half the neutral posture, i.e., roughly $\varDelta \phi$ = 13$^{\circ }$. As this value distributes among four IVD joints, thus, the L4/5 joint will go through about $\varDelta \phi _{L4/5}$ = 3.5$^{\circ }$ angular deflection within about half the duration of the acceleration phase (second half), i.e., about 70 ms (Best et al. 1993, table 3). This is a deflection of 0.062 rad, and as the stretch of a LIG for 1 rad deflection equals its lever arm, we calculate a strain of 0.062 (i.e., 6.2%) for 3.5$^{\circ }$ deflection. Within 70 ms, the SSL would thus be strained by 0.062 / 0.07 $\approx$ 0.89 s$^{-1}$ times its rest length of 50 mm, i.e., in absolute numbers about 45 mm s$^{-1}$ stretch rate. In the snatch discipline of weight lifting, the second phase (M2) from maximum extension to maximum flexion of the knee (Liu et al. 2019, fig. 2) may correspond (regarding SSL stretch) to the second half of the acceleration phase in javelin throw. Snatch phase M2 lasts about 100 ms (Liu et al. 2019, Table 3) in elite lifters, with a corresponding stretch rate of about 30 mm s$^{-1}$ being induced in the SSL.

Add (2): (Panjabi et al. 1998) stretched cervical ligaments very rapidly at rates of 920 mm s$^{-1}$. This is certainly an order of magnitude higher than our estimations of high physiological rates. Yet, from their experiments (Panjabi et al. 1998, fig. 4), one can roughly estimate the damping coefficient $\frac{maximum\,force}{stretch\,rate}$ of a cervical (alar) ligament, with the latter generating a physiological force (about 70 N) comparable to the SSL at about half the stretch (1.8 mm) but comparable strain: 0.16 in the alar ligament (rest length about 11 mm) as compared to 0.12 in the SSL. The maximum forces reached by the alar ligament during these rapid stretches were about 300–500 N, that is, four to seven times higher than its maximum elastic force. With this, the estimate of a value of a (cervical) ligament damping coefficient would then be 325–540 N s m$^{-1}$. Given this, we would then expect at the (high) physiological SSL stretch rates estimated above (30–45 mm s$^{-1}$) that the damping forces would be only a twentieth to thirtieth of 300–500 N, that is, 10–25 N. Compared to about 70 N near maximum elastic force, this would indicate significant hysteresis at physiological near-limit rates as in javelin throwing or snatching.

Experiments for identifying damping properties of ligaments, and other passive biological tissue, seems to be an exciting challenge that promises a lot of insight eventually in their role in movement dynamics.

4.8 Critical review of the mechanical analysis: determining a spinal characteristic such as $M_{L4/5}(\phi )$

At various occasions in this paper, the passive lumbar flexion characteristic $M_{L4/5}(\phi )$ as calculated by our model has been compared to our measured data. Here, we would like to reflect on different methods that can be applied to calculate the lumbar characteristic from known geometric and kinematic plus force and/or torque data, be it using measured or simulated data. For this, applying inverse dynamics analysis is a common approach in biomechanics. Here, we restrict ourselves to discussing the results of inverse statics as an approximation, because inertia terms were low in our quasi-static experiments, and some methodical issues in analyses can already be identified by applying statics. As we focus on solely addressing potential analysis errors, we compare different analysis methods by applying them to model simulation data, because then any indeterminate measurement error is excluded. Figure 11 shows both the generated machine torque around axis $\mathcal {A}$ and the results of three different methods that calculate the lumbar characteristic. Two of them apply inverse statics, with each using different assumptions and input data. Both may use data that are either provided by measurement or by a computer model. The third method practically demands computer synthesis of the movement in focus.

Straight away turning toward the third method, the generated joint torque component $M_{L4/5}$ in the table (global x–y) plane (Fig. 2) is denoted as ‘torque induced by driving elements (global)’ in Fig. 11 (green line; see also Fig. 4a–d). It is the sum of the corresponding torque components generated by any structure that actuates (passes or connects) the L4/5 joint (forces: MTUs, LIGs, and FACs; force and torque: an IVD). For this, the force vectors and their lever arms, or the respective torques if modeled accordingly, of all force-generating structures are required and, of course, completely known in model-based computer synthesis of a movement. This is the benchmark for any other method, as this method represents the exact numbers that any inverse dynamics analysis approach strives to calculate.

The method ‘torque assuming KS’ (red line in Fig. 11) calculates $M_{L4/5}$ from the known ‘applied machine torque’ $M_{\mathcal {A}}$ (blue line in Fig. 11), with the following assumptions: There is static equilibrium between external forces on HAUT and joint forces and torques at L4/5 (inverse statics), the machine torque $M_{\mathcal {A}}$ is transferred as an external force $\mathbf {F}$ to the subject exactly at a known point $\mathcal {K}$ (near the centre of the cushion role) of force transmission, with the line $\mathcal {A}-\mathcal {K}$ being the corresponding lever arm that is exactly known, the $\mathbf {F}$ points in direction of the line $\mathcal {S}-\mathcal {K}$, and the location of the L4/5 joint is known (e.g., exactly in the model or approximately from markers), thus the lever arm of the line from $\mathcal {K}$ to the L4/5 location. The difference between ‘applied machine torque’ and ‘torque assuming KS’ is thus simply due to the distance between the locations of the axis $\mathcal {A}$ and the L4/5 joint in the table (global x–y) plane (Fig. 2). As a function of time, the machine torque does not oscillate, it increases linearly (Sect. 2.5.12). The ’oscillation’ in both curves is due to the model definitely being underdamped—see the very narrow hysteresis effects in ‘torque induced by driving elements’—as compared to physiologically occurring material properties. As a consequence, HAUT together with the mobile table part actually oscillate in terms of angles $\phi _{A}$ and $\phi _{S}$ (Fig. 1a) around the joints in $\mathcal {S}$ (frictionless) and the $\mathcal {A}$ (machine-driven). These angular oscillations induce systematic errors in inverse statics calculations of $M_{L4/5}(t)$, as any inertia forces and torques are neglected in inverse statics.

Although assuming statics just alike the method ‘torque assuming KS’, the ‘torque induced by contacts’ (red line in Fig. 11) does not assume just one external force $\mathbf {F}$ to act, but acknowledges that there is a whole spatially distributed scenario of contact forces and torques acting externally on the HAUT in the shoulder and upper trunk region. For example, the HAUT lies with a whole contact area on the mobile table part. Therefore, an overall frictional torque between the contacting areas can be built up, which causes a deviation of the assumption ‘external force acts in direction of the line $\mathcal {S}-\mathcal {K}$’. We have calculated ‘torque induced by contacts’ by simply summing the torque contributions of all modeled contact force elements acting on the HAUT, just as if force plates had acquired all these in the experiment. The noticeable offset of the ‘torque induced by contacts’ calculated this way as compared with the other curves is due to three facts: (1) Although there is neglectable friction in the axis $\mathcal {S}$ at which the mobile table part is suspended, the constraint force vector transmitted via this axis does usually not align with the connection lines from $\mathcal {S}$ to the centre of mass of either the mobile part or the HAUT. (2) Torsional friction between HAUT and the mobile part can occur due to (a) multiple, partly counteracting, PPCEs acting and (b) each of them even in itself having the potential of taking up a torsional torque. (3) The whole subject–table interaction constitutes a closed force chain, with interaction forces and torques possible to arise from (1) and (2).

Two conclusions may be drawn at least. First, if in future experiments also the joint characteristics in more dynamic loading situations are to be examined, an elaborate inverse dynamics approach would seemingly be state of the art. For this however, measuring with force plates the complete contact force scenarios of the machine-trunk interaction would be strongly advisable, plus measuring by appropriate sensors the forces and torques transmitted in all machine joints.

Second, however, for extracting joint, and eventually even structural, characteristics from experimental data, a pure movement synthesis approach, like the present one, that accompanies experimental analysis seems eventually superior to even the most elaborate inverse dynamics. According to the example above, even with complete force and torque scenarios of the contacts and the sensors available, the accumulation of systematic measurement errors, the unavoidable existence of inconsistencies between a measured system and the biomechanical model required in any case, plus the challenge of solving the redundancy problem, make it very likely that data transformations in an inverse dynamics approach make the system information gained more diffuse than when applying synthetic movement generation, at least beyond a certain threshold of complexity of the movement system examined. This applies all the more, the more detailed and exact structural properties are sought after.

Appendix

1.1 The implemented point-to-plane contact elements (PPCEs)

There are six PPCEs at the HAUT body. Two are located at the HAUT’s right side and model the trunk of the subjects, which lie on their right sides in the experiment, being supported by the mobile table part of the machine. In these two PPCEs, their plane is fixed to the table, with their normal vector pointing upwards (to HAUT), while the contact points are fixed on HAUT: at shoulder height and width, each one 4 cm dorsally and ventrally, respectively.

Four further PPCEs are introduced to model the fastening of the subject’s trunk to the shoulder cushion roll by the fixation belt, both on their part fixed to the mobile table (Fig. 1b). The belt is for pulling the trunk back to the roll in case the trunk would tilt away from the roll down to the surface of the mobile table. The roll–shoulder interaction is implemented by two of these PPCEs which are fixed to the HAUT’s backside: their plane in common is located 5 cm dorsally from the HAUT’s centre of mass (COM) and its normal vector points dorsally. The belt fastening is simply implemented by the another PPCEs with a second plane in common. This plane is likewise fixed on the HAUT’s backside, however, located 6 cm dorsally from HAUT’s COM, and its normal vector points ventrally.

Each the dorsal and ventral PPCE plane on HAUT can interact with both a lower (1.5 cm above table surface) and an upper (33.5 cm above table surface) contact point locating the shoulder cushion roll. The modeled roll is fixed on the machine’s mobile table part (Fig. 1a) a distance of 18 cm away (at $\mathcal {K}$) from the axis $\mathcal {S}$ of the frictionless hinge joint by which the mobile table is linked to the lever construction A-B-$\mathcal {S}$ which is again linked by hinge A to the machine’s base table part. The latter is eventually fixed to the ground. The two possible contact points on the roll are chosen so as to enable its contacting with HAUT in the regions nearby the heights of both shoulder joints.

To sum shoulder fixation up, two PPCEs support the right shoulder region of HAUT against gravity and another four PPCEs make a ‘rail’ gap for HAUT of 1 cm width, roughly representing a subject’s trunk backside supported by the cushion roll and its front side being pulled back to the cushion roll by the fixation belt. During flexion movements (forward rotations), two PPCEs guide the HAUT body mainly by normal pressure to the trunk’s backside—partly superposed by reversible tangential stick-slip interaction. Enforced pronounced HAUT backward rotations (trunk overextension) can be enforced by the A-B-$\mathcal {S}$ lever arm system around the machine’s motor axis $\mathcal {A}$ pulling the HAUT shoulder region backwards by means of the fifth and sixth PPCEs.

Like the shoulder region is ‘railed’ by PPCEs, the pelvis is ‘clamped’ to the base table by another four PPCEs in accordance to the experiments (Fig. 1b). Their contact points are fixed to the base table, all located 5 cm footward of the axis $\mathcal {A}$ and either 6 cm or 30 cm, respectively, above the base table plane. The corresponding planes fixed to the pelvis are located such that all four PPCEs are usually strained by few millimeters: in the model, the pelvis is thus viscoelastically ‘clamped’. Similar to HAUT at the shoulder cushion roll, both model’s shanks are also ‘railed’ by four further PPCEs. In the shanks, however, the ‘railing’ planes are fixed to the base table instead of the bodies, in parallel to the posterior edge of the base table where the model is lying on its left side on. The contact points are fixed to the shanks at the positions of their respective COM positions in caudal–cranial direction.

Eventually, the pelvis on its right, lying side, the right thigh, the right shank, and the right foot are supported against gravity by altogether six PPCEs of which their planes, like at the right shoulder height of HAUT, all represent the surface of the base table. From proximal to distal (numbers given as distances from the body’s respective COM), the contact points fixed to the bodies are located on the pelvis at 17.5 cm laterally below its COM and 5.8 cm cranially, on the thigh at 6 cm laterally and 13.5 cm proximally as well as 4.5 cm laterally and 25.5 cm distally, on the shank at 4.5 cm laterally and 13.5 cm proximally as well as 4.5 cm laterally and 25.5 cm distally, and on the foot 4.5 cm laterally at about the heel position.

All main parameters of the PPCEs were chosen the same: normal stiffness as $1.5\times 10^{4}$ N m$^{-1}$, the nonlinear normal damping factor according to Eq. (3) as $d_{PPCE,damp}$ = 1 s m$^{-1}$, tangential (stick) stiffness as $2.0\times 10^{3}$ N m$^{-1}$, the coefficients of static and kinetic (sliding, slipping) friction as $\mu _{s}$ = 0.8 and $\mu _{k}$ = 0.7, respectively, and the critical velocity for the slip–stick transition as $v_{crit}$ = 1 cm s$^{-1}$.