Nonlinear modeling and dynamic analysis of bioengineering hyper-elastic tubes based on different material models

Abstract

In this research, nonlinear vibrations of a hyper-elastic tube accounting for large deflection and moderate rotation have been examined. The hyper-elastic tube is assumed to be surrounded by a nonlinear hardening elastic medium. Different types of hyper-elastic material models are presented and discussed including neo-Hookean, Mooney–Rivlin, Ishihara and Yeoh models. The efficacy of these models in nonlinear vibration modeling and analysis of hyper-elastic tubes has been examined. Modified von-Karman strain is used to consider both large deflection and moderate rotation. The governing equations are obtained based on strain energy function of above-mentioned hyper-elastic material models. The nonlinear governing equation of the tube contains cubic and quantic terms which is solved via extended Hamiltonian method leading to a closed form of nonlinear vibration frequency. The effect of hyper-elastic models and their material parameters on nonlinear vibrational frequency of tubes has been studied.

1 Introduction

Silicone rubber is classified in the category of hyper-elastic materials and possesses excellent biomedical compatibility and chemical resistance together with complex mechanical properties. Hyper-elastic materials undergo large strains under various loading conditions. Hence, their mechanical characteristics cannot be described using a linear stress–strain relationship (Shahzad et al. 2015). Therefore, hyper-elastic materials exhibit material nonlinearity and there is a need for nonlinear stress–strain relations to express their constitutive laws. Up to now, several models are proposed for modeling of hyper-elastic materials such as neo-Hookean, Mooney–Rivlin, Ishihara, Ogden and Yeoh models (Martins et al. 2006; Ogden et al. 2004; Horgan and Saccomandi 2006). These models require material parameters to define the stress–strain relation. The simplest approach to obtain these material parameters is performing uniaxial or biaxial tension tests (Marckmann and Verron 2006; Beda 2007). Then, the constitutive hyper-elastic material models can be fitted to the test data based on specified values of material parameters.

Structures made of hyper-elastic materials exhibit large deformation during their operational life. When investigating vibration behavior of hyper-elastic structures, it is important to consider large strain effects. Based on von-Karman’s strain model, many investigations consider large deflections in analysis of nonlinear structures (Li and Hu 2016; Barati and Shahverdi 2018a; Shahverdi et al. 2019; Besseghier et al. 2015; Bouiadjra et al. 2013; She et al. 2018a). In this model, only large deflection of the structures has been considered and rotations are considered to be small (Barati and Zenkour 2019; Sheng and Wang 2018; She et al. 2018b). This assumption is mostly used for elastic structures. When the rotations are not small enough, the modified von-Karman nonlinear strain is used to account for both large deflection and moderately large rotation of the structure (Reddy and El-Borgi 2014; Reddy and Srinivasa 2014).

Many investigations are published on nonlinear vibrations of hyper-elastic structures. Breslavsky et al. (2014) studied nonlinear vibration behavior of thin hyper-elastic plates made of rubber and soft biological tissues. They used neo-Hookean, Mooney–Rivlin and Ogden hyper-elastic laws to examine nonlinear vibration of the plate. Soares and Gonçalves (2018) examined nonlinear vibration of hyper-elastic plates rested on elastic foundations by considering pre-stretch effect. Wang et al. (2019) studied vibration behavior of axially moving beams made of hyper-elastic material accounting for large deformations. Also, Barforooshi and Mohammadi (2016) and Mohammadi and Barforooshi (2017) used hyper-elastic material laws to examine nonlinear vibrations of beam-type resonators. They used von-Karman strain type in order to capture large deflections of the beam under oscillation.

This paper is concerned with the study of nonlinear vibrational behavior of hyper-elastic tubes accounting for large deflection and moderate rotation. Hyper-elastic tubes have many applications especially at bioengineering and mechanical engineering fields. The hyper-elastic tube is assumed to be surrounded by a nonlinear hardening elastic medium. Various types of hyper-elastic material models have been introduced including neo-Hookean, Mooney–Rivlin, Ishihara and Yeoh models. Large deflections and also moderately large rotation of the tube have been considered based on modified von-Karman strain model. Nonlinear vibration frequency of the tube is obtained by solving the tube governing equation based on extended Hamiltonian approach. The effects of hyper-elastic material parameters, hyper-elastic material law, nonlinear elastic medium, length-to-thickness ratio and boundary condition on vibrational frequency of hyper-elastic tube have been studied in detail.

2 Different models for hyper-elastic materials

Based on the approach of developing strain energy function (W), there are three types of models for hyper-elastic materials (Marckmann and Verron 2006; Steinmann et al. 2012):

• 1. Phenomenological models: they are based on the mathematical development of strain energy function, for example Rivlin series.

• 2. Models based on direct determination of material parameters using experiment.

• 3. Physically based models: they consider the physical properties of polymeric chains network and statistical approaches to develop strain energy function.

In the following, some well-known models of hyper-elastic materials will be introduced and discussed. The strain energy function based on these models is based on strain invariants (I₁, I₂, I₃) which are (Steinmann et al. 2012; Ali et al. 2010):

$$\begin{aligned} I_{1} &= \lambda_{1}^{2} + \lambda_{2}^{2} + \lambda_{3}^{2} = {\text{tr}}(C) \hfill \\ I_{2} &= \lambda_{1}^{2} \lambda_{2}^{2} + \lambda_{1}^{2} \lambda_{3}^{2} + \lambda_{2}^{2} \lambda_{3}^{2} = \frac{1}{2}\left( {I_{1}^{2} - {\text{tr}}(C^{2} )} \right) \hfill \\ I_{3} &= \lambda_{1}^{2} \lambda_{2}^{2} \lambda_{3}^{2} = \det (C) \hfill \\ \end{aligned}$$

(1)

where λ_i (i = 1, 2, 3) denote the square roots for right Cauchy–Green strains tensor (C) and physically they are stretch ratios. Also, based on incompressibility assumption of materials, I₃ = 1. Also, the right Cauchy–Green strains tensor (C) is corresponding to strains tensor of the beam (E) as:

$$[C] = 2[E] + [I].$$

(2)

2.1 Neo-Hookean type

The neo-Hookean type has only one material constant (C₁) and is known as simplest model for hyper-elastic materials. It is a physically based model and introduces the strain energy function as follows:

$$W = c_{10} (I_{1} - 3)$$

(3)

where I₁ is the first strain invariant. For a rubber material, it is found that C₁₀ = 0.2 MPa. In literature, it is reported that such modeling does not have enough terms for mathematical description of beams or plates to obtain their governing equations. So, this model has been discarded in the present paper due to its limitations.

2.2 Mooney–Rivlin model

As reported by Mooney, the response of rubber subjected to simple shear is linear. Based on two material parameters (C₁₀ and C₀₁), the strain energy function based on this model can be expressed as:

$$W = c_{10} (I_{1} - 3) + c_{01} (I_{2} - 3)$$

(4)

where I₁ and I₂, respectively, denote the first and second strain invariants. This model is suitable for moderate deformations, lower than 200% and is erroneous for larger deformations. Similar to neo-Hookean model, Mooney–Rivlin model has not adequate terms to include nonlinear strains of the beam. So, the governing equations will not completely be derived. So, there is a need for another complete model of hyper-elastic materials.

2.3 Yeoh type

This type only depends on the first strain invariant (I₁) and is phenomenological type, but introduces three material parameters (c₁₀, c₂₀, c₃₀). The strain energy function based on this model can be expressed as:

$$W = c_{10} (I_{1} - 3) + c_{20} (I_{1} - 3)^{2} + c_{30} (I_{1} - 3)^{3} .$$

(5)

This model is successfully used by many researchers. The efficacy of this model in modeling of hyper-elastic material structures will be figured out in the following sections. For silicone rubber, the parameters are reported as (Martins et al. 2006): c₁₀ = 0.24162 MPa, c₂₀ = 0.19977 MPa, and c₃₀ = − 0.00541 MPa.

2.4 Three-parameter Mooney–Rivlin model

This modeling is an extension of Mooney–Rivlin type with two parameters, and it is also called Ishihara model. Hence, this model contains three material parameters and the strain energy function has the following form:

$$W = c_{10} (I_{1} - 3) + c_{01} (I_{2} - 3) + c_{20} (I_{1} - 3)^{2} .$$

(6)

3 Mathematical formulation

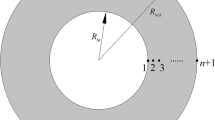
For modeling of hyper-elastic tube shown in Fig.1, the well-known Euler–Bernoulli beam model has been utilized for which the displacement field (u₁, u₂= 0, u₃) can be introduced as follows by neglecting shear deformation impacts (Bouadi et al. 2018; Bourada et al. 2018; Younsi et al. 2018; Mokhtar et al. 2018; Boutaleb et al. 2019; Abdelaziz et al. 2017; Faleh et al. 2018a, b; Al-Maliki et al. 2019; Fenjan et al. 2019; Ahmed et al. 2019):

$$u_{1} \left( {x,y,z,t} \right) = u\left( {x,y,t} \right) - z\frac{\partial w}{\partial x}$$

(7)

$$u_{3} (x,y,z,t) = w(x,y,t)$$

(8)

Fig. 1

Configuration of hyper-elastic tube embedded in elastic medium

Here, u and w, respectively, introduce longitudinal and lateral displacements. Based on modified von-Karman’s nonlinearity, the strain field in axial and transverse directions may be defined as (Reddy and Srinivasa 2014):

$$\begin{aligned} \varepsilon_{xx} & = \frac{{\partial u_{1} }}{\partial x} = \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} \\ \varepsilon_{zz} & = \frac{1}{2}\theta_{x}^{2} , \, \theta_{x}^{{}} = - \frac{\partial w}{\partial x} \\ \end{aligned}$$

(9)

where the transverse strain (ε_zz) is created due to moderate rotation ($\theta_{x}^{2}$). To derive the governing equations of hyper-elastic tube, the extended Hamilton’s principle may be defined as:

$$\int_{0}^{t} {\delta (W + V - K){\text{d}}t = 0} .$$

(10)

Herein, W defines strain energy function, $V$ defines work done by external forces, and K defines kinetic energy.

Based on Yeoh or three-parameter Mooney–Rivlin models, the first strain energy variation might be generally defined as:

$$\delta W = \delta W_{10} + \delta W_{01} + \delta W_{20} + \delta W_{30}$$

(11)

where using Eqs. (5) and (6) one can get to:

$$\begin{aligned} \delta W_{10} = 4C_{10} \int {\frac{\partial w}{\partial x}} \delta \left( {\frac{\partial w}{\partial x}} \right){\text{d}}V = 4AC_{10} \frac{\partial w}{\partial x}\delta w\left| {_{x = 0}^{x = L} } \right. - 4AC_{10} \int_{0}^{L} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \delta (w){\text{d}}x \hfill \\ \hfill \\ \end{aligned}$$

(12)

$$\begin{aligned} \delta W_{01} = & 4C_{01} \int {\left( {2\frac{\partial w}{\partial x}\delta \left( {\frac{\partial w}{\partial x}} \right) + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} \delta \left( {\frac{\partial u}{\partial x}} \right) + \frac{\partial u}{\partial x}\frac{\partial w}{\partial x}\delta \left( {\frac{\partial w}{\partial x}} \right) + \left( {\frac{\partial w}{\partial x}} \right)^{3} \delta \left( {\frac{\partial w}{\partial x}} \right)} \right)} {\text{d}}V \\ = & 8AC_{01} \frac{\partial w}{\partial x}\delta w\left| {_{x = 0}^{x = L} } \right. - 8AC_{01} \int_{0}^{L} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \delta (w){\text{d}}x + 2AC_{01} \left( {\frac{\partial w}{\partial x}} \right)^{2} \delta u\left| {_{x = 0}^{x = L} } \right. - 4AC_{01} \int_{0}^{L} {\frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \delta (u){\text{d}}x \\ & + 4AC_{01} \frac{\partial u}{\partial x}\frac{\partial w}{\partial x}\delta w\left| {_{x = 0}^{x = L} } \right. - 4AC_{01} \int_{0}^{L} {\left( {\frac{\partial u}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial w}{\partial x}\frac{{\partial^{2} u}}{{\partial x^{2} }}} \right)} \delta (w){\text{d}}x + 4AC_{01} \left( {\frac{\partial w}{\partial x}} \right)^{3} \delta w\left| {_{x = 0}^{x = L} } \right. \\ & - 12AC_{01} \int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \delta (w){\text{d}}x \\ \end{aligned}$$

(13)

$$\begin{aligned} \delta W_{20} = & 4C_{20} \int {\left( {2\frac{\partial u}{\partial x}\delta \left( {\frac{\partial u}{\partial x}} \right) + 2\left( {\frac{\partial w}{\partial x}} \right)^{2} \delta \left( {\frac{\partial u}{\partial x}} \right) + 4\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}\delta \left( {\frac{\partial w}{\partial x}} \right) + 2z^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}\delta \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + 4\left( {\frac{\partial w}{\partial x}} \right)^{3} \delta \left( {\frac{\partial w}{\partial x}} \right)} \right)} {\text{d}}V \\ = & 8C_{20} A\frac{\partial u}{\partial x}\delta u\left| {_{x = 0}^{x = L} } \right. - 8C_{20} A\int_{0}^{L} {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \delta (u){\text{d}}x + 8C_{20} A\left( {\frac{\partial w}{\partial x}} \right)^{2} \delta u\left| {_{x = 0}^{x = L} } \right. - 16AC_{20} \int_{0}^{L} {\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial w}{\partial x}} \delta (u){\text{d}}x \\ & + 16C_{20} A\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}\delta w\left| {_{x = 0}^{x = L} } \right. - 16AC_{20} \int_{0}^{L} {\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial u}{\partial x} + \frac{{\partial^{2} u}}{{\partial x^{2} }}\frac{\partial w}{\partial x}} \right)} \delta (w){\text{d}}x + 8C_{20} I\frac{{\partial^{2} w}}{{\partial x^{2} }}\delta \left( {\frac{\partial w}{\partial x}} \right)\left| {_{x = 0}^{x = L} } \right. \\ & - 8C_{20} I\frac{{\partial^{3} w}}{{\partial x^{3} }}\delta (w)\left| {_{x = 0}^{x = L} } \right. + 8C_{20} I\int_{0}^{L} {\frac{{\partial^{4} w}}{{\partial x^{4} }}} \delta (w){\text{d}}x \\ & + 16AC_{20} \left( {\frac{\partial w}{\partial x}} \right)^{3} \delta (w)\left| {_{x = 0}^{x = L} } \right. - 48C_{20} A\int_{0}^{L} {\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \delta (w){\text{d}}x \\ \end{aligned}$$

(14)

$$\begin{aligned} \delta W_{10} & = 8C_{30} \int {\left( {3\left( {\frac{\partial u}{\partial x}} \right)^{2} } \right.} \delta \left( {\frac{\partial u}{\partial x}} \right) + 6\frac{\partial u}{\partial x}\left( {\frac{\partial w}{\partial x}} \right)^{2} \delta \left( {\frac{\partial u}{\partial x}} \right) + 6\frac{\partial w}{\partial x}\left( {\frac{\partial u}{\partial x}} \right)^{2} \delta \left( {\frac{\partial w}{\partial x}} \right) + 3z^{2} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} \delta \left( {\frac{\partial u}{\partial x}} \right) \\ & \quad \quad + 6z^{2} \frac{\partial u}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }}\delta \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + 3\left( {\frac{\partial w}{\partial x}} \right)^{4} \delta \left( {\frac{\partial u}{\partial x}} \right) + 12\frac{\partial u}{\partial x}\left( {\frac{\partial w}{\partial x}} \right)^{3} \delta \left( {\frac{\partial w}{\partial x}} \right) + 6z^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} \delta \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \\ & \quad \quad + 6z^{2} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} \frac{\partial w}{\partial x}\delta \left( {\frac{\partial w}{\partial x}} \right) + 6\left( {\frac{\partial w}{\partial x}} \right)^{5} \left. {\delta \left( {\frac{\partial w}{\partial x}} \right)} \right){\text{d}}V \\ & = 24C_{30} A\left( {\frac{\partial u}{\partial x}} \right)^{2} \delta u\left| {_{x = 0}^{x = L} } \right. - 48C_{30} A\int_{0}^{L} {\frac{\partial u}{\partial x}\frac{{\partial^{2} u}}{{\partial x^{2} }}} \delta (u){\text{d}}x + 48C_{30} A\frac{\partial u}{\partial x}\left( {\frac{\partial w}{\partial x}} \right)^{2} \delta u\left| {_{x = 0}^{x = L} } \right. \\ & \quad - 48C_{30} A\int_{0}^{L} {\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} + 2\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \delta (u){\text{d}}x + 48C_{30} A\frac{\partial w}{\partial x}\left( {\frac{\partial u}{\partial x}} \right)^{2} \delta w\left| {_{x = 0}^{x = L} } \right. \\ & \quad - 48C_{30} A\int_{0}^{L} {\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial u}{\partial x}} \right)^{2} + 2\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}\frac{{\partial^{2} u}}{{\partial x^{2} }}} \right)} \delta (w){\text{d}}x + 24C_{30} I\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} \delta u\left| {_{x = 0}^{x = L} } \right. \\ & \quad - 48C_{30} I\int_{0}^{L} {\frac{{\partial^{3} w}}{{\partial x^{3} }}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \delta (u){\text{d}}x + 48C_{30} I\frac{\partial u}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }}\delta \left( {\frac{\partial w}{\partial x}} \right)\left| {_{x = 0}^{x = L} } \right. - 48C_{30} I\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial u}{\partial x}\frac{{\partial^{3} w}}{{\partial x^{3} }}} \right)\delta w\left| {_{x = 0}^{x = L} } \right. \\ & \quad + 48C_{30} A\int_{0}^{L} {\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{3} u}}{{\partial x^{3} }} + 2\frac{{\partial^{3} w}}{{\partial x^{3} }}\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial u}{\partial x}\frac{{\partial^{4} w}}{{\partial x^{4} }}} \right)} \delta (w){\text{d}}x + 24C_{30} A\left( {\frac{\partial w}{\partial x}} \right)^{4} \delta u\left| {_{x = 0}^{x = L} } \right. \\ & \quad - 96C_{30} A\int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{3} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \delta (u){\text{d}}x + 96C_{30} A\left( {\frac{\partial w}{\partial x}} \right)^{3} \frac{\partial u}{\partial x}\delta w\left| {_{x = 0}^{x = L} } \right. \\ & \quad - 96C_{30} A\int_{0}^{L} {\left( {3\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} \frac{\partial u}{\partial x} + \left( {\frac{\partial w}{\partial x}} \right)^{3} \frac{{\partial^{2} u}}{{\partial x^{2} }}} \right)} \delta (w){\text{d}}x \\ & \quad + 48C_{30} I\left( {\frac{\partial w}{\partial x}} \right)^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}\delta \left( {\frac{\partial w}{\partial x}} \right)\left| {_{x = 0}^{x = L} } \right. \\ & \quad - 48C_{30} I\left( {\left( {\frac{\partial w}{\partial x}} \right)^{2} \frac{{\partial^{3} w}}{{\partial x^{3} }} + 2\frac{\partial w}{\partial x}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} } \right)\delta (w)\left| {_{x = 0}^{x = L} } \right. \\ & \quad + 48C_{30} I\int_{0}^{L} {\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} + 6\frac{{\partial^{3} w}}{{\partial x^{3} }}\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial w}{\partial x} + 2\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{3} } \right)} \delta (w){\text{d}}x \\ & \quad + 48C_{30} I\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} \frac{\partial w}{\partial x}\delta w\left| {_{x = 0}^{x = L} } \right. - 48C_{30} I\int_{0}^{L} {\left( {2\frac{{\partial^{3} w}}{{\partial x^{3} }}\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial w}{\partial x} + \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{3} } \right)} \delta (w){\text{d}}x \\ & \quad + 48C_{30} A\left( {\frac{\partial w}{\partial x}} \right)^{5} \delta w\left| {_{x = 0}^{x = L} } \right. - 240C_{30} A\int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{4} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \delta (w){\text{d}}x. \\ \end{aligned}$$

(15)

The first variation applied to external load work may be written as follows:

$$\delta \,V = \int_{0}^{L} {q\delta w} {\text{d}}x.$$

(16)

Applied load by the substrate should be defined as (Bakhadda et al. 2018; Yazid et al. 2018; Kadari et al. 2018; Chaabane et al. 2019; Boukhlif et al. 2019; Boulefrakh et al. 2019):

$$q = k_{\text{w}} \,w - k_{\text{p}} \frac{{\partial^{2} w}}{{\partial x^{2} }} + k_{\text{nl}} w^{3}$$

(17)

where $k_{\text{w}}$ and $k_{\text{p}}$ are Winkler and Pasternak coefficients of the substrate, respectively. Next, k_nl denotes the nonlinear stiffness of the surrounding medium. The variation of kinetic energy is represented by:

$$\begin{aligned} \delta K & = \int_{0}^{L} {\left( {I_{0} \left[ {\frac{\partial u}{\partial t}\frac{\partial \delta u}{\partial t} + \left( {\frac{\partial w}{\partial t}} \right)\left( {\frac{\partial \delta w}{\partial t}} \right)} \right] - I_{1} \left( {\frac{\partial u}{\partial t}\frac{{\partial^{2} \delta w}}{\partial x\partial t} + \frac{{\partial^{2} w}}{\partial x\partial t}\frac{\partial \delta u}{\partial t}} \right)} \right)} \\ & \quad + \,I_{2} \left. {\left( {\frac{{\partial^{2} w_{{}} }}{\partial x\partial t}\frac{{\partial^{2} \delta w_{{}} }}{\partial x\partial t}} \right)} \right){\text{d}}x \\ \end{aligned}$$

(18)

where

$$(I_{0} ,I_{1} ,I_{2} ) = \int_{ - h/2}^{h/2} {(1,z,z^{2} )\rho } {\text{d}}z.$$

(19)

The nonlinear governing equations may be derived for hyper-elastic tube by using Eqs. (12)–(18) as:

$$\begin{aligned} & - 4AC_{01} \frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} - 8C_{20} A\frac{{\partial^{2} u}}{{\partial x^{2} }} - 16AC_{20} \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial w}{\partial x} - 48C_{30} A\frac{\partial u}{\partial x}\frac{{\partial^{2} u}}{{\partial x^{2} }} \\ & - 48C_{30} A\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} + 2\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) - 48C_{30} I\frac{{\partial^{3} w}}{{\partial x^{3} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} - 96C_{30} A\left( {\frac{\partial w}{\partial x}} \right)^{3} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} \\ \end{aligned}$$

(20)

$$\begin{aligned} & - 4AC_{10} \frac{{\partial^{2} w}}{{\partial x^{2} }} - 8AC_{01} \frac{{\partial^{2} w}}{{\partial x^{2} }} - 4AC_{01} \left( {\frac{\partial u}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial w}{\partial x}\frac{{\partial^{2} u}}{{\partial x^{2} }}} \right) \\ & - 12AC_{01} \left( {\frac{\partial w}{\partial x}} \right)^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} - 16AC_{20} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial u}{\partial x} + \frac{{\partial^{2} u}}{{\partial x^{2} }}\frac{\partial w}{\partial x}} \right) + 8C_{20} I\frac{{\partial^{4} w}}{{\partial x^{4} }} \\ & - 48C_{20} A\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} - 48C_{30} A\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial u}{\partial x}} \right)^{2} + 2\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}\frac{{\partial^{2} u}}{{\partial x^{2} }}} \right) \\ & + 48C_{30} A\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{3} u}}{{\partial x^{3} }} + 2\frac{{\partial^{3} w}}{{\partial x^{3} }}\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial u}{\partial x}\frac{{\partial^{4} w}}{{\partial x^{4} }}} \right) - 96C_{30} A\left( {3\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} \frac{\partial u}{\partial x} + \left( {\frac{\partial w}{\partial x}} \right)^{3} \frac{{\partial^{2} u}}{{\partial x^{2} }}} \right) \\ & + 48C_{30} I\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} + 6\frac{{\partial^{3} w}}{{\partial x^{3} }}\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial w}{\partial x} + 2\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{3} } \right) - 48C_{30} I\left( {2\frac{{\partial^{3} w}}{{\partial x^{3} }}\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial w}{\partial x} + \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{3} } \right) \\ & - 240C_{30} A\left( {\frac{\partial w}{\partial x}} \right)^{4} \frac{{\partial^{2} w}}{{\partial x^{2} }} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} \\ & \quad = + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + I_{1} \left( {\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }}} \right) - I_{2} \nabla^{2} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) - k_{w} w + k_{p} \nabla^{2} w - k_{nl} w^{3} . \\ \end{aligned}$$

(21)

Note that I₁ = 0 for isotropic hyper-elastic material.

4 Solution procedure

In this section, nonlinear vibration problem of hyper-elastic tubes is solved using a Hamiltonian approach and with the help of Galerkin’s method. First, it should be mentioned that the effect of axial displacement is ignorable compared to transverse displacement (She et al. 2018a). However, the transverse displacement is assumed to be:

$$w = \sum\limits_{i = 1}^{\infty } {W_{i} \varphi_{i} (x)}$$

(22)

where W_i is the vibration amplitude. The boundary conditions based on transverse displacement from Eqs. (12)–(15) can be expressed as:

$$w\left| {_{x = 0} } \right. = w\left| {_{x = L} } \right. = 0,\frac{{\partial^{2} w_{{}} }}{{\partial x^{2} }}\left| {_{x = 0} } \right. = \frac{{\partial^{2} w_{{}} }}{{\partial x^{2} }}\left| {_{x = L} } \right. = 0\quad {\text{Simply - Supported}}\,\left( {{\text{S}} - {\text{S}}} \right)$$

(23)

$$w\left| {_{x = 0} } \right. = w\left| {_{x = L} } \right. = 0,\quad \frac{{\partial w_{{}} }}{\partial x}\left| {_{x = 0} } \right. = \frac{{\partial w_{{}} }}{\partial x}\left| {_{x = L} } \right. = 0\,{\text{Clamped - Clamped}}\,\left( {{\text{C}} - {\text{C}}} \right).$$

(24)

To satisfy above-mentioned boundary condition, the function $\varphi_{i} (x)$ may be selected as (Bourada et al. 2018; Younsi et al. 2018; Mokhtar et al. 2018):

$$\varphi_{i} (x) = \sin \left( {\frac{i\pi }{L}x} \right)\quad {\text{for}}\,{\text{S}} - {\text{S}}$$

(25)

$$\varphi_{i} (x) = 0.5\left( {1 - \cos \left( {\frac{2i\pi }{L}x} \right)} \right)\quad {\text{for}}\,{\text{C}} - {\text{C}}$$

(26)

Now, placing Eq. (22) into the governing Eq. (21) and using Galerkin’s method lead to the following simplified nonlinear equation:

$$\begin{aligned} K_{1} W + K_{3} W_{{}}^{3} + K_{5} W_{{}}^{5} + M\ddot{W}_{{}} = 0. \hfill \\ \hfill \\ \end{aligned}$$

(27)

The symbol (.) represents the derivative with respect to time, M is mass matrix, and K_i are structural stiffness:

$$\begin{aligned} K_{1} & = - 4A(C_{10} + 2C_{01} ){\rm Z}_{20} + 8C_{20} I{\rm Z}_{40} + k_{w} {\rm Z}_{00} - k_{p} {\rm Z}_{20} \\ K_{3} & = - 12AC_{01} {\rm Z}_{2110} - 48C_{20} A{\rm Z}_{2110} + 48C_{30} I({\rm Z}_{4110} + 4{\rm Z}_{3210} + {\rm Z}_{2220} ) + k_{nl} {\rm Z}_{0000} \\ K_{5} & = - 240C_{30} A{\rm Z}_{211110} \\ M & = I_{0} {\rm Z}_{00} - I_{2} {\rm Z}_{20} . \\ \end{aligned}$$

(28)

In above equation, the constructed integrals are:

$$\begin{aligned} {\rm Z}_{00} & = \int_{0}^{L} {\,\varphi_{i} \varphi_{i} {\text{d}}x} \\ {\rm Z}_{20} & = \int_{0}^{L} {\,\varphi_{i}^{''} \varphi_{i} {\text{d}}x} \\ {\rm Z}_{40} & = \int_{0}^{L} {\,\varphi_{i}^{''''} \varphi_{i} {\text{d}}x} \\ {\rm Z}_{11} & = \int_{0}^{L} {\,\varphi_{i}^{'} \varphi_{i}^{'} {\text{d}}x} \\ {\rm Z}_{0000} & = \int_{0}^{L} {\,\left( {\varphi_{i} } \right)^{4} {\text{d}}x} \\ {\rm Z}_{2110} & = \int_{0}^{L} {\,\varphi_{i}^{''} \varphi_{i}^{'} \varphi_{i}^{'} \varphi_{i} {\text{d}}x} \\ {\rm Z}_{2220} & = \int_{0}^{L} {\,\varphi_{i}^{''} \varphi_{i}^{''} \varphi_{i}^{''} \varphi_{i} {\text{d}}x} \\ {\rm Z}_{3210} & = \int_{0}^{L} {\,\varphi_{i}^{'''} \varphi_{i}^{''} \varphi_{i}^{'} \varphi_{i} {\text{d}}x} \\ {\rm Z}_{4110} & = \int_{0}^{L} {\,\varphi_{i}^{''''} \varphi_{i}^{'} \varphi_{i}^{'} \varphi_{i} {\text{d}}x} \\ {\rm Z}_{211110} & = \int_{0}^{L} {\,\varphi_{i}^{''} \left( {\varphi_{i}^{'} } \right)^{4} \varphi_{i} {\text{d}}x} . \\ \end{aligned}$$

(29)

In above integrals, the symbol prime defines the derivatives with respect to x.

4.1 Extended Hamiltonian method

The nonlinear governing equation of hyper-elastic tube, Eq. (27), contains cubic and quantic terms. Hamiltonian approach (He 2010) is mostly used for Duffing-type oscillator having only cubic nonlinearity. In order to solve Eq. (27), an extended version of Hamiltonian method is used in the present research (Bayat et al. 2014).

Hamiltonian of a conservative system will be constant during vibrations. Hence, the Hamiltonian of the governing equation of the tube can be expressed as:

$$H = + \frac{1}{2}M\dot{W}^{2} + \frac{1}{2}K_{1} W^{2} + K_{3} \left( {\frac{1}{4}\tilde{W}^{4} } \right) + K_{5} \left( {\frac{1}{6}\tilde{W}^{6} } \right) = {\text{Constant}} = H_{0} .$$

(30)

Above relation gives that $H - H_{0} = 0$. Therefore, from mathematical point of view, it can be concluded that (Barati 2018a, b; Barati and Shahverdi 2018b):

$$\frac{\partial H}{{\partial W_{{}} }} = 0.$$

(31)

For this approach, the following function should be defined as:

$$\tilde{H}(t) = \int_{0}^{T/4} H {\text{d}}t = \frac{1}{4}TH.$$

(32)

Note that T defines the vibrations period and from above relation one can conclude that:

$$\frac{{\partial \tilde{H}(t)}}{\partial T} = \frac{1}{4}H.$$

(33)

According to Eqs. (31) and (33), it may be deduced that

$$\frac{\partial }{{\partial \tilde{W}_{{}} }}\left( {\frac{{\partial \tilde{H}(t)}}{\partial T}} \right) = 0.$$

(34)

The presented Eq. (34) can be also represented as:

$$\frac{\partial }{{\partial \tilde{W}_{{}} }}\left( {\frac{{\partial \tilde{H}(t)}}{{\partial \left( {1/\omega_{\text{NL}} } \right)}}} \right) = 0.$$

(35)

For nonlinear harmonic oscillation of the tube, the vibration amplitude can be defined as (Barati 2018a, b; Barati and Shahverdi 2018b):

$$\begin{aligned} W_{{}} (t) = \tilde{W}_{{}} \cos (\omega t) \hfill \\ \hfill \\ \end{aligned}$$

(36)

Now, with the use of Eq. (36), one can express Eq. (32) in detailed form as:

$$\begin{aligned} \tilde{H}(\omega_{\text{NL}} ) = & \frac{1}{{\omega_{\text{NL}} }}\int_{0}^{\pi /2} {\left[ { + \left( {\frac{1}{2}M\tilde{W}^{2} } \right)\omega_{\text{NL}}^{2} \sin^{2} (\theta ) + \left( {\frac{1}{2}K_{1} \tilde{W}^{2} } \right)\cos^{2} (\theta ) + K_{3} \left( {\frac{1}{4}\tilde{W}^{4} } \right)\cos^{4} (\theta )} \right.} \\ & \left. { + K_{5} \left( {\frac{1}{6}\tilde{W}^{6} } \right)\cos^{6} (\theta )} \right]{\text{d}}\theta . \\ \end{aligned}$$

(37)

The stationary conditions $\partial \tilde{H}/\partial \tilde{W} = 0$ result in

$$\frac{{K_{1} }}{M}\tilde{W} + \frac{3}{4}\frac{{K_{3} }}{M}(\tilde{W})^{3} + \frac{5}{8}\frac{{K_{5} }}{M}(\tilde{W})^{5} - \omega^{2} \tilde{W} = 0.$$

(38)

Finally, the nonlinear frequency of hyper-elastic tube is derived as:

$$\omega_{\text{NL}} = \frac{1}{2}\sqrt {\frac{{8\frac{{K_{1} }}{M} + 6\frac{{K_{3} }}{M}(\tilde{W})^{2} + 5\frac{{K_{5} }}{M}(\tilde{W})^{4} }}{2}} .$$

(39)

In the present article, results are presented based on the following normalized quantities:

$$\varOmega = \omega_{\text{NL}} L\sqrt {\frac{\rho }{{c_{10} }}} ,\;K_{\text{w}} = k_{\text{w}} \frac{{L^{4} }}{{c_{10} d_{2}^{4} }},\,\,K_{\text{p}} = k_{\text{p}} \frac{{L^{2} }}{{c_{10} d_{2}^{4} }},\;K_{\text{NL}} = k_{\text{nl}} \frac{{L^{4} }}{{c_{10} h}}.$$

(40)

5 Discussions on results

In present section, geometrically nonlinear vibrations characteristics of hyper-elastic tubes have been studied and figured out. Two types of hyper-elastic material models, called three-parameter Mooney–Rivlin model (Ishihara model) and Yeoh model, are considered. In previous section, closed form of nonlinear vibration frequency of the tube was obtained. The effects of hyper-elastic material parameters, hyper-elastic material law, nonlinear elastic medium, length-to-thickness ratio and boundary conditions on vibration frequency of the hyper-elastic tube will be studied in detail.

Vibration frequency validation of a hyper-elastic beam with rectangular cross section based on Yeoh model is presented in Fig. 2 with those of Barforooshi and Mohammadi (2016), and a good agreement has been achieved among the curves. The thickness of hyper-elastic beam is considered as h = 0.65. For this validation, the effect moderate rotations has been discarded due to the reason that in the paper of Barforooshi and Mohammadi (2016), and moderate rotations are not considered. However, the geometric nonlinearity in this figure is considered based on large deflection of the hyper-elastic beam.

Fig. 2

Validation of the nonlinear vibration frequency for a hyper-elastic beam

Nonlinear vibration frequency versus dimensionless amplitude of hyper-elastic tube based on Yeoh and three-parameter Mooney–Rivlin hyper-elastic models is plotted in Fig. 3 when L/h = 20. Both S–S and C–C boundary conditions have been considered. First of all, it must be pointed out that increasing of vibrational amplitudes is corresponding to greater frequency owing to inclusion of nonlinear stiffening impacts. However, the smallest frequency of the tube can be obtained at $\tilde{W}$/h = 0. Also, as the value of vibration amplitude increases, the difference between vibration frequencies of these two models becomes greater. This is due to the difference of these models in incorporation of strains for modeling of hyper-elastic materials. Also, consideration of mechanism of deformation has some differences for these models. Yeoh model contains the nonlinear strain up to third order, but three-parameter Mooney–Rivlin contains the strain up to second order. In fact, Yeoh model captures larger strains than Mooney–Rivlin in modeling of hyper-elastic materials.

Fig. 3

Nonlinear vibrational frequency versus dimensionless amplitude based on various hyper-elastic models (L/h = 20)

As it is well known on the literature, obtaining hyper-elastic material parameter is a complex task since they are dependent on various conditions such as loading type and environment. When using optimization to obtain material models, it is important to note that the answer is an approximation within predefined tolerances of the correct one. In Fig. 4, the effect of hyper-elastic material parameters of Yeoh model (c₁₀, c₂₀, c₃₀) with ± 10% and ± 20% tolerance is presented. One can see that increase in c₁₀ parameter reduces the nonlinear vibration frequency, but increase in c₂₀ parameter increases the nonlinear vibration frequency. This is due to the fact that increase in c₂₀ parameter increases structural stiffness of the tube. Also, c₃₀ is a material parameter related to larger strains, as can be seen from Eq. (5). Thus, from Fig. 4, it is obvious that the effect of c₃₀ material parameter is not sensible at small vibration amplitudes.

Fig. 4

Nonlinear vibrational frequency versus dimensionless amplitude based on various hyper-elastic material parameters (L/h = 20)

Effect of slenderness ratio (L/h) on nonlinear vibration behavior of hyper-elastic tubes with S–S and C–C boundary conditions is presented in Fig. 5. Yeoh model of hyper-elastic materials is considered in this figure. It is known that tubes become more flexible at greater values for slenderness ratio. Thus, derived nonlinear vibration frequencies become lower by increasing of slenderness ratios at constant normalized amplitudes ($\tilde{W}/h$). Moreover, derived nonlinear vibration frequencies related to several values for slenderness ratios rely on values of non-dimensional amplitudes. At a small slenderness ratio, nonlinear vibration frequency increases with higher slope with respect to non-dimensional amplitudes than a large slenderness ratio.

Fig. 5

Nonlinear vibration frequency versus dimensionless amplitude based on various slenderness ratios

Figures 6 and 7 show the dependency of nonlinear free vibration characteristics of geometrically nonlinear hyper-elastic tubes on elastic medium parameters. It is clear from the figure that increase in Winkler (K_w) and Pasternak (K_P) elastic medium coefficients only increases the value of vibration frequency and their influences are not dependent on the vibrational amplitudes. In fact, nonlinear vibration frequency is increased with the increase in elastic medium parameters regardless of the magnitude of vibration amplitude. In can be concluded that this observation is related to the increase in bending rigidity of the tube by considering the influence of elastic medium.

Fig. 6

Nonlinear vibration frequency versus dimensionless amplitude based on various Winkler parameters (L/h = 50, K_p = 0)

Fig. 7

Nonlinear vibration frequency versus dimensionless amplitude based on various Pasternak parameters (L/h = 50, K_w = 100)

The effect of nonlinear parameter of elastic medium (K_NL) on vibration frequency of hyper-elastic tubes is depicted in Fig. 8 when K_w = 100, K_p = 10. It is obvious based on the figure that the influences of nonlinear elastic medium constant (K_NL) on vibrational frequencies are negligible near the zero vibrational amplitudes. Hence, its impacts become more announced at great vibrational amplitudes. Actually, nonlinear elastic medium coefficient cannot vary the value of natural frequency, the frequency at $\tilde{W}/h = 0$, because the natural frequency is independent of nonlinear stiffness. However, as the magnitudes of vibration amplitudes become higher, the influence of nonlinear elastic medium parameter on the vibration frequency becomes more prominent because of the enhancement of nonlinear hardening influences.

Fig. 8

Nonlinear vibration frequency versus dimensionless amplitude based on various nonlinear elastic medium parameters (L/h = 20, K_w = 100, K_p = 10)

6 Conclusions

The present paper dealt with nonlinear vibration analysis of a hyper-elastic tube made of silicone rubber which is embedded in a nonlinear elastic medium. Yeoh and three-parameter Mooney–Rivlin models were used for modeling of hyper-elastic material. Extended Hamiltonian approach was used for solving the nonlinear governing equation of the tube possessing cubic and quintic nonlinearity types. It was found that as the value of vibration amplitude increased, the difference between vibration frequencies of Yeoh and three-parameter Mooney–Rivlin models became greater. This is due to the difference of these models in incorporation of strains for modeling of hyper-elastic materials. Also, it was reported that increase in c₁₀ and c₂₀ parameters, respectively, reduced and increased the nonlinear vibration frequency, Also, the effect of c₃₀ material parameter was not sensible at small vibration amplitudes.