Patient-specific in silico endovascular repair of abdominal aortic aneurysms: application and validation

Abstract

Non-negligible postinterventional complication rates after endovascular aneurysm repair (EVAR) leave room for further improvements. Since the potential success of EVAR depends on various patient-specific factors, such as the complexity of the vessel geometry and the physiological state of the vessel, in silico models can be a valuable tool in the preinterventional planning phase. A suitable in silico EVAR methodology applied to patient-specific cases can be used to predict stent-graft (SG)-related complications, such as SG migration, endoleaks or tissue remodeling-induced aortic neck dilatation and to improve the selection and sizing process of SGs. In this contribution, we apply an in silico EVAR methodology that predicts the final state of the deployed SG after intervention to three clinical cases. A novel qualitative and quantitative validation methodology, that is based on a comparison between in silico results and postinterventional CT data, is presented. The validation methodology compares average stent diameters pseudo-continuously along the total length of the deployed SG. The validation of the in silico results shows very good agreement proving the potential of using in silico approaches in the preinterventional planning of EVAR. We consider models of bifurcated, marketed SGs as well as sophisticated models of patient-specific vessels that include intraluminal thrombus, calcifications and an anisotropic model for the vessel wall. We exemplarily show the additional benefit and applicability of in silico EVAR approaches to clinical cases by evaluating mechanical quantities with the potential to assess the quality of SG fixation and sealing such as contact tractions between SG and vessel as well as SG-induced tissue overstresses.

1 Introduction

An abdominal aortic aneurysm (AAA) is a local enlargement of the abdominal aorta which is exposed to the immanent risk of rupture with high mortality rates (Ockert et al. 2007). In the intervention of an endovascular aneurysm repair (EVAR), a stent-graft (SG) is deployed inside the AAA to exclude the aneurysm sac from the main blood flow, remove the load of the pulsatile blood pressure from the aneurysm wall, prevent the aneurysm from ongoing aneurysm growth and consequently prevent the aneurysm from rupture. Most marketed SGs are a combination of a wire mesh (stent) that is attached on a polymeric fabric (graft). Compared to open AAA repair, EVAR is less invasive and has a reduced 30-day mortality rate (Greenhalgh et al. 2010). However, EVAR is not applicable to all patients and might not have the same longevity as open AAA repair. The complexity of the vessel geometry, especially extensive tortuosity and the lack of a sufficient sealing zone, might preclude the proper use of EVAR. Most frequent complications after EVAR are endoleaks (Greenhalgh and Powell 2008; Chang et al. 2013; Shiraev et al. 2018; Sampaio et al. 2004), SG migration (Altnji et al. 2015; van Prehn et al. 2009; Rafii et al. 2008; Zarins et al. 2003), SG fatigue (Kleinstreuer et al. 2008; Beebe et al. 2001; Jacobs et al. 2003), aortic neck dilatation (Vukovic et al. 2018; Cao et al. 2003; Sampaio et al. 2006; Kouvelos et al. 2017; Sternbergh et al. 2004) and SG kinking associated with the occlusion of blood vessels (Cochennec et al. 2007; Maleux et al. 2009). Since the potential success of EVAR, i.e., the EVAR treatment free of short-term and long-term complications, depends on various factors, computational vascular mechanics models can be a valuable tool in the preinterventional planning.

The objective of this work is the application of the in silico EVAR methodology that was recently published by our group (Hemmler et al. 2018) to patient-specific cases with bifurcated, marketed SGs. This involves the development of a continuous process chain which includes the following steps: (1) medical imaging of preinterventional CT data, (2) automated model generation of patient-specific vessels and SGs, (3) application of the in silico EVAR methodology as well as (4) postprocessing and mechanical interpretation of simulation results. Postinterventional CT data of patients treated by marketed, bifurcated SGs are used to qualitatively and quantitatively validate the in silico EVAR approach.

As the only patient-specific information for assessment of the applicability of EVAR, the SG selection and the SG sizing is the data obtained from medical imaging, this assessment is a great challenge, requires a lot of experience and is the subjective choice of the interventionalist. Hence, in silico EVAR applied to patient-specific cases can be used as predictive tool in four respects:

• Risk assessment of the EVAR intervention to number the potential likelihood of SG-related complications.

• Improvement of the device selection process. The risk of SG-related complications is affected by the device choice (Perrin et al. 2015b; Tonnessen et al. 2005) as not all marketed SGs fit to a specific vessel geometry to the same extent.

• Improvement of the SG sizing process. The optimal degree of SG oversizing is difficult to estimate as it depends on various factors such as the morphology and condition of the vessel (Wyss et al. 2011; van Prehn et al. 2009).

• Objectivity of preinterventional planning process and tool for education.

In this study, the in silico EVAR methodology based on finite element methods (FEM) that was proposed in Hemmler et al. (2018) is applied to three patient-specific cases treated by Cook Zenith Flex^® and Cook Zenith Spiral-Z^® SGs. Model and model parameter uncertainties inherent to patient-specific modeling as well as the variety of vessel geometries and complex shapes of marketed SGs are further challenges compared to the application of the in silico EVAR methodology to synthetic AAAs in Hemmler et al. (2018). The in silico EVAR methodology aims at finding the final deployed SG configuration in the vessel geometry rather than reproducing the intrainterventional steps of EVAR. The methodology considers in vivo non-stress-free vessel geometries extracted from in vivo CT images by the prestressing methodology proposed in Gee et al. (2010). A stent predeformation methodology (Hemmler et al. 2018) is applied to account for residual strains and stresses that exist in most marketed SGs. Attention is paid to detailed modeling of all vessel and aneurysm constituents as they can have a distinct impact on the outcome of EVAR (Wyss et al. 2011; Sampaio et al. 2004; Wolf et al. 2001). This means the vessel model considers both a “healthy” vessel wall by an anisotropic and hyperelastic constitutive law and an “aneurysmatic” vessel wall by an isotropic and hyperelastic constitutive law. Furthermore, intraluminal thrombus (ILT) and calcifications are considered in the vessel model. The deployed SG configuration is considered at static, but physiologically meaningful blood pressure states at the diastolic and at the systolic level.

The presented validation methodology of the in silico EVAR results is based on a qualitative and quantitative comparison between in silico EVAR results and the stent configuration extracted from postinterventional CT data. The average stent diameters in slices orthogonal to the SG centerline are compared pseudo-continuously along the total length of the deployed SG. The methodology has to cope with distracting artifacts that frequently occur when imaging metallic objects such as SGs by computed tomography (Boas and Fleischmann 2012; Mahnken 2012; Pugliese et al. 2006). Additionally, the variety of different shapes of marketed SGs makes it difficult to find a generally valid validation methodology for all types of SGs.

Several studies have already been conducted in the field of in silico EVAR approaches in idealized vessel geometries (e.g., Prasad et al. 2012; De Bock et al. 2012, 2014; Perrin et al. 2015b; Hemmler et al. 2018). Some studies have been published on the virtual deployment of stents in patient-specific vessels (e.g., Morlacchi et al. 2013; Iannaccone et al. 2016; Auricchio et al. 2011; Holzapfel et al. 2005) which is closely related to in silico EVAR simulations. However, only few patient-specific in silico EVAR studies exist (Auricchio et al. 2013; Romarowski et al. 2018; Perrin et al. 2015a, 2016). Auricchio et al. (2013) first published the in silico deployment of a SG in a patient-specific ascending aortic aneurysm. This pioneering achievement of Auricchio et al., however, suffered from the assumption of a rigid vessel. More elaborated in silico SG deployment simulations applied to AAA were performed by Perrin et al. (2015a, 2016). Perrin et al. (2015a, 2016) performed patient-specific in silico EVAR simulations of patients treated by bifurcated, marketed SGs. Both studies (Perrin et al. 2015a, 2016) considered elastically deformable vessel and SG models, however, were limited to linearized vessel constitutive models and did not consider ILT and calcifications of the vessel.

The in silico results mostly are validated by qualitative or quantitative comparison to in vivo imaging data (Perrin et al. 2015a, 2016; Auricchio et al. 2013; Iannaccone et al. 2016; Morlacchi et al. 2013) or in vitro experiments (Iannaccone et al. 2016; De Bock et al. 2012). Auricchio et al. (2013) used the mean stent diameter in three distinct slices orthogonal to the postinterventional vessel centerline to compare in silico EVAR results with in vivo data of one patient. Perrin et al. (2015a, 2016) measured one mean diameter for each stent limb for quantitative comparison between in silico EVAR results of patient-specific cases with postinterventional CT data. In addition to the diameter comparison, Perrin et al. compared the position of each stent limb quantitatively between in silico EVAR results and the stent extracted from postinterventional CT data.

The outline of this paper is organized as follows: in Sect. 2, we present the models of SG and vessel, give an overview of the in silico EVAR methodology with regard to patient-specific cases and present the validation methodology based on a comparison between in silico results and postinterventional CT data. In Sect. 3, the results of the in silico EVAR approach are presented for three patient-specific cases and are validated using the proposed validation methodology. Also, we show some potential applications of in silico EVAR such as the prediction of wall stresses as well as contact tractions between SG and vessel. The results of Sect. 3 are discussed in Sect. 4. Finally, limitations and conclusions of this study are drawn in Sects. 5 and 6, respectively.

2 Materials and methods

2.1 Clinical summary

Fig. 1

Patient-specific vessel models (I) and corresponding preassembled SG models (II) of the three clinical cases; visualization of vessel wall in dark red, ILT in light pink and calcifications in white

Three clinical cases are considered in this study with patient characteristics provided in Table 1 and visualized in Fig. 1. All three patients were treated by SGs from Cook Medical (Bloomington, Indiana, USA) which consist of a main body of type Cook Zenith Flex^® (CZ-Flex) and two iliac components of type Cook Zenith Spiral-Z^® (CZ-Spiral). The lengths of prosthesis overlaps between the main SG component and the iliac SG components are chosen such that the distal ends of the SG do not cover the bifurcation of the common iliac arteries to the external and internal iliac arteries. The prosthesis overlaps between the main SG component and the iliac components used in the EVAR interventions of the three patient-specific cases are provided in Table 1. For each patient, pre- and postinterventional CT data are available. Based on the preinterventional vessel diameters $D^{\mathrm {Ao}}$ and the nominal diameter D of the SG, the degree of SG oversizing is given by

$$\begin{aligned} o&=\frac{D}{D^{\mathrm {Ao}}}-1 \end{aligned}$$

(1)

and is provided in Table 1 for the proximal and distal landing zones of all three patients. SG landing zones are regions where the SG is directly attached to the luminal vessel surface and which are responsible for the seal between SG and vessel. The proximal landing zone is defined by the region from the most inferior renal artery to the beginning of the vessel dilatation of the AAA. In the three patient-specific cases, the distal landing zones are in the common iliac arteries.

Table 1 Clinical summary of the three patients treated by EVAR

2.2 Model assumptions

We incorporate the following basic assumptions in the patient-specific in silico EVAR approach:

• The intrainterventional steps of the EVAR intervention are strongly simplified. No medical tools, other than the SG itself, are considered.

• Treatment as 3D nonlinear elastostatic problem including frictional contact as given in detail in Hemmler et al. (2018). Fluid dynamics of the blood flow is neglected. A quasi-static pressure state is considered.

• Friction between SG and vessel is modeled assuming Coulomb’s law. Lubrication is neglected.

• Inter- and intrapatient variability in vessel material properties is neglected. Instead, population-averaged mean values are used.

• Constant vessel wall thickness of 1.5 mm is assumed.

• Modeling of the three SG components (main component and two iliac extensions) as one preassembled SG.

2.3 Vessel modeling

The patient-specific vessel geometries including ILT are segmented from preinterventional CT data in a semi-automatic fashion using the segmentation software Mimics 12.1 (Materialise, Leuven, Belgium). The vessel geometries are cut approximately 20 mm above the branching of the renal arteries and distally approximately 20 mm below the branching of the common iliac arteries into the internal and external iliac arteries. Renal arteries and internal iliac arteries are not part of the model. A uniform vessel wall thickness of 1.5 mm is assumed (Reeps et al. 2013).

Constitutive models and discretization techniques of the vessel are taken from Hemmler et al. (2018). A summary of the vessel constitutive models and model parameters is given in Table 2 where $\varPsi$ denotes the strain energy function (SEF) of the hyperelastic constitutive models, the superscript $(\bullet )^{\mathrm {wall}}$ stands for the total vessel wall, the superscript $(\bullet )^{\mathrm {AA}}$ for the “healthy” vessel wall, the superscript $(\bullet )^{\mathrm {AAA}}$ for the “aneurysmatic” vessel wall, the superscript $(\bullet )^{\mathrm {ILT}}$ for the intraluminal thrombus and the superscript $(\bullet )^{\mathrm {calc}}$ for calcifications. $\bar{I}_1$ as well as $\bar{I}_2$ are modified invariants of the right Cauchy–Green strain tensor. $\bar{I}_4$ as well as $\bar{I}_6$ are the squares of the stretches in mean fiber direction of the anisotropic two-fiber model with transversely isotropic fiber dispersion of the “healthy” vessel wall as defined in Gasser et al. (2006). The mean fiber direction of the two fibers $i=\{4,6\}$ in the local radial, axial and circumferential coordinate system of the vessel is defined by ${\varvec{M}}_{i}=[0,{\mathrm {sin}}(\theta _{i}),{\mathrm {cos}}(\theta _{i})]^{\mathrm {T}}$. J is the determinant of the deformation gradient and $\varPsi _{\mathrm {vol}}$ is an Ogden volumetric SEF (Doll and Schweizerhof 2000; Ogden 1972) whose volumetric bulk modulus is chosen sufficiently large to sustain almost incompressibility of the vessel constituents.

Table 2 Overview of constitutive models and material parameters of vessel and SG

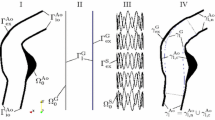
The material model of the vessel differentiates between the “healthy” and the “aneurysmatic” vessel wall as substantial differences between the two conditions of the vessel wall can be identified (Niestrawska et al. 2016). The blend between the “healthy” and the “aneurysmatic” vessel wall is regulated by the blend parameter $\lambda (d) \in [0;1]$ which is a function of the local diameter d of the vessel (Fig. 2I). Consequently, at locations of $\lambda =0$ the vessel material behavior is fully described by the SEF $\varPsi ^{AA}$ of a “healthy” vessel and at locations of $\lambda =1$ by the SEF $\varPsi ^{\mathrm {AAA}}$ of an “aneurysmatic” vessel (Table 2). In-between a smooth transition zone of partly “healthy” and partly “aneurysmatic” material exists as defined in Hemmler et al. (2018).

The hyperelastic constitutive model of the ILT with the SEF $\varPsi ^{\mathrm {ILT}}$ resolves three different ILT layers with decreasing stiffness $c^{\mathrm {ILT}}$ according to Gasser et al. (2008): luminal $c_{\mathrm {lum}}$, medial $c_{\mathrm {med}}$ and abluminal $c_{\mathrm {abl}}$. Calcifications are modeled implicitly within the domains of ILT and aortic wall by adding a hyperelastic SEF $\varPsi ^{\mathrm {calc}}$ contribution to the SEF of the vessel wall and the ILT at locations of high Hounsfield values in the patient-specific preinterventional CT data (Fig. 2I+II). The vessel is embedded in spring boundary conditions with a spring stiffness of $2.0\,{\mathrm {kPa/mm}}$ to mimic the surrounding tissue of the abdominal aorta (Moireau et al. 2012).

The vessel geometry is discretized by a conforming mesh with linear, tetrahedral and pyramid elements in the domain of the ILT and linear, hexahedral elements with F-bar-based element technology (de Souza Neto et al. 1996) in the domain of the vessel wall (Fig. 2III).

Fig. 2

Cut view of the vessel model of patient 1 (I) and visualization of the different vessel constituents: “healthy” vessel wall, “aneurysmatic” vessel wall, ILT and calcifications; transversal CT image (II) with contour lines of blood lumen (blue), abluminal ILT surface (red) and calcifications (green); detail view of the vessel mesh (III)

2.4 Stent-graft modeling

The considered SG devices from Cook Medical consist of three separate components: a main body of type CZ-Flex (Fig. 3I) and two iliac components of type CZ-Spiral (Fig. 3II). Both CZ-Flex SGs and CZ-Spiral SGs are composed of stent limbs that are sewn on the polymeric fabric graft. The following SG specific simplifications are used:

• The geometry of the marketed SGs is approximated based on measurements in Demanget et al. (2012, 2013) and information given in the Cook Zenith^® manual (Medical 2018).

• The three SG components are modeled as one preassembled SG with fixed overlap distances between the main component and the left iliac component and the right iliac component, respectively (Fig. 3III).

• The uncovered proximal stents with barbs (Fig. 3I) are not modeled explicitly in a geometrical sense. In order to account for the axial fixation of the SG by the proximal barbs, we apply mortar-based frictional contact in pure stick (no tangential sliding) between SG and luminal vessel surface in the most proximal region of the SG of 5 mm length.

• Mortar-based mesh tying is applied to model the suture between stent and graft.

• CZ-Flex and CZ-Spiral SGs consist of interior and exterior stent limbs. Interior stent limbs are sewn on the inner surface of the graft, whereas exterior stent limbs are sewn on the outer surface of the graft. In our SG model, all stent limbs are modeled as interior stent limbs with respect to the graft.

• Circularly shaped cross sections of the stent struts are modeled as quadratic cross sections with equivalent bending stiffness to ensure hexahedral meshing of the stent and to provide proper surfaces for the mortar-based mesh tying between stent and graft.

Fig. 3

Image of a CZ-Flex SG (I), a CZ-Spiral SG (II) and the preassembled, meshed SG model (III); illustration of the model generation of a ring-shaped stent limb (IV) and a spiral-shaped stent limb (V); stent cross section (VI) and meshing of a CZ-Flex stent limb (VII)

All stent limbs are ring-shaped with exception of the intermediate stent limbs of the CZ-Spiral SGs which are spiral-shaped. The single stent limbs are sinusoidally shaped (Demanget et al. 2012). Hence, the generation of one ring-shaped stent limb is based on

$$\begin{aligned} {\varvec{X}}_{{\mathrm {R}}}&=\left( \begin{array} {c} \frac{D_{{\mathrm {R}}}}{2}{\mathrm {cos}}(\varphi ) \\ \frac{D_{{\mathrm {R}}}}{2}{\mathrm {sin}}(\varphi )\\ \frac{h_{{\mathrm {R}}}}{2}\,{\mathrm {sin}}(\varphi p_{{\mathrm {R}}})\end{array} \right) , \quad \varphi \in [0;2\pi ] \end{aligned}$$

(2)

which defines the position vectors ${\varvec{X}}_{{\mathrm {R}}}$ of the centers of the stent cross sections. $D_{{\mathrm {R}}}$ is the diameter, $h_{{\mathrm {R}}}$ is the height and $p_{{\mathrm {R}}}$ is the number of periods of the stent limb (Fig. 3IV). The most distal stent limb of the CZ-Flex SG before the bifurcation is slightly elliptical which is approximated by a maximum to minimum diameter ratio of 1.2. The spiral-shaped geometry of the intermediate stent limb of the CZ-Spiral SGs is defined by

$$\begin{aligned} {\varvec{X}}_{\mathrm {Sp}}&=\left( \begin{array} {l} \frac{D_{\mathrm {Sp}}}{2}{\mathrm {cos}}(\varphi ) \\ \frac{D_{\mathrm {Sp}}}{2}{\mathrm {sin}}(\varphi )\\ \frac{h_{\mathrm {Sp}}}{2}\,{\mathrm {sin}}(\varphi p_{\mathrm {Sp}}) + l_{\mathrm {Sp}} \frac{\varphi }{2\pi }\end{array} \right) , \quad \varphi \in [0;2\pi n_{\mathrm {Sp}}] \end{aligned}$$

(3)

where $D_{\mathrm {Sp}}$ is the diameter, $h_{\mathrm {Sp}}$ is the height, $p_{\mathrm {Sp}}$ is the number of periods per turn of the stent limb. $l_{\mathrm {Sp}}$ is the lead of the stent limb and $n_{\mathrm {Sp}}$ is the number of turns per CZ-Spiral stent limb (Fig. 3V). Graft thickness and stent strut diameters are taken from the literature (Demanget et al. 2013) and are summarized in Table 3. The geometrical parameters $D_{{\mathrm {R}}}$, $h_{{\mathrm {R}}}$, $p_{{\mathrm {R}}}$, $D_{\mathrm {Sp}}$, $h_{\mathrm {Sp}}$, $p_{\mathrm {Sp}}$, $l_{\mathrm {Sp}}$ and $n_{\mathrm {Sp}}$ depend on the size of the SG and are extracted from the Cook Zenith^® manual (Medical 2018).

All ring-shaped stent limbs consist of stainless steel, whereas the spiral-shaped stent limbs of the CZ-Spiral SGs consist of nitinol. The material behavior of nitinol is modeled by a purely elastic model as proposed in Perrin et al. (2016) and Mortier et al. (2010). Stainless steel stent limbs as well as the graft are modeled by isotropic and hyperelastic material models proposed in Hemmler et al. (2018). The models are stated in Table 2 where the superscript $(\bullet )^{\mathrm {G}}$ stands for the graft, the superscript $(\bullet )^{{\mathrm {S}}}$ for stainless steel stents and the superscript $(\bullet )^{\mathrm {N}}$ for nitinol stents. $I_{1}$ is the first invariant of the right Cauchy–Green strain tensor and J is the determinant of the deformation gradient.

Linear, hexahedral elements with enhanced assumed strain (EAS) technology with adaptive element size and mesh refinement in the curved parts of the stent limbs are used for the discretization of the stent (Fig. 3VI + VII). Hexahedral solid-shell elements (Vu-Quoc and Tan 2003) with EAS as well as assumed natural strain (ANS) technology with an element edge length of 0.4 mm are used for the graft discretization (Fig. 3IV).

Table 3 Geometric SG parameters

2.5 In silico EVAR in patient-specific geometries

Fig. 4

Steps of the in silico EVAR methodology applied to patient 1 according to the in silico EVAR methodology proposed in Hemmler et al. (2018): stent predeformation (I), vessel prestressing (II), SG placement (IIIa–c) and final deployed state under static conditions (IV). Overview of the control curves ${\mathcal {C}}$ of the proximal part $(\bullet )^{{\mathrm {P}}}$, the left iliac part  $(\bullet )^{{\mathrm {L}}}$ and the right iliac part  $(\bullet )^{{\mathrm {R}}}$ in the initial $(\bullet )_{\mathrm {I}}$ and the target configuration $(\bullet )_{\mathrm {T}}$ (IIIa); colors of the SG indicate affiliation to the proximal control curve (blue), the left iliac control curve (orange) and the right iliac control curve (green) (IIIc)

This section provides the outline of the in silico EVAR methodology proposed in Hemmler et al. (2018) plus relevant aspects for patient-specific cases. The in silico EVAR methodology aims at finding the final configurations of the deployed SG and the vessel after the intervention under static conditions rather than reproducing the intrainterventional steps of EVAR. The methodology consists of four main steps: stent predeformation (Fig. 4I), vessel prestressing (Fig. 4II), SG placement in the interior of the vessel (Fig. 4III) and SG deployment (Fig. 4IV). Within the scope of the in silico EVAR methodology, we clearly distinguish between SG placement and SG deployment. SG placement defines the process of positioning the SG within the vessel. SG deployment defines all processes subsequent to the SG placement, i.e., the processes that let the SG freely deform within the vessel.

Stents of Cook Zenith^® SGs are manufactured with a larger diameter than the associated graft. During the assembling process of the SGs, stents are radially compressed and are sewn on the graft in this compressed state resulting in an assembled SG with residual strains and stresses. This effect called stent predeformation can have a major impact on the mechanical behavior of the SG in the deployed state (Hemmler et al. 2018; Roy et al. 2016). It is modeled by using the stent predeformation methodology proposed in Hemmler et al. (2018) (Fig. 4I). Similar degree of stent predeformation of 15% is assumed for all stent limbs.

As the patient-specific vessel geometry is reconstructed from in vivo medical imaging (Sect. 2.3), the initial geometric configuration is not stress-free. In order to initialize the model to this stressed configuration, we use a vessel prestressing methodology based on a modified updated Lagrangian formulation proposed in Gee et al. (2010). The vessel is prestressed to an assumed diastolic pressure of $p_{\mathrm {diast}}=80\,{{\mathrm {mmHg}}}$ (Fig. 4II).

The maximum length of the proximal landing zone is proximally limited by the bifurcations to the renal arteries which must not be covered by the covered part of the SG after the deployment. The proximal landing zone of the SG is assumed to be as long as possible. Hence, the SG is positioned slightly below the branches to the renal arteries according to the preinterventional CT data. The distal landing zones are not a priori determined but evolve from the deployment process.

The deformation of the SG during the in silico SG placement relies on a morphing algorithm based on 1D control curves ${\mathcal {C}} \subset {\mathbb {R}}^3$ (“Appendix 1”). Each node i of the SG is described in local cylindrical coordinate systems tangentially aligned to the control curve ${\mathcal {C}}$ with the local cylindrical coordinates $r^{i}$, $\theta ^{i}$, $\hat{z}^{i}$ (Fig. 5). In the following we distinguish between the proximal SG part (blue), the left iliac SG part (orange) and the right iliac SG part (green) (Fig. 4IIIc). The in silico EVAR methodology for bifurcated SGs demands three control curves: one control curve of the proximal part ${\mathcal {C}}^{{\mathrm {P}}}$, one control curve of the left iliac part ${\mathcal {C}}^{{\mathrm {L}}}$ and one control curve of the right iliac part ${\mathcal {C}}^{{\mathrm {R}}}$ of the SG. Each of the three control curves has to be given in the initial ${\mathcal {C}}_{\mathrm {I}}^{(\varPi )}$ and the target configuration ${\mathcal {C}}_{\mathrm {T}}^{(\varPi )}$ with $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$ (Fig. 4IIIa). The initial configurations of the control curves ${\mathcal {C}}_{\mathrm {I}}^{(\varPi )}$ are the centerlines of the three SG components in the undeformed configuration. These three centerlines are known from the SG generation process described in Sect. 2.4. The target configurations of the control curves ${\mathcal {C}}_{\mathrm {T}}^{(\varPi )}$ correspond to the centerlines of the vessel in the preinterventional imaged configuration which are known from the segmentation process (Sect. 2.3).

Fig. 5

Illustration of local cylindrical coordinates $r^{i}$, $\theta ^{i}$, $\hat{z}^{i}$ and the bounding box $\mathbb {B}^{j}$ (red) around point j of the control curve ${\mathcal {C}}_{\mathrm {I}}$; $({\varvec{t}}{\varvec{n}}{\varvec{b}})^{j}$ is the local triad tangentially aligned to the control curve ${\mathcal {C}}_{\mathrm {I}}$ at point j as defined in Hemmler et al. (2018)

The SG placement is a transformation of the SG from the undeformed SG configuration into the vessel geometry according to the evolution of the control curves ${\mathcal {C}}_{\mathrm {I}}^{(\varPi )}$ from their initial configuration into their target configuration  ${\mathcal {C}}_{\mathrm {T}}^{(\varPi )}$ with $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$ (Fig. 4III). During the SG placement step, the deformation of the SG is completely prescribed by the morphing algorithm based on control curves where each SG component (proximal part, left iliac part, right iliac part) is morphed individually. This means the deformation of the proximal SG part (blue) is fully described by the evolution of the control curve ${\mathcal {C}}^{{\mathrm {P}}}$ from ${\mathcal {C}}_{\mathrm {I}}^{{\mathrm {P}}}$ to ${\mathcal {C}}_{\mathrm {T}}^{{\mathrm {P}}}$ and independent of the evolution of the control curves ${\mathcal {C}}^{{\mathrm {L}}}$ and ${\mathcal {C}}^{{\mathrm {R}}}$. Similar independencies are given for the left iliac SG part and the right iliac SG part, respectively (Fig. 4III). To ensure continuity between the three SG components during the entire SG placement, the control curve continuity conditions provided in “Appendix 2” have to be satisfied.

Fig. 6

Validation methodology using postinterventional CT data visualized for patient 3: stents from simulation and segmentation of stents from postinterventional CT data (I); rigid registration of stents from simulation and postinterventional CT data (II); cut of stents into three SG parts (proximal part, left iliac part and right iliac part) (III); exemplary illustration of one set ${\mathsf{A}}_{\mathrm{I,postIV}}^{{\mathrm {S,P}},j}$ and ${\mathsf {A}}_{\mathrm {I,sim}}^{{\mathrm {S,P}},j}$ of the proximal stent part (IV); exemplary comparison of the stent diameter $\bar{d}^{{\mathrm {S}}}_{\mathrm {sim}}(s^{{\mathrm {P}},j})$ from simulation and the stent diameter $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}}}(s^{{\mathrm {P}},j})$ from postinterventional CT data at the same arc length $s^{{\mathrm {P}},j}$ (V)

Two different nonlinear traction loads

$$\begin{aligned} {\varvec{\hat{t}}}_{\mathrm {l}}&=-p_{\mathrm {l}} \cdot {\varvec{n}}_{\mathrm {l}} \quad {\mathrm {on}}\,(\gamma _{\mathrm {l,n}}^{{\mathrm {Ao}}} \cup \gamma _{\mathrm {l}}^{{\mathrm {G}}}) \end{aligned}$$

(4a)

and

$$\begin{aligned} {\varvec{\hat{t}}}_{\mathrm {c}}&=-p_{\mathrm {c}} \cdot {\varvec{n}}_{\mathrm {c}} \quad {\mathrm {on}}\,\gamma _{\mathrm {l,c}}^{{\mathrm {Ao}}} \end{aligned}$$

(4b)

are applied after the SG placement, where ${\varvec{n}}_{\mathrm {l}}$ is the outward surface normal on the Neumann boundary of the luminal vessel surface $\gamma _{\mathrm {l,n}}^{{\mathrm {Ao}}}$ not covered by the SG and the luminal surface of the graft $\gamma _{\mathrm {l}}^{{\mathrm {G}}}$. ${\varvec{n}}_{\mathrm {c}}$ is the outward surface normal on the luminal vessel surface $\gamma _{\mathrm {l,c}}^{{\mathrm {Ao}}}$ covered by the SG, i.e., the luminal surface of the vessel between the most proximal SG attachment and the most distal SG attachment. We consider the final deployed configuration of SG and vessel at the assumed diastolic blood pressure state of $p_{\mathrm {diast}}=80\,{\mathrm {mmHg}}$, i.e., $p_{\mathrm {l}}=p_{\mathrm {diast}}$, as well as at the assumed systolic blood pressure state of $p_{\mathrm {sys}}=130\,{\mathrm {mmHg}}$, i.e., $p_{\mathrm {l}}=p_{\mathrm {sys}}$. In both cases a zero AAA sac pressure after the insertion of the SG is assumed, i.e., $p_{\mathrm {c}}=0\,{\mathrm {mmHg}}$.

During the in silico SG placement, the deformation of the SG is fully prescribed by morphing constraints. After the placement of the SG in the interior of the vessel, we gradually remove the morphing constraints of the SG starting at the proximal end of the SG. After the in silico SG deployment, i.e., after the release of all morphing constraints, the SG can elastically deform within the elastically deformable vessel. The final state of SG and vessel after the in silico deployment of patient 1 at the systolic blood pressure state is visualized in Fig. 4IV.

Frictional contact between SG and vessel as well as contact between the two iliac components of the SG is modeled by a penalty contact formulation based on mortar methods (Popp et al. 2009, 2010) with a friction coefficient of 0.4 (Vad et al. 2010; Perrin et al. 2015a).

An implicit, quasi-stationary nonlinear solver with a semi-smooth Newton approach with consistent linearization (Gitterle et al. 2010) is used to solve the 3D nonlinear elastostatic problem including frictional contact. The large system of linearized equations is solved every Newton step by a parallel iterative GMRES method preconditioned using algebraic multigrid (Heroux et al. 2005).

2.6 Validation methodology

In this section, the validation methodology of the in silico EVAR results is described. We qualitatively and quantitatively compare the final configuration of the stent after the in silico SG deployment with the configuration of the stent extracted from postinterventional CT data. This comparison requires the assumption that within the time period between the EVAR intervention and the day of the postinterventional CT scan (Table 1), no growth and remodeling and other reasons have changed the configurations of vessel and SG. Due to the short time period between the EVAR intervention and the day of the postinterventional CT scan as well as relatively slow growth and remodeling rates of vessel tissue, this assumption seems reliable.

In the quantitative validation, we compare the diameters of the stent from the in silico EVAR approach with the diameters of the stent from postinterventional CT data. The single steps of the proposed validation methodology are discussed in the following and are summarized in Fig. 6.

The in silico EVAR simulation is based on the vessel geometry of preinterventional CT data which in general is aligned in a different coordinate system than the postinterventional CT data. Hence, after the segmentation of the stent from postinterventional CT data, a rigid registration based on a minimal point distance filter of the stent from postinterventional CT data onto the stent from the in silico EVAR simulation is used to align both stent configurations in the same coordinate system (Fig. 6II). Next, the three stent components $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$ (proximal part, left iliac part and right iliac part) are considered separately (Fig. 6III).

All nodes with the reference coordinates ${\varvec{X}}^{(\varPi ),i} \in ({\Omega }^{{\mathrm {S}},(\varPi )}_{\mathrm {0}} \cap {\Omega }^{\mathrm {G},(\varPi )}_{\mathrm {0}})$ of the SG model in its undeformed configuration with $i=1,2,\ldots ,n^{{\mathrm {SG}},{(\varPi)}}$ are grouped into subsets ${\mathsf {A}}^{(\varPi ),j}_{\mathrm {I}}$ (“Appendix 1”). ${\Omega }^{{\mathrm {S}},(\varPi )}_{\mathrm {0}}\subset {\Omega }^{{\mathrm {S}}}_{\mathrm {0}}$ and ${\Omega }^{\mathrm {G},(\varPi )}_{\mathrm {0}}\subset {\Omega }^{\mathrm {G}}_{\mathrm {0}}$ are the undeformed configurations of stent and graft of SG part $\varPi$. To ease the notation, we do not write the superscript $(\bullet )^{(\varPi )}$ in the following. Unless specified differently, the variables are valid for any of the three components of the SG $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$.

Based on the valid assumption that the relative deformation of the SG tangentially to its centerline is small, the centerline ${\mathcal {C}}_{\mathrm {De}}$ of the deployed SG can be computed. The points of the centerline ${\mathcal {C}}_{\mathrm {De}}$ are the centers of gravity of the SG nodes i in the sets ${\mathsf {A}}_{\mathrm {I}}^{j}$ according to

$$\begin{aligned} {\varvec{x}}_{\mathrm {C,De}}^{j}&=\frac{1}{\underset{i\in {\mathsf {A}}_{\mathrm {I}}^{j}}{\sum }\bar{\theta }^{i}}\underset{i\in {\mathsf {A}}_{\mathrm {I}}^{j}}{\sum } \bar{\theta }^{i} {\varvec{x}}^{i}=\frac{1}{2\pi }\underset{i\in {\mathsf {A}}_{\mathrm {I}}^{j}}{\sum } \bar{\theta }^{i} {\varvec{x}}^{i}, \nonumber \\&\quad \forall j=1,2,\ldots ,n_{\mathrm {C}}, \end{aligned}$$

(5)

where $n_{\mathrm {C}}$ is the number of points of the centerline ${\mathcal {C}}_{\mathrm {I}}$ of the SG in the undeformed configuration, ${\varvec{x}}^{i}$ are the current coordinates of all nodes i in the set ${\mathsf {A}}_{\mathrm {I}}^{j}$ and $\bar{\theta }^{i}=\frac{1}{2}(\theta ^{i+1}-\theta ^{i-1})$ is the mean angular distance between two adjacent nodes in set ${\mathsf {A}}_{\mathrm {I}}^{j}$. The nodes i in the sets ${\mathsf {A}}_{\mathrm {I}}^{j}$ are ordered counterclockwise according to the local angular coordinate $\theta ^{i}$ of the local cylindrical coordinate systems tangentially aligned to the centerline ${\mathcal {C}}_{\mathrm {I}}$ (Fig. 5). Hence, the nodes i and $i+1$ are adjacent nodes. The mean angular distance $\bar{\theta }^{i}$ is used as weighting to account for irregularly distributed nodes in the set ${\mathsf {A}}_{\mathrm {I}}^{j}$. In case of a regular SG mesh, i.e., the mean angular distance $\bar{\theta }^{i}$ is the same for all nodes i, Eq. (5) reduces to the arithmetic mean as shown in “Appendix 3.”

Further, we introduce the arc length parameterization

$$\begin{aligned} s^{j}=s^{j-1}+||{\varvec{x}}_{\mathrm {C,De}}^{j}-{\varvec{x}}_{\mathrm {C,De}}^{j-1}||,\quad&\forall j=2,3,\ldots ,n_{\mathrm {C}}, \nonumber \\&s^{1}=0, \end{aligned}$$

(6)

where ${\varvec{x}}_{\mathrm {C,De}}^{j}$ is the position vector of point j of the centerline ${\mathcal {C}}_{\mathrm {De}}$ according to Eq. (5) and $n_{\mathrm {C}}$ is the total number of points $j=1,2,\ldots ,n_{\mathrm {C}}$ that describe the piecewise linear centerline ${\mathcal {C}}_{\mathrm {De}}$ of the SG in the deployed state. Consequently, $s^{j}$ are discrete values of the arc length of the centerline ${\mathcal {C}}_{\mathrm {De}}$ with

$$\begin{aligned} \{s^{j}|0\le s^{j} \le L, \forall j=1,2,\ldots ,n_{\mathrm {C}}\}, \end{aligned}$$

(7)

where L is the total arc length of the centerline ${\mathcal {C}}_{\mathrm {De}}$.

Using the local cylindrical coordinates $\theta _{\mathrm {De}}^{{\mathrm {S}},i}$ and $r_{\mathrm {De}}^{{\mathrm {S}},i}$ (cf. Fig. 5), we can determine the average diameter of each set ${\mathsf {A}}_{\mathrm {I}}^{j}$. In contrast to Fig. 5 where the local coordinate systems are aligned to the undeformed centerline ${\mathcal {C}}_{\mathrm {I}}$, the local coordinates $\theta _{\mathrm {De}}^{{\mathrm {S}},i}$ and $r_{\mathrm {De}}^{{\mathrm {S}},i}$ correspond to the local coordinate systems that are tangentially aligned to the centerline ${\mathcal {C}}_{\mathrm {De}}$ of the deployed SG which is given by Eq. (5). For reasons of comparability with postinterventional CT data, where the graft is not visible, we only use the nodes of the stent (not the graft) to calculate the average diameter $\bar{d}^{{\mathrm {S}},j}$ of all nodes in the set ${\mathsf {A}}^{{\mathrm {S}},j}_{\mathrm {I}}$. This is indicated by the superscript $(\bullet )^{{\mathrm {S}}}$. In contrast to ${\mathsf {A}}_{\mathrm {I}}^{j}$, ${\mathsf {A}}^{{\mathrm {S}},j}_{\mathrm {I}}$ holds only nodes of the stent. Hence, the average stent diameter of all nodes in the set ${\mathsf {A}}^{{\mathrm {S}},j}_{\mathrm {I}}$ is given by

$$\begin{aligned} \bar{d}^{{\mathrm {S}},j}&=\bar{d}^{{\mathrm {S}}}(s^{j})=\frac{1}{2\pi }\underset{i \in {\mathsf {A}}^{{\mathrm {S}},j}_{\mathrm {I}}}{\sum }2\bar{\theta }_{\mathrm {De}}^{{\mathrm {S}},i}r_{\mathrm {De}}^{{\mathrm {S}},i}, \nonumber \\&\quad \forall j=1,2,\ldots ,n_{\mathrm {C}}, \end{aligned}$$

(8)

where $r_{\mathrm {De}}^{{\mathrm {S}},i}$ is the local radius of node i in set ${\mathsf {A}}^{{\mathrm {S}},j}_{\mathrm {I}}$.

$\bar{\theta }_{\mathrm {De}}^{{\mathrm {S}},i}=\frac{1}{2}(\theta _{\mathrm {De}}^{{\mathrm {S}},i+1}-\theta _{\mathrm {De}}^{{\mathrm {S}},i-1})$ is the mean angular distance between two adjacent nodes in the set ${\mathsf {A}}^{{\mathrm {S}},j}_{\mathrm {I}}$ according to the local cylindrical coordinate systems tangentially aligned to the centerline ${\mathcal {C}}_{\mathrm {De}}$ of the deployed SG (Fig. 5). At this point, it is important to clearly distinguish between $r_{\mathrm {De}}^{{\mathrm {S}},i}$ and $\bar{d}^{{\mathrm {S}},j}$. $r_{\mathrm {De}}^{{\mathrm {S}},i}$ is the local radius of node i in set  ${\mathsf {A}}^{{\mathrm {S}},j}_{\mathrm {I}}$ according to the local cylindrical coordinate system that is tangentially aligned to the centerline ${\mathcal {C}}_{\mathrm {De}}$. $\bar{d}^{{\mathrm {S}},j}$ is the average diameter of all nodes belonging to one common set ${\mathsf {A}}^{{\mathrm {S}},j}_{\mathrm {I}}$. The term average refers to the average of the diameters $2r_{\mathrm {De}}^{{\mathrm {S}},i}$ of a all nodes i in the set ${\mathsf {A}}^{{\mathrm {S}},j}_{\mathrm {I}}$.

Fig. 7

Visualization of the average stent diameters $\bar{d}_{\mathrm {sim}}^{{\mathrm {S}}}$ from simulation and the average stent diameters $\bar{d}_{\mathrm {postIV}}^{{\mathrm {S}}}$ from postinterventional CT data for the proximal SG part (I), the left iliac SG part (II) and the right iliac SG part (III) of patient 3

Until this point we only considered the deployed configuration of the stent from the in silico EVAR approach. In the following, we will apply the same methods to evaluate the deployed stent configuration extracted from postinterventional CT data with a resolution of $0.75\times 0.75\times 1.0\,{{\mathrm {mm}}}^3$ for patient 1, $0.79\times 0.79\times 1.0\,{{\mathrm {mm}}}^3$ for patient 2 and $0.76\times 0.76\times 1.0\,{{\mathrm {mm}}}^3$ for patient 3. We use the same centerlines ${\mathcal {C}}_{\mathrm {De}}$ and the same methods as for the simulated SG to evaluate the average diameters $\bar{d}^{{\mathrm {S}},j}$ [Eq. (8)] of the stent segmented from postinterventional CT data (Fig. 7). To distinguish between variables of the simulation and variables of the postinterventional CT data, we introduce the subscripts $(\bullet )_{\mathrm {sim}}$ and $(\bullet )_{\mathrm {postIV}}$, respectively.

Measuring the diameter of the stent from postinterventional CT data at distinct locations, i.e., measuring the average diameter of distinct sets ${\mathsf {A}}_{\mathrm {I,postIV}}^{{\mathrm {S}},j}$, can be sensitive to small variations of the location due to local artifacts in the postinterventional CT data. The main source of these artifacts is given by the well-known problem of imaging metallic objects by computed tomography (Boas and Fleischmann 2012; Mahnken 2012; Pugliese et al. 2006). Due to these metal-related artifacts, stent struts appear to be thicker than they are and a clear segmentation process of the stent is more difficult. Additionally, calcifications often cannot be separated clearly from stents.

Perrin et al. (2015a) used only one average diameter per stent limb in their quantitative validation methodology. Calculating only one average diameter for each stent limb is less susceptible to local artifacts in the postinterventional CT data. However, this method is not able to capture nonuniform stent shapes such as a conical shape. But particularly in the landing zones of the SG, nonuniform vessel shapes and consequently nonuniform stent shapes can have a major impact on the applicability and the success of EVAR (Moll et al. 2011; Chuter et al. 1997b). Hence, a validation methodology should also be able to assess how well such nonuniform stent shapes are represented.

In our validation methodology with the objective to measure the stent diameter pseudo-continuously along the total SG length, an outlier detection by a moving average filter is applied to reduce the variance of the measured average stent diameters from postinterventional CT data due to the presence of local artifacts (“Appendix 4”). Filtered data is indicated by the subscript $(\bullet )_{\mathrm {f}}$ in the following. A quality estimation of the segmented data from postinterventional CT scans, i.e., an estimation to which extent the stent diameter measurement from postinterventional CT data is influenced by the vagueness in the segmentation process, is provided in “Appendix 5.”

The quantitative comparison of the simulation results with the postinterventional CT data is done by comparing the average stent diameters $\bar{d}_{\mathrm {sim}}^{{\mathrm {S}}}(s^{(\varPi ),j})=\bar{d}_{\mathrm {sim}}^{{\mathrm {S}},(\varPi ),j}$ from simulation with the average stent diameters $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}}}(s^{(\varPi ),j})=\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}},(\varPi ),j}$ from postinterventional CT data (Fig. 6V) at same arc length $\{s^{(\varPi ),j}|0\le s^{(\varPi ),j} \le L^{(\varPi )}, \forall j=1,2,\ldots ,n_{\mathrm {C}}^{(\varPi )}\}$. As the exact blood pressure state of the patients in the postinterventional CT data is unknown, we use the simulation results at an assumed diastolic blood pressure state of $p_{\mathrm {diast}}=80\,{\mathrm {mmHg}}$ as lower bound and the simulation results at an assumed systolic blood pressure state of $p_{\mathrm {sys}}=130\,{\mathrm {mmHg}}$ as upper bound for the validation. Hence, the postinterventional CT data is compared to the in silico EVAR results at the internal diastolic pressure state and at the internal systolic pressure state. The relative error $e_{(\varLambda )}(s^{(\varPi ),j})$ of the in silico EVAR approach at the respective pressure state is

$$\begin{aligned} e_{(\varLambda )}(s^{(\varPi ),j}) =\frac{\bar{d}_{\mathrm {sim,}(\varLambda )}^{{\mathrm {S}}} (s^{(\varPi ),j})-\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}}} (s^{(\varPi ),j})}{\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}}} (s^{(\varPi ),j})} \end{aligned}$$

(9)

with $\varLambda =\{{\mathrm {diast,sys}}\}$. The mean error e at the discrete location $s^{(\varPi ),j}$ out of the error at the diastolic pressure state $e_{\mathrm {diast}}$ and the error at the systolic pressure state $e_{\mathrm {sys}}$ is given by

$$\begin{aligned} e(s^{(\varPi ),j})=\frac{1}{2}\left( e_{\mathrm {diast}}(s^{(\varPi ),j}) +e_{\mathrm {sys}}(s^{(\varPi ),j})\right) . \end{aligned}$$

(10)

In the following section we will consider three patients ${\Xi }=\{1,2,3\}$ for validation. We calculate the mean error $\mu _{e,(\varXi )}^{(\varPi )}$ and standard deviation $\sigma _{e,(\varXi )}^{(\varPi )}$ for each SG part $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$ and each patient ${\Xi }=\{1,2,3\}$ over all discrete locations $s_{(\varXi )}^{(\varPi ),j}$ according to

$$\begin{aligned} \mu _{e,(\varXi )}^{(\varPi )}=\frac{1}{n_{\mathrm {C},(\varXi )}^{(\varPi )}}\sum _{j=1,2,\ldots ,n_{\mathrm {C},(\varXi )}^{(\varPi )}}e(s_{(\varXi )}^{(\varPi ),j}) \end{aligned}$$

(11)

and

$$\begin{aligned} \sigma _{e,(\varXi )}^{(\varPi )}&=\sqrt{\frac{1}{n_{\mathrm {C},(\varXi )}^{(\varPi )}}\sum _{j=1,2,\ldots ,n_{\mathrm {C},(\varXi )}^{(\varPi )}}\left( e(s_{(\varXi )}^{(\varPi ),j})-\mu _{e,(\varXi )}^{(\varPi )}\right) ^2} \end{aligned}$$

(12)

In Eqs. (11) and (12), $s_{(\varXi )}^{(\varPi ),j}$ are discrete values of the arc length of the centerline ${\mathcal {C}}_{\mathrm {De},(\varXi )}^{(\varPi )}$ with $\{s_{(\varXi )}^{(\varPi ),j}|0\le s_{(\varXi )}^{(\varPi ),j} \le L_{(\varXi )}^{(\varPi )}, \forall j=1,2,\ldots ,n_{\mathrm {C},(\varXi )}^{(\varPi )}\}$. The discrete values of the arc length $s_{(\varXi )}^{(\varPi ),j}$ describe the discrete locations at which the average diameters $\bar{d}_{{{\text{sim}}}}^{{\text{S}}} (s_{\varXi }^{{(\varPi ),j}} ) = \bar{d}_{{{\text{sim, (}}\varXi {\text{)}}}}^{{{\text{S,}}(\varPi ),j}}$ as well as $\bar{d}_{{{\text{postIV}}}}^{{\text{S}}} (s_{\varXi }^{{(\varPi ),j}} ) = \bar{d}_{{{\text{postIV, (}}\varXi {\text{)}}}}^{{{\text{S,}}(\varPi ),j}}$ and consequently the relative errors $e(s_{(\varXi )}^{(\varPi ),j})=e_{{(\varXi )}}^{(\varPi ),j}$ are measured. $n_{\mathrm {C},(\varXi )}^{(\varPi )}$ is the total number of these discrete locations and $L_{(\varXi )}^{(\varPi )}$ is the total arc length of the centerline ${\mathcal {C}}_{\mathrm {De},(\varXi )}^{(\varPi )}$ of patient $\varXi$ and SG part $\varPi$ in the deployed state.

We speak of a pseudo-continuous diameter measure, since the number of discrete locations $s^{j}$ at which the average diameters $\bar{d}^{{\mathrm {S}},j}=\bar{d}^{{\mathrm {S}}}(s^{j})$ [Eq. (8)] are measured is very high. Hence, the average diameters of the stent $\bar{d}^{{\mathrm {S}}}$ are given almost continuously along the total length L of the deployed SG. Therefore, in the following we use the abbreviated continuous representation of (7) given by $s\in [0;L]$. Variables with superscript $(\bullet )^{j}$ denote discrete variables, and variables without superscript $(\bullet )^{j}$ denote variables that are given pseudo-continuously along $s\in [0;L]$.

3 Results

3.1 Validation using postinterventional CT data

The results of the in silico EVAR approach, i.e., the configurations of SG and vessel in the deployed state, for the three patient-specific cases are visualized in Fig. 9I. We validate the in silico EVAR methodology by qualitative and quantitative comparison between the simulation results and postinterventional CT data.

Fig. 8

Qualitative (I) and quantitative (II) validation of the three clinical cases; comparison of the average diameters of the stent from the in silico approach and the stent from postinterventional CT data qualitatively at four distinct slices per patient (I) and pseudo-continuously along the total arc length $s_{(\varXi )}^{(\varPi )}\in [0;L_{(\varXi )}^{(\varPi )}]$ of the respective SG part $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$ of patient ${\Xi }=\{1,2,3\}$

Table 4 Measured average diameters $\bar{d}_{\mathrm {sim}}^{{\mathrm {S}}}$ and $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}}}$ as well as relative errors e at the assumed diastolic pressure state (80 mmHg) and at the assumed systolic pressure state (130 mmHg) according to Eq. (9) in the exemplary four slices per patient visualized in Fig. 8I

3.1.1 Qualitative comparison

In Fig. 8I, the simulated stent configurations of the three patient-specific cases at an internal pressure state of 80 mmHg are superimposed to the stent configuration segmented from postinterventional CT data. Qualitatively, the simulated and postinterventional stent shapes are almost identical by visual comparison in Fig. 8I. Even specific SG deformations, such as the conical stent shape of the most proximal stent limb of patient 3 or the highly curved SG part of the left iliac part of patient 1 are properly predicted as can be seen in Fig. 8I. Only slight mismatches in the relative position of the right iliac SG parts of all three patients exist, whereas for the proximal and the left iliac SG part no significant position mismatches are visible.

For each patient four slices are considered qualitatively: one slice through the first stent limb of the proximal part (slice ${\mathrm {S}}_{({\Xi })}^{1}$), one slice through the second stent limb of the proximal part (slice ${\mathrm {S}}_{({\Xi })}^{2}$), one slice through the last stent limb of the left iliac part (slice ${\mathrm {S}}_{({\Xi })}^{3}$) and one slice through the last stent limb of the right iliac part (slice ${\mathrm {S}}_{({\Xi })}^{4}$), where ${\Xi }=\{1,2,3\}$ denotes the number of the patient. The slices ${\mathrm {S}}_{({\Xi })}^{1}$, ${\mathrm {S}}_{({\Xi })}^{3}$ and ${\mathrm {S}}_{({\Xi })}^{4}$ are of elevated relevance as they are within the proximal and the distal landing zones that are involved in several EVAR-related complications such as endoleaks type 1a and 1b.

The deployed stent diameters in the slices ${\mathrm {S}}_{1}^{1}$, ${\mathrm {S}}_{2}^{1}$ and ${\mathrm {S}}_{3}^{1}$, which define slices through the proximal landing zone, are well predicted. Slight discrepancies in slice ${\mathrm {S}}_{2}^{1}$ of patient 2 can be observed where the simulated stent diameter is slightly larger than the stent diameter extracted from postinterventional CT data. In the slices ${\mathrm {S}}_{1}^{2}$ and ${\mathrm {S}}_{3}^{2}$ some mismatches in the predicted stent expansion can be identified, whereas the prediction of the stent expansion in slice ${\mathrm {S}}_{2}^{2}$ is almost perfect.

The diameter of the simulated stents and the diameter of the stents from postinterventional CT data in the slices ${\mathrm {S}}_{1}^{3}$, ${\mathrm {S}}_{2}^{3}$ and ${\mathrm {S}}_{3}^{3}$, which are slices through the landing zone of the left iliac part, are almost identical from a qualitative perspective. The slices ${\mathrm {S}}_{1}^{4}$, ${\mathrm {S}}_{2}^{4}$ and ${\mathrm {S}}_{3}^{4}$ through the landing zone of the right iliac part highlight the previously mentioned relative position error of the simulated right iliac SG part compared to the postinterventional CT data. The prediction of the diameter expansion is relatively good. The largest discrepancies by visual comparison can be identified for patient 2 (slice ${\mathrm {S}}_{2}^{4}$) where the simulated stent diameter is too large.

3.1.2 Quantitative comparison

In Table 4, we plot the average stent diameters and relative errors of the distinct slices that were qualitatively discussed in Sect. 3.1.1 and which are visualized in Fig. 8I. We quantitatively evaluate the in silico EVAR results at the assumed diastolic pressure state of 80 mmHg and at the assumed systolic pressure state of 130 mmHg.

In Fig. 8II, we plot the average stent diameters of the in silico EVAR approach at 80 mmHg ($\bar{d}_{\mathrm {sim,diast}}^{{\mathrm {S}}}(s^{(\varPi )}_{(\varXi )})$) and at 130 mmHg ($\bar{d}_{\mathrm {sim,sys}}^{{\mathrm {S}}}(s^{(\varPi )}_{(\varXi )})$) as well as the filtered average diameters $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}}}(s^{(\varPi )}_{(\varXi )})$ of the stent from postinterventional CT data pseudo-continuously along the arc length $s_{(\varXi )}^{(\varPi )}\in [0;L_{(\varXi )}^{(\varPi )}]$ for all three SG parts $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$ and all three patients ${\Xi }=\{1,2,3\}$. Each asterisk corresponds to a discrete average diameter $\bar{d}_{\mathrm {sim},(\varXi )}^{{\mathrm {S}},(\varPi ),j}$, $\bar{d}_{\mathrm {postIV,f,},(\varXi )}^{{\mathrm {S}},(\varPi ),j}$ measured in a distinct set ${\mathsf {A}}_{\mathrm {I,sim},(\varXi )}^{{\mathrm {S}},(\varPi ),j}$ and ${\mathsf {A}}_{\mathrm {I,postIV},(\varXi )}^{{\mathrm {S}},(\varPi ),j}$, respectively (Sect. 2.6). Additionally, the relative error $e(s^{(\varPi )}_{(\varXi )})$ between the in silico EVAR approach and the postinterventional CT data according to Eq. (10) is visualized in Fig. 8II (right scale). At the bifurcations of the SG, the stent diameters of the postinterventional CT data could not be measured properly as the proximal part and the iliac parts of the stent are slightly overlapping. Further, in the range $s^{{\mathrm {L}}}_{2}\in [34\,{\mathrm {mm}}; 65\,{\mathrm {mm}}]$ of the left iliac part of patient 2, the quality of the segmented stent from postinterventional CT data is inappropriate to be able to measure stent diameters. Those regions, in which the average stent diameters of the postinterventional CT data could not be measured, are highlighted by orange color in the plots of Fig. 8II and are neglected in the calculation of the relative errors $e(s^{(\varPi )}_{(\varXi )})$. Table 5 provides a summary of the mean $\mu _{e,(\varXi )}^{(\varPi )}$ and the standard deviation $\sigma _{e,(\varXi )}^{(\varPi )}$ of the relative errors $e(s^{(\varPi )}_{(\varXi )})$ according to Eqs. (11) and (12) over all SG parts $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$ for each patient-specific case ${\Xi }=\{1,2,3\}$.

Referring to Fig. 8II, in the proximal parts of the three patients, average stent diameters $\bar{d}_{\mathrm {sim,diast}}^{{\mathrm {S}}}(s^{{\mathrm {P}}}_{(\varXi )})$ of the in silico EVAR approach at 80 mmHg (blue curve) and at 130 mmHg (red curve) are very close to the average stent diameters $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}}}(s^{{\mathrm {P}}}_{(\varXi )})$ of the postinterventional CT data (black curve). Largest discrepancies between in silico EVAR and postinterventional CT data can be observed in the proximal SG part of patient 2. The relative error is $|e(s^{{\mathrm {P}}}_{(\varXi )})|<12\%$ for any of the three patients with $s^{{\mathrm {P}}}_{(\varXi )}\in [0; L^{{\mathrm {P}}}_{(\varXi )}]$. The good prediction of the average stent diameters of the proximal SG part results in a mean relative error of $\mu _{e}^{{\mathrm {P}}}=6.4\%$ and a small standard deviation of $\sigma _{e}^{{\mathrm {P}}}=3.4\%$ (Table 5). $\mu _{e}^{{\mathrm {P}}}$ and $\sigma _{e}^{{\mathrm {P}}}$ denote the mean and standard deviation of the error e for the proximal SG part over all three patients according to Eqs. (11) and (12). It is also worth mentioning that the in silico approach is able to reproduce the conical shapes of the stent in the proximal landing zone (indicated by green color in Fig. 8II). Whereas the most proximal stent limb of patient 1 is only slightly conical, the most proximal stent limbs of patient 2 and 3 are strongly conical with a smaller average diameter at the proximal end and a larger average diameter at the distal end. The SGs of all three patients are strongly compressed in the proximal landing zone, i.e., the measured average stent diameters (blue, red and black curve in Fig. 8II) are significantly smaller than the nominal diameter $D(s^{{\mathrm {P}}}_{(\varXi )})$ (cyan curve in Fig. 8II). In the aneurysm sac ($s^{{\mathrm {P}}}_{(\varXi )}\gtrsim 30\,{\mathrm {mm}}$), the SG fully expands to its nominal diameter $D(s^{{\mathrm {P}}}_{(\varXi )})$ with exception of patient 1. Due to a pronounced ILT layer, patient 1 has a relatively small luminal diameter in the aneurysm sac of the preinterventional vessel. The SG cannot fully expand to its nominal diameter in this region.

Table 5 Mean and standard deviation of the relative errors $e(s^{(\varPi )}_{(\varXi )})$ according to Eqs. (11) and (12) over all SG parts $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$ of each patient-specific case ${\Xi }=\{1,2,3\}$

Very similar behavior of the left and right iliac SG parts can be observed in Fig. 8II. A relative error in the left iliac SG parts of $|e(s^{{\mathrm {L}}}_{(\varXi )})|<20\%$ and a relative error in the right iliac SG parts of $|e(s^{{\mathrm {R}}}_{(\varXi )})|<25\%$ is found for any $s^{{\mathrm {L}}}_{(\varXi )}\in [0; L^{{\mathrm {L}}}_{(\varXi )}]$ and $s^{{\mathrm {R}}}_{(\varXi )}\in [0; L^{{\mathrm {R}}}_{(\varXi )}]$, respectively. The mean error and the standard deviation of the iliac parts are given by $\mu _{e}^{{\mathrm {L}}}\,\pm \,\sigma _{e}^{{\mathrm {L}}} =2.1\,\pm \, 9.3 \%$ for the left iliac part and $\mu _{e}^{{\mathrm {R}}}\,\pm \,\sigma _{e}^{{\mathrm {R}}} =6.6\,\pm \, 9.8 \%$ for the right iliac part (Table 5). $\mu _{e}^{{\mathrm {L}}}$ and $\sigma _{e}^{{\mathrm {L}}}$ denote the mean and standard deviation of the relative error e for the left iliac SG part over all three patients. $\mu _{e}^{{\mathrm {R}}}$ and $\sigma _{e}^{{\mathrm {R}}}$ is the mean and standard deviation of the relative error e for the right iliac SG part over all three patients according to Eqs. (11) and (12). In contrast to the proximal SG parts, where the simulated average diameters $\bar{d}_{\mathrm {sim,diast}}^{{\mathrm {S}}}$ are slightly larger than the average diameters $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}}}$ from postinterventional CT data for the total length of the SG part $s^{{\mathrm {P}}}_{(\varXi )}\in [0; L^{{\mathrm {P}}}_{(\varXi )}]$, in the iliac SG parts there are regions where the simulated stent diameters are too large and regions where the simulated stent diameters are too small. This is the reason for the relatively small mean relative errors but higher standard deviations for the iliac SG parts as provided in Table 5. The prediction of the stent expansion diameters in the landing zones of the iliac SG parts (indicated by green color in Fig. 8II) is relatively good with exception of the landing zone of the right iliac SG part of patient 2. In the landing zone of the right iliac SG part of patient 2, the predicted average stent diameters of the in silico EVAR approach are too large compared to the postinterventional CT data with relative errors up to $25\%$. The average stent diameters of the deployed SG (blue, red and black curve) in the iliac SG parts are close to the nominal diameter (cyan curve) with exception of the regions of the distal landing zones (indicated by green color) where the SG is strongly compressed.

In summary, the mean and the standard deviation of the relative error e are very similar for all three patients with $\mu _{e,1}\,\pm \, \sigma _{e,1}=6.7\,\pm \, 8.7 \%$, $\mu _{e,2}\,\pm \, \sigma _{e,2}=5.5\,\pm \, 7.4 \%$ and $\mu _{e,3}\,\pm \, \sigma _{e,3}=5.0\,\pm \, 8.2 \%$. $\mu _{e,(\varXi )}$ and $\sigma _{e,(\varXi )}$ are the mean and the standard deviation of the relative error e of all three SG parts of patient $\varXi =\{1,2,3\}$ according to Eq. (11) and (12). The total relative error over all patients and all SG parts is $\mu _{e}\,\pm \, \sigma _{e}=5.6\,\pm \, 8.1 \%$ (Table 5).

Considering the change of the average stent diameters induced by the blood pressure change, the average diameters of the stent at 80 mmHg ($\bar{d}_{\mathrm {sim,diast}}^{{\mathrm {S}}}(s^{(\varPi )}_{(\varXi )})$) (blue curve in Fig. 8II) are only slightly smaller than the average diameters of the stent at 130 mmHg ($\bar{d}_{\mathrm {sim,sys}}^{{\mathrm {S}}}(s^{(\varPi )}_{(\varXi )})$) (red curve in Fig. 8II).

3.2 In silico EVAR application

To demonstrate the motivation of using in silico EVAR approaches as predictive tool, we evaluate the mechanical state of SG and vessel in the deployed state for the three patient‐specific cases. We consider the deployed SG configurations (Fig. 9I), the normal contact tractions between SG and vessel (Fig. 9II), the tissue stresses of the vessel before EVAR (Fig. 9III) and the tissue stresses of the vessel after EVAR (Fig. 9IV) at the systolic pressure state of 130 mmHg. Further, in Fig. 9V, the von Mises tissue overstress

$$\begin{aligned} \bar{\sigma }_{\mathrm {Mises}}&=\sigma _{\mathrm {Mises}}^{\mathrm {post}}-\sigma _{\mathrm {Mises}}^{\mathrm {pre}} \end{aligned}$$

(13)

is visualized, where $\sigma _{\mathrm {Mises}}^{\mathrm {pre}}$ are the von Mises Cauchy stresses in the vessel before EVAR (Fig. 9III) and $\sigma _{\mathrm {Mises}}^{\mathrm {post}}$ are the von Mises Cauchy stresses after EVAR (Fig. 9IV).

Fig. 9

Results of the in silico EVAR approach for all three clinical cases at 130 mmHg blood pressure: deployed configuration of the SG (I), normal contact tractions between SG and vessel (II), vessel von Mises Cauchy stresses before EVAR (III), vessel von Mises Cauchy stresses after EVAR (IV) and vessel von Mises overstresses (V)

For patients 2 and 3, radial graft buckling only is apparent in the proximal and distal landing zones and longitudinal graft buckling in the curved iliac parts. In contrast, for patient 1 radial graft buckling is apparent almost across the total SG since the SG is in contact with the vessel even in the aneurysm sac. Additionally, patient 1 possesses the highest degree of calcification, i.e., additional stiffening of the vessel, which might reduce the widening of the vessel by the SG and might lead to increased buckling of the SG (Fig. 9I). The SG almost fully adapts to the vessel geometry in all three cases, i.e., straightening of the vessel is insignificantly small even in the strongly angulated iliac arteries.

Maximal normal contact tractions above 100 kPa occur in the in silico model in the proximal and distal landing zones but also in the curved iliac parts of patient 1 (Fig. 9II). The SG yields vessel stresses above 300 kPa in the proximal and distal landing zones in the model of all three patient-specific cases (Fig. 9IV) as well as in the highly curved iliac parts of patient 1. The insertion of the SG reduces the wall stresses in the aneurysm sac in case 2 and 3. In case of patient 2, the SG is not in contact with the ILT in the aneurysm sac. Hence, the load on the vessel wall is fully removed resulting in zero vessel stresses in the aneurysm sac. In case of patient 1 the luminal diameter in the aneurysm sac is relatively small due to a relatively thick ILT layer. This means the SG is almost fully in contact with the ILT in the aneurysm sac. Therefore, the wall stresses in the aneurysm sac do not decrease in the model. In all three patient-specific cases local tissue overstresses $\bar{\sigma }_{\mathrm {Mises}}$ of up to 100 kPa exist mainly in the proximal and distal landing zones where passive fixation by SG oversizing is aspired (Fig. 9V).

4 Discussion

It was shown that the in silico EVAR methodology proposed in Hemmler et al. (2018) is applicable to patient-specific geometries with bifurcated SGs. The qualitative comparison of the deployed stent configuration of the in silico EVAR approach and the deployed stent extracted from postinterventional CT data showed very good agreement despite that certain model parameters, such as constitutive vessel parameters and the vessel wall thickness, are uncertain. Instead of fully patient-specific parameters, cohort-averaged and literature-based values had to be used.

Since the exact blood pressure state of the patients at time of the postinterventional CT scans is unknown, we computed the average diameters of the deployed stent from the in silico EVAR approach at the assumed diastolic blood pressure of 80 mmHg and at the assumed systolic blood pressure of 130 mmHg. The in silico results at the systolic blood pressure can be seen as upper bound and the in silico results at the diastolic blood pressure as lower bound when comparing to postinterventional CT data. However, the difference of the deployed stent diameters induced by the blood pressure change of 50 mmHg is rather small (${\mathrm {mean}}\pm {\mathrm {std}}=2.0\,\pm \, 1.2 \%$ at the proximal SG parts and ${\mathrm {mean}}\,\pm \, {\mathrm {std}}=0.7\,\pm \, 0.8 \%$ at the iliac SG parts).

The newly developed quantitative validation methodology allowed to plot the average diameters of the stents from the in silico EVAR approach and the stents extracted from postinterventional CT data pseudo-continuously along the total length of the SG in the deployed state. The quantitative comparison of the average stent diameters of the deployed SG from the in silico EVAR approach and the average stent diameters from postinterventional CT data showed very good agreement for the proximal SG parts with the maximum error smaller than 12% and $\mu _{e}^{{\mathrm {P}}}\,\pm \,\sigma _{e}^{{\mathrm {P}}} =6.4\,\pm \, 3.4 \%$ over all three patient-specific cases. The comparison of the iliac SG components showed good agreement with $\mu _{e}^{{\mathrm {L}}}\,\pm \,\sigma _{e}^{{\mathrm {L}}} =2.1\,\pm \, 9.3 \%$ for the left iliac parts and $\mu _{e}^{{\mathrm {R}}}\,\pm \,\sigma _{e}^{{\mathrm {R}}} =6.6\,\pm \, 9.8 \%$ for the right iliac parts. In total, the prediction of the stent diameters by the in silico approach led to slightly too large diameters compared to the stents extracted from postinterventional CT data.

In contrast to Perrin et al. (2015a), we only used the comparison of stent diameters for validation of the in silico EVAR methodology. We did not compare the position of the stent since pre- and postinterventional CT data generally are aligned in different coordinate systems. Hence, the results of the position comparison strongly depend on the quality of the registration between pre- and postinterventional CT data. Further, the results of the position comparison depend on the exact position of the patient during CT scanning. As the order of the position comparison should be in the range of a few millimeters, these effects would dominate the results. In contrast to the position comparison, the diameter comparison is independent of the global position of the stent.

Although the preinterventional vessel diameters and the degree of SG oversizing in the proximal landing zone are in the same range for all three patients ($o=17-20\%$, Table 1), the deployed SG configurations of the three patient-specific cases are very different in the proximal landing zone. The SG diameter in the deployed state in the proximal landing zone of patient 1 with a mean diameter of 22.9 mm is significantly smaller than the corresponding SG diameters of patient 2 with a mean diameter of 25.9 mm and patient 3 with a mean diameter of 24.5 mm. Here, the mean diameter corresponds to the in silico EVAR results in the proximal landing zones at 130 mmHg blood pressure. This observation of different stent expansion diameters goes hand in hand with the highest degree of graft buckling in the proximal landing zone of patient 1. One possible explanation is the highest degree of calcification of patient 1 compared to the other two patient-specific vessels. Calcifications are very stiff vessel constituents which reduce the widening of the vessel by the oversized SG. Hence, the deployed SG diameter is smaller and the degree of graft buckling is higher. These different characteristics of the deployed SGs in the landing zones of potentially similar clinical cases (similar with respect to the preinterventional proximal vessel diameter and the degree of SG oversizing) raise the need for patient-specific simulations which consider the patient-specific geometry of the vessel and which incorporate ILT and calcifications as additional vessel constituents. However, as in this study only three clinical cases were considered, these results do not allow for general conclusions.

Using the in silico EVAR methodology, it was shown that the insertion of the SG reduced the vessel stresses in the aneurysm sac and led to instant shrinkage of the sac diameter in two of three cases. Shrinkage of the sac diameter often is considered as evidence of clinical success (Ellozy et al. 2006; Sonesson et al. 2003) as this is an indicator that the luminal pressure is removed from the vessel in the aneurysm sac. But the SG yields tissue normal contact tractions between SG and vessel above 100 kPa and local tissue overstresses of up to 100 kPa in the landing zones of the SG which can lead to negative effects such as tissue remodeling and aortic neck dilatation (Kouvelos et al. 2017; Vukovic et al. 2018; Sternbergh et al. 2004).

In future studies, a metric combining mechanical and geometrical parameters should be developed to make in silico EVAR approaches a valuable tool that facilitates the preinterventional planning process. These parameters have to be able to assess the quality of the in silico EVAR outcome quantitatively. Possible parameters are tissue overstresses, contact tractions, SG fixation forces and SG drag forces. The metric combining these mechanical and geometrical parameters should group the in silico EVAR results in the range between “high risk of complications” and “no risk of complications” and hence make the in silico EVAR outcome easily interpretable by a clinician.

5 Limitations

Apart from the basic model simplifications stated in Sect. 2.2, this study is affected by the following limitations. First, compared to the real-world medical intervention the in silico EVAR approach is a strongly simplified process. The final deployed state of SG and vessel is the only point of interest. Any intrainterventional results cannot be obtained by this in silico EVAR methodology.

Second, inter- and intrapatient variability of vessel wall material parameters and vessel wall thickness (Biehler et al. 2015) were neglected. Instead, population-averaged mean values were used. Furthermore, we used the same material parameters and the same wall thickness for iliac arteries and the abdominal aorta.

Third, we did not consider any residual sac pressure after EVAR (Chuter et al. 1997a; Kwon et al. 2011). Instead, we assumed zero sac pressure after the insertion of the SG in our in silico approach.

Fourth, the blood pressure at time of imaging had not been recorded. Hence, the blood pressure corresponding to the stent configuration segmented from postinterventional CT data is unknown. Instead, diastolic and systolic blood pressures are considered in the in silico EVAR approach and were used as lower and upper bound in the comparison between in silico results and postinterventional CT data.

Fifth, the quantitative comparison of in silico results and postinterventional CT data was based on average diameters only. In future work, the cross-sectional shape, such as the ovalization of stents, could be compared as well.

Sixth, setting up the computational model is a largely automated process. Nevertheless, the semi-automated segmentation process of the patient-specific vessel geometry required approximately 3 h per patient and should be further automated for clinical applicability. Running the simulations required approximately 36 h per patient on 112 cores (Intel Haswell nodes). Algorithmic optimizations and model reduction techniques (Santamaría et al. 2018) should be considered in future studies to use in silico EVAR methods in clinical practice.

Finally, in this study we only considered short-term results after EVAR. The model did not include any tissue growth and remodeling after EVAR which often is observed in reality (Kouvelos et al. 2017; Vukovic et al. 2018; Sternbergh et al. 2004). However, in silico results were compared to postinterventional CT data shortly after EVAR treatment such that the influence of tissue growth and remodeling can be assumed to be negligibly small. Nevertheless, consideration of tissue growth and remodeling might be indispensable if long-term results shall be evaluated.

6 Conclusions

High complexity and non-negligible complication rates of EVAR raise the need for better preinterventional planning tools. As first steps toward a patient-specific, predictive tool, we applied the in silico EVAR methodology proposed in Hemmler et al. (2018) to three clinical cases with bifurcated SGs and sophisticated models of the vessel that include ILT, calcifications and an anisotropic model for the vessel wall.

Furthermore, we developed a qualitative and quantitative validation methodology that is based on a comparison of average stent diameters between in silico results and postinterventional CT data. The methodology measures average stent diameters pseudo-continuously along the total length of the deployed SG and is applicable to any SG type.

The good agreement between in silico results and postinterventional CT data makes in silico EVAR approaches very promising for the preinterventional planning of EVAR.

Appendices

Appendix 1: Definition of control curves and assignment of stent-graft nodes to the subsets ${\mathsf {A}}^{j}_{\mathrm {I}}$

This section provides the definition of control curves ${\mathcal {C}} \subset {\mathbb {R}}^3$ associated with the morphing algorithm that is used for the in silico SG placement. For a detailed description of the morphing algorithm, the reader is referred to Hemmler et al. (2018).

These control curves are given in the initial configuration ${\mathcal {C}}_{\mathrm {I}}$ and in the target configuration ${\mathcal {C}}_{\mathrm {T}}$. At each point $j=1,2,\ldots ,n_{\mathrm {C}}$ of the piecewise linear control curve ${\mathcal {C}}_{\mathrm {I}}$ in the initial configuration described by $n_{\mathrm {C}}$ discrete points with the coordinates ${\varvec{x}}_{\mathrm {C},\mathrm {I}}^{j}\in {\mathcal {C}}_{\mathrm {I}}$, a semi-infinite bounding box ${\mathbb {B}^{j} \subset {\mathbb {R}}^3}$ is used to assign the nodes i of the SG with the reference coordinates ${\varvec{X}}^{i} \in ({\Omega }^{{\mathrm {S}}}_{\mathrm {0}} \cap {\Omega }^{\mathrm {G}}_{\mathrm {0}})$ to one point on the control curve ${\mathcal {C}}_{\mathrm {I}}$. ${\Omega }^{{\mathrm {S}}}_{\mathrm {0}}$ and ${\Omega }^{\mathrm {G}}_{\mathrm {0}}$ describe the undeformed configurations of stent and graft, respectively. The semi-infinite bounding box ${\mathbb {B}^{j} \subset {\mathbb {R}}^3}$ is defined by two parallel, infinite planes with a distance of h (Fig. 5). All nodes i of the SG with ${\varvec{X}}^{i} \in \mathbb {B}^{j}$ are assigned to point j of the centerline ${\mathcal {C}}_{\mathrm {I}}$ and are put into the subset ${\mathsf {A}}^{j}_{\mathrm {I}}\subseteq {\mathsf {A}}_{\mathrm {I}}=\{1,2,\ldots ,n^{\mathrm {SG}}\}$ where $n^{\mathrm {SG}}$ is the number of nodes of the SG and where

$$\begin{aligned}&\overset{n_{\mathrm {C}}}{\underset{j=1}{\bigcup }} {\mathsf {A}}^j_{\mathrm {I}}={\mathsf {A}}_{\mathrm {I}}, \end{aligned}$$

(14a)

$$\begin{aligned}&{\mathsf {A}}^j_{\mathrm {I}}\cap {\mathsf {A}}^k_{\mathrm {I}}=\varnothing,\nonumber \\&\forall k \ne j,\,j=1,2,\ldots ,n_{\mathrm {C}},\,k=1,2,\ldots ,n_{\mathrm {C}} \end{aligned}$$

(14b)

holds.

Appendix 2: Control curve continuity conditions

The deformation of the SG during the in silico SG placement is fully described by the linear interpolation between two given configurations of the control curve, the initial configuration ${\mathcal{C}}_{\mathrm {I}}^{(\Pi)}\in {\mathbb {R}}^3$ and the target configuration ${\mathcal{C}}_{\mathrm {T}}^{(\Pi)}\in {\mathbb {R}}^3$. To ensure continuity between the three SG components $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$ during the entire SG placement, the following conditions between the initial configurations ${\mathcal {C}}_{\mathrm {I}}^{(\varPi )}$ and the target configurations ${\mathcal {C}}_{\mathrm {T}}^{(\varPi )}$ of the control curves have to be satisfied (Fig. 4IIIb):

• The distal end of the control curve ${\mathcal {C}}_{\mathrm {I}}^{{\mathrm {P}}}$ and the proximal ends of the control curves ${\mathcal {C}}_{\mathrm {I}}^{{\mathrm {L}}}$ and ${\mathcal {C}}_{\mathrm {I}}^{{\mathrm {R}}}$ have to be parallel and have to be in one plane. Same holds for the target configurations of the control curves ${\mathcal {C}}_{\mathrm {T}}^{{\mathrm {P}}}$, ${\mathcal {C}}_{\mathrm {T}}^{{\mathrm {L}}}$ and ${\mathcal {C}}_{\mathrm {T}}^{{\mathrm {R}}}$.

• The longitudinal overlap $l_{\mathrm {a}}$ of the three control curves as well as the transverse distance $l_{\mathrm {b}}$ between the three control curves has to be the same in the initial configurations ${\mathcal {C}}_{\mathrm {I}}^{(\varPi )}$ and the target configurations ${\mathcal {C}}_{\mathrm {T}}^{(\varPi )}$.

Appendix 3: Center of gravity calculation for regular stent-graft meshes

For a regular SG mesh, the mean angular distance $\bar{\theta }^{i}=\frac{1}{2}(\theta ^{i+1}-\theta ^{i-1})$ between two adjacent nodes in the set ${\mathsf {A}}_{\mathrm {I}}^{j}$ is $\bar{\theta }^{i}=\frac{2\pi }{n^{j}}$ for each node i where $n^{j}$ is the number of nodes in the set ${\mathsf {A}}_{\mathrm {I}}^{j}$. Hence, the calculation of the center of gravity of all nodes i in the set ${\mathsf {A}}_{\mathrm {I}}^{j}$ [Eq. (5)] reduces to the arithmetic mean

$$\begin{aligned} {\varvec{x}}_{\mathrm {C,De}}^{j}&=\frac{1}{2\pi }\underset{i\in {\mathsf {A}}_{\mathrm {I}}^{j}}{\sum } \bar{\theta }^{i} {\varvec{x}}^{i}=\frac{1}{n^{j}}\underset{i\in {\mathsf {A}}_{\mathrm {I}}^{j}}{\sum }{\varvec{x}}^{i}, \nonumber \\&\quad \forall j=1,2,\ldots ,n_{\mathrm {C}}, \end{aligned}$$

(15)

where ${\varvec{x}}^{i}$ are the current coordinates of all nodes i in the set ${\mathsf {A}}_{\mathrm {I}}^{j}$.

Appendix 4: Filtering of postinterventional CT data

A moving average filter with a span of

$$\begin{aligned} l_{\mathrm {span}}&=2 n_{\mathrm {postIV}} \left\lceil \frac{\varDelta z_{\mathrm {CT}}}{\bar{\varDelta s}_{\mathrm {postIV}}} \right\rceil + 1 \end{aligned}$$

(16)

is used to limit the impact of obvious artifacts in the stent diameter measurement from postinterventional CT data. In Eq. (16), $\varDelta z_{\mathrm {CT}}=1\,{\mathrm {mm}}$ is the slice thickness of the postinterventional CT data, $n_{\mathrm {postIV}}=3$ is a filtering constant that scales the length of the moving average filter. $\bar{\varDelta s}_{\mathrm {postIV}}$ is the mean edge length of the piecewise linear curve ${\mathcal {C}}_{\mathrm {De}}$, i.e., the mean distance between the centers of gravity of the sets ${\mathsf {A}}_{\mathrm {I,postIV}}^{{\mathrm {S}},j}$ defined by Eq. (5). The result of the filtering process is visualized for patient 3 in Fig. 10. Each asterisk denotes the measured average diameter $\bar{d}_{\mathrm {postIV}}^{{\mathrm {S}},(\varPi ),j}$ of one distinct set ${\mathsf {A}}_{\mathrm {I,postIV}}^{{\mathrm {S}},(\varPi ),j}$ of SG part $\varPi =\{{\mathrm {P}},{\mathrm {L}},{\mathrm {R}}\}$.

Fig. 10

Difference between measured average stent diameters $\bar{d}_{\mathrm {postIV}}^{{\mathrm {S}},j}$ from postinterventional CT data and filtered average stent diameters $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}},j}$ as well as visualization of the standard deviation $\sigma _{\mathrm {f}}$ for the proximal SG part (I), the left iliac SG part (II) and the right iliac SG part (III) of patient 3

Appendix 5: Quality estimation of segmented data from postinterventional CT scans

The quality of the postinterventional CT data is crucial for the reliability of a quantitative validation of the in silico EVAR results, but local artifacts have a non-negligible effect on the segmentation of the stent from postinterventional CT data. To obtain an estimation of the measurement inaccuracy due to the vagueness in the segmentation process of the stent from postinterventional CT data, we define the relative difference between the measured average diameter $\bar{d}_{\mathrm {postIV}}^{{\mathrm {S}},j}$ and the average diameter of the filtered data $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}},j}$ by

$$\begin{aligned} \epsilon _{f}^{j}&=\frac{\bar{d}_{\mathrm {postIV}}^{{\mathrm {S}},j}-\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}},j}}{\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}},j}}, \quad \forall j=1,2,\ldots ,n_{\mathrm {C}}. \end{aligned}$$

(17)

Further, the standard deviation

$$\begin{aligned} \sigma _{f}&=\sqrt{\frac{1}{n_{\mathrm {C}}}\sum _{j=1,2,\ldots ,n_{\mathrm {C}}}\left( \epsilon _{f}^{j}-\mu _{f}\right) ^{2}} \end{aligned}$$

(18)

is calculated, where

$$\begin{aligned} \mu _{f}&=\frac{1}{n_{\mathrm {C}}}\sum _{j=1,2,\ldots ,n_{\mathrm {C}}}\epsilon _{f}^{j} \end{aligned}$$

(19)

is the mean relative difference. $n_{\mathrm {C}}$ is the number of points describing the piecewise linear curve ${\mathcal {C}}_{\mathrm {De}}$ which is equivalent to the number of discrete sets ${\mathsf {A}}_{\mathrm {I,postIV}}^{j}$. In Fig. 10 we oppose the plain stent diameters from postinterventional CT data $\bar{d}_{\mathrm {postIV}}^{{\mathrm {S}},j}$, the filtered stent diameters $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}},j}$ and the standard deviation $\sigma _{f}$ for patient 3.

A large standard deviation $\sigma _{f}$ of the relative difference $\epsilon _{f}^{j}$ is an indicator that the measurements are strongly affected by local artifacts of the segmented stent. The standard deviation $\sigma _{\mathrm {f}}$ is very small for the proximal SG parts ($\sigma _{\mathrm {f}}^{{\mathrm {P}}}\le 2.0\%$) but more significant for the iliac SG parts (Table 6) due to two main reasons:

• The segmentation process of the CZ-Spiral SGs from postinterventional CT data is more difficult as those stent limbs are less clearly visible.

•  $\sigma _{\mathrm {f}}$ is the standard deviation of the relative difference between the measured average diameters $\bar{d}_{\mathrm {postIV}}^{{\mathrm {S}},j}$ and the filtered average diameters $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}},j}$. Hence, local artifacts in the postinterventional CT data of equivalent size would have a larger relative impact on $\sigma _{\mathrm {f}}$ in regions of small stent diameters such as in iliac SG parts.

Table 6 Standard deviation $\sigma _{\mathrm {f}}$ of the relative difference between the measured average diameter $\bar{d}_{\mathrm {postIV}}^{{\mathrm {S}}}$ and the average diameter of the filtered data $\bar{d}_{\mathrm {postIV,f}}^{{\mathrm {S}}}$ of the postinterventional CT data in [%] according to Eq. (18) for the three patient-specific cases and the three SG parts