1 Introduction

The study of physical oceanography traditionally focusses on situations in which the surface and bottom Ekman layers are spatially well separated; that is, in which the total water depth exceeds the combined thickness of both Ekman layers (e.g., Csanady 1982; Cushman-Roisin 1994; Tomczak and Godfrey 2003; Olbers et al. 2012). Indeed, this concept applies to most continental shelves except for relatively narrow zones adjacent to coasts. This concept does also not apply to shallow shelf seas at low latitudes where Ekman layer thicknesses in the absence of density stratification substantially increase (e.g., Olbers et al. 2012). Many shelf seas of the ecologically highly significant Coral Triangle of the Indonesian seas fall into the latter category. The oceanography of such low-latitude shelf seas has received little attention in the past.

Similar to the oceanographic approach, the circulation in inland waters is often decomposed into barotropic and baroclinic components, whereby the barotropic flow refers to the density-independent flow and the baroclinic flow is affiliated with density effects. Limnologists have long realized that depth-averaged circulation models are insufficient for the study of barotropic flows in homogeneous lakes (e.g., Wang et al. 2001; Hutter et al. 2014 and references therein), as these models miss the complex vertical structure of horizontal flows, for instance, leading to undercurrents and overturning features.

The creation of undercurrents and upwelling due to offshore winds, historically referred to as lee effect (Hela 1976), is a frequently observed feature in lakes (Monismith 1985, 1986; Stevens and Imberger 1996; Farrow and Stevens 2003) and coastal oceans (Svannsson 1975). Myrberg and Andrejev (2003) also identified this effect in the Baltic Sea. The lee effect is created by offshore winds leading to an onshore pressure gradient due to the sea surface sloping against the wind direction. The onshore pressure gradient induces an undercurrent, and upwelling follows at the upwind coastal boundary. An interesting question is as to whether such undercurrents and associated upwelling features also exist in shallow shelf seas at low latitudes, such as the Arafura Sea in the Indonesian seas.

Traditionally, the study of limnology often neglects Coriolis effects in cases when the width of a stratified lake is small compared with the internal Rossby radius of deformation (Hutter et al. 2014). Based on the external (barotropic) Rossby radius of deformation, a similar argument can be made for lakes of constant density. While this definition is based on characteristic horizontal length scales of flows and associated rotational effects on seiches, it does not account for the possible creation of Ekman layers that can substantially modify the circulation in lakes. The model findings by Hutter et al. (2014) for Lake Zurich, for instance, demonstrate that the Coriolis force is non-negligible even when barotropic Rossby radii are much larger than the width of the basin. Hence, in terms of Ekman layer influences, it should also be argued that Coriolis effects can only be ignored if the total depth of a water body (D) is much smaller than the theoretical thickness of the Ekman layer (d E ); that is,

$$ \delta =\frac{D}{d_E}<<1 $$
(1)

Based on this scaling, findings of this study will show that rotational effects due to the Coriolis force, which lead to vertical veering of horizontal flows in Ekman layers, need to be included in circulation studies of most inland waters.

To improve the understanding of the wind-driven dynamics in homogeneous water bodies under the influence of the Coriolis force and on time scales exceeding the inertia period, this work revitalizes the classical Ekman layer theory for a one-dimensional water column with a focus on interference situations in which the surface and bottom Ekman layers overlap. A three-dimensional hydrodynamic model is then applied to explore the wind-forced circulation in a large and shallow oceanic bay of constant density at low latitudes in more detail.

2 Methodology

2.1 Ekman layer dynamics with flow decomposition: vertical structures

For simplicity, we assume lateral uniformity of all variables, constant density (ρo), constant eddy viscosity (A z), and validity of the shallow-water approximation, which eliminates non-hydrostatic effects. Under these assumptions, the momentum equations on the f-plane can be written as:

$$ \frac{\partial u}{\partial t}-fv=-g\frac{\partial \eta }{\partial x}+{A}_z\frac{\partial^2u}{\partial {z}^2} $$
(2)
$$ \frac{\partial v}{\partial t}+fu=-g\frac{\partial \eta }{\partial y}+{A}_z\frac{\partial^2v}{\partial {z}^2} $$
(3)

where u and v are the components of horizontal flow velocity, t is time, x, y, and z are Cartesian coordinates (z points upward), g is acceleration due to gravity, η is sea-level elevation, A z is vertical eddy viscosity and f is the Coriolis parameter. Surface boundary conditions are:

$$ {A}_z\frac{\partial \left(u,v\right)}{\partial z}=\frac{\left({\tau}_x,{\tau}_y\right)}{\rho_o}\kern1em \mathrm{at}\ z=0 $$
(4)

where τ x and τ y are the components of the wind stress vector. For simplicity, a no-flow condition is prescribed at the bottom of the water column; that is, u = 0 and v = 0. Bottom-stress components are given by:

$$ \left({\tau}_{x,b},{\tau}_{y,b}\right)={\rho}_o{A}_z\frac{\partial \left(u,v\right)}{\partial z}\kern0.75em \mathrm{at}\ z=-D $$
(5)

which are indirectly determined by the resultant vertical shear near the seafloor and the setting of A z. Given the linearity of the momentum equations (2–3), the velocity field can be decomposed into wind-driven and pressure gradient-driven flow components:

$$ \left(u,v\right)=\left({u}_W+{u}_P,{v}_W+{v}_P\right) $$
(6)

The wind-driven flow component is governed by momentum equations representing the dynamics of the surface Ekman layer (Ekman 1905) (potentially modified by D):

$$ \frac{\partial {u}_W}{\partial t}-f{v}_W={A}_z\frac{\partial^2{u}_W}{\partial {z}^2} $$
(7)
$$ \frac{\partial {v}_W}{\partial t}+f{u}_W={A}_z\frac{\partial^2{v}_W}{\partial {z}^2} $$
(8)

The boundary conditions for the wind-driven flow component are:

$$ {A}_z\frac{\partial \left({u}_W,{v}_W\right)}{\partial z}=\frac{\left({\tau}_x,{\tau}_y\right)}{\rho_o}\kern0.75em \mathrm{at}\ z=0 $$
(9)
$$ {u}_W={v}_W=0\kern1em \mathrm{at}\ z=-D $$
(10)

On the other hand, the pressure gradient-driven flow component, leading to establishment of a potentially modified bottom Ekman layer (Cushman-Roisin 1994), is given by:

$$ \frac{\partial {u}_P}{\partial t}-f{v}_P=-g\frac{\partial \eta }{\partial x}+{A}_z\frac{\partial^2{u}_P}{\partial {z}^2} $$
(11)
$$ \frac{\partial {v}_P}{\partial t}+f{u}_P=-g\frac{\partial \eta }{\partial y}+{A}_z\frac{\partial^2{v}_P}{\partial {z}^2} $$
(12)

The boundary conditions for the pressure gradient-driven flow component are:

$$ \frac{\partial \left({u}_P,{v}_P\right)}{\partial z}=0\kern1em \mathrm{at}\ z=0 $$
(13)
$$ {u}_P={u}_w=0\kern0.5em \mathrm{at}\ z=-D $$
(14)

Under the assumptions made, both Ekman layers attain the same thickness, given by d E = (2A z/|f|)1/2. Note that A z in homogenous water bodies depends strongly on the wind stress magnitude (e.g., Svensson 1979).

For given values of total water depth D, eddy diffusivity A z , and Coriolis parameter f, we can now derive the steady-state velocity structures for wind stress and pressure gradient forcing on their own. It is important to stress that the individual results are scalable; that is, the steady-state solutions for each velocity part can be:

  1. (i)

    rotated in horizontal space in alignment with the direction of the individual force, and

  2. (ii)

    multiplied by an amplification factor in proportion to the magnitude of the individual force.

The resultant flow field is the superposition, or interference, of two linearly independent solutions. To this end, the individual vertical structures of the velocity components exclusively depend on δ = D/d E (noting that the d E is the same here for the surface and the bottom Ekman layers) and the magnitudes and orientations of the wind stress and pressure gradient forces.

The above equations are solved by using the numerical scheme described in Kämpf (2010). Vertical eddy viscosity is set to A z = 0.01 m2/s. The Coriolis parameter is set to −1 × 10−5 s−1, corresponding to ~5°S. This gives a theoretical Ekman layer thickness of ~45 m. The resultant vertical profiles of wind-driven and pressure gradient-driven flow components are derived for total water depths spanning a range from 10 to 200 m, that is, the ratio δ = D/d E is varied from 0.23 to 4.5. For convenience, the discussion is restricted to the case of a wind stress magnitude of 0.1 Pa and a pressure gradient force corresponding to a theoretical geostrophic flow of a speed of 0.25 m/s. The wind stress is directed northward in all cases. The orientation of the pressure gradient force is varied. The wind stress magnitude is linearly increased to its final value over 5 days of simulation to avoid the creation of inertial oscillations.

The depth-integrated lateral transport can be described by into three individual components, given by:

$$ \left({U}_s,{V}_s\right)=\frac{1}{\rho_of}\left({\tau}_y,-{\tau}_x\right) $$
(15)
$$ \left({U}_{geo},{V}_{geo}\right)=\frac{gD}{f}\left(-\frac{\partial \eta }{\partial y},\frac{\partial \eta }{\partial x}\right) $$
(16)
$$ \left({U}_b,{V}_b\right)=-\frac{d_E}{2D}\left({U}_{geo}+{V}_{geo},{V}_{geo}-{U}_{geo}\right) $$
(17)

where the subscript s refers to the surface Ekman layer, the subscript geo to the geostrophic regime, and the subscript b to the bottom Ekman layer.

2.2 Hydrodynamic case study

This part of the study employs the hydrodynamic COHERENS model (Luyten et al. 1999), which is based on terrain-following (sigma) coordinates. This model is applied with a horizontal grid spacing of 1 km and 10 vertical sigma levels to an idealized oceanic bay (Fig. 1). The bay is 100-km long and 100-km wide, and it has a maximum depth of 50 m. The minimum water depth is set to 10 m along the coasts. The bay deepens to 100 m at its entrance. The water column is devoid of density stratification in the reference simulation. To illustrate the upwelling process, the temperature of seawater deeper than 60 m is lowered by 2 °C in another simulation. A constant horizontal eddy diffusivity/viscosity of 1 m2/s is used. Vertical eddy viscosity is parameterized using the algebraic Pacanowski and Philander (1981) scheme. Eddy diffusivity is assumed the same as eddy viscosity. Note that, for a homogenous density field, this scheme returns an eddy viscosity of A z = 0.01 m2/s. The Coriolis parameter is set to f = −1 × 10−5 s−1. Both A z and f (and, accordingly, d E) are the same as in the one-dimensional water-column model. The ratio δ = D/d E varies from 0.227 in shallower near-shore waters to 1.14 in the bay’s center. Zero-gradient conditions are used for all variables at the western open boundary with the additional assumption that the averaged value of the sea level along this boundary remains the same during the simulations.

Fig. 1
figure 1

Model bathymetry used for the bay simulations. The arrows indicate the wind direction

Full size image

The model is exclusively forced by a uniform wind stress of a magnitude of 0.1 Pa (the same as used in the one-dimensional water-column model). The wind stress is gradually increased from zero to its final value over the initial 5 days of simulation to avoid the creation of unwanted gravity waves and inertial oscillations. Two uniform wind scenarios are discussed in this paper. In the first scenario, the wind blows westward. In the second scenario, the wind direction is changed to northwestward.

Three-dimensional flushing times are calculated to illustrate the exchange between the bay with the ambient ocean. To this end, a conservative tracer of a concentration of unity is introduced after the wind-adjustment period of 5 days to the bay eastward of x = 40 km. The concentration is kept at zero values for x < 40 km. The flushing time for a grid cell is then defined by the time it takes until the concentration has decreased to an e-folding threshold of exp(−1) = 0.368; that is, 36.8 %. Sadrinasab and Kämpf (2004), for instance, have applied this method to the Persian Gulf, and Sandery and Kämpf (2007) to Bass Strait, Australia. In addition, non-buoyant Lagrangian tracers are used to illustrate flow trajectories. For simplicity, diffusive effects on tracer movements are ignored. Luyten et al. (1999) give details on the tracer module.

Indeed, the methodology used here is highly simplified and process oriented. In reality, eddy viscosity is variable and surface buoyancy fluxes in conjunction with density stratification induce a much higher level of complexity than assumed in this work.

3 Results and discussion

3.1 One-dimensional water-column simulations

If the total water depth D substantially exceeds the thickness of the surface Ekman layer, then the wind forcing on its own creates the classical Ekman spiral with a surface flow deflected 45° to the left with respect to the wind direction (southern hemisphere) (Fig. 2a). For δ ≈ 1.4, the frictional influence of the seafloor only slightly modifies the near-bottom structure of the surface Ekman layer, whereas the remainder profile remains largely unchanged (Fig. 2b). The reader may wonder why this modification already starts for δ > 1. The classical Ekman layer thickness is based on an e-folding value of exp(−1) ≈ 0.368; that is, as the depth at which the surface speed of the classical Ekman spiral has dropped by 63.2 %. In fact, there are still substantial flows below this depth, which explains the observed modification. Note that the surface speed slightly increases compared to the deep-water case. More dramatic changes occur once D falls below the thickness of the surface Ekman layer (δ < 1). In this case, the entire flow field aligns more parallel to the wind direction (Fig. 2c).

Fig. 2
figure 2

Vertical structures of the steady-state flows as a function of the ratio (δ) between total water depth and Ekman layer depth. a–c Wind-driven flow components. The arrow indicates the wind direction. d–f Pressure gradient-driven flow components. Stars display the velocity of the geostrophic flow. The arrow indicates the direction of the pressure gradient force

Full size image

For δ ≫ 1, the pressure gradient forcing on its own creates a barotropic geostrophic flow that turns into the classical bottom Ekman spiral near the seafloor (Fig. 2d). For δ ≈ 1.4, most of flow field is already substantially modified, which is different to the wind-driven flow component. The signature of the geostrophic flow is no longer evident in the velocity profile and the surface flow has turned by 30° towards the direction of the pressure gradient force (Fig. 2e). As D falls below the thickness of the bottom Ekman layer (δ < 1), the resultant flow tends to align more parallel to the pressure gradient flow and the speed of the flow markedly decreases (Fig. 2f). As D decreases from δ ≈ 4.5 to δ ≈ 0.7, the pressure gradient-driven surface flow experiences a much more dramatic change in direction (by ~70°) than the wind-driven surface flow, changing only by 28°.

In the deeper water column (δ ≈ 4.5), the surface and bottom Ekman layers are spatially separated, such that an undisturbed geostrophic flow regime can develop (Fig. 3a). In this case, the velocity profiles of both Ekman layers attain exponential vertical structures. In stark contrast to this, the vertical structures of the surface and bottom Ekman are substantially altered in shallower water (Fig. 3b–c). The wind-driven flow tends to establish a constant vertical shear in order to connect the surface boundary condition of a prescribed vertical current shear (Eq. 9) with the no-flow condition at the seafloor (Eq. 10). On the other hand, the pressure gradient-driven flow tries to connect the full-slip (zero-gradient) condition at the sea surface (Eq. 13) with the no-flow condition at the seafloor (Eq. 14). This implies that the vertical structure of the horizontal flow has to have a pronounced curvature. The principally different shapes of wind-driven and pressure gradient-driven velocity profiles imply that full cancelation of the flow components leading to vanishing flow is physically impossible.

Fig. 3
figure 3

Vertical profiles of horizontal speed of wind-driven and pressure gradient-driven flow components for different ratios (δ) between total water depth and Ekman layer depth, with values of a δ = 4.5, b δ = 1.4, and c δ = 0.7

Full size image

We can now consider interference patterns between the wind-driven and pressure gradient-driven flow components for different orientations of the pressure gradient-driven flow. In deeper water (δ ≈ 4.5), the geostrophic flow is well developed below the base of the surface Ekman layer, irrespective of the direction of the pressure gradient force (Fig. 4a). Note that interference between the wind-driven and pressure gradient-driven flows occurs at depths below the vertical reach of the surface Ekman layer. At an orientation of the pressure gradient force of 210°, for instance, the residual flow almost vanishes at the sea surface, and the flow speed increases to the speed of the geostrophic flow at the base of the surface Ekman layer.

Fig. 4
figure 4

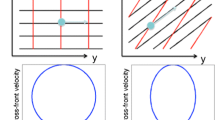
Hodographs of residual horizontal flows for southerly (northward) winds and different orientations (given in degrees) of the pressure gradient force for different ratios (δ) between total water depth and Ekman layer depth, with values of a δ = 4.5, b δ = 1.4 and c δ = 0.7. Arrows show the wind direction. Directions of the pressure gradient force refer to 0° as northward, turning clockwise. Each line refers to a different direction of the pressure gradient force. The endpoint of each curve gives the surface flow. Dashed curves are used for angles of 0°, 90°, 180°, and 270° for visualization purposes. The 180° angle (i.e., pressure gradient force is antiparallel to wind stress force) is highlighted in red

Full size image

Partial or full interference takes place when the surface and bottom Ekman layers partially or fully interfere. For the forcing parameters used, for instance, there is a broad range of directions of the pressure gradient force between 90° and 180° for which the residual flow is roughly parallel to the wind direction in shallower water (δ ≈ 1.4) (Fig. 4b). Moreover, the angle of 180° (the wind stress and pressure gradients are opposite to each other) stands out as it creates an undercurrent running opposite to the surface flow.

In very shallow water (δ ≈ 0.7), the assumed pressure gradient force is too weak to substantially change the direction of the residual mainly wind-driven flow (Fig. 4c). Hence, for a pressure gradient force of the same magnitude and direction, undercurrents may develop in deeper portions of a shelf sea, whereas unidirectional flows develop in the shallower regions. Nevertheless, it should be pointed out that increase of the magnitude of the pressure gradient force in the situation δ ≈ 0.7 can again create an undercurrent (results not shown).

The residual volume transport is the sum of the wind-driven and the pressure gradient-driven volume transports, each being modified by δ and D (the latter influencing the geostrophic transport). Given the linearity of the solutions, the resultant residual transport lies on a circle (where exactly depends on the direction of the pressure gradient force) of a certain radius centered over the endpoint of the wind-driven volume transport vector (Fig. 5a–b). Both the location of the center and the radius of the circle depend on δ, D, and the magnitudes of the wind stress and the pressure gradient force. In the case of δ ≈ 1.4, for instance, the individual volume transports almost cancel each other when both forces are opposite to the each other (Fig. 5a). This situation does not imply that the flow vanishes in the entire water column, which is physically impossible. Instead, there is a wind-driven flow in the surface layer and a counter flow in the bottom layer, each of approximately the same individual volume transports.

Fig. 5
figure 5

Residual volume transports (diamonds) for southerly winds and different orientations of the pressure gradient force for different ratios (δ) between total water depth and Ekman layer depth, with values of a δ = 1.4 and b δ = 0.7. Red circles display the wind-driven transport component. Directions of the pressure gradient force are defined as in Fig. 4. The direction of the pressure gradient force is changed clockwise in steps of 30°. Red arrows show the wind direction. The yellow diamond refers to the case when the pressure gradient force is parallel to the wind stress force

Full size image

In the case of lateral boundaries (coasts), a steady state of the dynamics implies that the depth-integrated flow is aligned parallel to coastlines. Hence, near coastlines, the pressure gradient force has to adjust to a prescribed wind forcing such that the resultant volume transport vector points into the direction of the coastline. It should be highlighted that this situation does not imply that pressure gradients vanish normal to the coast, which is often assumed in hydrodynamic models.

The magnitude of the wind-induced volume transport starts to reduce due to shallow-water effects once the total water depth falls below a value of δ ≈ 1.5 (Fig. 6a). Note that the magnitude of the wind-induced volume transport approximately halves near δ ≈ 1 when compared to the deep-water value. In this situation, the wind-driven transport is still deflected by almost 45o to the left with respect to the wind direction (Fig. 7a). The pressure gradient-driven transport (including the transport carries by the bottom-friction layer) seems to be proportional to the total water depth (Figs. 6b and 7b), but deviations from a linear relationship become apparent in vicinity of the seafloor. However, it is possible to extract bottom-boundary-layer effects from this via subtraction of the theoretical geostrophic transport; that is, U b  = U p  − U geo and V b  = V p  − V geo . This approach reveals the modification of the bottom Ekman layer as D decreases, even though the geostrophic flow does no longer exist. While the geostrophic transport decreases linearly with decreasing D, the seabed friction-driven transport does not decrease until δ < 1 (Fig. 6c) which is a lower threshold than the wind-driven transport has. In this situation, the seabed friction-driven transport starts to align more antiparallel to the theoretical geostrophic transport vector (Fig. 7c), such that the pressure gradient-driven transport is aligned more parallel with the pressure gradient force.

Fig. 6
figure 6

Magnitudes of a wind-driven, b pressure gradient-driven and c seabed friction-driven volume transport as a function of the ratio (δ = D/d E) between total water depth and Ekman layer depth. Vertical bars in (a) and (c) indicate values of δ below which the respective magnitude of volume transports decreases with reference to the deep-water value

Full size image
Fig. 7
figure 7

Steady-state direction and magnitude of a wind-driven, b pressure gradient-driven and c seabed friction-driven volume transport as a function of the ratio (δ = D/d E) between total water depth and Ekman layer depth. The arrow in (a) shows the wind direction. Arrows in (b) and (c) display the direction of the pressure gradient force

Full size image

3.2 Bay simulation

The easterly (westward) wind stress creates westward surface flows in the entire bay with the strongest flows (speed ≈ 1 m/s) developing in shallower regions along the northern and southern coasts (Fig. 8a). Flows along the eastern coast are weak. Due to the initial westward export of water, the resultant steady-state sea-level field slopes opposite to the wind. The steady-state sea-level anomaly at the eastern coast is −0.28 m. The slight asymmetry of pressure contours is the consequence of (week) rotational effects. The resultant pressure gradient force creates undercurrents in deeper portions of the bay, whereas unidirectional, mainly wind-driven coastal jets prevail in shallower waters along the northern and southern coasts (Fig. 8b). This total-depth dependency reflects the situation in Fig. 4b, c in which wind stress and pressure gradients are opposite to each other. These findings are consistent with the evidence of undercurrents in lakes (e.g., Hutter et al. 2014). Near the northeastern and southeastern corners of the model domain, the pressure gradient force slightly changes and facilitates a transition between the eastward undercurrent in deeper water and the westward currents in shallower water.

Fig. 8
figure 8

Steady-state flow field after 5 days of simulation for easterly winds. a Surface currents (maximum speed is 1 m/s; shown are every 6th vector in both directions) and sea level elevations (colors and contours). The arrow indicates the wind direction. b Near-bottom currents (maximum speed in 0.38 m/s) and sine of the angle between near-bottom and surface flows (colors and contours). The white arrow indicates the direction of the pressure gradient force. Black arrows indicate flow trajectories near the northwestern and southwestern corners of the domain

Full size image

The undercurrents operate to rapidly flush most near-bottom water of the bay within times scales <5 days, except for the southern regions of the bay where the flushing takes slightly longer (8–10 days) (Fig. 9a). In contrast, a localized region of rapid flushing of ~5 days appears in surface waters near the northeastern corner of the domain (Fig. 9b). This localized flushing time minimum is the signature of upwelling of near-bottom waters, already flushed into the domain, to the surface. Hence, what we see in this simulation is the classical lee effect (Hela 1976) but occurring in a large oceanic bay over a distance of ~100 km.

Fig. 9
figure 9

Steady-state distribution of flushing times T f (colors and thick lines, days) of a near-bottom water and b surface water for easterly winds. Thin black lines are bathymetry contours

Full size image

When adding colder water to depths below 60 m outside the bay, it becomes apparent that the pressure gradient-driven underflow operates as an upwelling mechanism moving slope-derived sub-surface water largely undiluted (assisted by reduced turbulence levels due to density stratification) across the entire length (100 km) of the bay (Fig. 10a). The region of upwelling of this cold sub-surface water to the sea surface coincides with the area of relatively rapid flushing of surface waters (Fig. 10b, compared with Fig. 9b).

Fig. 10
figure 10

Snapshots of the distributions of temperature anomalies (colors) after 8 days of simulation in a near-bottom water and b surface water for easterly winds. Thin black lines are bathymetry contours

Full size image

A change of the wind direction to southeasterly (northwestward) creates again a situation in which the sea surface tends to slope against the wind direction (Fig. 11a). Variations are seen near the northern and southern coasts, where pressure gradients have to adjust such that the volume transport vector is parallel to the coast. Again, the strongest flows of 1 m/s in speed develop along these coasts. In contrast to the easterly wind scenario, a northward unidirectional flow of moderate speed develops along the eastern coast (Fig. 11b). The resultant pressure gradient force creates undercurrents in deeper portions of the bay. The near-bottom currents are deflected slightly to the left with respect to the orientation of the pressure gradient, which is the signature of the modified bottom Ekman layer. Interestingly, a closed circulation pattern (swirl) of a diameter of 30–40 km appears in near-bottom waters near the northeastern corner of the bay. This closed circulation pattern, only existing in near-bottom waters, becomes evident in the trajectories of Lagrangian particles released in a depth range of 40–50 m in the northwestern corner of the domain (Fig. 12b). In contrast, particles released near the southeastern corner of the bay are upwelled to the sea surface from where they are rapidly moved out of the bay by the swift coastal boundary currents (Fig. 12a).

Fig. 11
figure 11

Same as Fig. 8, but for southeasterly winds as indicated by the arrow in (a). The circle in (b) indicates a closed circulation pattern

Full size image
Fig. 12
figure 12

Trajectories of 1000 Lagrangian drifters released in water depths >40 m near a the south-eastern corner or b the north-eastern corner of the domain. Trajectories extend over a time span of 5 days

Full size image

The undercurrent operates to rapidly flush the bay within time scales of 6 days, except for the northern portion of the bay which is not within the pathway of the undercurrent (Fig. 13a). Consequently, a shadow zone of reduced flushing develops in this region, noting that the circulation around the near-bottom swirl in the northwestern corner of the bay operates as a barrier for flushing. In surface waters, an elongated zone of flushing times ~5 days develops near the southern coast (Fig. 13b). In this wind scenario, the undercurrent leads to upwelling along the southern coast, which becomes apparent in the experiment where colder water is introduced to depths below 60 m outside the bay (Fig. 14a). It should be noted that most of the upwelled water leaves the bay in the surface outflow, while only a reduced fraction continues to spread eastward into the bay (Fig. 14b).

Fig. 13
figure 13

Same as Fig. 9, but for southeasterly winds

Full size image
Fig. 14
figure 14

Same as Fig. 10, but for southeasterly winds. The closed white line in (b) shows the region of pronounced upwelling; the arrow the main export path of upwelled water

Full size image

In reality, eddy viscosity, A z , in the surface mixed layer is strongly linked to the wind stress magnitude (e.g., Fischer et al. 1979; Svensson 1979; Wenegrat et al. 2014). While the models in this study only use fixed values of A z for demonstration purposes, it should be clear that variation of A z (giving Ekman layer thickness) can lead to a lateral shift of the boundary between flow regimes with undercurrents and flow regimes in which the wind-driven flow component prevails.

3.3 When are Ekman layer dynamics significant?

From the above findings, it becomes obvious that Ekman layer effects and the Coriolis force can only be ignored if the total water depth is very small compared to the theoretical Ekman layer thickness. How shallow does a lake or coastal ocean have to be so that Ekman layer dynamics become irrelevant? To address this question, we can take published relationships between wind stress magnitude, τ, and eddy viscosity, A z , in order to derive the Ekman layer depth in relation to total water depth. Previous lake studies, for instance, have adopted relations of the form (e.g., Fischer et al. 1979):

$$ {A}_z={c}_1\sqrt{\tau /{\rho}_o}D $$
(18)

where c 1 is a non-dimensional coefficient. Effler (1996) used a value of c 1 = 0.026 for circulation studies of Onondaga Lake, New York. Note that Eq. (18) includes total water depth D. For oceanic application, eddy viscosity can be estimated from (Svensson 1979):

$$ {A}_z={c}_2\tau /{\rho}_o{\left|f\right|}^{-1} $$
(19)

where c 2 = 0.026. Relation (19) is not applicable at low latitudes. For the near-equatorial Atlantic, Wenegrat et al. (2014)) derived a relationship of

$$ {A}_z={c}_3\tau $$
(20)

where c 3 is approximately 0.113 m2 s-1 Pa-1. Note that Eq. (20) returns a value of ~0.01 m2/s at τ = 0.1 Pa, which corresponds to the setting used in this study. From the relations (18)–(20), we can now estimate the ratio δ as a function of wind stress magnitude, total water depth, and geographical latitude for a reference value of τ = 0.1 Pa. For lakes at mid-latitude (~45° N or S) lakes, for instance, the surface and bottom Ekman layers already separate once the total water depth exceeds 20 m (Fig. 15a). This threshold depth scale changes to 18 m when halving τ or 30 m when doubling τ. Partial interference between the surface and bottom Ekman layers occurs for a range of D between 5 and 30 m. Hence, Ekman layer dynamics can only be ignored when dealing with very shallow (D ≪ 5 m) mid-latitude lakes. In contrast, Ekman layer dynamics are irrelevant for low-latitude (5° N or S) lakes if these are much shallower than ~40 m.

Fig. 15
figure 15

Ratios (δ) between total water depth (D) and Ekman layer depth as a function of D at different geographical latitudes for a wind stress magnitude of τ = 0.1 Pa and using Eq. (18) for a river applications, and Eq. (19) or Eq. (20) for b ocean applications

Full size image

In oceanic application, the transition regime 1 < δ < 2 occurs for total water depths between 20 and 40 m at mid-latitudes. This transition regime shifts to the range 40–85 m at low latitudes (Fig. 15b). The Arafura Sea (located between 5 and 10° S) has total water depths of only 40–50 m (Rochford 1966) and therefore is a likely candidate for the creation of interference-created undercurrents, as identified in this paper.

4 Summary and conclusions

This study focuses on the interdisciplinary boundary of the scientific fields of oceanography and limnology. While the findings are relevant to inland waters, they are also highly relevant for shallow shelf seas at low latitudes, such as those of the Indonesian Seas. The first important finding of this study is that Ekman layer dynamics cannot be ignored in most lakes. Hence, the Coriolis force needs to be included in most river simulations, no matter whether the lake is homogeneous or stratified. Another important finding of this study is that counter flows (undercurrents) appear to be typical circulation features of semi- or fully enclosed homogeneous water bodies. It is obvious from the findings that such wind-opposed undercurrents can only exist in relatively shallow water; that is, when the surface and bottom Ekman layers interfere. An interesting side result is that, in certain situations, undercurrents can trigger the formation of near-bottom swirls possibly acting as a trap for benthic organisms. The third important finding of this study is that the lee effect can operate as an efficient upwelling mechanism in large oceanic bays moving sub-surface water into a bay over large distances (~100 km). The author postulates that such undercurrents were a dominant cross-shelf exchange mechanism globally during geological time period of substantially lower sea levels falling within the range of δ < 2.