A 1D model for tides waves and fine sediment in short tidal basins—Application to the Wadden Sea

Abstract

In order to simulate the dynamics of fine sediments in short tidal basins, like the Wadden Sea basins, a 1D cross-sectional averaged model is constructed to simulate tidal flow, depth-limited waves, and fine sediment transport. The key for this 1D model lies in the definition of the geometry (width and depth as function of the streamwise coordinate). The geometry is computed by implementing the water level and flow data, from a 2D flow simulation, and the hypsometric curve in the continuity equation. By means of a finite volume method, the shallow-water equations and sediment transport equations are solved. The bed shear stress consists of the sum of shear stresses by waves and flow, in which the waves are computed with a depth-limited growth equation for wave height and wave frequency. A new formulation for erosion of fines from a sandy bed is proposed in the transport equation for fine sediment. It is shown by comparison with 2D simulations and field measurements that a 1D schematization gives a proper representation of the dynamics in short tidal basins.

1 Introduction

The Wadden Sea is formed by the dynamic interaction between hydrodynamics, sediment transport, morphology, and biology. The uniqueness of this area of intertidal flats, channel networks, and salt marshes is established by the attribution as a UNESCO world heritage in 2009, requiring preservation of the characteristics of the area. The area is, however, also subjected to anthropogenic activities. A proper understanding of the system from hydrodynamic, morphological, ecological, and biological points of view is a prerequisite to manage the system. In this paper, we consider a specific aspect, namely the modeling of transport of fine sediment.

The presence of fine sediment in the water column and in the seabed has an influence on biota. In the water column, the presence of fine sediment reduces the penetration of light. In general, this leads to a reduction of primary productivity, unless the system is limited by other factors, such as nutrients. This is generally not the case in the Wadden Sea. In the bed, the effect of the presence of fine sediment on biota is not straightforward. Sandy flats dry out quickly as soon as the flat emerges. Flats dominated by fine sediment tend to hold both water and nutrients for much longer when the area is dry, i.e., when light availability is maximal. This is favorable for diatoms and subsequently for other species. Some benthic species have very specific requirements regarding sediment composition, particularly burrowing species that ventilate their burrows. Cozzoli et al. (2013) show that species have a clear preference for a particular type of environment, specifically the sediment composition (mud percentage) and the hydrodynamic stress. Modeling of fine sediments, to give better predictions for the type of habitats, should therefore result in proper estimates for both the concentration in the water column and the fine sediment fraction in the bed.

The basins of the Wadden Sea have been modeled with different types of models. Simplifications are made in box models (Van Goor et al. 2003; Kragtwijk et al. 2004; Maas 1997; Burchard et al. 2008), where a basin is schematized into a few connected entities. On the other side of the spectrum, process-based models are applied in two or three dimensions (Elias et al. 2006; Dastgheib et al. 2008; Stanev et al. 2007). As stated by Townend (2010), each type of model is suited for a specific combination of processes, temporal and spatial scales. The simple models give a fast, but aggregated result. The process-based models give a high level of detail, but the results are sometimes difficult to interpret and take long computation times. There is also a range of models in between, like 2D simulations with simplified geometries (e.g., Marciano et al. 2005) or 1D simulations.

We have chosen to continue the development of 1D models to simulate the transport of fine sediments, specifically aiming at representing the concentration in the water column and the mud fraction in the bed. Previous work has shown that such an approach can capture the dominant processes at low computational costs. However, several shortcomings of previous modeling studies have to be overcome. A hydrodynamic module to simulate the tidal flow forms the basis of the model. The first 1D simulations of tidal flow in the Wadden Sea were carried out by Lorentz (1926). These simulations were done to determine the effect of the closure of the Zuiderzee by the Afsluitdijk. By means of the simplified 1D momentum equation (inertia, pressure gradient, and linearized friction) and the continuity equation, the water levels and velocities were calculated for a network of channels. Each channel consisted of maximum four parallel subchannels with different widths and depths. Intertidal areas were taken into account as subchannel, implying no direct interaction with the neighboring channel(s). The flow on the intertidal flats is parallel to the flow in the channel. This makes transport from the channels to the tidal flats difficult. The model of Lorenz can be regarded as one of the first applications of the divided channel method. Another classical approach is described by Dronkers (1964) and further elaborated on by Savenije (2005). The basin is divided in channels and flats. The momentum equation is solved for the channels only. The intertidal flats are accounted for by considering them as storage area (additional width) in the continuity equation, implying that the flow on the intertidal flats is (approximately) perpendicular to the flow in the channel. Such an approach is especially suitable for long tidal basins. Although the flow in the channels can rather well be simulated, no flow information is available at the intertidal flats. For the simulation of the dynamics of fine sediment, these areas are, however, of importance.

In more recent studies, the basin is schematized to a 1D channel with constant (in time) and uniform (in space) width (Schuttelaars and de Swart 2000; Van Leeuwen et al. 2000; Van Ledden 2003; Ter Brake and Schuttelaars 2010). As mentioned by Ter Brake and Schuttelaars (2010), such a uniform width is a crude assumption. This has consequences for the flow. For example, the Frisian inlet of the Wadden Sea is schematized by Van Leeuwen et al. (2000) and Ter Brake and Schuttelaars (2010) to a rectangular basin with a width of 2 km and a length of 20 km. The storage area is then 40 km². In reality, the total storage area (including intertidal flats) is approximately 300 km². As a result, the tidal volume is much smaller than the real volume, implying an underestimation of the velocities at the mouth. Van Leeuwen et al. (2000) give a velocity amplitude at the mouth of approximately 0.3 m/s, whereas the velocities should be in the order of magnitude of 1 m/s (see Postma (1961)). This affects the erosion rates and sediment transport, as these scale with the velocity to a power larger than 1. A new geometry therefore requires a nonuniform width to simulate the tidal volume and the velocities in the mouth correctly.

The abovementioned previous studies with 1D models on sediment transport and morphology in the Wadden Sea consider only tidal flow as forcing for sediment transport. This was partly done because their focus was on the sediment transport in the channels. In case of a forcing with an M2 and an M4 tide in combination with suspended sediment transport, no equilibrium is found for morphological simulations. Mud accumulation is found in the simulations of Van Ledden (2003) at the land side of the basin, and the basin length decreases. As the tidal forcing decreases to zero at the land side of the basin, a deposition area develops. These self-stimulating processes continue until the mud content reaches 100 % and, in case of morphodynamic simulations, until the bed level reaches the maximum water level. In reality, the bed shear stresses do not reduce to zero at the land side of the basin. Waves result in high bed shear stresses, especially on the tidal flats. These high bed shear stresses cause erosion, which can keep the basin open.

The largest part of the Wadden Sea consists of a sandy seabed with a low fraction of mud (< 10 %). The formulations for the erosion rate of fines from such a bed are still very empirical. An erosion rate formulation has been derived by Van Kessel et al. (2011), by multiplying van Rijn’s erosion rate formulation for sand (Van Rijn 1984) with the mud fraction in the bed. However, the calibration parameter for the erosion rate was required to be significantly lower than the one proposed by van Rijn. As the availability of measurements is limited, it is not aimed in this paper to focus on the development of a new erosion rate formulation. However, some more insights and an improvement is required.

Summarizing, several 1D models have been proposed for the simulation of hydrodynamics and sediment transport in short tidal basins. Most models for short tidal basins (a) use a uniform width, which leads to underestimation of the basin area and therefore underestimation of the velocities, and (b) do not take into account the effects of waves. In this paper, we therefore primarily aim at improving the schematization, in such a way that both the tidal volume and the tidal velocities are properly simulated. Furthermore, we account for the effects of waves in the erosion formulation for sediment transport as far as possible in a 1D schematization. In this way, we aim at modeling the concentration of fines in the water column and the mud fraction in the bed with an accurate, but efficient, model.

2 Geometry

2.1 Model area: Vlie Basin in the Wadden Sea

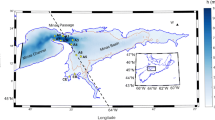
The Wadden Sea consists of a series of connected mesotidal basins (see Fig. 1a). The total Wadden Sea stretches from the Dutch coast, via the German coast, to the Danish coast. The basins are separated from the North Sea by barrier islands. However, through the openings in between the island water, sediment and other suspended or dissolved matter exchanges between the North Sea and the Wadden Sea. Characteristic for the basins is that they are relatively shallow and consist of a large part of intertidal areas that fall dry at low water. This makes them attractive habitats for various species.

Fig. 1

a Bathymetry of the Vlie Basin for 2007. The contour −1.3 m is the low water spring (LWS) level, indicating the separation between intertidal flat and channel. The contour +1 m is the high water spring (HWS) level. Almost the complete area is below this level. The x- and y-coordinates are based on the Rijks Driehoeken coordinates and represent the distance to Paris. The locations refer to suspended sediment sampling stations Vliestroom (VS) and Blauwe Schenk (BS), water level station WL, and wind station W . b Hypsometric curve (bed level as function of the submerged area) of the Vlie Basin with lines for HWS and LWS

In this paper, we only consider the Vlie Basin, the third basin from the west. This basin is hardly influenced by river discharges, so density-driven flow is expected to be negligible. Note that density-driven flow due to rainwater might be of importance (see Burchard et al. (2008)). Furthermore, this basin has a clear dendretic structure and is not elongated. As will be described later on, these characteristics are prerequisites for the proposed schematization. The bathymetric map is given in Fig. 1a and the hypsometric curve in Fig. 1b. The basin has an area of approximately 660 km², which is debatable as the Vlie Basin is connected to the Marsdiep Basin (southwestern neighbor). Since the building of the Afsluitdijk, the Marsdiep Basin is expanding (Wang et al. 2013). A clear definition of the watershed is therefore difficult. Here, the definition as used by the Dutch Ministry of Public Works is used. The semidiurnal tide varies between NAP −1.3 m (LWS) and NAP + 1.0 m (HWS) during spring tide and NAP −0.95 m (LWN) and NAP + 0.65 m (HWN) during neap tide. The reference datum NAP stands for Normaal Amsterdams Peil or Amsterdam Ordnance Datum. This implies that 350 km² falls dry at low water spring and 250 km² during low water neap (in case of a uniform water level in the basin). Almost the complete area is below mean sea level (650 km²).

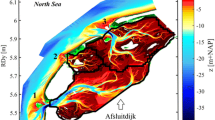
Figure 2 gives a map of the mud fraction in the bed of the Wadden Sea. The sediment characteristics for the inter- and supra-tidal areas are measured within the Synoptic Intertidal Benthic Survey (SIBES) project (see Kraan et al. (2010)). The bed of the Wadden Sea consists mainly of sand with a low fraction of fines. More than 80 % of the total area has a mud fraction smaller than 10 %. Peaks above 50 % are found along the borders, mainly at the Frisian coast in the southeast. Possible seasonal differences are not considered, as all the measurements have been carried out in summer.

Fig. 2

Map of the mud fraction in the Vlie Basin, based on the SIBES measurement campaign (Kraan et al. 2010). The contour line gives the LWS level. Unfortunately, no measurements are available in the deeper channels

2.2 From 2D basin to 1D basin

The key to a sound simulation of the tidal flow in short tidal basins is the determination of the geometry. It is aimed to meet the following requirements: (a) the hypsometry of the 1D schematization equals exactly the real hypsometry (submerged area as function of the bed level); (b) the width at the mouth in the 1D schematization equals the width of the channel at the mouth; and (c) the length of the 1D basin should be in the order of magnitude of the diameter of the basin. These criteria are essential for a proper simulation of the tidal flow. The 1D basin is defined by the width W and bed level η as function of the streamwise coordinate s. As the streamwise coordinate s is not known a priori, we start with the determination of the hypsometric curve. Then, the width is determined as function of the submerged area A. Finally, s is set as it follows directly from A and W , resulting in the geometry of the 1D basin.

The hypsometric curve is obtained from the measured 2D bathymetry. A submerged area A _n (η _n ) is determined for the area with a bed level η smaller than η _n , where the index n refers to the volume number. Figure 1b shows the hypsometry of the Vlie Basin. The hypsometric curve is discretized into N cells which have a width W _n , length Δs _n , and area a _n = W _n Δs _n . The width and length are not known yet, and the submerged area is defined by $A_{n}=\sum a_{n}$. The width is determined as a function of the submerged area, by means of substitution of the results of a 2D flow simulation into the continuity equation. The conservation equation can be written for each cell by the following:

$$ \frac{\mathrm{d} V_{n}}{\mathrm{d}t} = Q_{n-\frac{1}{2}} - Q_{n+\frac{1}{2}} $$

(1)

or

$$ a_{n} \frac{ h_{n}^{i+1} - h_{n}^{i}}{\Delta t}=(uWh)_{n-\frac{1}{2}} - (uWh)_{n+\frac{1}{2}} $$

(2)

with discharge Q, time t, and time step Δt. A staggered grid is used with the fluxes defined at the faces at $n\pm \frac {1}{2}$. The index i refers to the sequence in time. If the depth and velocities would be known, the width can be determined. These data (h and u) are obtained from 2D simulations. In principle, only two subsequent maps of the velocity and water depth are sufficient to determine the width, but we use the average over several tides.

An existing 2D simulation of the Wadden Sea is used, within the model package Delft3D. Details of the numerical model are given by Lesser et al. (2004). The grid and calibration are described by Borsje et al. (2008). The full model contains all Dutch basins and a large part of the North Sea. We only use the results of the Vlie Basin here. In order to implement the results of the 2D simulation into Eq. 2, the 2D information has to be transformed into the 1D schematization. This operation is similar to the determination of the hypsometric curve. All computation cells from the 2D simulation are ordered by the bed level and related to the volumes as used in the conservation equation. Per 1D volume, a number of 2D grid cells and related depths and velocities are found. In such a way, the averaged depth and absolute velocity per 1D volume can be determined. The direction of the flow from a 2D simulation is not trivial to transform to the 1D schematization. We assume that the flow always follows the same path, implying a constant streamline. Our 1D schematization therefore follows the streamline.

Per volume, the median and the 25th and 75th percentile values are determined. Figure 3 shows a snapshot of the transformed results. Fifty percent of the data (dots) is in between the (dashed) lines representing the 25th and 75th percentiles. A 1D approach would be perfectly valid if all velocities and water levels per bin would collapse on the median value (solid line). This is obviously not the case. Potential causes are discussed later. However, there is a clear trend in both the water level plots and the velocity plots, giving sufficient confidence for the application of a 1D schematization.

Fig. 3

a Water levels as function of the submerged area. The dots represent the water levels at each grid cell within the Vlie Basin at a certain time. The solid line represents the median value, and the dashed lines are the 25th and 75th percentiles. The thick solid line is the bed level. b Absolute velocity (see a for definition of lines and markers)

Now, the water levels and velocities are determined as functions of the submerged area, and the width can be determined, using the continuity equation. Resolving the width from the continuity equation requires a boundary condition, either at the mouth side or the land side. We have chosen to impose the width at the land side. This gave better convergence properties than imposing the width at the mouth side, as the width is much smaller at the mouth than at the land side. The width at the landside (or watershed in case of bordering another basin) should approximately be equal to the perimeter of the basin. For the Vlie Basin, the perimeter is determined at 80 km. The resulting width as a function of the storage area is plotted in Fig. 4. As for each cell, the width is determined and the length can be defined by Δs _n = a _n / W _n , resulting in the streamwise coordinate s. The bed level η and width W can now be mapped onto the streamwise coordinate s. The total length of the 1D basin (22 km) and the width at the mouth (2 km) follow from these settings. Both values are well in the expected range. A bird’s-eye view of the 1D basin is given in Fig. 5. The basin is narrow and deep at the mouth, representing the channels. At the other end (land or watershed), the basin is wide and shallow, representing the intertidal flats. A striking agreement is found with the sketch as given by Van Straaten and Kuenen (1957) (see Fig. 5c). Unfortunately, they gave no further explanation on how they obtained this figure, except that “It shows that the water which oscillates with the tides between the inlets and the shores and watersheds is alternately spread out horizontally over the shallow inner parts, at high tide, and piled up in high, narrow prisms in the deeper parts in or at least closer to the tidal inlets, at low tide.”

Fig. 4

Width as function of the storage area. The green lines represent the widths obtained from implementation of different instantaneous velocity and depth maps into Eq. 2. The blue line represents the median of the green lines. The red lines indicate the 25th and 75th percentiles. The black line is the fit used in the 1D simulations

Fig. 5

a Bed level η (solid line) on the left axis and width W (dashed line) on the right axis as function of the streamwise coordinate (s). b Bird’s-eye view of the resulting geometry. Note that both the vertical axis and the streamwise axis are elongated compared to the transverse axis. c Sketch of a tidal basin by Van Straaten and Kuenen (1957)

No further simplification is made for the width or bed level as a function of the submerged area. It is, however, striking that the width increases almost linearly with the submerged area for the subtidal area z < −1.3 m), and that the width is almost constant for the intertidal area (z > −1.3 m). Another notable relation is the almost linear increase of the bed level as function of the streamwise coordinate for the subtidal range (s = 1.5 − 15 km). The obtained geometry implies a very strong variation in width and bed level. The width at the intertidal areas is approximately 40 times as large as at the mouth. Furthermore, the width at the watershed is approximately four times as large as the length of the basin. Also, the bed level changes significantly from − 35 m at the mouth to above the mean sea level at the watershed/land.

2.3 Assumptions and implications

The geometry of the 1D basin has been explained, without mentioning the underlying assumptions and consequences. The first assumption is already made by assuming that the bed level is continuously increasing from the mouth into the basin. This is a direct consequence of aligning the 1D basin along the hypsometric curve. In general, this assumption is reasonable, as the depth at the mouth is larger than on the tidal flats, close to the watersheds. In more detail, deviations are found. For example, the deepest point does not lie in the mouth, but somewhat more into the basin. Furthermore, shallow areas are found close to the mouth, and deep areas are found close to the land. The implicit assumption of a correlation between the distance to the mouth and the bed level is then violated.

The 1D basin can be interpreted by considering the real basin as a self-similar structure of channels. The system starts at the mouth with a narrow deep channel and splits into several branches. A branch can only connect to a branch which is one order higher or lower. All branches of the same order have the same shape (width, bed level, and length), although the cross section does not necessarily have to be uniform in streamwise direction. The branching continues until the landside is reached and the full area is covered. We can now identify a number of streamlines, equal to the number of the smallest branches. They all come together at the mouth. Aligning all these branches gives the geometry of the 1D basin. Although the Wadden Sea basins have a fractal structure, as determined by Cleveringa and Oost (1999), the above assumptions are not fully fulfilled. As indicated by Cleveringa and Oost (1999), the fractal structure is valid for the length scales larger than approximately 500 m. For smaller scales, no clear fractal structure was found. In reality, the branches are not always strictly ordered. Short cuts of small channels dewatering on large channels are especially found close to the mouth. The branches are also not all equal in width, length, and bed level. Another implicit assumption of 1D models is that the ebb flow follows the same path as the flood flow. In reality, this is not the case. It is expected that the flood flow is not always following the channel pattern nor the ebb flow. Those circulation can not be accounted for in 1D models.

These assumptions limit the use of such a schematization to dendretic short tidal basins. A simple check can be made by considering the relation between the bed level and the distance to the mouth (along a streamline). If there is no such a relation, the schematization is not valid. Examples are elongated estuaries with channels and bordering tidal flats. In those cases, the schematization of Savenije (2005) is more suitable.

3 Hydrodynamics

3.1 Tides

In the previous chapter, the geometry of the 1D basin is defined. A 1D finite volume model is set up for the shallow water equations, based on the discretization of Stelling and Duinmeijer (2003). The flow can then be simulated by imposing a boundary condition at the mouth and a closed wall at the land side. In order to calibrate the model, it is run for the same conditions as the 2D model. The water level fluctuations as found at the mouth of the basin from the 2D simulation are imposed (see Fig. 6). In order to compare the 1D results with the 2D results, the 2D results are transformed as a function of the submerged area A (see Section 2.2). We use the median water levels and median absolute velocities for comparison.

Fig. 6

a Time series of the water level at the mouth (black) and at A = 300 km² for the 2D simulation (blue) and the 1D simulation (red). b Time series of the streamwise velocity. The sign of the velocities from the 2D simulations is based on the minimum absolute velocity and the sign of the change in water level

The only parameter left for calibration is the bed friction coefficient. The Manning formulation is used with coefficient n [s m^−1/3], consistent with the 2D simulations. For calibration, the mean values and amplitudes of the tidal constituents of the water level and flow velocity are determined. The constituents M2 and M4 are extracted by means of a harmonic analysis with T-TIDE (see Pawlowicz et al. (2002)). A period of only 2 days is considered. This period is sufficient for calibration of the 1D model.

The best results were obtained with a Manning value of n = 0.031 s m^−1/3. This value is higher than the value used in the 2D simulations n = 0.022 s m^−1/3. The friction term in the 1D simulation does not only represent the bed friction. It also includes all kinds of other momentum losses due to, e.g., turbulent exchange between channels and intertidal areas. It is therefore not surprising that the friction coefficient in the 1D model is higher than in the 2D simulations.

A first impression of the performance of the 1D model is shown in Fig. 6. At A = 300 km²(z = −1.2 m), the water level is shown. A spin-up period of a few hours is required. Both the phase and amplitude of the 1D simulation are in agreement with the 2D simulation. The velocity is also fairly well represented by the 1D model. The strongest deviations are found for the low water periods. For these periods, local processes play an important role. It is noted that the sign of the velocity of the 2D simulations is not known. Therefore, the sign is determined by using the minimum absolute velocity and the change in water level. A positive change in water level should correspond to a positive velocity (flood).

Figure 7a shows the mean value and the amplitudes of semidiurnal fluctuation (referred to by M2) and quarter-diurnal fluctuation (M4) for the water level. Going into the basin, the M2 amplitude decreases as a consequence of bed friction. Especially at the far end, the amplitude drops. This is a direct consequence of flooding and drying. The sinusoidal oscillation is truncated at low water. The mean water level is increasing. During ebb, the dewatering of the intertidal areas is strongly slowed down by friction. The amplitude of M4 decreases until A ≃ 300 km², which coincides with the low water level. Truncating the lower levels of an M2 dominated signal induces an M4 component, explaining the increase in M4 amplitude. The phases of M2 and M4 for the water level are given in Fig. 7b. The M2 phase slightly increases, resulting in a phase shift of approximately 1 h at the end of the basin for the 2D results. The 1D results show a larger phase shift, namely approximately 1.7 h. The M4 phase shows a remarkable change around A ≃ 300 km². As explained above, this can be ascribed to the drying from this position on.

Fig. 7

Tidal constituents of the aggregated 2D results (markers) and of the streamtube model (solid line), as function of the submerged area A. Two constituents are shown: M2 (□) and M4 (*). The mean value is plotted with (○). a Water level amplitude. b Water level phase. c Velocity amplitude. d Velocity phase

The 1D model results in a mean seaward velocity. This can be explained by the estuarine Stokes drift due to the phase difference between the water level and velocity of the M2 tide (see Dyer and Soulsby (1988)). The M2 amplitude decreases strongly from the mouth into the basin. The 1D model is well capable of representing the spatial distribution as follows from the 2D simulations. The amplitudes are, however, somewhat underestimated for A ≃ 0 − 150 km² and A ≃ 450 − 650 km². The M2 phase of the velocity of the 2D simulation is uniform, whereas a slight increase up till half an hour is found till A ≃ 300 km² for the 1D results. The phase shift increases continuously for the M4 component up till approximately 6 h. This shift is well represented by the 1D model.

Concluding, the spatial variation of both the amplitudes and phases of tidal components is well reproduced by the 1D model. This subscribes the validity of the assumptions made for the schematization of the geometry.

3.2 Waves

The 1D schematization reduces the possibilities for wave modeling. Where it is reasonable to assume that the flow follows the channel pattern, this is generally not the case for waves. The wave direction is often in the same direction as the wind. A method that neglects the wave direction therefore has to be adopted. We use the formulations of Young and Verhagen (1996), relating the dimensionless wave height to the dimensionless depth. According to Young and Verhagen (1996), the dimensionless wave energy for fetch-limited wave growth in an area with finite depth is determined by the following:

$$ \frac{g^{2} E}{U_{10}^{4}}=3.64 \times 10^{-3} \left(\tanh A_{1} \tanh \left[\frac{B_{1}}{\tanh A_{1}}\right]\right)^{1.74} $$

(3)

with

$$\begin{array}{@{}rcl@{}} A_{1}&=&0.493 \left(\frac{gh}{U_{10}^{2}} \right)^{0.75}\\ B_{1}&=&3.13 \times 10^{-3} \left(\frac{g F}{U_{10}^{2}} \right)^{0.57}\\ E&=&\frac{1}{16}H_{s}^{2} \end{array} $$

and with U ₁₀ as the wind speed at a height of 10 m and h as the averaged water depth over fetch length F. Due to the complexity of the bathymetry of the Wadden Sea basins, it is intrinsically difficult to determine h and F as these will not be constant, nor uniform. The formulation is, however, not very sensitive to the depth and fetch. Waves are mainly effective at shallow water, as the bed friction scales nonlinearly with the depth. Prediction of waves at larger depth is therefore not essential. Following from Eq. 3, the smaller the depth, the smaller is the influence of the fetch length. Figure 8 illustrates the effect of water depth and fetch length on the wave height. If we first consider the thick lines for a fetch of 5 km, we can state that the influence of a difference in depth (1 or 3 m) is small. The influence of the fetch increases with water depth. Taking a constant fetch of 5 km overestimates the wave height for a fetch of 1 km with approximately 30 % and underestimates the wave height with a fetch of 20 km with approximately 30 % for a depth of 3 m. For smaller depths, these values are smaller—overestimation of approximately 15 % and underestimation of approximately 25 %. In this paper, we consider a uniform fetch of 5 km.

Fig. 8

Wave height as function of the wind speed, according to Eq. 3. The red lines represent the relations for a water depth of 3 m and the blue lines for a depth of 1 m. The thick lines indicate the lines with a fetch of 5 km (as used in further simulations); the thin lines of 1, 2, 10, and 20 km. Waves break for Hs / h > 0.7

Similar to the wave energy, the peak frequency f _p can be estimated based on Young and Verhagen (1996):

$$\begin{array}{@{}rcl@{}} \frac{f_{p} U_{10}}{g}&=&0.133 \left({\tanh} A_{2} {\tanh} \left[\frac{B_{2}}{{\tanh} A_{2}} \right] \right)^{-0.37} \end{array} $$

(4)

with

$$\begin{array}{@{}rcl@{}} A_{2}&=&0.331 \left(\frac{gh}{U_{10}^{2}} \right)^{1.01}\\ B_{2}&=&5.215 \times 10^{-4} \left(\frac{gF}{U_{10}^{2}} \right)^{0.73} \end{array} $$

3.3 Bed shear stress

The total bed shear stress is a combination of the bed shear stress by waves (τ _w ) and by flow (τ _f ). Following Van Rijn (1993), the time-averaged bed shear stress for waves is defined by the following:

$$\begin{array}{rll} \tau_{w} &=& \frac{1}{4}\rho_{w} f_{w} U_{\delta}^{2} \\ U_{\delta}&=&\frac{\pi H}{T \sin kh} \end{array} $$

(5)

with water density ρ _w , friction coefficient f _w , orbital velocity at the bed U _δ , wave height H, wave period T, wave number k, and depth h. The friction coefficient is based on the grain size of the sediment only. The bed shear stress for flow is determined by the following:

$$\begin{array}{@{}rcl@{}} \tau_{f} &=& \frac{1}{2}\rho_{w} f_{f} u^{2} \end{array} $$

(6)

with friction coefficient f _f , which is also based on a Nikuradse roughness of k _s = 2.5d ₅₀. Both bed shear stresses are vectors and should be added accordingly. The direction of the flow and waves is, however, reduced to one direction. The bed shear stress is therefore added, implying that this is an overestimation of the real total bed shear stress:

$$ \tau=\tau_{w}+\tau_{f} $$

(7)

The bed shear stress due to waves is determined by imposing the wind speed, as measured at Terschelling (see Fig. 1). Equations 3 and 4 are used for the determination of the wave height and period and Eq. 5 for the bed shear stress. The tidal flow is simulated by imposing the water level as measured close to the mouth (see Fig. 1) and implemented in Eq. 6. Figure 9 shows the results of the bed shear stress due to currents and waves, separately and summed. The bed shear stress in the deeper parts, the channels, is dominated by the tidal flow. Further into the basin, the bed shear stress by currents decreases as the velocity decreases there as well (see Fig. 7). The bed shear stress by waves is small in the channels, as the waves do not penetrate to the bed. On the shallower part, the waves dominate. The total bed shear stress shows a maximum in the channel, due to the tidal current contribution. Further into the basin, the tidal shear stress reduces, and the shear stress due to waves increases. It is worth to notice that the total bed shear stress becomes almost uniform for A > 100 km². Friedrichs and Aubrey (1996) reported that a uniform maximum bed shear stress is linked to an equilibrium condition. This is, however, not further elaborated in this paper.

Fig. 9

Bed shear stresses as function of the distance from the mouth: median values for waves only (blue), median values for tidal flow only (red), median values for waves and tidal flow (black)

4 Fine sediment dynamics

Fine sediments play an important role in in the ecology of the Wadden Sea. In suspension, the sediment particles reduce light penetration, leading to less primary production. The mud fraction in the bed influences the permeability and the water content, which are important for many benthic species. We therefore aim with these computations to simulate the suspended sediment and the sediment fraction in the bed. Compared to previous 1D fine sediment simulations of the Wadden Sea (Van Ledden et al. 2004), several improvements are made. As mentioned in the previous parts of this paper, the tidal flow is better simulated with the newly proposed geometry, and waves are taken into account. In this chapter, we also propose a modified definition for the erosion rate formulation.

4.1 Model setup

The dynamics of fine sediments are determined by the transport equation for suspended sediment and the mass balance equation of sediments in the bed. As we consider a 1D schematization with spatially varying width and bed level, we write these equations in the conservative form:

$$ \frac{\partial W h c}{\partial t} + \frac{\partial Qc}{\partial s} - \frac{\partial}{\partial s} \left(\epsilon W h \frac{\partial c}{\partial s} \right) = W(E - D) $$

(8)

$$ \frac{\partial m}{\partial t} = D - E $$

(9)

with width W , water depth h, depth-averaged concentration c, time t, discharge Q, spatial coordinate s, diffusion coefficient 𝜖, erosion rate E, deposition rate D, and sediment mass per area in the active bed layer m. Based on the mass of fine sediment in the active layer, the mud fraction in the bed p _m is determined. The mud fraction or fine sediment fraction (p _m ) is defined by the mass of fine sediments divided by the total mass in the active layer. The total mass in the active layer is defined by the volume times the bulk density (ρ _b = ϕ _s ρ _s ), which is based on the sediment volume ϕ _s and the sediment density ρ _s . The mud fraction is then defined by p _m = m / (ρ _b δ∗), with δ∗ the active layer thickness. The bulk density ρ _b and the active layer thickness are considered constant and uniform. The deposition rate is defined as follows:

$$ D = \alpha w_{s} c $$

(10)

$$ w_{s} = a \left(\frac{c}{c_{0}}\right)^{b} $$

(11)

α represents the ratio between the concentration at the bed and the depth-averaged concentration. Although this ratio depends on the velocity and the particles, we adopt a simple constant value: α = 2.5. The settling velocity stems from Stanev et al. (2007) and is assumed to be dependent on the concentration. The concentration c ₀is an arbitrary concentration to obtain convenient dimensions for the parameters a and b and is set to c ₀ = 1 kg m⁻³. Many combinations of a and b are used in literature. An overview is given by Pejrup and Mikkelsen (2010), showing that the values can vary approximately two orders of magnitude. The values will be determined later.

The relatively low mud fractions ( < 10 %) (see Fig. 2) imply that the fines are in the pores of the sand skeleton. We assume that the fines do not travel through the pores within the bed, and that erosion of fines takes place only due to erosion of sand. This approach is comparable to the one used by Van Ledden (2003) and Van Kessel et al. (2011). The erosion of sand is hardly influenced by such a small mud fraction. Erosion of the mud fraction is then fully determined by the erosion of sand.

Generally, the sand flux due to bed-load transport is defined by Fernandez Luque and Van Beek (1976):

$$ E_{b}=\frac{q}{L} $$

(12)

with transport capacity q (in kilogram per meter per second) and length scale L. In many papers on sand transport (like those of Fernandez Luque and Van Beek 1976 or Van Rijn 1984), the saltation length is used for L, which is in the order of magnitude of O(10 − 100)d ₅₀. This erosion rate can, however, not be used in our case. We are interested in the time scale needed to erode the typical active layer. This first requires a definition of the active layer thickness. We take the layer with bed ripples as active layer. These have a length of approximately λ = (500 − 1,000)d ₅₀ ≈ 0.1– 0.2 m and a height of approximately δ = (50 − 200)d ₅₀ ≈ 0.0075 – 0.03 m for d ₅₀ = 150μm (see Van Rijn (1993)). Let us consider an area with length λ and arbitrary width. The sediment mass per width in the bed is then defined as follows:

$$ m_{\lambda}=\rho_{b} \delta_{\ast} {\lambda} $$

(13)

with m _λ as the sediment mass per width for length λ, ρ _b as the bulk density, and δ∗ as the representative layer thickness, taking into account the shape of the bed forms. The time needed to refresh the sand in this area is defined as follows:

$$ T=\frac{\rho_{b} \delta_{\ast} {\lambda}}{q} $$

(14)

The erosion rate is now determined by:

$$ E_{b}= \frac{\rho_{b} \delta_{\ast} {\lambda}}{T \lambda} = \frac{q}{\lambda} $$

(15)

Instead of the saltation length, the length of the ripples is determining the erosion rate. We can now define the erosion rate for the mud fraction as follows:

$$ E_{m}= p_{m} \frac{q}{\lambda} $$

(16)

The difference between the erosion rate based on the saltation length and the one based on the bed form length is that the first one can be considered as a gross erosion rate, whereas the second one is the net erosion rate for ripples. Ripples are not the only bed forms in estuarine environments. Megaripples and sand dunes are also found. These could be considered in a similar way. As the length scales of the bed forms are much larger (1–100 m), the erosion rates will be much smaller. They are therefore not considered here, although they start playing a role for simulations over larger periods. A single bed layer is assumed in this paper to keep the number of parameters as low as possible. In a later stage, a multilayer approach can be applied.

Finally, the bed-load transport capacity needs to be specified. Many formulations are derived in the past. Here, we use the method of Ribberink (1998), derived for waves and currents:

$$ q= \sqrt{\Delta g D_{50}^{3}} \gamma (\theta-\theta_{c} )^{n} $$

(17)

with relative density Δ = ρ _s − ρ _w / ρ _w ; shield parameter $\theta =\frac {u_{\ast }^{2}}{\Delta g D_{50}}$ and critical value indicated with _c ; and coefficients γ = 10.4 and n = 1.67. The final erosion rate for fine sediments then reads as follows:

$$ E_{m}= \frac{p_{m}}{\lambda} \sqrt{\Delta g D_{50}^{3}} \gamma (\theta-\theta_{c} )^{n} $$

(18)

In order to run the model, boundary conditions have to be imposed at the mouth and at the landside. At the land side, no sediment passes. At the mouth, a concentration has to be set for incoming flow. By defining a constant mud fraction in the bed, the equilibrium concentration (deposition = erosion) is determined. In this way, storms and tidal fluctuations can be accounted for, although in reality, processes in the ebb-tidal delta will influence the concentration at the mouth for incoming flow.

4.2 Parameter settings

Two data sets are available to calibrate the model: suspended sediment concentrations and mud fractions in the bed. Suspended sediment measurements are available at two locations (Vliestroom and Blauwe Schenk; see Fig. 1) with a relatively low frequency, approximately once per month. Samples are taken 1 m below the water surface. These data are part of the MWTL data set ( www.waterbase.nl). The sediment distribution in the bed is given in Fig. 2.

In order to run the sediment module, several parameters have to be set: layer thickness δ∗; the ripple length λ for the erosion flux; a and b for the deposition flux; and the diffusion coefficient 𝜖. The bed layer thickness δ∗ = 15 mm and the ripple length λ = 0.2 m are based on typical dimensions of ripples. The settling velocity parameters a = 0.017 m s⁻¹ and b = 1.33 are chosen equal to the values used by Stanev et al. (2007). The diffusion coefficient 𝜖 = 100 m² s⁻¹ is chosen similar to the values used by Ter Brake and Schuttelaars (2010). This parameter represents a number of mixing processes as we have reduced the complex bathymetry to a relatively simple 1D channel. The model is run with a real-time forcing over a complete year (2007). This implies that the measured water level (intervals of 10 min) at the entrance is imposed as boundary condition, and the hourly measured wind speed is used for the wave forcing. At the mouth, a mud fraction of 1 % is imposed. Table 1 gives an overview of the parameters and their values for the reference run.

Table 1 Parameter settings and boundary conditions for the model for fine sediment dynamics

Additional to the reference run, simulations are carried out to determine the sensitivity of the model. Specifically, we determine the sensitivity of the model to the length and height of the considered bed forms. The length λ is directly influencing the erosion rate. Sensitivity runs with λ = 0.4 m and with λ = 0.1 m are made. The height represents the thickness of the active layer δ∗ and influences the active sediment mass in the bed. Additional simulations are carried out for active layer thicknesses δ∗ = 7.5 mm and δ∗ = 30 mm.

4.3 Results and discussion

Time series of the concentrations are plotted in Fig. 10 for the locations Vliestroom and Blauwe Schenk, at respectively s = 1 km and s = 15 km. Fluctuations in concentration are found due to the semidiurnal tides and the spring–neap cycle. The tidal pattern is most clear in the deeper part Vliestroom, as the bed shear stresses due to tides dominate. Storms result, however, in peak values in the concentrations. At the shallower location (Blauwe Schenk), the concentrations are more influenced by wave forcing, giving a more scattered response due to fluctuations in wind speed. The measured concentrations of fine sediment are measured at low frequency. Unfortunately, no high-frequency measurements are available for the concentrations. The measurements are therefore not sufficient to verify the processes over time scales of hours to days. However, the modeled and measured concentrations are in the same order of magnitude. High concentrations in shallow areas and low concentrations in the deeper parts are also found by Postma (1961) for the basin Amelander Zeegat. Mechanisms due to tidal asymmetry as described by Van Straaten and Kuenen (1957) bring fines to the shallow flats. This is also reflected in the mud fraction in the bed, shown in Fig. 11. Based on the measurements of the SIBES campaign (Kraan et al. 2010), the measured mud fraction is plotted as function of the submerged area. The median value is plotted, as well as the 25th and 75th percentiles. This scatter is largely caused by nonuniformity in space. For locations with the same bed level, different mud fractions are found. This could be ascribed to the spatially varying exposure to waves. The modeled mud fraction is given as well in Fig. 11. The modeled mud fraction is of the same order of magnitude as the measured median value. The measured distribution shows a more pronounced peak at the intertidal flats.

Fig. 10

Time series of the suspended sediment concentrations at Vliestroom (a) and Blauwe Schenk (b). See Fig. 1 for the locations. The continuous line represents the model results; and the markers represent the measurements ( www.waterbase.nl)

Fig. 11

Mud percentage in the bed as function of the submerged area A. The measurements (blue) are obtained from the results as shown in Fig. 2. The median value is indicated with the blue solid line. The spatial variation is indicated with the 25th and 75th percentiles by means of the dashed blue lines. There are no measurements available for the deeper part (until 250 km²). The modeled mud fraction in the bed is indicated for simulations with length scales of λ = 0.1 m (black), λ = 0.2 m (red), and λ = 0.4 m (green)

The model makes use of a relatively simple erosion rate formulation with the length scale λ as calibration parameter. The parameter λ is therefore containing all uncertainties in the erosion rate formulation. Changing the erosion rate has a direct effect on the erosion rate and affects the mud fraction in the bed. The larger the length scale, the smaller is the erosion rate, and the higher is the mud fraction in the bed. This is shown in Fig. 11. The mud fraction for the simulation with a length λ = 0.4 m gives an increase of the mud fraction. The concentration also shows an increase. The effect of the difference in λ is therefore partly compensated by the concentration and the mud fraction in the bed.

The thickness of the active layer δ∗ does not lead to a significant change in the mean concentration or mud fraction. As shown in Fig. 12, the thickness of the layer results in more intense short-term fluctuations. The smaller the thickness, the smaller is the mass in the active layer and the faster is the response of the mud fraction to deposition and erosion fluxes. This behavior can also be deduced from the mass balance equation of the active layer. A dynamic equilibrium is found when erosion balances with deposition, averaged over a certain period: 〈D〉 = 〈E〉. The bulk density and layer thickness determine the time scale to reach the equilibrium. If the system is in dynamic equilibrium, the bulk density and the layer thickness determine the magnitude of the fluctuations around the dynamic equilibrium. As the fluctuations of the mud fraction in the bed are small compared to the equilibrium value, no significant nonlinear interactions are found. The long-term averaged mud fraction in the bed is therefore hardly dependent on the thickness of the layer. Note that a similar way of reasoning is used for morphodynamic modeling by Roelvink (2006) to derive the morphological factor.

Fig. 12

Mud percentage in the bed at A = 350 km² as function of time. The model results are shown for a period of 2 years for simulations with active layer thicknesses of δ* = 0.075 m (red), δ* = 0.15 m (black) and δ* = 0.3 m (green)

Although the simulated concentration and mud fraction in the bed are in reasonable agreement with the measurements, there are several reasons for a discrepancy between the model and reality. One of the main assumptions of the model is a direct relation between the distance to the mouth and the variables depth, concentration, mud fraction, wave forcing, etc. No spatial variation is considered in that sense. As already indicated, there is a spatial variation for locations with the same distance to the mouth (or same depth). High mud fractions are, for example, found in the southeastern part of the Vlie Basin, close to the Frisian coast. These areas are less exposed to waves, as the dominant wind direction is from the southwest. This directly shows the limitation of the schematization in which the forcing is uniform for a certain bed level. Local wave action, leading to variation in forcing for equal bed levels, can not be accounted for. Uniform and constant values are used for the critical bed shear stress, active layer thickness, and ripple length. In reality, these will be dependent on flow and/or wave magnitudes and local sediment properties. Furthermore, biological effects could be of importance. On the muddier flats, critical shear stresses can become higher by the development of biofilms, or benthic fauna can increase the active layer thickness (Montserrat et al. 2008).

5 Conclusions and recommendations

A new way of schematizing a complex tidal basin into a 1D basin is proposed. The key lies in the definition of the width as function of the streamwise coordinate. The proposed method ensures that the 1D basin has the same hypsometry as the real basin, which is a prerequisite for a proper modeling of the tidal volume. The resulting geometry can be seen as a quantification of the sketch as suggested by Van Straaten and Kuenen (1957). We emphasize that the proposed method is only suitable for short tidal basins with a clear dendritic channel structure. In longer basins, there is no relation between the bed level and the distance to the mouth (along a streamline).

The determination of the width as function of the streamwise coordinate requires the results of a 2D simulation. Although this is a restriction for “unexplored” tidal basins, 1D models will often/always be used in combination with 2D simulations. The 1D model can be used as quick tool or for long-term simulations, whereas the 2D model will be applied to obtain higher accuracies. A possible way to circumvent the use of a 2D model is the determination of the bed level as function of the streamwise coordinate, by following the fractal structure. This is, however, not further elaborated here.

Although the waves are simulated with a relatively simple model, reasonable results are obtained. It is shown that waves dominate the bed shear stress in shallow areas. Subsequently, neglecting the waves will significantly reduce the bed shear stresses and therefore the sediment dynamics at the intertidal flats. Reduction of waves results in an increase in mud fraction in the bed. The areas with very high mud contents (> 40 %), as found in the measurements, could be explained by less wave exposure. As a uniform wind direction and fetch length is assumed in this model, such spatial variations could not be accounted for. Further analysis of 2D wave simulations could reveal a better representation of the wave-induced bed shear stress.

Fine sediment dynamics are simulated with empirical relations for the erosion and deposition rate. The erosion rate formulation is defined by dividing the bed-load transport formulation by a length scale. Contrary to previous studies, the length scale is not based on the saltation length of a grain, but on the length scale of bed forms. Although this length scale still needs calibration, the order of magnitude is in reasonable agreement with the length scales of bed forms. Further testing of the underlying hypothesis by comparison with laboratory experiments and/or field measurements is necessary to improve the proposed concept for erosion of fine sediment from a sandy bed. Improvements could also be made in the definition of the bed layer thickness. A uniform value was used here, where bed layer thicknesses could be based on bed shear stresses. Deposition was computed by a relatively simple formulation for the settling velocity. The formulation includes effects of increased flocculation for higher concentrations. Breakup of the flocs is, however, not taken into account.

The complexity of the 1D model is in between the complexity of basin-integrated models, like ASMITA, and 2D/3D models, like Delft3D, ROMS, or GETM. The level of detail of the results is therefore also in between—more detailed differentiation of the results over the basin compared to results of box models—but site-specific results can not be obtained. The 1D-model can therefore be applied to determine the response of the basin on large-scale interventions, but is less applicable for small-scale local interventions.

In conclusion, a 1D model schematization for short tidal basins is built, based on physically sound schematizations, that gives a proper representation of tidal flow and sediment dynamics. The model gives direct insights in the variation of bed shear stresses, suspended sediment concentrations, and mud fractions in the bed.