Effects of bottom slope, flocculation and hindered settling on the coupled dynamics of currents and suspended sediment in highly turbid estuaries, a simple model

Abstract

This study aims at gaining basic understanding about two specific phenomena that are observed in the highly turbid estuaries tidal Ouse, Yangtze and Ems, i.e. (1) the accumulation of suspended matter in the deeper parts of the estuaries and (2) the relatively high values of turbidity near the surface in the area of the turbidity maximum. A semi-analytical model is analysed to verify the hypothesis that these phenomena result from bottom slope-induced turbidity currents and from hindered settling, respectively. The model governs the dynamics of residual flow, driven by fresh water discharge, salinity gradients and turbidity gradients. It further uses the condition of morphodynamic equilibrium (no divergence of net sediment transport) to compute the residual sediment concentration. New aspects are that depth variations on flow and mixing processes, as well as flocculation and hindered settling of sediment, are explicitly accounted for. Tides act as a source of mixing and erosion of sediment only, thus processes like tidal pumping are not considered. Model results show that the estuarine turbidity maximum (ETM) shifts in the down-slope direction, compared to the case of a constant depth. Slope-induced turbidity currents, which are directed down-slope near the bottom and up-slope near the surface, are responsible for this shift, thereby confirming the first part of the hypothesis above. The down-slope shift of the ETM is reduced by currents resulting from gradients in depth-dependent mixing, which counteract turbidity currents, but which are always weaker. Including flocculation and hindered settling yields increased surface sediment concentrations in the area of the turbidity maximum, compared to the situation of a constant settling velocity, thereby supporting the second part of the hypothesis. Sensitivity experiments reveal that the conclusions are not sensitive to the values of the model parameters.

1 Introduction

Estuarine turbidity maxima (ETMs) are found in many estuaries (see examples in Schoellhamer 2001; Brenon and Le Hir 1999; Uncles et al. 1999; de Jonge 2000). In some of these estuaries, suspended sediment concentrations (hereafter SSC) of more than 10 kg m^-3 are observed (cf. Allen et al. 1980; Uncles et al. 2002). Large concentrations of suspended matter in estuaries have a big impact on the environment. Since suspended sediment contains organic material, which consumes oxygen, high SSC values in the water will decrease the oxygen available for lifeforms (cf. Lin et al. 2006; Talke et al. 2009b). Large navigational problems for ships can occur when sediment is transported into harbour areas and settles there (Wurpts and Torn 2005; Jiang et al. 2012). Thus, knowledge about the processes causing spatial shifts and/or intensification of turbidity maxima is important for proper management of estuaries.

It was argued by Postma (1967) that the location and intensity of turbidity maxima depend on the amount of suspended material, the settling velocity of suspended sediment and the estuarine circulation. A quantitative numerical study on the mechanisms behind the ETM was carried out by Festa and Hansen (1978). They considered the dynamics of sub-tidal flow in an estuary with constant width and depth. Forcing of the flow is due to prescribed salinity and concentration values on the upstream and downstream boundaries and a prescribed fresh water discharge. Tides are only parametrically accounted for, in the sense that they set the constant values of the eddy viscosity and eddy diffusion coefficients. Moreover, they cause local erosion of sediment that balances local settling. In general, these coefficients depend on tidal flow, distance to the bed and the Richardson number (Bowden and Fairbairn 1952; Burchard et al. 2008). The numerical solutions obtained confirm the qualitative arguments of Postma (1967). Later studies demonstrated there are many more processes that affect the formation of turbidity maxima. Examples of these processes are barotropic tidal velocity asymmetry (Allen et al. 1980; Chernetsky et al. 2010; Huijts et al. 2011), velocity asymmetries induced by asymmetry in tidal mixing caused by tidal straining (Jay and Musiak 1994; Scully and Friedrichs 2003), longitudinal variations in cross-sectional area (Lin and Kuo 2001) and flocculation and hindered settling (Winterwerp 2002, 2011). Flocculation will cause an increase in the settling velocity due to an increase in particle size. At high concentration, the settling of sediment will become hindered, due to the large amount of particles, and thus the settling velocity will decrease.

Despite all these processes, the study of Festa and Hansen (1978) reveals that it is possible to gain fundamental insight into the major characteristics of ETM by employing simple models that are based on ’classical estuarine scaling’ of which the concepts were developed by Hansen and Rattray (1965). This means that effects of tides are only accounted for by suitable choices of turbulent mixing and sediment erosion coefficients. Adopting the simple model approach, as outlined above, Talke et al. (2009a), hereafter T09, developed a diagnostic, analytical model, in which they investigated the influence of flow generated by density gradients due to both salinity and SSC on the spatial distribution of SSC. They found that turbidity currents induced by horizontal gradients in SSC explain the observed asymmetrical distribution of SSC (steep gradients on the seaside, weaker gradients on the river side) in the highly turbid Ems estuary. At the same time, their model cannot explain why observations in highly turbid estuaries show elevated concentrations of SSC in deeper parts of the estuary and why the observed SSC at the surface are higher than computed. The postulate that will be investigated in this paper is that there are two potential reasons for these discrepancies. First, allowing for variations in depth will induce bottom slope-induced turbidity currents, and according to measurements (Schoellhamer 2001), the latter affect the location of the ETM. The depth variations will also cause variations in values of eddy viscosity and eddy diffusivity. Second, allowing for hindered settling is crucial to explain the observed high turbidity values near the surface. The approach adopted in this study follows the concepts of ‘exploratory modelling’, as explained by Murray (2003), in which the focus is on explaining observed phenomena, rather than on quantitative prediction.

Therefore, in Section 2, a new model will be derived that accounts for depth variations, spatially varying mixing conditions and for flocculation/hindered settling. The model is designed to gain fundamental understanding about ETM dynamics in highly turbid estuaries, of which three of them will be discussed: the Ems, the tidal Ouse and the Yangtze. In Section 3, results will be presented, followed by a discussion (Section 4) in which the role of other processes, like tidal pumping, will be assessed. The final section contains the conclusions.

2 Field data and Model

2.1 Field sites

2.1.1 Ems estuary

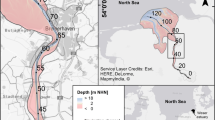
The Ems estuary is located in the north-east of the Netherlands and the north west Germany (Fig. 1a). The total length of the estuary is approximately 100 km, when measured from the island Borkum to the weir near Herbrum. The main inflow of freshwater is from the Ems River, with a mean discharge of 100 m³s^-1. The seaward border of the estuary is formed by the Wadden Sea. The water depth varies in the part seaward of Emden between 10 and 20 m, while the landward part has an average depth of 7 m. The estuary has a typical tidal range of 3.5 m around Emden, which increases in the upstream direction. The Ems estuary is characterised by high concentrations of suspended sediment. Up until 1984 only dredging activities have taken place to maintain the water depth of the Ems. Due to the increase of the size of the cruise ships made in Papenburg since 1984, three dredging campaigns have taken place to deepen the Ems estuary. Since then, maximum concentrations of suspended sediment in the Ems estuary have increased up to 30 kg m^-3 near the bed (de Jonge 2000, T09). Measured distribution of salinity and turbidity during ebb and flood tide are shown in Fig. 2 a,b.

Fig. 1

Geographic setting of the studied estuaries. a Map of the Ems estuary; b map of the tidal Ouse; and c map of the Yangtze estuary. Note: in b and c, the sea is at the right. Blue lines represent transects over which salinity and turbidity measurements are performed, of which the results are displayed in Fig. 2. For the Yangtze estuary, the North Passage of the estuary is studied. Large blue circles represent the location of the 0 km locations for these figures

Fig. 2

Salinity and turbidity measurements for the Ems (T09) (a and b), tidal Ouse (Uncles et al. 2006) (c and d) and the North passage of the Yangtze estuary (Liu et al. 2011) (e and f). a: Measured salinity (top) and turbidity (bottom) during ebb tide on the 2nd of August 2006. b: as a, but during flood tide on the 2nd of August 2006. c Measured salinity (bottom) and turbidity (top) during high water for the tidal Ouse on the 20th of March 1995. d: as c, but during high water on the 18th of August 1995. Note that here, the salinity intrusion is larger than in the previous panel due to a small freshwater discharge. e: salinity for the Yangtze estuary on the 20th of August 2005 during low water slack and the turbidity (bottom) at early flood measured a day earlier. f: as e, but on the 20th of August 2005 during high water slack and the turbidity at early ebb measured a day earlier

2.1.2 Tidal Ouse

The tidal Ouse is part of the Humber system, which is located on the east coast of England (Fig. 1b). The tidal Ouse discharges freshwater into the Humber estuary, with an average rate of 130 m³s^-1 (Uncles et al. 1999). The tidal Ouse is about 60 km long, measured from the weir near Naburn to the apex near Blacktoft. The average tidal range is 4.8 m at the apex and reduces to half of that at the weir near Naburn. The concentrations of suspended sediment in the Ouse estuary are high and show a strong variation with seasons and tidal conditions (Mitchell et al. 2003; Uncles et al. 2006), as is illustrated in Figure 2 c,d.

2.1.3 Yangtze estuary

The Yangtze estuary is located on the east coast of China near the city of Shanghai (see Fig. 1c) (Liu et al. 2011) and is characterised by multiple channels. The present model will be applied to the North passage of the Yangtze estuary, which on average discharges 5,000 m³s^-1 of fresh water originating from the Yangtze river to the South China Sea. The estuary has a tidal range of 4 m at the mouth. In the area, dredging maintains the depth of the main channel. These interventions have resulted in significant morphological changes as well as in the formation and intensification of turbidity maxima (Liu et al. 2011; Jiang et al. 2012). Measured salinity and turbidity patterns around high and low water slack tide are shown in Fig. 2e,f.

2.2 Model

2.2.1 Momentum and mass balance

A semi-analytical model is designed to gain insight in the dynamics of sub-tidal flow and sediment transport in a highly turbid estuary. As was motivated in the introduction, the model solves sub-tidal flow and distribution of suspended sediment in an idealised estuary (Fig. 3). A Cartesian coordinate system is used, of which the origin is located at the undisturbed water surface at the seaside. The x-axis points in the upstream direction, i.e. from sea (on the left) towards the river (on the right). The z-axis points vertically upward. The depth h(x) and width b(x) in the longitudinal direction can be chosen arbitrarily. The upstream boundary of the estuary is located at x = L; this is the location where the salinity vanishes. This can either be at a weir (i.e. for the Ems) or at the limit of salt intrusion. The cross section is assumed to have a rectangular shape. The equations governing the water motion are similar as those used by Hansen and Rattray (1965) and T09. The main differences are that here arbitrary depth and width profiles can be selected and that vertical eddy viscosity and eddy diffusivity depend on depth. The momentum equation governing the tidally and width-averaged sub-tidal velocity in the along-estuary direction is given by

$$ 0=-g\int_z^0\frac{\partial \rho}{\partial x}dz'-g\rho_0 \frac{d\eta}{dx}+\frac{\partial}{\partial z} \left\{ \rho_0 A_v \frac{\partial u}{\partial z}\right\}. $$

(1)

In this equation, u is the local along-channel velocity component of the water, $\rho$ the local density of the fluid, $\rho _0$ the density of fresh water and A _v is the vertical eddy viscosity coefficient. The surface elevation with respect to the undisturbed water level z = 0 is given by $\eta$. Finally, g represents the local acceleration due to gravity. The momentum equation describes a balance between the baroclinic pressure force, which is induced by density differences, the barotropic pressure force, which is induced by a spatial variation of the surface slope, and the internal friction force. The following constraint, which is derived from the continuity equation, states that the integrated horizontal velocity over a cross section is equal to the discharge of fresh water,

$$ \int_{-h}^0ub dz=Q. $$

(2)

Here, Q is the freshwater discharge, which has a negative value since the water is transported in the seaward direction. Strictly speaking, the upper bound in the integral in Eq. 2 should read $\eta$, but the rigid-lid approximation ($\| \eta \|<<h$) allows it to be replaced by the undisturbed free surface level. At the bottom, a no-slip condition is applied which means that there is no horizontal motion at the bottom, thus

$$ u\big\vert_{z=-h}=0. $$

(3)

Furthermore, a no-stress condition is applied at the surface:

$$ \rho_0 A_v \frac{\partial u}{\partial z}\big\vert_{z=0}=0. $$

(4)

Hence, effects of wind are neglected.

Fig. 3

Overview of the modelled situation. The upper panel shows a top view and the lower panel shows a side view. Note that the sea is at the left, as in all subsequent figures. The origin is located at the water surface on the seaside. In the figure u is the along-channel component of the flow, C the sediment concentration and $z=\eta$ the location of the free surface. The rigid-lid approximation means that sea surface elevation is negligible with respect to local water depth, but gradients in the sea level (inducing a pressure gradient force) are maintained

2.2.2 Density

The local density is described by the following expression:

$$ \rho=\rho_0+\beta S+\gamma C, $$

(5)

where S is the salinity and C is the SSC by mass. In this equation, the density change per salinity unit is given by $\beta \sim 0.83~$kgm^-3psu^-1. The coefficient $\gamma =(\rho _s-\rho )/\rho _s \simeq 0.62$, in which $\rho _s$ (~2650 kgm^-3) is the density of the suspended material. The salinity is assumed to be a given function of the longitudinal coordinate and to be constant over the vertical (well mixed conditions). The longitudinal salinity profile is modelled, following Warner et al. (2005), as

$$ S(x)=0.5S_*\left\{1-\tanh\left(\frac{x-x_c}{x_L}\right)\right\}, $$

(6)

in which S _* is the salinity at sea, x _c is the location of the maximum salinity gradient and x _L is the length scale on which the salinity varies.

2.2.3 Sediment mass balance and morphodynamic equilibrium

The sediment mass balance expresses a balance between settling and vertical turbulent diffusion of sediment:

$$ w_s C + K_v \frac{\partial C}{\partial z} = 0, $$

(7)

with corresponding boundary condition

$$ C=C_b\quad\mathrm{at}\quad z=-h(x). $$

(8)

In Eq. 7, w _s is the settling velocity of sediment particles, and K _v is the vertical eddy diffusion coefficient. The value for bottom concentration C _b is determined by application of the condition of morphodynamic equilibrium

$$ \int_{-h(x)}^0\left(uC-K_h\frac{\partial C}{\partial x}\right)dz=0 $$

(9)

for all x in which K _h is the horizontal eddy dispersion coefficient. This condition states that there is no net sediment transport through any estuarine cross section (cf. Friedrichs et al. 1998).

2.2.4 Formulation for mixing coefficients

When the water depth decreases, also the mixing length in the water decreases. The reason for this behaviour is that the size of turbulent eddies which provide for mixing in the water becomes smaller. The reduced mixing leads to a decrease in eddy viscosity and eddy diffusivity in the fluid. In the present study, the effect of depth change on the vertical eddy viscosity and diffusion coefficients is taken into account. A mathematical formulation for this dependence is presented in Friedrichs and Hamrick (1996). This leads to the power law

$$ A_v(x)=A_{v0}\tilde{h}(x)^n, $$

(10)

in which A _v0 is the viscosity coefficient at the water depth at the origin H, and $\tilde {h}(x)$ is the local water depth scaled with the water depth at the origin. Parameter n is the power of the depth dependence. Friedrichs and Hamrick (1996) suggested that n should have a value which ranges between 1 and 1.5. Schramkowski and de Swart (2002) found that for the Western Scheldt, $n=1.28\pm 0.48$. In the model, the vertical eddy diffusion coefficient has the same dependency on the local water depth as that of the vertical eddy viscosity coefficient,

$$ K_v(x)=K_{v_{0}}\tilde{h}(x)^n. $$

(11)

The horizontal dispersion coefficient k _h in Eq. 9 is assumed to be a constant.

2.2.5 Formulation for settling velocity

In this study, it is assumed that the settling velocity of suspended sediment depends only on the bottom concentration of suspended sediment (C _b ). This means the near-bed SSC is assumed to be representative for the concentration of suspended sediment in the whole water column. Consequently, the settling velocity will depend on distance x to the seaward boundary. This is a first, crude assumption to account for cohesive properties of the sediment. Following Mehta (1984), the dependence of the settling velocity on the bottom concentration is divided in three regimes. In the first regime, the concentrations are low and the settling velocity is constant, i.e.

$$ w_s=w_{s_{low}}\; \mathrm{ for: }\;\;C_b(x)< 0.3~\mathrm{kgm}^{-3}. $$

(12)

Here, $w_{s_{low}}$ is the settling velocity for sediment particles at low concentrations. In the second regime, flocculation dominates. The relation between the bottom concentration of suspended sediment and settling velocity for this regime is given by

$$ w_s=d_1\,C_b(x)^{\alpha_w }\;\; \mathrm{ for: } \;\; 0.3~\mathrm{kgm}^{-3}<C_b(x)<3.5~\mathrm{kgm}^{-3}. $$

(13)

Here, d ₁ is a constant which depends on the composition of sediment and is empirically determined. In the third regime, hindered settling dominates and the expression for the settling velocity in this regime reads

$$ w_s=w_{s0}\,(1-d_2C_b(x))^{\beta_w}\;\; ;\;C_b(x)>3.5~\mathrm{kgm}^{-3}, $$

(14)

in which d ₂, the floc volume per kilogramme of suspended sediment, has a value of 0.008 m³ kg^-1, $\beta _w= 5$ and w _s0 a reference settling velocity. Values for d ₁ and $\alpha _w$ follow by imposing that w _s is continuous in C _b .

2.3 Explicit solutions and expressions

First, an explicit solution is derived for the sediment mass balance (7). Using boundary condition (8), it reads

$$ C(x,\zeta)=C_b(x)\exp\Big(-Pe_v(x)\big(\zeta+\tilde{h}(x)\big)\Big), $$

(15)

in which $\zeta =z/H$ is a scaled vertical coordinate. Furthermore,

$$ Pe_v(x)=w_s(x)H/K_v(x) $$

(16)

is the local Péclet number, which describes the ratio between the water depth at the origin and the typical thickness of the sediment layer, $K_v/w_s$ at a specific location. Note that, because vertical eddy diffusivity can be written as $K_v\sim k u_* H$, with u _* the friction velocity and k a constant, it follows that $Pe_v= (w_s)/(k\, u_*)\equiv R$, where R is the Rouse number.

Next, the solution for the sub-tidal flow in the estuary is derived. This is done by substituting Eqs. 5 and 15 in the momentum (Eq. 1). The momentum equation is subsequently integrated twice with respect to the vertical. Then, by using volume constraint (Eq. 2), the following expression for the horizontal velocity is found:

$$ \begin{array}{rll} u&=&\underbrace{\frac{g\beta H^3}{48\rho_0 A_v(x)}m_1(\zeta,x)\frac{ds(x)}{dx}}_{\mathrm{Salinity~gradient~flow}}\\ &&+\underbrace{\frac{g\gamma H^3}{48\rho_0 A_v(x)}m_2(\zeta,x)\frac{dC_b(x)}{dx}}_{\mathrm{Turbidity~gradient~flow}}\\ &&+\underbrace{\frac{g\gamma H^3}{48\rho_0 A_v(x)}m_3(\zeta,x)\frac{d\tilde{h}(x)}{dx}C_b(x)}_{\mathrm{Gravitational~turbidity~flow}}\\ &&+\underbrace{\frac{3Q}{2b(x)H\tilde{h}(x)^3}(\tilde{h}(x)^2-\zeta^2)}_{\mathrm{Discharge}}\\ &&-\underbrace{\frac{g\gamma H^3}{48\rho_0 A_v(x)}m_4(\zeta,x)\frac{1}{K_v(x)}\frac{dK_v(x)}{dx}(x)C_b(x)}_{\mathrm{Mixing~gradient~flow}}\\ &&+\underbrace{\frac{g\gamma H^3}{48\rho_0 A_v(x)}m_4(\zeta,x)\frac{1}{w_s(x)}\frac{dw_s(x)}{dx}(x)C_b(x)}_{\mathrm{Settling~velocity~gradient~flow}} \end{array} $$

(17)

In this expression, functions $m_{\#}$ depend on the along-estuary coordinate x and scaled depth, of which the formulations of these expressions are given in Appendix. In Eq. 17, the first and the fourth term describe the classic tidally averaged formulation of the water flow, as discussed by Hansen and Rattray (1965). The second term describes the flow induced by longitudinal variations in density caused by variations in the bottom concentration. This turbidity gradient term was first described by T09. The third term is new and describes the flow induced by longitudinal variations in the density caused by variations in water depth. The fifth and sixth are also new and represent the flow induced by longitudinal changes in the vertical diffusivity and the flow induced by longitudinal changes in the settling velocity, respectively. By inserting Eq. 17 in the morphodynamic equilibrium condition (Eq. 9) and elaborating this expression, the following differential equation for the bottom concentration is obtained:

$$ \begin{array}{rll} 0&=&\underbrace{\frac{-T_s g\beta H^3}{48\rho_0 A_v(x)}\frac{ds}{dx}C_b(x)}_{\mathrm{Salinity~gradient}}+\underbrace{\frac{3T_Q Q}{2b(x)h(x)}C_b(x)}_{\mathrm{Freshwater~discharge}}\\ &&-\underbrace{\frac{T_t\gamma H^3}{48\rho_0 A_v(x)}\frac{dC_b}{dx}C_b(x)}_{\mathrm{Turbidity~gradient}}-\underbrace{\frac{T_hg\gamma H^3}{48 \rho_0 A_v(x)}\frac{d\tilde{h}(x)}{dx}C_b(x)^2}_{\mathrm{Bottom~slope}}\\ &&-\underbrace{\frac{T_{p}g\gamma H^3}{48 \rho_0 A_v(x)}\frac{1}{K_v(x)}\frac{dK_v(x)}{dx}C_b(x)^2}_{\mathrm{Mixing~gradient}}\\ &&+\underbrace{\frac{T_{p}g\gamma H^3}{48 \rho_0 A_v(x)}\frac{1}{w_s(x)}\frac{dw_s(x)}{dx}C_b(x)^2}_{\mathrm{Settling~velocity~gradient}}\\ &&-\underbrace{T_{K_h} K_h(x)\frac{dC_b}{dx}}_{\mathrm{Dispersion~by~the~turbidity~gradient}}\\ &&-\underbrace{T_{hK_h} K_h(x) \frac{d\tilde{h}(x)}{dx}C_b(x)}_{\mathrm{Dispersion~by~the~bottom~slope}}\\ &&-\underbrace{T_{pK_h} K_h(x)\frac{1}{K_v(x)}\frac{dK_v(x)}{dx}C_b(x)}_{\mathrm{Dispersion~by~the~mixing~gradient}}\\ && +\underbrace{T_{pK_h} K_h(x)\frac{1}{w_s(x)}\frac{dw_s(x)}{dx}C_b(x)}_{\mathrm{Dispersion~by~the~settling~velocity~gradient}}. \end{array} $$

(18)

Expressions for $T_{\#}$ are given in Appendix. The first six terms represent the transport of suspended sediment by all terms of the momentum (Eq. 17). The last four terms represent the dispersion caused by density variations of suspended sediment. These density changes are caused by variations in the bottom concentration (term 7), variations in water depth (term 8), longitudinal changes in the vertical diffusivity (term 9) and longitudinal changes in the settling velocity (term 10). Equation 18 is a non-linear differential equation for the bottom concentration (C _b ). It extends the one by T09 in the sense that the new mechanism yield additional non-linear terms that scale with $C_b^2$. The constraint used is that the total amount of sediment which is available for transport in the system is given (cf. Friedrichs et al. 1998). The total amount of suspended matter in the estuary reads

$$ M_{C_b}=\int_0^L b(x) \int_0^1C_b(x)\mathrm{exp}(-Pe_v(x)(\zeta+\tilde{h}(x)))Hd\zeta dx. $$

(19)

The constraint is used that $M_{C_b}=M_{tot}$, where $M_{tot}$ is derived by evaluating Eq. 19 with a constant bottom concentration ($C_b(x)=c_*$). Parameter c _* is an average bottom concentration, which is used as a tuning parameter. Solutions are obtained by numerically solving differential Eq. 18 from the mouth to the head of the estuary, starting from an arbitrarily chosen bottom concentration at the mouth. The starting concentration at the mouth is updated after each iteration by comparing the total modelled mass of suspended sediment with M _tot . This method is repeated until the modelled total mass of the suspended sediment in the estuary is equal (within a relative error of 1 %) to M _tot .

3 Results

The model derived in Sections 2.2–2.3 will now be applied to the three estuaries discussed in Section 2.1. To model these estuaries, smoothed versions of their bottom profiles shown in Fig. 2 are used, and model parameters are chosen to represent the respective estuaries. For the width profile, an exponential decreasing profile is used, i.e.

$$ b(x)=B_0\exp\left(-\frac{x}{\alpha_b}\right), $$

(20)

in which $\alpha _b$ is the e-folding length of the estuary width. An overview of the used model parameters is presented in Table 1.

Table 1 Model parameters and their representative values for the three estuaries

3.1 Longitudinal distribution of SSC

The effect of the added processes described in the previous section on the modelled longitudinal distribution of SSC is now investigated. This is done by turning off the added processes one after another. For each model result, the modelled near-bed concentration is compared with the observed near-bed concentration. This is first done for the Ems estuary, of which the used depth and salinity profiles are shown in Fig. 4a. In Fig. 4b, the modelled longitudinal and vertical distribution of suspended sediment is shown for the default case in which vertical mixing coefficients depend on depth and the settling velocity depends on concentration. The calculated distribution of SSC shows a strong increase in concentration towards the salt toe in the upstream direction until a near-bed concentration of 11 kg m$^{-3}$ at ($\tilde {x}\sim 0.75$); after which, the concentration gradually decreases. Near the upstream boundary, the concentration reduces again to zero. Next, in Fig. 4c, the longitudinal distribution of SSC pattern is shown for a model run in which a constant settling velocity is used ($w_{s_0}$), so no flocculation and hindered settling. The pattern resembles that the default case, albeit some of the suspended sediment is pushed seaward. Furthermore, the suspended sediment is located closer to the bed. In Fig. 4d, the depth dependence of the mixing length is also switched off. Here, the longitudinal distribution in SSC shows a peak in suspended sediment at the upstream side of the area with high SSC. The vertical distribution of SSC reveals that less sediment is found near the bed and higher SSC are found higher up in the water column. Finally, in Fig. 4e, the result of a model run is shown in which variations in depth are switched off and we return to a flat bed. Compared to the previous results, the turbidity maximum is located more upstream. The vertical distribution of suspended sediment is similar to Fig. 4c, i.e. small values higher up in the water column.

Fig. 4

Modelled distribution of suspended sediment in the $\tilde {x}$-$\zeta$ plane for the Ems estuary with the different additions to the model on and off. Top panels show the depth and salinity profiles that represented the Ems estuary. In b, all additions to the model are switched on. In c, the concentration-dependent settling velocity is turned off. In d, both the depth dependence of the mixing length and the concentration-dependent settling velocity are switched off. In e, depth-dependent mixing is switched off and a constant depth is assumed

The longitudinal distribution of the SSC is modelled for both the tidal Ouse and the north passage of the Yangtze estuary; results are shown in Fig. 5. The model results are compared with those retrieved by a model setting that assumes a constant depth $H$ and constant settling velocity. The model results for the tidal Ouse are shown in Fig. 5c for the present model and in Fig. 5e for the case that $H$ and w _s are constants. A large upstream shift in the turbidity maximum occurs when the new effects are accounted for. Furthermore, higher concentrations of SSC are found at larger distance from the bed. Results for Yangtze estuary for the two different configurations (all new processes switched on, versus the case that $H$ and w _s are constants) are shown in Fig. 5d, f. Here, similar results are found as for the Ems estuary. The turbidity maximum becomes more pronounced, and higher concentrations are observed at large distances from the bed.

Fig. 5

The modelled distribution of suspended sediment for the tidal Ouse (left-hand panels) and the North Passage of the Yangtze estuary (right-hand panels). Top panels show the depth and salinity profiles used. Middle panels show the modelled suspended sediment concentration in the $\tilde {x}$-$\zeta$ plane for the model with all additions switched on. Bottom panels show the modelled suspended sediment concentration in the $\tilde {x}$-$\zeta$ plane using a constant depth

3.2 Sensitivity analysis

Our results show that our newly added processes confirm our results that adding these lead to better representation of the observations. The model now produces higher SSC near the surface and accumulation in the deeper parts of the estuaries. To test the robustness of the newly added parameters, the sensitivity of the these parameters is now investigated. The model parameters for the Ems is taken as a standard case in this sensitivity analysis; the bed profile is, however, replaced with an artificial one,

$$ h(x)=H\exp\left(-\frac{x}{\alpha_h}\right). $$

(21)

with $H$ the depth at the mouth of the estuary and, $\alpha _h$ the e-folding length of the depth of the estuary. For our standard case, we chose $H=13$ m and $\alpha _h=208$ km. The artificial depth profile allows us to investigate the sensitivity of the model with respect to the bottom slope. We double the value for $\alpha _h$ for this analysis and we adapt $H$ such that at $\tilde {x}=0.6$, the location at which sediment starts accumulating and the depths are equal. The used depth profiles for this analysis as well as the results are shown in Fig. 6a, b, respectively. Results show that an increasing bed slope leads to a more downstream and more pronounced turbidity maximum. Next, the sensitivity of results to the value of exponent $n$, which controls the depth dependence of vertical viscosity and diffusivity, is analysed. The results, shown in Fig. 6c, reveals that an increase of the exponent results in narrowing of the turbidity maximum. The location of the turbidity maximum appears not to be influenced by variations in $n$. The modelled location of the ETM is not sensitive to an increase $w_{s_{low}}$; however, altering the value leads through the formulation of the boundary condition to a change in the total amount of sediment available in the estuary (see Eq. (19)). When lowering $w_{s_{low}}$, this leads to an overestimation of the total amount of sediment in the estuary, resulting in an unrealistic distribution of SSC in the estuary; this can be corrected by reducing $C_*$. Variations in $d_2$ and $\beta _w$ show similar results, i.e. by reducing their respective values, narrowing of the turbidity maximum occurs, whilst the location of the maximum moves slightly upstream.

Fig. 6

Sensitivity of modelled near-bed suspended sediment concentration (SSC) with respect to the newly added model parameters. a: depth profiles used for the analysis of variations in the bed slope in b. c: near-bed SSC for different values of exponent $n$, which controls the depth dependence vertical viscosity and diffusion. d: as c, but for different values of the settling velocity at low concentrations $ws_{low}$. e: as c, but for different values of $d_2$, which controls the relation between the SSC and the settling velocity. f: as c, but for different values of $\beta _w$, which controls the relation between the SSC and the settling velocity. Dashed vertical lines indicate location at which residual currents are shown in Fig. 7e, f

3.3 Residual currents

The longitudinal distribution of SSC is determined by the net flow $u$, which itself, however, is again influenced by the SSC. In order to increase understanding of this feedback mechanism, we discuss the five flow components of the residual flow, as given by Eq. 17. To assess the effects of the residual currents around the turbidity maximum, four locations in the model of the Ems estuary will be investigated. The first location is at $\tilde {x}=x/L=0.57$ in Fig. 4a, which is in a region where the salinity gradient is still large and the SSC is beginning to increase and is subject to flocculation. The second location is a bit more upstream at $\tilde {x}=0.65$, where the SSC is larger and is now in the hindered settling regime. The third location is upstream of the turbidity maximum at $\tilde {x}=0.87$. At this location, the salinity gradient is small, and the SSC is still in the hindered settling regime. At the final location $\tilde {x}=0.99$, the SSC concentration is still in the hindered settling regime, but in contrast to the previous locations, here, the depth increases in the landward direction. For each location, the vertical distributions of the residual flow components are shown in Fig. 7.

Fig. 7

Residual currents at several locations for the model run representing the Ems estuary. Except for the location of d, the water depth decreases at all locations in the upstream direction. Note, that the discharge term $u_Q$ is not shown. a: the residual currents downstream of the turbidity maximum at a location with concentrations such that sediment is in the flocculation regime. b: as a, but at a location where the sediment is in the hindered settling regime. c: as b, but upstream of the turbidity maximum with concentration in the hindered settling regime. d: as c, but at a location where the bed is upward sloping in downstream direction. e: residual current caused by gravity flow for the sensitivity analysis of the bed slope presented in Fig. 6b at $\tilde {x}=0.9$ (dashed vertical line). f: residual flow current by variations in mixing length for the sensitivity analysis of exponent $n$ presented in Fig. 6c at $\tilde {x}=0.9$ (dashed vertical line)

The residual current induced by a gradient in the salinity, which does not depend on the suspended sediment concentration, is directed in the upstream direction close to the bottom and in the downstream direction near the surface. The current induced by the turbidity gradient is directed away from high concentrations of suspended sediment near the bed. Thus, around the turbidity maximum, this results in downstream near-bottom residual currents away from the turbidity maximum.

The first new aspect in our model is the introduction of depth variations. These depth variations induce additional horizontal density differences which result in residual currents. As shown in Fig. 7a, this gravity flow is directed in the down-slope direction near the bed. The absolute value of its residual current depends both on the slope and the local SSC. To model the effect of depth variations on local mixing, the vertical mixing coefficients $A_v$ and $K_v$ are related to the local water depth, as shown in Eqs. 10 and 11,respectively. The residual current induced by depth-dependent mixing is directed opposite to that of the slope-induced turbidity current residual current, but it has a smaller magnitude.

The final addition to the model is the concentration-dependent settling velocity. For low concentrations, the settling velocity is constant in this regime, so no additional residual current component is generated. At locations where the SSC increases in the upstream direction, the residual currents due to variations in the settling velocity in the flocculation regime and in the hindered settling regime are shown in Fig. 7a, b, respectively. They reveal that the effect of variations in the settling velocity on the residual current, and thus on horizontal transport of suspended sediment, is small compared to all other residual current components. Secondly, residual currents have opposite direction in the flocculation and hindered settling regime. In the flocculation regime, the near-bottom residual current is directed away from high SSC, while in the hindered settling regime, the current is directed toward high SSC. In all cases, relative strength of the residual current caused by variations in settling velocity is small.

Finally, the residual currents of the sensitivity analysis of the bed slope (Fig. 6b) and exponent n (Fig. 6c) are compared. Both results are compared near the turbidity maximum at $\tilde {x}=0.9$. The residual flow caused a sloping bed, shown Fig. 7e for three different slopes, which increases with increasing bed slopes (the concentrations are similar). The residual flow caused by variations in mixing, shown in Fig. 7f for three different values of exponent $n$, increases with increase depth dependence of the vertical mixing. For the highest investigated value $n=2$, the effect of dampening the mixing is larger than the gravitational flow; this would lead to up-slope transport of suspended sediment.

3.4 Vertical distribution of suspended sediment

Two of the newly added processes directly influence the vertical distribution of suspended sediment. The vertical distribution of suspended sediment is given by Eq. 15. The vertical distribution of suspended sediment at a certain location in our model depends only on the near-bed SSC (C _b ) and the Péclet number, where the latter depends on the settling velocity w _s and the vertical diffusivity $K_v$. The e-folding height ($\delta =K_v/w_s$), i.e. the height above the bed at which the concentration has decreased by $e^{-1}$ with respect to its near-bed value, is plotted in Fig. 8 as a function of both concentration (at constant depth) and water depth (at constant near-bed SSC) with respect to its near-bed value. A decrease in water depth leads to decreased vertical mixing resulting in a lower e-folding height, this is shown in Fig. 8a. The slope of the e-folding height as a function of depth is, however, smaller than 1; thus in absolute sense, the suspended sediment will appear closer to the surface at lower water levels. Furthermore, for the settling velocity the e-folding height decreases with increasing concentration in the flocculation regime and then increases again in the hindered settling regime. The effect of high bottom concentrations on the surface concentration is thus increased by incorporating hindered settling in the model.

Fig. 8

a: e-folding height $\delta =K_v/w_s$ versus water depth for a near-bed concentration ($C_b=1$ kg m$^{-3}$ and $w_s=0.008$ $\mathrm {ms}^{-1}$). b: as a, but e-folding height versus C _b for a depth $\mathrm {H}=11$ m

4 Discussion

4.1 Effects of new physical aspects on turbidity dynamics

Three new aspects have been added to the model of T09. First, the incorporation of bottom slopes in the model. Second, eddy viscosity and eddy diffusivity depend on the local water depth. Third, the settling velocity has been made dependent on the local bottom concentration. Here, consequences of adding these three new aspects will be discussed. Furthermore, processes are discussed that are not accounted for in the present model and which may affect flow and sediment patterns.

The incorporation of bottom slopes in the model results in important new physics. In the classical model of Hansen and Rattray (1965), in which a constant depth is considered, sub-tidal flow is driven by freshwater discharge and horizontal gradients in salinity. As shown by Festa and Hansen (1978), this results in the formation of a single estuarine turbidity maximum. T09 demonstrated that if sediment concentrations are high, they affect the density of water and thereby force an additional, turbidity-driven flow. In the present model, variations in depth cause additional turbidity currents. When the sediment is located on a sloping bed, decrease of sediment concentration toward the surface leads to a horizontal gradient in the density, thereby generating a gravity-driven flow toward the deeper parts (Wright et al. 2001). The magnitude of this turbidity flow component scales with the bottom concentration of suspended sediment squared and with the local bottom slope. Thus, this term is only important for high concentrations of suspended sediment and for large bottom slopes. This down-slope residual current explains the trapping of high concentrations of suspended sediment in the deeper parts, as is shown in the turbidity measurements displayed in Fig. 2. This effect shows to be strong in the tidal Ouse which has the largest slopes of the three estuaries that are considered in this study.

The effects of depth-dependent mixing intensity on residual flow and turbidity dynamics is observed best by considering the vertical profiles of horizontal velocity shown in Fig. 7. The increase of vertical mixing with depth generates a flow that is directed from larger to smaller depths. Generally, eddy mixing that increases with depth causes all density-driven flow components to become larger in shallower water. Moreover, trapped sediment accumulates closer to the bottom in shallow water. However, the flow component driven by fresh water discharge is not affected, as it does not depend on eddy viscosity. Close to the bottom, the residual current in the up-slope direction will thus be stronger and induces a larger transport of sediment in the up-slope direction. The consequence of all this is that the turbidity maximum is shifted in the up-slope direction with respect to the situation without depth-dependent mixing.

The third new aspect of this model concerns a formulation of the settling velocity that depends on the bottom concentration. In estuaries like the Ems and tidal Ouse, high concentrations are found, also close to the surface. This was not modelled by any of the previous models. In this study, formulations of Mehta (1984) have been adopted to link settling velocity w _s to bottom concentration C _b . In particular, for high SSC, the settling of particles is hindered by other sediment particles, and w _s decreases with increasing C _b . In Section 3.1, the model was used to test the hypothesis that this hindered settling is responsible for the high surface concentrations. Results shown in Fig. 8 indeed support this hypothesis.

Finally, note that a simple formulation for settling velocity is used that depends on bottom concentration only. More sophisticated expressions for w _s , which depend on local concentration and turbulent shear rate, were developed by Winterwerp (2002, 2011) and implemented in a 1dv-model (no horizontal gradients). Results of that model agree quite well with data of the Ems estuary. The motivation to use a simpler formulation in this study is that it aims at gaining basic understanding about observed phenomena. Thus, decisions were made to keep the model tractable, whilst maintaining the essential physics. In this case, support for the decisions made was found from qualitative comparison between the model results and the data.

4.2 The role of tides in trapping sediment

In the present model, sediment transport is the result of along-channel advection of mean SSC by sub-tidal flow. Tides are only parametrically accounted for, i.e. they act as a source for mixing and pick-up of sediment from the bed. Mechanisms resulting in net sediment transport by tidal pumping are thus ignored. The primary reason for this choice is identical to that for selecting simple formulations for the settling velocity of sediment, i.e. to design a minimum model that explains the observed accumulation of fine sediment in the deeper parts of estuaries and the relatively high turbidity values near the surface. The key hypothesis is that, for understanding these two phenomena, it is essential to account for turbidity currents and for hindered settling of sediment. In line with Murray (2003), this hypothesis can be (and has been) tested with an exploratory model that only includes the essential physics. As the results of Section 3 confirm the hypothesis, the conclusion is that tidal pumping of sediment is not crucial to understand the two specific features that set the motivation for this study. At the same time, this does not alter the fact that, to obtain better quantitative comparison between model results and field data, more elaborated models are required. The clue of the present study is that any model governing hydrodynamics and sediment dynamics of highly turbid estuaries should account for turbidity currents, as well as flocculation and hindered settling.

One mechanism resulting in net sediment transport is due to spatial settling lag (Postma 1954; 1961), which induces net transport of sediment towards areas where tidal current amplitudes and depth are small. Other mechanisms are net sediment transport due to overtides in the currents and tide-induced residual flow, which are generated due to non-linear effects. These mechanisms include temporal spatial lag (Groen 1967), barotropic velocity asymmetry (Allen et al. 1980), asymmetry in tidal mixing caused by tidal straining (Jay and Musiak 1994), non-linear advective processes related to lateral tidal advection of along-channel tidal momentum (Lerczak and Geyer 2004; Huijts et al. 2011) and tidal variations in settling velocity due to flocculation and hindered settling (Winterwerp 2002; 2011).

Chernetsky et al. (2010) investigated several mechanisms leading to net sediment transport by tidal currents in an idealised model for the Ems estuary. They found that net sediment transport induced by the external M₄ overtide is necessary to accurately model the turbidity maximum in the Ems. This conclusion is interesting, yet site-specific, as for example, the Yangtze estuary has no external overtides. In this regard, note that their results reveal that already the transport contributions due to sub-tidal flow yield a good, first-order estimate of the distribution of turbidity over the domain. Furthermore, note that their model does not account for net sediment transport due to spatial lag, asymmetry in tidal mixing, turbidity currents and non-linear advective processes driven by lateral tidal flow. The significance of non-linear advective processes and asymmetry in mixing in generating estuarine residual circulation has been demonstrated in several studies (cf. Scully et al. 2009; Stacey et al. 2010, Burchard et al. 2011). The direction (landward/seaward) and magnitude of the resulting net sediment transports depend in a complex way on bathymetry, tidal forcing, stratification and sediment characteristics. This becomes particularly evident from the results of Scully et al. (2009) who, in a numerical study on sub-tidal flow in the Hudson estuary, found that residual flow driven by lateral advective processes and by asymmetry in mixing have opposite effects on driving along-channel estuarine circulation. Clearly, assessing the relative importance of all the processes driving net sediment transport in dependence of forcing conditions, geometry, etc. deserves further attention. However, that is beyond the scope of the present paper.

4.3 Morphodynamic equilibrium

A final issue to discuss concerns the concept of morphodynamic equilibrium, which is used to calculate the SSC. It is thus assumed that the bed level rapidly adjusts to changes in estuarine forcing conditions, where the latter typically vary on a timescale of a week. An estimate of the morphodynamic adjustment timescale is derived from computing the rate of bottom change that results from gradients in the flow-induced sediment transport:

$$ \begin{array}{rll} &&\hspace*{-7.5pt} \left[\rho_s\,(1-p)\frac{\partial H}{\partial t}\right]\sim \left[\frac{\partial }{\partial x}\int_{-H}^0 u\,C\,dz \right]\,, \hspace{1cm} \mathrm{or} \\ && \left[\frac{\partial H}{\partial t}\right] \sim \frac{U\,[C]\, H}{\rho_s\,(1-p)L}\,. \end{array} $$

(22)

Here, the brackets indicate an order of magnitude; $\rho _s\simeq 2650~\mathrm {kg m}^{-3}$ is the density of grains, $p(\sim 0.4)$ is the bed porosity, $U(\sim 0.1~\mathrm {m s}^{-1})$ is the sub-tidal flow velocity, $[C]\sim 5~\mathrm {kg m}^{-3}$ is a characteristic sediment concentration, $H(\sim 10~m)$ is a typical depth and $L(\sim 10$ km) is a length over which the transport varies. Substitution of these numbers yields a change of bed level of about 3 cm per day. Thus, adjustment of mudbanks takes place in 1–2 days, i.e. in a time that is short compared to the timescale of the forcing.

5 Conclusions

In this paper, an explanation is sought for two specific phenomena that are observed in three highly turbid estuaries, viz. the Ems, the tidal Ouse and the Yangtze. First, high values of turbidity occur in the deep parts of the systems. Second, values of suspended sediment concentrations are larger than what would be expected based on the overall grain size of the sediment. The key hypothesis investigated is that these phenomena result from bottom slope-induced turbidity currents and from hindered settling of sediment, respectively. Here, this hypothesis is verified by deriving and analysing a simple, exploratory model that governs the along-channel distribution of sub-tidal flow and residual suspended sediment concentration in an estuary. The model is based on the width-averaged momentum and continuity equation, the mass balance of suspended sediment and the condition of morphodynamic equilibrium. The salinity is prescribed in the model. The model extends those of Hansen and Rattray (1965), Festa and Hansen (1978) and T09 in three ways. First, the flat bottom is replaced by an arbitrary bottom profile. Second, vertical diffusion and vertical viscosity depend on the local water depth, while those were constant in the previous models. Third, the settling velocity is not constant, but depends on local bottom concentration to represent effects of flocculation and hindered settling. Net sediment transport due to tidal pumping is neglected, based on the arguments discussed in Section 4.2.

It is demonstrated that bottom slope-induced turbidity currents result in accumulation of sediment in deeper areas. Around the turbidity maximum, the net transport induced by the turbidity current is of the same order of as that caused by salinity gradients. The bottom slope thus has a major impact on model results for all three estuaries. This is mainly attributed to the larger variations in water depth and larger bed slopes in both the Ems and tidal Ouse. The turbidity currents cause a shift of the turbidity maximum in the down-slope direction compared to a flat bottom case.

The dependence of vertical diffusion and vertical eddy viscosity on the water depth causes a current that is directed in the up-slope direction. The strength of the current caused by the depth dependence of the vertical diffusion is always smaller than that of the bottom slope-induced turbidity current. Since both current components have opposite directions, it can be concluded that depth dependence of the vertical diffusion results in a reduction of the bottom slope-induced turbidity current. This also reduces the sediment transport and contributes to an up-slope shift of the ETM with respect to the case with constant vertical mixing parameters.

Making the settling velocity dependent on bottom concentration, such that processes like flocculation and hindered settling are parametrically accounted for, leads to higher surface SSC in the area near the ETM. This change is consistent with measurements. Results of sensitivity experiments show that these conclusions are qualitatively robust.

Appendix: Expressions

Description of the model parameters values for the model. All model parameters are functions of the scaled vertical coordinate ζ, the Péclet number Pe _v depends on horizontal coordinate x (see Eq. (16)) and the scaled depth $\tilde{h}$ which is defined as h(x)/H.

$$ m_1 = (\tilde{h}^3-9\zeta^2\tilde{h}-8\zeta^3), $$

(23)

$$ m_2 = \frac{12G_1}{Pe_v^{4}\tilde{h}^3}\mathrm{exp}\Big(-Pe_v\big(\zeta+\tilde{h}\big)\Big), $$

(24)

$$ m_{3} = -m_{2}Pe_{v}, $$

(25)

$$ m_{4} = \Bigg(\frac{24G_2}{Pe_v^5\tilde{h}^3}\mathrm{exp}\Big(-Pe_v\big(\zeta+\tilde{h}\big)\Big)-m_2\tilde{h}\Bigg)Pe_v, $$

(26)

in which

$$ \begin{array}{rll} G_1&=&4\tilde{h}^3Pe_v \\ &&+\,\Big(-6\zeta^2+6\tilde{h}^2+\tilde{h}^2Pe_v^2(\zeta+\tilde{h})(3\zeta+\tilde{h})\Big) \\ &&{\kern12pt}\times\,\mathrm{exp}\Big(Pe_v\zeta\left.\right)\Big) \\ &&+\Big(6\zeta^2-6\tilde{h}^2-6\zeta^2\tilde{h}Pe_v+2\tilde{h}^3Pe_v\Big) \\ &&{\kern12pt}\times\,\mathrm{exp}\Big(Pe_v\big(\zeta+\tilde{h}\big)\Big),\\ G_2&=&6\tilde{h}^3Pe_v+2\zeta Pe_v^2\tilde{h}^3 \\ &&+\,\Big(\tilde{h}^4Pe_v^2+4\zeta\tilde{h}^3Pe_v^2+12\tilde{h}^2 \\ &&+\,3\zeta^2Pe_v^2\tilde{h}^2-12\zeta^2\Big)\mathrm{exp}\Big(Pe_v\zeta\left.\right)\Big) \\ &&+\,\Big(-12\zeta^2\tilde{h}Pe_v-\tilde{h}^4Pe_v^2+6\tilde{h}^3Pe_v \\ &&-\,12\tilde{h}^2+3\tilde{h}^2\zeta^2Pe_v^2+12\zeta^2\Big)\mathrm{exp}\Big(Pe_v\big(\zeta+\tilde{h}\big)\Big). \end{array} $$

$$ \begin{array}{rll} T_s&=&\frac{1}{Pe_v^4}\Big\{\Big(-48+Pe_v^3\tilde{h}^3-18Pe_v\tilde{h}\Big)\\ &&{\kern18pt}-\times\,\mathrm{exp}\big(Pe_v\tilde{h}\big)+48-30Pe_v\tilde{h}\\ &&{\kern18pt}+\,6Pe_v^2\tilde{h}^2\Big\}, \end{array} $$

(27)

$$ T_t = \frac{-12H_1}{Pe_v^{7}\tilde{h}^3}\mathrm{exp}\big(-2Pe_v\tilde{h}\big), $$

(28)

$$ T_h = -T_tPe_v, $$

(29)

$$ T_{p} = \Bigg(T_t\tilde{h}-\frac{-12H_2}{Pe_v^{8}\tilde{h}^3}\mathrm{exp}\big(-2Pe_v\tilde{h}\big)\Bigg)Pe_v, $$

(30)

$$ \begin{array}{rll} T_Q &=& \frac{-2}{Pe_v^3\tilde{h}^3}\Big\{(-1+\frac{1}{2}Pe_v^2\tilde{h}^2)\mathrm{exp}\big(-Pe_v\tilde{h}\big)\\ &&+\,1-\tilde{h}Pe_v\Big\}, \end{array} $$

(31)

$$ T_{K_h} = \frac{1-\mathrm{exp}\big(-Pe_v\tilde{h}\big)}{Pe_v}, $$

(32)

$$ T_{hK_h} = \mathrm{exp}\big(-Pe_v\tilde{h}\big)-1, $$

(33)

$$ \begin{array}{rll} T_{pK_h} &=& \Bigg(T_{hK_h}\tilde{h}-\frac{\mathrm{exp}\big(-Pe_v\tilde{h}\big)+Pe_v\tilde{h}-1}{Pe_v^2}\Bigg) \\ &&\times\,Pe_v, \end{array} $$

(34)

in which

$$ \begin{array}{rll} H_1&=&12-\tilde{h}^2Pe_v^2\Big(12+\tilde{h}Pe_v\big(6+\tilde{h}Pe_v\big)\Big) \\ &&+\,\Big(-24+4\tilde{h}Pe_v\big(6+3\tilde{h}Pe_v-\tilde{h}^2Pe_v^2\big)\Big) \\ &&\times\,\mathrm{exp}\Big(Pe_v\tilde{h}\Big)\\ &&+\,\Big(12-2\tilde{h}Pe_v\big(12-6\tilde{h}Pe_v+\tilde{h}^2Pe_v^2\big)\Big) \\ &&\times\,\mathrm{exp}\Big(2Pe_v\tilde{h}\Big),\\ H_2&=&48-\tilde{h}^2Pe_v^2\big(36+15\tilde{h}Pe_v+2\tilde{h}^2Pe_v^2\big) \\ &&+\,\Big(2\tilde{h}Pe_v\big(48+\tilde{h}Pe_v\big(-6+\tilde{h}Pe_v\big) \\ &&\times\,\big(-2+\tilde{h}Pe_v\big)\big)-96\Big)\times\mathrm{exp}\Big(Pe_v\tilde{h}\Big) \\ &&-\,\Big(\tilde{h}Pe_v\big(4-\tilde{h}Pe_v\big)\big(24+\tilde{h}Pe_v \\ &&{\kern12pt}\times\big(-9+2\tilde{h}Pe_v\big)\big)+48\Big)\times \mathrm{exp}\Big(2Pe_v\tilde{h}\Big). \end{array} $$