Reports in the literature agree that distance has a crucial role in affecting patients’ choice with reference to health care services (see [3, 8]). Patients accept meeting monetary and nonmonetary costs inherent to distance, if they expect a positive return in terms of enhanced quality from the hospital located furthest away. To understand what we intend for nonmonetary costs of distance we refer to the fact that if the stay in hospital is long, and the hospital is located far away, patients’ relatives may be unable to come to visiting (or at least they could reduce the visiting) or, alternatively, the patient could feel uncomfortable because of the new environment.

This behavior can be explained in terms of utility maximization where quality, distance, and transportation costs enter as arguments. This studied the secondary health care market through a Hotelling [6] spatial competition model which assumes that: (a) only two hospitals serve the market, (b) they are located at the extremes of a line of unit length, and (c) patients are uniformly distributed on that line.

The model uses a linear utility function where utility increases in quality and decreases in distance. Patients are free to choose the hospital that they prefer, i.e., the quality/distance mix that maximizes their utility. The health care services that they receive are free at the point of use; we assume a tax financed health system where the purchaser (which pays for health treatment received by patients) is assumed to be a government agency that freely chooses contract terms and payment forms. The purchaser aims to induce all patients to be treated. He achieves this goal by defining a fixed price per treated patient payment scheme in such a way as to meet both the hospital rationality constraint and, indirectly, the patient participation constraint (granting them at least with their reservation utility). Obviously the purchaser’s goal is to obtain this result at minimum cost.

In this study hospital and consumer behavior are jointly analyzed under the condition that a prospective diagnosis-related group (DRG) payment system is implemented. The goal is to better understand the hospital’s strategic choices which are affected by the reimbursement scheme, patient behavior, and market structure, in particular with reference to the horizontal differentiation given by Hotelling spatial competition. This contribution complements the existing literature both in health and industrial economics, but its originality consists in the application of the standard Hotelling spatial competition model to the secondary health care market.

Hotelling spatial differentiation has been widely studied by the literature since its original publication in 1929, but it has been implemented mainly in the industrial economics field. With reference to health economics relatively few recent analyses have been published. In particular, Gravelle [4] analyses the competition among providers in the private and public systems for the quality of service and the number of care providers. The study focuses on capitation contracts in which providers receive an initial payment for each patient who registers with them. It is concerned with the way in which competition between providers affects the quality of service, via the number of providers, and patient access to services. Gravelle and Masiero [5] investigated the case in which general practitioners are horizontally and vertically differentiated and compete for patients via their imperfect observed quality. They consider the extent to which switching costs and imperfect patient information about quality interact to blunt incentives for quality. Patients improve their knowledge of the characteristics of the practice that they join after experiencing its services. There are initial errors in judging quality and switching costs which lock some of the mistaken patients into the wrong general practitioner. Furthermore they are interested in whether competition between general practitioners leads to appropriate levels of information and switching costs or whether additional regulation is required. They are concerned with errors and welfare consequences.

This contribution shows that the hospital monopolistic rent directly relates to patient behavior. The rent increases in distance disutility and decreases in patients’ quality perception. The monopolistic rent curbs, ceteris paribus, the provider’s incentives in producing quality.

Because of the asymmetry of information that characterizes the health market, patients are generally unable to observe the true quality provided, and their decisions reflect a perceived quality, affected by bias. Therefore the second part of this contribution presents the case in which quality is observed with error. Using the mean-variance method, the equilibrium previously found is investigated in a stochastic framework. Providers face a new demand affected by uncertainty which does not reflect the true but the perceived quality.

The basic framework

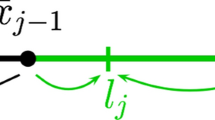
The study refers to a population (normalized to 1) of patients affected by a specific illness which refers to a single DRG. Patients are assumed to be uniformly distributed along a line of unit length. To recover from their illness patients demand hospital health care. Only two hospitals serve the market, and they are located at the extremes of the unit length line (Fig. 1). The patient’s utility depends on the quality of the treatment received and on the cost incurred to move from patient’s location to the hospital:

figure 1
$$ U_{{pz}} = \left\{ \begin{aligned} & \alpha q_{a} - \gamma d \\ & \alpha q_{b} - \gamma {\left( {1 - d} \right)} \\ \end{aligned} \right. $$
(1)

with α, γ >0, where α describes the preferences for quality, γ is the unit transportation cost, qa, and qb are the quality levels supplied by hospital A and hospital B, respectively, and d is the distance incurred by the patient.

Patients are indifferent between hospital A and hospital B if:

$$ \alpha q_{a} - \gamma d = \alpha q_{b} - \gamma {\left( {1 - d} \right)} $$
(2)
$$ {\text{solving}}\;{\text{for}}\;d\;{\text{yields}}:\;d = \frac{\alpha } {{2\gamma }}{\left( {q_{a} - q_{b} } \right)} + \frac{1} {2} $$
(3)

Multiplying the distance d by the population density (equal to 1), we obtain Hospital i demand (D i ):

$$ D_{i} = \frac{\alpha } {{2\gamma }}{\left( {q_{i} - q_{j} } \right)} + \frac{1} {2};\;i \ne j;\;\;\;i,j = A,B $$
(4)

Patients decide to be admitted to hospital if their expected utility is at least equal to their reservation utility Ū. We assume that Ū=0, that is, a patient prefers not to be treated when the distance disutility exceeds utility deriving from the treatment. Each hospital sets its quality to maximize its surplus. Because of the payment scheme adopted by the purchaser, each hospital i receives a fixed price M per patient treated. M is set to satisfy the hospital’s participation constraint. M must cover all the costs hospital i incurs in treating D i patients at q i (i=a, b) quality level. Hospital i revenues (R) are:

$$ R = MD_{i} {\left( {q_{i} ,q_{j} } \right)};i = A,B;i \ne j $$
(5)

where M is arbitrarily chosen by the purchaser. Hospital i revenue increases with the number of patients treated, i.e., with its demand.

The monetary costs (C) to hospital i are:

$$ C_{i} {\left( {q_{i} ,q_{j} } \right)} = c{\left[ {\frac{\alpha } {{2\gamma }}{\left( {q_{i} - q_{j} } \right)} + \frac{1} {2}} \right]}q_{i} + F_{i} $$
(6)

The cost function is linear in quality and in the number of treated patients; c is a cost parameter associated with the number of patients. The hospital will maximize the following surplus function:

$$ \left. {\prod _{i} {\left( {q_{i} } \right)}} \right|_{{q_{j} = \ifmmode\expandafter\bar\else\expandafter\=\fi{q}_{j} }} = R{\left( {q_{i} } \right)} - c{\left( {q_{i} } \right)} - F_{i} $$
(7)

The maximization problem can be written as:

$$ \begin{aligned} & {\mathop {Max}\limits_{q_{i} } }\Pi _{i} = M{\left[ {\frac{\alpha } {{2\gamma }}{\left( {q_{i} - q_{j} } \right)} + {\left( {\frac{1} {2}} \right)}} \right]} - c{\left[ {\frac{\alpha } {{2\gamma }}{\left( {q_{i} - q_{j} } \right)} + {\left( {\frac{1} {2}} \right)}} \right]}q_{i} - F_{i} \\ & s.t. \\ & U_{{pz}} \geqslant \ifmmode\expandafter\bar\else\expandafter\=\fi{U} \\ \end{aligned} $$
(8)

The choice variable to the hospital is its own quality level. A higher quality implies higher costs, but at the same time it can be exploited to increase the demand, given the other competitor’s quality level.

Simultaneous quality choices

We presume that the two hospitals compete on quality, and we assume complete information on revenues and cost functions. The two hospitals are identical and therefore they show an equivalent reaction function. Solving the maximization problem presented in the previous section, we obtain the following reaction function:

$$ q_{i} {\left( {q_{j} } \right)} = \frac{1} {2}{\left( {q_{j} + \frac{M} {c} - \frac{\gamma } {\alpha }} \right)} $$
(9)

The quality increases with the competitor’s quality, the fixed price M set by the purchaser and the parameter associated with the quality relevance in the patient utility function. It decreases in the cost parameter and in the patient’s private transportation cost parameter. The term γ/α relates the hospital decision about quality to the marginal cost of distance (γ) and to the marginal benefit of quality (α) entering the patients’ utility function.The symmetric Nash-equilibrium is given by:

$$ q_{a} = q_{b} = \frac{M} {c} - \frac{\gamma } {\alpha } $$
(10)

The quality provided can be shifted by the purchaser through the fixed price M. A greater value of M allows for a quality rise. The purchaser sets M to meet the hospital participation constraint, i.e., nonnegative profits. (The fixed price M must be set greater then cγ/α; in fact in case M≤cγ/α, both hospitals will choose a nonpositive quality level, and patients’ participation constraint would not be met, i.e., hospitals would face no demand for health treatment.)

If we assume that the purchaser is a government agency, it is reasonable to assume that it aims to provide at least a nonnegative utility to all citizens, regardless of their spatial location. This goal is reached when the marginal consumer can meet its participation constraint. Because the two hospitals behave symmetrically, the marginal consumer is located at 1/2. The quality requirement to obtain the above social welfare objective is: q=γ/2α. (The quality level can be easily obtained by setting the fixed price M according to Eq. 6, i.e., M=3γc/2α.)

A price per patient treated lower than 3γc/2α would reduce quality (q<γ/2α), and a certain share of the market would not ask for health services. Because the government agency wishes to obtain the social objective at minimum cost, it would not set M above 3γc/2α. Given this price, the profit that each firm can attain is: Π i =γc/2α−F i ≥0; i=A,B. We assume γc/2α≥F in order to meet the hospital participation constraint. It is straightforward to see the invariance in hospital’s profit regardless of M: any increase in M intensifies the hospitals’ competition on costly quality in order to obtain the marginal consumer. Thus the additional reimbursement, from the hospital’s point of view, is completely “wasted” to boost upwards the quality level, not allowing for a profit expansion.

If γc/2α>F, the hospital earns positive surplus. Only if F=γc/2α does hospital profit turns out to be zero. The latter represents a corner solution in which private or public provision of health services determine the same outcome. In fact it is generally assumed that a public hospital would transform the entire reimbursement in quality, under the zero profit condition:

$$ \Pi _{{pu}} = Md_{{pu}} - cd_{{pu}} q_{{pu}} - F = 0; $$
(11)

where the subscript pu refers to public (hospital). Then a public hospital would set q pu = (M/c)+(F/cd pu ), which coincides with the private quality rule only if F=γc/2α and d=1/2.

Apart from this hypothesis, a first best is not attainable because of the monopolistic rent which determines the market failure, but, at least, the purchaser is able, following the price definition rule given in Eq. 6, to induce the hospital into producing the optimal quality.

Uncertainty

In the market for health care patients are usually unable to observe the true quality level. Thus the demand for health care services is assumed to depend on perceived quality. Expectations and errors are introduced in the model. The new utility function for the patient depends on the provider’s distance and on perceived quality:

$$ U_{{pz}} = u{\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q},d} \right)} $$
(12)

where \( \ifmmode\expandafter\tilde\else\expandafter\~\fi{q} \) is the perceived quality which we assume to be equally and normally distributed with \( \bar{q}\;{\text{mean}}\;{\text{and}}\;\sigma ^{2}_{q} \;{\text{variance:}}\;\tilde{q} \sim N{\left( {\bar{q},\sigma ^{2}_{q} } \right)}{\text{;}}\;d\;{\text{is}}\;{\text{the}}\;{\text{distance}}{\text{.}} \)

Furthermore we assume: \( \frac{{\partial U_{{pz}} }} {{\partial \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}}} \geqslant 0;\frac{{\partial ^{2} U_{{pz}} }} {{\partial \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}^{2} }} \leqslant 0;\frac{{\partial U_{{pz}} }} {{\partial d}} \leqslant 0;\frac{{\partial ^{2} U_{{pz}} }} {{\partial d^{2} }} \leqslant 0 \)The patient chooses hospital i when the expected utility from the uncertain quality \( \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}_{i} \) is greater than the expected utility from hospital j with uncertain quality \( \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}_{j} : \)

$$ E{\left[ {u{\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}_{a} ,d} \right)}} \right]} \geqslant E{\left[ {u{\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}_{b} ,d} \right)}} \right]} $$
(13)

If we assume a bounded uncertainty, i.e., the “random” quality \( \ifmmode\expandafter\tilde\else\expandafter\~\fi{q} \) is very close to the expected quality \( \ifmmode\expandafter\bar\else\expandafter\=\fi{q} = E{\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}} \right)} \) for every state of the world, we can use the following approximation:

$$ u{\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q},d} \right)} \approx u{\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{q},d} \right)} + {\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q} - \ifmmode\expandafter\bar\else\expandafter\=\fi{q}} \right)}{u}\ifmmode{'}\else$'$\fi_{{ \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}}} {\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{q}} \right)} + {\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q} - \ifmmode\expandafter\bar\else\expandafter\=\fi{q}} \right)}^{2} \frac{{{u}\ifmmode{''}\else$''$\fi_{{ \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}}} {\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{q}} \right)}}} {2} $$
(14)

Using expectations:

$$ \begin{aligned} & E{\left[ {u{\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q},d} \right)}} \right]} \approx u{\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{q},d} \right)} + \frac{{\operatorname{var} {\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}} \right)}{u}\ifmmode{''}\else$''$\fi_{{ \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}}} {\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{q}} \right)}}} {2} \\ & {\text{given}}:\;\operatorname{var} {\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}} \right)} = E{\left[ {{\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q} - \ifmmode\expandafter\bar\else\expandafter\=\fi{q}} \right)}^{2} } \right]} \\ \end{aligned} $$
(15)

Having assumed the perceived quality as equally and normally distributed with q̄ mean and \( \sigma ^{2}_{q} \) variance, the new utility function for the patient, in its explicit form, can be written as:

$$ \begin{aligned} & U_{{pz}} = \left\{ \begin{aligned} & \alpha \ifmmode\expandafter\bar\else\expandafter\=\fi{q}_{a} - \gamma d - \beta \sigma ^{2}_{{q_{a} }} \\ & \alpha \ifmmode\expandafter\bar\else\expandafter\=\fi{q}_{b} - \gamma + \gamma d - \beta \sigma ^{2}_{{q_{b} }} \\ \end{aligned} \right. \\ & {\text{with}}:\;\alpha ,\beta ,\gamma > 0 \\ \end{aligned} $$
(16)

Patients maximize an expected utility function where two new elements enter: the perceived quality mean and its variance. Patient utility increases with the average quality \( {\left[ {\ifmmode\expandafter\bar\else\expandafter\=\fi{q} = E{\left( { \ifmmode\expandafter\tilde\else\expandafter\~\fi{q}} \right)}} \right]} \) and decreases with its variance (σ q 2). This assumption allows us to model a trade-off between expected quality and its variance. In other words, if both hospitals present an equal expected (average) quality, patients will naturally choose the hospital characterized by a lower variance (given the distance d).

The demand that the hospital i faces is defined as:

$$ D_{i} = \frac{\alpha } {{2\gamma }}{\left( {\bar{q}_{i} - \bar{q}_{j} } \right)} - \frac{\beta } {{2\gamma }}{\left( {\sigma ^{2}_{{q_{i} }} - \sigma ^{2}_{{q_{j} }} } \right)} + \frac{1} {2} $$
(17)

The resulting demand for each hospital will not depend directly upon the quality provided because of the observation bias. Under the hypothesis that hospitals’ control is limited to the quality choice variable, they will behave in the same way as in the deterministic scenario, but with a different expected payoff.

Simultaneous quality choices under uncertainty

Under simultaneous quality choices hospitals maximize the quality according to Eq. 4. The profit function is given by:

$$ \Pi _{i} = M{\left[ {\frac{\alpha } {{2\gamma }}{\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{q}_{i} - \ifmmode\expandafter\bar\else\expandafter\=\fi{q}_{j} } \right)} - \frac{\beta } {{2\gamma }}{\left( {\sigma ^{2}_{{q_{i} }} - \sigma ^{2}_{{q_{j} }} } \right)} + \frac{1} {2}} \right]} - c{\left[ {\frac{\alpha } {{2\gamma }}{\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{q}_{i} - \ifmmode\expandafter\bar\else\expandafter\=\fi{q}_{j} } \right)} - \frac{\beta } {{2\gamma }}{\left( {\sigma ^{2}_{{q_{i} }} - \sigma ^{2}_{{q_{j} }} } \right)} + \frac{1} {2}} \right]}q_{i} - F_{i} $$
(18)

If the average quality is assumed equal to the true quality, we can rewrite Eq. 18 as:

$$ \Pi _{i} = M{\left[ {\frac{\alpha } {{2\gamma }}{\left( {q_{i} - q_{j} } \right)} - \frac{\beta } {{2\gamma }}{\left( {\sigma ^{2}_{{q_{i} }} - \sigma ^{2}_{{q_{j} }} } \right)} + \frac{1} {2}} \right]} - c{\left[ {\frac{\alpha } {{2\gamma }}{\left( {q_{i} - q_{j} } \right)} - \frac{\beta } {{2\gamma }}{\left( {\sigma ^{2}_{{q_{i} }} - \sigma ^{2}_{{q_{j} }} } \right)} + \frac{1} {2}} \right]}q_{i} - F_{i} $$
(19)

Hospitals will maximize their profit with respect to “true quality” q i . Setting first order conditions we derive the hospital’s reaction function:

$$ \begin{aligned} & q_{i} = \frac{1} {2}{\left[ {q_{j} + \frac{M} {c} + \frac{\beta } {\alpha }{\left( {\sigma ^{2}_{i} - \sigma ^{2}_{j} } \right)} - \frac{\gamma } {\alpha }} \right]} \\ & i = A,B \\ \end{aligned} $$
(20)

This result is closely related to a simultaneous deterministic reaction function. The new term \( \frac{\beta } {{2\alpha }}{\left( {\sigma ^{2}_{i} - \sigma ^{2}_{j} } \right)} \) which enters the quality function represents the uncertainty hospitals face in their demand. It shifts quality upwards or downwards to compensate the variance in the perceived quality. Generally hospitals would tend to reduce quality variance when possible. The most recent literature on this subject shows the relevance of reputation, closely related to the concept of perceived quality, in determining the demand for health care services. Hospitals aim to reduce asymmetric information by a number of ways, for example, by advertising (see [9]). Although hospitals are not able directly to influence the variance of quality (at least in this model), which is not a choice variable, they are informed about it, and they know its value. What matters is not the absolute level of the variance but the relative difference with respect to the competitor. In general, a lower variance than that of the market competitor allows for a lower quality, given the market share. Symmetrically the competitor faces higher costs to provide higher quality to obtain the same market share, causing himself lower profit. Solving the reaction function equations system, we can derive the quality level each hospital sets: \( q_{i} = \frac{M} {c} - \frac{\gamma } {\alpha } + \frac{\beta } {{3\alpha }}{\left[ {\sigma ^{2}_{i} - \sigma ^{2}_{j} } \right]},\;{\text{where}}\;{\text{i}} \ne {\text{j}}. \) In the case that the two hospitals present the same variance, uncertainty does not matter, and we are back to the deterministic outcome.

Conclusion

In many developed countries the expenditure for hospital care is publicly financed. It represents a large portion of public expenditure, and it increases constantly. Most recent health system reforms are intended to contain this growth. A number of articles have analyzed the trade-off between quality and cost: a higher quality implies higher production costs and vice versa [1, 2, 7]. Some countries, including Italy, have introduced a prospective payment scheme (DRG based) and patients’ choice in an attempt to overcome the quality/cost trade-off. The expected outcome is efficiency in production and a high quality level. The former should be attained by the prospective payment: if the reimbursement depends on the expected cost, the hospital is stimulated to cost minimization. Unfortunately, the cost containment effort could induce the hospital to undesirably skimp on quality. Improved quality might be induced by the demand mechanism, consistent with natural competition between providers for the marginal consumers. Providers need to invest in the quality supplied to obtain the marginal patient and consequently increase the demand.

This contribution investigates this scenario through the standard Hotelling spatial competition model. The purchaser is assumed to be a government agency which aims to provide hospital care to all its citizens at minimum cost. The patient participation goal is attained when each patient is granted with at least the reservation utility. The model shows that the viable way to get all patients treated is inefficient. If the purchaser sets the price to induce hospitals to provide the suitable quality level to meet the marginal patient participation constraint, hospitals would earn positive profits. Because a tax-financed health system is assumed, the hospital surplus turns out to be a “social excess burden.” This implies that a social welfare function, as defined for example, by Chalkley and Malcomson [1], cannot be maximized in this framework; the hospital horizontal monopolistic rent avoids the system to reach a first best equilibrium outcome.

In the second part of this contribution the patients are assumed to be unable to observe the true quality provided. The demand for health care services depends on a perceived quality level. The patient utility function is modified to take into account the effects of information asymmetry. Analyzing the simultaneous quality choices scenario under uncertainty, it is possible to verify that hospitals do not have incentives to deviate from the deterministic equilibrium. We expect the hospitals to provide the same true quality level. Hospitals might face changes in demand and profit (caused by marginal variations), even providing the same quality level, but the simultaneous (Nash) equilibrium remains stable in the long run. The model suggests that both the hospitals and the purchaser have an interest in reducing information asymmetry. Hospitals aim to reduce the variance in quality in order to boost their demand, the purchaser aims to decrease uncertainty to avoid hospital incentives on quality curbing.

A natural extension of this study concerns the analysis of mixed oligopoly in which a private profit-maximizing hospital competes with a public (and benevolent) hospital. In this case a sequential structure would be required. The context of sequential quality choices also turns out to be suitable in analyzing the case in which the two hospitals are different in costs, revenues, or scale economies.