Improving clustering with pairwise constraints: a discriminative approach

Abstract

To obtain a user-desired and accurate clustering result in practical applications, one way is to utilize additional pairwise constraints that indicate the relationship between two samples, that is, whether these samples belong to the same cluster or not. In this paper, we put forward a discriminative learning approach which can incorporate pairwise constraints into the recently proposed two-class maximum margin clustering framework. In particular, a set of pairwise loss functions is proposed, which features robust detection and penalization for violating the pairwise constraints. Consequently, the proposed method is able to directly find the partitioning hyperplane, which can separate the data into two groups and satisfy the given pairwise constraints as much as possible. In this way, it makes fewer assumptions on the distance metric or similarity matrix for the data, which may be complicated in practice, than existing popular constrained clustering algorithms. Finally, an iterative updating algorithm is proposed for the resulting optimization problem. The experiments on a number of real-world data sets demonstrate that the proposed pairwise constrained two-class clustering algorithm outperforms several representative pairwise constrained clustering counterparts in the literature.

1 Introduction

The goal of clustering is to split a collection of data into meaningful groups or clusters. It has been extremely valuable for data analysis and plays a key role in various application domains ranging from engineering, bioinformatics, earth science, medical science, social science to economics [1–5]. In practice, it is, therefore, of great importance to obtain a user-desired and accurate grouping of data, that is, the clusters obtained by a clustering algorithm correspond to the true semantic categories of the data [6]. However, due to its unsupervised nature, a traditional unsupervised clustering algorithm may fail to provide the desired partitions, for example, several documents that talk about different topics but with many words in common may be grouped into the same cluster. One solution for this problem is to introduce prior information that may guide the partitioning of the data. In this paper, we are particularly interested in how to incorporate pairwise constraints to improve the clustering performance. Specifically, two kinds of pairwise constraints are additionally provided for the clustering task at hand: One is the must-link constraint describing that the pair of instances should belong to the same cluster; the other is the cannot-link constraint specifying that the pair of instances should be assigned to different clusters. Although pairwise constraints provide weak supervision information as they only indicate the relationship between the splits rather than the splits themselves, it is generally believed that they can boost the clustering performance [7, 8]. A simple example for pairwise constrained clustering is illustrated in Fig. 1.

Fig. 1

An example for clustering guided with pairwise constraints. Samples from different true categories are represented by circle and triangle, respectively. The ellipses denote the clusters. The result in (a) does not correspond to the true semantic categories of data, while the result in (b) has been greatly improved with the guidance of pairwise constraints

In practice, pairwise constraints can be often obtained conveniently. First, in many application areas, pairwise constraints can be collected automatically along with the unlabeled data. For example, the protein co-occurring information in the Database of Interacting Proteins (DIP) data set can be used as the must-link constraints when performing gene clustering [9]. In video surveillance applications, any two faces from the same frame must come from two different persons, thus forming a cannot-link constraint, whereas those from temporally adjacent frames with spatial overlap can be assumed to be must-link [10]. Second, pairwise constraints can also be collected by human specification with little efforts. Unlike labels that would require users to have prior knowledge or experience with a data set, it is less difficult for a user, who is even not an expert in a domain, to make a judgement whether two objects are similar or not than to provide them with the exact class labels.

Since the last decade, a number of approaches have been developed, which have achieved reasonable performance improvement in clustering tasks using pairwise constraints. The most predominant strategy of these methods is to learn a better distance metric or similarity matrix by leveraging pairwise constraints first and then to apply standard clustering algorithms like K-means or spectral methods with the resulting metric or similarity matrix to determine the cluster assignments [9, 11–20]. Despite the success in their application domains, several existing works [9, 13–16] simply utilize the limited number of prespecified pairwise constrained samples in the metric learning step, while the abundant unconstrained ones are not taken into account. As a result, the obtained metric or similarity may not be reliable for the whole data set [21]. Thereby, it is more rational to make use of valuable intrinsic information with the unconstrained data in addition to the given pairwise constraints, in order to boost the effect of such scarce supervision information. Nevertheless, since the task of clustering is to split a collection of data into meaningful clusters, it may make more sense for pairwise constraints to directly guide the learning for the partitioning boundaries with the largest margins between categories, than to help in modeling the metrics of data with which to perform the clustering afterwards. The plausible reason is that the partitioning boundaries might be simpler to estimate by such margin-based approaches, whereas the ground-truth distance metrics might be considerably complex or against the model assumption [10, 22]. Thus, by extending maximum margin clustering (MMC) algorithm [23] that directly finds the hyperplanes that well separate different groups of data by a generalized large margin criterion, Hu et al. have proposed a pairwise constrained two-class MMC and a pairwise constrained multi-class MMC in [25]. Moreover, they have shown that it is much easier for the pairwise constrained variants of MMC to obtain the cluster memberships for out-of-sample data points, because the discriminative partitioning boundaries can be established using the available data [25]. Such a merit is important for generalization, predictive purposes and large-scale data. By contrast, it is generally nontrivial for some existing semi-supervised clustering methods (e.g., the pairwise constrained variants of spectral clustering approaches [11, 12, 16, 18–20]) to determine the cluster memberships for new samples, as no partitioning model is built in such methods. Nevertheless, our previous work [26] finds that the multi-class constrained clustering method in [25] may not be able to robustly detect whether the cannot-link constraints have been violated, particularly when the cannot-link pair of samples actually belong to different semantic categories yet with very similar appearance. Furthermore, we find that the constrained two-class clustering algorithm in [25] also suffers from such a drawback. Besides, we have further observed that it may generate unexpected high penalty even though some given must-link constraints are not violated, especially for the case where the must-link pair of samples are from far away subgroups in a semantic class.

In this paper, aimed at improving the clustering performance on the two-class data set, we propose a novel approach to adapt the unsupervised MMC for its pairwise constrained variant. In particular, to overcome drawbacks of the preliminary pairwise constrained two-class MMC approach [25], a new set of pairwise loss functions is proposed based on a two-class discriminative classification model. It is sensitive to detect the violations of pairwise constraints and is able to provide robust penalization to such violations based on the margin principle. Meanwhile, it would not produce unexpected high penalty if the pairwise constraints are satisfied. In addition, as the extension of MMC, there are also three other advantages of the proposed method over some pairwise constrained clustering counterparts in the literature. Firstly, it makes fewer assumptions on the distance metric or similarity which might be complicated in practice. Secondly, it is able to exploit the limited number of pairwise constraints together with abundant unconstrained samples in a unified discriminative learning framework. Thirdly, it is much easier for the proposed method to determine the cluster memberships for out-of-sample examples than its constrained spectral clustering counterparts. For the resulting optimization problem, we have developed an effective and efficient iterative algorithm to solve it. Experimental results evaluated on extensive benchmark real-world data sets demonstrate that the proposed pairwise constrained clustering method outperforms state-of-the-art constrained clustering counterparts for two-class clustering tasks.

The remainder of the paper is organized as follows. In Sect. 2, we present related work on pairwise constrained clustering. We formulate the basic pairwise constrained two-class maximum margin clustering problem in Sect. 3. In Sect. 4, the proposed constrained two-class MMC approach is given in detail. Experimental results are given in Sect. 5. Finally, some concluding remarks are given in Sect. 6.

2 Related work

A lot of efforts have been made in pairwise constrained classification [10, 33–36] and pairwise constrained clustering [8, 9, 11, 13–21, 25–29, 31, 32] for improving the performance of the learning algorithms. In the following, we will only focus on the work utilizing the pairwise constraints for clustering. Generally, the current pairwise constrained clustering methods can be divided into four categories: constraint-based ones, metric-based ones, similarity-based ones and penalty-based ones.

The constraint-based methods: The seminal effort on constraint-based semi-supervised clustering, that is, the COP-K-means algorithm, has been made by Wagstaff et al. in [8]. It follows the same clustering procedure of K-means while respecting the pairwise constraints, requiring that none of the constraints is violated in the clustering process. Nevertheless, such a strict enforcement of constraints often suffers from great performance degradation in case of possibly noisy constraints.

The metric-based methods: In these approaches, a distance metric is firstly trained to satisfy the prespecified pairwise constraints as much as possible, and then K-means clustering is performed with the obtained metric. The algorithm in [13] learns a Mahalanobis distance metric which corresponds to a linear transformation of the data features, by minimizing the distance between must-link data points while keeping cannot-link data points apart. Nevertheless, it is computationally too expensive to be applied to practical applications. Bar-Hillel et al. thus proposed the relevant components analysis (RCA) [14], which is efficient and achieves comparable results as the algorithm in [13]. The main drawback with RCA is that it is unable to handle the cannot-link constraints. Such a problem has been addressed by discriminative component analysis (DCA) in [15], which can make use of both the must-link and cannot-link constraints to learn the optimized transformation. Most recently, Wu et. al assert that the Mahalanobis distance metric model is unable to effectively handle binary-class data with multi-modal distribution, which is, however, common in practice, because it simply assumes a fixed metric for the entire input space [22]. Furthermore, these metric-based pairwise constrained clustering algorithms exclude unconstrained data from the metric training step, therefore leading to less reliable metric for the whole data set [17, 31, 32].

The similarity-based methods: These approaches resort to seeking an appropriate similarity matrix with the assistance of pairwise constraints for conducting the spectral clustering. With a given affinity matrix, the methods of [9, 16] simply modify the similarities between constrained objects only. Not surprisingly, such an ad-hoc modification usually does not work well in practice due to insufficient pairwise constraints, and the obtained similarity matrix generally may not be a valid kernel matrix. The methods in [18, 19] resolve this problem by introducing the manifold regularizer when optimizing the similarity matrix with respect to the pairwise constraints. However, they require semi-definite programming (SDP) whose computation cost is considerably intensive and prohibits such approaches applicable to real applications, even for data sets of moderate size. In a way consistent with the given affinities, a much more efficient work in [20] propagates the pairwise constraints from a few specified sample pairs to the rest of the entries in the similarity matrix using Gaussian process.

The penalty-based methods: These approaches augment penalty functions for violating the pairwise constraints with the original clustering objective function; therefore, they can utilize the unconstrained samples and the constrained ones in a single framework. The proposed method also follows this line. In this way, the paper [21] and references in [27–30] adapt the K-means and the nonnegative matrix factorization (NMF) clustering to their constrained variants, respectively, but with no extension to new points. Most recently, preliminary efforts on constrained MMC have been made in [25, 26] along this direction. Despite their success, we find that the loss function for violating the pairwise constraints in [25] may not be able to detect and discourage the violation of given constraints robustly. We further find that the performance of the pairwise constrained multi-class clustering algorithm in [26] may degrade for two-class clustering tasks, when the number of must-link constraints and that of cannot-link constraints are imbalanced.

3 Problem formulation

In this paper, only the two-class clustering problem is considered where we group the data into two clusters. Motivated by the success of large margin methods in supervised learning, MMC [23] aims at extending such methods to unsupervised learning. Specifically, for a given set of data points, it tries to find the maximum margin hyperplane that can separate the data into two different clusters among all possible binary labels. Formally, let $\mathcal{X }=\{\mathbf{x }_{i}\}_{i=1}^{m}(\mathbf x _{i}\in \mathbb{R }^{d})$ denote the set of data points. Suppose the hyperplane is parameterized by the weight vector $\mathbf w \in \mathbb{R }^{d\times 1}$ and the bias term $b\in \mathbb{R }$, that is, the discriminative function can be written as $f(\mathbf x )=\mathbf w ^{T}\mathbf x +b$ , and then the MMC problem is cast into the following optimization problem [38], that is,

$$\begin{aligned}&\min _{f}~\left\{ \frac{1}{2}\Vert f\Vert _{\mathcal{I }}^2 + \lambda \sum _{i=1}^{m}L(|f(\mathbf x _{i})|)\right\} ,\nonumber \\&\quad subject~to:~ -s\le \sum _{i=1}^{m}f(\mathbf x _{i})\le s, \end{aligned}$$

(1)

where $\Vert f\Vert _\mathcal{I }^2$ is the regularization term controlling the complexity of the hypothesis space, and $\Vert \mathbf w \Vert ^2$ is often adopted for $\Vert f\Vert _\mathcal{I }^2$. The item $\lambda$ is a positive trade-off constant. The item $L(|f(\mathbf x _{i})|)$ is the “generalized” margin constraint violation cost function with $L(z)=\max (1-z,0)$. Such a cost function is similar to that for the transductive support vector machine (SVM) [24], forcing the unlabeled samples far away from the hyperplane. The constraint in (1) is a cluster balance constraint introduced to avoid the trivially optimal solutions because a large margin value can be always achieved by assigning all the samples to a single cluster [37]. The constant $s\ge 0$ controls the cluster imbalance. Ultimately, MMC learns the hypothesis $f$ via solving (1), and finally, the cluster assignment for $\mathbf x _{i}$ can be determined as follows: It belongs to group 1 if $f(\mathbf x _{i})\ge 0$, or group 2 otherwise. Moreover, the clustering memberships of the unseen data can be obtained similarly with the obtained partitioning hypothesis. Recently, several efforts [39–43] have been made to enhance the efficiency of the basic MMC [37], while some extend the basic MMC with subspace learning [44], feature selection [45] and multiple kernel learning [46] for improving its effectiveness. Nevertheless, such extensions are all unsupervised.

In this paper, to further improve the performance of MMC, we focus on introducing more informative supervision for adapting it to its semi-supervised variant. Specifically, a set of pairwise constraints is provided, that is, $\mathcal{C }=\{C_{j}=(\mathbf x _{j1},\mathbf x _{j_{2}},\ell _{j})\}_{j=1}^{n}$, where $\ell _{j}=1$ indicates that the pair of samples $(\mathbf x _{j_{1}},\mathbf x _{j_{2}})$ must link, while $\ell _{j}=-1$ means that the pair of samples $(\mathbf x _{j_{1}},\mathbf x _{j_{2}})$ cannot link. We denote the sets of prescribed must-link constraints and cannot-link constraints by $\mathcal{ML }$ and $\mathcal{CL }$, respectively, with $\mathcal{C }=\mathcal{ML }\cup \mathcal{CL }$. To derive the constrained MMC, the key lies in the way that the pairwise constraints are being incorporated into MMC. Under the same discriminative learning framework, they can be introduced, as another set of cost functions which attempts to penalize the violation of the given constraints, into the original MMC objective function, that is,

$$\begin{aligned} \min _{f}\left\{ \frac{1}{2}\Vert \mathbf w \Vert ^2 + \lambda \sum _{i=1}^{m}L(|f(\mathbf x _{i})|)+\gamma \sum _{j=1}^{n}L^{\prime }(f(\mathbf x _{j_{1}}),f(\mathbf x _{j_{2}}),\ell _{j})\right\} , \end{aligned}$$

(2)

where $\mathbf x _{i}$ represents the sample that does not involve in the constraints set, the item $L^{\prime }(f(\mathbf x _{j_{1}}),f(\mathbf x _{j_{2}}),\ell _{j})$ denotes the cost function for violating the pairwise constraint $C_{j}$, and the coefficient $\gamma$ is the another positive trade-off constant. Note that the cluster imbalance constraint is excluded in (2) because the cannot-link constraints are able to prevent the trivially optimal solutions [25]. From now on, we will use the shorthands $f_{i}$, $f_{j_{1}}$ and $f_{j_{2}}$ for $f(\mathbf x _{i})$, $f(\mathbf x _{j_{1}})$ and $f(\mathbf x _{j_{2}})$, respectively.

A preliminary work on constrained two-class MMC has been proposed in [25], in which $|f_{1}-\ell f_{2}|$ is adopted for the pairwise loss function, that is,

$$\begin{aligned} L^{\prime }(f_{1},f_{2},\ell )=|f_{1}-\ell f_{2}|. \end{aligned}$$

(3)

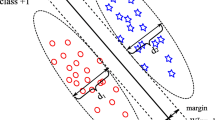
Although the improvement over unsupervised MMC has been observed in [25], we find that this work with such a pairwise loss function may not work robustly in practice. Its robustness will be investigated through two cases as shown in Fig. 2.

Fig. 2

Two intermediate clustering results with premature hyperplanes. Samples from different true categories are represented by circle and triangle, respectively. The premature hyperplane for each clustering task is depicted with a straight line across the two-dimensional space. The ellipses indicate the clusters determined by the hyperplane. As can be seen, the clustering result has violated the prespecified constraints. The pairwise loss function in [25] is able to provide appropriate penalization to the constraint violation for the case shown in (a), but may fail for the case in (b)

For the case described in Fig. 2a, the premature hyperplane has resulted in the must-link pair ($\ell _{j}=1$) of samples, which are close to each other, residing on its two sides with opposite signs. Therefore, it will incur a large cost for penalizing such an violation, according to the pairwise loss function $|f_{j_{1}}-f_{j_{2}}|$. The same figure depicts a constraint ($\ell _{j}=-1$) that is posed on two far apart samples from different ground-truth classes. Such a pair of samples have been incorrectly placed on the same side of the hyperplane with the hyperplane with the same sign (i.e., the constraint is not fulfilled). Moreover, they are both far off the hyperplane. Therefore, the significant cost $|f_{j_{1}}+f_{j_{2}}|$ will effectively drive the algorithm to find a better hyperplane.

However, in practical applications, users are more inclined to specify some highly informative pairwise constraints for dealing with cases in which samples are much more difficult to be partitioned correctly. For instance, samples from different classes usually show serious overlap in real problems, that is, there are many samples belonging to different categories but seeming to be very similar (e.g., some face images may have similar appearance but belong to different persons, several documents may get many words in common but discuss different topics, etc.). Therefore, the cannot-link constraints are particularly provided to guide the partitioning in such difficult scenarios. As shown in Fig. 2b, a cannot-link constraint is specified in the severely overlapping region and the premature hyperplane passes through such a region. Consequently, the cannot-link pair of samples will also be close to the premature hyperplane in this case, for example, see Fig. 2b. As a result, the values of the decision function $f$ for both samples, that is, $f_{j_{1}}$ and $f_{j_{2}}$, will be near zero, and then $|f_{j_{1}}+f_{j_{2}}|$ would naturally reduce to zero as if the constraint was not violated. That is to say, even though the current partition does not fulfill such a cannot-link constraint in the case where the constraint is specified from a severe overlapping regions as shown in Fig. 2b, the pairwise loss function of [25] would not be able to discourage such a violation effectively.

Meanwhile, we often expect that two points belonging to the same true class but with a large distance (e.g., experimental samples from two subtypes of lung cancer [47]) could still be grouped in the same cluster. Thus, a must-link constraint is usually provided for such a pair of samples. In Fig. 2b, the must-link pair of samples happens to be correctly put into the same partition by the hyperplane. In other words, the must-link constraint is not violated. Nevertheless, because these two points are very different from each other, the form of $|f_{j_{1}}-f_{j_{2}}|$ might trigger an unexpected high cost, leading to a possibly poor hyperplane instead.

On the other hand, for the difficult case in Fig. 2b, the paper [22] argues that a fixed metric for the entire input space (e.g., the Mahalanobis metric) may not be able to effectively model the desired distance metric, with which originally far away samples from subgroups of a single semantic class (see the data points with the must-link constraints in Fig. 2b) are near to each other, while the samples belonging to different categories but with similar appearance (see the data points with the cannot-link constraints in Fig. 2b) become far apart. By contrast, it can be observed from Fig. 2 that it may be much easier to find a hyperplane which can well separate the samples into two clusters and fulfill the given constraints by the constrained MMC.

To this end, we will propose a new discriminative pairwise constrained two-class MMC algorithm. In particular, we put forward a set of pairwise loss functions, which could overcome the drawbacks of the work in [25] and features robust penalization to the violation of constraints.

4 The proposed discriminative pairwise constrained maximum margin clustering approach

Recall that the unsupervised two-class MMC is to find a binary labeling for the samples, so that the obtained hyperplane under such a labeling result has the largest margin from both the two labeled clusters [23]. With the given pairwise constraints, the main idea of our proposed pairwise constrained two-class clustering approach is as follows: The labeling for a pair of constrained samples should fulfill the must-link/cannot-link constraint on the cluster memberships of them; meanwhile, the corresponding hyperplane with such a labeling should possess the maximum margin from the constrained samples. Base on such an idea, the proposed new pairwise loss functions are presented first.

4.1 The proposed pairwise loss functions

Concerning the definitions for must-link and cannot-link constraints in the context of binary maximum margin clustering, we propose the following pairwise loss function $H_{j}(f)$ for $L^{\prime }(f_{j_{1}},f_{j_{2}},\ell _{j})$:

$$\begin{aligned} H_{j}(f)\triangleq \min \{L(f_{j_{1}})+L(\ell _{j}f_{j_{2}}), L(-f_{j_{1}})+L(-\ell _{j}f_{j_{2}})\}. \end{aligned}$$

(4)

It essentially requires that if $\mathbf x _{j_{1}}$ is labeled with 1 (or $-1$), then $\mathbf x _{j_{2}}$ ought be labeled with $\ell _{j}$ (or $-\ell _{j}$) correspondingly; furthermore, $\mathbf x _{j_{1}}$ and $\mathbf x _{j_{2}}$ should be far away from the hyperplane at the same time. To evaluate the robustness of the proposed pairwise loss functions, the following two propositions are presented.

Proposition 1

If $C_{j}$ is violated, the pairwise loss for violating such a constraint $H_{j}(f)$ is always not less than 1.

Proof

Suppose $C_{j}$ is a must-link constraint ($\ell _{j}=1$) and is violated, recall that a sample $\mathbf x _{i}$ belongs to cluster 1 if $f_{i}\ge 0$, or cluster 2 otherwise; therefore, either $f_{j_{1}}$ or $f_{j_{2}}$ should be negative. Because $L(z)=\max (1-z,0)$ is a nonnegative and monotonic decreasing function, we have

$$\begin{aligned} \left\{ \begin{array}{l} L(f_{j_{1}})+L(f_{j_{2}})\ge L(0)=1,\\ L(-f_{j_{1}})+L(-f_{j_{2}})\ge L(0)=1. \end{array} \right. \end{aligned}$$

Thereby, $H_{j}(f)\ge 1$ holds if a must-link constraint $C_{j}$ is violated. In a similar way, we can prove that $H_{j}(f)\ge 1$ also holds if a cannot-link constraint $C_{j}$ is violated. $\square$

Proposition 2

If $C_{j}$ is not violated, the pairwise loss $H_{j}(f)$ is always less than 2.

Proof

Suppose $C_{j}$ is a must-link constraint ($\ell _{j}=1$) and is not violated. Without loss of the generality, we assume $f_{j_{1}}\ge 0$ and $f_{j_{2}}\ge 0$, and then we have $H_{j}(f)=\min \{L(f_{j_{1}})+L(f_{j_{2}}), L(-f_{j_{1}})+L(-f_{j_{2}})\}=L(f_{j_{1}})+L(f_{j_{2}})$. Furthermore, recall that $L(z)=\max (1-z,0)$; we, therefore, obtain that $L(f_{j_{1}})\le 1$ and $L(f_{j_{2}})\le 1$. Consequently, $L(f_{j_{1}})+L(f_{j_{2}})\le 2$ holds. In a similar way, we can prove that $H_{j}(f)\le 2$ also holds if a cannot-link constraint $C_{j}$ is not violated. $\square$

According to Proposition 1 and Proposition 2, several remarks can be made as follows:

• When $C_{j}$ is violated, the pairwise loss for violating such a constraint $H_{j}(f)$ is always not less than 1. Furthermore, $H_{j}(f)$ will produce a greater value than 1 when the hyperplane is close to either $\mathbf x _{j_{1}}$ or $\mathbf x _{j_{2}}$ (i.e., $|f_{j_{1}}|<1$ or $|f_{j_{2}}|<1$). Therefore, in comparison with (3) which may fail to effectively penalize the violation of cannot-link constraints specified in seriously overlapped region as depicted in Fig. 2b, $H_{j}(f)$ is expected to be able to overcome such a drawback in this case.

• The value of $H_{j}(f)$ is upper bounded if $C_{j}$ is not violated. Moreover, when $C_{j}$ is satisfied, no matter how different $\mathbf x _{j_{1}}$ and $\mathbf x _{j_{2}}$ may be, as both of them are far away from the hyperplane (i.e., $|f_{j_{1}}|>1$ and $|f_{j_{2}}|>1$), $H_{j}(f)$ will be near $0$. Thereby, compared to (3), it would not trigger an undesired significant cost for the aforementioned case in Fig. 2b, where a must-link pair of samples stay in the same partition yet have a large distance.

4.2 Pairwise constrained maximum margin clustering algorithm

Subsequently, the corresponding constrained two-class MMC optimization problem can be written as follows:

$$\begin{aligned} Q(f)\triangleq \frac{1}{2}\Vert \mathbf w \Vert ^2 + \lambda \sum _{i=1}^{m}L(|f_{i}|)+\gamma \sum _{j=1}^{n}H_{j}(f). \end{aligned}$$

(5)

Note that pairwise constraints have already been proposed to be incorporated into SVMs [10, 33]. However, the classification problem is the main focus in [10, 33], where the labels for some examples are known during training. By contrast, we handle the clustering problem where no labels are provided in (5).

Although $H_{j}(f)$ may be a preferred choice compared to the loss function (3), it is generally intractable to optimize. Therefore, we will introduce several auxiliary functions as follows:

$$\begin{aligned} H^{(1)}_{j}(f)&\triangleq L(f_{j_{1}})+L(\ell _{j}f_{j_{2}}),\\ H^{(2)}_{j}(f)&\triangleq L(-f_{j_{1}})+L(-\ell _{j}f_{j_{2}}). \end{aligned}$$

Further, we define

$$\begin{aligned} \widetilde{H}_{j}(f,p)=p\cdot H^{(1)}_{j}(f)+(1-p)\cdot H^{(2)}_{j}(f), \end{aligned}$$

(6)

where $p\in [0,1]$. We have

$$\begin{aligned} H_{j}(f)=\min _{p\in [0,1]}\widetilde{H}_{j}(f,p). \end{aligned}$$

(7)

Moreover, it can be verified that

$$\begin{aligned} p^{*}\triangleq \arg \min _{p\in [0,1]} \widetilde{H}_{j}(f,p), \end{aligned}$$

(8)

should be either $0$ or $1$, which can thus be viewed as a selector for $H_{j}(f)$ from $\{H^{(1)}_{j}(f),H^{(2)}_{j}(f)\}$. For the proposed constrained MMC objective function in (5) and the following formulation

$$\begin{aligned} \widetilde{Q}(f,\{p_{j}\}_{j=1}^{n})\triangleq \frac{1}{2}\Vert \mathbf w \Vert ^2 + \lambda \sum _{i=1}^{m}L(|f_{i}|)+\gamma \sum _{j=1}^{n}\widetilde{H}_{j}(f,p), \end{aligned}$$

(9)

with (6)–(8), we have

$$\begin{aligned} Q(f)=\min _{\{p_{j}\}_{j=1}^{n}\in [0,1]^{n}}\widetilde{Q}(f,\{p_{j}\}_{j=1}^{n}). \end{aligned}$$

(10)

Consequently, the problem of minimizing $Q(f)$ with respect to $f$ can be equivalently cast into the one of the minimizing $\widetilde{Q}(f,\{p_{j}\}_{j=1}^{n})$ with respect to $f$ and $\{p_{j}\}_{j=1}^{n}\in [0,1]^{n}$, that is,

$$\begin{aligned} \min _{f}Q(f)=\min _{f,\{p_{j}\}_{j=1}^{n}}\widetilde{Q}(f,\{p_{j}\}_{j=1}^{n}). \end{aligned}$$

(11)

Under the circumstances, we have developed an iterative optimization algorithm for the proposed pairwise constrained MMC problem. In each iteration, it minimizes $\widetilde{Q}(f,\{p_{j}\}_{j=1}^{n})$ by iteratively keeping either $f$ or $\{p_{j}\}_{j=1}^{n}$ fixed and optimizing $\widetilde{Q}(\cdot )$ with respect to the other, that is,

• Fixing $f$ at $f^{(t-1)}$, we will solve the following problem for $\{p_{j}^{(t)}\}_{j=1}^{n}$, that is,

  $$\begin{aligned} \{p_{j}^{(t)}\}_{j=1}^{n}=\arg \min _{\{p_{j}\}_{j=1}^{n}}\widetilde{Q}(f^{(t-1)},\{p_{j}\}_{j=1}^{n}). \end{aligned}$$

  (12)

• Fixing $\{p_{j}\}_{j=1}^{n}$ at $\{p_{j}^{(t)}\}_{j=1}^{n}$, we then optimize the following problem for $f^{(t)}$, that is,

  $$\begin{aligned} f^{(t)} = \arg \min _{f}\widetilde{Q}(f,\{p_{j}^{(t)}\}_{j=1}^{n}). \end{aligned}$$

  (13)

Based on (7), it can be seen that the problem (12) can be directly solved by

$$\begin{aligned} p_{j}^{(t)}= \left\{ \begin{array}{ll} 1,&\quad \text{ if} H^{(1)}_{j}(f^{(t-1)})<H^{(2)}_{j}(f^{(t-1)})\text{;}\\ 0,&\quad \text{ otherwise.} \end{array} \right. \end{aligned}$$

(14)

In the following, we will develop the detailed procedure for (13). Specifically, the corresponding optimization problem can be written below:

$$\begin{aligned} \min _{f}\left\{ \frac{1}{2}\Vert \mathbf w \Vert ^2 + \lambda \sum _{i=1}^{m}L(|f_{i}|)+\gamma \sum _{j=1}^{n}\widetilde{H}_{j}(f,p^{(t)})\right\} . \end{aligned}$$

(15)

By introducing slack variables as in the support vector machine algorithm, (15) can be equivalently formulated as follows:

$$\begin{aligned}&\min _{f,\varvec{\xi }}\left\{ \frac{1}{2}\Vert \mathbf w \Vert ^2 + \lambda \sum _{i=1}^{m}\xi _{i} +\gamma \sum _{j=1}^{n}\widetilde{H}_{j}(f,p^{(t)})\right\} \nonumber \\&\quad subject~to:~|f(\mathbf x _{i})|\ge 1-\xi _{i},\xi _{i}\ge 0,i=1,\ldots ,m, \end{aligned}$$

(16)

where $\varvec{\xi }=[\xi _{1},\ldots ,\xi _{m}]^{T}$. From Eq. (6), it is clear that $\widetilde{H}_{j}(f,p^{(t)})$ is just the linear combination of the convex loss functions with nonnegative coefficients; thus, it is still convex. Consequently, the objective function in (16) is convex. However, the inequality constraints are not convex, but can be viewed as a difference of two convex functions. Fortunately, such a nonconvex optimization problem in (16) can be efficiently solved by resorting to the constrained concave–convex procedure (CCCP) [48, 49], which will be described in the following subsection.

4.2.1 The constrained concave–convex procedure for the optimization

CCCP is an effective technique proposed recently to solve problems with concave–convex objective function under the concave–convex constraints in the following form [38, 48, 49]:

$$\begin{aligned}&\min _\mathbf{z }~\Big \{h_{0}(\mathbf z )-g_{0}(\mathbf z )\Big \}\nonumber \\&\quad \text{ subject} \text{ to}:~h_{i}(\mathbf z )-g_{i}(\mathbf z )\le c_{i},i=1,\ldots ,q, \end{aligned}$$

(17)

where $h_{0}, g_{0}, h_{i}, g_{i}~(i=1,\ldots ,q)$ are convex and differentiable functions, and $c_{i}\in \mathbb{R }$. Given an initial guess on $\mathbf z _{0}$, in the $(r+1)$-th iteration, CCCP first replaces $g_{0}(\mathbf z ), g_{i}(\mathbf z )$ in (17) with its linearization at $\mathbf z _{r}$ and then solves the resulting convex problem for $\mathbf z _{r+1}$:

$$\begin{aligned}&\min _\mathbf{z }~\Big \{h_{0}(\mathbf z )-\big [g_{0}(\mathbf z _{r})+\varvec{\nabla }g_{0}(\mathbf z _{r})^{T}(\mathbf z -\mathbf z _{r}) \big ]\Big \}\nonumber \\&\quad \text{ subject} \text{ to}:~h_{i}(\mathbf z )-\big [g_{i}(\mathbf z _{r})+\varvec{\nabla }g_{i}(\mathbf z _{r})^{T}(\mathbf z -\mathbf z _{r}) \big ]\le c_{i}, i=1,\ldots ,q, \end{aligned}$$

(18)

where $\varvec{\nabla }g_{0}~(\mathbf z _{r}), \varvec{\nabla }g_{i}~(\mathbf z _{r})(i=1,\ldots ,q)$ are the gradients of $g_{0}(.), g_{i}(.)$ at $\mathbf z _{r}$, respectively. It can be shown that the objective (18) in each CCCP iteration decreases monotonically [48]. When CCCP converges, it will arrive at a local minimum of (17) [49].

For our problem, as $|\mathbf w ^{T}\mathbf x _{i}+b|$ is nonsmooth, the gradient in (18) should then be replaced by the subgradient¹. Let $f_{r}(\mathbf x _{i})=\mathbf w _{r}^{T}\mathbf x _{i}+b_{r}$; we have

$$\begin{aligned} \frac{\partial }{\partial \mathbf w }|\mathbf w ^{T}\mathbf x _{i}+b|\Big |_\mathbf{w _{r},b_{r}}&= sgn(\mathbf w _{r}^{T}\mathbf x _{i}+b_{r})\mathbf x _{i},\\ \frac{\partial }{\partial b}|\mathbf w ^{T}\mathbf x _{i}+b|\Big |_\mathbf{w _{r},b_{r}}&= sgn(\mathbf w _{r}^{T}\mathbf x _{i}+b_{r}), \end{aligned}$$

where $sgn(~)$ denotes the sign function. Following CCCP, the $|f(\mathbf x _{i})|$ term in (16) is replaced by its first-order Taylor expansion

$$\begin{aligned}&|\mathbf w _{r}^{T}\mathbf x _{i}+b_{r}|+sgn(\mathbf w _{r}^{T}\mathbf x _{i}+b_{r})[(\mathbf w -\mathbf w _{r})^{T}\mathbf x _{i}+(b-b_{r})]\\&\quad =sgn(\mathbf w _{r}^{T}\mathbf x _{i}+b_{r})(\mathbf w ^{T}\mathbf x _{i}+b)=sgn(f_{r}(\mathbf x _{i}))f(\mathbf x _{i}). \end{aligned}$$

Then, we obtain the following convex optimization problem for each iteration of CCCP:

$$\begin{aligned}&\min _{f,\varvec{\xi }}\left\{ \frac{1}{2}\Vert \mathbf w \Vert ^2 + \lambda \sum _{i=1}^{m}\xi _{i} +\gamma \sum _{j=1}^{n}\widetilde{H}_{j}(f,p^{(t)})\right\} \nonumber \\&\quad subject~to:.~sgn(f_{r}(\mathbf x _{i}))f(\mathbf x _{i})\ge 1-\xi _{i},~\xi _{i}\ge 0, ~i=1,\ldots ,m, \end{aligned}$$

(19)

which can be reformulated into

$$\begin{aligned} \min _{f}\left\{ \frac{1}{2}\Vert \mathbf w \Vert ^2 + \lambda \sum _{i=1}^{m}L(sgn(f_{r}(\mathbf x _{i}))f(\mathbf x _{i})) +\gamma \sum _{j=1}^{n}\widetilde{H}_{j}(f,p^{(t)})\right\} . \end{aligned}$$

(20)

Subsequently, starting with $f_{0}$, we will solve (20) for $f_{r+1}$. Suppose it converges in the $R$-th CCCP iteration, the solution to (15), that is, $f^{(t)}$, is then obtained by $f^{(t)}=f_{R}$.

For solving (20), let

$$\begin{aligned} \hat{y}_{i}&\triangleq&\left\{ \begin{array}{ll} 1&\quad \text{ if}\,f_{r}(\mathbf x _{i})\ge 0;\\ -1&\quad \text{ otherwise.} \end{array} \right.\end{aligned}$$

(21)

$$\begin{aligned} \hat{y}_{j_{1}}&\triangleq&\left\{ \begin{array}{llll} 1&\quad \text{ if}\,\,C_{j}\in \mathcal{ML } \ \text{ and}\ p_{j}^{(t)}=1;\\ -1&\quad \text{ if}\,\,C_{j}\in \mathcal{ML } \ \text{ and} \ p_{j}^{(t)}=0;\\ 1&\quad \text{ if}\,\,C_{j}\in \mathcal{CL } \ \text{ and} \ p_{j}^{(t)}=1;\\ -1&\quad \text{ if}\,\,C_{j}\in \mathcal{CL } \ \text{ and} \ p_{j}^{(t)}=0. \end{array} \right.\end{aligned}$$

(22)

$$\begin{aligned} \hat{y}_{j_{2}}&\triangleq&\left\{ \begin{array}{llll} 1&\quad \text{ if}\,C_{j}\in \mathcal{ML }\ \text{ and} \ p_{j}^{(t)}=1;\\ -1&\quad \text{ if}\,C_{j}\in \mathcal{ML }\ \text{ and}\ p_{j}^{(t)}=0;\\ -1&\quad \text{ if}\,C_{j}\in \mathcal{CL }\ \text{ and}\ p_{j}^{(t)}=1;\\ 1&\quad \text{ if}\,C_{j}\in \mathcal{CL }\ \text{ and}\ p_{j}^{(t)}=0. \end{array} \right. \end{aligned}$$

(23)

We further let $\gamma$ equal to $\lambda$, and then it can be observed that (20) is just a standard SVM problem, with $\{(\mathbf x _{i},\hat{y}_{i})\}_{i=1}^{m}$, $\{(\mathbf x _{j_{1}},\hat{y}_{j_{1}})\}_{j=1}^{n}$ and $\{(\mathbf x _{j_{2}},\hat{y}_{j_{2}})\}_{j=1}^{n}$ being the training examples. The problem in (20) can be efficiently solved by directly applying an off-the-shelf SVM solver, for example, SVM-perf² which is used in this paper. Therefore, subjecting to pairwise constraints, we finally reformulate the two-class clustering problem into a series of supervised binary learning problems and then make use of an effective and efficient SVM solver for optimizing such supervised problems. This makes our proposed method theoretically attractive. Its effectiveness in practice is demonstrated through experiments in Sect. 5.

The detailed procedure for solving (13) using CCCP is summarized in Algorithm 1. We stop the algorithm when the relative difference between objective values of the convex problem in (20) is less than $\epsilon _{1}$ in two successive iterations, which means the current objective value of (20) is only larger than $(1-\epsilon _{1})$ of the objective value in the last iteration. In this paper, $\epsilon _{1}$ is set at $0.01$.

4.2.2 The complete algorithm

A proper initialization for $f$ is critical because the original problem in (5) is nonconvex. We, therefore, provide a heuristic method for the initialization. Since MMC projects each sample to a one-dimensional space with the projection vector $[\mathbf w ^{T}~b]^{T}$, it is expected that the cannot-link pairs of samples should be as far away as possible, while the must-link pairs should be as close as possible. To this end, we try to find a projection vector $\mathbf u \in \mathbb{R }^{d+1}$ to map the data, formed by appending 1 to each instance, into such a space by solving

$$\begin{aligned}&\max _\mathbf{u }\left\{ \frac{1}{N_{c}} \sum _{j:\ell _{j}=-1} \left(\left(\mathbf x _{j_{1}}^{T}~1\right)^{T}\mathbf u -\left(\mathbf x _{j_{2}}^{T}~1\right)^{T}\mathbf u \right)^{2} = \mathbf u ^{T}\mathbf S _{c}\mathbf u \right\} ,\nonumber \\&subject~to:~ \nonumber \\&\frac{1}{N_{m}} \sum _{j:\ell _{j}=1} \left(\left(\mathbf x _{j_{1}}^{T}~1\right)^{T}\mathbf u -\left(\mathbf x _{j_{2}}^{T}~1\right)^{T}\mathbf u \right)^{2}= \mathbf u ^{T}\mathbf S _{m}\mathbf u =1, \end{aligned}$$

(24)

where $N_{c}$ and $N_{m}$ denote the total number of must-link and cannot-link constraints, respectively, and

$$\begin{aligned} \mathbf S _{c}&= \frac{1}{N_{c}}\sum _{j:\ell _{j}=-1}\left[\left(\mathbf x _{j_{1}}^{T}~1\right)-\left(\mathbf x _{j_{2}}^{T}~1\right)\right]^{T}\left[\left(\mathbf x _{j_{1}}^{T}~1\right)-\left(\mathbf x _{j_{2}}^{T}~1\right)\right],\end{aligned}$$

(25)

$$\begin{aligned} \mathbf S _{m}&= \frac{1}{N_{m}}\sum _{j:\ell _{j}=1}\left[\left(\mathbf x _{j_{1}}^{T}~1\right)-\left(\mathbf x _{j_{2}}^{T}~1\right)\right]^{T}\left[\left(\mathbf x _{j_{1}}^{T},1\right)-\left(\mathbf x _{j_{2}}^{T}~1\right)\right]. \end{aligned}$$

(26)

By the Lagrange method, the variable vector $\mathbf u$ can be easily solved, that is, the optimal $\mathbf u$ should be the first eigenvector of $(\mathbf S _{m})^{-1}\mathbf S _{c}$ (it can be obtained by the “eigs( )” function in Matlab). Ultimately, the solution for $\mathbf u$ is used to initialize $f$.

The complete algorithm for the proposed pairwise constrained MMC is summarized in Algorithm 2. We stop the algorithm when the relative difference between objective values of the problem in (9) is less than $\epsilon _{2}$ in two successive iterations. In our later experiments, $\epsilon _{2}$ is set at $0.01$.

Proposition 3

The proposed pairwise constrained two-class MMC algorithm in Algorithm 2 always converges.

Proof

By (14), we have

$$\begin{aligned} \widetilde{Q}\left(f^{(t+1)},\left\{ p_{j}^{(t)}\right\} _{j=1}^{n}\right)\ge \widetilde{Q}\left(f^{(t+1)},\left\{ p_{j}^{(t+1)}\right\} _{j=1}^{n}\right). \end{aligned}$$

Moreover, by the CCCP in Algorithm 1 which solves (13), we have

$$\begin{aligned} \widetilde{Q}\left(f^{(t)},\left\{ p_{j}^{(t)}\right\} _{j=1}^{n}\right)\ge \widetilde{Q}\left(f^{(t+1)},\left\{ p_{j}^{(t)}\right\} _{j=1}^{n}\right). \end{aligned}$$

We, therefore, have

$$\begin{aligned} Q(f^{(t)})&\!=\!&\widetilde{Q}\left(f^{(t)},\left\{ p_{j}^{(t)}\right\} _{j=1}^{n}\right)\!\ge \widetilde{Q}\left(f^{(t+1)},\left\{ p_{j}^{(t)}\right\} _{j=1}^{n}\right)\!\ge \widetilde{Q}\left(f^{(t+1)},\left\{ p_{j}^{(t+1)}\right\} _{j=1}^{n}\right)\\&\!= Q(f^{(t+1)}). \end{aligned}$$

Hence, the objective function $Q(f^{(t)})$ does not increase throughout the iterations in Algorithm 2. Furthermore, note that the objective function for the proposed method in (5) is nonnegative. In other words, its lower bound is $0$. Then, we can conclude that the Algorithm 2 shall converge to a local optimum according to the Gauchys criterion for convergence [52]. $\square$

4.2.3 Time complexity analysis

This section analyzes the time complexity of the proposed pairwise constrained MMC algorithm. For the initialization, it takes $O(nd^{2})$ time to build $\mathbf S _{c}$ and $\mathbf S _{m}$, and the time complexity for solving the eigen problem is $O(d^{2})$ by the eigs() function in Matlab. Therefore, the initialization by finding the projection vector generally takes $O(nd^{2})$ time. In each iteration of the Algorithm 2, the computational cost of calculating $\{p_{j}^{(t)}\}_{j=1}^{n}$ by (14) is $O(nd)$. Algorithm 1 actually performs a sequence of SVM training with the linear kernel. Thanks to the cutting plane optimization techniques utilized by the off-the-shelf SVM solver SVM-Perf [53], the SVM training scales with time $O(d(m+2n))$. Hence, the time complexity of Algorithm 1 can be denoted as $O(d(m+2n))$. Eventually, the overall complexity of the proposed pairwise constrained binary MMC in Algorithm 2 is $O(nd^{2})+O(\bar{T}d(m+2n))$, where $\bar{T}$ is the number of iterations for Algorithm 2 to converge.

4.3 Discussions

In our previous work [26], we have proposed a pairwise constrained multi-class MMC algorithm, whose possible drawback will be discussed when applied for the two-class clustering task in this section. Regarding to a two-class clustering task, [26] reduces to optimize the following problem:

$$\begin{aligned}&\min _\mathbf{w _{1},\mathbf w _{2}}\Bigg \{\frac{\beta }{2}\sum _{r=1}^{2}\Vert \mathbf w _{r}\Vert ^2+\sum _{i=1}^{m}\sum _{r=1}^{2}L\left(\max _{p\in \{1,2\}}\mathbf w _{p}^{T}\mathbf x _{i}-\mathbf w _{r}^{T}\mathbf x _{i}\right) \nonumber \\&\quad +\sum _{j=1}^{n}L\left(\ell _{j}\Big [\max _{r_{1}=r_{2}}\left(\mathbf w _{r_{1}}^{T}\mathbf x _{{j}_{1}}+\mathbf w _{r_{2}}^{T}\mathbf x _{{j}_{2}}\right)-\max _{r_{1}\ne r_{2}}\left(\mathbf w _{r_{1}}^{T}\mathbf x _{{j}_{1}}+\mathbf w _{r_{2}}^{T}\mathbf x _{{j}_{2}}\right)\Big ]\right)\Bigg \}, \end{aligned}$$

(27)

where $\beta$ is a positive constant, $r_{1},r_{2}\in \{1,2\}$, and $\mathbf w _{r}$ is the weight vector for cluster $r$ ($r\in \{1,2\}$). The value $\mathbf w _{r}^{T}\mathbf x _{i}$ is the score for the sample $\mathbf x _{i}$ associated with the cluster $r$, and $\mathbf w _{r_{1}}^{T}\mathbf x _{{j}_{1}}+\mathbf w _{r_{2}}^{T}\mathbf x _{{j}_{2}}$ with $r_{1}=r_{2}$ denotes the score for the pair of samples $\mathbf x _{{j}_{1}}, \mathbf x _{{j}_{2}}$ assigned to the same cluster. $\mathbf w _{r_{1}}^{T}\mathbf x _{{j}_{1}}+\mathbf w _{r_{2}}^{T}\mathbf x _{{j}_{2}}$ with $r_{1}\ne r_{2}$ represents the score for the pair of samples $\mathbf x _{{j}_{1}}, \mathbf x _{{j}_{2}}$ assigned to different clusters. Optimizing such an objective function of the algorithm in [26] essentially requires that the score for assigning a sample to some cluster to which it is most likely to belong should be greater than the score for assigning it to other cluster by at least a margin, and the score for the most possible assigning scheme satisfying the specified pairwise constraint should be always greater than that for any assigning scheme which violates the constraint by at least a margin. It has been demonstrated that the algorithm in [26] features robust penalty for violating the pairwise constraints.

To solve the nonconvex optimization problem in (27), the CCCP is applied to decompose (27) into a series of convex problems [26]. In addition, according to [26], we have $\mathbf w _{1}=-\mathbf w _{2}$ in such convex problems for the two-class clustering case. Therefore, the convex optimization problem in the $t$-th CCCP iteration can be rewritten as follows:

$$\begin{aligned} \min _\mathbf{w _{1},\mathbf w _{2}}\left\{ \frac{\beta }{2}\sum _{r=1}^{2}\Vert \mathbf w _{r}\Vert ^2\!+\!\sum _{i=1}^{m}L\left(2\mathbf w _{p^{*}}^{T}\mathbf x _{i}\right)\!+\sum _{j=1}^{n}L\left(\ell _{j}\big [\mathbf w _{u^{*}}^{T}(\mathbf x _{j_{1}}\!+\mathbf x _{j_{2}})\!-\mathbf w _{v^{*}}^{T}(\mathbf x _{j_{1}}\!-\mathbf x _{j_{2}})\big ]\right)\right\} ,\nonumber \\ \end{aligned}$$

(28)

where

$$\begin{aligned} q^{*}&= \arg \max _{r\in \{1,2\}}\mathbf w _{r}^{(t-1)T}\mathbf x _{i},\\ u^{*}&= \arg \max _{r\in \{1,2\}}\mathbf w _{r}^{(t-1)T}(\mathbf x _{j_{1}}+\mathbf x _{j_{2}}),\\ v^{*}&= \arg \max _{r\in \{1,2\}}\mathbf w _{r}^{(t-1)T}(\mathbf x _{j_{1}}-\mathbf x _{j_{2}}), \end{aligned}$$

and $\mathbf w _{r}^{(t-1)}$ denotes the solution of $\mathbf w _{r}$ in the $(t-1)$-th iteration of CCCP. Considering $\mathbf w _{1}=-\mathbf w _{2}$, it is easy to verify that the item $\big [\mathbf w _{u^{*}}^{T}(\mathbf x _{j_{1}}+\mathbf x _{j_{2}})-\mathbf w _{v^{*}}^{T}(\mathbf x _{j_{1}}-\mathbf x _{j_{2}})\big ]$ takes one of the four values listed in Table 1.

Table 1 The possible values for $\big [\mathbf w _{u^{*}}^{T}(\mathbf x _{j_{1}}+\mathbf x _{j_{2}})-\mathbf w _{v^{*}}^{T}(\mathbf x _{j_{1}}-\mathbf x _{j_{2}})\big ]$

Then (28) can be reformulated as:

$$\begin{aligned} \min _\mathbf{w _{1}}\left\{ \beta \Vert \mathbf w _{1}\Vert ^2+\sum _{i=1}^{m}L\left(\widehat{\ell _{i}}2\mathbf w _{1}^{T}\mathbf x _{i}\right)+\sum _{j=1}^{n}L\left(\ell _{j}2\mathbf w _{1}^{T}\tilde{\mathbf{x }}_{j}\right)\right\} , \end{aligned}$$

(29)

where

$$\begin{aligned} \widehat{\ell _{i}}\triangleq \left\{ \begin{array}{ll} 1&\quad \text{ if}\,\,q^{*}=1;\\ -1&\quad \text{ if}\,\,q^{*}=2, \end{array} \right. \end{aligned}$$

and $\tilde{\mathbf{x }}_{j}$ can be one of the samples from the set $\{\mathbf{x }_{j_{1}},\mathbf x _{j_{2}},-\mathbf x _{j_{1}},-\mathbf x _{j_{2}}\}$ depending on $\mathbf w _{r}^{(t-1)T}$ (see Table 1). Subsequently, let $\mathbf w =2\mathbf w _{1}$, (29) is equivalent to:

$$\begin{aligned} \min _\mathbf{w }\left\{ \frac{\beta }{2}\Vert \mathbf w \Vert ^2+2\sum _{i=1}^{m}L\left(\widehat{\ell _{i}}\mathbf w ^{T}\mathbf x _{i}\right)+2\sum _{j=1}^{n}L\left(\ell _{j}\mathbf w ^{T}\tilde{\mathbf{x }}_{j}\right)\right\} . \end{aligned}$$

(30)

Hence, in essence, for the case of two-class pairwise constrained MMC, optimizing the problem in (30) requires that the sample $\mathbf x _{i}$ $(i=1,\ldots ,m)$ and one of the samples from $\{\mathbf{x }_{j_{1}},\mathbf x _{j_{2}},-\mathbf x _{j_{1}},-\mathbf x _{j_{2}}\}$ $(j=1,\ldots ,n)$ should be as far away from the hyperplane as possible.

In [26], in order to find a good initial model for performing the CCCP, it utilizes only the more reliable supervisory information (i.e., the pairwise constraints) other than the unconstrained samples in the first few iterations of CCCP, that is, it solves the following problem for initializing $\widehat{\ell _{i}}$’s $(i=1,\ldots ,m)$ in (30):

$$\begin{aligned} \min _\mathbf{w }\left\{ \frac{\beta }{2}\Vert \mathbf w \Vert ^2+2\sum _{j=1}^{n}L(\ell _{j}\mathbf w ^{T}\tilde{\mathbf{x }}_{j})\right\} , \end{aligned}$$

(31)

which is a binary SVM problem but without the bias term $b$, and $\ell _{j}$’s $(j=1,\ldots ,n)$ can be viewed as the binary labels for $\tilde{\mathbf{x }}_{j}$’s $(j=1,\ldots ,n)$. However, it is known that the bias term plays a crucial role when the distribution of the labels is uneven [54–57]. Thereby, in a common case, for example, when the positive $\ell _{j}$’s greatly outnumber the negative ones, it may result in an improper hyperplane by the unbiased SVM in (31). Consequently, the so-obtained hyperplane may not be a good initialization for the problem (30). Furthermore, since the original optimization problem of [26] in (27) is nonconvex and CCCP only converges to a local minimum [49], such an initialization may lead to poor solutions eventually. In other words, for the two-class pairwise constrained clustering, when the number of must-link constraints greatly deviates from the number of cannot-link ones, the performance of our previous work in [26] may degrade.

To this end, this paper particularly has designed a new pairwise constrained two-class MMC method. The proposed one and our previous work [26] when applied in two-class clustering differ from each other in two aspects. One is that they use different pairwise loss functions, which lead to different objective functions in the CCCP iterations. Specifically, for a pair of constrained samples, there is only one sample or its negative involved in the objective function in (20), while both of the two samples from the constraint are included in (30). The other is that the proposed new method does include the bias term $b$ in the hyperplane model. Therefore, for the case where the number of must-link constraints and the one of cannot-link constraints are imbalanced, the proposed method is expected to be more robust than our previous work [26] which is, however, particularly developed for handling the multi-class clustering tasks.

5 Experiments

In this section, we evaluated the accuracy and efficiency of our proposed algorithm on a couple of real-world binary-class data sets. Moreover, the generalization capability of the proposed approach, that is, the performance on the out-of-sample data points, was investigated as well. All the experiments were conducted with Matlab 7.0 on a 2.62GHz Intel Dual-Core PC running Windows 7 with 2GB main memory.

5.1 Evaluation metrics

To evaluate the effectiveness of clustering algorithms, we used the clustering accuracy (ACC) and the normalized mutual information (NMI) in this paper. The efficiency of each clustering algorithm was assessed by the central processing unit (CPU) time in seconds during the execution.

Following the strategy in [11, 25, 41], we firstly take a set of labeled data, remove the labels and run the clustering algorithms. Then, we label each of the resulting clusters with the majority class according to the original training labels. Finally, the clustering accuracy (ACC) is defined as the matching degree between the obtained labels and the original true labels [11, 25, 41]:

$$\begin{aligned} ACC=\frac{\sum _{i=1}^{N}I(\hat{t}_{i}=t_{i})}{N}, \end{aligned}$$

(32)

where $N$ is the number of samples in the data set, $\hat{t}_{i}$ is the label obtained by the above steps for $\mathbf x _{i}$, and $t_{i}$ is the ground-truth label. The NMI is defined by [58]:

$$\begin{aligned} NMI=\frac{\sum _{i=1}^{C}\sum _{j=1}^{C}n_{i,j}\log \left(\frac{N\cdot n_{i,j}}{n_{i}\tilde{n}_{j}}\right)}{\sqrt{\left(\sum _{i=1}^{C}n_{i}\log \frac{n_{i}}{N}\right)\left(\sum _{j=1}^{C}\tilde{n}_{j}\log \frac{\tilde{n}_{j}}{N}\right)}} \end{aligned}$$

(33)

where $n_{i}$ denotes the number of data contained in the cluster $\mathcal{C }_{i}(1\le i\le C),\,\tilde{n}_{j}$ is the number of data belonging to the ground-truth class $\mathcal{C }^{^{\prime }}_{j}$ ($1\le j\le C$), and $n_{i,j}$ denotes the number of data that is in the intersection between the cluster $\mathcal{C }_{i}$ and the class $\mathcal{C }^{^{\prime }}_{j}$. The NMI ranges from 0 to 1. The larger the value it is, the more similar the groupings by clustering and those by the true class labels.

5.2 Competing algorithms

We compared the proposed algorithm, denoted as TwoClaCMMC, with the following competing clustering algorithms.

• 1) K-means [59]: This is the traditional unsupervised K-means algorithm without any pairwise constraints incorporated, and it served as the baseline.

• 2) DCA+K-means [15]: The discriminative component analysis (DCA) firstly learns a distance metric based on the pairwise constraints.³ Then, K-means is performed with this metric. This method is a typical metric-based one.

• 3) AffPropag [20]: AffPropag⁴ is a representative pairwise constrained spectral clustering algorithm, which belongs to the similarity-based methods.

• 4) CPCMMC [25]: This is a penalty-based approach, and it is a preliminary work on pairwise constrained two-class maximum margin clustering.

• 5) MultiClaCMMC [26]: This is our previous approach, which is also a penalty-based one. It is proposed in order to overcome the drawbacks of multi-class clustering algorithm in [25].

5.3 Experiments for evaluating the effectiveness and the efficiency

This set of experiments compare the effectiveness and the efficiency of TwoClaCMMC and its competing algorithms.

5.3.1 Evaluation data sets

We used four categories of data sets in this set of experiments for evaluating the effectiveness and the efficiency of all the algorithms. Specifically, those data sets are as follows:

• UCI data: live-disorder, pima, sonar are from the UCI repository.⁵

• Image data: COIL2 ⁶ is a subset from the Columbia object image library (COIL-100), including color images of objects taken from different angles. It is known that there are subgroups within a single semantic class for this data set [60].

• Gene expression data: We performed experiments on two gene expression data sets, and they have high dimensionalities, with many features (i.e., genes) in common for samples from different classes. colon cancer data set consists of samples from two classes of patients: the normal healthy ones and the tumor ones [61]. We preprocessed the raw data by carrying out a base 10 logarithmic transformation. leukemia data set contains samples from two classes of leukemia: the acute lymphoblastic leukemia (ALL) and the acute myeloid leukemia (AML). It has been reported that there are subgroups in the class ALL [62]. The raw leukemia data set was preprocessed following the protocol in [63].

• Text data: 20NewsGroup-Similar2, 20NewsGroup-Related2 are from the 20 newsgroup document databases,⁷ and WebKBPage is from [64]. 20NewsGroup-Similar2 data set consists of 2 newsgroups on similar topics (comp.os.ms-windows, comp.windows.x) with significant cluster overlap. 20NewsGroup-Related2 contains articles from two related topics (talk.politics.misc, talk.politics.guns). The WebKBPage data set is a subset of web documents of the computer science departments of four universities. The two categories are course or noncourse. Each document is represented by the textual content of the webpage. It is known that the articles from these two classes often have a lot of words in common [64].

In a word, most of the data sets used in this set of experiment may feature the multi-modal data distribution within a single semantic class and severe overlap among samples from different classes, thus are quite appropriate for evaluating the robustness of the pairwise constrained clustering algorithms. A summary of all the binary-class data sets used in this set of experiments is shown in Table 2. Note that the values in the parentheses denote sample numbers of the two classes.

Table 2 The data sets used in experiments for evaluating the effectiveness and the efficiency

5.3.2 Evaluation settings

For our method (TwoClaCMMC) and CPCMMC, $\gamma$ was set to be equal to $\lambda$; thus, they both have only one free parameter. Then, $\lambda$ was searched from $\{10^{-3}, 10^{-2}, 10^{-1}, 1{,} 10^{1}, 10^{2}{,} 10^{3}\}$, and the best result was reported on each data set for TwoClaCMMC and CPCMMC. The only one free parameter $\beta$ in MultiClaCMMC was set by searching from the grid $\{10^{-3}, 10^{-2}, 10^{-1}, 1, 10^{1}, 10^{2}, 10^{3}\}$. For AffPropag, to build the basic similarity matrix, the width of the Gaussian kernel was set by exhaustive search from the grid $\{10^{-4}, 10^{-3}, 10^{-2}, 10^{-1}, 1, 10^{1}, 10^{2}, 10^{3}, 10^{4}\}$. The K-means and DCA+K-means do not have free parameters.

Moreover, all the data sets were preprocessed so that their features have zero mean and unit standard deviation, except the three text data sets whose features are already sparse enough. In the experiments, we let the number of clusters be the true number of classes (i.e., $2$) in each data set for all the algorithms, although the selection of the number of clusters is a crucial issue, which is, however, beyond the scope of this paper. For each data set, we evaluated the performance with different numbers of pairwise constraints. As in [20, 25, 26], each constraint was generated by randomly selecting a pair of samples. If the samples belong to the same class, a must-link constraint was formed. Otherwise, a cannot-link constraint was formed. Then, the same constraints are applied to different algorithms. For a fixed number of pairwise constraints, the results were averaged over 10 realizations of different pairwise constraints.

5.3.3 Evaluation results on the effectiveness and the efficiency

To compare the clustering effectiveness, the ACC and NMI curves for the clustering results of all the algorithms are shown in Figs. 3 and 4.⁸

Fig. 3

Comparison of clustering accuracy over the different number of pairwise constraints

 

Fig. 4

Comparison of normalized mutual information over the different number of pairwise constraints

It can be observed that TwoClaCMMC indeed can improve the performance of the baseline K-means, even though the maximum number of constraints provided for each data set in our experiment is only an extremely small fraction of the total number of constraints that can be generated (e.g., $0.12$ % for the COIL2 data set for which only up to 1,000 pairwise constraints are provided, and 0.04 % for the WebKBPage data set for which up to 250 pairwise constraints are provided). Therefore, such a result indicates that the proposed method may be competent in the practical scenarios where the nonexpert users generally label only a small portion of sample pairs for guiding the clustering.

In contrast, the ACC/NMI curves for DCA+K-means often show a slow rise on some data sets with the increase in the amounts of pairwise constraints, or even fall behind those for the baseline. On the one hand, such phenomena may be due to the fact that the unconstrained samples are not involved in the DCA metric learning algorithm. As a result, useful supervision information contained in the insufficient pairwise constraints may not be effectively propagated to the whole data set. On the other hand, the degrading performance of DCA+K-means suggests that the ground-truth metrics for the data used in this set of experiments might be considerably complex in general. Furthermore, one can also observe that the clustering performance of AffPropag is always inferior to that of the proposed algorithm. These observations corroborate the advantage of the proposed discriminative approach, which directly searches the possibly much simpler partitioning boundary and thus makes fewer assumptions about the possibly complicated underlying metric or similarity for the data.

It is also observed that the improvement made by CPCMMC on most data sets is often less significant than those by TwoClaCMMC and MultiClaCMMC. This phenomenon may be due to the reason that there is generally severe overlap in most used data sets and the ground-truth categories may contain subgroups as well, but the loss function for violating the cannot-link constraints in CPCMMC [25] may not be able to effectively discourage the violation of constraints in such scenarios, and the pairwise loss function for the must-link constraints may produce unexpected high penalty even when the must-link constraints are not violated.

Besides, from Figs. 3 and 4, one can observe that although MultiClaCMMC is comparable to TwoClaCMMC on the sonar, COIL2, 20NewsGroup-Similar2, 20NewsGroup-Related2 data sets, its performance is inferior to that of the newly proposed TwoClaCMMC on the remaining data sets, especially when the number of pairwise constraints is small. Recall in our experiment setups a pairwise constraint was generated as follows: randomly selecting a pair of samples and then forming a must-link or cannot-link constraint based on whether the ground-truth labels of such a pair of samples are the same or not. From Table 2, it can be seen that the numbers of positive and negative samples are imbalanced in the live-disorder, pima, colon cancer, leukemia and WebKBPage data sets. Then, for such data sets, according to the permutation and combination theories, such a scheme for producing the pairwise constraints will be prone to result in significantly less cannot-link constraints than must-link constraints (e.g., the average number of must-link constraints is about two times of that of cannot-link constraints, when 30 and 100 constraints were generated for the leukemia and WebKBPage data set, respectively). Then, as we have discussed in Sect. 4.3, the performance of MultiClaCMMC is likely to degrade under such circumstances.

To compare the efficiency, the average and standard deviation of the CPU time consumption for the 10 trials of each constrained clustering algorithm are demonstrated in Fig. 5. It can be seen that the proposed method TwoClaCMMC is generally time efficient. For instance, in this set of experiments, it takes about 30 s to partition the COIL2 data set with the largest number of sample size, and around 10 s to handle the leukemia data set with the largest dimensionality. Although it is not always the fastest algorithm on all the data sets, it is much more advantageous than its counterparts in terms of the accuracy. Moreover, the average and standard deviation of the number of iterations for the proposed approach to converge are shown in Fig. 6. As can be seen from Fig. 6, the proposed method usually converges fast, and the number of iterations for the proposed approach to converge never exceeded $20$ on all the data sets tried so far in this set of experiments.

Fig. 5

Comparison of execution time for the pairwise constrained clustering algorithms

Fig. 6

Number of iterations for convergence of the proposed algorithm

5.4 Experiments for evaluating the generalization performance

In practice, it is often desirable for a clustering algorithm to use the partitioning model or metric, which is learned with a small amount of currently available data, for determining the cluster memberships for newly observed samples. Such a merit is particularly useful for handling the large-scale data, because many clustering algorithms cannot be run on the whole large data sets due to memory problem. The proposed constrained clustering method TwoClaCMMC is essentially based on SVM model, which can achieve small generation error on new data; thus, it is expected to naturally inherit such a merit. In this subsection, a set of experiments compares the generalization performance for some competing algorithms.

5.4.1 Evaluation data sets

We performed experiments on three data sets from UCI repository. Two confusing classes (“I” vs. “J”, “3” vs. “8”) were chosen from the letter and pendigit databases to construct the letterIJ data set and pendigit38 data set, respectively. In addition, magic was used, which is a large-scale data set. The basic information about those data sets is summarized in Table 3.

Table 3 The data sets used in experiments for evaluating the generalization performance

5.4.2 Evaluation settings

For each data set, it was first divided into 10 nonoverlapping folds. Then, we sequentially picked onefold of samples as the out-of-sample points for testing the generalization performance, and the samples in the remaining folds were used as the training set to learn the partitioning model or metric.

With regard to TwoClaCMMC, MultiClaCMMC and CPCMMC, we used the discriminative model learned on the training data to directly cluster the testing data. For DCA+K-means, the metric obtained on the training data was used to perform K-means clustering on the testing data. Note that AffPropag does not provide such a generalization ability; even worse, the large-scale data set magic cannot be run by AffPropag on our machine due to the out-of-memory problem.

5.4.3 Evaluation results on the generalization performance

Figure 7 shows the average results on the previously available data (marked by “train”) and the out-of-sample data (marked by “test”) in the 10-fold runs. As can been seen from Fig. 7, TwoClaCMMC and MultiClaCMMC again outperform CPCMMC as well as DCA+K-means on the out-of-sample data points. Moreover, for TwoClaCMMC and MultiClaCMMC, the clustering performance on out-of-sample examples is comparable with that on the training subset. In other words, for handling large-scale data sets from a practical viewpoint, we may firstly perform TwoClaCMMC on a small subset and then use the learned model to cluster the remaining points.

Fig. 7

Comparison of generalization performance over the different number of pairwise constraints in the 10-fold runs

6 Conclusion

We have presented a discriminative pairwise constrained maximum margin clustering approach. In particular, a new set of pairwise loss functions featuring robust detection and penalization for the violation to the constraints have been proposed. In this way, without explicitly estimating the possibly complex underlying distance metric or similarity matrix, the proposed method directly models the partitioning boundary that separates the data into two groups and fulfills the pairwise constraints as much as possible. An iterative updating algorithm has been developed for the resulting optimization problem. Extensive experiments on real-world data sets demonstrate that the proposed pairwise constrained two-class clustering algorithm could considerably improve the baseline unsupervised clustering. It also outperforms the state-of-the-art pairwise constrained clustering counterparts with the same number of constraints. In addition, the experimental results show that the proposed method generalizes well on the out-of-sample data points.

There are several potential directions for future research. Firstly, we mainly focus on developing a pairwise constrained two-class maximum margin clustering algorithm in this paper; however, it is more common to perform multi-class clustering tasks in real applications. We plan to derive the multi-class extension of the proposed method in the future research. Secondly, the time complexity of the initialization procedure for the proposed method is $O(nd^{2})$, which may be time consuming for very high-dimensional data. More efficient initialization scheme should be developed. Thirdly, it would be also interesting to study how to actively identify the most informative pairwise constraints during the clustering. Lastly, instead of prespecifying the constraints in batch, we will explore the situation where the constraints are incrementally given. We plan to consider the problem of efficiently updating a clustering to satisfy the new and old constraints rather than re-clustering the entire data set.