Instability in spatial error models: an application to the hypothesis of convergence in the European case

Abstract

This paper focuses on the hypothesis of stability in the mechanisms of spatial dependence that are usually employed in spatial econometric models. We propose a specification strategy for which the first step is to solve a local estimation algorithm, called the Zoom estimation. The aim of this stage is to detect problems of heterogeneity in the parameters and to identify the regimes. Then we resort to a battery of formal Lagrange Multipliers to test the assumption of stability in the processes of spatial dependence. The alternative hypothesis consists of the existence of several regimes in these parameters. A small Monte Carlo serves to confirm the behaviour of this strategy in a context of finite size samples. As an illustration, we solve an application to the case of the hypothesis of convergence for the per capita income in the European regions. Our results reveal the existence of a strong Centre-Periphery dichotomy in which instability extends to all the elements (coefficients of regression as well as parameters of spatial dependence) that intervene in a classical conditional β-convergence model.

1 Introduction

The topics of autocorrelation and heterogeneity constitute the nucleus of the research program in spatial econometrics (Anselin 1988a, b). There is widespread literature devoted to both subjects (Anselin et al. 2004), whose recent development may be attributed to the challenges posed by the necessity of disentangling the role played by space in the mechanisms of economic growth. In short, the positive feed-back that exists between the two research agendas, spatial econometrics and economic growth, should be acknowledged.

However, it is rather surprising that, until recently, the topics of autocorrelation and heterogeneity (or interdependence and instability) have been treated separately. The works of Durlauf et al. (2001), Lopez-Bazo et al. (2004), Parent and Riou (2005) and Ertur and Koch (2007), among others, are singular because they introduce local peculiarities into the mechanisms of spatial interaction in neoclassical-type growth models. Each one of them uses a different approach such as technological externalities, investment spillover effects, knowledge diffusion processes, etc, but they coincide in attaining more flexible specifications. Similar efforts to integrate the two topics are also evident in the most recent literature on spatial econometrics. Let us mention the pioneering work of Brunsdon et al. (1998) and the more recent papers of Páez et al. (2002a, b), LeSage and Pace (2004), Ertur et al. (2007) and Mur et al. (2008, 2009).

The purpose of our paper is to progress in this direction by developing a new approach that facilitates the simultaneous treatment of the features of interdependence and heterogeneity. We focus the discussion on the introduction of instability into the mechanisms of spatial dependence. Our proposal combines two different techniques. In the first place, we will solve the local estimation of the model with the objective of identifying clusters of regions which interact differently with their neighbours (López et al. 2009a). We use the local estimation algorithm as a merely descriptive, exploratory technique which produces valuable information in order to test for the existence of parameter instability. This is the purpose of the battery of Lagrange Multipliers that we use in the second stage: testing for the breaks detected previously.

We apply this discussion to the modelling of regional convergence mechanisms. In recent years, several works have appeared which review the situation of the literature on economic growth and convergence (Fingleton 2003; Magrini 2004; Abreu et al. 2005; Durlauf et al. 2005; Arbia 2006). Overall, they confirm the maturity of the discussion and the variety of techniques used to address the problem. Some of the most interesting pieces explicitly consider the role played by space as stated, for example, in Quah (1996, p. 954): ‘physical location and geographical spillover matter more than do national, macro factors’. Spatial econometric techniques occupy a prominent role here, focusing on two distinctive features of the growth processes, namely, spatial interdependence and the lack of uniformity across space. The former is related to the concept of externality (Kubo 1995) whereas the disparity in the initial conditions appears to be ‘crucial to an improved understanding of regional dynamics’ (Rey and Janikas 2005, p. 160). Specifically, the aim is to show that, at least for the European case, these processes are strongly interdependent but far from being homogeneous over space.

The structure of the paper is as follows. In Sect. 2, we present the combination of techniques that, in our opinion, are most adequate to analyse the assumption of parameter stability in cross-sectional equations. In the third section we discuss the results of a small simulation experiment which confirms the adequacy of these techniques. In the fourth section, we review the case of the distribution of per capita income for the regions of the 27 member states of the current European Union, NUTS II level, in the period 1995–2005. We find clear signs of instability in all the β-convergence equations that we specify. Moreover, there emerges a strong centre-periphery regime that needs to be properly treated. The paper finishes with a section of conclusions.

2 Instability in cross-section econometric models

By instability we mean lack of constancy in some, or all, of the parameters of the model, assuming that the functional form and the group of regressors remain effectively unchanged. This is a very well-known problem in mainstream econometrics where there exists a huge amount of literature devoted to the subject, beginning with Chow (1960) and still in progress (see, for example, Zeileis et al. 2005, for a recent review). The difference is that, in our models, the instability will occur over space in such a way that this element, space, should play a prominent role.

This situation has much in common with the problems addressed in the cases of the LISA (Local Indicators of Spatial Association; Anselin 1995) and the GWR (Geographically Weighted Regressions; Fotheringham et al. 1999). However, we are not only interested in detecting ‘pockets of spatial nonstationarity’ (Anselin 1995, p. 94) as in the case of LISA, but also in testing the extent to which the intensity of the spatial dependence in different zones of space is similar (in fact, the detection of spatial nonstationarities is part of the first stage of our approach). With respect to the GWR, we share the reasoning of Fotheringham et al. (1999): the local estimation will provide biased and inconsistent estimations of the parameters, but the size of the bias will probably be smaller than that of other alternatives that do not deal with the problem of heterogeneity. The local estimation is not the best solution, although it could be acceptable in some circumstances.

LeSage and Pace (2004) transfer the discussion to the autoregressive parameter of a Spatial Lag Model (SLM in what follows), proposing an estimation algorithm that they call SALE (the acronym of Spatial Autocorrelation Local Estimation). Ertur and Koch (2007) resort to the SALE algorithm to estimate a heterogeneous spatially-augmented Solow model specified using data at country level. The Bayesian version of this technique, BSALE, appears in Ertur et al. (2007). Mur et al. (2008) follow a similar approach, introducing the Zoom estimation. The idea is to develop an algorithm which solves, for each point in space, the estimation of an equation with a spatial structure. For example, in the case of an SLM:

(1)

y, u and l (R × 1) being vectors of, respectively, the endogenous variable, the error terms and of ones, x an (R, k) matrix of regressors and W an (R, R) weighting matrix; α, β and γ are the (vectors of) parameters that intervene in the ‘global’ model of 1a. Equations 1a and 1b make sense under the assumption of structural parameter homogeneity. However, if the parameters are not stable across space, it is advisable to use the ‘local’ equation which appears in Eq. 1b. The double upper-index ‘(r, m)’ indicates that the data corresponds to the system made up of the (m − 1) nearest regions to the rth. W ^{(r, m)} is the weighting matrix corresponding to this local system, which must reflect the (local) connection network used in the original W matrix and $\mathop y\nolimits_{(r)}^{(r,m)}$ is the corresponding (m, 1) vector of the endogenous (local) variable. Moreover, $\left\{ {\alpha_{r}^{(r,m)} ,\beta_{r}^{(r,m)} ,\gamma_{r}^{(r,m)} ;\; r = 1,2, \ldots ,R} \right\}$ are the local parameters that intervene at point r.

Both models can be estimated by maximum-likelihood methods (ML in what follows), as explained in Mur et al. (2008) and the results can be represented graphically using maps. If there is homogeneity in the parameters, the local estimates will be very similar but, if the parameters (all or some) vary across space, we will obtain heterogeneous maps. As stated, the aim of the Zoom estimation is merely descriptive and should be combined with other, more formal, approaches to gain a better insight into the problem (López et al. 2009a; Mur et al. 2009, for different extensions).

Obviously the two models of Eqs. 1a, 1b are extreme situations of complete homogeneity and full heterogeneity. In some cases, it would be more interesting to allow some parameters to vary while the others remain fixed. By way of an example, if we assume an SLM with a simple centre-periphery break that only affects the parameter of spatial dependence, we may write:

$$ \left. \begin{array}{l} y = \gamma_{0} {\mathbf{W}}y + \gamma_{1} {\mathbf{W}}^{*} y + x\beta + u \hfill \\ u\sim N(0,\sigma^{2} I) \hfill \\ \end{array} \right\} $$

(2)

where γ₀ is the autocorrelation parameter that dominates in one part of space (the periphery, for example) while, in the other part (the centre), a different parameter intervenes whose value is $\gamma_{0} + \gamma_{1}$ ($\gamma_{1}$ measures the difference between the two regimes). Furthermore, W is the weighting matrix that describes the interaction produced in the whole system. This interaction presents some peculiarities in the form of a different intensity in the centre and in the periphery. We use matrix W* to affect one of these groups (the periphery, for example). It is important to highlight that, in order to assure the interpretation of the model, the structure of the interactions should be respected. That is, matrix W* must reproduce exactly the same information that appears in W for the regions involved; the other regions will have a value of zero. Accordingly, $w_{ij}^{*} = w_{ij}$ if the ith or the jth region belongs to the centre, otherwise $w_{ij}^{*} = 0.$

The discussion does not change if we use a Spatial Error Model (SEM). The specification that corresponds to this case is:

$$ \left. \begin{array}{l} y = x\beta + u \hfill \\ u = \rho_{0} {\mathbf{W}}u + \rho_{1} {\mathbf{W}}^{*} u + \varepsilon \hfill \\ \varepsilon \sim N\left( {0,\sigma^{2} I} \right) \hfill \\ \end{array} \right\} $$

(3)

The treatment of a discrete break in the parameter of spatial dependence, of an SLM or an SEM, in two or more regimes does not pose special difficulties and may be solved by ML methods. Huang (1984), Anselin (1990), Rietveld and Wintershoven (1998), LeGallo et al. (2003) and Lacombe (2004), among others, used specifications similar to Eqs. 2 or 3. However, the complexity of the ML algorithm increases rapidly with the number of regimes. For this reason, we think that it is a good idea to test, beforehand, whether it is necessary to introduce some break into the autocorrelation parameter.

This is the approach taken by Mur et al. (2008, 2009), obtaining a test for the existence of a structural break in the parameter of spatial dependence of an SLM, like that of Eq. 2. The final expression of this statistic is the following (see Sect. 6):

$$ \left. {\begin{array}{*{20}c} {\mathop H\nolimits_{0} :\mathop \gamma \nolimits_{1} = 0} \\ {\mathop H\nolimits_{A} :\mathop \gamma \nolimits_{1} \ne 0} \\ \end{array} } \right\} \Rightarrow {\text{LM}}_{\text{break}}^{\text{LAG}} = {\frac{{\left[ {{\frac{{y^{\prime } {\mathbf{W}}^{*} \tilde{u}}}{{\tilde{\sigma }^{2} }}} - {\text{tr}}{\tilde{\mathbf{B}}}^{ - 1} {\mathbf{W}}^{*} } \right]^{2} }}{{\tilde{\sigma }_{\text{lag}}^{2} }}}\mathop \sim \limits_{\text{as}} \chi^{2} (1) $$

(4)

where $\tilde{u}$ is the vector of residuals of the ML estimation of Eq. 2, under the null hypothesis of Eq. 4, ${\tilde{\mathbf{B}}} = I - \mathop {\tilde{\gamma }}\nolimits_{0} {\mathbf{W}},$ $\mathop {\tilde{\sigma }}\nolimits^{2}$ and $\mathop {\tilde{\gamma }}\nolimits_{0}$ are the ML estimates of the two parameters, also under the null hypothesis of Eq. 4, and $\mathop {\tilde{\sigma }}\nolimits_{\text{lag}}^{2}$ is the ML estimation of the variance of the restriction that we are testing. In Sect. 6 we complete this test with the corresponding Lagrange Multiplier associated with the SEM of Eq. 3:

$$ \left. {\begin{array}{*{20}c} {\mathop H\nolimits_{0} :\mathop \rho \nolimits_{1} = 0} \\ {\mathop H\nolimits_{A} :\mathop \rho \nolimits_{1} \ne 0} \\ \end{array} } \right\} \Rightarrow \mathop {\text{LM}}\nolimits_{\text{break}}^{\text{ERR}} = {\frac{{\mathop {\left[ {{\frac{{\tilde{u}^{\prime } \mathop {\mathbf{W}}\nolimits^{*} {\tilde{\mathbf{B}}}\tilde{u}}}{{\mathop {\tilde{\sigma }}\nolimits^{2} }}} - {\text{tr}}\mathop {{\tilde{\mathbf{B}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \right]}\nolimits^{2} }}{{\mathop {\tilde{\sigma }}\nolimits_{\text{err}}^{2} }}}\mathop \sim \limits_{\text{as}} \mathop \chi \nolimits^{2} (1) $$

(5)

All the elements that intervene in the last Multiplier come from the model of Eq. 3, estimated under the null hypothesis. Specifically, $\tilde{u}$ is the vector of ML residuals, ${\tilde{\mathbf{B}}} = I - \mathop {\tilde{\rho }}\nolimits_{0} {\mathbf{W}},$ $\mathop {\tilde{\sigma }}\nolimits^{2}$ and $\mathop {\tilde{\rho }}\nolimits_{0}$ are the ML estimations of the two parameters, and $\mathop {\tilde{\sigma }}\nolimits_{\text{err}}^{2}$ is the estimated variance of the linear restriction of Eq. 5.

Finally, we include a brief reference to the test of common factors of Burridge (1981), a useful technique for discriminating between SLM and SEM (Mur and Angulo 2006). Assuming the existence of a structural break in the mechanisms of spatial dependence, we need (1) to estimate the model of the null hypothesis; (2) to estimate the model of the alternative hypothesis and (3) to compare their likelihoods with the $\mathop {\text{LR}}\nolimits_{\text{break}}^{\text{COM}}$statistic:

(6)

where $l(y)_{{\left| {\mathop H\nolimits_{0} } \right.}}$ and $l(y)_{{\left| {\mathop H\nolimits_{A} } \right.}}$ are the log-likelihoods obtained under the null and alternative hypotheses, respectively. The asymptotic distribution of the test assumes that there are k parameters in vector β which lead to 2k non-linear restrictions in Eq. 6.

3 Small sample behaviour of the $\mathop {\text{LM}}\nolimits_{\text{break}}^{\text{ERR}}$ Lagrange Multiplier

In this section, we will study the behaviour of the $\mathop {\text{LM}}\nolimits_{\text{break}}^{\text{ERR}}$ test by means of a Monte Carlo experiment.¹ In the first part, we present the usual results about the size and power of the test under different scenarios. Then, we check the capacity of the test to identify the spatial units that form part of each of the regimes present in the sample.

The Data Generating Process (DGP in what follows) corresponds to Eq. 3:

$$ \left. \begin{array}{l} y = \alpha + x\beta + u \hfill \\ u = \mathop \rho \nolimits_{0} {\mathbf{W}}u + \mathop \rho \nolimits_{1} \mathop {\mathbf{W}}\nolimits^{*} u + \varepsilon \hfill \\ \varepsilon \sim N(0,\mathop \sigma \nolimits^{2} I) \hfill \\ \end{array} \right\} $$

(7)

Only one regressor appears in the right-hand side of the equation; its values have been obtained from a normal unit distribution, the same as in the case of the random error term ε. The coefficient associated with x takes a value of 3 (β = 3) whereas the value of the intercept is 2 (α = 2). Both values guarantee that, in the absence of spatial effects, the R ² of the regression will be approximately 0.8. We have used a square regular lattice of order (16 × 16) which results in a sample size of 256 observations. This sample size roughly coincides with the application solved in Sect. 4. The weighting matrix W has been specified following a contiguity criterion and rook-type movements. The matrix has been row-standardised. In order to develop the alternative hypothesis, we have introduced a break in the parameter ρ into two regimes, as is indicated in Eq. 7. One of the regimes is located in the centre and the second in the periphery of the lattice. We tried several configurations of the central regime: made up of 36 cells (grouped in a 6 × 6 grid), of 64 cells (a grid of 8 × 8) and of 100 (10 × 10). Each combination has been repeated 1,000 times.

3.1 Size and power of the $\mathop {\text{LM}}\nolimits_{\text{break}}^{\text{ERR}}$ test

Table 1 shows the rate of rejections of the null hypothesis of homogeneity in the spatial dependence parameter for different combinations of the parameters ρ₀ and ρ₁. The size of the test, in the italic row, corresponds to value zero in ρ₁. In general, we can confirm that the empirical size of the test does not differ substantially from the nominal size. Specifically, the composition and shape of the central region does not affect the behaviour of the test.

Table 1 Percentage of rejections of the null hypothesis with the $\mathop {{\rm LM}}\nolimits_{{\rm break}}^{{\rm ERR}}$ test

As expected, the power of the $\mathop {\text{LM}}\nolimits_{\text{break}}^{\text{ERR}}$ test increases when the difference between the spatial dependence parameters of both regimes increases, as measured by ρ₁. Also, the results are slightly better when the coefficient of spatial dependence of the central region is higher than that of the periphery (that is, for positive values of ρ₁). Lastly, it is evident that the lack of symmetry in the composition of the regimes negatively affects the behaviour of the test: the worst results are produced for central regions composed of a small number of units.

3.2 Identification of the regimes by means of the $\mathop {\text{LM}}\nolimits_{\text{break}}^{\text{ERR}}$ test

There is no doubt that the behaviour of the test $\mathop {\text{LM}}\nolimits_{\text{break}}^{\text{ERR}}$ depends on the a priori correct identification of the spatial units that should appear in each regime. In some cases, there will be a well-defined hypothesis that leads us to an initial division of the whole set of regions into a finite number of regimes. In other cases, this information will not be available or the information will be insufficient. The idea is to apply a previous exploratory analysis which may help us in the difficult task of dividing the space into regimes.

Let us call ${\text{LM}}(i,m)_{\text{break}}^{\text{ERR}}$ the value of the statistic $\mathop {\text{LM}}\nolimits_{\text{break}}^{\text{ERR}}$ obtained for the case of a spatial regime made up of the ith region plus the (m − l) regions nearest to it. Also, for each pair (i, m) we will obtain the corresponding specification of matrix W*. With each of these matrices we can solve the corresponding instability test in the parameter of spatial dependence. Finally, if there is really a break in the parameter of spatial dependence, the sequence of statistics ${\text{LM}}(i,m)_{\text{break}}^{\text{ERR}}$ will show a peak when the tentative regime better overlaps the real one.

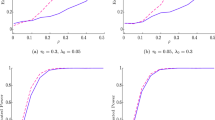
Due to space limitations, we are going to present only the case of a break produced around a central spatial unit and mad up of 64 spatial units in an 8 × 8 regular grid. The combinations simulated in the coefficients are (ρ₀ = 0.5; ρ₁ = 0.4) and (ρ₀ = 0.5; ρ₁ = 0.2), respectively. The most important results appear in Fig. 1 where we present the average of the p-values of the ${\text{LM}}(i,m)_{\text{break}}^{\text{ERR}}$ statistic after 1,000 simulations:

$$ \bar{{\rm L}}\bar{{\rm M}}(i,m)_{{\rm break}}^{{\rm ERR}} = {\frac{1}{1,000}}\sum\limits_{j = 1}^{1,000} {{\rm LM}(i,m)_{{\rm break}}^{{\rm ERR}} } $$

(8)

The results are promising given that, overall, the procedure tends to correctly identify the spatial units involved in the problem of parameter instability. The identification is more precise when the difference between the coefficients of spatial dependence (ρ₀; ρ₁) of the two regimes increases. When this difference is small the procedure is not so well-behaved. Other proposals to deal with the same problem can be found in López et al. (2009a), where they develop a kind of cluster analysis using the local estimates, and in López et al. (2009b), that contains a more formal solution.

Fig. 1

p-Values corresponding to the average of the simulated multipliers: $\bar{\rm L}\bar{\rm M}(i,m)_{\rm break}^{\rm ERR}$

4 Instability and heterogeneity: an application to the case of the European regions

In this section, we are going to apply the proposal developed in the previous two sections to a well-known case in spatial analysis, the hypothesis of convergence. The literature on this subject reveals a tendency to give greater flexibility to the equation that develops the assumption of convergence. Specifically, we are interested in the simultaneous treatment of the features of heterogeneity and spatial dependence. The papers of LeGallo and Dall’Erba (2006), Fischer and Stirböck (2006) and Ramajo et al. (2008) are some of the most recent on the subject. In general, they use a dummy variables framework with the aim of introducing differences into the convergence rates of regions. This technique is of a discrete nature (that is, there is finite number of regimes) and gives support to the concept of convergence clubs. Ertur and Koch (2007) and Ertur et al. (2007) are exceptions to the discrete approach because they adopt a local approach to the processes of convergence.

We focus on the per capita Gross Domestic Product (GDPpc from now on), in purchasing power parity units, corresponding to a total of 262 regions, NUTS II level, from the 27 countries that are currently members of the European Union (EU27). For different reasons, various regions have been excluded, among them the Canary Islands, Ceuta, Melilla and the Portuguese archipelagos of the Azores and Madeira. The data used in our analysis comes from the Cambridge Econometrics and REGIO databanks and covers the period 1995–2005.

4.1 A first look at the problem of instability in regional convergence models: the European case

Let us call y _rt the regional per capita income in region r at the beginning of the period, year t, and $g_{{y_{rt,t + n} }}$ its corresponding growth rate between the years t and t + n; in our case t = 1,985 and n = 10. In the literature devoted to the topic, there is a clear preference for conditional β-convergence equations such as:

$$ \mathop g\nolimits_{{\mathop y\nolimits_{rt,t + n} }} = \alpha + \beta \mathop {{ \ln }y}\nolimits_{{\mathop 0\nolimits_{rt} }} + \sum\limits_{j = 1}^{k} {\mathop x\nolimits_{{\mathop j\nolimits_{rt} }} \mathop \delta \nolimits_{j} } + \mathop u\nolimits_{rt} $$

(9a)

where ${ \ln }y_{{0_{rt} }}$ is the logarithm of the per capita income in region r, t is the base year and $\{ \mathop x\nolimits_{{\mathop 1\nolimits_{rt} }} ;\,\mathop x\nolimits_{{\mathop 2\nolimits_{rt} }} ; \ldots ;\mathop x\nolimits_{{\mathop k\nolimits_{rt} }} \}$ are a set of conditioning factors. These variables, in our case, are the weight of the agricultural sector in the regional product, x ₁, the percentage of the regional working population occupied in technological activities, x ₂, and the regional population density, x ₃.² The results of the estimation of this model appear in the first column of Table 2. There are clear signs of misspecification due to an omitted spatial structure.

Table 2 Models of β-convergence estimated with spatial regimes

The second column of Table 2 contains the estimation of an SLM:

$$ \mathop g\nolimits_{{\mathop y\nolimits_{rt,t + n} }} = \alpha + \beta \mathop {{ \ln }y}\nolimits_{{\mathop 0\nolimits_{rt} }}\,+\,\theta \sum\limits_{s = 1}^{R} {\mathop w\nolimits_{rs} \mathop {{ \ln }y}\nolimits_{{\mathop 0\nolimits_{st} }} } + \sum\limits_{j = 1}^{k} {\mathop x\nolimits_{{\mathop j\nolimits_{rt} }} \mathop \delta \nolimits_{j} } + \gamma \sum\limits_{s = 1}^{R} {\mathop w\nolimits_{rs} \mathop g\nolimits_{{\mathop y\nolimits_{st,t + n} }} } + \mathop u\nolimits_{rt} $$

(9b)

and the third column the estimation of an SEM:

$$ \mathop g\nolimits_{{\mathop y\nolimits_{rt,t + n} }} = \alpha + \beta \mathop {{ \ln }y}\nolimits_{{\mathop 0\nolimits_{rt} }} + \sum\limits_{j = 1}^{K} {\mathop x\nolimits_{{\mathop j\nolimits_{rt} }} \mathop \delta \nolimits_{j} } + \sum\limits_{s = 1}^{R} {\mathop b\nolimits_{rs}^{ - 1} \mathop u\nolimits_{rt} } $$

(9c)

In both cases, w _rs refers to the (r, s) element of a W weighting matrix specified by combining the criteria of distance (with an interaction radius of 100 km) and of the two nearest neighbours (as in Mur et al. 2008, 2009); $b_{rs}^{ - 1}$ is the corresponding element of the diffusion matrix $\mathop {\mathbf{B}}\nolimits^{ - 1} = \mathop {\left( {I - \rho {\mathbf{W}}} \right)}\nolimits^{ - 1}$. Clearly the symptoms of misspecification, due to an omitted cross-sectional dependence structure, have almost disappeared. Finally, note that the LRCOM shows a clear preference for the SEM of Eq. 9c.

The question now is what happens with the (maintained) assumption of stability. We begin by solving the local Zoom estimation of the conditional β-convergence model of Eq. 9a, which can be expressed as:³

$$ \mathop g\nolimits_{y}^{(r,m)} = \mathop \alpha \nolimits^{(r,m)} \,+\, \beta^{(r,m)} \mathop {{ \ln }y}\nolimits_{0}^{(r,m)} \,+\, x^{\prime}\delta^{(r,m)} + \mathop u\nolimits^{(r,m)} ;\quad \mathop u\nolimits^{(r,m)} \sim N(0,\mathop \sigma \nolimits_{(r,m)}^{2} I_{m} ) $$

(10)

The results corresponding to the series of local estimates, $\left\{ {\beta^{(r,m)} ,r = 1,2, \ldots ,R} \right\}$ for different values of m, are summarized in Fig. 2.

Fig. 2

Local estimation of the parameter of β-convergence: Eq. 9a

The regions where the local estimate of β^{(r, m)} is not significant are coloured in light grey. If the coefficient is significant and negative the region appears in black and if it is significant and positive in dark grey. It is clear that, as we increase the size of the Zoom (using a higher value of m), a more regular spatial pattern emerges. There is a homogenous block made up of French, British, Dutch, Belgian and German regions always in light and dark grey, implying the absence of convergence at a local scale; on the contrary, the colour black, synonym of convergence at a local scale, extends towards the periphery of the continent.

In Fig. 3, we present the results of the procedure of identifying regimes based on the sequence of values of the ${\text{LM(}}i,m)_{\text{break}}^{\text{ERR}}$ statistic. Depending on the simulation, we used two values for the parameter m, 40 and 80.

Fig. 3

Regimes of spatial interaction according to a SEM approach

Once again, in Fig. 3 a central-periphery structure which affects the mechanisms of spatial dependence clearly emerges. Specifically, the regions situated in the centre of the continent maintain a greater interaction with their neighbours than those situated in the exterior zones.

Figure 4 shows the quartiles of the local estimation of the parameter of spatial dependence of the SEM of Eq. 9c:

$$ \mathop g\nolimits_{{\mathop y\nolimits_{rt,t + n} }} = \mathop \alpha \nolimits^{(r,m)}\,+\, \beta^{(r,m)} \mathop {{ \ln }y}\nolimits_{{\mathop 0\nolimits_{rt} }} + \sum\limits_{j = 1}^{k} {\mathop x\nolimits_{{\mathop j\nolimits_{rt} }} \mathop \delta \nolimits_{j}^{(r,m)} } + \sum\limits_{s = 1}^{R} {\mathop b\nolimits_{rs}^{{\mathop {(r,m)}\nolimits^{ - 1} }} \mathop u\nolimits_{rt} } $$

(11)

where $\mathop b\nolimits_{rs}^{{\mathop {(r,m)}\nolimits^{ - 1} }}$ refers to the (r, s) element of the local diffusion matrix $\mathop {\mathbf{B}}\nolimits^{{\mathop {(r,m)}\nolimits^{ - 1} }} = \mathop {( {I - \mathop \rho \nolimits_{r}^{(r,m)} \mathop {\mathbf{W}}\nolimits^{(r,m)} } )}\nolimits^{ - 1}$ that operates around region r and $\mathop \rho \nolimits_{r}^{(r,m)}$ is the corresponding local spatial dependence parameter.

Fig. 4

Locally estimated spatial dependence parameter $\mathop \rho \nolimits_{r}^{(r,m)}$. SEM case. m = 40

Lastly, Fig. 5 summarizes the structure of spatial regimes that emerges by combining all the previous information.

Fig. 5

Regimes of spatial dependence for the European case: centre and periphery

The centre is made up of a macro-region characterized by weak symptoms of convergence but strong relationships of spatial dependence. This cluster includes a total of 125 units from Western Germany, Holland, Belgium, Luxembourg, Austria, the South of the United Kingdom, Ireland, Northern France and Italy. The other 137 regions constitute the periphery and are characterized by a lower income, the existence of an apparently homogeneous tendency towards convergence and weaker spatial relations.

4.2 Duality in the mechanisms of convergence and of spatial dependence

According to this Centre-Periphery dichotomy, we can not accept the null hypothesis of homogeneity in the coefficient of regression in any of the models in Eqs. 9a–9c, as indicated by the Chow test that appears in Table 2. This evidence confirms the suspicions of structural instability. Below, in Eqs. 12a and 12b, we allow the mechanism of β-convergence to differ between the two groups of regions:

$$ \left. \begin{aligned} g_{y} &= \alpha + \beta_{c} D_{c} \ln y_{0} + \beta_{p} D_{p} \ln y_{0} + D_{c} x^{\prime } \delta_{c} + D_{p} x^{\prime } \delta_{p} \\&\quad + \theta_{c} D_{C} {\mathbf{W}} \ln y_{0} + \theta_{p} D_{P}{\mathbf{W}}\ln y_{0} + \gamma {\mathbf{W}}g_{y} + u \hfill\\ \end{aligned} \right\} $$

(12a)

$$ \mathop g\nolimits_{y} = \alpha + \beta_{c} D_{c} \mathop {{ \ln }y}\nolimits_{0}\,+\,\beta_{p} D_{p} \mathop {{ \ln }y}\nolimits_{0} \,+\, D_{c} x^{\prime } \delta_{c} + D_{p} x^{\prime } \delta_{p} + \left[ {I - \rho {\mathbf{W}}} \right]^{ - 1} u $$

(12b)

The estimations included in the respective columns of Table 2 corroborate the importance of the break. In general, there is a higher speed of convergence in the periphery than in the central regions. The differences also extend to the other parameters. Interestingly, the LRCOM test continues in favour of the SEM of Eq. 12b.

Nevertheless, there are still signs of instability in the parameters of spatial dependence in both equations, as shown by the ${\text{LM}}_{\text{break}}^{\text{LAG}}$ and ${\text{LM}}_{\text{break}}^{\text{LAG}}$ tests. The solution is to extend the break also to the spatial dependence mechanisms, as in the specifications of 12c and 12d:

$$ \left. \begin{aligned} \mathop g\nolimits_{y}& = \alpha + \beta_{c} D_{c} \mathop {{ \ln }y}\nolimits_{0} + \beta_{p} D_{p} \mathop {{ \ln }y}\nolimits_{0} + \mathop \theta \nolimits_{c} D_{c} {\mathbf{W}}\mathop {{ \ln }y}\nolimits_{0} + \mathop \theta \nolimits_{p} D_{P} {\mathbf{W}}\mathop {{ \ln }y}\nolimits_{0} \hfill \\ &\quad + D_{c} x^{\prime}\delta_{c} + D_{p} x^{\prime}\delta_{p} + \gamma {\mathbf{W}}\mathop g\nolimits_{y} + \mathop \gamma \nolimits_{c}^{*} \mathop {\mathbf{W}}\nolimits^{*} \mathop g\nolimits_{y} + x^{\prime}\delta + u \hfill \\ \end{aligned} \right\} $$

(12c)

$$ g_{y} = \alpha + \beta_{c} D_{c} \mathop {{ \ln }y}\nolimits_{0} + \beta_{p} D_{p} \mathop {{ \ln }y}\nolimits_{0} \,+\, D_{c} x^{\prime}\delta_{c} + D_{p} x^{\prime}\delta_{p} + \left[ {I - \rho {\mathbf{W}} - \mathop \rho \nolimits_{c}^{*} \mathop {\mathbf{W}}\nolimits^{*} } \right]^{ - 1} u $$

(12d)

The matrix W* affects only the regions belonging to the Central regime and has been specified according to Fig. 5. Both equations appear to be acceptable in the sense that they do not fail the specification tests. Moreover, the estimations, which now differ only slightly, are always produced in the expected sense. The ${\text{LR}}_{\text{break}}^{\text{COM}}$ test indicates that we cannot reject the restrictions of common factors underlying the model of Eq. 12d, although the evidence in favour of SEM structures is weaker than in previous cases. So we may conclude by choosing Eq. 12d as the best specification for explaining the European experience in the period 1995–2005.

According to our estimates, it is clear that the discrepancy between the two regimes directly affects the processes of cross-sectional dependence. For example, in model given by Eq. 12d, where these mechanisms are assumed to be constant, the estimation of the coefficient of spatial dependency is relatively high, 0.614, compared to other studies. If we introduce a break into the two regimes, as is done in Eq. 12d, we obtain a significantly lower estimation for the periphery, with a value of 0.493, while the coefficient corresponding to the regions of the centre of the continent is almost 50% higher, with a value of 0.713 (adding the values of γ = 0.493 and γ _c  = 0.238).

Except for this issue, our results largely coincide with others in the literature dealing with the convergence hypothesis for the European regions. For example, as underlined by Fingleton and Lopez-Bazo (2006), there exists a preference in favour of SEM structures that, in our case, is consistently corroborated by the LRCOM test. The same can be said in relation to the differences in the rate of convergence (Baumont et al. 2003): after discounting the differences in the long-run steady state between the centre and the periphery, there is still a slightly higher speed of convergence in the central regions (of almost four hundredths). The recent incorporation of a large group of regions from Eastern Europe, with a much lower income level, has not significantly altered this situation; on the contrary, it has served to accentuate the centre-periphery dichotomy. There are also some discrepancies, especially in the estimated values, that may be attributed to differences in the temporal span, in the spatial breakdown or, simply, to the source of the data used in our analysis.

5 Conclusions

Heterogeneity and dependence are characteristic features of econometric models with a spatial base and are very often confused because they produce similar symptoms. In this work, we have explored a new approach which combines the two mechanisms in a more general framework of spatial instability.

Some other authors have previously discussed the same problem (as in Brunsdon et al. 1998; Páez et al. 2002a, b; LeSage and Pace 2004; Egger and Pfaffermayr 2006). The contribution of our paper focuses on the part of the diagnostic, as a necessary previous step before resorting to costly algorithms of local estimation. We present a strategy organized in three steps. The first one is of an exploratory nature and consists of the application of an intensive local estimation algorithm, looking for spatial regimes and symptoms of structural breaks. The second stage is of a confirmatory nature and we have to test the significance of the spatial break identified in the first stage, using some of the Lagrange Multipliers presented in Sect. 3. The third stage estimates the corresponding specification.

To illustrate our proposal, we present an application to the case of the per capita income of the European regions. Using data for 262 regions observed during a rather short time period (1995–2005), our evidence reveals the existence of a strong break in the process of convergence in terms of a classical centre-periphery model. Some of the results found in the paper are similar to other studies like, for example, the preference for SEM structures or the detection of a slightly higher rate of convergence in the central regions of the continent. Our work completes this picture by extending the break also to the mechanisms of spatial dependence that operate in both areas, centre and periphery. We find that the dependence is stronger in the central regions, probably due to the existence of more and better infrastructures of transport and communications that facilitate the interaction between them.

Appendix: Tests for the existence of a structural break in the mechanisms of spatial interaction

In this Appendix, we are going to obtain the expressions of the Lagrange Multipliers of Eqs. 4 and 6 with which we test for the existence of a break in the parameter of spatial dependence. The first part of the appendix is dedicated to the SLM and the second to a SEM.

1.1 The case of the SLM⁴

The equation for this case appears in expression given by Eq. 4 in the text:

$$ \left. \begin{array}{l} y = \mathop \gamma \nolimits_{0} {\mathbf{W}}y + \mathop \gamma \nolimits_{1} \mathop {\mathbf{W}}\nolimits^{*} y + x\beta + u \hfill \\ u\sim N(0,\mathop \sigma \nolimits^{2} I) \hfill \\ \end{array} \right\} $$

(A1)

whose log-likelihood function is:

$$ l(y;\varphi ) = -\, {\frac{R}{2}}{ \log }(2\pi ) - {\frac{R}{2}}{ \log }(\mathop \sigma \nolimits^{2} ) - {\frac{{\left( {{\mathbf{B}}y - x\beta } \right)^{\prime } \left( {{\mathbf{B}}y - x\beta } \right)}}{{2\mathop \sigma \nolimits^{2} }}} + { \log }\left| {\mathbf{B}} \right| $$

(A2)

where φ is the vector of parameters of the model, φ = [β, γ₀, γ₁, σ²]′, and B is a square matrix of order (R, R), ${\mathbf{B}} = I - \mathop \gamma \nolimits_{0} {\mathbf{W}} - \mathop \gamma \nolimits_{1} \mathop {\mathbf{W}}\nolimits^{*}$. The score vector is the following:

$$ g(y;\varphi ) = {\frac{\partial l(y;\varphi )}{\partial \varphi }} = {\frac{1}{{\mathop \sigma \nolimits^{2} }}}\left[ {\begin{array}{*{20}c} {x^{\prime}\left( {{\mathbf{B}}y - x\beta } \right)} \\ {y^{\prime}{\mathbf{W^{\prime}}}\left( {{\mathbf{B}}y - x\beta } \right) + \mathop \sigma \nolimits^{2} {\frac{{\partial { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \gamma \nolimits_{0} }}}} \\ {y^{\prime}{\mathbf{W}}^{*\prime } \left( {{\mathbf{B}}y - x\beta } \right) + \mathop \sigma \nolimits^{2} {\frac{{\partial { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \gamma \nolimits_{1} }}}} \\ { - {\frac{R}{2}} + {\frac{{\left( {{\mathbf{B}}y - x\beta } \right)^{\prime } \left( {{\mathbf{B}}y - x\beta } \right)}}{{2\mathop \sigma \nolimits^{2} }}}} \\ \end{array} } \right] $$

(A3)

Under the assumption that there is no break in the coefficient of spatial dependence, this vector simplifies to:

$$ \left. {\begin{array}{*{20}c} {\mathop H\nolimits_{0} :\mathop \gamma \nolimits_{1} = 0} \\ {\mathop H\nolimits_{A} :\mathop \gamma \nolimits_{1} \ne 0} \\ \end{array} } \right\} \Rightarrow \mathop {g(y;\varphi )}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {{\frac{{y^{\prime}{\mathbf{W}}^{*\prime } \tilde{u}}}{{\mathop {\tilde{\sigma }}\nolimits^{2} }}} - {\text{tr}}\left[ {\mathop {\left( {I - \mathop {\tilde{\gamma }}\nolimits_{0} {\mathbf{W}}} \right)}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \right]} \\ 0 \\ \end{array} } \right] $$

(A4)

where $\mathop {\tilde{\gamma }}\nolimits_{0}$ and $\mathop {\tilde{\sigma }}\nolimits^{2}$ are the ML estimations of γ₀ and σ² and $\tilde{u}$ is the corresponding series of residuals of the restricted model:

$$ \left. \begin{array}{l} y = \mathop \gamma \nolimits_{0} {\mathbf{W}}y + x\beta + u \hfill \\ u\sim N(0,\mathop \sigma \nolimits^{2} I) \hfill \\ \end{array} \right\} $$

(A5)

The structure of the Hessian matrix is a bit complex:

$$ \begin{gathered} {\frac{{\mathop \partial \nolimits^{2} l(y;\varphi )}}{{\partial \varphi \partial \varphi^{\prime}}}} = - {\frac{1}{{\mathop \sigma \nolimits^{2} }}}\left[ {\begin{array}{*{20}c} {x^{\prime}x} & {x^{\prime}{\mathbf{W^{\prime}}}y} & {x^{\prime}{\mathbf{W}}^{*\prime } y} & {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}x^{\prime}u} \\ {y^{\prime}{\mathbf{W}}x} & {y^{\prime}{\mathbf{W^{\prime}W}}y - \mathop \sigma \nolimits^{2} {\frac{{\mathop \partial \nolimits^{2} { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \gamma \nolimits_{0}^{2} }}}} & {y^{\prime}{\mathbf{W^{\prime}}}\mathop {\mathbf{W}}\nolimits^{*} y - \mathop \sigma \nolimits^{2} {\frac{{\mathop \partial \nolimits^{2} { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \gamma \nolimits_{0} \partial \mathop \gamma \nolimits_{1} }}}} & {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}y^{\prime}{\mathbf{W^{\prime}}}u} \\ {y^{\prime}\mathop {\mathbf{W}}\nolimits^{*} x} & {y^{\prime}{\mathbf{W}}^{*\prime } {\mathbf{W}}y - \mathop \sigma \nolimits^{2} {\frac{{\mathop \partial \nolimits^{2} { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \gamma \nolimits_{0} \partial \mathop \gamma \nolimits_{1} }}}} & {y^{\prime}{\mathbf{W}}^{*\prime } \mathop {\mathbf{W}}\nolimits^{*} y - \mathop \sigma \nolimits^{2} {\frac{{\mathop \partial \nolimits^{2} { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \gamma \nolimits_{1}^{2} }}}} & {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}y^{\prime}{\mathbf{W}}^{*\prime } u} \\ {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}u^{\prime}x} & {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}u^{\prime}{\mathbf{W}}y} & {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}u^{\prime}\mathop {\mathbf{W}}\nolimits^{*} y} & { - {\frac{R}{{\mathop {2\sigma }\nolimits^{2} }}} + {\frac{{u^{\prime}u}}{{\mathop \sigma \nolimits^{4} }}}} \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(A6)

The information matrix evaluated under the null hypothesis is the following:

$$ \begin{gathered} {\mathbf{I}}(\varphi ) = - \mathop {E\left[ {{\frac{{\mathop \partial \nolimits^{2} l(y;\varphi )}}{{\partial \varphi \partial \varphi^{\prime}}}}} \right]}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} = {\frac{1}{{\mathop \sigma \nolimits^{2} }}}\left[ {\begin{array}{*{20}c} {x^{\prime}x} & {x^{\prime}{\mathbf{W^{\prime}}}\mathop {\mathbf{B}}\nolimits^{ - 1} x\beta } & {x^{\prime}{\mathbf{W}}^{*\prime } \mathop {\mathbf{B}}\nolimits^{ - 1} x\beta } & 0 \\ {\beta^{\prime}x^{\prime}\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} {\mathbf{W}}x} & \begin{gathered} \left\{ {\beta^{\prime}x^{\prime}\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{'} } \right.{\mathbf{W}}\mathop {\mathbf{B}}\nolimits^{ - 1} x\beta \hfill \\ \left. { + 2\mathop \sigma \nolimits^{2} {\text{tr}}\mathop {\mathbf{B}}\nolimits^{ - 1} {\mathbf{W}}\mathop {\mathbf{B}}\nolimits^{ - 1} {\mathbf{W}}} \right\} \hfill \\ \end{gathered} & \begin{gathered} \left\{ {\beta^{\prime}x^{\prime}\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} {\mathbf{W^{\prime}}}} \right.\mathop {\mathbf{W}}\nolimits^{*} \mathop {\mathbf{B}}\nolimits^{ - 1} x\beta \hfill \\ \left. { + 2\mathop \sigma \nolimits^{2} {\text{tr}}\mathop {\mathbf{B}}\nolimits^{ - 1} {\mathbf{W}}\mathop {\mathbf{B}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \right\} \hfill \\ \end{gathered} & {{\text{tr}}\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} {\mathbf{W}}} \\ {\beta^{\prime}x^{\prime}\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} x} & \begin{gathered} \left\{ {\beta^{\prime}x^{\prime}\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} {\mathbf{W^{\prime}}}} \right.\mathop {\mathbf{W}}\nolimits^{*} \mathop {\mathbf{B}}\nolimits^{ - 1} x\beta \hfill \\ \left. { + 2\mathop \sigma \nolimits^{2} {\text{tr}}\mathop {\mathbf{B}}\nolimits^{ - 1} {\mathbf{W}}\mathop {\mathbf{B}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \right\} \hfill \\ \end{gathered} & \begin{gathered} \left\{ {\beta^{\prime}x^{\prime}\mathop {\mathbf{B}}\nolimits^{ - 1} {\mathbf{W}}^{*\prime } } \right.\mathop {\mathbf{W}}\nolimits^{*} \mathop {\mathbf{B}}\nolimits^{ - 1} x\beta \hfill \\ \left. { + 2\mathop \sigma \nolimits^{2} {\text{tr}}\mathop {\mathbf{B}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} \mathop {\mathbf{B}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \right\} \hfill \\ \end{gathered} & {{\text{tr}}\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \\ 0 & {{\text{tr}}{\mathbf{W^{\prime}}}\mathop {\mathbf{B}}\nolimits^{ - 1} } & {{\text{tr}}{\mathbf{W}}^{*\prime } \mathop {\mathbf{B}}\nolimits^{ - 1} } & {{\frac{R}{{\mathop {2\sigma }\nolimits^{2} }}}} \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(A7)

The Lagrange Multiplier for the test of Eq. A4 is obtained in the usual way:

$$ \begin{aligned} \left. {\begin{array}{*{20}l} {\mathop H\nolimits_{0} :\mathop \gamma \nolimits_{1} = 0} \\ {\mathop H\nolimits_{A} :\mathop \gamma \nolimits_{1} \ne 0} \\ \end{array} } \right\} &\Rightarrow \mathop {{\rm LM}}\nolimits_{{\rm break}}^{{\rm LAG}} = \left[ {\mathop {g\left( \varphi \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]^{\prime } \mathop {\left[ {\mathop {I\left( \varphi \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]}\nolimits^{ - 1} \left[ {\mathop {g\left( \varphi \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]\mathop \sim \limits_{{\rm as}} \mathop \chi \nolimits^{2} (1) \\ \mathop {{\rm LM}}\nolimits_{{\rm break}}^{{\rm LAG}} &= {\frac{{\mathop {\left[ {{\frac{{y^{\prime } \mathop {\mathbf{W}}\nolimits^{*} \tilde{u}}}{{\mathop {\tilde{\sigma }}\nolimits^{2} }}} - {\rm tr}\mathop {{\tilde{\mathbf{B}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \right]}\nolimits^{2} }}{{\mathop {\tilde{\sigma }}\nolimits_{{\rm lag}}^{2} }}}\mathop \sim \limits_{{\rm as}} \mathop \chi \nolimits^{2} (1) \\ \end{aligned} $$

(A8)

The term $\mathop {\tilde{\sigma }}\nolimits_{\text{lag}}^{2}$ in the denominator is the asymptotic variance of the restriction corresponding to the null hypothesis, obtained as:

$$ \begin{gathered} {\tilde{\sigma }}_{\text{lag}}^{2} = \tilde{a} - \tilde{b}^{\prime} {{\tilde{\mathbf{V}}}\left[ {\tilde{\varphi }} \right]}_{{\left| { H_{0} } \right.}} \tilde{b} \hfill \\ \begin{array}{*{20}c} \to & {\tilde{a} = {\frac{{\tilde{\beta }^{\prime}x^{\prime}{{\tilde{\mathbf{B}}}}^{ - 1} {\mathbf{W}}^{\prime *} {\mathbf{W}}^{*} {{\tilde{\mathbf{B}}}}^{ - 1} x\tilde{\beta }}} {{{\tilde{\sigma }}^{2} }}} + 2{\text{tr}}{{\tilde{\mathbf{B}}}}^{ - 1} {\mathbf{W}}^{*} {{\tilde{\mathbf{B}}}}^{ - 1} {\mathbf{W}}^{*} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} \to & {\tilde{b} = {\frac{1}{{{\tilde{\sigma }}^{2} }}} \left[ {\begin{array}{*{20}c} {x^{\prime}{\mathbf{W}}^{\prime *} {{\tilde{\mathbf{B}}}}^{ - 1} x\tilde{\beta }} \\ {\tilde{\beta }^{\prime}x^{\prime} {{\tilde{\mathbf{B}^{\prime}}}} ^{ - 1} {\mathbf{W^{\prime}}} {\mathbf{W}}^{*} {{\tilde{\mathbf{B}}}}^{ - 1} x\tilde{\beta } + 2 {\tilde{\sigma }}^{2} {\text{tr}} {{\tilde{\mathbf{B}}}}^{ - 1} {\mathbf{W}} {{\tilde{\mathbf{B}}}}^{ - 1} {\mathbf{W}}^{*} } \\ {{\text{tr}} {{\tilde{\mathbf{B}^{\prime}}}}^{ - 1} {\mathbf{W}}^{*} } \\ \end{array} } \right]} \\ \end{array} \hfill \\ \end{gathered} $$

(A9)

Matrix $\mathop {{\tilde{\mathbf{V}}}\left[ {\tilde{\varphi }} \right]}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}}$ is the ML estimation of the corresponding variance matrix of the vector of parameters under the null hypothesis of Eq. A8. The Lagrange Multiplier of Eq. A8 can easily be generalized to the more general case in which there are p different regimes in the coefficient of autocorrelation. The extended model corresponding to this case is:

$$ \left. \begin{array}{l} y = \mathop \gamma \nolimits_{0} {\mathbf{W}}y + \sum\limits_{s = 1}^{p} {\mathop \gamma \nolimits_{s} \mathop {\mathbf{W}}\nolimits_{s}^{*} y} + x\beta + u \hfill \\ u\sim N(0,\mathop \sigma \nolimits^{2} I) \hfill \\ \end{array} \right\} $$

(A10)

The null hypothesis will be of the joint type:

$$ \begin{aligned} & \left. {\begin{array}{*{20}l} {\mathop H\nolimits_{0} :\mathop \gamma \nolimits_{1} = \mathop \gamma \nolimits_{2} = \ldots = \mathop \gamma \nolimits_{p} = 0} \hfill \\ {\mathop H\nolimits_{A} :\exists \mathop \gamma \nolimits_{j} \ne 0} \hfill \\ \end{array} } \right\} \hfill \\ & \quad \Rightarrow \mathop {{\rm LM}}\nolimits_{{\rm break}}^{{\rm LAG}} = \left[ {\mathop {g\left( \varphi \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]^{\prime } \mathop {\left[ {\mathop {{\mathbf{I}}\left( \varphi \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]}\nolimits^{ - 1} \left[ {\mathop {g\left( \varphi \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]\mathop \sim \limits_{{\rm as}} \mathop \chi \nolimits^{2} (p) \hfill \\ \end{aligned} $$

(A11)

The score will reproduce the structure indicated in Eq. A4, with an equation such as ${\frac{{y^{\prime}\mathop {\mathbf{W}}\nolimits_{s}^{*} \tilde{u}}}{{\mathop {\tilde{\sigma }}\nolimits^{2} }}} - {\text{tr}}\mathop {{\tilde{\mathbf{B}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits_{s}^{*}$ for each regime. The Hessian and information matrices must be similarly extended.

1.2 The case of the SEM

The specification that we must use in this case is that of Eq. 5:

$$ \left. \begin{array} {l}y = x\beta + u \hfill \\ u = \mathop \rho \nolimits_{0} {\mathbf{W}}u + \mathop \rho \nolimits_{1} \mathop {\mathbf{W}}\nolimits^{*} u + \varepsilon \hfill \\ \varepsilon \sim N(0,\mathop \sigma \nolimits^{2} I) \hfill \\ \end{array} \right\} $$

(A12)

The log-likelihood function is the following:

$$ l(y;\varphi ) = - \,{\frac{R}{2}}{ \log }(2\pi ) - {\frac{R}{2}}{ \log }(\mathop \sigma \nolimits^{2} ) - {\frac{{\left( {y - x\beta } \right)^{\prime } {\mathbf{B^{\prime}B}}\left( {y - x\beta } \right)}}{{2\mathop \sigma \nolimits^{2} }}} + { \log }\left| {\mathbf{B}} \right| $$

(A13)

where φ is the vector of parameters φ = [β, ρ₀, ρ₁,σ²]′ and B is the diffusion matrix, of order (R, R), ${\mathbf{B}} = I - \mathop \rho \nolimits_{0} {\mathbf{W}} - \mathop \rho \nolimits_{1} \mathop {\mathbf{W}}\nolimits^{*}$. The score vector is:

$$ g(y;\varphi ) = {\frac{\partial l(y;\varphi )}{\partial \varphi }} = {\frac{1}{{\mathop \sigma \nolimits^{2} }}}\left[ {\begin{array}{*{20}c} {x^{\prime}{\mathbf{B^{\prime}}}\varepsilon } \\ {u^{\prime}{\mathbf{W^{\prime}}}\varepsilon + \mathop \sigma \nolimits^{2} {\frac{{\partial { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \rho \nolimits_{0} }}}} \\ {u'{\mathbf{W}}^{*\prime } \varepsilon + \mathop \sigma \nolimits^{2} {\frac{{\partial { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \rho \nolimits_{1} }}}} \\ { - {\frac{R}{{2\mathop \sigma \nolimits^{2} }}} + {\frac{{\varepsilon^{\prime } \varepsilon }}{{2\mathop \sigma \nolimits^{2} }}}} \\ \end{array} } \right] $$

(A14)

with $u = y - x\beta$ and $\varepsilon = {\mathbf{B}}u = {\mathbf{B}}(y - x\beta )$. Under the assumption that there is no break in the coefficient of spatial dependence, the model of Eq. A12 simplifies to:

$$ \left. \begin{array} {l}y = x\beta + u \hfill \\ u = \mathop \rho \nolimits_{0} {\mathbf{W}}u + \varepsilon \hfill \\ \varepsilon \sim N(0,\mathop \sigma \nolimits^{2} I) \hfill \\ \end{array} \right\} $$

(A15)

so the score becomes:

$$ \left. {\begin{array}{*{20}c} {\mathop H\nolimits_{0} :\mathop \rho \nolimits_{1} = 0} \\ {\mathop H\nolimits_{A} :\mathop \rho \nolimits_{1} \ne 0} \\ \end{array} } \right\} \Rightarrow \mathop {g(y;\varphi )}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {{\frac{{\tilde{u}^{\prime}\mathop {\mathbf{W}}\nolimits^{*} {\mathbf{B}}\tilde{u}}}{{\mathop {\tilde{\sigma }}\nolimits^{2} }}} - {\text{tr}}\left[ {\mathop {\left( {I - \mathop {\tilde{\rho }}\nolimits_{0} {\mathbf{W}}} \right)}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \right]} \\ 0 \\ \end{array} } \right] $$

(A16)

where $\mathop {\tilde{\rho }}\nolimits_{0}$ and $\mathop {\tilde{\sigma }}\nolimits^{2}$ are the ML estimations of ρ₀ and σ² in the model of Eq. A15 and $\tilde{u}$ is the associated series of residuals. From the score of Eq. A14, it is straightforward to obtain the Hessian matrix:

$$ \begin{gathered} {\frac{{\mathop \partial \nolimits^{2} l(y;\varphi )}}{{\partial \varphi \partial \varphi^{\prime}}}} = - \frac{1}{{\mathop \sigma \nolimits^{2}}} \hfill \\ \left[ {\begin{array}{*{20}c} {x^{\prime}{\mathbf{B^{\prime}B}}x} & {x^{\prime}{\mathbf{WB}}u} & {x^{\prime}\mathop {\mathbf{W}}\nolimits^{*} {\mathbf{B}}u} & {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}x^{\prime}{\mathbf{B^{\prime}B}}u} \\ {u^{\prime}{\mathbf{B^{\prime}W^{\prime}}}x} & {u^{\prime}{\mathbf{W^{\prime}W}}u - \mathop \sigma \nolimits^{2} {\frac{{\mathop \partial \nolimits^{2} { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \rho \nolimits_{0}^{2} }}}} & {u^{\prime}{\mathbf{W^{\prime}}}\mathop {\mathbf{W}}\nolimits^{*} u - \mathop \sigma \nolimits^{2} {\frac{{\mathop \partial \nolimits^{2} { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \rho \nolimits_{0} \partial \mathop \rho \nolimits_{1} }}}} & {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}u^{\prime}{\mathbf{W^{\prime}B}}u} \\ {u^{\prime}{\mathbf{B^{\prime}W}}^{{*^{\prime}}} x} & {u^{\prime } \mathop {\mathbf{W}}\nolimits^{*\prime } {\mathbf{W}}u - \mathop \sigma \nolimits^{2} {\frac{{\mathop \partial \nolimits^{2} { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \rho \nolimits_{0} \partial \mathop \rho \nolimits_{1} }}}} & {u^{\prime}\mathop {\mathbf{W}}\nolimits^{*\prime } \mathop {\mathbf{W}}\nolimits^{*} u - \mathop \sigma \nolimits^{2} {\frac{{\mathop \partial \nolimits^{2} { \log }\left| {\mathbf{B}} \right|}}{{\partial \mathop \rho \nolimits_{1}^{2} }}}} & {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}u^{\prime}\mathop {{\mathbf{W^{\prime}}}}\nolimits^{*} {\mathbf{B}}u} \\ {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}u^{\prime}{\mathbf{B^{\prime}B}}x} & {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}u^{\prime}{\mathbf{B^{\prime}W}}u} & {{\frac{1}{{\mathop \sigma \nolimits^{2} }}}u^{\prime}\mathop {{\mathbf{B^{\prime}W}}}\nolimits^{*} u} & { - {\frac{R}{{\mathop {2\sigma }\nolimits^{2} }}} + {\frac{{u^{\prime}{\mathbf{B^{\prime}B}}u}}{{\mathop \sigma \nolimits^{4} }}}} \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(A17)

as well as the information matrix corresponding to the null hypothesis:

$$ \begin{gathered} {\mathbf{I}}(\varphi ) = - \mathop {E\left[ {{\frac{{\mathop \partial \nolimits^{2} l(y;\varphi )}}{{\partial \varphi \partial \varphi^{\prime}}}}} \right]}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} = {\frac{1}{{\mathop \sigma \nolimits^{2} }}}\left[ {\begin{array}{*{20}c} {x^{\prime}{\mathbf{B^{\prime}B}}x} & 0 & 0 & 0 \\ {0^{\prime}} & {2\mathop \sigma \nolimits^{2} {\text{tr}}\left( {\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} {\mathbf{W^{\prime}}}\mathop {\mathbf{B}}\nolimits^{ - 1} {\mathbf{W}}} \right)} & {2\mathop \sigma \nolimits^{2} {\text{tr}}\left( {\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*'} \mathop {\mathbf{B}}\nolimits^{ - 1} {\mathbf{W}}} \right)} & {{\text{tr}}\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} {\mathbf{W}}} \\ {0^{\prime}} & {2\mathop \sigma \nolimits^{2} {\text{tr}}\left( {\mathop {{\mathbf{W^{\prime}B^{\prime}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} \mathop {\mathbf{B}}\nolimits^{ - 1} } \right)} & {2\mathop \sigma \nolimits^{2} {\text{tr}}\left( {\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*\prime } \mathop {\mathbf{B}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \right)} & {{\text{tr}}\mathop {{\mathbf{B^{\prime}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \\ 0 & {{\text{tr}}{\mathbf{W^{\prime}}}\mathop {\mathbf{B}}\nolimits^{ - 1} } & {{\text{tr}}\mathop {\mathbf{W}}\nolimits^{\prime *} \mathop B\nolimits^{ - 1} } & {{\frac{R}{{\mathop {2\sigma }\nolimits^{2} }}}} \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(A18)

Finally, the Lagrange Multiplier for the hypothesis of Eq. A16 takes the following expression:

$$ \begin{aligned} \left. {\begin{array}{*{20}c} {\mathop H\nolimits_{0} :\mathop \rho \nolimits_{1} = 0} \\ {\mathop H\nolimits_{A} :\mathop \rho \nolimits_{1} \ne 0} \\ \end{array} } \right\} &\Rightarrow \mathop {{\rm LM}}\nolimits_{{\rm break}}^{{\rm ERR}} = \left[ {\mathop {g\left( \theta \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]^{\prime } \mathop {\left[ {\mathop {\mathbf{I}\left( \theta \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]}\nolimits^{ - 1} \left[ {\mathop {g\left( \theta \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]\mathop \sim \limits_{{\rm as}} \mathop \chi \nolimits^{2} (1) \\& \mathop {{\rm LM}}\nolimits_{{\rm break}}^{{\rm ERR}} = {\frac{{\mathop {\left[ {{\frac{{\tilde{u}^{\prime}\mathop {\mathbf{W}}\nolimits^{*} {\tilde{\mathbf{B}}}\tilde{u}}}{{\mathop {\tilde{\sigma }}\nolimits^{2} }}} - {\rm tr}\mathop {{\tilde{\mathbf{B}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \right]}\nolimits^{2} }}{{\mathop {\tilde{\sigma }}\nolimits_{{\rm err}}^{2} }}}\mathop \sim \limits_{{\rm as}} \mathop \chi \nolimits^{2} (1) \\ \end{aligned} $$

(A19)

$\mathop {\tilde{\sigma }}\nolimits_{err}^{2}$ is the asymptotic variance of the restriction of the null hypothesis, which is equal to:

$$ \begin{array}{l} \mathop {\tilde{\sigma }}\nolimits_{err}^{2} = \mathop {\left[ {{\frac{{\mathop {\tilde{\sigma }}\nolimits^{2} }}{{2\mathop {\tilde{\sigma }}\nolimits^{2} {\text{tr}}\mathop {{\tilde{\mathbf{B}^{\prime}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} \mathop {{\tilde{\mathbf{B}}}}\nolimits^{ - 1} \mathop {{\mathbf{W^{\prime}}}}\nolimits^{*} - \mathop {\tilde{b}{\tilde{\mathbf{D}}}}\nolimits^{ - 1} \mathop {\tilde{b}}\nolimits^{{}} }}}} \right]}\nolimits^{ - 1} \hfill \\ \to \tilde{b} = \left[ {\begin{array}{*{20}l} {2\mathop \sigma \nolimits^{2} {\text{tr}}\mathop {{\tilde{\mathbf{B}^{\prime}}}}\nolimits^{ - 1} {\mathbf{W^{\prime}}}\mathop {{\tilde{\mathbf{B}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \\ {\mathop {{\text{tr}}{\tilde{\mathbf{B}^{\prime}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits^{*} } \\ \end{array} } \right] \hfill \\ \to {\tilde{\mathbf{D}}} = \left[ {\begin{array}{*{20}c} {2\mathop \sigma \nolimits^{2} {\text{tr}}\mathop {{\tilde{\mathbf{B}^{\prime}}}}\nolimits^{ - 1} {\mathbf{W}}\mathop {{\tilde{\mathbf{B}}}}\nolimits^{ - 1} {\mathbf{W^{\prime}}}} & {\mathop {{\text{tr}}{\tilde{\mathbf{B}^{\prime}}}}\nolimits^{ - 1} {\mathbf{W}}} \\ {\mathop {{\text{tr}}{\tilde{\mathbf{B}^{\prime}}}}\nolimits^{ - 1} {\mathbf{W}}} & {{\frac{R}{{2\mathop {\tilde{\sigma }}\nolimits^{2} }}}} \\ \end{array} } \right] \hfill \\ \end{array} $$

(A20)

As in the previous case, the Multiplier of Eq. A19 can be generalized to treat with p different regimes. The extended model will be:

$$ \left. \begin{array} {l}y = x\beta + u \hfill \\ u = \mathop \rho \nolimits_{0} {\mathbf{W}}u + \sum\limits_{s = 1}^{p} {\mathop \rho \nolimits_{s} \mathop {\mathbf{W}}\nolimits_{s}^{*} u} + \varepsilon \hfill \\ \varepsilon \sim N(0,\mathop \sigma \nolimits^{2} I) \hfill \\ \end{array} \right\} $$

(A21)

The null hypothesis is again of the joint type:

$$ \begin{gathered} \left. {\begin{array}{*{20}l} {\mathop H\nolimits_{0} :\mathop \rho \nolimits_{1} = \mathop \rho \nolimits_{2} = \cdots = \mathop \rho \nolimits_{p} = 0} \hfill \\ {\mathop H\nolimits_{A} :\exists \mathop \rho \nolimits_{j} \ne 0} \hfill \\ \end{array} } \right\} \hfill \\\quad \Rightarrow \mathop {{\rm LM}}\nolimits_{{\rm break}}^{{\rm ERR}} = \left[ {\mathop {g\left( \varphi \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]^{\prime } \mathop {\left[ {\mathop {{\mathbf{I}}\left( \varphi \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]}\nolimits^{ - 1} \left[ {\mathop {g\left( \varphi \right)}\nolimits_{{\left| {\mathop H\nolimits_{0} } \right.}} } \right]\mathop \sim \limits_{{\rm as}} \mathop \chi \nolimits^{2} (p) \hfill \\ \end{gathered} $$

(A22)

The score will be obtained as in A16, with an equation of the type ${\frac{{\tilde{u}^{\prime}\mathop {\mathbf{W}}\nolimits_{s}^{*} {\tilde{\mathbf{B}}}\tilde{u}}}{{\mathop {\tilde{\sigma }}\nolimits^{2} }}} - {\text{tr}}\mathop {{\tilde{\mathbf{B}}}}\nolimits^{ - 1} \mathop {\mathbf{W}}\nolimits_{s}^{*}$ for each of the p regimes considered. The Hessian and information matrices must be similarly extended.