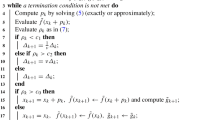Recent advances in trust region algorithms

Abstract

Trust region methods are a class of numerical methods for optimization. Unlike line search type methods where a line search is carried out in each iteration, trust region methods compute a trial step by solving a trust region subproblem where a model function is minimized within a trust region. Due to the trust region constraint, nonconvex models can be used in trust region subproblems, and trust region algorithms can be applied to nonconvex and ill-conditioned problems. Normally it is easier to establish the global convergence of a trust region algorithm than that of its line search counterpart. In the paper, we review recent results on trust region methods for unconstrained optimization, constrained optimization, nonlinear equations and nonlinear least squares, nonsmooth optimization and optimization without derivatives. Results on trust region subproblems and regularization methods are also discussed.

1 Introduction

Trust region algorithms are a class of numerical methods for optimization, which have been extensively studied for many decades. Historical development of trust region methods can be traced back to Levenberg [72], where a modified Gauss–Newton method is given for solving nonlinear least square problems. Levenberg’s method was re-discovered independently by Morrison [80] and Marquardt [76]. The method was popularized due to the influential paper of Marquardt [76], thus it is called as Levenberg–Marquardt method (see [48]). Though Morrison’s paper was not widely known because it was published in a conference proceeding instead of a journal, many leading experts now favor the name “Levenberg–Morrison–Marquadt method” as an acknowledgment of the important contribution of Morrison [80]. Levenberg–Marquardt method modifies Gauss–Newton method by adding a damping term to restrict the length of the Gauss–Newton step, in order to avoid a too long step when the Jacobian matrix of the nonlinear functions is nearly singular at the current point. Thus, a more imaginable name for trust region method is restricted step method which was used by Fletcher [48]. Pioneer researches on trust region methods were given by Powell [88–91], Fletcher [47], Hebden [67], Madsen [74], Osborne [86], Moré [78], Toint [118–122], Dennis and Mei [37], Sorensen [113, 114], and Steihaug [115]. Moré [79] gave an excellent survey of early works on trust region methods, which popularized trust region methods and standardized the term “trust region”. An invited plenary talk on trust region methods was given by Yuan [148] at the Fourth International Congress on Industrial and Applied Mathematics, which was held in Edinburgh, July 1999. The huge comprehensive monograph by Conn et al. [24] is the first published book on trust region methods, which gives a very good summary of works being done until the time of publication and is regarded as an encyclopedia of the subject.

Unlike line search algorithms, where a line search is carried out along a search direction in each iteration, trust region algorithms obtain the new iterate point by searching in a trust region which is normally a neighbourhood of the current iterate point. To be more exact, at the $k$th iteration, a trust region algorithm for the general optimization problem

$$\begin{aligned} \min _{x\in X} f(x) , \end{aligned}$$

(1.1)

where $f(x)$ is the objective function to be minimized and $X \subset \mathfrak {R}^n$ is the feasible set, obtains the trial step $s_k$ by solving the following trust region subproblem

$$\begin{aligned} \min _{ d \in X_k}&m_k(d ) \end{aligned}$$

(1.2)

$$\begin{aligned} \hbox {s.t.}&\Vert d \Vert _{W_k} \le \varDelta _k , \end{aligned}$$

(1.3)

where $m_k (d)$ is a model function that approximates the objective function $f(x_k +d)$ near the current iteration point $x_k$, $X_k$ is an approximation to the shifted feasible set $X-x_k$, $\Vert . \Vert _{W_k}$ is a norm in $\mathfrak {R}^n$ and $\varDelta _k >0$ is the trust region radius.

The framework of a trust region method for optimization problem (1.1) is as follows

Thus, the essential parts of a trust region algorithm are the construction of the trust region subproblem and how to judge the trial step. In order to define the trust region subproblem, we need to build up an approximate model $m_k(d)$, and to select the trust region $\{d \in \mathfrak {R}^n \, | \, \Vert d \Vert _{W_k} \le \varDelta _k\}$. Once the trial step $s_k$ is obtained by solving the trust region subproblem exactly or inexactly, we can use the information at the trial point $x_k + s_k$ to judge the quality of the trial step $s_k$. Based on certain criteria, if the trial point $x_k +s_k$ is (sufficiently) better than the current iterate $x_k$, we accept the trial step. At the end of each iteration, we need to choose the trust region for the next iteration and construct the new model function $m_{k+1}(d)$.

Due to the trust region constraint (1.3), the feasible region of a trust region subproblem is always a bounded set, which enables us to use nonconvex approximation model functions $m_k(d)$. This is one of the advantages of trust region methods over line search methods. The trust region constraint can be viewed as an implicit regularization and preconditioning can be used by selecting proper norm $\Vert .\Vert _{W_k}$. These make trust region algorithms reliable and robust, as they can be applied to nonconvex and ill-conditioned problems.

An advantage of trust region methods is that it is easier to establish convergence results for trust region algorithms than for line search algorithms. For example, in order to prove the global convergence of line search type quasi-Newton methods, one needs to use sophisticated techniques to estimate the growing of the quasi-Newton matrices (see Powell [92]), while the global convergence of trust region type quasi-Newton methods can be easily established as long as the trace of the quasi-Newton matrices does not increase faster than linearly (see Powell [90]). In [128], it is explained also why the assumptions for line searches are stronger. Another advantage of trust region methods over line search methods is that trust region methods using second order information can normally converges to second-order stationary points while line search type methods could converges to saddle points (for example, see [24] and [117]).

In this paper, we review recent results on trust region methods. In Sect. 2, we consider trust region methods for unconstrained optimization, particularly on results about subspace techniques, non-standard updating techniques for trust region radius, and non-standard shaped trust regions that are not defined by Euclidean balls. In Sect. 3, we discuss trust region methods for constrained optimization, where emphases are given on subspace techniques, and recent results on augmented Lagrangian function methods. Trust region techniques for nonlinear equations and nonlinear least squares are presented in Sect. 4. In Sect. 5, trust region algorithms for nonsmooth optimization are discussed. Trust region methods for optimization without derivatives are reviewed in Sect. 6 and some regularization methods are discussed in Sect. 7. A brief discussion is given at the end of the paper.

2 Unconstrained optimization

In this section, we consider unconstrained optimization, that is the case where the feasible region $X$ is the whole space $\mathfrak {R}^n$. This case is fundamental and relatively simple, because we can simply let $X_k = X = \mathfrak {R}^n$. Thus, the trust region subproblem in the $k$th iteration has the following form:

$$\begin{aligned} \min _{d \in \mathfrak {R}^n}&m_k(d)\end{aligned}$$

(2.1)

$$\begin{aligned} \hbox {s.t. }&\Vert d \Vert _{W_k} \le \varDelta _k . \end{aligned}$$

(2.2)

Let $s_k$ be a trial step which is an exact or inexact solution of (2.1)–(2.2). We compute the predicted reduction $Pred_k= m_k(0) - m_k(s_k)$, which is the reduction in the model function, and the actual reduction of the objective function $Ared_k = f(x_k ) - f(x_k + s_k)$. In general, if $x_k$ is not a stationary point of $f(x)$, the predicted reduction $Pred_k >0$. For example, a quadratic model function with the Euclidean norm trust region constraint leads to the standard trust region subproblem (TRS):

$$\begin{aligned} \min _{d\in \mathfrak {R}^n}&m_k(d) = f(x_k) + g_k^T d + \frac{1}{2} d^T B_k d \end{aligned}$$

(2.3)

$$\begin{aligned} \hbox {s.t. }&\Vert d \Vert _2 \le \varDelta _k , \end{aligned}$$

(2.4)

where $g_k = g(x_k) = \nabla f(x_k)$ and $B_k\in \mathfrak {R}^{n\times n}$ is a symmetric matrix approximating the Hessian of the objective function. Subproblem (2.3)–(2.4) is widely used in many trust region algorithms as it is easy to solve and it has nice theoretical properties including that the Hessian of the Lagrangian function of (2.3)–(2.4) is positive semi-definite [53, 113], and that it has at most one non-global local minimizer [77]. For convex quadratic model functions $m_k(d)$, it is shown that the truncated conjugate gradient method can obtain a very good inexact solution of (2.3)–(2.4), namely the reduction of the objective function obtained by the truncated conjugate gradient method will be at least half of the maximum reduction in the trust region [149]. Let $s_k$ be the exact solution of (2.3)–(2.4), we have that

$$\begin{aligned} Pred_k \ge \frac{1}{2} \Vert g_k \Vert _2 \min \left\{ \varDelta _k , \quad \frac{\Vert g_k\Vert _2}{ \Vert B_k \Vert _2} \right\} \!, \end{aligned}$$

(2.5)

which was first proved by Powell [91]. However, it is not necessary for $s_k$ to be the exact solution of (2.3)–(2.4) to satisfy (2.5). For example, a minimizer of the quadratic model $m_k(d)$ in (2.3) along the steepest descent direction within the trust region (2.4) also satisfies (2.5). Inequalities of the type (2.5) indicate that certain sufficient reduction can be achieved in the approximate model provided that $x_k$ is not a stationary point of the objective function. The quadratic model (2.3) is not the only possible model for $m_k(d)$. For example, the following conic model

$$\begin{aligned} m_k(d) = \frac{g_k^T d}{1- h_k^T d } + \frac{1}{2} \frac{d^T B_k d}{(1- h_k^T d )^2} \end{aligned}$$

(2.6)

is used in a trust region algorithm given by Di and Sun [38], where $h_k \in \mathfrak {R}^n$. No matter what kind of model function $m_k(d)$ is chosen, we normally require that the trial step $s_k$ obtained satisfies some “sufficient descent” condition similar to (2.5), in order to establish the global convergence of the algorithm.

The ratio between the actual reduction and the predicted reduction

$$\begin{aligned} r_k = \frac{Ared_k}{Pred_k} \end{aligned}$$

(2.7)

plays a very important role in trust region algorithms, since it gives a measure for judging how good the trial step $s_k$ is. Intuitively, a larger $r_k$ corresponds to a better trial step because it achieves a lower objective function value for the same predicted reduction $Pred_k$. Thus, a general strategy is to accept the trial step as long as $r_k$ is larger than a preset non-negative constant.

The value of the trust region radius $\varDelta _k$ decides the size of the trust region in which we replace the original problem by the approximate model. A larger trust region radius shows that we are more confident about our model while a smaller trust region indicates that we are more conservative. Thus, the ratio (2.7) is also used to adjust the new trust region radius.

For unconstrained optimization problem, a model trust region method is given as follows.

Different choices for the parameters $\tau _i (i=0,1,2,3,4)$ are discussed in Yuan [148], Chapter 17.1 of Conn et al. [24], and Gould et al. [55]. Global convergence of the trust region method can be easily established as long as the trial step $s_k$ satisfies a sufficient descent condition similar to (2.5). To prove the local superlinear convergence of a trust region method, the general approach is to show that the trust region constraint $\Vert d \Vert _{W_k} \le \varDelta _k$ is inactive for all sufficiently large $k$. In order to ensure $\Vert s_k \Vert _{W_k} < \varDelta _k$, the standard technique is to show that $s_k \rightarrow 0$ and $\varDelta _k$ is bounded away from zero. This explains why we set $\varDelta _{k+1} \ge \varDelta _k$ when $r_k \ge \tau _2$ in the model algorithm.

However, $\varDelta _k$ bounded away from zero is only a sufficient condition for the local superlinear convergence, but not a necessary one. Therefore, it is worthwhile to study techniques that allow $\varDelta _k \rightarrow 0$. The reason for preferring $\varDelta _k \rightarrow 0$ is that for ill-conditioned and even degenerate problems, it is more reliable and robust to have $\varDelta _k \rightarrow 0$. Moreover, in trust region methods for derivative-free optimization, $\varDelta _k$ also goes to zero, because of the so-called criticality step (for example, see [30]).

One approach is to let the new trust region radius $\varDelta _{k+1}$ depend on $s_k$. Hei [68] suggests to update the trust region radius by

$$\begin{aligned} \varDelta _{k+1}=R_{\eta }(r_k) \Vert s_k\Vert _2 , \end{aligned}$$

(2.10)

where $R_{\eta } (t)$ is a monotonically increasing function satisfying

$$\begin{aligned} 0<\beta \le R_\eta (t)\le 1-\gamma _1<1,&\qquad \forall t\in (-\infty , \eta ),\\ 1<1+\gamma _2\le R_\eta (t)\le M<+\infty ,&\qquad \forall t\in [\eta , +\infty ), \end{aligned}$$

with $0<\beta <1, 0<\gamma _1<1-\beta , \gamma _2>0, M>1+\gamma _2, 0<\eta <1$.

Suppose the algorithm converges to a local minimizer $x^*$ of $f(x)$ at which the second order sufficient condition is satisfied. The algorithm is locally superlinearly convergent if we can prove that $s_k$ is close to Newton’s step $- (\nabla ^2 f(x_k))^{-1} g_k$, namely,

$$\begin{aligned} \Vert s_k + (\nabla ^2 f(x_k))^{-1} g_k \Vert _2 = o ( \Vert s_k \Vert _2 ) , \end{aligned}$$

(2.11)

and that the trust region constraint is inactive ($\Vert s_k \Vert _2 < \varDelta _k$). Assuming that the minimum eigenvalue of $\nabla ^2 f(x^*)$ is $\xi$, (2.11) implies that $\Vert s_k \Vert _2 \le \frac{2}{\xi } \Vert g_k \Vert _2$ for all sufficiently large $k$. Thus, it is reasonable to let $\varDelta _k$ depend on $\Vert g_k \Vert _2$. Fan and Yuan [45] suggested to use

$$\begin{aligned} \varDelta _k:=\mu _{k}\Vert g_{k}\Vert _2 \end{aligned}$$

(2.12)

where

$$\begin{aligned} \mu _{k+1}= \left\{ \begin{array}{ll} c_1\mu _k &{} \quad \hbox {if} \ r_k< \eta _2,\\ c_2\mu _k &{} \quad \hbox {if} \ r_k\ge \eta _2\quad \hbox {and}\quad \Vert s_k\Vert _2 > \dfrac{1}{2} \varDelta _k, \\ \mu _k &{} \quad \hbox {otherwise}, \end{array}\right. \end{aligned}$$

with $0<\eta _2<1, 0<c_1<1<c_2$ and $\mu _1 >0$ being given (2.12) can be generalized to

$$\begin{aligned} \varDelta _k = \mu _k \Vert g_k \Vert _2^{\alpha } , \end{aligned}$$

where $\alpha \in (0, 1]$ is a parameter.

Recently, motivated by applications in adaptive techniques which exploit the information made available during the optimization process in order to vary the accuracy of the objective function computation, Bastin et al. [5] proposed an interesting way of updating the trust region radius. In their retrospective trust region algorithm, they use the model function at the current iteration to compute the ratio of the actual reduction and the predicted reduction in the previous trial step, and use this ratio to update the trust region radius. Namely, if $x_{k+1} = x_k +s_k$, a new model function $m_{k+1}$ is constructed. Then, the new ratio

$$\begin{aligned} \tilde{\rho }_k=\dfrac{f(x_k)-f(x_k+s_k)}{m_{k+1}(-s_k)-m_{k+1}(0)} \end{aligned}$$

(2.13)

is computed, and the trust region radius is updated by the following formula:

$$\begin{aligned} \varDelta _{k+1}= \left\{ \begin{array}{ll} \max [\gamma _2 \Vert s_k\Vert , \varDelta _k] &{}\quad \hbox {if}\ \tilde{\rho }_k \ge \tilde{\eta }_2 , \\ \varDelta _k &{}\quad \hbox {if}\ \tilde{\rho }_k\in [\tilde{\eta }_1, \tilde{\eta }_2] , \\ \gamma _1\Vert s_k\Vert &{}\quad \hbox {if}\ \tilde{\rho }_k\in [0, \tilde{\eta }_1) \, , \\ \min [\gamma _1\Vert s_k\Vert , \max [\gamma _0, \tilde{\theta }_k]\varDelta _k] &{}\quad \hbox {if}\ \tilde{\rho }_k<0 , \end{array}\right. \end{aligned}$$

(2.14)

where

$$\begin{aligned} \tilde{\theta }_k=\dfrac{-(1-\tilde{\eta }_2)\langle \nabla _xf(x_{k+1}), s_k\rangle }{ (1-\tilde{\eta }_2) [f(x_{k+1})-\langle \nabla _xf(x_{k+1}), s_k\rangle ]+ \tilde{\eta }_2 m_{k+1}(-s_k)-f(x_k)} , \end{aligned}$$

and the constants satisfy $0 < \gamma _0 < \gamma _1 \le \gamma _2>1$ and $0 < \tilde{\eta }_1 \le \tilde{\eta }_2 < 1$. $\tilde{\theta }_k\varDelta _k$ is used to ensure $\tilde{\rho }_{k+1}\ge \tilde{\eta }_2$. Please notice that $\tilde{\theta }_k$ uses the gradient at $x_{k+1}$.

For large-scale optimization problems, namely when $n$ is very large, trust region subproblems are also large-scale. Thus, it is valuable to investigate subspace properties of trust region subproblems. Consider the standard trust region quasi-Newton method where the model functions $m_k(d)$ are quadratic functions with the Hessian matrices being updated by quasi-Newton formulae. Wang and Yuan [130] gave the subspace properties of the trial steps $s_k$:

Lemma 1

Suppose $B_1 =\sigma I$, $\sigma > 0$. The matrix updating formula is any one chosen from PSB and Broyden family (where the updates may be singular), and $B_k$ is the $k$th update matrix. Let $s_k$ be a solution of subproblem (2.3)–(2.4), $g_k = \nabla f (x_k)$, ${\mathcal {G}}_k =Span \{ g_1, g_2, \dots , g_k \}$ and $x_{k+1} = x_k + s_k$ ($x_1 \in \mathfrak {R}^n$ is any given initial point). Then for all $k\ge 1$, $s_k \in {\mathcal {G}}_k$. Moreover for any $z\in {\mathcal {G}}_k$ and any $u \in {\mathcal {G}}_k^\perp$ , we have

$$\begin{aligned} B_k z \in {\mathcal {G}}_k , \qquad B_k u = \sigma u \, . \end{aligned}$$

(2.15)

This result extends a similar result for line search type quasi-Newton methods given by Siegel [112]. Based on this result, it can be shown that the full space trust region quasi-Newton method is equivalent to the subspace counterpart provided that the approximate Hessian is updated by quasi-Newton formulae and the initial Hessian approximation is appropriately chosen. In the subspace algorithm, the trial step can be obtained by solving the trust region subproblem in the subspace spanned by all the gradient vectors computed so far. To be more exact, the trial step can be defined by minimizing the quasi-Newton quadratic model in the subspace spanned by all the computed gradients. The advantage of subspace trust region algorithms is that the subproblems are defined in lower dimension, thus they are more suitable for large scale problems. Subproblems of general subspace trust region algorithms for unconstrained optimization have the following form

$$\begin{aligned} \min _{d\in \mathfrak {R}^n}&m_k(d) \end{aligned}$$

(2.16)

$$\begin{aligned} \hbox {s.t. }&\Vert d \Vert _{W_k} \le \varDelta _k , \quad d \in {{\mathcal {S}}}_k , \end{aligned}$$

(2.17)

where ${{\mathcal {S}}}_k \subset \mathfrak {R}^n$ is a low dimensional subspace. Possible choices for ${{\mathcal {S}}}_k$ are

$$\begin{aligned} {{\mathcal {S}}}_k= & {} Span \{ g_1, g_2, ..., g_k \} , \end{aligned}$$

(2.18)

$$\begin{aligned} {{\mathcal {S}}}_k= & {} Span \{ g_k, s_{k-1}, ..., s_{k-r} \} ,\end{aligned}$$

(2.19)

$$\begin{aligned} {{\mathcal {S}}}_k= & {} Span \{ g_k, y_{k-1}, ..., y_{k-r} \} , \end{aligned}$$

(2.20)

and

$$\begin{aligned} {{\mathcal {S}}}_k = Span \left\{ e_{k(1)}, e_{k(2)}, ..., e_{k(r)} \right\} , \end{aligned}$$

(2.21)

where $r \ll n$ is a non-negative integer, $y_i = g_{i+1} - g_i$, and $e_i$ is the $i$th coordinate unit vector in $\mathfrak {R}^n$. For more detailed discussions on subspace selection, please see Yuan [151].

Regarding the choices for the norm $\Vert . \Vert _{W_k}$ in the trust region subproblem, it is common to use the Euclidean norm $\Vert . \Vert _2$, since the Euclidean norm trust region subproblem (2.3)–(2.4) is widely studied and easy to solve. However, in some special cases, we can use different norm $\Vert . \Vert _{W_k}$ other than the Euclidean norm $\Vert . \Vert _2$. For example, for the quadratic model function (2.3) with $B_k$ being updated by limited memory quasi-Newton updates (for example, see [73]), the matrix $B_k$ has the form

$$\begin{aligned} B_k = \sigma _k I + P_k D_k P_k^T , \end{aligned}$$

(2.22)

where $\sigma _k >0$, $P_k \in \mathfrak {R}^{n \times r}$ satisfying $P_k^TP_k = I_r$ and $D_k \in \mathfrak {R}^{r \times r}$ is diagonal and positive definite. Normally, $r$ is much smaller than $n$. Burdakov et al. [9] suggested to use the norm

$$\begin{aligned} \Vert d \Vert _{W_k} = \max \left\{ \Vert P_k^T d \Vert _\infty , \, \, \Vert {(P_k)}^T_{\perp } d \Vert _2 \right\} , \end{aligned}$$

(2.23)

where $(P_k)^T_\perp$ is the projection onto the subspace orthogonal to $Range(P_k)$. In this case, the solution $s_k$ for the trust region subproblem (2.1)–(2.2) can be expressed (by orthogonal decomposition) as $P_k s_1 + (P_k)_{\perp } s_2$. Both $s_1$ and $s_2$ have closed-form solutions [151], due to the fact that $s_1$ is the solution of the box constrained QP (in $\mathfrak {R}^r$)

$$\begin{aligned} \min _{s\in \mathfrak {R}^n}&\frac{1}{2} s^T \left( \sigma _k I + D_k \right) s + s^T \left( P_k^T g_k \right) \end{aligned}$$

(2.24)

$$\begin{aligned} \hbox {s.t.}&\Vert s\Vert _\infty \le \varDelta _k \end{aligned}$$

(2.25)

while $s_2$ solves the 2-norm constrained special QP

$$\begin{aligned} \min _{s\in \mathfrak {R}^n}&\frac{1}{2} \sigma _k s^T s + s^T (P_k)^T_{\perp } g_k \end{aligned}$$

(2.26)

$$\begin{aligned} \hbox {s.t.}&\Vert s\Vert _2 \le \varDelta _k \, . \end{aligned}$$

(2.27)

Encouraging numerical results for trust region algorithms using the cylinder-shape trust region (2.23) were reported in Gong [54] and Zikrin [158].

A class of recursive trust region methods for multiscale nonlinear optimization, often arising in systems governed by partial differential equations, is given by by Gratton et al. [63]. The standard trust region method for unconstrained optimization is a special case of this class. A remarkable result obtained by Gratton, Sartenaer and Toint [63] is that the unconstrained trust region algorithm needs at most $O(\epsilon ^{-2})$ iterations to achieve $||g(x_k)||$ below $\epsilon$.

3 Constrained optimization

Normally, trust region methods for constrained optimization problem (1.1) are more complicated than line search methods due to the difficulty that the approximate feasible region $X_k$ may not have points in the trust region of the current iteration, namely $x_k + d \not \in X_k$ as long as $\Vert d \Vert _{W_k } \le \varDelta _k$. Consider the case that the feasible set $X$ is defined by equality and inequality constraints

$$\begin{aligned} X = \{ x \, \, | \, \, c_i(x) = 0,\,\, i=1,...,\quad m_e; c_i(x) \ge 0,\,\, i=m_e+1, ..., m\} \, . \end{aligned}$$

(3.1)

At the $k$th iteration point $x_k$, line search type SQP methods normally compute the search direction $d_k$ by solving the QP subproblem:

$$\begin{aligned} \min&m_k(d)\end{aligned}$$

(3.2)

$$\begin{aligned} \hbox {s.t.}&d \in X_k \, \end{aligned}$$

(3.3)

where $m_k(d)$ is a quadratic function approximating the Lagrangian function and

$$\begin{aligned} X_k= & {} \{ d \, \, | \, \, c_i(x_k) + d^T \nabla c_i(x_k) = 0, i=1,...,m_e; \nonumber \\&\quad c_i(x_k) + d^T \nabla c_i(x_k)\ge 0, i =m_e+1, ..., m \} \, \end{aligned}$$

(3.4)

is the feasible set of the linearized constraints. To overcome the possible difficulty that $X_k \cap \{ d \, | \, \Vert d \Vert _{W_k} \le \varDelta _k \} = \emptyset$, instead of using (1.2)–(1.3), we can use the following trust region subproblem

$$\begin{aligned} \min _{d \in \mathfrak {R}^n}&m_k(d) \end{aligned}$$

(3.5)

$$\begin{aligned} \hbox {s.t. }&\Vert d \Vert _{W_k} \le \varDelta _k \end{aligned}$$

(3.6)

$$\begin{aligned}&d \in \theta _k X_k , \end{aligned}$$

(3.7)

for some $\theta _k \in (0, 1]$. It is easy to see that $\theta _k X_k \cap \{ d \, | \, \Vert d \Vert _{W_k} \le \varDelta _k \} \ne \emptyset$ for sufficiently small $\theta _k \in (0,1]$ provided that $\varDelta _k >0$ and $X_k$ is nonempty. In the special case of equality constrained optimization problems, subproblem (3.5)–(3.7) is equivalent to null-space approach, detailed discussions can be found in Bryd et al. [12], Vardi [126] and Omojukun [85]. Normally, the model function $m_k(d)$ in (3.5) is a quadratic function. Similar to unconstrained case, it is also possible to use non-quadratic models such as conic models [117].

Intuitively, we should choose $\theta _k \in (0,1]$ in (3.7) as large as possible since a larger $\theta _k$ corresponding to the case that $\theta _k X_k$ is a better approximation to the shifted feasible set $X-x_k$. Thus, one way to achieve this is to replace $\theta _k$ by a variable $\theta \in (0,1]$ and penalize the term $(1-\theta )$ in the object. Namely we can use the following subproblem

$$\begin{aligned} \min _{d \in \mathfrak {R}^n}&m_k(d) + \sigma (1-\theta )^2 \end{aligned}$$

(3.8)

$$\begin{aligned} \hbox {s.t. }&\Vert d \Vert _{W_k} \le \varDelta _k , \end{aligned}$$

(3.9)

$$\begin{aligned}&d \in \theta X_k , \quad \theta \in (0,1] \, . \end{aligned}$$

(3.10)

The shifted linearized feasible region $\theta X_k$, can be viewed as a null space of the linearized constraints. All the trust region algorithms that obtain the trial step by computing a range-space step (also called vertical step or normal step) and a null-space step (also called horizontal step or tangential step) can be regarded as trying to satisfy (3.7). Along this direction, a trust-funnel algorithm is given by Gould and Toint [58] where neither a penalty function nor a filter [52] is used. The algorithm converges to first-order stationary points by using different trust regions to cope with the nonlinearities of the objective function and the constraints and allowing inexact SQP steps that do not lie exactly in the null space of the constraints. Recently, a new algorithm is given by Curtis et al. [33] where global convergence is achieved by combining a trust region methodology with a funnel mechanism similar to [58]. The new algorithm has the additional capability that it solves problems with both equality and inequality constraints, and has prominent features such as that the subproblems that define each search direction may be solved approximately, that inexact sequential quadratic optimization steps may be utilized when advantageous, and that it may be implemented matrix-free so that derivative matrices need not be formed or factorized so long as matrix-vector products with them can be performed.

The condition $d\in \theta X_k$ is one particular way of approximating the linearized constraints. For trust region SQP algorithms that use null-space approach, the normal steps try to reduce the constraint violations whilst the tangential steps try to reduce the objective function or the Lagrangian function. In order to ensure convergence, conditions have to be imposed on normal steps and tangential steps. A detailed study was made on these condition in [69], where convergence results can be extended to the case that allow the use of inexact problem information originating from inexact first-order derivative information.

Another type of trust region subproblems has the following form

$$\begin{aligned} \min _{d\in \mathfrak {R}^n }&\phi _k(d) \,\end{aligned}$$

(3.11)

$$\begin{aligned} \hbox {s.t. }&\Vert d \Vert _{W_k } \le \varDelta _k , \end{aligned}$$

(3.12)

where $\phi _k (d)$ is a model function approximating some penalty function. For example, Fletcher [50] suggests the following $SL_1QP$ type trust region subproblem

$$\begin{aligned} \min _{d\in \mathfrak {R}^n}&g_k^T d + \frac{1}{2} d^T B_k d + \sigma _k \left\| \left( c_k + A_k^T d \right) ^{(-)}\right\| _1 \end{aligned}$$

(3.13)

$$\begin{aligned} \hbox {s.t. }&\Vert d\Vert _\infty \le \varDelta _k , \end{aligned}$$

(3.14)

where $( c_k + A_k^T d)^{(-)}$ is the vector of violations of the linearized constraints defined by

$$\begin{aligned} ( c_k + ( A_k)^T d)_i^{(-)} = \left\{ \begin{array}{ll} c_i(x_k) + d^T \nabla c_i(x_k) &{}\quad i=1,...,m_e , \\ \min \{ 0, \, c_i(x_k) + d^T \nabla c_i(x_k) \} &{} \quad i=m_e+1,...,m , \end{array} \right. \qquad \end{aligned}$$

(3.15)

where $A_k$ is the Jacobian of the constraints computed at $x_k$, The above trust region subproblem for constrained optimization can be viewed as the trust region subproblem for the $L_1$ exact penalty of the constrained problem. A similar subproblem based on the $L_\infty$ exact penalty function is given by Yuan [146]. The $L_\infty$ exact penalty function, comparing with the $L_1$ exact penalty, can reduce the maximum violation of constraints more quickly, whilst possibly increasing the violations overall. Trust region subproblems based on exact penalty functions are closely related to subproblems of trust region algorithms for nonlinear equations [40, 147] and nonlinear least squares that will be discussed in the next section. Trust region algorithms that use (3.13)–(3.14) are also similar to trust region algorithms for composite nonsmooth optimization [50, 51, 140–142].

For equality constrained optimization problems, Niu and Yuan [82] suggested a quadratic model function $Q_k(d)$ which approximates the augmented Lagrangian function at the $k$th iteration, and used the subproblem

$$\begin{aligned} \min _{d\in \mathfrak {R}^n}&{Q_k(d) }\end{aligned}$$

(3.16)

$$\begin{aligned} \hbox {s.t. }&\Vert d\Vert _2 \le \varDelta _k \, . \end{aligned}$$

(3.17)

One nice property of this approach is that (3.16)–(3.17) is exactly in the form of the standard trust region subproblem for unconstrained optimization (2.3)–(2.4). The model function in (3.16) is given by

$$\begin{aligned} Q_k (d) = (g_k-A_k\lambda _k)^T d +\frac{1}{2}d^{T}B_k d+ \sigma _k \Vert c_k + A_k^T d \Vert _2^2 , \end{aligned}$$

(3.18)

where $\lambda _k$ is the current approximate Lagrange multiplier and $\sigma _k > 0$ is the penalty parameter. In the algorithm of Niu and Yuan [82], the trial step is computed by solving (3.16)–(3.17). Then, the augmented Lagrange function is also used as a merit function to decide whether the trial step should be accepted. Their method extends the traditional trust region approach by combining a filter technique into the rules for accepting trial steps so that a trial step could still be accepted even when it is rejected by the traditional rule based on the merit function reduction. An estimate of the Lagrange multiplier is updated at each iteration, and the penalty parameter is updated to force sufficient reduction in the norm of the constraint violations. An active set technique is used to handle the inequality constraints. Numerical results for a set of constrained problems from the CUTEr collection [56] indicate that this approach is very efficient. However, no convergence results are given in Niu and Yuan [82] about their algorithm. Another possible way of handling inequality constraints is to use

$$\begin{aligned} Q_k (d) = (g_k-A_k\lambda _k)^T d +\frac{1}{2}d^{T}B_k d+ \sigma _k \Vert ( c_k + A_k^T d)^{(-)} \Vert _2^2 . \end{aligned}$$

(3.19)

The idea of approximating augmented Lagrangian by a quadratic function is also used in the trust region algorithm by Curtis et al. [34], in which global convergence is analyzed. However, when constraint violations converge to zero and the penalty parameter varies infinitely many times, first-order criticality could not be guaranteed, unless a much stronger assumption is enforced on the update of penalty parameters.

A modification to Niu and Yuan’s algorithm is given by Wang and Yuan [132] for equality constrained optimization, where a condition is introduced to decide whether the Lagrange multiplier should be updated. It also suggests a new strategy for adjusting the penalty parameters. Global convergence of the modified method is established under mild conditions by Wang and Yuan [132], in which the behavior of penalty parameters is analyzed. Recently, an extended trust region algorithm is given by Wang and Zhang [133] for nonlinear optimization with both equality constraints and simple bounds. At each iteration, an affine scaling trust region subproblem is constructed, where affine scaling technique is applied to handle bounds constraints. By adaptive update strategies of Lagrange multipliers and penalty parameters, global convergence can be achieved under mild conditions.

The shifted feasible set $X_k$ defined by (3.4) is the set containing all the points that satisfy the linearized constraints. We can equivalently write it as

$$\begin{aligned} X_k = \left\{ d \, \, | \, \, (c_k + A_k^T d )^{(-)} =0 \right\} \, . \end{aligned}$$

(3.20)

Thus, in order to handle the case when $X_k$ has no intersection with the trust region, instead of requiring zero residual of the linearized constraints, we can set an upper bound for the sum of squares of violations of the linearized constraints. Namely, we can let

$$\begin{aligned} X_k = \left\{ d \, \, | \, \, \Vert (c_k + A_k^T d )^{(-)}\Vert _2^2 \le \xi _k \right\} , \end{aligned}$$

(3.21)

where $\xi _k \ge 0$ is a parameter. If

$$\begin{aligned} \xi _k \ge \min _{\Vert d\Vert _{W_k} \le \varDelta _k} \Vert (c_k + A_k^T d )^{(-)}\Vert _2^2 , \end{aligned}$$

$X_k$ defined by (3.21) has nonempty intersection with the trust region. Thus, it is reasonable to consider the following trust region subproblem

$$\begin{aligned} \min _{d \in \mathfrak {R}^n}&m_k(d)\end{aligned}$$

(3.22)

$$\begin{aligned} \hbox {s.t. }&\Vert (c_k + A_k^T d )^{(-)}\Vert _2^2\le \xi _k \end{aligned}$$

(3.23)

$$\begin{aligned}&\Vert d\Vert _{W_k} \le \varDelta _k \, . \end{aligned}$$

(3.24)

The above subproblem with quadratic model $m_k(d)$ and $\Vert .\Vert _{W_k} = \Vert .\Vert _2$, called Celis–Dennis–Tapia (CDT) subroblem, is given by Celis et al. [18] and used by Powell and Yuan [107]. Properties of the CDT subproblem are discussed by many authors [2, 19, 87, 116, 144], and algorithms for solving the CDT subproblem are given by [145, 156]. Recently, Bienstock [6] shows that the CDT problem is polynomial-time solvable.

Subspace properties of the CDT problem are studied by Grapiglia, Yuan and Yuan [59], which establishes the following result.

Lemma 2

Let $S_k$ be an $r$ $(1\le r\le n)$ dimensional subspace in $\mathfrak {R}^n$, and $Z_k \in \mathfrak {R}^{n\times r}$ be an orthonormal basis matrix of $S_k$, namely

$$\begin{aligned} S_k = span \{ Z_k \}, \quad Z_k^T Z_k = I_r. \end{aligned}$$

Suppose that

$$\begin{aligned} \{ \nabla c_1(x_k) , ..., \nabla c_m(x_k) , g_k\} \subset S_k \end{aligned}$$

and $B_k \in \mathfrak {R}^{n \times n}$ is a symmetric matrix satisfying

$$\begin{aligned} B_k u = \sigma u , \quad \forall u \in S_k^\perp , \end{aligned}$$

where $\sigma > 0$. Then, the CDT subproblem

$$\begin{aligned} \min _{d\in \mathfrak {R}^n}&g_k^T d + \frac{1}{2} d^T B_k d \end{aligned}$$

(3.25)

$$\begin{aligned} \hbox {s.t. }&\Vert c_k + A_k^T d \Vert _2 \le \xi _k \end{aligned}$$

(3.26)

$$\begin{aligned}&\Vert d \Vert _2 \le \varDelta _k \end{aligned}$$

(3.27)

is equivalent to the following problem:

$$\begin{aligned} \min _{\bar{d}\in \mathfrak {R}^r}&{\bar{g}}_k^T \bar{d} + \frac{1}{2} {\bar{d}}^T {\bar{B}}_k \bar{d} \end{aligned}$$

(3.28)

$$\begin{aligned} \hbox {s.t. }&\Vert c_k + {\bar{A}}_k^T \bar{d} \Vert _2 \le \xi _k \end{aligned}$$

(3.29)

$$\begin{aligned}&\Vert \bar{d} \Vert _2 \le \varDelta _k , \end{aligned}$$

(3.30)

where $\bar{g}_k = Z_k^T g_k$, $\bar{B}_k = Z_k^T B_k Z_k$, and ${\bar{A}}_k = Z_k^TA_k$.

Due to the above lemma, a subspace version of the Powell-Yuan trust region algorithm is presented in Grapiglia, Yuan and Yuan [59]. Comparing with the full space implementation, the amount of computation of the subspace version algorithm can be reduced when the number of constraints is much smaller than the number of variables, especially in the early iterations. The subspace properties of the CDT subproblem described in the above lemma can be used in the same way to construct a subspace version of the CDT trust region algorithm for equality constrained optimization proposed by Celis et al. [18], as well of any algorithm based on the CDT subproblem.

Trust region interior-point methods are important class of numerical methods for general constrained optimization. Such methods are based on solving the KKT systems of barrier functions with trust region techniques. For more detailed discussions on trust region interior-point methods, please see Chapter 13 of [24]. The famous software package KNITRO [11] is an excellent example of the success of trust region interior-point methods. Other recent works on trust region interior-point methods include [129, 139] and [71].

When the constraints are simple bounds, we have the general bound constrained optimization problem

$$\begin{aligned} \min _{x\in \mathfrak {R}^n}&f(x) \end{aligned}$$

(3.31)

$$\begin{aligned} \hbox {s.t.}&l \le x \le u , \end{aligned}$$

(3.32)

where $l < u$ are two vectors in $\mathfrak {R}^n$. If $x_k$ is an interior point, namely

$$\begin{aligned} l < x_k < u , \end{aligned}$$

(3.33)

Coleman and Li [22, 23] suggested the following affine scaling trust region subproblem

$$\begin{aligned} \min _{d \in \mathfrak {R}^n}&m_k (d) \end{aligned}$$

(3.34)

$$\begin{aligned} \hbox {s.t.}&\Vert D_k^{-1} d \Vert _2 \le \varDelta _k \, \end{aligned}$$

(3.35)

where $D_k$ is a diagonal positive definite matrix. In Coleman and Li [22, 23], the affine scaling matrix $D_k$ is defined by

$$\begin{aligned} (D_k)_{ii} = \sqrt{ | v^{(i)} ( x_k ) | } , \quad i=1,..., n, \end{aligned}$$

(3.36)

where $v^{(i)}(x)$ is defined by

$$\begin{aligned} v^{(i)}(x) = {\left\{ \begin{array}{ll} x^{(i)} - u ^{(i)} &{} \hbox { if } (g(x))_i < 0 \quad \hbox { and } \quad u^{(i)} < \infty , \\ x^{(i)} - l^{(i)} &{} \hbox { if } (g(x))_i \ge 0 \quad \hbox { and } \quad l^{(i)} > - \infty , \\ \quad -1 &{} \hbox { if } (g(x))_i < 0 \quad \hbox { and } \quad u^{(i)} = \infty , \\ \quad \, \, 1 &{} \hbox { if } (g(x))_i \ge 0 \quad \hbox { and} \quad l^{(i)} = - \infty . \end{array}\right. } \end{aligned}$$

(3.37)

The derivation of the scaling matrix (3.36) is based on the Newton’s method for the diagonal system $D(x)^2 g(x) = 0$.

Wang and Yuan [131] suggested a new scaling matrix:

$$\begin{aligned} ( D_{k})_{ii}= {\left\{ \begin{array}{ll} t_k \cdot \sqrt{\frac{{a_{k}^{(i)}}}{ (g_{k} )_i }} , &{} \quad i\in {\mathcal {S}}_{k}^{1},\\ t_k \cdot \sqrt{\frac{{b_{k}^{(i)}}}{| (g_{k})_i | }} ,&{}\quad i\in {\mathcal {S}}_{k}^{2},\\ 1 ,&{}\quad i\notin {\mathcal {S}}_{k} \mathop {=}\limits ^{\vartriangle }{\mathcal {S}}_{k}^{1}\cup {\mathcal {S}}_{k}^{2}. \end{array}\right. } \end{aligned}$$

(3.38)

where

$$\begin{aligned} t_k =\dfrac{\sqrt{\sum \limits _{i\in {\mathcal {S}}_{k}^{1}} a_{k}^{(i)} ( g_{k})_i+\sum \limits _{i\in {\mathcal {S}}_{k}^{2}} b_{k}^{(i)}| (g_{k})_i|}}{\varDelta _{k}} , \end{aligned}$$

(3.39)

with the vectors $a_{k}$ and $b_{k}$ being defined componentwise by

$$\begin{aligned} a_{k}^{(i)}=x_{k}^{(i)}-l^{(i)},\quad b_{k}^{(i)}=u^{(i)}-x_{k}^{(i)},\quad i=1,\ldots ,n , \end{aligned}$$

and the two index sets are defined by

$$\begin{aligned} {\mathcal {S}}_{k}^{1}=\left\{ i \,\, | \,\, a_{k}^{(i)} \le \varDelta _{k}, \, (g_{k})_i \ge \epsilon a_{k}^{(i)}\right\} ,\quad {\mathcal {S}}_{k}^{2}=\left\{ i \, \, | \, \, b_{k}^{(i)} \le \varDelta _{k}, \, - (g_{k})_i \ge \epsilon b_{k}^{(i)}\right\} ,\nonumber \\ \end{aligned}$$

(3.40)

with $\epsilon \ll 1$ being a small positive constant. The scaling matrix (3.38) depends on the distances of the current iterate to the boundaries, the gradient of the objective function and the trust region radius. The motivation for choosing the scaling matrix by (3.38) is that the trust region step $s_k$ would head to the solution if the objective function is linear, which is proved in [131]. To be more exact, if the object function $f(x) = c^T x$ with $c_i \ne 0$ for all $i=1:n$, the minimizer $s_k$ of problem (3.34)–(3.35) with $m_k(d) = c^T d$ and the scaling matrix $D_k$ given by (3.38) implies that $x_k + s_k = x^*$ when $x_k$ is sufficiently close to $x^*$ which is the solution of (3.31)–(3.32).

4 Nonlinear equations and nonlinear least squares

In this section we consider trust region algorithms for nonlinear equations

$$\begin{aligned} F(x) = ( f_1(x) , f_2(x) , ..., f_m (x) )^T = 0 , \end{aligned}$$

(4.1)

where $F(x)$ is a nonlinear mapping from $\mathfrak {R}^n$ to $\mathfrak {R}^m$, and a closely related problem, the nonlinear least squares problem,

$$\begin{aligned} \min _{x\in \mathfrak {R}^n} \Vert F(x) \Vert _2^2 \, . \end{aligned}$$

(4.2)

Normally, a trust region algorithm for nonlinear Eq. (4.1) tries to minimize some penalty function $h(F(x))$. Thus, trust region algorithms for composite nonsmooth optimization [50, 51, 140–142] can be applied. The penalty function $h(\cdot )$ satisfies that $h(0)=0$ and

$$\begin{aligned} h(F) >0 , \qquad \forall F \ne 0 , \, F \in \mathfrak {R}^m \, . \end{aligned}$$

(4.3)

Thus, a general trust region subproblem for nonlinear equations is:

$$\begin{aligned} \min _{d\in \mathfrak {R}^n}&h (F_k + J_k d ) + \frac{1}{2} d^T B_k d \end{aligned}$$

(4.4)

$$\begin{aligned} \hbox {s.t. }&\Vert d \Vert _{W_k} \le \varDelta _k , \end{aligned}$$

(4.5)

where $F_k = F(x_k)$ and $J_k= [ \nabla f_1(x_k) , \nabla f_2(x_k) , ... , \nabla f_m(x_k) ]^T \in \mathfrak {R}^{m\times n}$ is the Jacobian matrix of $F(x)$ computed at $x_k$. Pioneer works on trust region algorithms for nonlinear equations and nonlinear least squares are given by Powell [90], Madsen [74], Moré [78], Duff et al. [40]. In these early papers, $B_k$ is set to be the zero matrix for all $k$, and $h(\cdot )$ is chosen as a simple penalty function such as $\Vert .\Vert _2$, $\Vert .\Vert _1$ or $\Vert .\Vert _\infty$. El Hallabi and Tapia [41] considered the case where $h(F) = \Vert F\Vert _\alpha$ is a general norm of $F$. The advantage of using a zero $B_k$ is that the subproblem is easy to solve as it can be converted into a linear programming problem when $\Vert d\Vert _{W_k} = \Vert d\Vert _\infty$ or $\Vert d\Vert _{W_k} = \Vert d\Vert _1$. However, the price that we have to pay for $B_k =0$ is that normally the convergence rate is at most linear. Powell and Yuan [106] studied conditions for superlinear convergence when $h(F) = \Vert F\Vert _1$ and $h(F) = \Vert F\Vert _\infty$.

Under certain non-degeneracy conditions, fast convergence results can be proved even if we let $B_k \equiv 0$ for all $k$. Consider the special case $h(F) = \Vert F\Vert _2^2$ and $\Vert . \Vert _{W_k} = \Vert .\Vert _2$, the trust region subproblem (for nonlinear equations and nonlinear least squares) becomes

$$\begin{aligned} \min _{d \in \mathfrak {R}^n}&\Vert F_k + J_k d \Vert _2^2 \end{aligned}$$

(4.6)

$$\begin{aligned} \hbox {s.t. }&\Vert d\Vert _2 \le \varDelta _k \, . \end{aligned}$$

(4.7)

Instead of using the standard technique [such as (2.9)] for updating trust region radii, Fan [42] suggests to use

$$\begin{aligned} \varDelta _k =\mu _{k}\Vert F_{k}\Vert _2^\delta , \end{aligned}$$

(4.8)

where $\delta \in (\frac{1}{2}, 1)$. Let $s_k$ be the solution of (4.6)–(4.7) with $\varDelta _k$ being defined by (4.8), and let

$$\begin{aligned} \rho _k={\dfrac{Ared_k}{Pred_k}}=\dfrac{\Vert F_k\Vert _2^2-\Vert F(x_k+s_k)\Vert _2^2}{\Vert F_k \Vert _2^2 - \Vert F_k +J_k s_k \Vert _2^2 } \, . \end{aligned}$$

Fan [42] updates the parameter $\mu _{k+1}$ by

$$\begin{aligned} \mu _{k+1}= {\left\{ \begin{array}{ll} c_5\mu _k &{} \text {if} \ \rho _k< c_2,\\ \mu _k &{} \text {if} \ \rho _k\in [c_2, c_4], \\ \min \{c_6\mu _k, M\} &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

where $0<c_2<c_4<1, \, 0<c_5<1<c_6, \, M\gg c_6\mu _1$ and $\mu _1>0$ are given. Fan [42] proves that the algorithm has the local $2 \delta$ order convergence rate in the sense that

$$\begin{aligned} {\text {dist}}(x_{k+1},X^*)\le {\text {dist}}(x_k,X^*)^{2\delta } , \end{aligned}$$

(4.9)

where $X^*$ is the solution set of $F(x) = 0$ if the local error bound condition holds. A similar technique is given by Zhang and Wang [154] in which the trust region radius has the form

$$\begin{aligned} \varDelta _k= \alpha ^p\Vert F_k\Vert _2^\delta , \end{aligned}$$

(4.10)

where $\alpha \in (0,1)$ and $p$ is the smallest positive integer that gives an acceptable trial step $s_k$. (4.10), as well as (4.8), implies that the trust region radius converges to zero when $k \rightarrow \infty$. Fan and Pan [44] proposed to use

$$\begin{aligned} \varDelta _{k}=\alpha ^p M\Vert F_k\Vert _2 , \end{aligned}$$

where $0<\alpha <1, M\gg 0$, and obtained local quadratic convergence rate:

$$\begin{aligned} \Vert x_{k+1}-x^*\Vert \le O(\Vert x_k-x^*\Vert ^2) \, . \end{aligned}$$

Recently, Fan and Lu [43] presented a new trust region algorithm which improves the algorithm given in Fan [42]. At each iteration, the new algorithm needs to compute the function value at an extra point and to solve an additional trust region subproblem. The algorithm is described as follows. At the $k$th iteration, the algorithm obtains $s_k$ by solving the trust region subproblem:

$$\begin{aligned}&\min _{s\in \mathbb {R}^n} \Vert F_k+J_ks\Vert _2^2\nonumber \\&\ s.t. \ \ \Vert s\Vert \le \varDelta _k:=\mu _k\Vert F_k\Vert _2^\delta \end{aligned}$$

where $\frac{1}{2}<\delta <1$. Denote $y_k=x_k+s_k$. Then, another subproblem:

$$\begin{aligned}&\min _{s\in \mathbb {R}^n} \Vert F(y_k)+J_ks\Vert _2^2,\nonumber \\&\ s.t. \ \ \Vert s\Vert \le \bar{\varDelta }_k:=\mu _k\Vert F(y_k)\Vert _2^\delta \end{aligned}$$

is solved to obtain $\bar{s}_k$. Define the new predicted reduction by

$$\begin{aligned} Pred_k=\Vert F_k\Vert _2^2-\Vert F_k+J_ks_k\Vert _2^2+\Vert F(y_k)\Vert _2^2-\Vert F(y_k)+J_k\bar{s}_k\Vert _2^2 , \end{aligned}$$

and $\rho _k={\dfrac{Ared_k}{Pred_k}}=\dfrac{\Vert F_k\Vert _2^2-\Vert F(x_k+s_k+\bar{s}_k)\Vert _2^2}{Pred_k}.$ The algorithm then updates $x_{k+1}$ and $\mu _{k+1}$ by

$$\begin{aligned} x_{k+1}=\left\{ \begin{array}{ll}x_k+s_k &{} \quad \hbox {if} \ \rho _k\ge p_0,\\ x_k &{}\quad \hbox {otherwise}, \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \mu _{k+1}=\left\{ \begin{array}{ll} 4\mu _k &{} \quad \hbox {if} \ \rho _k< \eta _1,\\ \mu _k &{} \quad \hbox {if} \ \rho _k\in [\eta _1, \eta _2],\\ \max \left\{ {\dfrac{\mu _k}{4}}, m\right\} &{} \quad \hbox {if} \ \rho _k> \eta _2 , \end{array}\right. \end{aligned}$$

where $m>0$ is a small constant. Under the local error bound condition, it can be shown that the modified trust region algorithm has the following property:

$$\begin{aligned} {\text {dist}}(x_{k+1}, X^*) \le {\text {dist}}(x_k, X^*)^{2{\delta }^2+\delta } \, . \end{aligned}$$

(4.11)

This result improves (4.9) because $2\delta ^2+\delta > 2\delta$ and the modified trust region algorithm is superlinearly convergent (in the sense of the rate of the distance ${\text {dist}}(x_k, X^*)$ converging to zero) for all $\delta \in (\frac{1}{2} , 1)$. Moreover, the convergence rate of ${\text {dist}}(x_k, X^*)$ is nearly cubic when $\delta$ is very close to 1.

Convergence results of several methods, including those allow the trust region radius to converge to zero, can be covered by a unified convergence theory given by Toint [124] under the framework of nonlinear stepsize control.

A derivative-free algorithm for nonlinear least squares was give by Zhang, Conn and Scheinberg [153]. Its local convergence properties are studied in [152].

5 Nonsmooth optimization

Non-smooth optimization problems are special problems where either the objective function or some constraints are nonsmooth. Trust region methods for nonsmooth optimization were first given by Fletcher [49–51], where the following composite nonsmooth optimization problem

$$\begin{aligned} \min _{x\in \mathfrak {R}^n} h(F(x)) \end{aligned}$$

(5.1)

is studied, where $F(x) = (f_1(x), ..., f_m(x))^T$ is a continuously differentiable mapping from $\mathfrak {R}^n$ to $\mathfrak {R}^m$ and $h(\cdot )$ is a nonsmooth convex function defined on $\mathfrak {R}^m$. Other pioneering researches on trust region algorithms for nonsmooth optimization include Powell [93], Burke [10] and Yuan [140–143]. A trust region subproblem for composite nonsmooth optimization problem (5.1) is

$$\begin{aligned} \min _{d\in \mathfrak {R}^n }&h(F(x_k) + J_k d ) + \frac{1}{2} d^T B_k d \end{aligned}$$

(5.2)

$$\begin{aligned} \hbox {s.t.}&\Vert d\Vert _{W_k} \le \varDelta _k , \end{aligned}$$

(5.3)

where $J_k = [\nabla f_1(x_k ), ... \nabla f_m(x_k) ]^T$ is the Jacobian matrix of $F(x)$ at $x_k$. The composite nonsmooth optimization (5.1) is studied by Sampaio, Yuan and Sun [110] where it is assumed that $F(x )$ is a nonsmooth locally Lipschitzian function while $h( \cdot )$ is a continuously differentiable function.

For the general nonsmooth optimization problem

$$\begin{aligned} \min _{x\in \mathfrak {R}^n} f(x) \end{aligned}$$

(5.4)

where $f(x) : \mathfrak {R}^n \rightarrow \mathfrak {R}$ is a nonsmooth function, we can build at each iteration a model $m_k(d) = m (x_k , p_k) (d)$ which is an approximation of $f(x_k +d)$ for small $d$, and $p_k\in \mathfrak {R}^l$ is an $l$-dimensional parameter vector which may change from iteration to iteration [36]. Consequently, the trust region subproblem at the $k$th iteration is

$$\begin{aligned} \min&m(x_k, p_k)(d) \end{aligned}$$

(5.5)

$$\begin{aligned} \hbox {s.t. }&\Vert d\Vert _{W_k} \le \varDelta _k \, . \end{aligned}$$

(5.6)

The Clarke generalized directional derivative [21] of $f$ at $x$ in the direction of $d \in \mathfrak {R}^n$ is defined by

$$\begin{aligned} f^\circ (x ; d ) = \lim _{y\rightarrow x} \sup _{t \downarrow 0} \frac{f(y + t d) - f(y)}{t} \, . \end{aligned}$$

(5.7)

Under some conditions which include

$$\begin{aligned} m(x, p )(0) = f(x) , \end{aligned}$$

(5.8)

and

$$\begin{aligned} m(x, p)^\circ (0; d) = f^\circ (x; d) \, \quad \forall d \in \mathfrak {R}^n\backslash \{ 0 \} , \end{aligned}$$

(5.9)

Dennis et al. [36] proved the convergence of a general trust region method for problem (5.4), where the trail step $s_k$ is obtained by solving subproblem (5.5)–(5.6) approximately. The results in [36] are extended by Qi and Sun [108] where the trust region subproblem

$$\begin{aligned} \min&f(x_k) + \phi (x_k , d) + \frac{1}{2} d^T B_k d \end{aligned}$$

(5.10)

$$\begin{aligned} \hbox {s.t. }&\Vert d\Vert _2 \le \varDelta _k \end{aligned}$$

(5.11)

is used. It is assumed in [108] that the function $\phi (x_k, d)$ satisfies

$$\begin{aligned} f(x_k + s_k ) - f(x_k) \le \phi (x_k , s_k)+ o ( \Vert s_k \Vert _2 ) \end{aligned}$$

(5.12)

if $s_k \rightarrow 0$, for any convergent subsequence $\{x_k \}$.

By converting nonsmooth convex minimization problems into differentiable convex optimization problems through Moreau-Yosida regularation, Zhang [155] gives a trust region algorithm for nonsmooth convex optimization. The Moreau-Yosida regularization of $f(x)$ is defined by

$$\begin{aligned} f_\lambda (x) = \min _{z\in \mathfrak {R}^n} \left\{ f(z) + \frac{1}{2\lambda } \Vert z- x\Vert _2^2 \right\} , \end{aligned}$$

(5.13)

where $\lambda > 0$ is a parameter.

In recent years, regularized minimization problems with nonconvex, nonsmooth, perhaps non-Lipschitz penalty functions have attracted considerable attention, owing to their wide applications in image restoration, signal reconstruction, and variable selection. Chen et al. [20] studied the following nonsmooth unconstrained minimization problem

$$\begin{aligned} \min _{x \in \mathfrak {R}^n} f(x) := \theta (x) + \lambda \sum _{i=1}^m \varphi \left( |d_i^T x|\right) , \end{aligned}$$

(5.14)

where $\theta : \mathfrak {R}^n \rightarrow \mathfrak {R}_+$ is twice continuously differentiable $\lambda \in \mathfrak {R}_+$, $d_i \in \mathfrak {R}^n, i=1,\ldots ,m$, and $\varphi : \mathfrak {R}_+ \rightarrow \mathfrak {R}_+$ may not be convex, differentiable, and perhaps not even Lipschitz. Chen et al. [20] proposed a smoothing trust region Newton method for solving (5.14). At each iteration, the method obtains the trial step by solving a model that approximates the smoothing problem

$$\begin{aligned} \min _{x \in \mathfrak {R}^n} \tilde{f}(x,\mu ): = \theta (x) + \lambda \sum _{i=1}^m \tilde{\varphi }(s(d_i^T x,\mu )), \end{aligned}$$

(5.15)

where $\tilde{\varphi }$ is a smoothing function of $\varphi$, and $s (d_i^T x , \mu )$ is a smoothing term for $|d_i^T x|$. For example, one possible choice of $s(t,\mu )$ is $\mu \hbox {ln} (2 + e^{t/\mu } + e^{-t/\mu } )$. The smoothing parameter $\mu$ is updated in order to ensure convergence. Assume that the penalty function $\varphi$ satisfies the following assumption.

Assumption 1

• 1. $\varphi$ is differentiable in $(0,\infty )$ and $\varphi '$ is locally Lipschitz continuous in $(0,\infty )$.

• 2. $\varphi$ is continuous at $0$ with $\varphi (0)=0$, $\varphi '(0^+) > 0$ and $\varphi '(t) \ge 0$ for all $t>0$.

Chen et al. [20] showed that the sequence generated by the smoothing trust region Newton method for (5.14) converges to a point satisfying the second order necessary optimality condition from any starting point.

Cartis et al. [13] studied the worst-case complexity of minimizing an unconstrained, nonconvex composite objective with a structured nonsmooth term by means of some first-order methods. [13] finds that it is unaffected by the nonsmoothness of the objective in the sense that a first-order trust region or quadratic regularization method (where the subproblem is to minimize the approximation function plus a quadratic regularization term $\sigma ||d||_2^2$) applied to it takes at most $O(\epsilon ^{-2} )$ function-evaluations to reduce the size of a first-order criticality measure below $\epsilon$.

6 Optimization without derivatives

In this section, we consider optimization without derivatives. Numerical methods for optimization problems without using derivatives are also called derivative-free methods. Derivative-free trust region methods date back to the algorithm of Winfield [137, 138], which is one of the pioneering works in trust region methods. The study of derivative-free trust region methods is very active in recent years. Excellent reviews on trust region algorithms for optimization without derivatives are given in [95, 97] and [29].

Comparing with derivative-based algorithms, derivative-free trust region algorithms have to build the model function $m_k(d)$ without using derivatives. Therefore, we can not apply Taylor expansions which are normally used in derivative-based algorithms. Instead, it is natural for derivative-free algorithms to construct model functions by interpolation.

The simplest nonlinear model is the quadratic model, which can be expressed by

$$\begin{aligned} m_k(d) = Q_k(x_k + d) = \hat{f}_k + \hat{g}_k^T d + \frac{1}{2} d^T B_k d , \end{aligned}$$

(6.1)

where $\hat{f}_k \in \mathfrak {R}$, $\hat{g}_k \in \mathfrak {R}^n$, $B_k \in \mathfrak {R}^{n \times n}$ symmetric. Because $B_k$ is symmetric, the number of independent elements is $\frac{1}{2} n (n+1)$. Thus, the total number of independent parameters in (6.1) is $\frac{1}{2} (n+1) (n+2)$. Hence it is reasonable to use $\frac{1}{2} (n+1)(n+2)$ function values and the interpolation conditions

$$\begin{aligned} Q_k(x^{(k)}_j ) = f(x^{(k)}_j) \, \quad j=1,..., \frac{1}{2}(n+1) (n+2) , \end{aligned}$$

(6.2)

to set the values $\hat{f}_k$, $\hat{g}_k$ and $B_k$, where $x^{(k)}_j (j=1,..., \frac{1}{2} (n+1)(n+2) \, )$ are the interpolation points at the $k$th iteration. Methods using (6.2) are given by Winfield [137, 138] and Powell [96].

However, even for a medium-size $n$ (for example, several hundred), evaluating the objective function at $\frac{1}{2}(n+1)(n+2)$ points can be prohibitively expensive. Thus, modern model-based trust region algorithms often build quadratic interpolation models using less than $(n+1)(n+2)/2$ points. Assume that the interpolation set has only $m$ points $x^{(k)}_j (j=1,...,m)$ with $m < \frac{1}{2} (n+1)(n+2)$ at the $k$th iteration. Consider the interpolation conditions

$$\begin{aligned} Q_k(x^{(k)}_j ) = f\left( x^{(k)}_j\right) \, \quad j=1,..., m \, . \end{aligned}$$

(6.3)

Normally we should choose $m \ge n+1$, since even for a linear model, we need at least $(n+1)$ function evaluations to define the model function by interpolation uniquely. Let ${\mathcal {Q}}$ be the linear space of all quadratic functions from $\mathfrak {R}^n$ to $\mathfrak {R}$. It is easy to see that the dimension of ${\mathcal {Q}}$ is $\frac{1}{2} (n+1)(n+2)$. Hence, the interpolation conditions (6.3) give an under-determined system for the parameters $\hat{f}_k$, $\hat{g}_k$ and $B_k$. Therefore, we need to impose more conditions on the model function in addition to interpolation conditions (6.3) in order to obtain the parameters $\hat{f}_k$, $\hat{g}_k$ and $B_k$, for example,

$$\begin{aligned} \min \Vert \hat{g}_k\Vert _F^2 + \Vert B_k \Vert _F^2 \end{aligned}$$

by Conn and Toint [31],

$$\begin{aligned} \min \Vert B_k\Vert _F^2 \end{aligned}$$

by Conn et al. [25, 26] and Conn, Scheigberg and Vicente (Chapter 5 of [29]), and

$$\begin{aligned} \min \Vert \mathrm {vec}(B_k)\Vert _1 , \end{aligned}$$

where ${\mathrm {vec}}(B_k)$ is a vector containing all the upper-triangular entries of $B_k$, by Bandeira, Scheinberg and Vicente [3].

Powell [97–99] suggests

$$\begin{aligned} \min \Vert B_{k} - B_{k-1} \Vert _F^2 , \end{aligned}$$

(6.4)

which is used in a series of software [100–102]. An extension of (6.4) is given by Powell [104] where the model function is obtained by

$$\begin{aligned} \min \Vert B_k -B_{k-1}\Vert _F^2 + \sigma _k \Vert \hat{g}_k - \nabla m_{k-1} ( x_k - x_{k-1} ) \Vert ^2 , \end{aligned}$$

(6.5)

subject to the interpolation conditions (6.3). Zhang [157] studies this extension using a Sobolev semi-norm which is defined by

$$\begin{aligned} | f |_{H^1(\Omega )} := \left[ \int _{\Omega } \Vert \nabla f(x) \Vert _2^2 dx \right] ^{1/2} \, . \end{aligned}$$

(6.6)

It is shown by Zhang [157] that

$$\begin{aligned} \min _{Q(x) \in {\mathcal {Q}}}&\Vert \nabla ^2 Q \Vert _F^2 + \sigma \Vert \nabla Q(\bar{x})\Vert _2^2\end{aligned}$$

(6.7)

$$\begin{aligned} \hbox {s.t. }&Q(x) = f(x) , x \in {{\mathcal {S}}} , \end{aligned}$$

(6.8)

where ${{\mathcal {S}}}$ is the set of interpolation points, is equivalent to

$$\begin{aligned} \min _{Q\in {\mathcal {Q}} }&| Q(x) |_{ H^1( {\mathcal {B}}_r )} \end{aligned}$$

(6.9)

$$\begin{aligned} \hbox {s.t. }&Q(x) = f(x) , x \in {{\mathcal {S}}} , \end{aligned}$$

(6.10)

where ${\mathcal {B}}_r = \{ x | \Vert x - \bar{x} \Vert \le r\}$ with $r = \sqrt{ (n+2) / \sigma }$. Based on this observation, Zhang [157] proposes a simple and efficient method to determine $\sigma _k$ in (6.5).

In some applications, it can also happen that the interpolation conditions (6.3) are overdetermined ($m>(n+1)(n+2)/2$), especially when the function evaluation is not very expensive but contaminated by noise. In this case, instead of requiring the exact interpolation conditions (6.3), one can define the quadratic model $m_k(d)$ to be a weighted least squares approximation of $f$ by solving

$$\begin{aligned} \min \sum _{i=1}^m w_i^2 \left( m_k\left( x^{(k)}_j - x_k \right) - f(x^{(k)}_j) \right) ^2 , \end{aligned}$$

(6.11)

which is used in the trust region method based on regression models [7, 28], and is also discussed in Chapter 4 of [29].

In addition to quadratic models, radial basis functions (RBF) models are also very popular for constructing derivative-free trust region algorithms. A radial basis function model has the following form

$$\begin{aligned} m_k(d) = \sum _{j=1}^m \lambda _j \phi ( \Vert d - x^{(k)}_j \Vert ) + p(d) , \end{aligned}$$

(6.12)

where $\phi : R_+ \rightarrow R$ is a univariate function and $p\in {\mathcal {P}}_{d-1}^n$ is a polynomial in the space of $n-$variate polynomials of total degree no more than $d-1$. Algorithms using radial basis function models are discussed in [84, 135, 136].

A special issue for derivative-free trust region methods based on interpolation and regression is the geometry of the interpolation/regression set, which is critical to the quality of the model. This interesting problem is discussed in [27, 28]. In order to keep the interpolation/regression set from becoming degenerate, many methods (for instances, DFO, UOBYQA, and NEWUOA) use explicit “geometry-improving” steps. Marazzi and Nocedal [75] proposed another strategy in which a “wedge constraint” is imposed to the trust region subproblem so that the geometry of the interpolation set will not be destroyed after the trial point is included into the set. Fasano, Morales and Nocedal [46] studied the numerical performance of a trust region method using interpolation models but without any “geometry phase”, where surprisingly good results are obtained. However, it is shown in [111] that the “geometry phase” cannot be completely omitted, otherwise the convergence will be jeopardized. In [111] they also propose a convergent trust region method that does not have any explicit “geometry-improving” step or wedge constraint but exploits “self-correcting geometry” of the interpolation set.

Convergence theory is more difficult to be established for a derivative-free trust region algorithm than a derivative-based trust region algorithm because no derivative information is used in the construction of the algorithm. Convergence results for derivative-free trust region algorithms are given in [26, 30, 103], and [136].

Recently, an interesting paper [4] was published in which it proves the almost-sure convergence of trust region method assuming that the models are “probabilistically fully linear”. Another recent paper [62] shows that the algorithm studied in [4] drives the gradient to zero at the rate of $\mathcal {O}(1/\sqrt{k})$ with “overwhelmingly high” probability, matching the rate of the deterministic trust region method using derivatives.

Derivative-free trust region algorithms for constrained problems were first discussed by Powell [94], where linearly constrained derivative-free optimization is studied. Powell [102] also studies another special case for bound constrained problems. An active set derivative-free trust region method is given for solving nonlinear bound constrained optimization by [64]. Recently, Troeltzsch [125] gives a derivative-free trust region algorithm based on SQP for equality constrained optimization.

Sampaio and Toint [109] gave a derivative-free trust-funnel method for general equality constrained nonlinear optimization problems. The algorithm is an generalization of the trust-funnel method of Gould and Toint [58], and preserves the main features of the method in [58] without using derivatives.

Trust region framework provides a way to rigorously handle surrogate models [65]. Grapiglia, Yuan and Yuan [61] presented a derivative-free trust region algorithm for composite nonsmooth optimization (5.1). The proposed algorithm is an adaptation of the derivative-free trust region algorithm of Conn, Scheinberg and Vicente [30] for unconstrained smooth optimization, with the techniques for composite nonsmooth optimization proposed by Fletcher [50, 51] and Yuan [141, 142]. Under suitable conditions, global convergence of the algorithm is proved. Furthermore, by introducing a slightly modified update rule for the trust region radius and assuming that the interpolation models are fully linear at all the iterations, it is proved that the function-evaluation complexity of the algorithm is $O(\epsilon ^{-2} )$ for the algorithm to reduce the first order criticality measure below $\epsilon$.

Hybrid of trust region and other methodology is also studied in the context of derivative-free optimization. For instances, [35] and [39] incorporate trust region techniques into direct search and stochastic search, and [65] studies a surrogate management framework using trust region steps for derivative-free optimization.

7 Regularization methods

One interesting result of the standard trust region subproblem is that the minimizer of (2.3)–(2.4) is also a global minimizer of the model function $m_k(d)$ with a suitable quadratic penalty term. Namely (2.3)–(2.4) is equivalent to

$$\begin{aligned} \min _{d\in \mathfrak {R}^n} g_k^T d + \frac{1}{2} d^T B_k d + \frac{1}{2} \lambda _k \Vert d\Vert _2^2 , \end{aligned}$$

(7.1)

for a proper penalty parameter $\lambda _k \ge 0$. Thus, trust region algorithms can be viewed as a regularization by using the quadratic penalty function. Consequently, extensions of trust region algorithms by other regularization techniques have been attracting attention from many researchers. Cartis et al. [14] proposed an adaptive regularisation algorithm using cubics (ARC) for unconstrained optimization. At each iteration of the ARC algorithm, the following cubic model

$$\begin{aligned} m_k(d) = f(x_k) + g_k^T d + \frac{1}{2} d^T B_k d + \frac{1}{3} \sigma _k \Vert d \Vert _2^3 \end{aligned}$$

(7.2)

is used to obtain the trial step $s_k$. To be more exact, $s_k$ satisfies

$$\begin{aligned} m_k(s_k ) \le m_k (s_k^C ) \end{aligned}$$

(7.3)

where $s_k^C = - \alpha _k^C g_k$ is the Cauchy point with

$$\begin{aligned} \alpha _k^C = \hbox {arg} \min _{\alpha \in \mathfrak {R}_+ } m_k ( - \alpha g_k ) \, . \end{aligned}$$

The ARC algorithm uses an adaptive estimation of the local Lipschitz constant and approximations to the global model-minimizer which remain computationally-viable even for large-scale problems. It is shown in [14] that the excellent global and local convergence properties obtained by Nesterov and Polyak are retained, and sometimes extended to a wider class of problems, by the ARC approach. Worst-case function- and derivative-evaluation complexity of the ARC method is studied in [15]. Recently, Grapiglia, Yuan and Yuan [60] extended the results of [15] by relaxing the boundedness of $B_k$ to the following weaker condition

$$\begin{aligned} \Vert B_k \Vert \le \delta _1 + \delta _2 k . \end{aligned}$$

In [16], the ARC method is adapted to the constrained optimization problem where a nonlinear, possibly nonconvex, smooth objective function is minimized over a convex domain.

The generalization of the model function (7.2) gives the following general regularised version of trust region subproblem:

$$\begin{aligned} \min _{d\in \mathfrak {R}^n} m(d) = g^T d + \frac{1}{2}d^T B d +\frac{\sigma }{p} \Vert d \Vert _2^p , \end{aligned}$$

(7.4)

where $\sigma >0$, $p>2$. (7.4) with $p = 3$ is the cubic reguarised subproblem used by Cartis et al. [14] in their ARC algorithm. This special case was first due to Griewank [66] and was considered later by many authors, see Nesterov and Polyak [81], Weiser et al. [134], and Cartis et al. [14]. Recently, Gould and Toint [57], and Hsia et al. [70] studied properties of subproblem (7.4) for the general case $p>2$.

The necessary global optimality condition for (7.4) was established by Cartis et al. [14, Thm. 3.1] and by Nesterov and Polyak [81, Thm. 10 when p = 3 ], see also [57]. Very recently, Hsia et al. [70] proved that the presented necessary condition is also sufficient. In the same paper, the $\ell _2$ norm of the global minimizers is shown to be unique.

Theorem 1

(Necessary and sufficient global optimality condition) The point $d^*$ is a global minimizer of (7.4) if and only if it is a critical point satisfying $\nabla m(d^*)=0$ and $B+\sigma \Vert d^*\Vert _2^{p-2}I\succeq 0$. Moreover, the $\ell _2$ norms of all the global minimizers are equal.

Following Martínez’s characterization [77] on necessary and sufficient conditions for the non-global local minimizer of (2.3)–(2.4), Hsia et al. [70] established the necessary and sufficient condition for the non-global local minimizer of (7.4) as follows.

Theorem 2

(Necessary and sufficient condition for non-global local minimizer) $\underline{d}$ is a non-global local minimizer of (7.4) if and only if

$$\begin{aligned} \underline{d} =- \left( \sigma \underline{t}^* I+ B\right) ^{-1}g, \end{aligned}$$

(7.5)

where $\underline{t}^*$ is a root of the secular function

$$\begin{aligned} h(t)=\Vert \left( \sigma t I+ B\right) ^{-1}g\Vert ^2-t^{\frac{2}{p-2}}, ~~t\in \left( \max \left\{ - \frac{\alpha _2}{\sigma },0\right\} , - \frac{\alpha _1}{\sigma }\right) \end{aligned}$$

(7.6)

such that $h'(\underline{t}^*)>0$, where $\sigma _1 \le \sigma _2$ are the two smallest eigenvalues of $B$.

Notice that, the secular function for (2.3)–(2.4) [cf. $h(t)$ in (7.6)] is defined by

$$\begin{aligned} \phi (\lambda )=\Vert (B_k +\lambda I)^{-1}g_k \Vert ^2. \end{aligned}$$

Martínez [77] proved that, if $\underline{d}$ is a non-global local minimizer of (2.3)–(2.4), then $\underline{d}$ satisfies $(B_k+\lambda ^*I)\underline{d}=-g_k$ with $\lambda ^*\in (-\alpha _2,-\alpha _1)$, $\lambda ^*\ge 0$ and $\phi '(\lambda ^*)\ge 0$. And, this necessary condition becomes sufficient when $\phi '(\lambda ^*)> 0$. To the best of our knowledge, it is unknown whether the gap between the necessary and sufficient conditions can be closed as in Theorem 2.

As a corollary of Theorem 2, it is shown in [70] that

Theorem 3

(7.4) with $p>2$ has at most one non-global local minimizer.

Interestingly, Theorem 3 is applied by Hsia et al. [70] to show that problem (7.4) with $m$ linear inequality constraints:

$$\begin{aligned} \min _{d\in \mathfrak {R}^n}&g^T d + \frac{1}{2}d^TBd +\frac{\sigma }{p} \Vert d\Vert _2^p \end{aligned}$$

(7.7)

$$\begin{aligned} \mathrm{s. t. }&l_i\le a_i^Td\le u_i,~i=1,\ldots ,m, \end{aligned}$$

(7.8)

can be solved in polynomial time when $p=4$ and $m$ is a fixed number. Notice that, when $m$ is also an input, (7.7)–(7.8) is generally NP-hard even when $p=4$, see a proof in [70].

In a recent paper, Cartis et al. [17] proved that a general nonlinear nonconvex optimization problem can be solved to the accuracy of $\epsilon$ by a second-order method using cubic regularization in at most $O(\epsilon ^{-3/2})$ function evaluations, the same order bound as in the unconstrained case. This result is obtained by first showing that the same result holds for inequality constrained nonlinear least-squares.

8 Discussions

In this paper, trust region and regularization algorithms for unconstrained optimization, constrained optimization, nonlinear equations and nonlinear least squares, nonsmooth optimization, and optimization without derivatives are reviewed. Trust region algorithms have been flourishing in nonlinear optimization over the past three decades, they can also been applied to other types of optimization problems.

The application of trust region methods to Nash equilibrium problems is studied in Yuan [150], which proposes a Jacobi-type trust region method for their solutions. The method includes different trust regions for each player, and the trial step for each player is computed and accepted (or rejected) based on each individual utility function. In order to ensure global convergence, an overall merit function is used to update the trust regions.

A trust region algorithm for unconstrained multi-objective optimization is given in Villacorta, Oliveira and Soubeyran [127]. At each iteration, instead of treating each object separably, the algorithm constructs a single nonsmooth trust region subproblem. It is shown that the algorithm generates a sequence that converges to Pareto critical points.

Recently, a Riemannian trust region method for low-rank matrix completion is given by Boumal and Absil [8], which studies the problem of recovering large scale low-rank matrices when most of the entries are unknown. It adapts an approach that exploits the geometry of the low-rank constraint to recast the problem as an unconstrained optimization problem on the Grassmann manifold. Consequently, the derived unconstrained optimization problem is solved by applying first- and second-order Riemannian trust region methods, which are studied in Absil, Baker and Gallivan [1].

Trust region is a powerful technique for ensuring global convergence and is particularly suitable for handling nonconvex and ill-conditioned problems. Trust region can be used with other techniques to construct efficient numerical algorithms, for example its combination with line search technique [83], and with a non-monotone technique [123]. Recently, in optimization, particularly for sparse problems, alternating direction minimization (ADM) techniques are attracting much attention from researchers. Yet, most ADM methods are globalized through line search techniques. It is worthwhile to explore the possibility of using trust region techniques in ADM type algorithms.