Strong LP formulations for scheduling splittable jobs on unrelated machines

Abstract

A natural extension of the makespan minimization problem on unrelated machines is to allow jobs to be partially processed by different machines while incurring an arbitrary setup time. In this paper we present increasingly stronger LP-relaxations for this problem and their implications on the approximability of the problem. First we show that the straightforward LP, extending the approach for the original problem, has an integrality gap of 3 and yields an approximation algorithm of the same factor. By applying a lift-and-project procedure, we are able to improve both the integrality gap and the implied approximation factor to $1+\phi$, where $\phi$ is the golden ratio. Since this bound remains tight for the seemingly stronger machine configuration LP, we propose a new job configuration LP that is based on an infinite continuum of fractional assignments of each job to the machines. We prove that this LP has a finite representation and can be solved in polynomial time up to any accuracy. Interestingly, we show that our problem cannot be approximated within a factor better than $\frac{e}{e-1}\approx 1.582\, (\hbox {unless } \mathcal {P}=\mathcal {NP})$, which is larger than the inapproximability bound of 1.5 for the original problem.

1 Introduction

The unrelated machine scheduling problem, $R||C_{\max }$ in the three-field notation of [9], has attracted significant attention within the scientific community. The problem is to find a schedule of jobs with machine-dependent processing times that minimizes the makespan, i.e., the maximum machine load. Lenstra et al. [14] designed a polynomial time linear programming based rounding algorithm and showed that the algorithm has a worst-case approximation ratio of 2, and that the existence of a polynomial time algorithm with ratio smaller than 3/2 would prove that $\mathcal {P}= \mathcal {NP}$.

A natural generalization of this problem is to allow jobs to be split and processed on multiple machines simultaneously, where in addition a setup has to be performed on every machine processing the job. This generalized scheduling problem finds applications in production planning, e.g., in textile and semiconductor industries [13, 22], and disaster relief operations [25]. Formally, we are given a set of $m$ machines $M$ and a set of $n$ jobs $J$ with processing times $p_{ij} \in \mathbb {Z}_+$ and setup times $s_{ij} \in \mathbb {Z}_+$ for every $i \in M$ and $j \in J$. A schedule corresponds to a vector $x \in [0, 1]^{M \times J}$, where $x_{ij}$ denotes the fraction of job $j$ that is assigned to machine $i$, satisfying $\sum _{i\in M} x_{ij}=1$ for all $j\in J$. If job $j$ is processed (partially) on machine $i$ then a setup of length $s_{ij}$ has to be performed on the machine. During the setup of a job the machine is occupied and thus no other job can be processed nor be set up. This results in the definition of load of machine $i\in M$ as $\sum _{j: x_{ij}>0}( x_{ij}p_{ij} + s_{ij})$. The objective is to minimize the makespan, the maximum load of the schedule. We denote this problem by $R|\text {split,setup}|C_{\max }$. Note that by setting $p_{ij}=0$ and interpreting the setup times $s_{ij}$ as processing requirements we obtain the classical problem without job splitting, $R||C_{\max }$.

Related work Reducing the approximability gap for $R||C_{\max }$ is a prominent open question [27]. Since the seminal work by Lenstra et al. [14] there has been a considerable amount of effort leading to partial solutions to this question. In the restricted assignment problem, the processing times are of the form $p_{ij}\in \{p_j,\infty \}$ for all $i,j \in J$. A special case of this setting, in which each job can only be assigned to two machines, was considered by Ebenlendr et al. [6]. They note that while the lower bound of 3/2 still holds, a $7/4$-approximation can be obtained. For the general restricted assignment problem Svensson [23] broke the barrier of 2, by showing that the optimal makespan can be estimated within a factor of $33/17 + \varepsilon \approx 1.9412 + \varepsilon$ by an algorithm based on a machine configuration linear programming relaxation where each variable indicates the subset of jobs assigned to a given machine. It is worth mentioning that this result only shows that the objective value can be approximated within said precision, but no polynomial time algorithm is known to find a schedule with this guarantee.

On the negative side, the machine configuration LP has an integrality gap of 2 for general unrelated machines [26], as was the case for the linear programming relaxation in [14]. This even holds for another special case called unrelated graph balancing, where each job has (possibly different) finite processing times on at most two machines [6, 26]. Configuration LPs have also been studied extensively for the max-min version of the problem [2, 3, 8, 11, 17, 26], which has become known as the Santa Claus problem.

The literature on scheduling problems with splittable jobs is significantly less abundant. To the best of our knowledge such a problem has been presented for the first time in a production problem in the textile industry [22]. It was modeled as a restricted assignment version, in which each job is associated to a specific subset of compatible machines on which it can be processed and can be split arbitrarily and processed independently on these machines. However no setup times are considered. The jobs are released over time and the goal is minimizing the maximum (weighted) tardiness. It turns out that this problem is solvable in polynomial time if machines are identical or uniform; the paper considers also the case of unrelated machines providing pseudopolynomial time algorithms. Another application of splittable jobs appears in production scheduling for semiconductor wafers [13], again with the objective of minimizing the total weighted tardiness. The authors provide different variants of a local search heuristic to solve the problem in practice.

Theoretical results on the subject are not only scarce, but also restricted to the special case of identical machines. In particular, Xing and Zhang [28] describe a $(1.75 - 1/m)$-approximation for makespan minimization, which was later improved to $5/3$ by Chen et al. [4]. The problem with splittable jobs, setup times, and the objective of minimizing the sum of completion times, having arisen in modeling a problem on disaster relief operations [25], is studied by Schalekamp et al. [19]. They give a polynomial time algorithm in the case of two machines and job- and machine-independent setup times, and a 2.781-approximation algorithm for arbitrary $m$. This was later improved to $2 + \varepsilon$ in [5], even in the presence of weights, in which case the problem is NP-hard [19].

Another setting that comes close to job splitting is preemptive scheduling with setup times [15, 18, 21], which does not allow simultaneous processing of parts of the same job. We also refer to the survey [1] and references therein for results on other scheduling problems with setup costs.

Our contribution Due to the novelty of the considered problem, our aim is to advance the understanding of its approximability, in particular in comparison to $R||C_{\max }$. We first study the integrality gap of a natural generalization of the LP relaxation by Lenstra et al. [14] to our setting and notice that their rounding technique does not work in our case. This is because it might assign a job with very large processing time to a single machine, while the optimal solution splits this job. On the other hand, assigning jobs by only following the fractional solution given by the LP might incur a large number of setups (belonging to different jobs) to a single machine. We get around these two extreme cases by adapting the technique from [14] so as to only round variables exceeding a certain threshold while guaranteeing that only one additional setup time is required per machine. This yields a 3-approximation algorithm presented in Sect. 2. Additionally, we show that the integrality gap of this LP is $3$, and therefore our algorithm is best possible for this LP.

In Sect. 3 we improve the approximation ratio by tightening our LP relaxation with a lift-and-project approach. We refine our previous analysis by balancing the rounding threshold, resulting in a $(1+\phi +\varepsilon )$-approximation for any $\varepsilon >0$, where $\phi \approx 1.618$ is the golden ratio. Surprisingly, we can show that this number is best possible for this LP; even for the seemingly stronger machine configuration LP mentioned above. This suggests that considerably different techniques are necessary to match the 2-approximation algorithm for $R||C_{\max }$. Indeed, we also show in Sect. 5 that it is $\mathcal {NP}$-hard to approximate within a factor $\frac{e}{e-1}\approx 1.582$, a larger lower bound than the 3/2 hardness result known for $R||C_{\max }$. For the restricted assignment case, where $s_{ij}\in \{s_j,\infty \}$ and $p_{ij}\in \{p_j,\infty \}$, we obtain a $(2+\varepsilon )$-approximation algorithm, for any $\varepsilon >0$, matching the 2-approximation of [14] in Sect. 4. We remark that the solutions produced by all our algorithms have the property that at most one split job is processed on each machine. This property may be desirable in practice since in manufacturing systems setups require labor causing additional expenses.

As the integrality gaps of all mentioned relaxations are no better than $1+\phi$, we propose a novel job based configuration LP relaxation in Sect. 6.2 that has the potential to lead to better guarantees. Instead of considering machine configurations that assign jobs to machines, we introduce job configurations, describing the assignment of a particular job to the machines. The resulting LP cuts away worst-case solutions of the other LPs considered in this paper, rendering it a promising candidate for obtaining better approximation ratios. While the set of job configurations is infinite, we show that we can restrict a priori to a finite subset of so-called maximal configurations. Applying discretization techniques we can approximately solve the LP within a factor of $(1+\varepsilon )$ by separation over the dual constraints. Finally, we study the projection of this polytope to the assignment space and derive an explicit set of inequalities that defines this polytope. An interesting open problem is to determine the integrality gap of the job configuration LP.

2 A 3-approximation algorithm

Our 3-approximation algorithm is based on a generalization of the LP by Lenstra, Shmoys, and Tardos [14]. Let $C^*$ be a guess on the optimal makespan. Consider the following feasibility LP, whose variable $x_{ij}$ denotes the fraction of job $j$ assigned to machine $i$.

$$\begin{aligned} {[\mathrm{LST}]}\!: \quad \qquad \qquad \sum _{i\in M} x_{ij}&= 1&\text {for all }j\in J,\end{aligned}$$

(1)

$$\begin{aligned} \sum _{j\in J} x_{ij}(p_{ij}+s_{ij})&\le C^*&\text {for all }i\in M,\end{aligned}$$

(2)

$$\begin{aligned} x_{ij}&= 0&\text {for all } i\in M,\, j\in J : s_{ij}> C^*,\nonumber \\ x_{ij}&\ge 0&\text {for all } i\in M,j\in J. \end{aligned}$$

(3)

Notice that the smallest value of $C^*$ such that $[\mathrm{LST}]$ is feasible can be computed in polynomial time. Indeed, there are at most $n\cdot m$ different thresholds for $C^*$ that changes the subset of equalities considered in (3). We solve one linear program for each of them, where $C^*$ is treated as a variable and the objective function is to minimize $C^*$. Among all these linear programs we select the one of the smallest $C^*$ and such that it is consistent with the corresponding threshold for the $s_{ij}$’s. The computed $C^*$ value satisfies that $C^* \le \mathrm{OPT}$, where $\mathrm{OPT}$ is the optimal solution of the original problem $R|\text {split,setup}|C_{\max }$.

Let $x$ be a feasible extreme point of $[\mathrm{LST}]$. We define the bipartite graph $G(x)=(J\cup M, E(x))$, where $E(x)=\{ij:0<x_{ij}\}$. Using the same arguments as in [14], not repeated here, we can show the following property.

Lemma 1

For every extreme point $x$ of $[\mathrm{LST}]$, each connected component of $G(x)$ is a pseudotree; a tree plus at most one edge that creates a single cycle.

We devise a procedure for rounding the extreme point $x$. To this end, we define

$$\begin{aligned} E_{+}=\{ij\in E(x):x_{ij} > 1/2\} \end{aligned}$$

and

$$\begin{aligned} J_{+}=\{j\in J:\text {there exists } i\in M \text { with } ij\in E_{+}\}, \end{aligned}$$

i.e., those jobs that the fractional solution $x$ assigns to some machine by a factor of more than $1/2$. In our rounding procedure each job $j\in J_+$ is completely assigned to the machine $i\in M$ for which $x_{ij}>1/2$. We now show how to assign the remaining jobs.

Let us call $G'(x)$ the subgraph of $G(x)$ induced by $(J\cup M){\setminus } J_+$. Notice that every edge $ij$ in $G'(x)$ satisfies $0 < x_{ij} \le 1/2$. Also, since $G'(x)$ is a subgraph of $G(x)$ every connected component of $G'(x)$ is a pseudotree.

Definition 1

Given $A\subseteq E(G'(x))$, we say that a machine $i\in M$ is $A$ -balanced, if there exists at most one job $j\in J{\setminus } J_{+}$ such that $ij\in A$. We say that a job $j\in J{\setminus } J_{+}$ is $A$ -processed if there is at most one machine $i\in M$ such that $ij\notin A$ and $x_{ij}>0$.

In what follows we seek to find a subset $A\subseteq E(G'(x))$ such that each job $j\in J{\setminus } J_+$ is $A$-processed and each machine is $A$-balanced. We will show that this is enough for a 3-approximation, by assigning each job $j\in J{\setminus } J_+$ to machine $i$ by a fraction of at most $2x_{ij}$ for each $ij\in A$, and not assigning it anywhere else. Since every job $j\in J{\setminus } J_+$ is $A$-processed and $x_{ij}\le 1/2$ for all $i\in M$ (including the only machine $i$ with $ij\notin A$, if it exists), job $j$ will be completely assigned. Also, since each machine is $A$-balanced, the load of each machine $i$ will be affected by at most the setup-time of one job $j$. This setup time $s_{ij}$ is at most $C^*$ by restriction (3). This and the fact that the processing time of a job on each machine is at most doubled are the basic ingredients to show the approximation factor of 3.

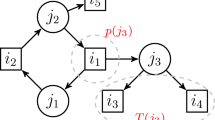
Construction of the set A In the following, we denote by $(T,r)$ a rooted tree $T$ with root $r$. Consider a connected component $T$ of $G'(x)$. Since $G'(x)$ is a subgraph of $G(x)$, Lemma 1 implies that $T$ is a pseudotree. We denote by $C=j_1i_1j_2i_2\cdots j_{\ell }i_{\ell }j_1$ the only cycle of $T$ (if it exists), which must be of even length. If such a cycle does not exist we choose any path in $T$ from $j_1$ to some $i_{\ell }$. The jobs in the cycle are $J(C)=\{j_1,\ldots ,j_{\ell }\}$ and the machines are $M(C)=\{i_1,\ldots ,i_{\ell }\}$. In the cycle, we define the matching $K_C=\{(j_k,i_k):k\in \{1,\ldots ,\ell \}\}$. In the forest $T{\setminus } K_C$, we denote by $(T_u,u)$ the tree rooted in $u$, for every $u\in J(C)$. Notice that by deleting the matching, no two vertices of $J(C)$ will be in the same component of $T{\setminus } K_C$.

For every $u\in J(C)$, by directing the edges of $(T_u,u)$ away from the root, we obtain a directed tree, each level of which consists either entirely of machine-nodes or entirely of job-nodes. We delete all edges going out of machine nodes, i.e., all edges entering job-nodes. The remaining edges we denote by $A_u$. We define $A:=\bigcup _{u\in J(C)}A_u$; see Fig. 1 for a depiction of the situation. The following two lemmas show that the set $A$ is indeed $A$-processed and $A$-balanced.

Fig. 1

Construction of set $A$. Circles represent job nodes, squares represent machines. Solid lines represent the edges in $A$, dashed lines represent edges deleted in the construction, double dashed lines represent the edges in $K_C$

Lemma 2

Every job $j\in J{\setminus } J_+$ is $A$-processed.

Proof

Consider first a job $j_k\in J(C)$. Since $j_k$ is the root of the tree $T_{j_{k}}$, the set $A$ contains all its incident edges apart from the edge $(i_{k},j_k)$, which was removed as part of the matching $K_C$. Therefore $j_k$ is $A$-processed for all $k\in \{1,\ldots ,\ell \}$. Now consider a job $j \notin J(C)$. This job $j$ is part of a directed tree $T_u$ and has exactly $1$ incoming edge in that tree. By construction of $A_u$, this edge is the only edge incident to the job-node that is deleted, hence it is $A$-processed. $\square$

Lemma 3

Every machine $i\in M$ is $A$-balanced.

Proof

Any machine $i \in M$ is a node of some tree $T_u$. By construction, the single incoming edge into $i$ of $T_u$ is the only edge incident to $i$ that survives in $A$, hence $i$ is $A$-balanced. $\square$

Given set $A$, we apply the following rounding algorithm that constructs a new assignment $\tilde{x}$. The algorithm also outputs a binary vector $\tilde{y}_{ij}\in \{0,1\}$ which indicates whether job $j$ is (partially) assigned to machine $i$ or not.

Theorem 1

There exists a $3$-approximation algorithm for $R|\text {split,setup}|C_{\max }$.

Proof

Let $x$ be an extreme point of $[\mathrm{LST}]$ and consider the output $\tilde{x},\tilde{y}$ of algorithm Rounding$(x)$. Clearly $\tilde{x},\tilde{y}$ can be computed in polynomial time. We show that the schedule that assigns a fraction $\tilde{x}_{ij}$ of job $j$ to machine $i$ has a makespan of at most $3C^*$. This implies the theorem since, as discussed before, $C^*\le \mathrm{OPT}$.

First we show that $\tilde{x}\ge 0$ defines a valid assignment, i.e., $\sum _{i\in M} \tilde{x}_{ij}=1$ for all $j$. Indeed, this follows directly by the algorithm Rounding$(x)$: If $j\in J_+$, then there exists a unique machine $i\in M$ with $ij\in E_+$ and therefore $j$ is completely assigned to machine $i$. If $j\not \in J_+$, then

$$\begin{aligned} \sum _{i\in M} \tilde{x}_{ij} = \sum _{i: ij\in A} \frac{x_{ij}}{\sum _{k:kj\in A}x_{kj}}=1. \end{aligned}$$

Now we show that the makespan of the solution is at most $3C^*$. First notice that for every $ij\in E_{+}$ we have that $1=\tilde{x}_{ij}=\tilde{y}_{ij}\le 2x_{ij}$, because $ij \in E_{+}$ implies that $x_{ij}>1/2$. On the other hand, for every $j\in J{\setminus } J_{+}$ we have that $\sum _{k:kj\in A}x_{kj}\ge 1/2$, because at most one machine that processes $j$ fractionally is not considered in $A$. We conclude that $\tilde{x}\le 2x$. Then for every $i \in M$ it holds that

$$\begin{aligned} \sum _{j\in J} (\tilde{x}_{ij}p_{ij}+\tilde{y}_{ij}s_{ij})&= \sum _{j:ij\in E_{+}} (\tilde{x}_{ij}p_{ij}+\tilde{y}_{ij}s_{ij})+\sum _{j:ij\in A} (\tilde{x}_{ij}p_{ij}+\tilde{y}_{ij}s_{ij})\\&\le \sum _{j:ij\in E_{+}}2x_{ij}(p_{ij}+s_{ij})+\sum _{j:ij\in A} \left( 2x_{ij}p_{ij}+s_{ij}\right) \\&\le 2C^*+\sum _{j:ij\in A} s_{ij}.\\ \end{aligned}$$

Recall that machine $i$ is $A$-balanced, and therefore there is at most one job $j$ with $ij\in A$. Also, $ij\in A$ implies that $ij\in E(x)=\{ij: x_{ij}>0\}$, and hence, by (3) in $[\mathrm{LST}], s_{ij}\le C^*$. We conclude that $\sum _{j:ij\in A} s_{ij}\le C^*$, and the theorem follows. $\square$

We finish this section by noting that our analysis is tight. Specifically, it can be shown that the gap between the LP solution and the optimum can be arbitrarily close to 3.

Theorem 2

For any $\varepsilon >0$, there exists an instance such that $(3-\varepsilon )C^*\le \text {OPT}$, where $C^*$ is the smallest number such that $[\mathrm{LST}]$ is feasible.

Proof

We give a family of instances $\{I_k\}_{k\in \mathbb {N}}$ such that $\text {OPT}/C^*$ approaches 3 as $k$ goes to infinity. This suffices for showing the theorem.

Instance $I_k$ has a set $J$ of $2k+1$ jobs. For each job $j\in J$ we introduce its own set of $k$ identical machines $M_j$, i.e., $M_{j}\cap M_{j'}=\emptyset$ if $j\ne j'$. We define $s_{ij}=1$ and $p_{ij}=2k$ for each $j\in J$ and $i\in M_j$, and $s_{ij}=p_{ij}=\infty$ if $i\in M_{j'}$ with $j'\ne j$. Additionally, we introduce a new family of $k$ machines $M'$, where for all $j\in J$ and $i\in M'$ we have $p_{ij}=0$ and $s_{ij}=1$. See Fig. 2 for a depiction of the construction.

Fig. 2

Example showing that $[\mathrm{LST}]$ has a gap of 3

We claim that the LP has a solution with $C^*=1+\frac{1}{2k}$ while $\text {OPT}=3$.

To see that $\text {OPT}=3$, notice that there are two possible cases. If all jobs in $J$ are completely assigned to machines in $M'$ then the makespan is clearly $3$ since there are $k$ machines in $M'$ and $2k+1$ jobs, and each job has to use a setup time of $1$ on each machine. Otherwise, there exists one job $j\in J$ that is completely assigned to machines in $M_j$. It is easy to see that the solution that minimizes the makespan on these machines assigns job $j$ up to a fraction of $1/k$ to each machine in $M_j$. Then the load on each machine $i\in M_j$ is $1+p_{ij}/k=3$. Therefore $\text {OPT}=3$.

We now give a feasible solution to $[\mathrm{LST}]$ with $C^*:=1+\frac{1}{2k}$. This is obtained with the following fractional assignment,

$$\begin{aligned} x_{ij}:= {\left\{ \begin{array}{ll} \frac{1}{2k} &{} \text {for each }j\in J \text { and } i\in M_j\cup M',\\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Since $|M_j\cup M'|=2k$ it is clear that every job is completely assigned. Then, to see that in $[\mathrm{LST}]$  (2) is satisfied, notice that for $i\in M'$ we have that

$$\begin{aligned} \sum _{j\in J} x_{ij}(p_{ij}+s_{ij}) = \sum _{j\in J} x_{ij} = \frac{2k+1}{2k}= 1 + \frac{1}{2k}= C^*, \end{aligned}$$

and similarly, for $i\in M_{j}$,

$$\begin{aligned} \sum _{j'\in J} x_{ij'}(p_{ij'}+s_{ij'}) = x_{ij}(p_{ij}+s_{ij})= \frac{2k+1}{2k}= C^*. \end{aligned}$$

We conclude that the gap for instance $I_k$ is $\frac{3}{1+\frac{1}{2k}}$, which converges to $3$ when $k$ goes to infinity. $\square$

3 An LP with integrality gap $1+\phi$

In this section we refine the previous algorithm and improve the approximation ratio. Since $[\mathrm{LST}]$ has a gap of 3, we strengthen it in order to obtain a stronger LP. To this end notice that inequalities (2) in $[\mathrm{LST}]$ are the LP relaxation of the following constraints of the mixed integer linear program with binary variables $y_{ij}$ for machine $i$ and job $j$:

$$\begin{aligned} \sum _{j\in J}(x_{ij}p_{ij}+ y_{ij}s_{ij})&\le C^*&\text {for all }i\in M,\end{aligned}$$

(4)

$$\begin{aligned} x_{ij}&\le y_{ij}&\text {for all }i\in M \text { and }j\in J. \end{aligned}$$

(5)

A stronger relaxation is obtained by applying a lift-and-project step [16] to the first inequality. For some fixed choice $ij$ multiplying both sides of the $i$-th inequality (4) by the corresponding variable $y_{ij}$ implies (by leaving out terms)

$$\begin{aligned} y_{ij}x_{ij}p_{ij}+ y_{ij}^2s_{ij}\le y_{ij}C^*. \end{aligned}$$

In case $C^*-s_{ij}>0$, this inequality implies the valid linear inequality

$$\begin{aligned} x_{ij}\frac{p_{ij}}{C^*-s_{ij}} \le y_{ij}, \end{aligned}$$

(6)

since every feasible integer solution has $y_{ij}x_{ij}=x_{ij}$ and $y_{ij}^2=y_{ij}$. Note that, in optimal solutions of the LP relaxation, $y_{ij}$ attains the smallest value that satisfies (5) and (6). Therefore, we define $\alpha _{ij} = \max \left\{ 1,\frac{p_{ij}}{C^*-s_{ij}}\right\}$ if $C^*>s_{ij}$, and $\alpha _{ij}=1$ otherwise, and substitute $y_{ij}$ by $\alpha _{ij}x_{ij}$ to obtain the strengthened LP relaxation

$$\begin{aligned} {[\mathrm{LST}_{\mathrm{strong}}]}\!: \quad \qquad \qquad \sum _{i\in M} x_{ij}&= 1&\text {for all }j\in J,\end{aligned}$$

(7)

$$\begin{aligned} \sum _{j\in J} x_{ij}(p_{ij}+ \alpha _{ij}s_{ij})&\le C^*&\text {for all }i\in M,\end{aligned}$$

(8)

$$\begin{aligned} x_{ij}&= 0&\text {for all } i\in M, \, j\in J: s_{ij} > C^*, \nonumber \\ x_{ij}&\ge 0&\text {for all } i\in M,j\in J. \end{aligned}$$

(9)

We remark that the stronger inequalities (8) obtained through the lift-and-project procedure also follow from the observation that at most a fraction of $(C^* - s_{ij})/p_{ij}$ of job $j$ can be processed on machine $i$. Notice that $[\mathrm{LST}_{\mathrm{strong}}]$ is at least as strong as $[\mathrm{LST}]$ since $\alpha _{ij}\ge 1$. Since the $\alpha _{ij}$ variables depend on $C^*$, we cannot use the approach of Sect. 3 to find the smallest $C^*$ value such that $[\mathrm{LST}_{\mathrm{strong}}]$ is feasible. Instead, for any $\varepsilon >0$, we find a value of $C^*$ such that $[\mathrm{LST}_{\mathrm{strong}}]$ is feasible and $C^*\le (1+\varepsilon )\mathrm{OPT}$. This follows by a straightforward binary search procedure on integer powers of $1+\varepsilon$. Note that the value of $C^*$ that we find here might be strictly larger than the one used in the previous section.

Let $x$ be an extreme point of this LP. We use a rounding approach similar to the one in the previous section. Consider the graph $G(x)$. As before, each connected component of $G(x)$ is a pseudotree, using the same arguments that justified Lemma 1. Also, we define again a set of jobs $J_+$ that the LP assigns to one machine by a sufficiently large fraction. In the previous section this fraction was 1/2. Now we parameterize it by $\beta \in (1/2, 1)$, to be chosen later. We define $E_+=\{j\in E(x): x_{ij}>\beta \}$ and $J_+=\{j\in J: \text { there exists } i\in M \text { with } ij\in E_+\}$.

Consider the subgraph $G'(x)$ of $G(x)$ induced by the set of nodes $(J\cup M){\setminus } J_+$. Let $A$ be a set constructed as in the previous section. Then, as in Sect. 2, every machine is $A$-balanced and every job is $A$-processed. Now we apply the algorithm Rounding$(x)$ of the last section to obtain a new assignment $\tilde{x},\tilde{y}$. We show that for $\beta = \phi -1$ this is a solution with makespan $(1+\phi )C^*$, where $\phi =(1+\sqrt{5})/2\approx 1.618$ is the golden ratio. The following technical lemma is needed.

Lemma 4

Let $\beta$ be a real number such that $1/2<\beta <1$. Then

$$\begin{aligned} \max _{0\le \mu \le 1}\left\{ \mu + \max \left\{ \frac{1}{\beta },\frac{1-\mu }{1-\beta } \right\} \right\} = \max \left\{ \frac{1}{1-\beta },1+\frac{1}{\beta }\right\} . \end{aligned}$$

Proof

Let $f(\mu )= \mu + \max \left\{ \frac{1}{\beta },\frac{1-\mu }{1-\beta } \right\}$. Clearly $f$ is a piece-wise linear function with at most two different slopes. Therefore, it is maximized when $\mu \in \{0,1\}$ or when $\mu$ is the breakpoint of the function, i. e., when $\mu$ solves the equation $\mu + 1/\beta =\mu + (1-\mu )/(1-\beta )$. Let $\mu _0$ be the solution of this equation. A simple computation shows that $f(\mu _0)=2$, which implies that $\max _{0\le \mu \le 1} f(\mu )=\max \{f(0),f(\mu _0),f(1)\}=\max \{1/(1-\beta ),2,1+1/\beta \}$. Since $1/2<\beta <1$, we have $1/(1-\beta ) > 2$ and $1+1/\beta >2$, which implies the lemma. $\square$

Theorem 3

For any $\varepsilon >0$, there exists a $(1+\phi +\varepsilon )$-approximation algorithm for the problem $R|split,setup |C_{\max }$.

Proof

By binary search we find $C^*$ such that $[\mathrm{LST}_{\mathrm{strong}}]$ is feasible, and such that $C^* \le (1+\varepsilon ')\mathrm{OPT}$. Let $x$ be an extreme point of $[\mathrm{LST}_{\mathrm{strong}}]$ with this value of $C^*$, and let $\tilde{x},\tilde{y}$ be the output of algorithm Rounding$(x)$ described in Sect. 2. The fact that $\tilde{x},\tilde{y}$ correspond to a feasible assignment follows from the same argument as in the proof of Theorem 1. We now show that the makespan of this solution is at most $(1+\phi )C^*$, which implies the approximation factor.

For any edge $ij\in E_{+}$, we have $x_{ij}>\beta$ and hence $1=\tilde{x}_{ij}=\tilde{y}_{ij}\le 1/\beta \cdot x_{ij}$. Additionally, for every $j\in J{\setminus } J_{+}$, we have again, by the choice of $A$, that it is $A$-processed. Hence, $\sum _{k:kj\notin A}x_{kj}\le \beta$, because at most one machine that processes $j$ fractionally is not considered in $A$. Thus, $\sum _{k:kj\in A}x_{kj}\ge 1-\beta$, which implies that $\tilde{x}_{ij}\le x_{ij}/(1-\beta )$. Hence, for machine $i$,

$$\begin{aligned} \sum _{j\in J} (\tilde{x}_{ij}p_{ij}+\tilde{y}_{ij}s_{ij})&=\sum _{j:ij\in E_{+}} (\tilde{x}_{ij}p_{ij}+\tilde{y}_{ij}s_{ij})+\sum _{j:ij\in A} (\tilde{x}_{ij}p_{ij}+\tilde{y}_{ij}s_{ij})\\&\le \frac{1}{\beta }\sum _{j:ij\in E_{+}}x_{ij}(p_{ij}+s_{ij})+\frac{1}{1-\beta }\sum _{j:ij\in A} x_{ij}p_{ij}+ \sum _{j:ij\in A}s_{ij}. \end{aligned}$$

Since machine $i$ is $A$-balanced, there exists at most one job $j$ with $ij\in A$ (if there is no such job then $i$ has load at most $C^*/\beta$). Let $j(i)$ be that job, and define $\mu _{i}= s_{ij(i)}/C^*$. Then notice that

$$\begin{aligned} x_{ij(i)}(p_{ij(i)}+\alpha _{ij(i)}s_{ij(i)})&\ge x_{ij(i)}p_{ij(i)}\left( 1+\frac{s_{ij(i)}}{C^*-s_{ij(i)}}\right) \\&= x_{ij(i)}p_{ij(i)}\left( 1+\frac{\mu _i}{1-\mu _i}\right) = x_{ij(i)}p_{ij(i)}\frac{1}{1-\mu _i}. \end{aligned}$$

Combining the last two inequalities we obtain that

$$\begin{aligned} \sum _{j\in J} (\tilde{x}_{ij}p_{ij}+\tilde{y}_{ij}s_{ij})&\le \frac{1}{\beta }\sum _{j:ij\in E_{+}}x_{ij}(p_{ij}+s_{ij})+\frac{1}{1-\beta }x_{ij(i)}p_{ij(i)}+ s_{ij(i)}\\&\!\le \! \frac{1}{\beta }\!\sum _{j:ij\in E_{+}}\!\!x_{ij}(p_{ij}\!+\!s_{ij})\!+\!\frac{1\!-\!\mu _i}{1\!-\!\beta }x_{ij(i)}(p_{ij(i)}\!+\!\alpha _{ij(i)}s_{ij(i)}) \!+\! \mu _i C^* \\&\le \max \left\{ \frac{1}{\beta },\frac{1-\mu _i}{1-\beta }\right\} \sum _{j\in J}x_{ij}(p_{ij}+\alpha _{ij}s_{ij})+ \mu _i C^* \\&\le C^* \left( \mu _i + \max \left\{ \frac{1}{\beta },\frac{1-\mu _i}{1-\beta }\right\} \right) . \end{aligned}$$

Therefore, by the previous lemma we have that the load of each machine is at most $C^* \cdot \max \{1/(1-\beta ),1+1/\beta \}$. The latter factor is minimized when $1/(1-\beta )=1+1/\beta$, hence $\beta =(-1+\sqrt{5})/2=(1+\sqrt{5})/2-1=\phi -1$. Together with the fact that $C^* \le (1+\varepsilon ')\mathrm{OPT}$, the approximation ratio becomes $(1+1/(\phi -1))(1+\varepsilon ')=(1+\phi )(1+\varepsilon ')$ and choosing $\varepsilon = (1+\phi )\varepsilon '$ completes the proof. $\square$

We close this section by showing that $1\,+\,\phi$ is the best approximation ratio achievable by $[\mathrm{LST}_{\mathrm{strong}}]$.

Theorem 4

For any $\varepsilon >0$, there exists an instance such that $C^*(1+\phi -\varepsilon )\le \text {OPT}$, where $C^*$ is the smallest number such that $[\mathrm{LST}_{\mathrm{strong}}]$ is feasible.

Proof

Consider the instance depicted in Fig. 3. It consists of two disjoint sets of jobs $J$ and $J'$. Each job $j_{\ell } \in J$ forms a pair with its corresponding job $j'_{\ell } \in J'$. Each such pair is associated with a parent machine $i_p(j_{\ell })=i_p(j'_{\ell })=i_p^{\ell }$ such that both $j_{\ell }$ and $j'_{\ell }$ can be processed on this machine with setup time $s_{i^{\ell }_{p}j_{\ell }} = s_{i^{\ell }_{p}j'_{\ell }} = \phi /2$ and $p_{i^{\ell }_{p}j_{\ell }} = p_{i^{\ell }_{p}j'_{\ell }} = 0$. Each job $j$ of each pair is furthermore associated with a child machine $i_c(j)$ such that $s_{i_c(j)j} = 0$ and $p_{i_c(j)j} = \phi +1 = 1/(2 - \phi )$. In addition, there is a single top job $j^t$ that can be processed on any of the parent machines with setup time $1$ and processing time $0$. All other setup and processing times are infinite.

Fig. 3

Example showing that $[\mathrm{LST}_{\mathrm{strong}}]$ has a gap of $1+\phi$

We will show that the makespan of any feasible solution is at least $1 + \phi$ while the LP relaxation has a value of $1 + 1/k$. First, it is easy to check that the following fractional assignment is a feasible solution to $[\mathrm{LST}_{\mathrm{strong}}]$ with $C^*=1+1/k$.

$$\begin{aligned} x_{ij} = {\left\{ \begin{array}{ll} \phi - 1 &{} \text {for } j\in J \cup J', i=i_p(j),\\ 2 - \phi &{} \text {for } j\in J\cup J', i=i_c(j),\\ \frac{1}{k} &{} \text {for } j=j^t, i=i_p^\ell \text { for all }\ell =1,\ldots ,k, \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

To see that the optimal makespan of the instance is $1+\phi$, let $i_p(j_\ell )$ be the machine that receives the top job $j^t$ in an optimal solution (note that $p_{j^t i}=0$ for all $i$, and hence this job is never split). Similarly, jobs $j_{\ell }$ and $j'_{\ell }$ are not split in an optimal solution. If either of these jobs is completely assigned to its child machine, then the makespan of the schedule is $1/(2 - \phi )=1\,+\,\phi$. Otherwise, $j_{\ell }$ and $j_{\ell }'$ are both assigned to $i_p(j_{\ell })=i_p(j_{\ell }')$, which then has a load of $1+1/(\phi - 1)=1+\phi$. The theorem follows by choosing $k$ large enough for the given $\varepsilon$. $\square$

4 A $(2+\varepsilon )$-approximation algorithm for restricted assignment

In this section we consider the restricted assignment setting, i.e., for every job $j$ there exists a set of machines $M_j$ such that $p_{ij}=p_j$ and $s_{ij}=s_j$ if $i\in M_j$, and $p_{ij}=s_{ij}=\infty$ if $i\notin M_j$. We use the same relaxation as in the previous section to show that this version admits a 2-approximation algorithm,

$$\begin{aligned} {[\mathrm{LST}_{\mathrm{strong}}]}\!: \quad \qquad \qquad \sum _{i\in M_j} x_{ij}&= 1&\text {for all }j\in J,\end{aligned}$$

(10)

$$\begin{aligned} \sum _{j\in J:i\in M_j} x_{ij}(p_{j}+ \alpha _{j}s_{j})&\le C^*&\text {for all }i\in M,\end{aligned}$$

(11)

$$\begin{aligned} x_{ij}&= 0&\text {for all } i\in M, \, j\in J: s_{ij} > C^*,\nonumber \\ x_{ij}&\ge 0&\text {for all }j\in J \text { and } i\in M_j, \end{aligned}$$

(12)

where $\displaystyle \alpha _j=\max \left\{ 1,p_{j}/(C^*-s_{j})\right\}$.

Let $x$ be an extreme point of this LP. As the basis for the rounding procedure we consider in this case the graph $G'(x)=(J'(x) \cup M, E'(x))$ defined by the set of edges $E'(x)=\{ij:0<x_{ij}<1 \}$ and the set of job-nodes $J'(x) = \{j \in J : j \text { is incident to some } e \in E'(x)\}$; i.e., we fix all variables $x_{ij}$ that have value $0$ or $1$. As before, each connected component of $G'(x)$ is a pseudotree. Let $A$ be the set constructed as in Sect. 2, now based on the graph $G'(x)$.

As each job $j \in J'(x)$ is $A$-processed, there is at most one machine $i^-_j$ such that $0 < x_{i^{-}_{j}j} < 1$ and $i^{-}_{j}j \notin A$. For each $j \in J'(x)$ we further choose an arbitrary machine $i^+_j$ with $i^{+}_{j}j \in A$. We construct a new solution $\tilde{x}$ by defining

$$\begin{aligned} \tilde{x}_{ij} := {\left\{ \begin{array}{ll} 0 &{} \text {if } i^-_j \text { exists and } i = i^-_j\\ x_{ij} + x_{i^{-}_{j}j} &{} \text {if } i^-_j \text { exists and } i = i^+_j\\ x_{ij} &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

for every $i\in M$ and $j \in J$. In other words, the amount of $j$ processed on $i^-_j$ is moved to $i^+_j$. We will show that this, together with the full setup time $s_j$, increases the load of $i^+_j$ by at most $C^*$, yielding the desired approximation ratio of $2+\varepsilon$.

Theorem 5

For any $\varepsilon >0$, there exists a $(2+\varepsilon )$-approximation algorithm for scheduling splittable jobs on unrelated machines under restricted assignment.

Proof

By binary search we find $C^*$ such that $[\mathrm{LST}_{\mathrm{strong}}]$ is feasible, and such that $C^* \le (1+ \varepsilon /2)\mathrm{OPT}$. We construct $\tilde{x}$ from the resulting solution $x$ as described above. It remains to show that

$$\begin{aligned} \sum _{j \in J \, : \, \tilde{x}_{ij} > 0} (p_j \tilde{x}_{ij} + s_{j}) \le 2C^*\quad \text { for every } i \in M. \end{aligned}$$

Consider a machine $i \in M$. First observe that (10), (11) and (12) imply $\alpha _j x_{ij}\le 1$ for all $j \in J$ and that further $C^* \ge p_j/\alpha _j + s_j$ by definition of $\alpha _j$. Combining these two observations yields $C^* \ge p_j x_{ij} + s_j$. Because $i$ is $A$-balanced, $i$ processes at most one job $j$ with $0 < x_{ij} < 1$. Note that $\tilde{x}_{ij} \le x_{ij} + x_{i^{-}_{j}j}$ (with equality if $i = i^+_j$) and $\tilde{x}_{ij'} \le x_{ij'}$ for all $j' \ne j$. Therefore

$$\begin{aligned} \sum _{j \in J \, : \, \tilde{x}_{ij} > 0} (p_j \tilde{x}_{ij} + s_{j}) \le \underbrace{\sum _{j' \in J} {x}_{ij'} (p_{j'} + \alpha _{j'} s_{j'})}_{\le C^*} + \underbrace{p_j x_{i^{-}_{j}j} + s_{j}}_{\le C^*} \le 2C^*, \end{aligned}$$

where the first inequality follows from the fact that $x_{ij'} \in \{0, 1\}$ for all $j' \ne j$. This proves the lemma. $\square$

Finally, note that if $p_j=0$ for all $j \in J$, then also $\alpha _j=1$ for $j \in J$, and therefore $[\mathrm{LST}_{\mathrm{strong}}]$ is equivalent to the classic LP relaxation of the restricted assignment version of $R||C_{\max }$ (with setup times fulfilling the roles of the processing times in the latter). This implies that the integrality gap of $2$ known for the latter LP also holds for $[\mathrm{LST}_{\mathrm{strong}}]$ in the restricted assignment case; see [14].

5 Hardness of approximation

By reducing from Max $k$ -Cover, we derive an inapproximability bound of $e / (e-1) \approx 1.582$ for $R|\text {split,setup}|C_{\max }$, indicating that the problem might indeed be harder from an approximation point of view compared to the classic $R||C_{\max }$, for which $3/2$ is the best known lower bound [14].

Theorem 6

For any $\varepsilon > 0$, there is no $\big (\frac{e}{e-1}-\varepsilon \big )$-approximation algorithm for $R|\text {split,setup}|C_{\max }$ unless $\mathcal {P} = \mathcal {NP}$.

Proof

We prove the hardness of $R|\text {split,setup}|C_{max}$ by providing a reduction from the Max $k$ -Cover problem defined as follows: given a universe of elements $e_1, \ldots , e_m$ and a family of subsets of this universe $S_1, \ldots , S_n$, find $k$ sets that maximizes the number of covered elements, i.e., the number of elements contained in the union of the selected sets. In a seminal paper [7], Feige showed that it is $\mathcal {NP}$-hard to distinguish between instances in which all elements can be covered with $k$ disjoint sets and instances where no $k$ sets can cover more than a $(1-\frac{1}{e}) + \varepsilon '$ fraction of the elements for any $\varepsilon ' > 0$. In addition, this hardness holds for instances where all sets have the same cardinality, namely $m/k$.

Given a Max $k$ -Cover instance where each set has cardinality $m/k$ we construct an instance of our problem in polynomial time as follows. We define $n$ jobs, one for each set $S_j$. We define a set of $n-k$ generic machines with the property that on each one of them each job $j$ has setup time $1$ and processing time $0$. Next, we create an element-machine $m_i$ for each element $e_i$, on which each job $j$ with $e_i \in S_j$ requires setup time $s_{m_{i}j}=0$ and processing time $p_{m_{i}j}=m/k=|S_j|$, and each job $j$ with $e_i \notin S_j$ has setup time $s_{e_i,j}=2$ and $p_{m_{i}j}=m/k=|S_j|$.

Assume all elements can be covered by $k$ disjoint sets. In the instance of $R|\text {split,setup}|C_{max}$, we can schedule the $k$ jobs corresponding to these sets on the element-machines by assigning each of them by equal fractions $k/m$ of length $1$ on each of its $m/k$ element-machines. Note that, as the sets are disjoint, no element-machine recieves more than one fraction of a job. The remaining $n - k$ jobs can be processed on the generic machines, yielding a makespan of $1$.

Now assume every set of $k$ sets can cover at most $((1-\frac{1}{e}) + \varepsilon ') m$ elements. Note that if more than $n - k$ jobs are scheduled on the generic machines, at least one of these machines has to process two jobs, resulting in a makespan of $2$. Thus, in order to achieve a makespan strictly less than $2$, at least $k$ jobs have to be scheduled on element-machines. Consider any subset of $k$ jobs scheduled on the element-machines. Note that we have to divide the total processing time of $m$ of these $k$ jobs over the at most $(1-\frac{1}{e} +\varepsilon ')m$ element-machines covered by the corresponding $k$ sets. In the best case this yields a makespan of $\frac{m}{(1-\frac{1}{e} +\varepsilon ')m}=\frac{e}{e-1} - \varepsilon$. This proves that it is $\mathcal {NP}$-hard to distinguish between instances that have optimal makespan $1$ and instances that have optimal makespan $\frac{e}{e-1} -\varepsilon$ for any $\varepsilon >0$. $\square$

Notice that the construction used in this lower bound makes it non-valid for the restricted assignment version of the problem. For that version the best known lower bound is still $3/2$, resulting from the basic makespan problem without splits [14].

6 Configuration LP relaxations

A basic tool of combinatorial optimization is to design stronger linear programs based on certain configurations. These LPs often provide improved integrality gaps and thus lead to better approximation algorithms as long as they can be solved efficiently and be rounded appropriately. We consider two configuration LPs in this section: a machine configuration LP, which we show to exhibit, surprisingly, the same integrality gap of $1 + \phi$ as already observed for $[\mathrm{LST}_{\mathrm{strong}}]$, and a job configuration LP, which we show to be much more promising.

Remark 1

Observe that $R|\text {split,setup}|C_{\max }$ can be formulated as a mixed integer program with rational coefficients. Hence there always exists an optimal solution in which all fractions $x_{ij}$ are rational numbers. We therefore will restrict all configurations throughout this section to consist only of rational numbers. In particular, although the sets of configurations in the LPs defined below might be infinite, they will always be countable, and we can thus define sums over these sets.

6.1 A machine configuration LP

In machine scheduling the most widely used configuration LP uses as variables the possible configurations of jobs on a given machine. These machine configuration LPs have been successfully studied for the unrelated machine setting since the pioneering work of Bansal and Sviridenko [3]. Recent progress in the area includes [6, 23, 24, 26].

The standard way to formulate a machine configuration LP relaxation for allocation problems is to have a variable for each machine $i$ and each subset (configuration or bundle) $B$ of jobs that can be feasibly assigned to $i$ with respect to a guessed makespan $C^*$. In the context of $R|\text {split,setup}|C_{\max }$ the natural extension of a configuration $B$ for machine $i$ is associated with a vector $x^B \in [0, 1]^J$ that specifies what fraction of job $j$ is scheduled on machine $i$ in the configuration. Given a guessed makespan $C^*$, we say a configuration $B$ is feasible, if and only if $\sum _{j : x^B_j > 0} (x^B_j p_{ij} + s_{ij}) \le C^*$. Note that the number of feasible configurations is infinite. Although we shall see that the machine configuration is in fact no stronger than $[\mathrm{LST}_{\mathrm{strong}}]$, we first prove that we can restrict to a finite subset of configurations, called maximal configurations in order to define the LP formally. A feasible configuration $B$ is maximal if $x^B_j \in \{0, 1\}$ for all $j \in J$, or if $\sum _{j : x^B_j > 0} p_{ij} x^B_{j} + s_{ij} = C^*$ and there is at most one job $j \in J$ with $0 < x^B_j < 1$. Note that the set of maximal configurations is finite.

Theorem 7

For any configuration $B$ for a machine $i \in M$, the corresponding vector $x^B$ is a convex combination of vectors corresponding to maximal configurations for $i$.

Proof

Let $B \in \mathcal {B}_i$ for some $i \in M$ and let $S = \mathrm{support }(x^B)$. Note that $x^B$ is contained in the polytope described by

$$\begin{aligned} \sum _{j \in S} (p_{ij}x_j + s_{ij})&\le C^* \\ 0 \le x_j&\le 1 \qquad \text {for all } j \in S. \end{aligned}$$

Any vertex of this polytope must fulfill at least $|S| - 1$ of the latter inequalities with equality and thus corresponds to a maximal configuration. Thus, any machine configuration is a convex combination of maximal configurations. $\square$

Given a guessed makespan $C^*$, we denote the set of maximal feasible configurations for each machine $i \in M$ by $\mathcal {B}_i$. The machine configuration LP is a feasibility LP with a variable $\rho _{B}$ for each $B \in \dot{\bigcup }_{i \in M} \mathcal {B}_i$ indicating whether or not the configuration $B$ is assigned to a machine $i$.

$$\begin{aligned} {[\mathrm{MCLP}]}\!: \quad \qquad \qquad \sum _{B\in \mathcal {B}_i} \rho _{B}&\le 1&\text {for all }\; i \in M,\\ \sum _{i \in M} \sum _{B \in \mathcal {B}_i} x^B_j \rho _{B}&\ge 1&\text {for all }\; j \in J,\\ \rho _{B}&\ge 0&\text {for all }\; B\in \dot{\bigcup }_{i \in M} \mathcal {B}_i. \end{aligned}$$

The first set of constraints says that we should (fractionally) assign at most one configuration to each machine and the second set of constraints says that each job should be (fractionally) assigned (at least) once.

It is easy to see that $[\mathrm{MCLP}]$ is a relaxation of our problem and that the minimum $C^*$ such that $[\mathrm{MCLP}]$ is feasible provides a lower bound on the optimal makespan $\mathrm{OPT}$. Rather surprisingly, we show that this seemingly stronger relaxation has the same integrality gap as the strengthened assignment LP $[\mathrm{LST}_{\mathrm{strong}}]$.

Theorem 8

For any $\varepsilon >0$, there exists an instance such that $C^* ( 1+ \phi - \varepsilon ) \le \mathrm{OPT}$, where $C^*$ is the smallest number such that $[\mathrm{MCLP}]$ is feasible.

Proof

The construction is similar to that in the proof of Theorem 4.

We first select the parameters of the construction. Let $\beta = \phi -1$ and select $k, G, d$ to be large integers (dependent on $\varepsilon$) so that

$$\begin{aligned} \left( 1-\frac{1}{k}\right) \frac{d}{G} \ge \beta \qquad \text{ and } \qquad \frac{G}{d} \ge \frac{1}{\beta } - \varepsilon . \end{aligned}$$

(13)

Based on these parameters we construct the integrality gap instance as follows. There are $k$ disjoint groups of jobs $J_1, \ldots , J_k$, each containing $G$ jobs, i.e., $J_1=\{j^{(1)}_1,\ldots ,j^{(G)}_1\}, \ldots , J_k=\{j^{(1)}_k,\ldots ,j^{(G)}_k\}$. For each job $j\in \bigcup _{\ell =1}^k J_\ell$ there is a child machine $i_c(j)$ and for each group $\ell =1, \dots , k$ there is a parent machine $i_p({j^{(1)}_\ell })= i_p(j^{(2)}_{\ell }) = \dots = i_p(j^{(G)}_{\ell })$ that can process all the jobs in $J_\ell$. Finally, there is a top job $j^t$ (see Fig. 4 and notice the tree structure with $j^t$ being the root).

Fig. 4

Example showing that $[\mathrm{MCLP}]$ has a gap of $1+\phi$

The processing times and setup times are as follows,

$$\begin{aligned} p_{ij}&= {\left\{ \begin{array}{ll} 0 &{} \text {for } j\in \bigcup \nolimits _{\ell =1}^k J_\ell , i=i_p(j),\\ \frac{1}{1-\beta } &{} \text {for } j\in \bigcup \nolimits _{\ell =1}^k J_\ell , i=i_c(j),\\ 0 &{} \text {for } j=j^t, i=i_p(j) \text { for any }j\in \bigcup \nolimits _{\ell =1}^k J_\ell ,\\ \infty &{} \text {otherwise}. \end{array}\right. } \\ s_{ij}&= {\left\{ \begin{array}{ll} \frac{1}{d} &{} \text {for } j\in \bigcup \nolimits _{\ell =1}^k J_\ell , i=i_p(j),\\ 0 &{} \text {for } j\in \bigcup \nolimits _{\ell =1}^k J_\ell , i=i_c(j),\\ 1 &{} \text {for } j=j^t, i=i_p(j) \text { for any }j\in \bigcup \nolimits _{\ell =1}^k J_\ell ,\\ \infty &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

First we prove that an optimal solution has makespan at least $1+\phi -\varepsilon$. To see this, let $i_p(j^{(i)}_\ell )$ be the machine that receives the top job $j^t$ in an optimal solution (since $p_{j^t i}=0$ for all $i$, this job is never split). Similarly, jobs $j^{(1)}_{\ell }, \ldots , j^{(G)}_\ell$ are not split in an optimal solution. If either of these jobs is completely assigned to its child machine, then the makespan of the schedule is $1/(1 - \beta )=1+\phi$. Otherwise, $j^{(1)}_{\ell },\ldots j^{(G)}_{\ell }$ are all assigned to $i_p(j^{(1)}_{\ell })=\cdots = i_p(j^{(G)}_{\ell })$, which will have a load of $1+G/d\ge 1+\frac{1}{\beta } - \varepsilon = 1+\phi - \varepsilon$, using that ${G}/{d} \ge {1}/{\beta } - \varepsilon$ by (13).

Having proved that an optimal solution has makespan at least $1+\phi -\varepsilon$, we complete the proof by showing that $[\mathrm{MCLP}]$ is feasible for $C^* = 1$. Since $j_t$ has setup time $1$ and processing time $0$ on all parent machines, we have that a configuration $B^i_t$ that schedules $j_t$ completely on machine $i$ and no other job is feasible for these machines. We choose $\rho _{B^i_t} = 1/k$ for each parent machine, i.e., for each machine $i = i_p(j)$ for some $j\in \bigcup \nolimits _{\ell =1}^k J_\ell$. Note that this will assign job $j_t$ fractionally and also leaves a $(1-1/k)$ fraction of space on each parent machine for other configurations.

It remains to assign the jobs in $\bigcup \nolimits _{\ell =1}^k J_\ell$. For any such a job $j$, define the configuration $B^c_j$, that assigns a $(1-\beta )$ fraction of it to its child machine $i_c(j)$ and nothing else; i.e., $x^{B^c_j}_j = 1-\beta$ and $x^{B^c_j}_{j'} = 0$ for any other job $j'\ne j. B^c_j$ is a feasible configuration for machine $i_c(j)$, because job $j$ has processing time $1/(1-\beta )$ and setup time $0$ on that machine. We choose $\rho _{B^c_j} = 1$ for each $j\in \bigcup \nolimits _{\ell =1}^k J_\ell$. Thus, so far we have assigned a fraction $1-\beta$ of each job $j\in \bigcup \nolimits _{\ell =1}^k J_\ell$, i.e., a $\beta$ fraction of these jobs remains to be assigned. We will assign this remaining fraction to the parent machine for each job. To construct the configurations necessary for this, we consider each group $\ell = 1, 2, \ldots , k$ separately. As the jobs in $J_\ell$ have processing time 0 and setup time $1/d$ on $i^\ell _p$, a feasible configuration for $i^\ell _p$ is to completely schedule any $d$ jobs in $J_\ell$. There are ${G \atopwithdelims ()d}$ different ways of forming such a configuration, i.e., by selecting $d$ jobs out of the $G$ jobs in $J_\ell$. Recall that $i^\ell _p$ has a $(1-1/k)$ fraction of remaining space for processing such configurations. We use this space completely, by assigning an equal fraction to each of the ${G \atopwithdelims ()d}$ configurations containing exactly $d$ jobs, i.e., we choose $\rho _{B} = (1-1/k)/{G \atopwithdelims ()d}$ for each configuration $B \in \mathcal {B}_{i^\ell _p}$ that completely schedules $d$ of the jobs in $J_\ell$ on machine $i^\ell _p$. This will schedule the remaining $\beta$ fraction of a job in $J_\ell$ because it is part of exactly ${G-1 \atopwithdelims ()d-1}$ such configurations and

$$\begin{aligned} \left( 1-\frac{1}{k}\right) \frac{{G-1 \atopwithdelims ()d-1}}{{G \atopwithdelims ()d}} = \left( 1-\frac{1}{k}\right) \frac{d}{G} \ge \beta , \end{aligned}$$

where the last inequality follows from (13). Since this holds for every group $\ell$, each job is completely assigned and each machine receives (fractionally) a configuration of makespan $1$. We have thus proved that $[\mathrm{MCLP}]$ is feasible for $C^* =1$ and the statement follows. $\square$

6.2 A job configuration LP

As the machine configuration LP does not provide any improvement over the assignment LP $[\mathrm{LST}_{\mathrm{strong}}]$, we introduce a new family of configuration LPs, which we call job configuration LPs. A configuration $f$ for a given job $j$ specifies the fraction of $j$ that is scheduled on each machine. The configuration consists of two vectors $x^f \in [0, 1]^M$ and $y^f \in \{0, 1\}^M$ such that $\sum _{i \in M} x^f_i = 1$ and $y^f_i = 1$ if and only if $x^f_i > 0$. On machine $i \in M$ configuration $f$ requires time $t_{i}^f := p_{ij} x^f_i + s_{ij} y^f_i$. Given a guess on the makespan $C^*$, configuration $f$ is feasible if $t_i^f \le C^*$ for all $i \in M$. A feasible configuration $f$ is maximal if there is at most one machine $i \in M$ with $0 < x^f_i < x_{ij}^{\max }$, where $x_{ij}^{\max } := (C^* - s_{ij})/p_{ij}$.

Note that the number of maximal configurations is finite because each configuration is uniquely determined by the set of machines to which the job is fully assigned and additionally the machine to which it is fractionally assigned if the configuration contains such a machine. The following theorem shows that we can restrict to the finite set of maximal configurations, which we denote by $\mathcal {F}_{j}$ for each $j \in J$. We say a vector $\tilde{f}$ (not necessarily a configuration) dominates another one $f$ if and only if $x^{f} \ge x^{\tilde{f}}$ and $y^{f} \ge y^{\tilde{f}}$.

Theorem 9

For any feasible configuration $f$ of job $j \in J$, there exists a convex combination of maximal configurations for $j$ which dominates $f$.

Proof

Take any feasible configuration $f$ for job $j$. Then the corresponding vector $x^f$ is contained in the polytope described by

$$\begin{aligned} \sum _{i \in M} x_i&= 1 \\ 0 \le x_i&\le x_{ij}^{\max } \qquad \text {for all } i \in M. \end{aligned}$$

Any vertex of this polytope must satisfy at least $|M| - 1$ of the latter inequalities with equality and thus corresponds to a maximal configuration. Therefore there exists a convex combination $\sum _{f' \in \mathcal {F}_{j}} \mu _{f'} x^{f'} = x^f$. In particular, this implies $\sum _{f' \in \mathcal {F}_{j}} \mu _{f'} y_i^{f'} \le y_i^{f}$ for all $i \in M$. $\square$

Thus, in a feasibility LP, we can replace any job configuration by a convex combination of maximal configurations. This makes the following feasibility LP well-defined and there is a one-to-one correspondence between its integer solutions and every feasible solution to $R|\text {split,setup}|C_{\max }$ with makespan at most $C^*$:

$$\begin{aligned} {[\mathrm{CLP}]}\!: \quad \qquad \qquad \sum _{f \in \mathcal {F}_j} \lambda _{f}&= 1&\text {for all }\; j \in J,\\ \sum _{j \in J} \sum _{f \in \mathcal {F}_j} \lambda _{f} t_{i}^f&\le C^*&\text {for all }\; i \in M,\\ \lambda _{f}&\ge 0&\text {for all }\; f \in \dot{\bigcup }_{j \in J} \mathcal {F}_j. \end{aligned}$$

Note that, though finite, the set of maximal configurations is still exponential in the input size. Also it is not hard to show that the separation problem for the dual is NP-complete. In order to approximately solve the LP in polynomial time, we will discretize $[\mathrm{CLP}]$. Given $\varepsilon >0$, the discretization will violate the makespan $C^*$ by a factor of $1+\varepsilon$: If $[\mathrm{CLP}]$ is feasible then the discretized LP, $[\mathrm{CLP}]^d$, will also be feasible, while if $[\mathrm{CLP}]^d$ is feasible then $[\mathrm{CLP}]$ is feasible for configurations with makespan $C^*(1+\varepsilon )$.

Given a maximal configuration $f \in \mathcal {F}_j$, we define the corresponding discretized configuration $\tilde{f}$ by

$$\begin{aligned} x_i^{\tilde{f}}:= \left\lfloor \frac{x_i^f \cdot m }{\varepsilon } \right\rfloor \cdot \frac{\varepsilon }{m} \quad \text { and } \quad y_i^{\tilde{f}} = y_i^f \qquad \text {for all }i\in M. \end{aligned}$$

Note that each value $x_i^{\tilde{f}}$ is a multiple of $\frac{\varepsilon }{m}$, but that the discretized configuration might not process the job completely. However, observe that $x_i^{\tilde{f}} \ge x_i^f-\varepsilon /m$ and therefore $\sum _{i\in M} x_i^{\tilde{f}} \ge 1-\varepsilon$. We denote the set of all discretized configurations by $\mathcal {F}_j^d$ and define the discretized configuration LP $[\mathrm{CLP}]^d$ exactly as $[\mathrm{CLP}]$, only replacing $\mathcal {F}_j$ by $\mathcal {F}_j^d$. We now prove $[\mathrm{CLP}]^d$ indeed approximates $[\mathrm{CLP}]$ arbitrarily well.

Lemma 5

If  $[\mathrm{CLP}]$ is feasible for makespan $C^*$, then $[\mathrm{CLP}]^d$ is feasible for makespan $C^*$. Also, if  $[\mathrm{CLP}]^d$ is feasible for makespan $C^*$, then $[\mathrm{CLP}]$ is feasible for makespan $(1+ O(\varepsilon ))C^*$.

Proof

Consider any maximal configuration $f \in \mathcal {F}_j$ and the corresponding discretized configuration $\tilde{f}$. Observe that $x_i^{\tilde{f}} \le x_i^f$ and therefore $t_i^{\tilde{f}} \le t_i^f$. This implies that any feasible solution to $[\mathrm{CLP}]$ yields a feasible solution to $[\mathrm{CLP}]^d$ by replacing every configuration in its support with the corresponding discretized configuration. Conversely, given a solution to $[\mathrm{CLP}]^d$ note that we can multiply the vector $(x_{i}^{f})_{i\in M}$ for each $f\in \mathcal {F}_j^d$ by a factor of $1/(1-\varepsilon ) = 1+O(\varepsilon )$, because $\sum _{i\in M} x_i^{\tilde{f}} \ge 1-\varepsilon$. This yields configurations that violate the makespan $C^*$ by a factor of $1+O(\varepsilon )$, and thus $[\mathrm{CLP}]$ is feasible for this increased makespan. $\square$

Lemma 6

The program $[\mathrm{CLP}]^d$ can be solved in polynomial time.

Proof

By Farkas’ Lemma (see e.g. [20]), $[\mathrm{CLP}]^d$ is feasible if and only if the following LP is infeasible,

$$\begin{aligned} 0&> \sum _{i\in M}C^*\cdot \delta _i + \sum _{j\in J} \mu _j,&\\ 0&\le \mu _j + \sum _{i\in M} t_i^f \delta _i&\text {for all }j\in J, f\in \mathcal {F}_j^d,\\ \delta _i&\in \mathbb {R}_+,\, \mu _j \in \mathbb {Q}&\text {for all } i\in M,j\in J. \end{aligned}$$

To determine the feasibility of this dual program we use the equivalence of separation and optimization [10]. Given a solution $\mu ,\delta$ the separation problem can be solved by fixing $j\in J$ and solving the minimization problem

$$\begin{aligned}{}[P_j]\!:\quad \min \left\{ \sum _{i\in M} t_i^f \delta _i : f\in \mathcal {F}_j^d\right\} . \end{aligned}$$

We use the maximality of the configurations in $\mathcal {F}_j^d$ to solve $[P_j]$ efficiently. First, we guess the machine $i^*\in M$ with $0 < x_{i^*}^f < x_{i^*j}^{\max }$ together with the fraction $x_{i^*}^f$. Recall that $x_{i^*}^f$ must be one of only $\lfloor m/\varepsilon \rfloor +1$ different values, thus this guessing takes only polynomial time. For a given $i^*$ and $x_{i^*}^f$, problem $[P_j]$ reduces to finding a set $S\subseteq M{\setminus }\{i^*\}$ such that $\sum _{i\in S} x_{ij}^{\max }\ge 1-\varepsilon - x_{i^*}^f$ while minimizing $\sum _{i\in S} \delta _i(x_{ij}^{\max }p_{ij} + s_{ij})$. Observe that this is a Knapsack Cover problem, which can be solved in pseudo-polynomial by adapting the dynamic program for the standard Knapsack problem [12]. This yields a polynomial algorithm in our case since the values $x_{ij}^{\max }$ are of the form $k_i\cdot m/\varepsilon$ for some $k_i\in \{0,\ldots ,\lfloor m/\varepsilon \rfloor \}$. $\square$

Projection of the job configuration LP Observe that any convex combination of job configurations $\lambda$ can be translated into a pair of vectors $x^{\lambda }, y^{\lambda } \in [0, 1]^{M \times J}$ in the assignment space by setting

$$\begin{aligned} x_{ij}^{\lambda } := \sum _{f \in \mathcal {F}_j} \lambda _{f} x^f_{i} \quad \text { and } \quad y_{ij}^{\lambda } := \sum _{f \in \mathcal {F}_j} \lambda _{f} y^f_i. \end{aligned}$$

We show that applying this projection to $[\mathrm{CLP}]$ leads to assignment vectors described by the following set of inequalities:

$$\begin{aligned} {[\mathrm{CLP}_{\mathrm{proj}}]}\!: \quad&\sum _{j \in J} (p_{ij} x_{ij} + s_{ij} y_{ij})&\le C^*&\quad \text {for all }\; i \in M, \end{aligned}$$

(14)

$$\begin{aligned}&\sum _{i \in M} (\beta _i x_{ij} + \gamma _i y_{ij})&\ge K(j, \beta , \gamma )&\quad \text {for all }\; j \in J,\ \beta , \gamma \in \mathbb {Q}^M, \end{aligned}$$

(15)

with $K(j, \beta , \gamma ) := \min \left\{ \sum _{i \in M} (\beta _i x^f_i + \gamma _i y_i^f) \, : \, f \in \mathcal {F}_j \right\} .$

Theorem 10

If $\lambda \in [\mathrm{CLP}]$ then $(x^{\lambda }, y^{\lambda })\in [\mathrm{CLP}_{\mathrm{proj}}]$. Conversely, if $(x, y)\in [\mathrm{CLP}_{\mathrm{proj}}]$ then there exists $\lambda \in [\mathrm{CLP}]$ such that $x = x^\lambda$ and $y = y^\lambda$.

Proof

Let $\lambda$ be a feasible solution to $[\mathrm{CLP}]$ and let $\beta , \gamma \in \mathbb {Q}^M_+$. By definition of $K(j, \beta , \gamma )$ for any $j \in J$ we have that

$$\begin{aligned} \sum _{i \in M} \beta _i x^{\lambda }_{ij} + \gamma _i y^{\lambda }_{ij} = \sum _{i \in M} \sum _{f \in \mathcal {F}_j} \lambda ^f \left( \beta _i x^f_i + \gamma _i y^f_i \right) \ge K(j, \beta , \gamma ). \end{aligned}$$

Furthermore by feasibility of $\lambda$ we obtain the following inequality, proving that $(x^{\lambda }, y^{\lambda })$ is a feasible solution to $[\mathrm{CLP}_{\mathrm{proj}}]$:

$$\begin{aligned} \sum _{j \in J} \left( p_{ij} x^{\lambda }_{ij} + s_{ij} y^{\lambda }_{ij}\right) = \sum _{j \in J} \sum _{f \in \mathcal {F}_j} \left( p_{ij} \lambda ^f x_i^f + s_{ij} \lambda ^f y_i^f\right) = \sum _{j \in J} \sum _{f \in \mathcal {F}_j} \lambda ^f t_i^f \le C^*. \end{aligned}$$

To prove the converse consider a feasible solution $(x, y)$ to $[\mathrm{CLP}_{\mathrm{proj}}]$. Clearly, there exists $\lambda \in [\mathrm{CLP}]$ with $x = x^\lambda , y = y^\lambda$ if and only if the following LP has a feasible solution.

$$\begin{aligned} \sum _{f \in \mathcal {F}_j} x^f_{i} \lambda _{f}&= x_{ij}&\text {for all }\; i \in M, \, j \in J,\\ \sum _{f \in \mathcal {F}_j} y^f_i \lambda _{f}&= y_{ij}&\text {for all }\; i \in M, \, j \in J,\\ \sum _{f \in \mathcal {F}_j} \lambda _{f}&= 1&\text {for all }\; j \in J,\\ \sum _{j \in J} \sum _{f \in \mathcal {F}_j} t_{i}^f \lambda _{f}&\le C^*&\text {for all }\; i \in M,\\ \lambda _{f}&\ge 0&\text {for all }\; f \in \dot{\bigcup }_{j \in J} \mathcal {F}_j. \end{aligned}$$

By duality, the latter holds if and only if the following LP is bounded.

$$\begin{aligned} \min \quad&\sum _{i \in M} \sum _{j \in J} (x_{ij} \beta _{ij} + y_{ij} \gamma _{ij}) + \sum _{j \in J} \mu _j&+ \sum _{i \in M} C^* \delta _i \\ \text {s.t.} \quad&\sum _{i \in M} \left( x^f_i \beta _{ij} + y^f_i \gamma _{ij}\right) + \mu _j + \sum _{i \in M} t_{i}^f \delta _i&\ge 0&\text {for all }\; j \in J, \, f \!\in \! \mathcal {F}_j,\\&\delta _i&\ge 0&\text {for all }\; i \!\in \! M. \end{aligned}$$

Applying inequality (14) to the term $C^*$ in the objective function of this dual, we obtain the lower bound

$$\begin{aligned} \sum _{i \in M} \sum _{j \in J} \big (x_{ij} (\beta _{ij} + p_{ij}\delta _i) + y_{ij} (\gamma _{ij} + s_{ij}\delta _i)\big ) + \sum _{j \in J} \mu _j. \end{aligned}$$

This, in turn, can be lower bounded using inequalities (15) by

$$\begin{aligned} \sum _{j \in J} K \big (j,\ (\beta _{ij} + p_{ij}\delta _i)_{i\in M},\ (\gamma _{ij} + s_{ij}\delta _i)_{i\in M}\big ) + \sum _{j \in J} \mu _j. \end{aligned}$$

To conclude observe that the constraints of the dual guarantee that each of the summands is non-negative, implying that the dual is bounded. $\square$

The following lemma shows that all inequalities of $[\mathrm{LST}_{\mathrm{strong}}]$ are special cases of the inequalities of $[\mathrm{CLP}_{\mathrm{proj}}]$ and therefore the latter linear program is at least as strong as the former.

Lemma 7

Let $x, y$ be a feasible solution to $[\mathrm{CLP}_{\mathrm{proj}}]$ for some value of $C^*$. Then $x$ is a feasible solution to $[\mathrm{LST}_{\mathrm{strong}}]$ for the same value of $C^*$.

Proof

Let $x, y$ be a feasible solution to $[\mathrm{CLP}_{\mathrm{proj}}]$ for the given value of $C^*$. For any $j \in J$ and any $f \in \mathcal {F}_j$, observe that $\sum _{i \in M} x_{i}^f = 1$ and also $x_{i}^f \ge 0$ for all $i \in M$. Therefore (15) implies $\sum _{i \in M} x_{ij} = 1$ and $x_{ij} \ge 0$ for all $i \in M$. Now assume $s_{ij} > C^*$ for some $i \in M$ and $j \in J$. Then $x_{i}^f = 0$ in all configurations $f \in \mathcal {F}_j$ and therefore (15) implies $x_{ij} = 0$ for any such pair of job and machine. Finally, observe that $x_i^f \le x_{ij}^{\max }$ in all configurations and therefore $-\alpha _{ij}x_{i}^f + y_{i}^f \ge 0$ for all $f \in \mathcal {F}_j$ with $\alpha _{ij}$ as defined in Sect. 3. Therefore, inequalities (15) imply $\alpha _{ij}x_{ij} \le y_{ij}$ for all $i \in M$ and $j \in J$ and thus inequalities (14) imply $\sum _{j \in J} x_{ij}(p_{ij} + \alpha _{ij}s_{ij}) \le C^*$ for all $i \in M$. Hence $x$ is a feasible solution for $[\mathrm{LST}_{\mathrm{strong}}]$ with makespan $C^*$. $\square$

In particular, Lemma 7 implies that the integrality gap of $[\mathrm{CLP}]$ is at most that of $[\mathrm{LST}_{\mathrm{strong}}]$. We conclude this section by showing that already a very special class of inequalities (15) from $[\mathrm{CLP}_{\mathrm{proj}}]$ is sufficient to eliminate the gap in the worst-case instances of $[\mathrm{LST}_{\mathrm{strong}}]$. For a set of machines $S \subseteq M$ let $L(j, S) := \sum _{i \in M\setminus S} \max \big \lbrace \frac{C^*-s_{ij}}{p_{ij}}, \, 0 \big \rbrace$ be the maximum fraction of job $j$ that can be processed within time $C^*$ by the machines in $M {\setminus } S$. The following inequalities are satisfied by the vector $x, y$ induced by any feasible solution to $R|\text {split,setup}|C^*_{\max }$ with makespan at most $C^*$.

$$\begin{aligned} \frac{\sum _{i\in S'}x_{ij}}{1-L(j,S\cup S')} + \sum _{i\in S} y_{ij} \ge 1 \ \ \text { for all } j \in J \text { and } S, S' \subseteq M \text { with } L(j,S\cup S') < 1. \end{aligned}$$

One way to validate these inequalities is to observe that they are a special case of inequalities (15), obtained by setting $\beta _i = \frac{1}{1-L(j,S\cup S')}$ for $j \in S'$ and $0$ everywhere else, and $\gamma _i = 1$ for $i \in S$ and $0$ everywhere else. The corresponding value $K(j, \beta , \gamma )$ can be verified to be at least $1$. However, for an alternative and more direct argument for the validity of the inequalities, observe that any feasible solution must process a total fraction of at least $1 - L(j, S \cup S')$ on the machines in $S \cup S'$. Therefore, either $\sum _{i \in S'} x_{ij} \ge 1 - L(j, S \cup S')$ or at least one machine in $S$ is used to process job $j$. In either case, the left hand side of the corresponding inequality is at least $1$.

Now consider the example instance given in the proof of Theorem 4 and depicted in Fig. 3. If $C^* < 1 + \phi$, then $L(j, \{i_p(j)\}) = C^*/p_{i_c(j)j} < 1$ and therefore $y_{i_p(j)j} = 1$ for all $j \in J \cup J'$ in any feasible solution to $[\mathrm{CLP}_{\mathrm{proj}}]$. This immediately implies infeasibility of $[\mathrm{CLP}_{\mathrm{proj}}]$ for any $C^* < \phi$. We also note that the exact same argument applies to the worst-case instance of the machine configuration LP.

It will be interesting to find out if this job configuration LP will indeed have a better integrality gap and accompanying approximation algorithm.