Bulk-Robust combinatorial optimization

Abstract

We commence an algorithmic study of Bulk-Robustness, a new model of robustness in combinatorial optimization. Unlike most existing models, Bulk-Robust combinatorial optimization features a highly nonuniform failure model. Instead of an interdiction budget, Bulk-Robust counterparts provide an explicit list of interdiction sets, comprising the admissible set of scenarios, thus allowing to model correlations between failures of different components in the system, interdiction sets of variable cardinality and more. The resulting model is suitable for capturing failures of complex structures in the system. We provide complexity results and approximation algorithms for Bulk-Robust counterparts of the Minimum Matroid Basis problems and the Shortest Path problem. Our results rely on various techniques, and outline the rich and heterogeneous combinatorial structure of Bulk-Robust optimization.

1 Introduction

This paper studies a natural new robust model for combinatorial optimization. Our model, called Bulk-Robustness is motivated by systems that feature highly correlated component failures. Most existing robust counterpart in combinatorial optimization assume a completely uniform failure model. Concretely, given a certain adversarial budget $k$, most models assume that the adversary is able to remove any subset of resources of total interdiction cost $k$. In fact, typically, unit interdiction costs are assumed, meaning that the adversary can simply remove any subset of $k$ resources. This paper strays from this main line of research, focusing on the opposite end of the uniformity scale. In our model, the input provides an explicit collection of interdiction sets, of potentially variable cardinality. Formally, the Bulk-Robust counterpart of a combinatorial optimization problem is defined as follows.

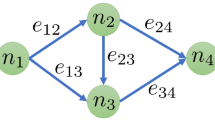
For a positive integer $b$ let $[b] = \{1,\ldots , b\}$. We denote the logarithm in base $2$ and the natural logarithm functions by $\log (\cdot )$ and $\ln (\cdot )$, respectively. We model a combinatorial optimization problem by means of a set system $\mathcal {S} = (A, \mathcal {X})$ (with $A$ being a finite set of elements—which we also call resources—and $\mathcal {X} \subseteq 2^A$ comprising the feasible set of solutions) and a nonnegative cost function $w:A \rightarrow \mathbb {Z}_+$. Given this input the goal is to find an element $X \in \mathcal {X}$ of the set system minimizing $w(X) = \sum _{a\in X} w(a)$. We assume that $\mathcal {X}$ is up-monotone, namely that for every $X_1 \subseteq X_2 \subseteq A$ it holds that $X_1\in \mathcal {X}$ implies $X_2 \in \mathcal {X}$. For example, the Minimum Spanning Tree problem is obtained by taking $A$ to be the edges of the input graph, and $\mathcal {X}$ the set of all subsets of edges connecting all vertices. We note that one could also consider robust counterparts in our model for non-monotone set systems. The obtained problems are, however, both harder to motivate and lose a lot of the problem structure exploited by our algorithms. An instance of the corresponding Bulk-Robust counterpart also includes a collection $\Omega = \{F_1, \ldots , F_m\}$ of interdiction sets with $F_i \subseteq A$ for every $i\in [m]$. The goal is to find the cheapest set $X^* \subseteq A$ with the property that $X^*{\setminus }F_i \in \mathcal {X}$ for every $i\in [m]$. Put differently, the Bulk-Robust counterpart asks to solve

$$\begin{aligned} z(\mathcal {S}, w, \Omega ) = \min _{X\subseteq A} \left\{ w(X): \, X{\setminus }F_i \in \mathcal {X} \quad \forall i\in [m] \right\} . \end{aligned}$$

To illustrate our definitions consider the Bulk-Robust Shortest Path problem. In our context, we would like to consider the Shortest Path problem as follows. Given a graph $G= (V,E)$, two vertices $s,t\in V$ and a weight function $w$ on the edges, the Shortest Path problem asks to find the cheapest set $P \subseteq E$ with the property that $P$ connects $s$ and $t$. Bulk-Robust Shortest Path additionally supplies a collection $\Omega = \{F_1, \ldots , F_m\}$ of subsets of edges, and asks to find a cheapest subset of edges $P$ with the property that $s$ and $t$ are connected by $P{\setminus }F_i$ for every $i\in [m]$.

Although for most graph problems, the Bulk-Robust counterpart is defined as having edge failures, the model also naturally allows for vertex failures. For example, to simulate a vertex failure in the Bulk-Robust Shortest Path problem, one simply includes in $\Omega$ an interdiction set that contains all incident edges to this vertex. This outlines an important advantage of Bulk-Robust counterparts, namely that the nonuniform scenario set allows for constructing interdiction sets that target arbitrary structures in the set system, thus mimicking some dependencies between failures of resources in the underlying system, or a potential adversarial behavior.

As we mentioned before, our motivation to study Bulk-Robust counterparts comes from many potential applications. Next, we bring a number of examples of such applications.

1.1 Motivation

We start with a rather general motivating example. Consider a system composed of $n$ components and $m < n$ regulators (with $n, m\in \mathbb {Z}_+$). Each regulator $i \in [m]$ controls the operation of some subset $C_i \subseteq [n]$ of the components, where some components may be controlled by more than one regulator. A component is active if all regulators that control it are active. The entire systems’ operational capability is expressed by a set system $\mathcal {S} = ([n], \mathcal {X})$ (with $\mathcal {X} \subseteq 2^{[n]}$) so that the system is operational if and only if the set $A \subseteq [n]$ of active components is an element of the set system, namely $A \in \mathcal {X}$. A system is said to be robust if for every regulator $i\in [m]$, the system remains operational if all regulators, but $i$ are active. In other words, the system is robust if $[n]{\setminus }C_i \in \mathcal {X}$ for every $i\in [m]$.

The latter definition bears a clear resemblance to Bulk-Robust counterparts. Indeed, we can identify components with resources of a set system and interdiction sets with inactive regulators. If a regulator becomes inactive, all components that it regulates get out of order. At the same time, this definition resembles an inherent structure in many applications. Concretely, many systems, some examples thereof we bring later, admit a clear hierarchical structure. While the system is built from a large set of autonomous components, different subsets of these components are controlled by other elements in the system. It is then natural to ask—which such elements are critical to the integrity of the system? Below, we mention some potential application areas, where dependent failure scenarios—as used in Bulk-Robust optimization—are a natural way to model failures or malicious attacks.

• Computer Systems. It is common place in computer systems to have certain machines responsible for some critical functionality of the system. Consider, for example an important database. Typically, databases are stored on high-performance designated server machines. Due to the high cost of such machines, most computer systems allocate a single or few special-purpose machines for this task. Consequently, during down-time of these machines access to the database is disrupted, keeping a potentially large number of processes in the system stranded.

• Health Care. Health care facilities are typically very large and cost intensive systems. Here, certain individual components are pivotal for the operations of relatively large parts of the system. This is true for some individuals in the work force, e.g., if a specialized surgeon cannot practice, the performance of an entire team decreases. This also applies to crucial parts of the technical equipment: malfunction of a costly, and therefore not backed-up, specialized device for diagnoses will inhibit the entire facility to perform treatments based on these diagnoses.

• Digitally Controlled Infrastructures. Many important infrastructures are controlled by a collection of central computers. A large number of heterogeneous components can rely on the operation of one such controller. Examples of such systems range from electricity grids to railway switching systems.

• Cascades. Many systems feature cascading failures triggered by a failure of a single, or a small number of critical components. For example in an financial investment network the bankruptcy of a few important companies can lead to further bankruptcies, eventually resulting in the downfall of large parts of the network. Such cascading effects were recorded in many other network-centric complex systems.

• Military. Consider a large military unit with a deep hierarchy, composed of many levels of commanders with various ranks. Each higher officer is responsible for some part of the entire military personnel available to this unit, potentially deployed over a large area in a battlefield. With the simplifying assumption that every soldier can only take commands from his direct commander, it is clear that a sophisticated enemy will be compelled to target higher officers, in command of a critical part of the entire force, rather than a simple soldier. In large, this remains true also without the latter assumption.

The previous examples illustrate that targeting a few critical components of a system can lead to the malfunction of large parts of the system. Bulk-Robustness models attacks of this nature. Note that a nonuniform scenario set arises naturally in this context, even if we assume that the adversary can choose to attack any one single component. This implies that from the point of view of many applications, even the assumption of a uniform scenario set leads to nonuniform failure patterns in the system. It is the goal of the current paper to commence a study of such nonuniform models of robustness.

1.2 Contribution

In this paper we commence an algorithmic study of Bulk-Robust counterparts of classical combinatorial optimization problems. We present results for Bulk-Robust counterparts of the Minimum Matroid Basis problem and the Shortest Path problem. Note that the former problem contains the Bulk-Robust Minimum Spanning Tree problem as a special case. Hereafter we state our complexity results, as well as our algorithmic results for the aforementioned problems.

Complexity Results. Our first result states that the Bulk-Robust counterpart of almost any combinatorial optimization problem contains the Set Cover problem as a special case. Concretely, we show that a polynomial-time $c \ln m$-approximation algorithm does not exist for any $c < 1$ under standard complexity assumptions. For the Bulk-Robust Minimum Matroid Basis problem, we are able to provide an algorithm with an approximation guarantee that almost matches this hardness bound.

The Bulk-Robust Shortest Path problem turns out to be considerably harder to approximate in general. We therefore study a parameterized version of it, that depends on a critical parameter of the instance, which we call width. The width $k$ of an instance is the maximum size over all interdiction sets, i.e.,

$$\begin{aligned} k = \max _{F\in \Omega } |F|. \end{aligned}$$

Bulk-Robust Shortest Path restricted to the case $k=1$ coincides with a robust path problem defined in [2], where it was shown to be polynomial-time solvable. We thus concentrate on the case $k\ge 2$. For $k=2$ we show that Bulk-Robust Shortest Path is APX-hard. We remark that in the case $k \ge 3$ this problem is APX-hard even when the input graph is restricted to be Series-Parallel. When $k$ is not bounded we show that unless $\mathrm {NP} \subseteq \mathrm {DTIME}(n^{\log \log n})$,¹ it is impossible to approximate Bulk-Robust Shortest Path in polynomial time within a factor of $O(2^{\frac{1}{4}k^{1-\epsilon }})$, or a factor of $O(2^{\log ^{1-\epsilon } n})$ for any $\epsilon > 0$.

Bulk-Robust Minimum Matroid Basis. For the Bulk-Robust Minimum Matroid Basis problem we develop an $O(\log m + \log r)$-approximation algorithm, where $r$ is the rank of the matroid. Our algorithm relies on an approximation algorithm for the Submodular Function Maximization problem. For the Bulk-Robust Minimum Spanning Tree problem this result gives an $O(\log n + \log m)$-approximation algorithm, which is asymptotically optimal in $m$ in view of the hardness results that we provide.

Bulk-Robust Shortest Path. We first propose a simple polynomial $O(\log m)$-approximation algorithm for instances of Bulk-Robust Shortest Path with fixed width $k$. This procedure is inspired by the greedy log-approximation for the Set Cover problems, and iteratively constructs a solution by solving a sequence of relaxations of the original problem.

Then, we refine our technique to obtain a constant-factor approximation algorithm for the case $k=2$. The algorithm is based on a linear programming relaxation to augment an initial solution for the case $k=1$ to a feasible solution of the given instance. We round a solution to this linear program by breaking the LP into at most 4 independent linear programs that are naturally integral, and whose costs can be bounded in terms of the value of the original LP. This leads to a $13$-approximation for Bulk-Robust Shortest Path for $k=2$.

Notice that since we showed this problem to be APX-hard, a constant-factor approximation is the best we can hope for from a qualitative point of view.

1.3 Related work

The field of robust optimization has received significant attention recently. We review here related work that has been carried out in the last twenty years in the field of robust discrete and combinatorial optimization. For a comprehensive survey on general models for robust optimization we refer the reader to the paper of Bertsimas, Brown and Caramanis [8].

The study of general models of robustness in discrete optimization was initiated by Kouvelis and Yu [28] and Yu and Yang [41]. The main model considered in the latter works is one that introduces uncertainty in the cost structure. Concretely, the input to the robust problem provides an instance of the nominal problem, as well as a collection $w^i, i\in I$ of cost functions, presented in one of several ways. The goal is to find a feasible solution $X$ for the problem minimizing $\max _{i\in I} w^i(X)$. Yu and Yang [41] study the Shortest Path problem in this model. They prove that the problem is weakly NP-hard already for two scenarios, and strongly NP-hard when the number of scenarios is unbounded. For the case of a bounded number of scenarios the authors provide two pseudo-polynomial algorithms. Their objective of minimizing the maximum weight of several weight functions $w^i$ can also be reinterpreted as a multi-budgeted problem, which is a class of problems that has received considerable attention recently (see  [6, 11, 12, 23, 32–34] and references therein). Using this connection, their algorithmic results for two objective functions are also implied by algorithms for the Restricted Shortest Path problem (see Warburton [40] and Hassin [25]).

Robust counterparts—in the spirit of the approach of Yu and Yang [41]—of various other problems were subsequently considered. These problems include robust counterparts of the Minimum Spanning Tree problem, the Minimum Cut problem, the Knapsack problem and the Linear Assignment problem. We refer to the book of Kouvelis and Yu [28] and the recent survey of Aissi et al. [4] for further details about results for this model.

Dhamdhere et al. [15] introduced a new model for robust combinatorial optimization, called Demand-Robustness. Unlike the previously mentioned model, this two-stage model incorporates uncertainty in the feasible set. Analogously to Bulk-Robustness, Demand Robust combinatorial optimization deals with up-monotone set systems. The uncertainty in the feasible set is problem-dependent. For example, the robust counterpart of the Shortest Path problem has as a scenario set a collection of potential terminal pairs $(s_i, t_i), i\in I$ that need to be connected by the chosen subgraph. The solution is constructed in two stages. In the first stage, a subset of resources is chosen at a reduced price, without the knowledge of what set of terminal pairs will materialize. In the second stage, the identity of the materialized scenario is revealed, and the first-stage solution is augmented to a feasible solution with an additional set of resources, the full cost of which is incurred. The cost is computed as the maximum cost of the obtained solution over all possible scenario realizations. The authors provide approximation algorithms for Demand-Robust counterparts of several problems, including the Minimum Cut problem, the Minimum Steiner Tree problem, the Uncapacitated Facility Location problem and the Minimum Vertex Cover problem. Some results were subsequently improved by Golovin et al. [22]. The model was extended to allow exponentially many scenarios by Feige et al. [18]. The authors replace the explicit list of scenarios by an implicitly defined scenario set. Approximation algorithms are provided for several problems in this model. Khandekar et al. [27] obtained algorithmic results for other robust problems in this model, and provided some hardness results.

Bertsimas and Sim [9] developed a model of robust optimization for mixed-integer linear programming (MIP). The uncertainty in this model lies in the coefficients of the constraint matrix. Each row of the matrix is associated with an upper bound on the number of coefficients that can deviate from their nominal values within prescribed bounds. The goal is to obtain a minimum-cost solution that is feasible in all possible scenarios. The authors show that the problem of solving this robust model can be transformed into a MIP of a moderately larger size.

Recently, Adjiashvili [2] proposed a new nonuniform model for robust combinatorial optimization. Again, this model assumes up-monotone feasible sets. Given an instance of the nominal problem, a subset $B$ of resources and a positive integer $r$, the goal is to obtain a minimum-cost set of resources $X$, with the property that $X{\setminus }F$ is a feasible solution of the nominal instance for every set $F\subseteq B$ with $|F| \le r$. The paper studies the Shortest Path problem in this robust model, providing exact algorithms for some special cases, an approximation algorithm for the general case and some complexity results. Note that any Bulk-Robust instance with width $k=1$ is also an instance of the latter robust model with $r=1$, and vice versa, thus these models coincide when $r=k=1$.

Various important network design problems are motivated by robust optimization. The Minimum $k$-Edge Connected Spanning Subgraph problem is one important example. Gabow, Goemans, Tardos and Williamson [20] developed a polynomial time $(1 + \frac{c}{k})$-approximation algorithm for the latter problem, for a fixed constant $c$. The authors also show that for some constant $c' < c$, the existence of a polynomial time $(1 + \frac{c'}{k})$-approximation algorithm implies P$=$NP. The first approximation algorithm for this problem with a guarantee tending to one as $k$ tends to infinity is due to Cheriyan and Thurimella [14]. The Minimum $k$-Edge Connected Spanning Subgraph problem can be seen as the uniform variant of the Bulk-Robust Minimum Spanning Tree problem, studied in the current paper.

The Shortest Path problem was studied in a number of robust setups. A setting related to Bulk-Robust optimization was considered by Adjiashvili and Zenklusen [3]. They study a two-stage $s$–$t$ connection problem in undirected graphs with a uniform scenario set. Given a limited adaptability budget, the goal is to choose a minimum-cost initial set of edges connecting $s$ and $t$, with the property that for any interdiction set chosen by the adversary that disconnects $s$ and $t$, there exists a set of other edges, whose cost is bounded by the adaptability budget, that reconnect $s$ and $t$. Without the second stage, which allows for adapting the solution, this problem can be interpreted as a Bulk-Robust optimization problem with uniform failure scenarios. The authors prove that the problem is NP-hard in general and provide exact and constant-factor approximations for special cases. We refer the reader to [3, 10] and references therein for further information on robust versions of shortest path problems.

Another related class of problems are so-called interdiction problems. These problems are defined on an underlying combinatorial optimization problem. To illustrate, consider the Maximum Cardinality Matching problem. A corresponding interdiction problem asks to find a subset of the edges that satisfy some budget constraint and whose removal from the graph leads to a new graph whose maximum cardinality matching is as small as possible. Hence, the order of removing elements and finding a solution is reversed compared to many other robust problem variants. First, a set is removed, and then any solution can be obtained. For more information on interdiction problems, see [26, 42] and references therein.

A further problem class with some reminiscence to Bulk-Robust variants, are problems where one is interested in computing an optimal solution of a combinatorial optimization problem for any possible failure set of a given size. A well-studied variant of this problem type is the replacement path problem (see e.g. [7, 24, 38, 39]). Similar questions have also been considered in the context of spanning trees (see [37]).

Various other robust variants of classical combinatorial optimization problems were proposed. For a survey of these results we refer the reader to the theses of Adjiashvili [1] and Olver [31].

1.4 Preliminaries and notation

Throughout the paper $n$ is reserved for the number of vertices in the input graph, or the number of elements of a matroid, and $m$ is reserved for the number of interdiction sets, namely $m= |\Omega |$. All graphs are allowed to have parallel edges and loops. Paths in graphs are edge disjoint. The vertex set and the edge set of a graph $G$ is denoted by $V(G)$ and $E(G)$, respectively. For a graph $G=(V,E)$ and a set of edges $A \subseteq E$ we denote $G-A = (V,E{\setminus }A)$. For two vertices $s,t\in V$ an $s$–$t$ cut is a set of edges $C\subseteq E$ with the property that $s$ and $t$ are in different connected components in $G-C$. The connected components containing $s$ and $t$ in $G-C$ are called the $s$-shore and the $t$-shore of $C$, respectively.

As it is common, we assume that matroids $\mathcal {M}=(A,\mathcal {I})$ are given by an independence oracle, which is a procedure that can be called for any $X\subseteq A$, and returns whether $X\in \mathcal {I}$. We recall that the rank function $r:2^A \rightarrow \mathbb {Z}_{\ge 0}$ of a matroid $\mathcal {M}=(A,\mathcal {I})$ is defined by

$$\begin{aligned} r(X) = \max \{|Y| : Y\subseteq X, \, Y\in \mathcal {I}\}, \end{aligned}$$

and as is well known, it can be computed efficiently given an independence oracle. We refer the reader to the book of Schrijver [36] for an introduction to matroid theory.

Let us briefly discuss two important properties of Bulk-Robust counterparts. For this discussion we fix an instance $(\mathcal {S},w,\Omega )$ of a Bulk-Robust counterpart of some combinatorial optimization problem $\mathcal {P}$, with $\mathcal {S} = (A, \mathcal {X})$ and $\Omega = \{F_1, \ldots , F_m\}$.

Consider first the complexity of the feasibility problem, which amounts to deciding whether there exists a set $X$ in

$$\begin{aligned} \mathcal {F} = \{Y \subseteq A : Y{\setminus }F_i \in \mathcal {X}\,\,\,\, \forall i\in [m]\}. \end{aligned}$$

We observe that this problem can be solved by invoking the feasibility oracle of $\mathcal {S}$. Concretely, if there exists a feasible solution $X\in \mathcal {F}$, then also the entire ground set $A \supseteq X$ is a feasible solution, due to monotonicity of $\mathcal {X}$. Thus, to verify that $\mathcal {F}$ is nonempty one simply needs to verify that $A{\setminus }F_i\in \mathcal {X}$ for every $i\in [m]$. Throughout this paper, when we consider Bulk-Robust problems, we always assume that they are feasible, to avoid trivial cases.

The second property of Bulk-Robust counterparts is related to their approximability. Observe that given an algorithm for the underlying combinatorial optimization problem that for every $B \subseteq A$ returns a solution

$$\begin{aligned} X^*(B) \in \mathrm {argmin} \{w(X) : X\in \mathcal {X} : X\subseteq B\}, \end{aligned}$$

one can obtain an $m$-approximation for the Bulk-Robust instance by simply taking

$$\begin{aligned} X = \bigcup _{i\in [m]} X^*(A{\setminus }F_i). \end{aligned}$$

From monotonicity of $\mathcal {X}$, $X$ is clearly a feasible solution, while

$$\begin{aligned} z(\mathcal {S}, w, \Omega ) \ge w(X^*(A{\setminus }F_i)) \end{aligned}$$

follows from the fact that $X^*(A{\setminus }F_i)$ is an optimal solution to the relaxation of the robust problem that only considers a single interdiction set $F_i$. The latter properties motivate us to focus on obtaining complexity results and better approximation algorithms for Bulk-Robust counterparts.

The remainder of the paper is organized as follows. The next section provides complexity results for Bulk-Robust combinatorial optimization problems. Sections 3 and 4 provide approximation algorithms for the Bulk-Robust counterparts of the Minimum Matroid Basis and the Shortest Path problems, respectively. We conclude the paper and discuss various promising directions for future research in Sect. 5.

2 Complexity of Bulk-Robust optimization

2.1 Inapproximability of Bulk-Robust counterparts

We begin by showing that the Set Cover problem can be modeled as the Bulk-Robust couterpart of essentially any combinatorial optimization problem. Recall that Set Cover is defined as follows. Given a ground set $S = \{a_1, \ldots , a_n\}$ of $n$ elements, a collection $\mathcal {R} = \{R_1, \ldots , R_t\}$ of subsets of $S$ with the property that $\cup _{R\in \mathcal {R}} R = S$, and weights $w(R)$ for each set $R \in \mathcal {R}$, the Set Cover problem asks to find a collection $\mathcal {Y} \subseteq \mathcal {R}$ covering $S$, namely satisfying $\cup _{R\in \mathcal {Y}} R = S$, while minimizing the total weight $\sum _{R\in \mathcal {Y}} w(R)$ of this collection. Feige [17] showed that unless $\mathrm {NP} \subseteq \mathrm {DTIME}(n^{\log \log n})$, Set Cover admits no polynomial $c \ln n$-approximation algorithm for any $c < 1$. Under the weaker assumption that $\mathrm {P}\ne \mathrm {NP}$, Raz and Safra [35] proved that Set Cover admits no polynomial approximation algorithms with guarantee $c \ln n$ for some $c > 0$.

Our goal is to prove that the latter result implies a conditional $c \ln m$ lower bound for approximation for Bulk-Robust counterparts. To achieve this we prove the result first for an extremely simple problem, namely the Minimum Matroid Basis problem when the matroid is the uniform matroid of rank one. Recall that the uniform matroid of rank one with $n$ elements $A = \{b_1, \ldots , b_n\}$ is the set system $U_{n,1} = (A, \mathcal {I})$ with $\mathcal {I} = \{B \subseteq A : |B| \le 1\}$. Its bases are all singletons of the ground set, and the optimal solution for the Minimum Matroid Basis problem is attained by the singleton containing the cheapest element in $A$. As we mentioned before, we are always considering the up–monotone variant of the nominal problem. For the case of the uniform matroid of rank one, this variant has as feasible sets all subsets $B\subseteq A$ which contain a basis of the matroid, namely which satisfy $|B|\ge 1$.

Proposition 1

Unless $\mathrm {NP} \subseteq \mathrm {DTIME}(n^{\log \log n})$, Bulk-Robust Minimum Matroid Basis admits no polynomial $c \ln m$-approximation algorithm for any fixed $c < 1$, even when the matroid is restricted to a uniform matroid of rank one, where $m$ is the number of interdiction sets.

Proof

The proof proceeds by a simple reduction from the Set Cover problem. Consider an instance of Set Cover as defined above. We construct an instance of Bulk-Robust Minimum Matroid Basis as follows. The matroid is chosen to be $U_{t,1} = (A, \mathcal {I})$, with the $i$-th element in $A$ corresponding to the $i$-th set $R_i$ in the Set Cover instance. The family of interdiction sets $\Omega = \{F_1, \ldots , F_n\}$ contains one interdiction set for every ground set element of the Set Cover instance. The set $F_i$ is chosen to contain all elements in $A$ corresponding to sets in the Set Cover instance that do not cover $a_i$. This concludes the construction of the instance. It is straightforward to verify that feasible solutions to the Set Cover instance are in one-to-one correspondence with feasible solutions to the Bulk-Robust Minimum Matroid Basis problem with identical costs. As the number of interdiction sets $m$ is equal to the cardinality of the ground set of the Set Cover instance, the result of Feige [17] concludes the proof.$\square$

The latter result easily extends to many other combinatorial optimization problems, including the Bulk-Robust counterparts of the Shortest Path problem and many others. The simplest explanation is that the Minimum Basis problem for the uniform matroid of rank one $U_{t,1}$ can be simulated with all these problems by considering a graph with two vertices $u$ and $v$, and $t$ parallel edges connecting $u$ and $v$. For example, the existence of a $u$-$v$ path in any subgraph of this graph is equivalent to the existence of an edge in this subgraph. We conclude with the following corollary.

Corollary 2

Unless $\mathrm {NP} \subseteq \mathrm {DTIME}(n^{\log \log n})$, the Bulk-Robust counterparts of the Minimum Matroid Basis problem and the Shortest Path problem admit no polynomial $c \ln m$-approximation algorithm for any fixed $c < 1$.

2.2 Complexity of the Bulk-Robust shortest path problem

In this section we focus on the Bulk-Robust Shortest Path problem, showing stronger inapproximability results, as well as various results for fixed-width instances. For our first reduction we use the Directed Steiner Forest problem, defined as follows.

Given a directed arc-weighted graph $G = (V, A)$, and a collection of ordered pairs $\mathcal {P} \subseteq V \times V$ of vertices, the Directed Steiner Forest problem asks to find a cheapest set of arcs $A^* \subseteq A$ with the property that it contains a $u$-$v$ path for every terminal pair $(u,v) \in \mathcal {P}$. Dodis and Khanna [16] showed that Directed Steiner Forest is at least as hard as the Label Cover problem. This implies that unless $\mathrm {NP} \subseteq \mathrm {DTIME}(n^{\log \log n})$, Directed Steiner Forest cannot be approximated in polynomial time within $O(2^{\log ^{1-\epsilon } n})$ for any fixed $\epsilon > 0$. The following proposition proves a similar result for the Bulk Robust Shortest Path problem.

Proposition 3

Unless $\mathrm {NP} \subseteq \mathrm {DTIME}(n^{\log \log n})$, there is no polynomial approximation algorithm with guarantee $O(2^{\log ^{1-\epsilon } n})$ for the directed Bulk-Robust Shortest Path problem, for any fixed $\epsilon > 0$.

Proof

We prove the claim by a reduction from the Directed Steiner Forest problem. Given an instance of the Directed Steiner Forest problem consisting of a graph $G = (V, A)$ and a collection of terminals $\mathcal {P}$, we construct an instance of Bulk-Robust Shortest Path as follows. The graph is constructed from $G$ by adding two new vertices $s,t$ and $2|\mathcal {P}|$ new arcs. For every terminal pair $(u,v)\in \mathcal {P}$, two zero-cost arcs $su$ and $vt$ are added to the graph. This concludes the construction of the graph. The scenario set $\Omega$ is chosen to contain one interdiction set $F_{(u,v)}$ for each terminal pair $(u,v)\in \mathcal {P}$. The interdiction set $F_{(u,v)}$ contains all arcs incident to $s$ and $t$, except for $su$ and $vt$. Finally, the terminals of the Bulk-Robust Shortest Path problem are chosen to be $s$ and $t$. It is straightforward to verify that every feasible solution to the Directed Steiner Forest instance corresponds to a feasible solution for the Bulk-Robust Shortest Path problem with the same cost (obtained by adding to this solution all arcs incident to $s$ and $t$), and vice versa. Finally, the result follows from the fact that the new graph has only two vertices more than the original one.$\square$

Our next goal is a hardness-of-approximation result in terms of the parameter $k$.

Proposition 4

Unless $\mathrm {NP} \subseteq \mathrm {DTIME}(n^{\log \log n})$ there is no $O(2^{\frac{1}{4}k^{1-\epsilon }})$-approximation algorithm for the directed Bulk-Robust Shortest Path problem for any $\epsilon > 0$, where $k$ is the width of the instance.

Proof

To this end we describe a simple modification of the reduction in Proposition 3. We assume without loss of generality that $|\mathcal {P}| = 2^l$ for some integer $l$. The new reduction connects the new vertices $s$ and $t$ to the terminals in the graph $G$ using a balanced binary tree. Formally, the reduced graph contains $2(2^l - 1)$ new vertices comprising two balanced binary trees $T_1$ and $T_2$, whose leaves are the sets of sources and the set of targets of the terminal pairs in $\mathcal {P}$, respectively. $s$ is the root of the tree $T_1$ and all arcs in $T_1$ are directed away from $s$ towards the source terminals, while $t$ is the root of $T_2$ and all arcs in $T_2$ are directed from the target terminals towards $t$. This concludes the construction of the graph. The terminals of the Bulk-Robust Shortest Path instance remain $s$ and $t$. Figure 1 illustrates the reduction.

The scenario set $\Omega$ is constructed as follows. Again, for every terminal pair $(u,v) \in \mathcal {P}$, $\Omega$ contains a single interdiction set $F_{(u,v)}$. This set is defined as follows. Consider the unique $s$–$u$ path in the graph, completely contained in $T_1$. This path contains $l-1$ vertices different from $u$. Each such vertex has an outgoing arc in $T_1$ that is not contained in the $s$–$u$ path. $F_{(u,v)}$ is chosen to contain all these arcs. Consider next the unique $v$–$t$ path completely contained in $T_2$. This path contains $l-1$ vertices different from $v$. Each such vertex contains one incoming arc not in the $v$–$t$ path. We include also all these arcs in $F_{(u,v)}$. This concludes the construction of $F_{(u,v)}$. Notice that by construction, any $s$–$t$ path in the graph, not containing arcs from $F_{(u,v)}$ must contain a $u$-$v$ path in the original graph. This implies the correspondence between Steiner forests in the original graph and robust paths in the transformed graph, thus the reduction is correct.

Finally, note that $k = \max _{F\in \Omega } |F| = 2l -2 \le 2 \log |\mathcal {P}|$. Let $\epsilon > 0$ and $f(x)=2^{\frac{1}{4}x^{1-\epsilon }}$.  The existence of a $O(f(k))$-approximation algorithm for Bulk-Robust Shortest Path implies an approximation algorithm for the Directed Steiner Forest problem with approximation guarantee of $O(f(2 \log |\mathcal {P}|)) = O(2^{\frac{1}{2}\log ^{1-\epsilon } |\mathcal {P}|}) = O(2^{\log ^{1-\epsilon } n})$, where in the last equality we used $|\mathcal {P}| \le n^2$. The result now follows from the result of Dodis and Khanna [16].$\square$

In the remainder of this section we prove that Bulk-Robust Shortest Path is already APX-hard for $k=2$ in both directed and undirected graphs. In light of the polynomial algorithm for the case $k=1$ in [2], this result is tight in terms of the parameter $k$. We prove the result for undirected graphs. The adaptation for directed graphs is straightforward. Our proof is based on a reduction from the Minimum Vertex Cover problem on subcubic graphs, i.e., graphs with degrees bounded by $3$. This is a well-known APX-hard problem [5]. Recall that given an undirected graph $G=(V,E)$, the Minimum Vertex Cover problem asks to find a smallest set $S \subseteq V$ of vertices with the property that every edge is incident to at least one vertex in $S$.

Fig. 1

An illustration of the reduction in Proposition 4. The interdiction set $F_{u_1,v_1}$, corresponding to the terminal pair $(u_1,v_1)$, is marked in red

Our reduction can be broken down into two steps. First, we introduce a property of graphs, which we call $k$-monotonicity, and which allows us to map Vertex Cover problems to Bulk-Robust Shortest Path problems. More precisely, we show that the Vertex-Cover problem on any graph that is $k$-monotone can be reduced to a Bulk-Robust Shortest Path problem of width $k$. We then prove that any subcubic graph is $2$-monotone.

We start by defining the notion of $k$-monotonicity.

Definition 5

A graph $G=(V,E)$ is $k$ -monotone, if there are $k$ orders $\pi _1, \dots , \pi _k$ of its edge set $E$, such that for every vertex $v\in V$, the set of edges incident to $v$ is an interval in at least one of the $k$ orders.

E.g., a path is $1$-monotone by simply ordering the edges in the order that they appear on the path. Note that every $n$-vertex graph is $n$-monotone since one can define for every vertex $v$ an edge order such that edges incident to $v$ appear consecutively in this order. More generally, every $t$-colourable graph is $t$-monotone; for each color class an edge ordering can be defined such that for all vertices $v$ of this color, the edges incident to $v$ appear consecutively.

In the following lemma we prove that instances of Minimum Vertex Cover on $k$-monotone graphs can be modeled as instances of Bulk-Robust Shortest Path with width $k$, given a corresponding family of $k$ orderings of the edges.

Lemma 6

Given a $k$-monotone graph $G=(V,E)$ with a corresponding collection of $k$ edge orderings $\pi _1,\dots , \pi _k$, there is a polynomial time transformation of the Minimum Vertex Cover instance on $G$ to an instance of Bulk-Robust Shortest Path with width $k$. Furthermore, any solution to the Vertex Cover problem can be transformed in polynomial time to a solution of identical value to the Bulk-Robust Shortest Path problem and vice versa.

Proof

We start by fixing some notation. Let $E=\{e_1,\dots , e_m\}$, and for $i\in [k]$, $\pi _i$ is a permutation on $[m]$, that defines the edge order $\{e_{\pi _i(1)}, \dots , e_{\pi _i(m)}\}$.

We construct an instance $(H, \Omega )$ of Bulk-Robust Shortest Path in the following way. We describe first the graph $H$ and then the interdiction sets. We include in $H$ $k$ vertex-disjoint $s$–$t$ paths $P_i$, $i\in [k]$, of length $|P_i|=m$. We use the term $P_i$ to represent the edges on the path.

Path $P_i$ corresponds to the permutation $\pi _i$, and we denote its edges by $f^i_1, \dots , f^i_m$ in the order when traversing $P_i$ from $s$ to $t$. All edges on any of the paths $P_i$ have cost zero, and we think of them as being in one-to-one correspondence with the initial edges, where the initial edge $e_j\in E$ corresponds to edge $f_{\pi _i(j)}^i$ of the path $P_i$. Furthermore, we add one additional edge to $H$ for every vertex $v\in V$ as follows.

We associate every vertex $v\in V$ with an index $i(v) \in [k]$, that corresponds to one ordering $\pi _{i(v)}$ that numbers the edges incident to $v$, i.e., $E_v = \{e \in E : v\in e\}$, consecutively. If there are several orderings where $E_v$ is consecutive, we break ties arbitrarily and let $i(v)$ be any one of them. Let $beg(v), end(v)$ be the end vertices in $H$ of the subpath of $P_{v(i)}$ that corresponds to the edges $E_v$. We conclude the construction of $H$ by adding the edge $\beta _v$ from $beg(v)$ to $end(v)$ with cost one, for every vertex $v$ of $G$. We interpret the inclusion of edges of type $\{beg(v),end(v)\}$ in a solution to the constructed Bulk-Robust Shortest Path problem instance, as signifying that we use $v$ in the Vertex Cover problem on $G$. Figure 2 illustrates the construction for an example graph $G$ with width $k=2$.

The interdiction sets are defined as follows. We have a interdiction set $F_{e_j}$ for every edge $e_j\in E$ defined by

$$\begin{aligned} F_{e_j} = \{f^i_{\pi _i(j)} \mid i\in k\}. \end{aligned}$$

Hence, $F_{e_j}$ includes on each path $P_i$ the edge that corresponds to $e_j$. This finishes our construction of the Bulk-Robust Shortest Path instance $(H,\Omega )$. Notice that the width of the instance is $k$, since all interdiction sets $F_{e_j}$ satisfy $|F_{e_j}|=k$. Furthermore, observe that the interdiction set $F_{e_j}$ for $e_j=\{u,v\}$ forces any feasible solution to $(H,\Omega )$ to contain either $\{beg(u), end(u)\}$ or $\{beg(v),end(v)\}$.

We now discuss how solutions map between the two problems. Let $C\subseteq V$ be a vertex cover in $G$. We claim that

$$\begin{aligned} S = \bigcup _{i\in [k]} P_i \cup \{\beta _u : u\in C\} \end{aligned}$$

is a feasible solution to the Bulk-Robust Shortest Path instance with cost equal to $|C|$. The fact that the cost matches $|C|$ is immediate from the definition of $S$. To check feasibility, consider any interdiction set $F_{e_j} \in \Omega$. Since $C$ is a vertex cover, there is some $u\in C$ with $u\in e_j$. The following is an $s$–$t$ path in $H$ only using edges in $S{\setminus }F_{e_j}$: start at $s$ and follow $P_{i(u)}$ until $beg(u)$, then take the edge $\beta _u$ to $end(u)$, and continue on $P_{i(u)}$ until $t$. One can easily observe that this is an $s$–$t$ path in $H$ that only contains edges in $S{\setminus }F_{e_j}$.

Conversely, consider a feasible solution $S$ of cost $d$ for the Bulk-Robust Shortest Path problem defined by $(H,\Omega )$. Let

$$\begin{aligned} C = \{v \in V : \beta _v \in S\}. \end{aligned}$$

We claim that $C$ is a vertex cover of $G$ with $|C|$ being equal to the cost of $S$. Again, the fact that $|C|$ matches the cost of $S$ follows immediately from the definition of $C$. To check that $C$ is a vertex cover, consider any edge $e_j \in E$, and consider its associated interdiction set $F_{e_j}$. Since $S$ is a feasible solution to the Bulk-Robust Shortest Path problem, there must be an $s$–$t$ path in $S{\setminus }F_{e_j}$. As mentioned previously, this is only possible if $S$ contains an edge of type $\{beg(v), end(v)\}$ for at least one of the endpoints $v\in e_j$ of $e_j$. Hence, $C$ is indeed a vertex cover.$\square$

Since Vertex Cover on subcubic graphs is APX-hard [5], it remains to show the following to obtain APX-hardness for the Bulk-Robust Shortest Path problem with width $k=2$.

Fig. 2

Top left A subcubic graph $G$. The numbering of the edges $f_1^i, f_2^i,\dots , f^i_{11}$ for $i\in \{1,2\}$ indicates two orderings of the edges that show $G$ to be $2$-monotone. Top right The partition into two sets $V_1$ and $V_2$ in Lemma 7, which gives rise to the orderings $\pi _1, \pi _2$. Bottom the transformation in Lemma 6 corresponding to the $2$-monotone graph $G$. The interdiction set $F_e$ with $e=\{u_3, u_4\}$ is highlighted with dashed edges

Lemma 7

Every subcubic graph is $2$-monotone. Furthermore, a corresponding pair of edge orderings that certifies $2$-monotonicity can be obtained from $G$ in polynomial time.

Proof

Let $G = (V,E)$ be a subcubic graph. We describe a procedure to obtain the two orderings of $E$. We start by obtaining a partition of the vertex set $V = V_1 \cup V_2$, which is obtained iteratively. We initialize by setting $V_1 = V$ and $V_2 = \emptyset$. We stop the procedure when it is true that for every $i\in [2]$ and for every $v\in V_i$, the number of neighbors of $v$ in $V_i$ is at most one. In every iteration we choose an arbitrary vertex $v \in V_i$ for some $i\in [2]$, which violates the condition, and move it to the other partition. Since the graph is subcubic, this operation strictly increases the number of edges with one endpoint in $V_1$ and the other one in $V_2$. Hence, this iterative algorithm will stop after $O(|E|)$ steps, with a partition $V_1,V_2$ of $V$ that satisfies the desired property.

It remains to define the desired orders $\pi _1,\pi _2$ of $E$. The edge ordering $\pi _i$, for $i\in [2]$, will be such that for any vertex $v\in V_i$, the edges adjacent to $v$ appear consecutively in $\pi _i$. We describe how to construct $\pi _1$, constructing $\pi _2$ is analogous.

To do so we first order the vertices in $V_1$ such that if $u, v \in V_1$ and $\{u,v\} \in E$, then $u$ and $v$ appear one after the other in the order of $V_1$ (see Fig. 2). This can easily be achieved, since the induced graph $G[V_1]$ contains only isolated edges. Let $\sigma = u_1, \ldots , u_{|V_1|}$ be the corresponding order. The ordering $\pi _1$ is then defined as follows. The first edges in the order are all edges with both endpoints in $V_2$. Those edges are included in an arbitrary order. We then add all edges $e\in U$ that are incident to $u_1$, followed by the edge $\{u_1,u_2\}$ if it exists. We continue with adding all edges $e\in U$ incident to $u_2$ etc. Clearly, the edges incident to a vertex $u\in V_1$ appear as an interval in the ordering given by $\pi _1$. See Fig. 2 for an illustration.$\square$

In light of Lemmas 6 and 7 we obtain the desired result for $k = 2$.

Theorem 8

The Bulk-Robust Shortest Path problem restricted to instances with $k = 2$ is APX-hard.

3 Bulk-Robust minimum matroid basis

In this section we develop a polynomial $(\log r + \log m)$-approximation algorithm for the Bulk-Robust Minimum Matroid Basis problem, where $r$ is the rank of the matroid. In light of Proposition 1, this result is tight with respect to the parameter $m$. Recall that the Minimum Matroid Basis problem is defined as follows. Given a matroid $\mathcal {M} = (A, \mathcal {I})$ and a linear cost function on its ground set, the goal is to find a basis of the matroid with minimum cost. In the Bulk-Robust Minimum Matroid Basis problem we are additionally given a collection $\Omega$ of interdiction sets and the goal is to find the cheapest subset $S$ of the ground set, such that $S{\setminus }F_i$ contains a basis of the matroid $\mathcal {M}$ for every $F_i\in \Omega$.

This problem can easily be seen to be a special case of the following problem, that we call Simultaneous Matroid Basis problem, and which is defined as follows. Given $t$ matroids $\mathcal {M}_1, \ldots , \mathcal {M}_t$ on the same ground set $A$, find a minimum cost subset $S$, which contains a basis of each matroid. Note that Bulk-Robust Minimum Matroid Basis can be transformed into a Simultaneous Matroid Basis problem by setting $\mathcal {M}_i = (A, \mathcal {I}_i)$ and

$$\begin{aligned} \mathcal {I}_i = \{X \subseteq A : X{\setminus }F_i \in \mathcal {I}\}, \end{aligned}$$

for all $i\in [t]$. In the remainder of this section, we will focus on the Simultaneous Matroid Basis problem, and present an approximation algorithm for this problem, which, by the above observation, carries over to the Bulk-Robust Minimum Matroid Basis problem.

We notice that the Simultaneous Matroid Basis problem can be reinterpreted as a matroid intersection problem. More precisely, instead of directly constructing a minimum weight set $S\subseteq A$ that contains a basis in each matroid, consider the problem of obtaining the complement $\overline{S}=A{\setminus }S$ of an optimal set. Hence, the problem can be rephrased as the task of finding a maximum weight set $\overline{S}$ such that $A\setminus \overline{S}$ contains a basis for each matroid. This is equivalent to saying that $\overline{S}$ should be a maximum weight set in the intersection of the dual matroids of all involved matroids. Whereas this observation is nice from a theoretical point of view, it seems hard to exploit it algorithmically, partially due to the difficulty of approximating matroid intersection problems with more than two matroids, and furthermore since this reduction is not approximation-preserving.

To introduce our approximation algorithm, let us fix an instance of Simultaneous Matroid Basis with $t$ matroids $\mathcal {M}_1, \ldots , \mathcal {M}_t$ and a cost function $w$. Let $r_i$ denote the rank function of the matroid $\mathcal {M}_i$ for $i\in [t]$. For brevity we let $\alpha _i = r_i(A)$ denote the rank of $\mathcal {M}_i$.

Since all matroids are defined with the same ground set $A$, we can define the aggregate rank of a set $X \subseteq A$ as

$$\begin{aligned} f(X) = \sum _{i\in [t]} r_i(X). \end{aligned}$$

Observe that $f(A) = \sum _{i\in [t]} \alpha _i$. Furthermore, a set $X\subseteq A$ is a feasible solution to the Simultaneous Matroid Basis instance if and only if

$$\begin{aligned} f(X) = f(A). \end{aligned}$$

The function $f$ is the key to our algorithm. An important feature of $f$ is submodularity, namely the property that for every two sets $X, Y \subseteq A$ we have

$$\begin{aligned} f(X) + f(Y) \ge f(X \cup Y) + f(X \cap Y). \end{aligned}$$

Submodularity of $f$ follows from submodularity of rank functions of matroids, and the fact that sums of submodular functions are also submodular. Let us briefly review an important operation on matroids called contraction. For a matroid $\mathcal {M} = (A, \mathcal {I})$ and $X \subseteq A$, the contraction of $\mathcal {M}$ by $X$ is a matroid with ground set $A{\setminus }X$, denoted by $\mathcal {M}/X$, and defined by the rank function

$$\begin{aligned} r(Y) = r(Y \cup X) - r(X), \end{aligned}$$

where $r$ is the rank function of $\mathcal {M}$. In other words, a set $S\subseteq A{\setminus }X$ is independent in $\mathcal {M}/X$, if for any maximal independent set $I\subseteq X$ in $M$, $I\cup S$ is independent in $M$.

We are ready to give a brief description of the algorithm. The algorithm is iterative. In each iteration, the algorithm maintains a partial solution obtained so far. Let $S_j$ denote the set of elements comprising the partial solution in the end of the $j$’th iteration and let $S_0 = \emptyset$. The invariant that the algorithm maintains is that

$$\begin{aligned} f(A) - f(S_{j+1}) \le \gamma (f(A) - f(S_j)) \end{aligned}$$

holds for every iteration $j$ and some constant $\gamma < 1$. Another feature is that

$$\begin{aligned} w(S_{j+1}{\setminus }S_j) \le \mathrm {OPT}, \end{aligned}$$

where $\mathrm {OPT}$ is the optimal solution value for this instance of Simultaneous Matroid Basis. Clearly, any algorithm satisfying the latter two conditions is a $O(\log f(A))$-approximation algorithm for Simultaneous Matroid Basis. Indeed, the former inequality guarantees that after $O(\log f(A))$ iterations the partial solution is feasible, and the latter inequality ensures that in each iteration, the set of elements added have a cost bounded by $\mathrm {OPT}$.

Let us focus next on a single iteration of the algorithm. In order to obtain the update set $Y_{j+1} = S_{j+1}{\setminus }S_j$ we use an algorithm for the Monotone Submodular Function Maximization problem with a linear budget constraint. More precisely, given a monotone submodular set function $g$ on some ground set $A$ and a budget constraints $w(X)\le B$ for $X\subseteq A$, this problem asks to find a set $X\subseteq A$ maximizing

$$\begin{aligned} \max \{g(X) : w(X) \le B\}. \end{aligned}$$

A result from Feige [17] implies that Monotone Submodular Function Maximization with a linear budget constraint is in general not possible to approximate within a factor of $1-\frac{1}{e}+\epsilon$, for any fixed $\epsilon >0$, unless P$\ne$NP.²

Lots of progress has been made recently on approximation algorithms for constrained and unconstrained submodular function maximization. In particular, several essentially optimal algorithms for monotone submodular function maximization with a single budget constraint were found (see [13, 19, 29] and references therein). More precisely, for any fixed $\epsilon >0$, these algorithms are efficient $(1-\frac{1}{e}-\epsilon )$-approximations.

Our algorithm iteratively calls a $O(1)$-approximation for the monotone submodular function maximization problem with a budget constraint as a subprocedure. The main loop of our algorithm is given as Algorithm 1. The algorithm assumes that the optimal solution value $\mathrm {OPT}$ is known. We will remove this assumption later.

Let us prove the following lemma, which bounds the approximation guarantee of Algorithm 1. We set $T = \sum _{i\in [t]} \alpha _i$.

Lemma 9

Algorithm 1 is an $O(\log T)$-approximation.

Proof

Note that in each iteration we increase the cost of the current solution by at most $\mathrm {OPT}$. It remains to bound the number of iterations performed by the algorithm. For this we will show that the quantity $\Delta = T-\sum _{i\in [t]}r_i(S)$ decreases by a constant factor at each iteration of the while loop.

Let $S^*$ be an optimal solution to the Simultaneous Matroid Basis problem. Hence, $w(S^*)=\mathrm {OPT}$, and therefore

$$\begin{aligned} \max \{f(X): X\subseteq A{\setminus }S, w(X)\le \mathrm {OPT}\}&\ge f(S^*{\setminus }S) \\&= \sum _{i\in [t]} \left( r_i((S^*{\setminus }S) \cup S) - r_i(S) \right) \\&= \sum _{i\in [t]} \left( r_i(S^*) -r_i(S) \right) \\&= T - \sum _{i\in [t]} r_i(S). \end{aligned}$$

Since we use a constant-factor approximation to solve the constrained submodular function maximization problem in step 6, we get a set $Y\subseteq A{\setminus }S$ satisfying

$$\begin{aligned} f(Y) \ge c \cdot \Delta , \end{aligned}$$

(1)

for some constant $c\in (0,1)$. It follows that in the following iteration of the while loop, the updated version $S'=S\cup Y$ of $S$ that we use satisfies

$$\begin{aligned} \sum _{i\in [t]} r_i(S\cup Y)&= \sum _{i\in [t]} \left( g_i(Y) + r_i(S)\right) \\&= f(Y) + \sum _{i\in [t]} r_i(S). \end{aligned}$$

Combining the above equality with (1), and reordering terms, we obtain

$$\begin{aligned} T - \sum _{i\in [t]}r_i(S\cup Y) \le (1-c) \left( T - \sum _{i\in [t]}r_i(S) \right) = (1-c) \Delta . \end{aligned}$$

We conclude that $\Delta$ decreases by a factor of $1-c<1$ in each iteration. Since at the first iteration we have $\Delta = T$, the total number of iterations is at most $O(\log T)$.

$\square$

It remains to remove the assumption that $\mathrm {OPT}$ needs to be known in advance. To this end, notice that for every value $T \ge \mathrm {OPT}$ it holds that the optimal solution $S^*$ to the Simultaneous Matroid Basis instance is feasible for the problem $\max \{f(X) : w(X) \le T\}$. Note that the only requirement we have from the update set $Y$ chosen in any iteration of Algorithm 1 is that $f(Y) \ge c \cdot \Delta$ holds. Although $S^*$ is not a feasible solution of $\max \{f(X) : w(X) \le T\}$ whenever $T < \mathrm {OPT}$ it can still happen, that a solution to the latter problem yields a set $Y$ with $f(Y) \ge c \cdot \Delta$. It follows that we cannot use binary search with the previous criterion to find $\mathrm {OPT}$ exactly. At the same time, we can still use this set $Y$ to update the current solution $S$, since it satisfies both required conditions: It has a cost which is at most $\mathrm {OPT}$ and it attains a large enough value for $f$. The latter discussion justifies the following approach.

Whenever we have to perform step 6 of Algorithm 1, our plan is to find a value $T \in \mathbb {Z}_+$ and two $c$-approximations $Y^T, Y^{T-1}$ to the following two Constrained Submodular Function Maximization problems

$$\begin{aligned} Y^{T} \leftarrow \max \{f(X) : w(X) \le T\} \,\, \text { and } \,\, Y^{T-1} \leftarrow \max \{f(X) : w(X) \le T-1\} \end{aligned}$$

that satisfy

$$\begin{aligned} f(Y^T) \ge c \cdot \Delta \,\, \text { and } \,\, f\left( Y^{T-1}\right) < c\cdot \Delta . \end{aligned}$$

Notice that such a value $T$ together with the two solutions $Y^T$ and $Y^{T-1}$ can be found in polynomial time by applying a binary search procedure to $T$ within the range $[0,\sum _{a\in A} w_a]$. Clearly, if $T$ satisfies the above property, then $T\le \mathrm {OPT}$: otherwise, $f(Y^{T-1})<c\cdot \Delta$ would violate the fact that $Y^{T-1}$ was obtained via a $c$-approximation. Hence, we can replace the role of $\mathrm {OPT}$ by such a $T$ in Algorithm 1, since $Y^T$ satisfies both criteria we need, namely $w(Y^T)\le \mathrm {OPT}$ and $f(Y^T)\ge c\cdot \Delta$.

This concludes the algorithm for Simultaneous Matroid Basis, and as a special case, for the Bulk-Robust Minimum Matroid Basis problem. We obtain the following theorem.

Theorem 10

There is a polynomial $O(\log (T))$-approximation algorithm for Simultaneous Matroid Basis. In particular, the Bulk-Robust Minimum Matroid Basis problem admits a polynomial $O(\log r + \log m)$-approximation algorithm.

Notice that the dependence of the approximation factor on $m$ is asymptotically optimal in view of Proposition 1.

Observe that for the Bulk-Robust Minimum Spanning Tree problem, which is a special case of Bulk-Robust Minimum Matroid Basis problem, we have $r=n-1$. Hence, Theorem 10 implies a polynomial $O(\log n + \log m)$-approximation for this problem.

4 Bulk-Robust shortest path

In this section we develop a constant-factor approximation algorithm for the Bulk-Robust Shortest Path problem restricted to instances with width $k=2$. In view of Theorem 8 this is qualitatively the best we can hope for.

Our algorithm relies on a simpler algorithmic framework that gives a $O(\log m)$-approximation algorithm for any fixed $k$ in polynomial time. We begin by presenting this algorithm, and later describe the required modification to obtain a constant-factor approximation algorithm for $k=2$. We present the algorithm for undirected graphs. The adaptation for directed graphs is straightforward.

Consider an instance $\mathrm {I}_k$ of Bulk-Robust Shortest Path with graph $G=(V,E)$, interdiction sets $\Omega = \{F_1, \ldots , F_m\}$, and terminals $s, t \in V$. We assume that the width $k = \max _{i\in [m]} |F_i|$ is constant.

We define a sequence of relaxations $\mathrm {I}_{k-1}, \ldots , \mathrm {I}_1$ of the instance $\mathrm {I}_k$. The instance $\mathrm {I}_j$ is defined with the same graph and terminals as $\mathrm {I}_k$, but with scenario set

$$\begin{aligned} \Omega _j = \left\{ R \subseteq E : |R| \le j \,\, \text { and } \,\, \exists F\in \Omega \,\, R\subseteq F\right\} . \end{aligned}$$

In words, the set $\Omega _j$ contains all subsets of cardinality at most $j$ of interdiction sets in $\Omega$. Clearly, for any $1 \le l\le j \le k$, any feasible solution for $\mathrm {I}_j$ is also a feasible solution for $\mathrm {I}_l$, since for any interdiction set $R \in \Omega _l$ there exists an interdiction set $R' \in \Omega _j$ with $R \subseteq R'$. Consequently, this is indeed a sequence of relaxations of the original problem instance.

The algorithm works as follows. It starts by solving the instance $\mathrm {I}_1$ to optimality, using the algorithm in [2]. In each subsequent iteration $j > 1$, the algorithm augments the current solution $S_{j-1}$, which is assumed to be feasible for $\mathrm {I}_{j-1}$, to a solution for $\mathrm {I}_j$, by solving an augmentation problem. The augmentation problem is a certain Set Cover problem that we define hereafter. We assume without loss of generality that $(V,S_{j-1})$ is connected. For otherwise, one can remove all edges in $S_{j-1}$ that are not in the connected component that contains $s$ and $t$, thus obtaining a cheaper solution for $\mathrm {I}_{j-1}$. A simple but very useful observation is the following.

Lemma 11

Let $F \in \Omega _j$ be some interdiction set such that $s$ and $t$ are disconnected in $(V,S_{j-1}{\setminus }F)$. Then we have the following

• (i) $F\subseteq S_{j-1}$,

• (ii) $(V,S_{j-1}{\setminus }F)$ consists of two connected components (one containing $s$ and the other one $t$).

Proof

• (i) Assume by the sake of contradiction $F\not \subseteq S_{j-1}$, and let $F'=F\cap S_{j-1}$. Hence, $S_{j-1}{\setminus }F' = S_{j-1}{\setminus }F$, and therefore, removing $F'$ from $S_{j-1}$ disconnects $s$ and $t$. This violates the assumption that $S_{j-1}$ is feasible for $\mathrm {I}_{j-1}$.

• (ii) Again, assume by contradiction that $(V,S_{j-1}{\setminus }F)$ consists of at least $3$ connected components. Then there is at least one connected component whose corresponding set of vertices $W\subseteq V$ does not contain $s$ or $t$. Since $(V,S_{j-1})$ is assumed to be connected, there is at least one edge $e\in F$ that has one endpoint in $W$ and one outside of $W$. However, this implies that the set $F'=F{\setminus }\{e\}$ satisfies that $(V,S_{j-1}{\setminus }F')$ is disconnected, thus contradicting that $S_{j-1}$ is feasible for $\mathrm {I}_{j-1}$.

$\square$

In the context of the $j$-th augmentation problem, we call a set $F\in \Omega _j$ critical if it disconnects $s$ and $t$ in $(V, S_{j-1})$. If we want to augment $S_{j-1}$ such that it is feasible for some critical interdiction set $F\in \Omega _j$, we can add to $S_{j-1}$ a path $P$ with the following properties: $P\subseteq E{\setminus }S_{j-1}$, and $P$ is a $u$–$v$ path, where $u$ and $v$ are vertices in the connected components of $(V,S_{j-1}{\setminus }F)$ that contain $s$ and $t$, respectively. We call such a path $P$ an $F$-fixing path.

Notice that Lemma 11 guarantees that adding an $F$-fixing path $P$ to $S_{j-1}$ leads to a set $S_{j-1}\cup P$ that is feasible for interdiction set $F$, since $F\subseteq S_{j-1}$, and hence, $F\cap P=\emptyset$. Furthermore, the second part of Lemma 11 makes sure that for any critical interdiction set $F$, there exists an $F$-fixing path, assuming that $\mathrm {I}_j$ is feasible, as usual. To see this, observe that if $\mathrm {I}_j$ is feasible, then there is a set of edges $U\subseteq E{\setminus }(S_{j-1}\cup F)$ such that $(V, (S_{j-1}{\setminus }F)\cup U)$ contains an $s$–$t$ path. Since $(V, S_{j-1}{\setminus }F)$ only has two connected components, this implies that one can choose $U$ to be a single path connecting the components, which by definition is an $F$-fixing path. Notice that if $(V,S_{j-1})$ had more than two connected components, then $U$ could consist of several paths that connected different connected components in $(V,S_{j-1})$, leading to a graph where $s$ and $t$ are connected.

To augment $S_{j-1}$ to a set $S_j \supseteq S_{j-1}$ that is feasible for $\mathrm {I}_j$, we will add to $S_{j-1}$ a set of edges that contains for every critical interdiction set $F\in \Omega _j$ an $F$-fixing path. A minimum-cost augmentation of this type is called an optimal augmenting set. We formalize these concepts in the following definition.

Definition 12

The $j$-th Augmentation problem is: given a feasible solution $S_{j-1}$ for $\mathrm {I}_{j-1}$, find a minimum-cost augmenting set $X^*_j \subseteq E{\setminus }S_{j-1}$, namely a set with the property that for every critical interdiction set $F\in \Omega _{j}$ with respect to $S_{j-1}$, $X^*_j$ contains an $F$-fixing path. The optimal solution value of the $j$-th augmentation problem is denoted by $\mathrm {AUG}_j$.

The following lemma states an important property of the augmentation problem. Concretely, it states that despite the possibly complicated structure of the optimal augmentation set $X_j^*$, one can restrict the search to unions of paths, by incurring a loss of at most a factor of two.

Lemma 13

There exists a collection of paths $Q_1, \ldots , Q_r \subseteq E{\setminus }S_{j-1}$, such that for each critical $F\in \Omega _j$, the collection contains at least one $F$-critical path and $\sum _{i=1}^{r}{w(Q_i)} \le 2\mathrm {AUG}_j$.

Proof

Let $X_j^*$ be the optimal solution to the $j$-th augmentation problem (with $w(X^*_j) = \mathrm {AUG}_j$). Observe that $X^*_j$ is a forest, since the graph is undirected. Consider any tree $T\subseteq X^*_j$. Let $W$ be the set of vertices incident to edges in $S_{j-1}$. By doubling all edges in $T$, we obtain an Eulerian subgraph. Consider any Eulerian tour in this subgraph. We cut the tour into edge-disjoint paths in the following way. We start at an arbitrary vertex in $W$ and follow the tour until it reaches another vertex in $W$. The edges traversed correspond to the first path $Q_1$. We continue to follow the tour until the next vertex in $W$ is reached. This part corresponds to $Q_2$ etc.

Let $Q_1, \ldots , Q_{r'}$ be the obtained paths. Clearly $\sum _{i=1}^{r'}{w(Q_i)} = 2w(T)$. Furthermore, every critical interdiction set that was fixed by $T$ is clearly also fixed by some path from the latter collection. By repeating the argument for every tree in $X^*_j$ we obtain the result.$\square$

Lemma 13 allows us to treat the augmentation problem as a Set Cover problem. Formally, for every pair of vertices $u, v\in V$ we compute $P_{u,v}$, a shortest $u$-$v$ path in $E{\setminus }S_{j-1}$. We call this path the $u$-$v$ link $\alpha _{u,v}$, and define its cost to be $w(P_{u,v})$. We say that a link $P_{u,v}$ covers a critical set $F\in \Omega _j$, if the path $P_{u,v}$ fixes $F$. Finally, the Set Cover instance is defined as having a ground set composed of the critical interdiction sets in $\Omega _j$, and a family of covering subsets corresponding to links, where the set corresponding to the link $P_{u,v}$ contains all critical interdiction sets which are fixed by $P_{u,v}$. We denote this Set Cover problem by $SC_j$. Exploiting this connection to the Set Cover problem, we obtain a first approximation algorithm for Bulk-Robust Shortest Path.

Theorem 14

For any constant $k$, there is polynomial $O(\log m)$-approximation algorithm for the Bulk-Robust Shortest Path problem restricted to the instances with width $k$.

Proof

Let $\mathrm {OPT}$ denote the optimal solution for the problem. The algorithm proceeds by solving the problem instance $\mathrm {I}_1$, followed by the sequence of $k-1$ augmentation problems. The correctness of the algorithm is a direct consequence of Lemma 11. The initial problem is solved to optimality using the algorithm in [2]. This incurs a cost of $\mathrm {OPT}$, at most. The augmentation problems are solved with the Set Cover problem $SC_j$, for $j=2, \ldots , k$. We use the greedy algorithm for the Set Cover problem to solve each problem. Lemma 13 and the fact that the greedy algorithm is a $(\log n + 1)$-approximation algorithm [36] imply that the obtained solution in the $j$-th iteration is a $2(\log n' + 1)$-approximation of $\mathrm {AUG}_j$, where $n' \le |\Omega _j| \le 2^km$ is the number of critical interdiction sets. Since $\mathrm {AUG}_j \le \mathrm {OPT}$ for every $j\in [k]$ and $k$ is a constant, the theorem is proved.$\square$

In the following section we show how to solve the Set Cover problem $SC_2$ with a more sophisticated algorithm that exploits the underlying structures, thus incurring a loss of only a constant factor in the approximation guarantee. This algorithm will therefore lead to constant-factor approximation algorithm for the case $k=2$.

4.1 A constant factor approximation algorithm for $k=2$

To solve the Set Cover problem $SC_2$ we need a result about the structure of minimal solutions for the Bulk-Robust Shortest Path problem for $k=1$. Concretely, it was shown in [2] that every inclusion-wise minimal solution for this problem is an $s$–$t$ bipath, formally defined as follows.

Definition 15

An $s$–$t$ bipath in the graph $G =(V,E)$ is a union of two $s$–$t$ paths $P_1, P_2 \subseteq E$, such that for every two nodes $u,v$ incident to both $P_1$ and $P_2$, the order in which they appear on $P_1$ and $P_2$, respectively, when traversed from $s$ to $t$ is the same.

Intuitively, an $s$–$t$ bipath is a alternating concatenation of paths and cycles, with endpoint $s$ and $t$. See Fig. 3 for an illustration.

Fig. 3

An illustration of an $s$–$t$ bipath

Consider a bipath $P_1 \cup P_2 = Q \subseteq E$ comprising an optimal solution for the instance $\mathrm {I}_1$, obtained using the algorithm in  [2]. We slightly abuse notation assuming that $\Omega _1$ is a set of edges, instead of a collection of sets, each containing a single edge. Clearly, from feasibility of $Q$, every bridge in $Q$ (i.e., a single edge separating $s$ and $t$) is an edge in $E{\setminus }\Omega _1$. Observe that this set of bridges is exactly $P_1 \cap P_2$. Let $H=(V,Q)$.

From our previous observation, every critical interdiction set $F\in \Omega _2 = \Omega$ must contain exactly one edge on $P_1$ and one edge on $P_2$. More precisely, since no edge $e\in P_1\cap P_2$ is part of a interdiction set $F\in \Omega$—otherwise $P_1\cup P_2$ would not be a feasible solution for the scenarios $\Omega _1$—a critical interdiction set $F\in \Omega _2$ must contain two edges of the same cycle of $P_1\cup P_2$, one from $P_1{\setminus }P_2$ and one from $P_2{\setminus }P_1$.

Let the edges on the path $P_i$ be numbered $e^i_1, \ldots , e^i_{d_i}$ according to their order on $P_i$ from $s$ to $t$. The following property is clearly satisfied for every $i \in [2]$.

Property 16

For every $j_1,j_2, j \in [d_i]$, $j_1 < j < j_2$ and critical $F \in \Omega$ such that $e^i_j \in F$, the edge $e^i_{j_1}$ is on the $s$-shore in $H-F$, and $e^i_{j_2}$ is on the $t$-shore in $H-F$.

For every critical $F \in \Omega$ denote by $\mathrm {PRE}(F)$ ($\mathrm {POST}(F)$, respectively) the subset of vertices in $H-F$, which is on the $s$-shore ($t$-shore, respectively) of the cut $F$. Note that a $u$-$v$ link fixes $F$ if and only if $u\in \mathrm {PRE}(F)$ and $v\in \mathrm {POST}(F)$, or vice versa. In the following lemma we describe a way to obtain a $6$-approximation for the Set Cover problem $SC_2$.

Lemma 17

There is a polynomial time $6$-approximation algorithm for the Set Cover problem $SC_2$.

Proof

We set $\ell (u,v) = w(P_{u,v})$. Recall that $P_i = \{e^i_{1}, \ldots , e^i_{d_i}\}$ for $i\in [2]$. We denote the vertex on $P_i$ that is incident to $e^i_j$ and $e^i_{j+1}$ by $v^i_j$ for every $i\in [2]$ and $j\in [d_i -1]$.

Let $Link$ be all pairs $\{u,v\}$ corresponding to the endpoints of a link $\alpha _{u,v}$. We start by partitioning $Link$ into three groups $Link_1,Link_2$ and $Link_3$. Let $Link_1$ be all pairs $\{u,v\}\in Link$ with $u$ and $v$ being vertices on the first path, i.e., $u=v^1_i, v=v^1_j$ for some $i,j$. Notice that both $u$ and $v$ may simultaneously be on $P_1$ and $P_2$ in this definition. The set $Link_2$ contains all pairs $\{u,v\}\in Link{\setminus }Link_1$ with $u$ and $v$ lying both on the second path. The set $Link_3$ contains all remaining pairs of endpoints $\{u,v\}\in Link$. In words, the endpoints $\{u,v\}$ of a link are in $Link_3$ if not both $u,v$ are on $P_1$ nor are both on $P_2$.

Based on these definitions, we distinguish between four different modes how a critical interdiction set $F$ can be fixed by a link $\alpha _{u,v}$. These modes will later allow us to decompose the problem into four simpler independent subproblems. Hence, let $\alpha _{u,v}$ be a link that fixes $F$. The first and second mode correspond to $\{u,v\}\in Link_1$ and $\{u,v\} \in Link_2$, respectively. The third mode corresponds to $\{u,v\}\in Link_3$, with $u$ on $P_1$ and $v$ on $P_2$, such that $u\in \mathrm {PRE}(F)$ and $v\in \mathrm {POST}(F)$. The forth mode corresponds to $\{u,v\}\in Link_4$, with $u$ on $P_1$ and $v$ on $P_2$, such that $u\in \mathrm {POST}(F)$ and $v\in \mathrm {PRE}(F)$. Figure 4 illustrates this definition.

The key observation is that if one restricts all failures to be covered in only one of the four modes, the resulting problem becomes an Interval Covering problem. Recall that the interval covering problem consists of selecting a minimum–cost set of intervals, out of a given set of closed weighted intervals $\mathcal {S} = \{[a_i,b_i] \,:\, i\in [m]\}$ with integer bounds $0\le a_i,b_i \le n$ such that the union of the selected intervals equals $[0,n]$. It is well–known that Interval Covering can be modeled as an integer program with a totally unimodular constraint matrix, thus this problem is integral, namely for any instance, the optimal solution value always equals the optimal solution value of its continuous relaxation (see e.g. [36] for details). For the first two modes this claim is easy to verify: Consider the first mode; here, the Interval Covering problem contains each faulty edge on $P_1$ as a point while the intervals stretch between pairs of vertices on the given path. We prove the claim for the third mode. The proof for the fourth mode is identical. Recall that an interdiction set $F$ is covered in the third mode by a link $\alpha _{v^1_i, v^2_j}$ with $\{v^1_i,v^2_j\}\in Link_3$, if $v^1_i \in \mathrm {PRE}(F) \cap P_1$ and $v^2_j \in \mathrm {POST}(F) \cap P_2$. To obtain the desired Interval Cover problem we first remove all interdiction sets $F$ from $\Omega$ that are redundant for the third mode in the following sense. Consider two critical interdiction sets $F_1= \{e^1_{i_1}, e^2_{j_1}\}$ and $F_2 =\{e^1_{i_2}, e^2_{j_2}\}$ such that $i_2 > i_1$ and $j_2 < j_1$. Clearly, if for some link $\alpha _{v^1_c, v^2_d}$ it holds that $v^1_c \in \mathrm {PRE}(F_1)$ and $v^2_d \in \mathrm {POST}(F_1)$ then it also holds that $v^1_c \in \mathrm {PRE}(F_2)$ and $v^2_d \in \mathrm {POST}(F_2)$, since $\mathrm {PRE}(F_1) \subseteq \mathrm {PRE}(F_2)$ and $\mathrm {POST}(F_1) \subseteq \mathrm {POST}(F_2)$. Consequently, we can simply eliminate $F_2$, as any solution that covers $F_1$ also covers $F_2$. Let $\Omega ' \subseteq \Omega$ be all remaining interdiction sets for the third mode obtained after removing all redundant ones in this way.

Critically, we now have the property that for distinct $F_1= \{e^1_{i_1}, e^2_{j_1}\}$ and $F_2 =\{e^1_{i_2}, e^2_{j_2}\}$ in $\Omega '$ it holds that $sign(i_1 - i_2) = sign(j_1 - j_2)$. Thus, $\Omega '$ can be ordered according to the appearance of the interdiction sets on the paths $P_1, P_2$ from $s$ to $t$. It is now straightforward to see that every link $\alpha _{u,v}$ fixes a set of interdiction sets in $\Omega '$, which corresponds to an interval in this order, hence the claim is proved. Figure 5 illustrates this procedure.

Consider next the following linear programming relaxation of the Set Cover problem $SC_2$. We include a variable $x_{u,v}\in [0,1]$ for each link $\alpha _{u,v}$, where $x_{u,v} =1$ is interpreted as including the link $\alpha _{u,v}$. Furthermore, we denote by $fix(F)$ all pairs $\{u,v\}$ such that the link $\alpha _{u,v}$ fixes $F$.

$$\begin{aligned} \min \left\{ \ell (x) : x_{u,v} \ge 0 \;\forall \{u,v\}\in Link, \quad \sum \limits _{\{u,v\}\in fix(F)} x_{u,v} \ge 1 \quad \forall F \in \Omega \right\} \end{aligned}$$

Let $x^*$ be an optimal fractional solution to the above LP. Such a solution can be obtained by standard linear programming algorithms. Notice that due to the minimization, no component of $x^*$ will be larger than $1$, for otherwise, one could set such a component to $1$, thus obtaining a better feasible solution. For $F \in \Omega$ and $q \in [4]$, let $fix_{q}(F)$ denote all pairs $\{u,v\}$ such that $F$ is fixed in the $q$-th mode by $\alpha _{u,v}$. Hence, $fix(F)=\cup _{q\in [4]} fix_{q}(F)$.

Since the links in $fix(F)$ fractionally cover the interdiction set $F$, at least one of the following must hold for every interdiction set $F\in \Omega$:

• (1) $\sum _{\{u,v\} \in fix_{1}(F)} x^*_{u,v} \ge \frac{1}{6}$,

• (2) $\sum _{\{u,v\} \in fix_{2}(F)} x^*_{u,v} \ge \frac{1}{6}$,

• (3) $\sum _{\{u,v\} \in fix_{3}(F)} x^*_{u,v} \ge \frac{1}{3}$,

• (4) $\sum _{\{u,v\} \in fix_{4}(F)} x^*_{u,v} \ge \frac{1}{3}$.

For each $F\in \Omega$, let $j(F)\in [4]$ be such that the above case number $j(F)$ holds for $F$. If several cases apply, then $j(F)$ is chosen to be an arbitrary case among those who apply.

We are now ready to partition the Set Cover problem into four independent problems with disjoint families of interdiction sets, according to the values of $j(F)$. More precisely, we partition $\Omega$ into $\Omega ^1,\dots , \Omega ^4$, where

$$\begin{aligned} \Omega ^{q} = \{F\in \Omega \mid j(F) = q\} \quad \forall q\in [4]. \end{aligned}$$

We then solve the following four independent subproblems

$$\begin{aligned}&\min \left\{ \ell (x) : x_{u,v} \ge 0\;\forall \{u,v\}\in Link, \quad \sum \limits _{\{u,v\}\in fix_{q}(F)} x_{u,v} \ge 1 \quad \forall F \in \Omega ^{q} \right\} \\&\qquad \qquad \forall q\in [4]. \quad \quad (LP_{q}) \end{aligned}$$

By the above discussion, each of these problems is naturally integral since the non-redundant constraints define an Interval Coloring problem. Hence, an optimal solution to each of these problems is a $\{0,1\}$-solution, and can therefore be interpreted as a set of links $L_q$ for $q\in [4]$. Clearly, the set $L = \cup _{q\in [4]} L_{q}$ corresponds to a solution of $SC_2$. It remains to show that it is a $6$-approximation. Notice, that $L_1$ and $L_2$ only contain links of $Link_1$ and $Link_2$, respectively, whereas $L_3$ and $L_4$ contain links only of $Link_3$.

By definition of the $\Omega ^{q}$ we have that the point $z^1\in \mathbb {R}_{\ge 0}^{Link}$ defined by $z^1_{u,v}= 6x^*_{u,v}$ for $\{u,v\}\in Link_1$, and $z^1_{u,v}=0$ otherwise, is feasible for $LP_1$. Similarly, $z^2\in \mathbb {R}_{\ge 0}^{Link}$ defined by $z^2_{u,v}=6 x^*_{u,v}$ for $\{u,v\}\in Link_2$ and $z^2_{u,v}=0$ otherwise, is feasible for $LP_2$. Finally, $z^3\in \mathbb {R}_{\ge 0}^{Link}$ defined by $z^3_{u,v}=3x^*_{u,v}$ for $\{u,v\}\in Link_3$ and $z^3_{u,v}=0$ otherwise, is feasible for both $LP_3$ and $LP_4$. Hence, the cost of $L_1$ and $L_2$ is bounded by $\ell (z^1)$ and $\ell (z^2)$, respectively, and the cost of each of $L_3$ and $L_4$ is bounded by $\ell (z^3)$.

Thus, the total cost of $L$ is upper bounded by

$$\begin{aligned} \ell (z^1) + \ell (z^2) + 2\ell (z^3) = 6 \ell (x^*), \end{aligned}$$

where we use $z^1 + z^2 + 2z^3 = 6x^*$. Hence, $L$ is a $6$-approximation for $SC_2$, as desired.$\square$

Putting things together we obtain the following.

Fig. 4

Four different modes of fixing the interdiction set $F = \{f_1, f_2\}$. The link $\alpha _{q}$ fixes $F$ in the $q$-th mode for $q\in [4]$

Fig. 5

An illustration of the third mode. The interdiction set $F' = \{f_1', f_2'\}$ is redundant in the presence of the interdiction set $F = \{f_1, f_2\}$

Theorem 18

There is a polynomial $13$-approximation algorithm for Bulk-Robust Shortest Path with $k = 2$.

Proof

The cost of the returned solution consists of the cost of $S_1$, which is bounded by $\mathrm {OPT}$, and the cost of the augmentation set, which by Lemmas 13 and 17 is bounded by $12 \mathrm {OPT}$.$\square$

5 Conclusion and future work

In this paper we considered a new robust model for combinatorial optimization. The proposed model allows for defining a collection of possible interdiction sets, thus giving the possibility to specify explicitly the list of subsets of resources that comprise all possible interdiction sets. This results in considerable modeling flexibility. Concretely, the ability to specify arbitrary scenario sets permits interdiction sets of variable cardinality, as well as interdiction sets that model failures of special structures in the network, and any combination thereof.

We provided both complexity results and approximation algorithms for the Bulk-Robust counterparts of the Minimum Matroid Basis problem and the Shortest Path problem. From the point of view of computational complexity, we showed that the Set Cover problem can be modeled as a special case of many Bulk-Robust problems, including Bulk-Robust Minimum Matroid Basis and Bulk-Robust Shortest Path. This result was strengthened with respect to various parameters for the Bulk-Robust Shortest Path problem. In particular, we showed that the problem is APX-hard when the input is restricted to instances with width two. In addition, we showed that the Bulk-Robust Shortest Path problem for general $k$ does not admit approximation algorithms with polynomial dependence on the width $k$ unless $\mathrm {NP} \subseteq \mathrm {DTIME}(n^{\log \log n})$.

On the algorithmic side we obtained the following results. We developed an algorithm for the Bulk-Robust Minimum Matroid Basis problem with an approximation guarantee of $O(\log m + \log r)$. As a special case, we obtain an $O(\log n + \log m)$-approximation algorithm for the Bulk-Robust Minimum Spanning Tree problem. This algorithm relies on an approximation algorithm for the Constrained Submodular Function Maximization problem. The dependence of the approximation guarantee of this algorithm on the parameter $m$ is essentially the best possible in light of our complexity results.

For the Bulk-Robust Shortest Path problem we provided algorithmic results for instances with fixed width. For arbitrary fixed $k$ we obtained an $O(\log m)$-approximation algorithm, using an iterative procedure that solves a sequence of relaxations of the original instance, in combination with an algorithm for the Set Cover problem. We then refined our method by replacing the Set Cover algorithm by an LP-based algorithm to obtain a $13$-approximation algorithm for instances with width two.

There is still a wide variety of interesting open problems linked to Bulk-Robust optimization. We conclude the paper by mentioning a number of such problems.

• It would be interesting to study different Bulk-Robust combinatorial optimization problems, and in particular, structural properties of the scenarios $\Omega$ that allow for designing strong approximation algorithms, or even exact algorithms.

• Do there exist constant-factor approximations for the Bulk-Robust Shortest Path problem for any fixed width $k\ge 3$?

• Even for the case $k=1$, the complexity of the Bulk-Robust counterpart of a polynomially solvable combinatorial optimization problem can vary significantly. While Bulk-Robust Shortest Path admits a polynomial-time algorithm in this case, one can easily see that Bulk-Robust Minimum Spanning Tree generalizes the Minimum $2$-Edge Connected Spanning Subgraph problem, which is already NP-hard. An analysis of other Bulk-Robust counterparts with $k=1$ would be interesting.

• The Bulk-Robust model admits several promising extensions. One way to extend the model is to allow a combination of an implicitly-given uniform family of interdiction sets, specified by a parameter $B \in \mathbb {N}$, and an explicitly-given family $\Omega$ of interdiction sets. A combined interdiction set in this model is composed of any union $F_1 \cup F_2$, where $|F_1| \le B$ and $F_2 \in \Omega$. On the one hand, this model allows for describing scenario sets $\Omega$ of exponential size, thus increasing the modeling flexibility. Furthermore, there is hope that one could design approximation algorithms for such problems whose approximation ratio primarily depends only on the maximum size of a set of type $F_2$. This hope is fostered by the fact that uniform failure models often allow for better approximation algorithms; for example, the Shortest Path problem with uniform failures of up to $k$ edges corresponds to finding a minimum cost set of $k+1$ arc-disjoint paths, which can easily be solved by minimum cost flow techniques.